Evaluation of a baseline for the study of azimuthal correlations of charmed mesons in heavy-ion collisions using PYTHIA 8 and Herwig++ models

Abstract

Measurements of azimuthal correlations of charmed mesons in high-energy heavy-ion collisions can shed light on transport properties of the Quark-Gluon Plasma. The STAR experiment collected in 2014 and 2016 a large sample of Au+Au reactions at $\sqrt{s_{NN}}$ = 200 GeV, making such a study possible. However, such a measurement in p+p collisions at the same energy is not feasible so far. To provide such a baseline, we report a model study of the azimuthal correlations between charmed mesons in p+p collisions at $\sqrt{s}$ = 200 GeV, 500 GeV and 1.96 TeV. We used two Monte Carlo generators, PYTHIA 8 and Herwig++. We compare their predictions and validate them against available data from the STAR and CDF experiments to provide a reliable p+p baseline for the correlation studies in heavy-ion collisions at experiments at RHIC. We also discuss prospects for such measurements.

1 Introduction

High-energy heavy-ion collisions at Relativistic Heavy Ion Collider (RHIC) at the Brookhaven National Laboratory (BNL) or at the Large Hadron Collider (LHC) at CERN allow one to create and study the Quark-Gluon Plasma (QGP) [1], which properties are determined by the quark and gluon degrees of freedom. Heavy quarks, especially charm quarks (c), are valuable tools to study the QGP properties. Because of their large mass (m$_{charm}$ = 1.27 GeV/c$^{2}$), they are produced in the initial interactions with large momentum transfer at the early stage of the collision, before the QGP phase. Therefore, they are expected to carry information on the entire evolution of the QGP.

A plethora of new results on charm quark interactions with the QGP has been reported recently by the RHIC and LHC collaborations (see, for instance, [2,3,4,5,6,7,8,9]). Most notably, charm mesons loose significant energy in the partonic medium [10, 11] and they experience a significant level of collectivity [12,13,14,15,16,17].

Interpretation of these results depends on models, which sometimes differ significantly in their assumptions and approaches. Two main categories of energy loss mechanisms are considered in the literature: radiative energy loss ($E_{rad}$) due to medium-induced gluon radiation and collisional energy loss ($E_{coll}$) due to binary interactions with other particles in the QGP. At low transverse momenta ($\textrm{p}_{\textrm{T}}$), collisional effects are expected to dominate [18]. A study of the distribution of the relative azimuth angle ($\Delta \phi$) between the $\textrm{D}$ and $\mathrm {\overline{D}}$ mesons can help to pin down the relative contribution of these mechanisms [19, 20]. It is expected that the $\Delta \phi$ distribution will be smeared in heavy-ion collisions compared to the p+p case if $E_{coll}$ plays a significant role [20, 21] while radiative effects would not substantially change $\Delta \phi$ [19, 20].

Notably, recent results from the STAR [22] and PHENIX [23] experiments demonstrate that there is a significant difference in the energy loss between charm and bottom quarks at RHIC. This effect is observed so far only at an intermediate-$\textrm{p}_{\textrm{T}}$ range; energy loss at high $\textrm{p}_{\textrm{T}}$ is dominated by radiative effects, and thus, mass dependence of the nuclear modification factor does not show up. A similar trend is observed at the LHC [24]: at high $\textrm{p}_{\textrm{T}}$  the nuclear modification for charm and bottom are similar. Furthermore, the measurement of azimuthal correlations of muon pairs from heavy-flavor decays in Pb+Pb collisions at $\sqrt{s_{NN}} = 5.02$ TeV [2] shows that the width of the observed correlation signal is approximately the same in p+p and Pb+Pb reactions, supporting conclusions that $E_{rad}$ overshadows $E_{coll}$ in the high-$\textrm{p}_{\textrm{T}}$ region.

These results stress the importance of the intermediate and low-$\textrm{p}_{\textrm{T}}$ regions at RHIC in terms of studying the interplay of $E_{rad}$ and $E_{coll}$. The STAR experiment is well positioned to conduct such research in heavy-ion reactions because it recorded a large sample of Au+Au collisions in 2014 and 2016 with high-precision microvertexing detector: Heavy Flavor Tracker (HFT) [25]. Unfortunately, the HFT was not available in p+p reactions; thus, an experimental study of $\textrm{D} - \overline{\textrm{D}}$ in p+p at $\sqrt{s} = 200\,\hbox {GeV}$ is not feasible. Therefore, it is not possible to experimentally obtain the essential baseline to look into the decorrelation effects in heavy-ion collisions in STAR.

This motivates our studies of the charm-anticharm meson correlations in p+p reactions using two models: PYTHIA 8 [26] and Herwig++ [27]. Compared to the existing work [28], we use Herwig++, which provides next-to-leading order perturbative QCD calculations (compared to the leading order in PYTHIA 8), and we include validation of model predictions for charmed mesons correlations against existing experimental data. Using these well-established and trustworthy tools and ensuring validation of their results, we expect our study to deliver a reliable baseline for the interpretation of the data from heavy-ion collisions at RHIC.

This paper is organized as follows. In Sect. 2, we briefly introduce the settings we used to model the azimuthal distributions. Section 3 presents the validation of the model predictions against available data, and then we present and discuss the simulation results in Sect. 4. Section 5 contains a feasibility study for a future $\textrm{D} - \overline{\textrm{D}}$ measurement in p+p collisions at RHIC. We conclude with the summary in Sect. 6.

2 Materials and methods

In this study, we used two Monte Carlo event generators: PYTHIA 8 (version 8.244) [26] and Herwig++ (version 7.2.2) [27]. We used them to simulate p+p collisions at the center-of-mass energies $\sqrt{s}$ = 200 GeV, 500 GeV and 1.96 TeV, and then study correlations between charmed mesons ($\textrm{D}^{0}, \overline{\textrm{D}^{0}}, \textrm{D}^{+}, \textrm{D}^{-}, \textrm{D}^{*+}, \textrm{D}^{*-}$).

For the PYTHIA 8 simulations, we used parameters and configurations given in Appendix A. These parameters are based on the STAR-HF Tune, which was developed to describe $J/\psi$ and so-called non-photonic electrons (electrons from decays of D and B mesons) measurements at RHIC.

We generated data for three classes of QCD processes: hard QCD and soft QCD, and for hard QCD heavy-flavor subset of charm production: HardQCD:hardccbar. We use events generated with HardQCD:hardccbar to provide a baseline: a correlation due to energy-momentum conservation in $2 \rightarrow 2$ reactions. They include two categories of processes: gluon–gluon fusion $g g \rightarrow c \bar{c}$ and quark-antiquark annihilation $q \bar{q} \rightarrow c \bar{c}$. We call this configuration charm pair in the following text. The soft QCD includes elastic, diffractive, and minimum bias events. The hard QCD configuration includes all the standard $2\rightarrow 2$ reactions and the soft QCD part. Thus, the hard QCD should provide a complete description of the $\textrm{D} - \overline{\textrm{D}}$ correlations.

In the case of Herwig++, we used the standard configuration for minimum bias p+p collisions, which is provided with the program (the “MB.in” configuration file), and we changed the energy to $\sqrt{s}$ = 200 GeV, 500 GeV, and 1.96 TeV.

3 Validation of the simulation results

The validation of the results consists of two steps. First, we compared the charm transverse momentum distributions from models to the data from the STAR experiment [29]. Then, we extracted the distribution of the relative azimuthal angle between charmed meson and its antiparticle ($\Delta \phi = \phi _{D} - \phi _{\overline{D}}$), and we confronted them with available experimental results [30, 31].

Fig. 1

The $\textrm{p}_{\textrm{T}}$-differential charm production cross section at mid-rapidity ($|y |< 1$) reported by the STAR experiment [29], compared to results from PYTHIA 8 and Herwig++. The Herwig++ simulations include minimum bias (a), while PYTHIA 8 ones (b) are obtained for hard QCD processes (red), soft QCD processes (blue) and charm production processes (green)

3.1 Transverse momentum spectrum of charm quark pair

The first condition in order to conduct further correlation analysis is to check the $\textrm{p}_{\textrm{T}}$ distribution. Correlations can change with $\textrm{p}_{\textrm{T}}$. Thus, incorrect $\textrm{p}_{\textrm{T}}$ spectrum shape would affect correlation results in finite $\textrm{p}_{\textrm{T}}$ bins (especially if bins are wide).

Figure 1 shows experimental data on charm quark production at mid-rapidity ($|y |< 1$) in p+p collisions at $\sqrt{s}$ = 200 GeV reported by the STAR experiment [29]. We compared these data with predictions of Herwig++ (Fig. 1a) and PYTHIA 8 (Fig. 1b) simulations with different settings. We also show the ratio of experimental and model results in Fig. 2. In the case of Herwig++, there is a very good agreement of minimum bias results with the experimental data in almost the entire $\textrm{p}_{\textrm{T}}$ range. The PYTHIA 8 results have a similar shape to that seen in the data. However, only the hard QCD settings are consistent with the experimental data. This is expected, as it is the most complete configuration setup. The distribution of transverse momentum for the charm pair creation (HardQCD:hardccbar) gives harder $\textrm{p}_{\textrm{T}}$ spectrum and provides a very good description of the experimental data at $\textrm{p}_\textrm{T}> 2$ GeV/c.

These comparisons indicate that Herwig++, with the default minimum bias settings, reproduces the shape of the charm $\textrm{p}_{\textrm{T}}$ spectrum very well, while PYTHIA 8 requires additional parameter tuning. The difference between the Herwig++ and PYTHIA 8 most probably arises due to the higher order of perturbative QCD calculations and the specific choice of additional parameters employed in the latter. As history shows, these settings can be tuned to reproduce the experimental results very well if the data with high quality are available (see, for example, the Monash tune for the LHC [32]). In the following, we will provide the results of studies with Herwig++ at the NLO and use PYTHIA 8 for the sake of comparison with the LO results.

Fig. 2

The ratio of the $\textrm{p}_{\textrm{T}}$-differential charm production cross section at mid-rapidity ($|y |< 1$) reported by the STAR experiment [29] and the results from PYTHIA 8 and Herwig++ (shown in Fig. 1))

3.2 Azimuthal correlations of charmed mesons

We benchmark the Herwig++ predictions for azimuthal correlations for p+p collisions at $\sqrt{s} = 500\,\hbox { GeV}$ and $\sqrt{s} = 1.96$ TeV against experimental data from the STAR and CDF experiments, respectively. These are the only available correlation results within the energy range close to the one of our interest ($\sqrt{s_{NN}} = 200$ GeV). Therefore, we do not consider the LHC results, where additional processes (like double parton scattering) may play a significant role.

Figure 3a compares PYTHIA 8 and Herwig++’s results with the experimental data. The results from STAR [30] for $\textrm{D}^{*+}-\textrm{D}^{*-}$ have sizable uncertainties and provide little discrimination power. It is a case in point why reliable model predictions are necessary to interpret charm correlation results in heavy-ion results at RHIC. Note that STAR defined the correlation function as $\Delta \phi$ distribution normalized by the number of trigger particles (a D meson that has $\textrm{p}_{\textrm{T}}$ above a given threshold), which is different from the definition of azimuthal correlation we use in the following sections. As far as we understand, these experimental data are not corrected for the reconstruction efficiency. Thus, for the sake of comparison of the shape of the correlations, we normalized the model results to the integral of the experimental points.

Fig. 3

The azimuthal correlations of charmed mesons from Herwig++ (minimum bias configuration) and PYTHIA 8 (hard QCD setup) compared to experimental data. Panel a shows results for p+p collisions at $\sqrt{s} = 500$ GeV for charmed mesons with $\textrm{p}_{\textrm{T}} > 2.5$ GeV/c, compared to the STAR results [30]. Panel b shows the azimuthal correlations between $\textrm{D}^{0}-\textrm{D}^{*-}$ measured by the CDF experiment [31] for $5.5< \textrm{p}_{\textrm{T}} <20$ GeV/c in p+$\overline{p}$ collisions at $\sqrt{s} = 1.96\,\hbox {TeV}$. For (b), the model results show combined $\overline{\textrm{D}^{0}}-\textrm{D}^{*+}$ and $\textrm{D}^{0}-\textrm{D}^{*-}$ pairs and the Herwig++ and PYTHIA 8 points are shifted horizontally for better visibility

Figure 3b shows the $\textrm{D}^{0}-\textrm{D}^{*-}$ correlations reported by the CDF experiment [31] compared to model results. The measured $\textrm{p}_{\textrm{T}}$ range is high ($5.5< \textrm{p}_{\textrm{T}}<$ 20 GeV/c); thus, the correlation signal is very prominent both at $\Delta \phi \approx 0$ and $\approx \pi$. Given the high-$\textrm{p}_{\textrm{T}}$ region, the correlations are dominated by charm production in back-to-back jets (correlations at $\Delta \phi \approx \pi$) and quark and gluon fragmentation into $c\bar{c}$ pair within a single jet (which gives a signal at $\approx 0$). Note, the CDF data are reported as a pair production cross section $d\sigma /\Delta \phi$. We note that we were not able to reproduce the absolute value $d\sigma /d \Delta \phi$ in our studies, and to compare the shapes of the azimuthal correlations, we normalized the model results to the integral of the experimental points.

Figure 3 demonstrates the shape of the $\Delta \phi$ correlation from models that match very well the CDF data. The fluctuations we observed for the model studies are due to the low cross section for charm meson production in the $\textrm{p}_{\textrm{T}}$ range reported by CDF ($5.5< \textrm{p}_{\textrm{T}} <20$ GeV/c) and thus the long time needed to obtain a sufficient number of $\textrm{D}^{0}-\textrm{D}^{*-}$ and $\overline{\textrm{D}^{0}}-\textrm{D}^{*+}$ in the simulations. Given we focus on p+p reactions at RHIC, we consider the results in Fig. 3 to be satisfactory with the current statistics.

Based on the results above, one can conclude that Herwig++ and PYTHIA 8 (with the hard QCD setup) are appropriate frameworks for predicting charmed mesons’ angular correlations. We find it interesting that both PYTHIA 8 (the hard QCD setup) and Herwig++ give similar shapes of $d\sigma /d \Delta \phi$ of D mesons at high-$\textrm{p}_{\textrm{T}}$ in p+p at $\sqrt{s} = 1.96$ TeV and describe reasonably well the experimental data by CDF. However, the results from PYTHIA 8 and Herwig++ differ significantly for $\sqrt{s} = 500$ GeV and $\textrm{p}_{\textrm{T}}>$ 2.5 GeV/c. This again points towards the importance of parameter tuning and verification against experimental results at $\sqrt{s} = 500$ or 200 GeV if data with better quality are available.

4 Results

In this section, we present the results of the azimuthal correlations obtained with the PYTHIA 8 and Herwig++ frameworks. The correlations are shown for various settings and transverse momenta conditions. For these studies, we select mesons at mid-rapidity ($|y |< 1$), and we define the trigger and associated particles, where the trigger one has higher transverse momentum ($\textrm{p}_{\textrm{T, trig}}$) than associated particle ($\textrm{p}_{\textrm{T, asso}}$). We focus on relatively low $\textrm{p}_{\textrm{T}}$ ($\textrm{p}_{\textrm{T, trig}}$ > 2, 3, and 4 GeV/c) since the low-$\textrm{p}_{\textrm{T}}$ region is probably most accessible in Au+Au collisions registered by STAR in 2014 and 2016. All the results are presented as $\Delta \phi$ distribution normalized by the number of $\textrm{D} - \overline{\textrm{D}}$ pairs $\textrm{N}_{\textrm{pair}}$. Thus the correlation function is given as $C(\Delta \phi ) = 1/\mathrm {N_{pair}} \times dN / d\Delta \phi$

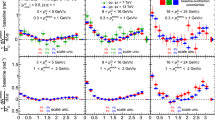
Figure 4 shows the summary of the azimuthal correlations obtained with PYTHIA 8 and Herwig++ for p+p collisions at $\sqrt{s}$ = 200 GeV for various combinations of $\textrm{p}_{\textrm{T, trig}}$ and $\textrm{p}_{\textrm{T, asso}}$. In the case of PYTHIA 8, a strong back-to-back correlation is clearly visible for charm pair production processes, which is expected given at the leading order, the charm quark production is dominated by $2 \rightarrow 2$ scatterings. Thus, charm quarks are produced mostly in jets going in opposite directions. The correlation signal is small for the hard QCD and soft QCD settings. Around $\Delta \phi \approx \pi$, it is between 0.15 and 0.20 1/rad, which is around 2 times less than the signal for Herwig++’s minimum bias and Pythia’s charm pair configurations. Most probably, the difference comes from the increasing role of c and $\bar{c}$ production in partonic showers for hard QCD and soft QCD configurations. It is worth noting that the azimuthal correlations in PYTHIA are sensitive to different model parameters, including the relative ratio of different types of hard scatterings for the production of charm pairs, for instance, $2 \rightarrow 2$ pair production, gluon splitting and flavor excitation (see [33] for an example discussion for the LHC energies).

Fig. 4

The $\textrm{D}^{0} - \overline{\textrm{D}^{0}}$ azimuthal correlations for Herwig++ minimum bias predictions and various PYTHIA 8 predictions. The predictions were obtained at the energy $\sqrt{s} =$ 200 GeV. There are a no $\textrm{p}_{\textrm{T}}$ cuts, b minimum $\textrm{p}_{\textrm{T}}$ for D mesons is 2 GeV/c, c minimum $\textrm{p}_{\textrm{T}}$ for a triggered particle is 3 GeV/c, and for associated is $\hbox {1 GeV/c}$

Overall, the correlation strength increases with increasing $\textrm{p}_{\textrm{T, trig}}$, which is well pronounced in Fig. 7 in the appendix B, where we compare results for a given PYTHIA 8 process with different conditions for $\textrm{p}_{\textrm{T, trig}}$ and $\textrm{p}_{\textrm{T, asso}}$. The hard QCD and soft QCD results also include feed-down from B-hadron decays. Still, we find this contribution negligible in the PYTHIA 8 simulations (relative contribution was less than a few per cent), and the $\Delta \phi$ distribution for inclusive D-mesons and those from c/$\overline{c}$ fragmentation have essentially the same shape.

On the other hand, a significant back-to-back correlation signal is predicted by Herwig++. It is larger than the one from PYTHIA 8, and it increases with increasing $\textrm{p}_{\textrm{T, trig}}$ and $\textrm{p}_{\textrm{T, asso}}$, which is clearly visible in Fig. 5. We do not observe a significant near-side ($\Delta \phi \approx 0$) correlation, which is consistent with predictions from PYTHIA 8 and also experimental data reported by the LHCb collaboration in [34] at the LHC. Figure 5b shows the impact of the B-hadron feed-down on the observed $\textrm{D} - \overline{\textrm{D}}$ correlations. The $\Delta \phi$ distribution for inclusive $\textrm{D}^{0} - \overline{\textrm{D}^{0}}$ pairs and pairs originated from c/$\overline{c}$ are similar, and we do not observe a significant effect of the feed-down on the measured correlations. It is expected to a large extent because, at the RHIC energies, the cross section for b-quark production is significantly lower than for charm quarks. It is a valuable observation since removing the B-hadron feed-down is not feasible within the STAR experiment so far.

Given the charm production cross section increases significantly with the colliding energy, the $\textrm{D} - \overline{\textrm{D}}$ correlation measurement in p+p collisions at the top RHIC energy provides a higher chance of successful experimental study. Thus, in Fig. 6 we show the inclusive $\textrm{D}^{0} - \overline{\textrm{D}^{0}}$ azimuthal correlations calculated with Herwig++ for p+p collisions at $\sqrt{s}$ = 500 GeV for four selection criteria: without imposing any $\textrm{p}_{\textrm{T}}$ threshold (inclusive $\textrm{p}_{\textrm{T}}$), $\textrm{p}_{\textrm{T, trig}}$ > 2 GeV/c, $\textrm{p}_{\textrm{T, trig}}$ > 3 GeV/c and $\textrm{p}_{\textrm{T, asso}}$ $> 1\,\hbox {GeV/c}$, and $\textrm{p}_{\textrm{T, trig}}$ > 4 GeV/c and $\textrm{p}_{\textrm{T, asso}}$ > 2 GeV/c. The correlation signal increases with $\textrm{p}_{\textrm{T, trig}}$ reaching $\approx 10\%$ at $\Delta \phi \approx \pi$, but also a significant near-side correlation shows up for the $\textrm{p}_{\textrm{T, trig}}$ > 4 GeV/c.

Fig. 5

Panel a shows $\textrm{D}^{0} - \overline{\textrm{D}^{0}}$ azimuthal correlations for p+p collision at the energy $\sqrt{s}$ = 200 GeV from Herwig++ for various $\textrm{p}_{\textrm{T, trig}}$ and $\textrm{p}_{\textrm{T, asso}}$ conditions. Panel b shows the effect of feed-down on the correlations for the inclusive-$\textrm{p}_{\textrm{T}}$ results

5 Prospects for measurement of angular correlations of charmed mesons at RHIC

The clear difference that we observe between results for $\Delta \phi$ from PYTHIA 8 and Herwig++ at RHIC energies calls for experimental verification of these predictions, if possible. In this section, we estimate if such measurements are feasible with the data collected so far by STAR at RHIC and planned for the operation of the sPHENIX experiment.

Fig. 6

The $\textrm{D}^{0} - \overline{\textrm{D}^{0}}$ azimuthal correlations for p+p collisions at the energy $\sqrt{s}$ = 500 GeV for Herwig++ minimum bias settings and various $\textrm{p}_{\textrm{T}}$ ranges

Table 1 Parameters of different experiments located at RHIC for p+p reactions

Table 1 gathers information on data sets collected (or planned) relevant for our studies [30, 35,36,37]. For the STAR experiment, the available $\Delta \phi$ results [30] (shown in Fig. 3a) used data from p+p collisions at $\sqrt{s}$ = 500 GeV collected in 2011, with integrated luminosity $\mathcal {L} =\text{ pb}^{-1}$. These results provide a reference, which we use to estimate the feasibility of studies at different energies and with different $\mathcal {L}$. We start with p+p at $\sqrt{s} = 200\,\hbox {GeV}$ since it is the most interesting as a reference for heavy-ion studies. The sPHENIX experiment includes the Monolithic Active Pixel Vertex (MVTX) detector [38], which increases capabilities in charm and beauty studies. However, the precision of the $\textrm{D}^{0} - \overline{\textrm{D}^{0}}$ correlation measurement in p+p collisions is strongly dependent on the size of the available data set, trigger setup and D-meson detection efficiency. The cross section for the charm production is significantly lower at $\sqrt{s}$ = 200 GeV compared to 500 GeV, and the data-taking plan for sPHENIX includes only $\mathcal {L} = 45~\text{ pb}^{-1}$ [36].

In the available sPHENIX technical notes and publications (including data-taking plans in the Beam User Proposal [39] and its Addendum for 20-Cryoweek Scenario [40]), we did not find feasibility studies for D-meson measurement in p+p collisions, while the expected $\textrm{D}^{0}$ reconstruction efficiency in Au+Au reaction is on the level of 0.1% at low $\textrm{p}_{\textrm{T}}$ and rises to $\approx 1\%$ at $\textrm{p}_{\textrm{T}}$ $\approx 4$ GeV/c [41]. These values are comparable to the performance observed in STAR [11].

At this point, we are not able to make a meaningful feasibility study of $\textrm{D} - \overline{\textrm{D}}$ correlation measurement in p+p reactions in sPHENIX, but based on the available information, we suspect such measurement will be challenging. Similarly, data collected by STAR at $\sqrt{s} = 200\,\hbox {GeV}$ are unlikely to yield satisfactory results. Thus, we turn to p+p collisions at $\sqrt{s}$ = 500 GeV at STAR.

To get quantitative estimates of the expected precision of the $\Delta \phi$ measurement, we start with information provided in Ref. [30] for STAR 2011 data. In that studies, $N_{\textrm{D}\overline{\textrm{D}}}^{2011} = 34 \pm 22$ pairs of charm mesons were registered. First, there is no significant change in the STAR detector configuration (relevant for $\textrm{D} - \overline{\textrm{D}}$ correlation studies) between 2011 and 2022. However, please note that data used for $\textrm{D}^{*+}-\textrm{D}^{*-}$ measurement at STAR in 2011 were collected with a trigger setup that required a high energy E deposited in a single tower of the Barrel Electromagnetic Caloritemer (BEMC). The trigger threshold for $\textrm{D}^{*+}-\textrm{D}^{*-}$ studies for 2011 was $E >4.3$ GeV, but for other data-taking campaigns, this trigger was used to sample only a fraction of the delivered luminosity. The full luminosity was sampled with higher thresholds: $E >5.9$ GeV.

At the time of conducting our study, there is no official information on the actual sampled luminosity for different trigger setups for the 2017 and 2022 runs. Additionally, the $\textrm{D}^{*+}$ studies are based on matching signal in the BEMC to a hadron from $\textrm{D}^{*+}$ decay. Thus, the relation between the BEMC trigger threshold and $\textrm{D}^{*+}$ reconstruction efficiency is not straightforward. For the sake of a first feasibility check, we make an optimistic assumption that one can use all the collected data and measure $\textrm{D}^{*\pm }$ with approximately the same efficiency as in 2011. Therefore, we use the STAR run 2011 results to estimate the expected $\textrm{D}^{0} - \overline{\textrm{D}^{0}}$ yield for other data sets listed in Table 1 by taking a simple scaling: $N_{\textrm{D}\overline{\textrm{D}}} = \mathcal {L} / \mathcal {L}_{2011} \times N_{\textrm{D}\overline{\textrm{D}}}^{2011}$, where $\mathcal {L}$ is the integrated luminosity of the data set of interest. This allows us to estimate the expected statistical uncertainty and compare it to the correlation signal predicted by Herwig++.

Table 2 The expected precision $\sigma$ of $\textrm{D}^{*+}-\textrm{D}^{*-}$ angular correlation measurement in STAR in p+p collisions at $\sqrt{s}$ = 500 GeV. The relative uncertainty $\sigma ^{\textrm{rel}}$ is calculated as $\sigma ^{\textrm{rel}} = \sigma /C(\Delta \phi )_{\textrm{max}}$. The statistical uncertainty of $C(\Delta \phi ) = 1/\mathrm {N_{pair}} \times dN /d\Delta \phi$ is given per a $\Delta \phi$ bin

Table 3 The expected size of the angular correlation effect for $\textrm{D}^{*+}-\textrm{D}^{*-}$ with inclusive $\textrm{p}_{\textrm{T}}$ from Herwig++ simulations of p+p collisions at $\sqrt{s} = 500\,\hbox {GeV}$, together with the estimation of a measurement uncertainty $\delta$ needed to observe the non-zero effect at a 5-standard-deviation level ($\delta = \Delta C/(5\sqrt{2}$))

One expects 12.8 times more $\textrm{D} - \overline{\textrm{D}}$ pairs in 2017 compared to the year 2011, 16 times more in the year 2022 data, and combined $\approx 30$ times more $\textrm{D} - \overline{\textrm{D}}$ pairs in combined 2017 and 2022 data sets compared to 2011. Given the $N_{\textrm{D}\overline{\textrm{D}}}^{2011}$ have a substantial statistical uncertainties, we calculated the expected $N_{\textrm{D}\overline{\textrm{D}}}$ for three cases: central value of $N_{\textrm{D}\overline{\textrm{D}}}^{2011}$, and $N_{\textrm{D}\overline{\textrm{D}}}^{2011} +$ one standard deviation and $N_{\textrm{D}\overline{\textrm{D}}}^{2011} +$ two standard deviations. Such an assumption should capture optimistic and pessimistic cases (due to statistical fluctuations in 2011) for the considered studies. We consider five bins to be sufficient to capture the shape of $\Delta \phi$ and $\textrm{D} - \overline{\textrm{D}}$ are evenly distributed among five bins in $\Delta \phi$. Table 2 shows the estimated statistical precision of $\Delta \phi$ correlation studies for projection using the central value of $N_{\textrm{D}\overline{\textrm{D}}}^{2011}$ (noted as $\sigma _{1}$), $N_{\textrm{D}\overline{\textrm{D}}}^{2011} +$ one standard deviation ($\sigma _{2}$) and the optimistic one $N_{\textrm{D}\overline{\textrm{D}}}^{2011} +$ two standard deviations ($\sigma _{3}$). In the most optimistic case, the uncertainty is below 0.01 for a correlation function value in a single $\Delta \phi$ bin.

To evaluate if such precision suffices for observation of the expected correlation, we calculated the size of the effect predicted by Herwig++ by taking a difference between the maximum and minimum value of $\Delta C = C(\Delta \phi )_{\textrm{max}} - C(\Delta \phi )_{\textrm{min}}$. Table 3 shows the expected $\Delta C$ for $\textrm{D}^{*+}-\textrm{D}^{*-}$ with inclusive $\textrm{p}_{\textrm{T}}$ in p+p reactions at $\sqrt{s}$ = 500 GeV from Herwig++. We assume the correlation is experimentally confirmed if one observes at least a $5\sigma _{\Delta }$ effect, where $\sigma _{\Delta }$ is the experimental uncertainty on the difference between the minimum and the maximum value of the correlation function.

Neglecting possible systematic uncertainties, this leads to a correlation observation condition $\sigma \le \delta = \Delta C/(5\sqrt{2})$, where $\sigma$ is an expected statistical precision listed in Table 2, and the factor $\sqrt{2}$ takes into account that computation of $\Delta C$ involves two $\Delta \phi$ bins.

By comparing results in Tables 3 and  2, we conclude that the successful study of azimuthal correlations of charmed mesons should be possible in STAR using combined data from 2017 and 2022 data-taking campaigns.

6 Conclusion

In the paper, we presented a model study of the azimuthal correlations of charmed mesons and compared the results from PYTHIA 8 and Herwing++ simulations with available data from the STAR and CDF experiments. Both Herwing++ and PYTHIA 8 (with the hard QCD setup) successfully withstood validation against available experimental data. However, while Herwing++ and PYTHIA 8 give consistent results for high-$\textrm{p}_{\textrm{T}}$ charmed mesons at Tevatron, we found that these models predict significantly different $\textrm{D} - \overline{\textrm{D}}$ correlation effects in p+p collisions at $\sqrt{s}$ = 200 GeV and 500 GeV at RHIC.

We have also shown that it is unlikely that experiments at RHIC can measure $\textrm{D} - \overline{\textrm{D}}$ correlations in p+p reactions at $\sqrt{s}$ = 200 GeV. Given STAR and sPHENIX should be able to perform $\textrm{D} - \overline{\textrm{D}}$ correlation study in Au+Au collisions at $\sqrt{s_{NN}}$ = 200 GeV, one needs to use models for obtaining a p+p baseline for this research.

Finally, we provided projections for experimental studies of azimuthal correlations of charmed mesons in p+p collisions at RHIC. Such a measurement should be feasible at STAR in p+p collisions at $\sqrt{s}$ = 500 GeV, exploiting large data sets collected in 2017 and 2022. These results would provide a necessary benchmark for modelling $\textrm{D} - \overline{\textrm{D}}$ correlations and discriminate between Herwing++ and PYTHIA 8 predictions to be used as a robust p+p baseline for charmed mesons correlation studies in heavy-ion collisions at RHIC.

Appendices

Appendix A PYTHIA 8 settings

We used the following parameters in our PYTHIA 8 studies:

• the type of particles being collided: p+p collisions,

• the collision central mass energy: $\sqrt{s} = 200\,\hbox {GeV}$,

• the seed of the random number generator,

• modification of scale choices of couplings and parton densities:

  • SigmaProcess:renormScale2 = 3,

  • SigmaProcess:factorScale2 = 3,

  • SigmaProcess:renormMultFac = 2,

  • SigmaProcess:factorMultFac = 2,

• the PDF function: LHAPDF6:MRSTMCal and the option: PDF:extrapolate = on,

• the relative production ratio vector/pseudo-scalar for the charm and bottom mesons:

  • StringFlav:mesonCvector = 1.5,

  • StringFlav:mesonBvector = 3,

• the heavy quarks’ masses:

  • 4:m0 = 1.43,

  • 5:m0 = 4.30.

• the type of process:

  • Soft QCD: SoftQCD:nonDiffractive = on,

  • Hard QCD: HardQCD:all=on and SoftQCD:nonDiffractive = on

  • Charm pair: HardQCD:gg2ccbar = on and HardQCD:qqbar2ccbar = on

Appendix B Azimuthal correlations from PYTHIA 8 for different configurations

Figure 7 shows the azimuthal correlations results for three various PYTHIA 8 settings. They are presented for different $\textrm{p}_{\textrm{T}}$ ranges.

Fig. 7

Azimuthal correlations of $\textrm{D}^0- \overline{\textrm{D}^{0}}$ for PYTHIA 8 charm pair (a), soft QCD (b), and hard QCD (c) configurations and various $\textrm{p}_{\textrm{T}}$ cut settings