The nature of kaons and antikaons is closely related to the chiral symmetry breaking pattern of low-energy QCD [1, 2]. Therefore, the study of kaon properties and their modification in dense nuclear matter has received the attention of the scientific community in the past decades. In particular, the hadronic interactions of charged kaons, K\(^+\) and K\(^-\), with nucleons (N) were investigated using kaonic atoms [3,4,5] and by studying the interaction or the production of kaons in light [6,7,8,9,10,11,12,13,14] and heavy nuclei [15,16,17,18,19,20,21,22,23]. Such measurements demonstrated the repulsive and attractive nature of the K\(^+\)N and K\(^-\)N strong interactions [1, 2], respectively. Information on the in-medium modification of the K\(^+\) and K\(^-\) potentials with the increasing baryon density was extracted from the comparison of kaon production yields and flow observables measured in nucleus–nucleus collisions [15,16,17] and pion- and proton-induced reactions [18,19,20,21,22,23] with the expectations from transport models. Several K\(^+\) nuclear potentials have been tested and the best agreement with the data results in a repulsive strength of 20–40 MeV at nuclear saturation density. On the other hand, the K\(^-\)N interaction is known to be sufficiently attractive in the isospin I = 0 channel to dynamically generate the \(\Lambda (1405)\) just below the K\(^-\)p threshold [24]. Such a state is interpreted as a quasi-bound antikaon–nucleon \(\mathrm {\overline{K}}\)N system which couples strongly to the \(\pi \Sigma \) channel, giving rise to a sizable K\(^-\) absorption [25]. In the case of K\(^-\) nuclear interaction, the influence of single- and multi-nucleon absorption processes in nuclei currently prevents extracting firm conclusions on the strength of the K\(^-\) in-medium attractive potential [1]. This ambiguity triggered a longstanding debate in the literature about the possible existence of exotic kaonic bound objects with nucleons (see [1] and references therein). Recently, the E15 Collaboration reported the first experimental evidence of the \(\mathrm {\overline{K}}\)NN state with a binding energy of about 42 MeV and a decay width of about 100 MeV [26]. From the theoretical side, binding energies in the range 9–95 MeV and decay widths between 16 and 110 MeV are expected [27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42]. The uncertainties in the models mainly arise from scarce knowledge of the full \(\mathrm {\overline{K}}\)NN three-body effects, such as three-body coupled channels and two-nucleon absorption processes. Additionally, three-body forces, which are relevant in the calculation of the nuclear binding energies [43, 44], are currently not included in kaonic bound state models. Further experimental investigations on the K\(^+\)NN and K\(^-\)NN three-body dynamics, in addition to the studies of K\(^+\) and K\(^-\) interaction in nuclei, are required to isolate and quantify the contribution from genuine three-body effects in such systems.

An alternative method to explore the three-body dynamics of K\(^+\) and K\(^-\) with nucleons is to employ the femtoscopy technique at high-energy collider facilities. In small colliding systems, such as pp and p–Pb at the Large Hadron Collider (LHC), the inter-hadron distances at the time of the particle emission range from a few femtometers down to scales compatible with the nucleon size. This leads to an enhancement of the strength of the signal due to the short-range strong interaction in the measured correlation function [45]. The femtoscopy method was proven to be able to test and constrain the hadron–hadron interaction for various two-particle systems [46,47,48,49,50,51,52,53,54,55,56,57], providing data with unprecedented precision on the hadronic interactions with strangeness at low relative momenta, down to the energy threshold of the produced pairs. Furthermore, the measured femtoscopic correlation functions are sensitive to the presence of bound states in the energy region below the threshold. Thus, they were also used to constrain the parameters of bound hadron–hadron systems [49, 58]. Recently, the ALICE Collaboration has extended the method to explore the correlation among three baryons, such as p–p–p and p–p–\(\Lambda \), to study the dynamics of three-body systems [59]. The analysis exploited Kubo’s cumulant expansion method [60] and the projector method [61] to isolate the genuine three-particle correlations from the measured correlation functions. As a result, a first experimental hint of genuine three-body effects in the unbound p–p–p system was found. The study in this Letter applies the same analysis procedure adopted in [59] to the case of p–p–K\(^+\) and p–p–K\(^-\) particle triplets to explore possible genuine three-body effects in the correlation functions induced by the strong interaction and bound state formation. The main advantage of the femtoscopy method with respect to the previous experimental techniques is the possibility to investigate for the first time the K\(^+\) and K\(^-\) three-body dynamics with nucleons, free from additional effects induced by the presence of the surrounding nucleons in nuclei.

The analysed data sample of pp collisions at \(\sqrt{s}~=~13\) TeV was recorded by ALICE [62,63,64] during the LHC Run 2 (2015–2018) data-taking period. In the following, the information from the V0 detector system [65], the inner tracking system (ITS) [66], the time projection chamber (TPC) [67] and the time-of-flight (TOF) detector [68] is used. The V0 detector is employed to trigger on high-multiplicity (HM) events. This trigger selects events within the 0.17% largest charged-track multiplicity of the INEL \(>0\) class, which is defined as inelastic collisions with at least one measured charged particle in the pseudorapidity range \(|\eta |<1\) [65]. This condition results in an average of about 30 charged particles in the range \(|\eta |<0.5\) [51], hence increasing the probability of finding triplets of the desired particle species with respect to the minimum-bias sample. The primary vertex position is reconstructed with the combined information of the ITS and the TPC, and, independently, with track segments in the two innermost layers of the ITS. Only events with a reconstructed primary vertex position along the beam axis within 10 cm from the centre of the ALICE detector are selected. A total of 10\(^9\) HM events are used in this analysis. The p–p–K\(^+\) and p–p–K\(^-\) data samples are built by combining three charged-particle tracks (triplets) reconstructed with the TPC. Assuming the same interactions in the particle and antiparticle systems, triplets of particles and the corresponding antiparticles are combined: p–p–K\(^+\) \(\equiv \) ( p–p–K\(^+\)  \(\oplus \) \(\overline{\textrm{p}}\) –\(\overline{\textrm{p}}\) –K\(^-\)) and p–p–K\(^-\) \(\equiv \) ( p–p–K\(^-\)  \(\oplus \) \(\overline{\textrm{p}}\)–\(\overline{\textrm{p}}\)–K\(^+\)). The agreement of the corresponding correlation functions confirmed the validity of this assumption.

Particles and antiparticles are identified using the same kinematic and topological selections. Protons and kaons are selected in the range \(|\eta | < 0.8\) and in the transverse momentum intervals \(p_{\textrm{T}} \in \) (0.5–4.05) \(\text {Ge}\hspace{-1.00006pt}V/c\) and \(p_{\textrm{T}} \in \) (0.2–2.5) \(\text {Ge}\hspace{-1.00006pt}V/c\), respectively. A minimum of 80 space points (hits) inside the TPC, out of the total 159, is required to guarantee track quality and good momentum resolution. Particle identification (PID) is conducted by requiring that the measured energy loss (\(\text {d}E/\text {d}x\)) in the TPC gas is compatible with the expected one from protons and kaons within three standard deviations (\(\sigma \)). For high momentum particles, the \(\text {d}E/\text {d}x\) information is combined with the time-of-flight measurement provided by the TOF, using a 3\(\sigma \) selection on the expected value for a given particle hypothesis at a given momentum. The PID selection for protons is described in detail in [46]. The selection of kaons is based on the procedure described in  [54] with several changes as explained in the following. TPC reconstructed tracks are identified as kaons either by using TPC PID information for momenta lower than 0.85 GeV/c, or, if a signal in the TOF is matched to the TPC track, by using the combined PID information from TPC and TOF up to a momentum of 2.5 GeV/c. To improve the purity of the kaon selection, the TPC and TOF information are also used to reject candidates that are compatible with the pion or electron hypothesis. To reject particles that are non-primary or come from pile-up collisions, the distance of closest approach (DCA) to the primary vertex of the tracks is required to be less than 0.1 cm in the transverse plane and less than 0.2 cm along the beam axis. The purity of the proton and kaon candidates is estimated employing Monte Carlo simulations based on PYTHIA 8 [69] (Monash 2013 Tune) event generator with a dedicated high-multiplicity selection to mimic the V0 high-multiplicity trigger and the \({\textsc {Geant4}}\) package [70, 71]. The purity averaged over the \(p_{\textrm{T}}\) ranges of the identified protons and kaons is about \(98\%\) for both particle species.

The number of selected and analysed triplets amounts to 4530 for p–p–K\(^+\), 3161 for \(\overline{\textrm{p}}\) –\(\overline{\textrm{p}}\) –K\(^-\), 6200 for p–p–K\(^-\) and 4937 for \(\overline{\textrm{p}}\)–\(\overline{\textrm{p}}\)–K\(^+\) in the femtoscopic region \(Q_3 < 0.4\) \(\text {Ge}\hspace{-1.00006pt}V/c\). The kinematic variable \(Q_3\), which is used in three-body analyses [59, 72], is a Lorentz-invariant scalar defined as \(Q_3=\sqrt{-q_{12}^2-q_{23}^2 -q_{31}^2}\), where \(q_{ij}\) is the norm of the relative four-momentum of the pair ij in the triplet \(q_{ij}^\mu = 2\ [ m_j/(m_i~+~m_j) ~p_i^\mu ~-~m_i/(m_i + m_j)\ p_j^\mu ]\). The systematic uncertainties of the correlation functions are evaluated by performing simultaneous variations of the selection criteria for particles and antiparticles. For protons and antiprotons, the same variations for the track selection and PID criteria as in [59] are performed. Similar variations are used for the kaons and antikaons. In order to account for the correlations between the systematic uncertainties, the variations are randomly combined in sets in which at least one selection criterion is changed. Large statistical fluctuations introduced by the variations of the selection criteria are avoided by requiring that the yield of the triplets changes by less than 10% with respect to the standard selection in the femtoscopic region \(Q_3 < 0.4\) \(\text {Ge}\hspace{-1.00006pt}V/c\). The main contribution at low \(Q_3\) (\(\approx 0.15\) \(\text {Ge}\hspace{-1.00006pt}V/c\)) is given by the variation of the DCA selection and it is found to be smaller than 5%.

The final state interactions (FSIs) among the hadrons emitted in the collisions can be explored using correlation functions [73, 74] in momentum space, defined as

$$\begin{aligned} C_3(\textbf{p}_1,\textbf{p}_2,\textbf{p}_3) = \frac{P_3(\textbf{p}_1,\textbf{p}_2,\textbf{p}_3)}{P_1(\textbf{p}_1) P_1(\textbf{p}_2) P_1(\textbf{p}_3)} \ , \end{aligned}$$
(1)

where \(\textbf{p}_i\) is the momentum vector of the i-th particle and \(P_3(\textbf{p}_1,\textbf{p}_2,\textbf{p}_3)\) and \(P_1(\textbf{p}_i)\) are the probabilities of finding three particles and one particle with the corresponding momentum, respectively. If the particles are not correlated \(P_3(\textbf{p}_1,\textbf{p}_2,\textbf{p}_3) = P_1(\textbf{p}_1) P_1(\textbf{p}_2) P_1(\textbf{p}_3)\) and then the correlation function becomes identical to unity. The presence of FSIs induces a correlation signal imprinted in the correlation function which causes deviations from unity depending on the nature of the interactions, attractive or repulsive, as well as on the properties of the emitting source (see [45, 75] for the details). In the case of three-particle systems, the correlation function can be evaluated in terms of \(Q_3\). Hence, three-particle correlation functions are experimentally obtained as

$$\begin{aligned} C_3(Q_3) = \mathcal {N}\ \frac{N_\textrm{same}(Q_3)}{N_\textrm{mixed}(Q_3)} \ , \end{aligned}$$
(2)

where \(\mathcal {N}\) is a normalisation parameter, \(N_\textrm{same}(Q_3)\) is the \(Q_3\) distribution of the particle triplets emitted in the same collision and \(N_\textrm{mixed}(Q_3)\) is the distribution of uncorrelated triplets. The latter are obtained by taking the three particles needed to form a triplet from three different collisions, thus called mixed event sample. Only events with similar multiplicity and position of the primary vertex along the beam axis are mixed. The number of events used for the mixing is set to 30. To account for the two-track merging and splitting effects due to the finite two-track resolution in the same event sample, a minimum value of the distance between the same charge tracks on the azimuthal–polar angle plane \(\Delta \eta \)–\(\Delta \varphi \) is applied to both the same and mixed event samples. The default selection is \(\Delta \eta ^2 + \Delta \varphi ^2 \ge (0.017)^2\) for  p–p tracks and \(\Delta \eta ^2/(0.012)^2 + \Delta \varphi ^2/(0.04)^2 \ge 1\) for p–K\(^+\) tracks. A systematic variation of about \(+\)10% for the values of the minimum distance is applied in the analysis. The correlation function is normalised to unity in the range \(1.0< Q_3 < 1.2\) GeV/c, where no signal from FSIs is expected. Variations of the normalisation range are performed and included in the systematic uncertainties. In the case of a particle triplet X–Y–Z, pairwise correlations with one uncorrelated particle (X–Y)–Z, X–(Y–Z) and (Z–X)–Y also occur in the system. Genuine three-particle correlations were isolated in [59] by applying the cumulant expansion method to the femtoscopic correlation functions. The three-particle cumulant \(c_3 (Q_3)\), which incorporates information about the three-body effects in the system, is computed from the measured correlation function \(C_3(Q_3)\) as follows

$$\begin{aligned} c_3 (Q_3) = C_{3}(Q_3) - C_\mathrm {two{-}body}(Q_3) \ , \end{aligned}$$
(3)

where pairwise correlations are evaluated following the cumulant decomposition as

$$\begin{aligned} C_\mathrm {two{-}body}(Q_3)&= C_{{(X-Y)-Z}}(Q_3) + C_{{X-(Y-Z)}}(Q_3)\nonumber \\&\quad + C_{{(Z-X)-Y}}(Q_3) - 2. \end{aligned}$$
(4)

Each component \(C_{{(i-j)-k}}(Q_3)\) of the lower-order contributions in Eq. (4) is computed using two methods [59, 61]: (i) a data-driven approach based on the event mixing technique, building triplets in which the correlated (i–j) pairs are emitted in the same collision and the uncorrelated particle –k from another collision; (ii) the projector method which uses as input the measured two-particle correlation function \(C(k^*)\) for the correlated pair (i–j), evaluated in terms of the relative momentum \(k^*\) in the pair rest frame (PRF), and calculates all the possible \(k^*\) configurations in the phase space for each \(Q_3\) value of the i–j–k triplet. The input correlation functions \(C(k^*)\) used in the projector method are obtained by selecting p–p, p–K\(^+\) and p–K\(^-\) pairs using the same dataset as for the three-body analysis. Unlike the p–p and p–K\(^+\) pairs, the p–K\(^-\) correlation is significantly affected by the contribution from jet-like events [76]. To use particles emitted in collisions with the same event shape as in the case of the analysed triplets, p–K\(^-\) pairs are selected from p–p–K\(^-\) triplets with \(Q_3 < 1\) GeV/c, while for p–p and p–K\(^+\) pairs such additional requirement is not used as the correlation functions with and without the \(Q_3\) selection are in agreement. A \(\pm 0.1\) GeV/c variation of the \(Q_3\) limit is included in the systematic uncertainties of the projector method and it is combined with the uncertainties propagated from the data points of the p–p, p–K\(^+\) and p–K\(^-\) correlation functions. The latter include the variations in the selection criteria for particles, variations in the track splitting/merging rejection criteria, and normalisation range.

Fig. 1
figure 1

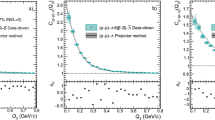
Correlation functions for (p–p)–K\(^+\) (\(\textrm{a}_1\)), (p–p)–K\(^-\) (\(\textrm{a}_2\)), p–(p–K\(^+\)) (\({\textrm{b}_1}\)), p–(p–K\(^-\)) (\({\textrm{b}_2}\)) as well as the total lower-order contributions for p–p–K\(^+\) (\(\textrm{c}_1\)) and p–p–K\(^-\) (\(\textrm{c}_2\)) as a function of \(Q_3\). The points represent the results obtained using the data-driven approach, with the statistical and systematic uncertainties represented by the error bars and the green boxes, respectively. The grey bands are the expectations of the projector method, with the band width representing the combined statistical and systematic uncertainties

Full size image

For the p–p–K\(^+\) and p–p–K\(^-\) systems, the lower-order contributions to the three-particle correlation functions are shown in Fig. 1, using the data-driven approach (data points) and the projector method (grey bands). The three-particle correlation functions of two correlated protons and an uncorrelated kaon, denoted as (p–p)–K\(^+\) and (p–p)–K\(^-\), are shown in panels (\(\mathrm {a_1}\)) and (\(\mathrm {a_2}\)), respectively. In both cases, the correlation functions are larger than unity in the low \(Q_3\) region as a result of the attractive p–p strong interaction, combined with the repulsive Coulomb and quantum statistics effects (see [46, 48] for more details). In the case of correlated p–K\(^+\) pairs with uncorrelated protons, p–(p–K\(^+\)), the correlation function shown in panel (\(\mathrm {b_1}\)) is lower than unity as a result of the repulsive p–K\(^+\) strong and Coulomb interactions, consistent with the measurement reported in [47]. In the p–(p–K\(^-\)) correlation function, shown in panel (\(\mathrm {b_2}\)), the main features of the p–K\(^-\) interaction are visible [47]: the cusp structure due to the opening of the \(\mathrm {\overline{K}^0}\)n channel as well as the bump due to the \(\mathrm {\Lambda (1520) \rightarrow p K^{-}}\) decay appear at \(Q_3 \approx \) 0.15 GeV/c and \(Q_3 \approx \) 0.7 GeV/c, respectively. The total lower-order contributions to the p–p–K\(^+\), panel (\(\mathrm {c_1}\)), and p–p–K\(^-\), panel (\(\mathrm {c_2}\)), correlation functions evaluated with the data-driven approach and the projector method are in agreement. The reduced \(\chi ^2\) between the two methods, evaluated in the \(Q_3\) range shown in Fig. 1 (21 degrees of freedom) by adding in quadrature the statistical and systematic uncertainties of the data, is 1.6 and 1.4 for p–p–K\(^+\) and p–p–K\(^-\), respectively. Since the projector method does not depend on the third particle mixing, it provides significantly smaller uncertainties than the data-driven approach and hence is used to extract the cumulants. This choice does not affect the final results of the analysis. Figure 2 shows the measured p–p–K\(^+\) (left panel) and p–p–K\(^-\) (right panel) correlation functions (data points) compared to the lower-order contributions evaluated using the projector method (grey bands).

Fig. 2
figure 2

Correlation functions (data points) for p–p–K\(^+\) (left panel) and p–p–K\(^-\) (right panel) compared to the lower-order contributions evaluated using the projector method (grey bands). Statistical and systematic uncertainties are represented by error bars and green boxes, respectively. The band widths represent the combined statistical and systematic uncertainties propagated from the two-particle correlation functions used as input to the projector method

Full size image
Fig. 3
figure 3

Cumulants for the p–p–K\(^+\) (left panel) and p–p–K\(^-\) (right panel) primary triplets. The error bars and the blue boxes on the data points represent the statistical and systematic uncertainties, respectively. The \(n_\sigma \) deviations from zero in each bin are shown in the bottom panels, adding in quadrature the statistical and systematic uncertainties of the data

Full size image

The corresponding cumulants are extracted using Eq. (3). The measured cumulants include the correlations of the primary particles as well as the feed-down from resonances and particle misidentifications, which need to be accounted for as discussed in [59]. The number of correctly identified primary triplets is about 66% of the total sample for both p–p–K\(^+\) and p–p–K\(^-\). The remaining contribution mainly stems from the feed-down of the \(\Lambda \) (17%) and \(\Sigma ^+\) (7%) hyperon decays into protons and from the \(\phi \) meson (4%) decay into charged kaons. These numbers are obtained combining the primary and secondary fractions with particle purities. The primary and secondary fractions are extracted using Monte Carlo template fits to the measured distributions of the DCA to the primary vertex [46]. The fraction of charged kaons from \(\phi \) decays is calculated using the expectations from a thermal model [77]. The correction of the measured cumulants to obtain the contribution from primary triplets is performed following the decomposition procedure adopted in [59]. Due to the absence of theoretical and experimental information on the genuine p–\(\Lambda \)–K\(^\pm \), p–\(\Sigma ^{+}\)–K\(^\pm \) and p–p–\(\phi \) correlations, the corresponding feed-down contributions to the p–p–K\(^{\pm }\) cumulants are considered to be flat, without any specific dependence on \(Q_3\). This assumption was tested in the case of p–p–p correlations [59], where a similar contribution (about 19%) for the \(\Lambda \) feed-down into protons was found. The results obtained by using the flat and non-flat corrections are found to be in agreement within the uncertainties. A flat feed-down contribution in the cumulant corresponds to negligible correlations from genuine three-body effects in the mother particle systems X–Y–Z decaying into p–p–K\(^{\pm }\). The dominant feed-down contributions coming from pairwise correlations in the triplets, such as (X–Y)–Z and X–(Y–Z), are already removed as they are included in the lower-order correlations. The resulting cumulants of the correctly identified primary p–p–K\(^+\) and p–p–K\(^-\) particle triplets are shown in left and right panels of Fig. 3, respectively.

In the absence of genuine three-particle correlations in the triplets, the measured three-particle correlation function would be identical to the lower-order contributions \(C_{3}(Q_3) = C_\mathrm {two{-}body}(Q_3)\). Consequently, from Eq. (3), the cumulant would be compatible with zero within the experimental uncertainties. In the case of the p–p–K\(^+\) and p–p–K\(^-\) systems, the agreement of the measured cumulants with zero is evaluated by performing a \(\chi ^2\) test in the region \(Q_3 < 0.4\) GeV/c. In this region, the relative momentum for all the pairs in the particle triplets is lower than 0.2 GeV/c, which is the kinematic region sensitive to the strong interaction. Larger \(Q_3\) values are dominated by kinematic configurations in which one of the pairs has a relative momentum larger than 0.2 GeV/c, meaning that only two of the three particles in the triplet can be in a kinematic configuration which is favourable for the strong interaction. Thus, at \(Q_3 > 0.4\) GeV/c the contributions from the two-body interaction dominate. The local statistical significance at \(Q_3 < 0.4\) GeV/c is obtained from the p-value of the \(\chi ^2\) distribution, which is converted in a number \(n_\sigma \) of Gaussian standard deviations. As the systematic uncertainties in different \(Q_3\) bins are correlated, the \(\chi ^2\) is calculated using the cumulants extracted from each systematic variation with the corresponding statistical uncertainties. Finally, the average \(\chi ^2\) in the interval \(Q_3 < 0.4\) GeV/c is extracted. The corresponding \(n_\sigma \) values are 2.5 and 1.5 for p–p–K\(^+\) and p–p–K\(^-\), respectively. As the \(Q_3\) range of the genuine three-body effects is not known a priori, the \(n_\sigma \) values have been evaluated as well in the region \(Q_3 < 0.2\) GeV/c and they are found to be 2.7 and 1.4 for p–p–K\(^+\) and p–p–K\(^-\), respectively. Such results indicate that the measured p–p–K\(^+\) and p–p–K\(^-\) correlation functions are compatible, within the quoted significance levels, with the assumption of pairwise correlations in the triplets without additional contributions from genuine three-body effects. More solid conclusions require a larger data sample to reduce the statistical uncertainties and full-fledged theoretical calculations for the three-particle correlation functions. In order to provide a comparison of the kinematic range accessible with this measurement to the study of K\(^+\) and K\(^-\) interactions in light nuclei, the momenta of the three particles in the triplets with \(Q_3 < 0.4\) GeV/c are evaluated in the PRF of the two protons. The momentum of each proton in the PRF is \(p_\textrm{p}^* < 180\) MeV/c, compatible with the typical Fermi momenta of nucleons in light nuclei (e.g. the Fermi momentum in Carbon-12 is about 220 MeV/c). In the rest frame of the two protons, the momentum of the K\(^+\) and K\(^-\) ranges from 30 MeV/c (in the first bin in Fig. 3) to 130 MeV/c (eighth bin in Fig. 3). This demonstrates that even for low kaon momenta, i.e. at energies close to the p–p–K\(^+\) and p–p–K\(^-\) thresholds, three-body effects such as kaonic bound state formation below threshold or three-body interactions do not contribute significantly to the measured correlation functions. These results provide additional experimental information for theoretical models aiming to understand the role of genuine three-body effects in p–p–K\(^+\) and p–p–K\(^-\) systems. The LHC Run 3 data taking will deliver a larger data set for more detailed studies of the K\(^+\) and K\(^-\) three-body dynamics in the low momentum region, down to the energy threshold of the triplets.