Abstract
The AGATA and GRETA spectrometers are large arrays of highly segmented HPGe detectors that use the technique of gamma ray tracking to reconstruct the scattering path of gamma rays interacting within the active material. A basic requirement is a precise reconstruction of the individual interaction locations within the detectors. This is possible through the use of pulse shape analysis which has to be conducted in real time due to the high data rates generated by the spectrometer. The methodologies that have been evaluated to perform this for AGATA are discussed along with the approaches used to calculate the pulse shape databases required by these algorithms. Finally, the performance and limitations of the existing approaches are reviewed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The AGATA [1] and GRETA [2] spectrometers [3] are large arrays of High Purity Germanium (HPGe) detectors that aim to deliver the highest possible \(\gamma \) detection efficiency while simultaneously providing the best possible energy resolution and spectrum quality (peak to total P/T). In order to achieve these goals \(\gamma \) tracking is required to reconstruct the multiple interactions that \(\gamma \) rays undergo while depositing their energy in the detectors. \(\gamma \) tracking requires the precise energy and interaction position of each interaction in order to enable the recovery of the full interaction sequence.
The identification of these unique interaction positions is achieved through the use of highly segmented germanium detectors and the use of Pulse Shape Analysis (PSA). The AGATA detectors provide a course degree of position information through the 36 segments on each detector. The resulting position resolution is however insufficient to precisely locate the interaction positions. PSA allows for the signal collected from each of the charge sensitive preamplifiers connected to these segments, and the core electrode, to be analysed. The unique shape profile of the charge signal can be used to identify the positions(s) of interaction. In practice PSA uses a database of pulse shapes (basis) to describe how these signals look at each interaction position inside the detector. By comparing the signals measured with the basis the unique interaction positions can be found. The basis is created from a calculation, and it is validated by experimental measurements which are obtained from detector characterisation systems.
For the experimental characterisation dedicated scanning tables have been developed for both the AGATA and GRETA detectors. The existing scanning tables use a collimated \(\gamma \)-ray source, producing a pencil beam of \(\gamma \) rays to select interactions taking place at a particular position inside the detector volume. The x, y-coordinate of the collimator position defines one part of the coordinates of the interactions, whereas the coincident detection of a Compton scattered \(\gamma \) ray inside a secondary collimation system completes the event selection also in the z direction.
In the AGATA collaboration scanning systems have been commissioned at the University of Liverpool [4, 5], IJC Orsay [6] and IPHC Strasbourg [1]. At GSI, Darmstadt a technique based on positron annihilation was developed [7, 8], a system based on this approach is being commissioned at the University of Salamanca. The scanning methods require time consuming measurements and/or analysis of the recorded signals to ensure the fidelity of the data.
Various methods to determine the interaction positions of \(\gamma \) rays in segmented germanium detectors have been developed that rely on PSA techniques. These methods typically analyse the profile of the induced real and transient charge signals. Real signals are measured at the electrode of the segment in which an interaction takes place with their measured charge terminating at a non-zero value. Transient signals are measured on the electrodes of segments neighbouring the interaction, due to the capacitive coupling between these segments and the moving charges a non-zero charge is induced which ultimately terminates at a zero value. The resulting large datasets of digitised preamplifier signals from the single crystal are compared with the calculated existing set of signal pulses known as a basis. The comparison includes the signal of the core electrode, the signal of the hit segment electrode and the signals from the neighbouring segment electrodes for every interaction. The profile of the core and hit electrode signals provides information regarding the radial position whilst signals from neighbouring segment electrodes contain information on the azimuthal and z-position of the interaction. The amplitude of the signals are proportional to the deposited energy.
2 Pulse shape calculation
Gamma rays interact within the active detector material producing a primary electron which subsequently creates electron–hole pairs. For the calculation, the interaction positions and the deposited energies are given as an input. Once the charges are created inside the active Ge material, they travel along the electric field of the reverse biased semiconductor detector and induce a signal in the electrodes. The quasistatic field approximation is typically applied such that the induced signals at all electrodes of the detector are instantaneously created. The time to collect all charge carriers is dependent on the geometry of the detector, the applied voltage and the impurity concentration of the semiconductor material.
The induced electrons and holes have distinctive mobility values resulting in different collection times. Specific models describe their mobilities with a complex azimuthal dependence. A basic model assumes a constant mobility. Refined descriptions like [9] p. 434, assume an empirical dependence of the drift velocities with the electrical field strength. Moreover, electron and hole mobilities in germanium are not isotropic, but depend on the orientation of the crystallographic axis of the cubic-centred germanium crystal structure with respect to the electrical field. Recent publications [10,11,12] show that such anisotropic treatment of electron and hole mobilities is crucial in non-planar coaxial detectors.
An AGATA detector crystal has a volume of \(\sim \)380 cm\(^3\). In order to achieve the position resolution required by the subsequent \(\gamma \) tracking algorithms, a calculated basis of waveforms that describe the response of the detector throughout the full volume is required. The current AGATA approach is to use a 2 mm Cartesian grid, which results in \(\sim \)48,000 basis sites throughout the full volume or \(\sim \) 700–2000 points per segment. Three different approaches for the simulation codes for AGATA have been pursued: the MATLAB-based Multi Geometry Simulation code (MGS) [13, 14], the Java-based AGATA Signal Simulation toolkit (JASS) [15] and the C-based AGATA Detector Library (ADL) [16]. Combined with the segmentation of the capsule, the PSA position resolution is expected to be \(\sim \) 5 mm FWHM for the AGATA detectors. The reader should note that there is an energy dependence to this value, which will be discussed in more detail later in this review.
2.1 MGS
The first results for the pulse shapes of a 36-fold segmented AGATA detector were described in pioneering publications on the MGS code [13, 14, 17]. These papers reviewed the mechanisms influencing the process of signal induction. The solution of the electric field and the charge carrier drift phenomena were considered for arbitrary crystal geometries crucial for the three irregularly tapered crystals that make up an AGATA triple cluster. The sequence of steps which were needed for the generation of a data set of position-dependent pulse shapes, included:
-
Calculation of the electric field starting from the solution of Poisson’s equation.
-
An implementation of charge carrier transport in a semiconducting medium.
-
Trajectories of charge carriers for arbitrary interaction positions inside the detector volume.
-
Application of the Shockley-Ramo theorem providing the resulting charge recovery at the contacts.
-
Weighting potential and weighting field resolution.
-
Scanning of selected areas in the crystal.
-
Simulation of the charge-collection efficiency.
The numerical algorithms were implemented using MATLAB [18]. This matrix-oriented programming language is adapted for grid-based solving algorithms enabling the modelling of general geometries with the support of a cubic grid. Emphasis was given to the proper numerical solution of Poisson’s equation and three distinct solving algorithms were implemented in the MGS software package.
In this work the dependence of the electron drift velocity anisotropy was taken from [11]. Electric conduction depends on several parameters, such as the strength of the applied electric field, the crystal orientation and the lattice temperature. The drift velocity magnitude and angle shift with respect to the electric field direction are affected by the fact that the tensor of differential mobility will become non-diagonal and field dependent, with decreasing diagonal elements as the strength of the electric field increases.
When an incoming \(\gamma \) ray interacts within a segmented detector, it generates free moving charges (electron hole pairs). The movement of these charges induces a signal in all segments during the carriers drift time. All AGATA pulse shape calculations are based on point like charges. In the segment where an interaction occurred and charge carriers are created, a net charge can be measured, while neighbouring segments yield transient signals. Ramo’s theorem provides the induced current as a function of time as the dot product of the drift velocity and the weighting field, independently of the bias voltage and space charge distribution. Its calculation involves solving Laplace’s equation (Poisson’s equation without any sources) with particular border conditions. The efficiency of implementation of Shockley-Ramo’s theorem was a key issue. MGS was utilised for the comparison with the first AGATA scan data from the Liverpool scanning apparatus [19].
2.2 JASS
JASS was developed specifically for the complex geometry of the AGATA HPGe detectors and its impact on the observed pulse shapes. A precise solver for the Poisson equation was developed together with an accurate interpolation method. The overall performance of this combination was found to be excellent since the boundary conditions were used to gauge the accuracy of the adaptive interpolation routine. It was demonstrated that the sum of all weighting potentials is equal to unity throughout the detector and the signal seen by the core contact is equal to the inverse sum of the segment signals. The condition holds on the calculated grid points at off-grid points for interpolated values for the potentials. The results for a 100 \(\mu \)m grid showed that for 97.6% of the detector volume the deviation was less than \(5\times 10^{-4}\). Small deviations occur in the last 0.5 mm from the detector surface.
The JASS results [15] illustrated that the agreement between simulated and experimental signals, i.e., the position resolution, depends significantly on the charge carrier mobility parameters for a given electric field configuration and to a lesser extent on the differential cross-talk correction. Systematic deviations were observed for the radial coordinate and emphasised the importance of a precise parameterisation in order to match to the experimental drift velocities. The precision of the electric field calculation depends on the grid size and on the model of the impurity distribution. At the time of development, the available computer memory limited the grid size that could be feasibly calculated.
The best match determined by the grid search algorithm of a random interaction scaled to the right energy compared with experimental data. The horizontal axis is split in 37 sections, each containing a 600 ns trace of the corresponding electrode. Top plot is scaled to full energy deposition. Middle plot is zoomed to emphasize the transient signals. Bottom plot shows the absolute difference between simulation and measurement. Adapted from [20]
2.3 ADL
ADL was developed for the calculation of signals from highly segmented large volume HPGe detectors. The ADL publication [16] introduced the general concepts and basic assumptions required to successfully form the calculation. Several approximations were discussed, justified and applied to simplify the problem. Again, all interactions by \(\gamma \) radiation are considered as point like interactions, as the range of the electrons cannot be resolved.
The solution to the Poisson equation for the complex AGATA detector geometry is obtained numerically by a finite difference technique on a cubic grid. The cubic grid simplifies drastically the equations after discretisation and allows for a fast lookup and interpolation of the values.
The numerical ADL signal calculation is separated into four parts:
-
Calculation of the fixed electric field in the reverse biased detector.
-
Trajectories under action of the external field are calculated taking into account the different mobility of electrons and holes.
-
Calculation of the instantaneously induced image charge in any electrode of the detector as a function of the positions of free electrons and holes in the depleted region of the detector.
-
The different inputs (potentials, mobilities, mirror charges, response functions) have to be generated and combined for the final calculation of the electric signals in the detector.
The electrical field inside the detector is obtained numerically by a finite difference technique on a cubic grid. Homogeneous Neumann boundary conditions are applied to the array boundaries. The potentials have no gradient component tangential to the array boundaries. The homogeneous boundary condition is also used for the passivated layer on the backside of the AGATA crystals. Key details regarding the passivation layer (geometrical size, thickness and charge density) are not available from the manufacturer, so assumptions were made.
The anisotropic behaviour of the moving charge carriers is of high importance in large coaxial detectors. The field orientation can take any direction with respect to the crystal orientation. The differences of charge carrier mobility between fields along different crystallographic axes amount up to about 30% in the high field regime. For the required mobility as function of field strength, three-dimensional mobility models were employed both for electrons and holes in germanium near liquid nitrogen temperature.
In the top plot the core signal for different interaction radii are shown. The effect of the different mobilities of electrons and holes is clearly visible. For small radii the faster electrons are collected immediately while the slower holes still have to drift to the segment electrode. The shortest rise time occurs at an intermediate position, for larger radii the time of the electrons to be collected is longer than for the holes. The bottom plot shows the transient signals in a segment next to the hit segment. Depending on the distance of the interaction to the non hit electrode, the amplitude of the transient signal changes. Colour code as indicated in the inset of the bottom graph. The slice is at 40.25 mm from the front of the detector. Adapted from [21]
Once the trajectories of all free charges in the detector are calculated as a function of time, the induced signals in each of the electrodes are determined. The weighting potential for each of the electrodes of interest is calculated for every position in the sensitive volume of the detector. The time evolution of the induced charge and the integral of the current into the electrode are given by the charge weighted sum of the weighting potential evaluated at the momentary position of the free charges.
In Fig. 2, examples of resulting simulated traces for an AGATA detector are given. The calculated charge signal is then subject of a convolution with a realistic response function of the acquisition electronics. The response function of the preamplifier is measured by injection of a clean fast rectangular pulse in the preamplifier’s pulser input. Since all channels in a highly segmented detector are not grounded, but connected to a preamplifier, the ideal Ramo currents will not strictly apply and need modification due to cross talk. The cross talk in segmented AGATA detectors was worked out in [21]. For AGATA detectors, two types of cross-talk have been observed to contribute: (1) Proportional cross-talk, which creates a cross-talk signal in neighbouring electrodes proportional to the capacities between the electrodes involved. This type of cross-talk is described by assuming the preamplifier acts at low frequencies as a large capacitance on the collecting electrode. Accurate routines were developed to measure and correct for this type of cross-talk within AGATA [22]. (2) Differential cross-talk, this produces a response which is proportional to the derivative of the induced signal and is therefore dependent on the rise time of this signal. Since the derivatives of active segment signals are only non-zero during the rise time of the inducing signal, this second type of cross-talk can have an impact on the performance of the PSA. A detailed discussion can be found in [22].
Schematic diagram of the ADL calculation approach taken from [10]. The routines are coloured in green and the user provided input is coloured blue. The main routine called Calculate Traces consists of three subroutines and takes the interaction position as input. The first subroutine calculates the path of the charge carriers through the detector material for every time step. It needs the electrical field and a mobility model of the charge carriers as an input. The second subroutine calculates for every time step the induced charges in all electrodes. It needs the weighting potentials to do this. The last subroutine convolves the signal with predefined functions
In Fig. 3 a block diagram of the ADL calculation approach is shown. ADL is now standard tool for calculating the pulse shape response of all AGATA detectors [16]. Each individual HPGe detector is characterised by its geometry, space-charge distribution, crystal-axis orientation, cross-talk properties and the response function of the electronics.
The interaction positions allocated by the PSA also depend on the grid-search algorithm that is employed to perform the comparison of the measured and simulated pulses. Moreover, the results of this comparison depend on the time alignment between measured and calculated pulses, the distance metric and the weighting of the individual segment pulses. Recent studies demonstrated that the AGATA PSA can resolve the interaction position of \(\gamma \) rays in segmented AGATA detectors with an energy-dependent position resolution of a few millimetres [23]. The comparisons of measured and simulated tracking efficiencies and peak-to-total ratios are given in [24, 25].
2.4 ADL PSA performance
The performance of ADL was reviewed and refined as reported in [26]). The position sensitivity of several AGATA detectors was determined by analysing the data of a \(^{22}\)Na source measurement. In the decay process of \(^{22}\)Na, a positron is emitted that annihilates with an electron very close to the point of emission. The positron has a maximum energy of 540 keV, a mean energy of 180 keV and a mean range of about 0.24 mm [27]. The annihilation photons produced which are emitted at an angle of near 180\(^\circ \), allows for the assessment of the quality of the PSA results. For this purpose, the shortest distance of a straight line connecting the two identified interaction points to the known source position is determined. It should be noted that variations in the momentum carried by the neighbouring nucleus and the positron range provide a physical limit to the position determination, however, this is below the functional limit of the germanium detectors themselves.
The pulses that are created by the ADL depend on a variety of detector properties and several input parameters for each individual HPGe detector are needed. Most of these input parameters are measured routinely, like the cross-talk properties of the detectors. However, some quantities, like the space charge distribution inside the crystal volume, are hard to access and are only partially available from the crystal manufacturer. The impurity concentration is only provided for the front and back of the crystal and a linear gradient is assumed in between.
In conclusion, the \(^{22}\)Na-coincidence method was established as a fast and reliable tool to study the results of the PSA. Whilst the method is currently limited by the existing PSA algorithm used by AGATA to single segments, the development of new PSA techniques could allow for the analysis of two annihilation photon interactions within a single segment and provide insight into the Compton behaviour of quantum-entangled photons.
2.5 The AGATAGeFEM software package
A number of software packages have been developed to calculate pulse shapes from the High-Purity Germanium detectors used in AGATA (e.g. see the references [12,13,14,15,16, 28, 29] and other sections of this article). The complex shapes of the AGATA crystals can be more accurately described using a finite element scheme and finite element methods (FEM) than with very dense rectangular grids. It is beyond the scope of the present work to describe FEM, and the interested reader is referred to [30] and references therein. AGATAGeFEM also uses a different model for the hole mobility with respect to ADL [10, 16] and JASS [15, 28, 29]. It is described in detail in [31].
The use of FEM allows AGATAGeFEM to have a varied precision of the mesh used to calculate the electric field, it varies from several millimetres in regions of weak fields to tens of micrometres where the combination of strong field gradients and complex geometry are combined. Another advantage of FEM is that the solution is an approximation of a function describing the electric potential and not the electric potential at the grid points. This removes possible ambiguities when calculating the electric field in the detector volume.
The AGATAGeFEM package, written in C++, uses high-quality open-source FEM software to calculate the electric and weighting potentials of AGATA type germanium detectors. The GNU Scientific Library [32] is used for solving the ordinary differential equation of charge-carrier transport. The geometry is described to within \(10^{-6}\) mm for charge transport and mesh generation. In AGATAGeFEM the solutions of the Poisson and Laplace equations are not projected down to a regular grid when used in the charge carrier-transport process. This is also the case for calculations of the induced signals via the Shockley-Ramo theorem. A weighting field as calculated by AGATAGeFEM together with pulse shapes from a net-charge segment and its nearest neighbour are shown in Fig. 4.
Using threads and the message passing interface [33] AGATAGeFEM is fully parallelised, both to calculate the field and the pulse-shapes. A graphical interface using the ROOT [34] interpreter interface allows for the calculation and display of the E-fields and pulses from ROOT. Furthermore, a very simple server client mechanism allows other programs to ask the server to calculate pulse shapes.
The AGATAGeFEM package also contains miscellaneous codes for:
-
Applying preamplifier response.
-
Applying cross-talk.
-
Re-sampling of pulse shapes.
-
Comparison of pulse shapes.
-
Calculation of pulse shapes from the output of the AGATA GEANT4 MC [35].
-
Creation of bases for PSA.
AGATAGeFEM has been used to investigate the influence of the different parameters that enter in pulse-shape calculations. This includes variations in the assumed geometry of the crystals and electrodes, and their impact on the result of the PSA for both simulated and experimental data. For details the reader is referred to [31].
Left: Example of a front segment weighting field. The field strength goes from 0 (blue) to 1 (red). Shown is also the mesh used for solving the Poisson equation. Right: Examples of net-charge signals and transient signals with and without convolution with the transfer function. The modulating effect of the response of the electronics is clearly seen (red shape). The effect of linear (green shape) and derivative (blue shape) cross-talk is also shown. For the net-charge segment the effect of the derivative cross-talk is too small to be seen
2.6 PSA and neutron damage
The AGATA n-type HPGe detectors are considered to be less sensitive to neutron damage than p-type detectors [36]. This is primarily due to reduced electron trapping in the net charge signal collected on the central core contact. However, for the AGATA detectors, the segments exhibit a higher sensitivity to trapping because the holes are the charge carriers that are collected. It was confirmed that these segments are more sensitive to neutron induced traps than the core electrode during the first weeks of the experimental campaign with the AGATA demonstrator at LNL. The new AGATA crystals were exposed for the first time to the flux of fast neutrons from deep inelastic collisions, fission and fusion evaporation reactions. Fast neutrons are well known to produce specific lattice defects in germanium crystals that act as efficient hole traps. This leads to a reduction in the charge collection efficiency of the detectors and an observable low energy tailing on the energy peak shape.
Since AGATA crystals are large, (4 cm radius \(\times \) 9 cm length), they have an increased sensitivity to neutron trapping. AGATA is designed with digital electronics allowing high count rate capability, which can lead to increased neutron doses applied to the detector. However, the energy resolution of the central core electrode did not deteriorate beyond expected limits with respect to the applied neutron dose during these early experiments.
The crystals can recover from neutron damage by annealing. However, for practical reasons and in view of the rate at which neutron damage becomes visible, this treatment cannot be applied after every experiment. Correction methods were therefore developed [37] aiming to minimise the unwanted effects due to trapping as much as possible, in between consecutive annealing procedures. These methods have gained renewed interest [38, 39] with the arrival of digital front-end electronics.
Fortunately, pulse shape analysis is not influenced by neutron trapping [39], PSA is only sensitive to changes in the signal shape of the order of the one percent level, while the energy resolution is already sensitive below the per mille level. Therefore energy resolution will deteriorate far earlier. Since the energy loss will in first approximation only depend on the interaction position in the detector, the high position sensitivity of the AGATA array allows for the correction of trapping effects using the pre-calculated trapping sensitivities. Such a correction method was described in [40] and applied successfully to neutron damaged AGATA detectors.
The theoretical model for the specific case of neutron induced hole trapping detailed in [40] demonstrates the sensitivity to trapping of both the core and hit segment signals. The peak height deficiency due to trapping is calculated as function of the interaction position of the \(\gamma \) rays within the crystal. These calculations are adequate to explain that segments show a higher sensitivity to neutron trapping than the core. The experimental observation is in agreement with collection efficiency calculations. A definition for the trapping sensitivity was proposed for highly segmented, n-type HPGe detectors.
The sensitivities are crucial quantities because they provide a simple but accurate approximation to the collection efficiency. This allows for a correction of the trapping effects and for a recovery of the energy resolution, which will prolong the operation time of the detectors. The approach was calculated to high precision although a first-order approximation and was shown to yield satisfactory results.
Using data taken with AGATA detectors, it was shown that this method indeed allows recovery for the mean position dependent energy losses in the detector [40]. A simple two-parameter optimization of the a priori unknown electron trap density and hole trap density is sufficient to describe the charge losses throughout the entire detector volume. The statistical variations in the charge loss, however, cannot be corrected for. This minimum loss in energy resolution is also position dependent and can be described as function of the sensitivities. The experimental data compares very well with theory (for details see [40]). An example of the efficacy of the neutron damage correction is shown in Fig. 5 where the energy as function of depth in the detector for selected 1332 keV single events at 15 mm radius are shown before and after the correction is applied. For the selected events, the width of the energy distribution (FWHM) is improved by the procedure from 4.14 keV to 2.85 keV with a small remaining shift which is still observed after correction.
3 Generating a basis and characterisation
3.1 Experimental performance
To be able to fully understand and model the bulk performance of a detector with complex geometry and electronic segmentation, it is crucial to understand its response as a function of \(\gamma \) ray interaction position. A number of techniques have been developed within the AGATA collaboration to extract this information. Each of these techniques uses the same basic procedure: a \(\gamma \) ray of a known energy interacts at a known position within the detector and the response of the detector is digitised, recorded and analysed in software. This process is repeated over multiple positions within the detector and a basis of detector responses as a function interaction position and energy is created. This can then be used for further PSA of experimental or simulated data. The techniques employed by the various characterisation laboratories can be separated into four distinct techniques of increasing complexity:
-
Singles Scanning
-
Coincidence Scanning
-
Pulse Shape Comparison Scanning (PSCS) with collimated beams
-
Pulse Shape Comparison Scanning with electronic collimation
In addition, another direct technique, using a Jacobian method, allows for the extraction of a basis directly from the experimental signals. Each of these is described below.
3.2 Singles scanning
The simplest scanning technique, often used as a first stage of a full characterisation (and the basis for PSCS as described in Sect. 3.4) is ‘Singles’ scanning. Here, the \(\gamma \)-ray interaction position is only known in two dimensions and so a fully constrained study of the detector cannot be made but geometrical information as well as surface and bulk performance can be studied by appropriate choice of the \(\gamma \) ray energy used.
Singles scans using a collimated \(\gamma \) beam, are performed at the University of Liverpool, IJC Lab Orsay and IPHC Strasbourg. A \(\gamma \)-ray source is collimated to a pencil beam with diameter of 0.5\(-\)2.0 mm. The collimated source is mounted on an automated 2-axis (X, Y) positional table which allows the position of the source to be precisely controlled with an accuracy of around 100 \(\mu \)m in both the x- and y-axes. The detector being characterised is then mounted above the table, in either the vertical or horizontal orientation, such that the beam of \(\gamma \) rays impinges on an active area of the detector. The XY position of interaction within the detector is inferred from the position of the scanning table and thus the collimated source. There are no constraints on the depth of interaction, along the z-axis. The source is raster scanned across the detector in a uniform grid, typically of 0.5\(-\)2.0 mm steps, and a database of detector response as a function of interaction position is recorded. Transmission through the collimator is of the order 10\(^{-6}\) and so a source activity of hundreds of MBqs is required to give sufficient number of \(\gamma \)-rays exiting the collimator. \(^{137}\)Cs is typically used as the \(\gamma \) energy of 662 keV is high enough to allow penetration into the bulk of the detector but not so high as to be difficult to shield and collimate. The 60 keV \(\gamma \) ray from \(^{241}\)Am can be used to investigate the surface of the detector being characterised. A wide range of \(\gamma \) energies given by a \(^{152}\)Eu source has also been used.
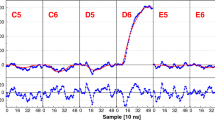
For each event, the 37 preamplifier signals from the detector are digitised and recorded along with the position of the source / scanning table. From this, basic characterisation information can be investigated such as the count rate response (intensity) and charge collection time (rise time) plots, as is shown in Fig. 6.
Example plots from 2D scans of AGATA capsule A006. Left: Intensity plot from \(^{241}\)Am scan with the detector in the vertical orientation showing surface effects. Centre: T90 rise time plot from \(^{137}\)Cs scan. Right: \(^{137}\)Cs scan with the detector in the horizontal orientation showing interactions throughout the detector bulk. Adapted from [41]
3.3 Coincidence scanning
A technique developed at the University of Liverpool [4] and IJC Lab, Orsay for localising the depth of interaction in the z-axis is referred to as ‘Coincidence’ scanning. This is an extension of the previously described ‘Singles’ scanning but allows \(\gamma \)-ray interaction positions to be constrained in three-dimensions through the use of secondary collimation and ancillary detectors.
In the system developed at the University of Liverpool, the detector being characterised is surrounded by a series of lead collimators, with 2–3 mm spaces between them, which are aligned with specific depths in the detector undergoing characterisation. This collimation is perpendicular to the primary collimation of the \(\gamma \) source, as shown in Fig. 7. These secondary collimators allow \(\gamma \) rays to escape if they scatter within the detector at 90\(^\circ \) with respect to the primary collimation. Each secondary collimator is surrounded by a number of scintillator detectors to detect the scattered \(\gamma \) rays. In excess of 40 custom BGO detectors are used in order to maximise the detection efficiency. Compton kinematics indicate that a 662 keV \(\gamma \) ray undergoing a single 90\(^\circ \) scattering interaction will deposit 374 keV in the AGATA crystal and the remaining 288 keV in the scintillator. Setting appropriate energy gates on both detectors in the offline data analysis allows only true single-site interactions to be selected and processed.
Schematic diagram of the University of Liverpool Coincidence scanning system. A \(^{137}\)Cs source is positioned along the X- and Y-axes by the scanning table. \(\gamma \)-rays emitted from the source, that scatter \(\sim \) 90\(^\circ \) inside the detector, can pass through the secondary collimators and are stopped in the scintillators. The secondary collimation constrains the interaction position along the z-axis. Adapted from [42,43,44]
Signals are digitised by Caen V1724 digitisers, using the DPP-PHA firmware for energy evaluation. These record the incoming waveform with 100 MHz clock frequency (10 ns per sample) and 14-bit resolution. A hardware trigger is set to only record events for which the AGATA core and at least one BGO detector trigger within a coincidence window of 325 ns of each other. The signals are then written to disk for offline analysis. The digitised signals from each detector for a given event are combined into a single signal showing the response of the entire detector (36 segments & core) over a given time window. Once a statistically significant number of signals have been recorded for a given interaction position, the signals corresponding to each individual event are averaged to minimise the effects of noise. Comprehensive details of the averaging process are given in [19, 43], a brief summary is given below and a flow chart illustrating the steps involved is shown in Fig. 8.
Flow diagram showing the analysis procedure for processing the array of pulse shapes at each precisely determined 3D interaction position [19]
Initially, each signal is gain matched and any baseline offset is corrected for. The signals are then expanded from the native 10 ns sampling of the digitisers to 2 ns via a five point linear interpolation followed by a three point moving average. The preamplifier decay of the signals is then corrected for and the signal heights normalised such that the core and hit segment are scaled to a maximum of 1. The hit and non-hit segments are scaled by the same factor. Signals are then time aligned to a common point to remove any time walk / jitter. Time alignment is not a trivial process and the reader is referred to [19, 43] for further details. All the time aligned signals are then used to produce a mean pulse representation. An iterative \(\chi ^2\) minimisation method is then used to compare each individual signal with the preliminary mean signal. A threshold is set on the maximum deviation between each individual event and the mean. Events, which do not pass this threshold, are discarded and a new mean is formed from the accepted events only. An example mean signal for the core, hit and adjacent segments is shown in Fig. 9. The final mean representation for each interaction position is then stored in a database of known detector responses, for use in subsequent PSA.
Mean signal formation for the core (left), hit segment (centre), and an adjacent segment (right) for a single position. Individual contributions are shown in blue, those that were rejected because they did not match the initial mean sufficiently closely in red, and the final mean in green. Adapted from [45]
The coincidence scanning system developed at the IJC Lab, Orsay, uses the same basic principle as the Liverpool system except that the secondary collimators are mounted directly onto the front of the six ancillary NaI(Tl) TOHR detectors and constrain the scattering angles to \(\sim \) 80\(^\circ \) and \(\sim \) 100\(^\circ \) as described in [6] and shown in Fig. 10. Signals from the AGATA detector are digitised using TIGRESS digitisers [46], giving the same 100 MHz clock frequency and 14 bit resolution as the Caen system used at Liverpool.
Left: Schematic diagram of the IJC Lab Orsay Coincidence scanning system. The \(^{137}\)Cs source is positioned along the x- and y-axes by the scanning table. \(\gamma \)-rays emitted from the source that scatter \(\sim \)80\(^\circ \) or \(\sim \)100\(^\circ \) can pass through the secondary collimators in front of the NaI detectors. Right: TOHR detector module and collimator stack with schematic. Adapted from [6]
The benefits of this technique are that it gives a very precise knowledge of the position of interaction (\(\sim \) 2 mm\(^3\)) within the detector. The Compton kinematics ensure that each event recorded is a true single-site interaction, the position of which is defined by the primary and secondary collimation. In addition, the timing of the interaction within the AGATA detector can be deduced from the ancillary scintillator detectors. The fast and predictable response of the scintillator provides precise measure of the start of the charge collection (\(t_0\)) than what is possible using the AGATA detector alone. The correct identification of \(t_0\) is crucial for comparison of experimental and simulated data and is often difficult to determine from experimental data. The disadvantages are that the secondary collimation results in a very low efficiency and so measurement times can be very long (many hours per position leading to partial scans taking several months to complete) to ensure sufficient statistics are recorded. This means that it is not practical to scan the entire volume of a capsule. Therefore, a subset of positions must be chosen that represent the most interesting areas of the crystal for comparison with and validation of more comprehensive simulated datasets.
3.4 Pulse shape comparison scanning (PSCS) with collimated beams
The upper left panel sketches the experimental configuration proposed for a straightforward implementation of the PSCS technique (the two measurements shown, with the \(^{137}\)Cs source in positions “a” and “b” respectively, are done separately). The other panels are the results of a GEANT4 simulation [50] showing interaction positions determined from comparison of pulse shapes with more and more stringent conditions on the similarity of the signal shapes imposed: finally (in the bottom right panel), only hits concentrated around the collimator line crossing points are present
In the initial phase of the AGATA project, it was common belief that the only feasible way to get the full-volume 3D position response of a crystal, i.e., association between the detector output signal shapes and all possible single-hit positions, was through solving the appropriate electrostatic equations [10, 12, 16, 17, 29, 31, 47, 48]. This was because the experimental techniques available were based only on coincidence \(\gamma \)-ray measurements with collimators [49], that are time consuming for extracting the full 3D response. A novel characterisation technique, the pulse Shape Comparison Scan (PSCS), was proposed in 2008 [50] that opened the possibility of effectively extracting the full 3D detector position response of an AGATA detector several tens of times faster, using only singles measurements. In essence, the PSCS principle is simple. It is to perform a consistency check on the pulse-shape signals for events acquired with different sets of measurements, allowing to select only those signals associated to \(\gamma \)-ray hits that took place in a specific and known location inside the HPGe crystal. The straightforward application of this concept [50] consists of performing two separate \(\gamma \) singles measurements, where the respective pencil \(\gamma \)-beam directions are perpendicular to one another (see the upper-left panel in Fig. 11). The spatial region corresponding to the intersection of the two pencil \(\gamma \) beams is now one single voxel (a few mm\(^3\)) inside the detector volume. In this experimental situation, a signal shape is found to be very similar in one set of data and in the other when the associated events correspond to \(\gamma \) singles interactions taking place in the position where the \(\gamma \) pencil beams intersect each other. This allows a specific detector output signal shape to be associated with a precise position inside the detector. The proof of principle for the PSCS method was obtained through a dedicated GEANT4 simulation (see Fig. 11 and [50]), while the experimental implementation of the technique was done at IPHC.
3.4.1 IPHC scanning apparatus
The IPHC scanning table is composed of two, perpendicular, 300 mm range, X and Y axes holding a collimator composed of W, Pb and Fe which generates a thin \(\gamma \) ray pencil beam (see red arrows in Fig. 12). Intense sources of \(^{241}\)Am (1.5 GBq), \(^{137}\)Cs (1.85 GBq) and \(^{152}\)Eu (0.75 GBq) can be placed in front of a 165 mm long collimator. The central part of the collimator is interchangeable and allows for the different collimator diameters (1.0, 0.50 and 0.21 mm). The detector can be mounted in two distinct positions with its axis either parallel or perpendicular to the \(\gamma \)-ray pencil beam, corresponding to the two perpendicular scans. An adjustment frame enables fine positioning of the detector in addition to a laser beam used as an alignment reference.
Figure 12 shows the experimental configurations and the principle of a PSCS scan. A vertical 2D scan is performed with a 2 mm pitch, the pulse shapes being registered in files associated to each (X, Y) position. Events with energy detected in only one segment and with equal energy deposit in the central contact and the segment are considered. A horizontal 2D scan with the same pitch is performed after alignment. The scan grid is chosen to ensure that interaction positions, defined by the pencil beams from the vertical and horizontal scans, intersect each other. The pulse shapes are registered in files associated to each (Y, Z) position. A \(\chi ^2\) test between pulse shapes from vertical and horizontal scan files of intersecting beams allows the selection of about 200 pairs of pulse shapes corresponding to position (X, Y, Z). A refinement procedure leads to about 140 pulse shapes used to calculate the mean pulse shape associated to the (X, Y, Z) coordinates.
A simple schematic diagram representing the procedure developed at IPHC for performing the PSCS technique. Contrary to Fig. 11 where two side scans are considered, front and side scans are preferred at IPHC. On the left (centre) panel, the detector is in vertical (horizontal) position. The red arrows show the direction of the pencil beam at the positions during data acquisition whereas the green arrows show the positions for which data are already acquired. The right panel shows, in green, the scan-grid points and, in red, the point corresponding to the crossing of the two red arrows
3.4.2 IPHC scanning procedure
The scanning procedure was optimised as reported in [51] where the AGATA detector, B006, was 3D scanned for the first time with this technique. Prior to the scanning using the PSCS technique, the detector position was aligned along the X axis. Scans of 100 \(\mu \)m pitch across the EF segmentation line are performed and the crystal is rotated accordingly for proper alignment (see fig. 3.9 in Ref. [51]). As a by-product, the segmentation width is deduced with an uncertainty of ±40 \(\mu \)m. A second preliminary scan across the bore hole of the crystal is performed along the X and Y axes with 100 \(\mu \)m pitch. The shift of the bore hole borders in each of the 5 segment slices (2–6) is determined and corrected leading to a final vertical alignment of the crystal better than (\(6\times 10^{-2}\))\(^\circ \). These data also allowed the borehole diameter to be determined.
In addition to the preliminary scans, the crystal lattice orientation may be deduced from a 2D scan with a 1 mm pitch using the pulse rise time T\(_{10-90}\) (i.e., between 10% and 90% of the pulse amplitude). The variation of T\(_{10-90}\) along a circle of a given radius indicates the main germanium lattice \(\langle 100\rangle \) and \(\langle 110\rangle \) axes with a precision of about 1–2\(^\circ \) (now improved to 0.4\(^\circ \) on average [52] ).
A \(^{137}\)Cs 3D scan with a 2 mm pitch of the AGATA capsule B006, following the procedure described above. This yielded the construction of a 48,500 point pulse-shape basis which is composed of 6 signals, for each (X, Y, Z) scanned crystal coordinates. These were, the total energy (central contact), the net charge signal of the hit segment and the four transient signals induced in the neighbouring segments. The 3D segmentation pattern is reconstructed using the PSCS technique. Using the pulse-shape database, several crystal parameters could be studied in slices of 2 mm thickness parallel or perpendicular to the crystal axis. Comparison of vertical/horizontal and horizontal/horizontal scans were performed showing similar detector responses [51].
3.4.3 Simulation of the PSCS technique
The PSCS technique applied at IPHC was simulated for the first time in [52, 53]. The scan of the full-volume of a symmetric crystal, was performed using GEANT4 simulations for the \(\gamma \)-ray interactions in the crystal coupled to the ADL software [16] for pulse-shape generation. The latter were convoluted with the preamplifier response and realistic noise was added. The percentages of single interactions in the selected events for different energies ranging from 122 to 1408 keV were deduced. On average for energies above 600 keV, about 50% of the events are singles. This value increases drastically for lower energies. The influence of multiple interactions in a single segment on the average pulse shape at each point was studied. The simulations indicate that:
-
Several interactions of multi-scattering events occur rather close to each other, on average about 2 mm away from the scan-grid point.
-
The pulse shapes of single and multiple-interaction events are very similar.
-
The larger the distance between the first and the furthest interaction point, the smaller the energy deposit at the latter point thus reducing its influence on the final pulse shape.
Following this study it was concluded that the multi-scattering events do not contaminate the pulse-shape database. The impact of the input statistics, i.e., the number of pulse shapes in each vertical and horizontal data set, shows a larger effect than \(\gamma \)-ray energy, the PSCS performance being improved with higher statistics. Improvements of the PSCS technique may be further studied such as the metrics used and the weight associated to the transient signals in the neighbouring segments, the use of a smaller pitch and smaller collimator diameter.
The PSCS technique gathers some of the advantages of the different scanning techniques. It is rather fast as it allows scanning of the full volume of a crystal within 2 weeks and offers the possibility to use several \(\gamma \)-ray energies to perform different types of studies (surface inspection with low-energies and volume study with higher energies). The disadvantage is that it is very difficult to identify the \(t_0\) from the germanium detector signals alone.
3.5 Pulse shape comparison scanning with electronic collimation
A development of the PSCS technique has been implemented at GSI [8, 54, 55] and at the University of Salamanca [56]. This utilises the principle of electronic collimation to further reduce the total time required to characterise a detector from weeks to days. The technique uses the two 511 keV photons emitted in opposite directions, 180\(^\circ \) apart, following the positron annihilation in a \(^{22}\)Na source and a position sensitive LYSO \(\gamma \)-camera as shown in Fig. 13. The source is positioned between the detector being characterised and the \(\gamma \)-camera such that one of the 511 keV annihilation photon pair is detected in each detector. The (X, Y) trajectories of the annihilation photons entering the detector being characterised can be determined from the position information recorded by the \(\gamma \)-camera. With the source and \(\gamma \)-camera in a given location, a database containing pulse shapes for all the trajectories coming inside the coincidence cone of the characterisation detector and the \(\gamma \)-camera are recorded. In this way, data are collected from all positions simultaneously, rather than one at a time as in collimated beam measurements, leading to a significant reduction in data collection time.
A second measurement is then taken with the source and \(\gamma \)-camera together rotated by 90\(^\circ \) around the characterisation detector (moving from position a to position b in Fig. 13) and data for this new configuration are recorded. The data sets from the two source/camera positions are then compared in a similar method as described in Sect. 3.4. The point for which identical signals are observed in both data sets correspond to the crossing point of two lines inside the coincidence cone. In this way, it is possible to gather 3-dimensional (X, Y, Z) position of interaction information from the two trajectories measured in the \(\gamma \)-camera.
A schematic diagram of the generalised Pulse Shape Comparison technique employed at GSI and Salamanca adapted from [8]
SALSA (Salamanca Lyso-based Scanning Array) was designed, set up and run by the group of the University of Salamanca. Its main aim was to explore in depth the capabilities of the AGATA highly segmented HPGe detectors. For this, a maximum position accuracy in the characterisation must be achieved and, therefore, some R &D needed to be accomplished on the characterisation method used by SALSA. SALSA is based on the same concepts as GSI system: virtual collimation [57], where two collinear 511 keV photons and a PSCS algorithm are used to achieve the three-dimensional position determination in the HPGe [50]. The optimized design of SALSA, aimed at minimising the impact of uncertainty sources in the calculated position, consists of high-spatial resolution \(\gamma \)-camera with large field of view and a point-like \(^{22}\)Na source. These are mounted on a high precision mechanical structure that holds the AGATA detector in a known position as shown in Fig. 14 [58]. The mechanics enable controlled 90\(^\circ \) rotations of both the \(\gamma \)-camera and source. This allowed their relative distances to be optimised in order to reduce position uncertainties in the propagation to the calculated values [58]. The \(\gamma \)-camera is a position sensitive detector made up of 4 LYSO detectors with their respective 64-fold pixelated PSPMTs, giving a total of 256 electronic channels, whose position determination algorithm has been developed to obtain an accuracy lower than 1 mm [56]. To obtain the three coordinates of every interaction point in the HPGe detector, scans are performed for at least two different angular positions of the \(\gamma \)-camera-source set with respect to the HPGe detector. A PSCS method is then applied to identify the signals corresponding to the same interaction points coming from different angular position measurements. The self-developed PSCS method employed is based on the Wilcoxon signed-rank test and considers the signal electronic noise to establish statistically the decision level [59]. This algorithm has been tested with net signals and testing with transient signals is currently ongoing.
Left: The mechanics of the SALSA system. The AGATA detector is placed with the central axis of the detector at (0, 0, 0). The \(\gamma \)-camera can be placed at two positions highlighted in green, denoted as S1 and S2. The red colour represents the position of the \(^{22}\)Na source. Right: Photo of the detector, source & \(\gamma \)-camera setup
3.6 Direct method: extraction of the basis from the experimental signals
A Jacobian method was proposed in [60] to build a signal basis directly from a set of signals delivered by the detector in situ, that is, in the actual accelerator/target/detection-system conditions corresponding to data acquisition during a physics experiment. The method avoids the need to use signal bases obtained by simulation or through a detector scanning device. The usual online PSA algorithms can apply this basis to perform signal decomposition. The method also provides Jacobian transforms that can be used to compute very quickly the hit locations in situations when signals are not overlapping.
The method relies on the fact that the distribution of hits inside the detector is known: it decreases exponentially along the z-axis and is homogeneous perpendicularly. For the sake of simplicity, we first explain it in the case of a grid of square segments. The first step consists in choosing so-called ordering variables, \(x_{\textrm{o}}\) and \(y_{\textrm{o}}\), for the x and y coordinates of the crystal. For example, inside a given segment, the ordering variable for the x coordinate can be calculated from the amplitudes r and l of the signals in its right and left neighbour segments:
If the distribution of hits on the front face of the segment is homogeneous, then the PDF \(f_x\) is flat. If the distribution \(f_{x_{\textrm{o}}}\), obtained from the experiment, was also flat, then the estimator \(x_{\textrm{e}}\) of x would be given as a simple linear transformation of \(x_{\textrm{o}}\). However, in the general case, the two distributions are different. If the relation between \(x_{\textrm{o}}\) and x is monotonously increasing then \(f_x(x_{\textrm{e}}) = f_{x_{\textrm{o}}}(x_{\textrm{o}}) / |\frac{\textrm{d}x_{\textrm{e}}}{\textrm{d}x_{\textrm{o}}}|\), where the denominator is the Jacobian of the transform. After integration, the relation can be conveniently rewritten as:
where \(F_x\) and \(F_{x_{\textrm{o}}}\) are the cumulatives of \(f_x\) and \(f_{x_{\textrm{o}}}\). Equations (1) and (2) give an estimate of x whose distribution is the same as \(f_x\) (i.e., flat in this case). The same procedure is applied to produce an estimator of the y coordinate. Better results can be obtained by iterating the procedure. Indeed, Eq. (2) was obtained under the hypothesis that the relation between x and \(x_{\textrm{o}}\) is the same whatever y. Let us suppose \(y_{\textrm{e}}\) is evaluated first. The cumulative distribution functions, \(F_{x\textrm{l}y_{\textrm{e}}}\) and \(F_{x_{\textrm{o}}\mathrm{|}y_{\textrm{e}}}\), corresponding to a small range around \(y_{\textrm{e}}\), can be calculated. Using these CDFs in Eq. (2) usually improves the estimation of x.
In the case of the AGATA crystals, the same procedure is applied using the cylindrical coordinates \(r, \phi \) and z (in the first ring, spherical coordinates may be more appropriate). The PDFs \(f_r\), \(f_\phi \) and \(f_z\) are no longer flat. They are calculated segment by segment from their geometries, considering a homogenous illuminance and an exponential decrease from the entrance face. The tabulated resulting \(r_{\textrm{e}}, \phi _{\textrm{e}}\) and \(z_{\textrm{e}}\) estimators can be used to calculate the hit location when only one segment is hit (which accounts for about 50% of the events), avoiding the use of the time-consuming PSA algorithm.
Another way to use the method, consists of building a signal basis by averaging the non-overlapping signals corresponding to given, regularly spaced, values of \(r_{\textrm{e}}, \phi _{\textrm{e}}, z_{\textrm{e}}\). This signal basis can then be used in the PSA code. Such a basis can be built just before the actual experiment with the signals obtained during the energy calibration with a radioactive source. This way, the basis is composed of signals delivered by the detectors in working conditions and including effects from aging (neutron damages and annealing of the crystal).
The method has been tested [60] using signals simulated using the MGS [17] and the AGATAGeFEM [31] simulation codes. The signals were altered by a 3 keV noise and a 5 ns (standard deviation) time-jitter. For \(\gamma \)-rays over 100 keV, the average location errors are about 4 mm. The method was then tested [61] using the signals delivered by the University of Liverpool scanning system [4, 62] showing average location errors of about 4.5 mm.
Motivated by the encouraging results found using calculated signals, the Jacobian method was applied to the source data taken with AGATA at GANIL [63]. Based on the work described above, GEANT4 simulations [35] were used to create simulated data sets to provide the expected 3D distribution of \(\gamma \)-ray interactions. To allow effective correlations between the simulated distributions of interaction points and ordering variables two different coordinate systems were used and combined with five different ordering variables. For the front slice segments a spherical coordinate system was used, with its origin at a depth of 30 mm into the detectors. For the other five slices of segments, a cylindrical coordinate system was used. For the r-coordinates the same ordering variable was used independently of the coordinate system. The \(\phi \) ordering variable selected was the asymmetry of the peak-to-peak amplitudes of the signals in the right and left neighbour segments. To have efficient estimators for the z-component (or approximately theta in the first slice) three different ordering variables were used. For the four middle slices, the normalised peak-to-peak amplitude asymmetry of the transient signals of the upper and lower neighbours was used. The last ring used a normalised peak-to-peak amplitude of the neighbour. A normalised averaged derivative of the net-charge signal is used as an ordering variable for the first ring.
Experimental in situ bases were produced for six AGATA detectors. Examples for three different detectors are given in Fig. 15. They were compared with the standard ADL bases by evaluating the achieved position resolution by the performance of AGATA after \(\gamma \)-ray tracking. It was shown that the efficiency of AGATA remained the same using the experimental bases. Somewhat disappointing, on the basis of comparing Doppler correction capabilities, it was shown that the experimental bases gave a slightly worse position resolution than the standard ADL bases. Possible reasons for this were stated as the difficulties in determining the true shape of the segments and the difficulties in correctly time aligning the pulse shapes when averaging them to produce the data bases. For details see [63].
Pulse shapes coming from two same shaped detectors of type A and one type B detector for the same position (\(x=31\) mm, \(y=5.5\) mm, \(z=63\) mm) in the detectors. The core signal is shown in more detail in inset (a), the net-charge signal in inset (b), and the transient signals from the nearest neighbours are shown in detail in insets (c)–(e). Figure taken from [63]
4 Pulse shape analysis
Pulse shape analysis is an essential step in the recovery of the true interaction position of incident \(\gamma \) rays as they deposit energy in the AGATA spectrometer. The technique facilitates the recovery of the individual energy deposition points following the interaction of a \(\gamma \) ray with matter by photoelectric absorption, Compton scattering and/or Pair Production. The output of the PSA provides the input to the subsequent gamma tracking algorithms that probabilisticaly combine the information returned by the PSA to reconstruct the individual gamma tracks. The aim of PSA is to determine the number of interactions in a segment or crystal and to reconstruct their individual positions, times and the deposited energies by analysing the experimental preamplifier signals, continuously sampled at 100 MHz from the front energy digital electronics (digitisers). The real-time processing requirements of the AGATA Data Acquisition system and the requirements of the tracking algorithms impose stringent performance constraints on the PSA algorithm. To perform a Doppler correction and to achieve the best possible peak-to-total ratio (P/T) the interaction locations have to be resolved with a precision of \(\sim \) 5 mm (FWHM). For PSA to be used in experiments with high beam intensities the reconstruction should take \(\sim \)1 ms per event and CPU. In the AGATA spectrometer PSA is performed at the pre crystal or local level, while gamma ray tracking is performed at the array or global level. The AGATA collaboration have investigated the performance of a number of different approaches to achieving the optimum PSA performance.
For information on the GRETINA project (Gamma-Ray Energy In-Beam Nuclear Array), which is the first phase of the GRETA project, and associated information on the performance of the implemented PSA algorithms, see [64].
4.1 The adaptive grid search
The Adaptive Grid Search (AGS) algorithm is based on a comparison between measured signals (real and transient signals of the segments) and calculated signals from a fine grid of points in the crystal (typically 2 mm spacing). It works by searching one or two interaction points per segment. In the standard implementation, which was utilised due to computational limitations, the algorithm searches one interaction point in a segment. This approach then considers the energetic barycentre if multiple hits occur. The final position is determined as the point on the grid which is the closest match to the experimental signal. The interaction positions are determined by the optimisation of a Figure of Merit (FoM) as shown in Eq. (3) that compares experimental signals (\(A_m\)) against the basis (\(A_s\)). The approach allows for the energy and time calibration to be applied and the \(T_0\) value is extracted using a digital Constant Fraction Discriminator or leading edge fit of the first traces. Any cross-talk correction is also applied at this stage. Due to the significant trace length and number of electrodes used in AGATA, individual signal comparisons are computationally intensive and an exhaustive search does not meet the execution rates necessary for online PSA. Instead a coarse grid approximation is applied using the AGS algorithm [65] that determines the coarse optimum of the basis followed by a refined search in the immediate euclidean vicinity of the optimum.
The AGS algorithm produced a position resolution of \(\sim \)5 mm (FWHM) at 1382 keV (\(3/2^- \rightarrow 7/2^-\) line in \(^{49}\)Ti [23] with a performance of \(\sim \)2000 events/s/core. The reader should note that the achievable position resolution is impacted by the signal to noise ratio of the signal waveforms and the location of the interaction position of the \(\gamma \) ray inside the AGATA detector. Low energy \(\gamma \) rays (<300 keV) will interact close to the front face of the detector, a region of the crystal where the electric field lines are non uniform. This coupled with the small signal size, both for the primary induced signal and the transient signals, presents a worst case scenario. Here the position resolution could potentially be limited to the half the size of the interaction segment. For a detailed discussion on the impact of the energy on the position resolution see [66].
In [26] some improvements to the FoM were proposed to minimise experimental deviation from the \(^{22}\)Na coincidence method, the FoM was modified by implementing a weighting factor for the transient signals of the nearest neighbours of the hit segment. A weighting factor (\(w_j\)) of 2.75 was obtained by experimental optimisation. An energy dependent weighting factor which increases for higher energies is being considered for future implementation. For low-energy depositions the signal to noise ratio is small, especially for the transient signals. In these cases, a larger weighting of these signals might not be favourable. The \(^{22}\)Na-coincidence method is restricted to energy depositions of 511 keV. Future investigations will also consider the influence of multiple interactions in different segments of the detector on the optimal weighting coefficient.
4.2 The particle swarm algorithm
A version of the particle swarm algorithm has been evaluated as a potential pulse shape analysis approach for AGATA [28]. In order to enable the evaluation a simulated basis was produced using JASS on a 3D regular rectangular grid with 1 mm spacing. For each point on the grid a full set of 37 pulse shapes of 1 ns step size and a trace length of 600 ns was generated and stored in the basis. The fully informed particle swarm (FIPS) approach was used, this is a special sub form of the particle swarm optimisation (PSO) algorithm. The PSO comprised of a very simple concept to optimize non-linear functions that was easily implemented and computationally inexpensive. The work concluded that single gamma ray interactions were well resolved in less than 1 ms/event. The case of multiple hit segments was shown to be much more demanding. FIPS was capable of resolving the higher energetic interaction very well. Conversely, the resolution of the lower energetic interaction deteriorated to levels outside AGATA requirements. The same effect was observed for the case of two interactions in a single segment [28].
4.3 The matrix method
The process of determining the positions of a set of hits from the resulting pulse shapes, using a signal basis, is by essence an inverse problem expressed in the matrix formalism. Using the usual tools of matrix theory, the problem can be characterised and solved in an optimum way.
The property of signal additivity can be expressed in the following way:
where s(t) is the detected signals, \(e(\textbf{x})\) is the energy deposited at \(\textbf{x}\) due to an interaction of the \(\gamma \) ray with the crystal and \(b(\textbf{x},t)\) is the signal corresponding to a unit energy. Both s and b are the concatenations of all the segment signals. The function b is tabulated as a signal basis matrix \(\textbf{B}\) corresponding to discrete points on a given grid. The jth column of the matrix is the signal \(b(\textbf{x}_j,t)\) discretised into time bins. In the same way, the energy function is discretised into a vector \(\textbf{e}\) which jth component corresponds to the energy deposit in the voxel of the jth grid point. Finally, s(t) is also discretised as a vector \(\textbf{s}\) and the previous equation is rewritten as [67, 68]:
In principle, the least square solution is given by \(\textbf{e}=({^{\textrm{t}}\textbf{B}}\,\textbf{B})^{-1}\,{^{\textrm{t}}\textbf{B}}\,\textbf{s}\). However, for many reasons (discretisation of the problem, electric signal noise and time jitter, approximate basis signals, conditioning of the matrix, etc.), the resulting solution would be wrong and non-physical (too many non-zero energy components, even negative components). Non-negative solutions with a maximum of null components can be computed using dedicated algorithms such as Backtracking [69], NNLS [70] and NNLC [71]. However, any inversion algorithm would be too slow to solve on line such a large system. Moreover, the found solution would be greatly affected by the properties of the \(\textbf{B}\) matrix.
The accuracy of the hit found locations depends on the fineness of the grid. However, a very fine grid does not entail good precision for two reasons. First, the matrix system would become even larger (up to become under-determined), second, because the response function of the detector is not purely bijective. In other words, the signal resulting from the sum of two hits may not be discriminated from the signal resulting from a single hit with the same total deposited energy at the weighted centre of both hits. This is especially true when the energy deposits are small or very unbalanced or in the central part of the segments. Another connected problem is that the matrix is very badly conditioned (the condition number, which measures the amplification of the uncertainties to the solution, for a full detector and a grid step of 2 mm is of the order of \(10^{50}\)). This means that small uncertainties on the basis matrix and on the detected signal, entails (very) large uncertainties on the \(\textbf{e}\) solution, which is on the hit locations. All these problems can be optimally addressed using Singular Value Decomposition (SVD) as shown in the following (the method is described in detail in [68]).
The basis matrix can be decomposed into the product of three matrices:
such that \(\textbf{W}\) is a diagonal positive matrix with diagonal components (singular values) arranged in a decreasing order, and \(\textbf{U}\) and \(\textbf{V}\) are column-orthonormal matrices (\({^{\textrm{t}}\textbf{U}}\,\textbf{U}= {^{\textrm{t}}\textbf{V}}\,\textbf{V}= \textbf{I}\)). The condition number of \(\textbf{B}\) is given as the ratio of the smallest non-zero singular value to the largest. Hence, the optimum way of reducing the condition number while minimizing the resulting bias on the solution consists in setting to zero all the smallest singular values. The number of singular values to keep depends on their distribution. In the case of matrix \(\textbf{B}\), the first 36 singular values are much larger than the following ones, indicating that the determination of the segments where the hits took place is reliable, which does not come as a surprise. The next singular values are organized, on a log scale, in a long, slowing decreasing, plateau followed by an exponential fall. This singular value spectrum shape indicates that our inverse problem belongs to the ill posed rather than rank deficient type. Thus, the cut-off corresponding to the singular values set to zero has to be determined empirically, somewhere on the plateau, with experimental or simulated signals. One notes r the number of remaining singular values (rank). The bottom and right parts of the \(\textbf{W}\) matrix are now composed of zeros only, which means that the right part of the \(\textbf{U}\) and lower part of the \({^{\textrm{t}}\textbf{V}}\) matrices play no role. Therefore, the three matrices can be reduced in size by keeping only the r first columns of \(\textbf{U}\), rows of \(\textbf{V}\) and row and columns of \(\textbf{W}\). The resulting matrices are noted \(\textbf{U}_r\), \({^{\textrm{t}}\textbf{V}_r}\) and \(\textbf{W}_r\) and \(\textbf{B}_r= \textbf{U}_r\,\textbf{W}_r\,{^{\textrm{t}}\textbf{V}_r}\). It can be noted that, at this point, the size of the basis matrix is not reduced but its condition number \(w_r/w_1\) is (much) improved. Nevertheless, Eq. (5) can be rewritten as:
The SVD of \(\textbf{B}\) is performed offline, before the experiment. Matrices \(\textbf{R}_r\) (used to compress the signals to r components only [72]) and \({^{\textrm{t}}\textbf{V}_r}\) are tabulated for on-line use. The new system to be solved for each experimental event is Eq. 7, which is smaller and better conditioned than the initial one Eq. 5. It can be even more reduced in size owing to the fact that, in most events, not all the segments are hit. As a result, only the components of vector \(\textbf{e}\) and the columns of matrix \({^{\textrm{t}}\textbf{V}_r}\) belonging to the hit segments have to be included in Eq. 7. The inversion algorithm shown to give the best solution, in terms of precision on the hit locations, is NNLC (non-negative least \(\chi ^2\)) [71] because it can take into account the signal fluctuations (noise and time jitter). It is to be noted that Eq. 7 can also be used to speed-up the grid search algorithm, \({^{\textrm{t}}\textbf{V}_r}\) playing the role of a basis of optimally compressed signals \({\textbf{s}_r}_j\).
After solving Eq. 7, the number, locations and energy deposits of the hits have to be deduced from vector \(\textbf{e}\). One hit corresponds to a set of non-zero components at close grid points. The energy of each hit is the sum of its set of components \(E=\sum _j e_j\) and its location is calculated as the weighted centre \(\textbf{g}= \sum _j e_j\,\textbf{x}_j\,/E\). Therefore, the precision of the location is not limited by the grid step. The discrimination of the hits can be done automatically using a classification algorithm such as k-means clustering or Ward’s method.
Although the method is rigorous and gave satisfactory results using simulated signals [68], its implementation for on-line PSA appeared to be too cumbersome and affected by the diversity of computing times of the inversion algorithm.
4.4 The recursive subtraction PSA algorithm
It has been illustrated that the PSA is a computationally expensive process and therefore the collaboration put effort into finding ways to optimise the methodology. The “folding” algorithm was proposed in [73] as part of this process. This was based on the fact that information about the radial spatial coordinate of the \(\gamma \) hits inside one specific segment, and also about the exact number of them, can be extracted quickly from the net-charge segment signal just by performing a second derivative operation. In fact, the second derivative enhances the amplitude of the net-charge signal in correspondence to the time instants where it is characterised by sudden changes in slope (i.e exactly when the charge carriers are collected, reaching the detector electrode). Then, knowing the velocity of the charge carriers, it is possible to determine the radial position of the hits and also count the number of them. This information could then be provided to the next part of the PSA to reduce the final computation overhead. Unfortunately, the simple concept of the “folding” algorithm was shown to have some problems in its application [74], mainly due to limitations connected to the presence of electronic noise.
A generalisation of the folding algorithm, aimed at bypassing these limitations was then proposed (the Recursive subtraction, RS algorithm [75, 76]). The RS algorithm applies, as a first step, an electronic filter to maximize the signal to noise ratio, particularly in the region of the signal where the more relevant information is concentrated. This is obtained, in practice, performing a single derivative and a subsequent low-pass filter. The shape of the signal resulting from this filtering operation corresponds to the smoothed current pulse (see the red-line signal in Fig. for an example). Next a shape comparison of the signal, in a selected and limited region, with all the basis signals is performed. The basis signals represent the full-volume 3D position response of an AGATA crystal. A primary assumption of RS algorithm is that the current signal shape, in this selected and limited region, depends mainly on the most energetic interaction (this is fundamental to speed up the process). See Fig. for a graphical representation of this shape comparison process. Finally, the signal of the basis that is found to have the best agreement is subtracted from the initial experimental signal and the procedure is iterated until the remaining signal amplitude is below a certain threshold. The red-line signal in Fig. is an example of a double-peak current pulse, originated by an event with two, radially well separated, \(\gamma \) hits in the same detector segment. If the two hits are spatially separated but have very similar radial coordinate (i.e., less than 5 mm distance) it is more difficult to disentangle the two overlapped hit signals. However, the shape of the current pulse also depends on the other two spatial coordinates (not only the radial one).
The results reported in [75, 76] demonstrate that the assumptions at the basis of the algorithm were sufficiently verified. In fact, the RS algorithm was initially tested with simulated signals, obtained including real electric noise and the effect of the preamplifier response [75, 76]. Then, it was applied to experimental signals [76] acquired in the in-beam test of the 25-fold segmented coaxial HPGe prototype detector MARS at LNL-INFN [77,78,79] and also signals acquired in the first in-beam test of an AGATA symmetric triple cluster at IKP Cologne [80, 81]. It showed good determination of the radial coordinate and hits number distribution [76]. The performance of the RS algorithm for the extraction of the full 3D \(\gamma \) localisation was also studied [82].
5 Future perspectives
Largely led by advances in the fields of Computer Science and Machine Learning, several methods have been trialled by the AGATA collaboration for improving the prediction accuracy and execution rate of the PSA. These methods ranged from genetic algorithms, particle swarm optimisers, wavelet deconvolution and neural-network based approaches [67, 83, 84]. Whilst initial development of these methods produced promising results during testing, the challenges of implementing multi-interaction PSA within the AGATA pipeline restricted their deployment, as a result a combination of the AGS method using Recursive Subtraction was chosen for online PSA in AGATA [85].
The requirement to process data through the AGATA DAQ system at higher count rates while simultaneously enabling the PSA with multiple hit processing per segment requires the implementation of efficiency savings in the current approaches or more novel approaches to signal processing. The existing AGS algorithm has been optimised to make its execution more efficient, potentially enabling it to process data at up to 10 kHz per core. However such performance would be limited to single interactions per segment or would require a reduction in the processing rate. Methods to perform the search of the basis more efficiently by using machine learning and artificial intelligence approaches have been investigated.
By considering the signals from AGATA as a generalisation of the notion of a triangle or tetrahedron to arbitrary dimensions (discrete geometrical simplices), the analysis of the underlying response of the detectors can be quantified. Feature extraction using Principal Component Analysis has proven useful in forming lower-dimensional representations of the signals produced by AGATA. The AGATA bases are used to train a dimensionality reduction model that can map experimental signals from the full space into feature extracted embeddings existing in a lower-dimensional space. These embeddings are then indexed into a hierarchical structure (graph) that exploits the distance geometry inherent to the dimensionally reduced space for significant improvements to execution rate. A k-Nearest Neighbour (k) search of these structures has proven to be incredibly efficient with approximate-kNN methods such as FAISS [86] capable of operating at 400 kHz on dimensionally-reduced representations with minimal cost to prediction accuracy [87].
Whilst a significant fraction of the events within AGATA are localised to single-site interactions the presence of multiple-interaction events has prevented conventional PSA methods from forming reliable predictions at execution rates acceptable for online processing. Transient signals similar to the one featured in Fig. () show distinct features that can be identified, however the reliance on identification of the number of interactions imposes a bias into the PSA that favours well-separable signals. Instead, a formalism as shown in Fig. 17 was developed to describe the possible combinations of signals present in AGATA and directly infer the best linear combination that fits the data regardless of the underlying pulse profile. By describing multiple interaction signals as convex simplices the optimum combination of signals and their respective contributing energy depositions can be inferred directly with minimal prior input. This technique allows for PSA to be performed on signals within the same segment that have significant covariance and cannot be separated conventionally.
Smoothed current signal calculated for a \(\gamma \) event with two hits in a single detector segment (continuous red line). With the black dashed line, the signal component relative only to the first hit (which released the 60% of the energy) plus a constant value is plotted. The plot shows that in a region of about 100 ns around the first peak the shape of the signal depends mainly on the most energetic hit signal component
This formalism has been demonstrated on up to 4 interactions within a single segment, however the computational complexity that arises from the exponential number of linear combinations is observed to quickly exhaust CPU-based hardware. Limitations on the amount of positional information contained within the signal impose a limit on the achievable resolution. Developments into GPU-acceleration have allowed for the online processing of 2 interaction events, however, 3 interaction signals are not possible to solve exhaustively online and incur significant memory costs. Graph-based approaches have been investigated with reasonable success.
Conceptual diagram for a 2-interaction signal in response space. The relative areas of the green and red simplices in relation to the (\(p_1, p_2, q\))-simplex provide the barycentric weights. Due to orthogonality in the system these are equivalent to the parameters \(\alpha \) & \(\beta \) respectively. Reproduced from [87]
Improvements are required in the both the PSA algorithms and the underlying data they use in order to enable the reliable extraction of the true interaction positions of the \(\gamma \) rays from experimental data [20]. This is particularly important for multiple interaction events in a single segment where small uncertainties can have a particularly big impact on the successful identification of the interaction positions.
The PSA relies on there being a good understanding of the operational parameters of each detector in the array. Factors such as the crystal temperature, the unique charge trapping profile in each crystal and the electron–hole mobility values need further work to be properly understood. Closed end coaxial detectors such at the AGATA detector will also suffer from divergence of the charge cloud at the holes approach the outer segmented contact, this can result in a miss-identification of a single interaction event as a multiple site event (for example). Again improvements to the models used to describe the detector response function may be required.
Improvements to the signal basis continue to be a focus of the collaboration. The calculated basis requires improved knowledge of the key input parameters required for each detector, factors such as the impurity gradients and knowledge of the passivated surface at the back of the crystal require more comprehensive information from the detector manufacturer to be made available or more detailed characterisation measurements to be made by the collaboration. There are dynamic effects to consider as well, such as the effective size of the core bore hole with the potential migration of the diffused lithium contact over time potentially impacting the PSA performance.
The multiple independent sources of uncertainty discussed above illustrate how complex the AGATA detector is to fully understand. This has led the AGATA collaboration to continue to investigate the possibility of producing a reliable experimental basis directly. A novel technique enabling the AGATA spectrometer to perform a self calibration of the response of each detector in-situ has recently been proposed [88]. It is currently being evaluated for use with the AGATA spectrometer. This would have the advantage that any dynamic change in this complex array of input parameters would be calibrated out, in the same way as a regular energy calibration.
There are also opportunities to improve the connectivity between the PSA and \(\gamma \) tracking algorithms. The PSA is performed at the per crystal level while the \(\gamma \) tracking is at the global array level, this means the information available to enable probabilistic decision making is different in each case. The PSA must proceed the \(\gamma \) tracking in the processing order, but this provides the opportunity for the PSA algorithm to pass the probability or confidence in the hit position identification onto the \(\gamma \) tracking algorithm. This would enable the \(\gamma \) tracking algorithm to include these probabilities in the decision making process when ordering scattered events, offering the potential for improved performance.
From a computational perspective, the development of more efficient PSA algorithms is critical in ensuring that AGATA can be fully utilised. Development into GPU-accelerated PSA algorithms will be necessary to interpret complex multi-interaction signals for online processing. The advent of Machine Learning assisted approaches such as in [89] will likely prove useful for building a set of in-situ bases that will handle nonlinear corrections for neutron damage and electrical degradation. This will ensure the maximum number of detectors remain operational. The potential improvements outlined above will enable the performance expected for the AGATA spectrometer to be realised.
Finally, there has been innovation in the underlying HPGe detector technology itself. The requirement for a high efficiency detector with the best possible energy resolution led to the development of point contact HPGe detectors in an inverted coaxial geometry [90, 91]. The small contact enables a much improved energy resolution when compared with an AGATA detector and an excellent signal to noise performance. Further developments of the inverted coaxial Ge detector are in progress with the production of highly segmented crystals. These developments include n-type [92] and p-type [44, 93, 94] prototype detectors. The demonstrated performance of these detectors indicates not only an improvement the energy resolution, but perhaps more importantly an improvement in the achievable position resolution. In future these designs could be exploited in the next generation of \(\gamma \) spectrometers.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: There is no data deposited because this is a review article further details can be found in the references cited.]
References
S. Akkoyun, A. Algora, B. Alikhani, F. Ameil, G. de Angelis, L. Arnold, A. Astier, A. Ataç, Y. Aubert, C. Aufranc et al., AGATA—Advanced GAmma tracking array. Nucl. Instrum. Methods A 668, 26 (2012). https://doi.org/10.1016/j.nima.2011.11.081
I.Y. Lee, M.A. Deleplanque, K. Vetter, Rep. Progress Phys. 66(7), 1095 (2003). https://doi.org/10.1088/0034-4885/66/7/201
I.-Y. Lee, J. Simpson, Nucl. Phys. News 20(4), 23 (2010). https://doi.org/10.1080/10619127.2010.506124
L. Nelson, M. Dimmock, A. Boston, H. Boston, J. Cresswell, P. Nolan, I. Lazarus, J. Simpson, P. Medina, C. Santos et al., Characterisation of an AGATA symmetric prototype detector. Nucl. Instrum. Methods Phys. Res. 573, 153 (2007)
A. Boston, M. Dimmock, C. Unsworth, H. Boston, R. Cooper, A. Grint, L. Harkness, I. Lazarus, M. Jones, P. Nolan et al., Performance of an AGATA asymmetric detector. Nucl. Instrum. Meth. A 604(1–2), 48 (2009). https://doi.org/10.1016/j.nima.2009.01.228.www.sciencedirect.com/science/article/pii/S0168900209001132
T. Ha, A. Korichi, F.L. Blanc, P. Désesquelles, N. Dosme, X. Grave, N. Karkour, S. Leboutelier, E. Legay, D. Linget et al., New setup for the characterisation of the AGATA detectors. Nucl. Instrum. Methods A 697, 123 (2013). https://doi.org/10.1016/j.nima.2012.08.111
C. Domingo-Pardo, N. Goel, T. Engert, J. Gerl, I. Kojouharov, H. Schaffner, F. Didierjean, G. Duchêne, M. Sigward, A novel imaging method for the pulse-shape characterization of position sensitive semiconductor radiation detectors. Nucl. Instrum. Meth. A 643(1), 79 (2011). https://doi.org/10.1016/j.nima.2011.04.021.www.sciencedirect.com/science/article/pii/S0168900211007595
N. Goel, C. Domingo-Pardo, T. Engert, J. Gerl, I. Kojouharov, H. Schaffner, Spatial calibration via imaging techniques of a novel scanning system for the pulse shape characterisation of position sensitive HPGe detectors. Nucl. Instrum. Meth. A 652(1), 591 (2011). https://doi.org/10.1016/j.nima.2011.01.146.www.sciencedirect.com/science/article/pii/S0168900211002488
G. F. Knoll, Radiation Detection and Measurement, 3rd edn. (Wiley, 2000)
B.Bruyneel, P. Reiter, and G. Pascovici, Characterization of large volume hpge detectors. part i: Electron and hole mobility parameterisation, Nucl. Instrum. Methods Phys. Res. 569, 764 (2006)
L. Mihailescu, W. Gast, R. Lieder, H. Brands, H. Jäger, The influence of anisotropic electron drift velocity on the signal shapes of closed-end HPGe detectors. Nucl. Instrum. Meth. A 447(3), 350 (2000). https://doi.org/10.1016/S0168-9002(99)01286-3.www.sciencedirect.com/science/article/pii/S0168900299012863
B.Bruyneel, P. Reiter, and G. Pascovici, Characterization of large volume hpge detectors. part ii: Experimental results., Nucl. Instrum. Methods Phys. Res. 569, 774 (2006)
P. Medina et al. http://www.iphc.cnrs.fr/-MGS-.html
I. Mateu, P. Medina, J. Roques, E. Jourdain, Simulation of the charge collection and signal response of a HPGe double sided strip detector using MGS. Nucl. Instrum. Meth. A 735, 574 (2014). https://doi.org/10.1016/j.nima.2013.09.069.www.sciencedirect.com/science/article/pii/S0168900213013521
M. Schlarb, R. Gernhäuser, S. Klupp, R. Krücken, Pulse shape analysis for \(\gamma \)-ray tracking (part i): Pulse shape simulation with JASS. Eur. Phys. J. A 47(10), 132 (2011). https://doi.org/10.1140/epja/i2011-11132-2
B. Bruyneel, B. Birkenbach, and P. Reiter, Pulse shape analysis and position determination in segmented hpge detectors: the agata detector library., Euro. Phys. J. A 52, 70 (2016). https://doi.org/10.1140/epja/i2016-16070-9
P. Medina, C. Santos, and D. Villaume, in Proceedings of the 21st IEEE instrumentation and measurement technology conference, vol. 21 (2004), vol. 21, pp. 1828–1832
T. M. Inc. Matlab version: 9.13.0 (r2022b) (2022). https://www.mathworks.com
M. Dimmock, Characterisation of agata symmetric prototype detectors. Ph.D. thesis, University of Liverpool (2008). https://livrepository.liverpool.ac.uk/3065959
A. Korichi and T. Lauritsen, Tracking \( \gamma \) rays in highly segmented HPGe detectors: a review of AGATA and GRETINA, The European Physical Journal A 55(7) (2019). https://doi.org/10.1140/epja/i2019-12787-1
B. Bruyneel, P. Reiter, A. Wiens, J. Eberth, H. Hess, G. Pascovici, N. Warr, D. Weisshaar, Crosstalk properties of 36-fold segmented symmetric hexagonal HPGe detectors. Nucl. Instrum. Methods A 599(2–3), 196 (2009). https://doi.org/10.1016/j.nima.2008.11.011
B. Bruyneel, P. Reiter, A. Wiens, J. Eberth, H. Hess, G. Pascovici, N. Warr, S. Aydin, D. Bazzacco, F. Recchia, Crosstalk corrections for improved energy resolution with highly segmented HPGe-detectors. Nucl. Instrum. Methods A 608(1), 99 (2009). https://doi.org/10.1016/j.nima.2009.06.037
F. Recchia, D. Bazzacco, E. Farnea, A. Gadea, R. Venturelli, T. Beck, P. Bednarczyk, A. Buerger, A. Dewald, M. Dimmock et al., Position resolution of the prototype AGATA triple-cluster detector from an in-beam experiment. Nucl. Instrum. Methods A 604(3), 555 (2009). https://doi.org/10.1016/j.nima.2009.02.042
N. Lalovic̀, C. Louchart, C. Michelagnoli, R. Perez-Vidal, D. Ralet, J. Gerl, and D. Rudolph, Performance of the AGATA \(\gamma \)-ray spectrometer in the PreSPEC set-up at GSI, Nucl. Instrum. Methods A 806, 258 (2016). https://doi.org/10.1016/j.nima.2015.10.032
A. Korichi, T. Lauritsen, A. Wilson, J. Dudouet, E. Clément, N. Lalović, R. Perez-Vidal, S. Pietri, D. Ralet, O. Stezowski, Performance of a gamma-ray tracking array: characterizing the agata array using a \(^{60}\)co source. Nucl. Instrum. Methods Phys. Res. A 872, 80 (2017). https://doi.org/10.1016/j.nima.2017.08.020
L. Lewandowski, P. Reiter, B. Birkenbach, B. Bruyneel, E. Clement, J. Eberth, H. Hess, C. Michelagnoli, H. Li, R. Perez-Vidal, Pulse-shape analysis and position resolution in highly segmented hpge agata detectors. Euro. Phys. J. A 55(5), 1 (2019)
J. Dryzek, in Proceedings of the 35th Polish Seminar on Positron Annihilation (2004)
M. Schlarb, R. Gernhäuser, S. Klupp, R. Krücken, Pulse shape analysis for \(\gamma \)-ray tracking (part ii): Fully informed particle swarm algorithm applied to agata. Eur. Phys. J. A 47(10), 131 (2011). https://doi.org/10.1140/epja/i2011-11131-3
R.K.M. Schlarb, R. Gernhäuser, Simulation and real-time analysis of pulse shapes from hpge detectors. GSI Sci. Rep. 2008, 232 (2008)
S. Brenner and L. Scott, The Mathematical Theory of Finite Element Methods (Springer, 1994)
J. Ljungvall, Pulse-shape calculations and applications using the agatagefem software package. Euro. Phys. J. A 57, 198 (2011). https://doi.org/10.1140/epja/s10050-021-00512-w
Gnu general public license, version 3. http://www.gnu.org/licenses/gpl.html (2007). Last retrieved 2020-01-01
Message Passing Interface Forum. MPI: A message-passing interface standard version 4.0 (2021). https://www.mpi-forum.org/docs/mpi-4.0/mpi40-report.pdf
R. Brun and F. Rademakers, Root - an object oriented data analysis framework, Nucl. Inst. & Meth. in Phys. Res. A 389, 81 (1997)
E. Farnea, F. Recchia, D. Bazzacco, T. Kröll, Z. Podolyák, B. Quintana, A. Gadea, Conceptual design and monte carlo simulations of the AGATA array. Nucl. Instruments Methods Phys. Res. Sect. A 621, 331 (2010). https://doi.org/10.1016/j.nima.2010.04.043
T.W. Raudorf, R.H. Pehl, Effect of charge carrier trapping on germanium coaxial detector line shapes. Nucl. Instruments Methods Phys. Res. Sect. A 255(3), 538 (1987)
M. Eschenauer, R. Wirowski, D. Marcus, P. Von Brentano, Resolution enhancement of gamma-spectroscopy data from neutron-damaged coaxial n-type hpge-detectors. Nucl. Instruments Methods Phys. Res. Sect. A 340(2), 364 (1994)
W. Ho, S. Boggs, R. Lin, S. Slassi-Sennou, N. Madden, R. Pehl, E. Hull, Pulse-shape discrimination techniques for correcting the effects of radiation damage in germanium coaxial detectors. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 412(2–3), 507 (1998)
M. Descovich, I. Lee, P. Luke, R. Clark, M. Cromaz, M. Deleplanque, R. Diamond, P. Fallon, A. Macchiavelli, E. Rodriguez-Vieitez, Effects of neutron damage on the performance of large volume segmented germanium detectors. Nucl. Instruments Methods Phys. Res. Sect. A 545(1–2), 199 (2005)
B. Bruyneel, B. Birkenbach, J. Eberth, H. Hess, G. Pascovici, P. Reiter, A. Wiens, D. Bazzacco, E. Farnea, C. Michelagnoli, Correction for hole trapping in agata detectors using pulse shape analysis. Euro. Phys. J. A 49(5), 1 (2013)
S. Colosimo, S. Moon, A. Boston, H. Boston, J. Cresswell, L. Harkness-Brennan, D. Judson, I. Lazarus, P. Nolan, J. Simpson et al., Characterisation of two agata asymmetric high purity germanium capsules. Nucl. Instrum. Methods Phys. Res. 773, 124 (2015)
M. Dimmock, A. Boston, H. Boston, C. Cresswell, L. Nelson, P. Nolan, C. Unsworth, I. Lazarus, J. Simpson, Characterisation results from an agata prototype detector. IEEE Trans. Nuc. Sci. 56, 1593 (2009)
C. Unsworth, A. Boston, H. Boston, L. Harkness-Brennan, D. Judson, P. Nolan, O. Thomas, J. Wright, A. Adekola, J. Colaresi, et al., Characterisation of a small electrode hpge detector, Nucl. Instrum. Methods Phys. Res 927 (2019)
F. Pearce, Characterisation of the first \(p\)-type segmented inverted-coaxial germanium detector. Ph.D. thesis, University of Liverpool (2020). https://livrepository.liverpool.ac.uk/3124117/
C. Unsworth, Characterisation of an asymmetric agata detector. Ph.D. thesis, University of Liverpool (2011). https://livrepository.liverpool.ac.uk/3062842/
J. M. et al, Ieee transactions on nuclear science, NS-55 (2007)
P. Pulic, Master’s thesis, Politecnico di Milano (2004)
T. Kröll, D. Bazzacco, Simulation and analysis of pulse shapes from highly segmented hpge detectors for the \(\gamma \)-ray tracking array mars. Nucl. Instrum. Methods Phys. Res. 463, 227 (2001)
A. Boston, H. Boston, J. Cresswell, M. Dimmock, L. Nelson, P. Nolan, S. Rigby, I. Lazarus, J. Simpson, P. Medina et al., Gamma-ray tracking: Characterisation of the AGATA symmetric prototype detectors. Nucl. Instrum. Meth. B 261(1–2), 1098 (2007). https://doi.org/10.1016/j.nimb.2007.04.305.www.sciencedirect.com/science/article/pii/S0168583X07010270
F. Crespi, F. Camera, B. Million, M. Sassi, O. Wieland, A. Bracco, A novel technique for the characterization of a hpge detector response based on shape pulse comparison. Nucl. Instr. Meth. A 593, 440 (2008). https://doi.org/10.1016/j.nima.2008.05.057
M. Ginsz, Characterization of high-purity, multi-segmented germanium detectors. Ph.D. thesis, University of Strasbourg (2015). http://www.theses.fr/2015STRAE047
B. D. Canditiis, 3d characterization of multi-segmented hpge detectors. simulation and validation of the pscs technique and its application for different energies with a 152eu source. Ph.D. thesis, University of Strasbourg (2020). http://www.theses.fr/2020STRAE008
G.D.B. De Canditiis, Simulations using the pulse shape comparison scanning technique on an agata segmented hpge gamma-ray detector. Eur. Phys. J. A 56, 276 (2020)
. Kojouharov, in IEEE Nuclear Science Symposium Conference Record (2007)
A. Sharma, R. Palit, I. Kojouharov, J. Gerl, M. Gorska-Ott, H. Schaffner, T. Habermann, S. Saha, B. Das, P. Dey, et al., in EPJ Web of Conferences 253 (2021)
A.H. Prieto, B. Quintana, Characterization of a high spatial resolution \(\gamma \) camera for scanning hpge segmented detectors. IEEE TNS 60, 4719 (2013)
P. Suetens, Fundamentals of Medical Imaging (Cambridge University Press, 2009)
A.H. Prieto, B. Quintana, Study of accuracy in the position determination with salsa, a \(\gamma \)-scanning system for the characterization of segmented hpge detectors. Nucl. Instr. Meth. A 823, 98 (2016)
S. Martín, B. Quintana, D. Barrientos, Wilcoxon signed-rank-based technique for the pulse-shape analysis of hpge detectors. Nucl. Instr. Meth. A 823, 32 (2016)
P. Désesquelles, Determination of the hit locations in segmented HPGe detectors without the use of simulations or scanning systems. Nucl. Instrum. Methods A 654(1), 324 (2011). https://doi.org/10.1016/j.nima.2011.06.099
P. Désesquelles, A. Boston, H. Boston, J. Cresswell, M. Dimmoc, I. Lazarus, J. Ljungvall, L. Nelson, D.-T. Nga, P. Nolan et al., Direct determination of the hit locations from experimental hpge pulses. Nucl. Instruments Methods Phys.Res.A 729, 198 (2013)
A. Boston, H. Boston, J. Cresswell, M. Dimmock, L. Nelson, P. Nolan, S. Rigby, I. Lazarus, J. Simpson, P. Medina et al., Direct determination of the hit locations from experimental hpge pulses. Nucl. Instruments Methods Phys. Res. Sect. B 261, 198 (2007)
H. Li, J. Ljungvall, C. Michelagnoli, E. Clément, J. Dudouet, P. Désesquelles, A. Lopez-Martens, G. de France, Experimental determination of reference pulses for highly segmented hpge detectors and application to pulse shape analysis used in \(\gamma \)-ray tracking arrays. Euro. Phys. J. A 54, 198 (2018). https://doi.org/10.1140/epja/i2018-12636-9
S. Paschalis, I. Lee, A. Macchiavelli, C. Campbell, M. Cromaz, S. Gros, J. Pavan, J. Qian, R. Clark, H. Crawford et al., The performance of the gamma-ray energy tracking in-beam nuclear array gretina. Nucl. Instrum. Methods A 709, 44 (2013). https://doi.org/10.1016/j.nima.2013.01.009
R. Venturelli, D. Bazzacco, Adaptive grid search as pulse shape analysis algorithm for \(\gamma \)-tracking and results. LNL Ann. Rep. 2004, 220 (2005)
P.-A. Söderström, F. Recchia, J. Nyberg, A. Al-Adili, A. Ataç, S. Aydin, D. Bazzacco, P. Bednarczyk, B. Birkenbach, D. Bortolato et al., Interaction position resolution simulations and in-beam measurements of the AGATA HPGe detectors. Nucl. Instruments Methods Phys.Res.Sect.A 638(1), 96 (2011). https://doi.org/10.1016/j.nima.2011.02.089
A. Olariu, P. Desesquelles, C. Diarra, P. Medina, C. Parisel, Pulse shape analysis for the location of the \(gamma\)-interactions in agata. IEEE Trans. Nucl. Sci. 1028, 1028 (2006). https://doi.org/10.1109/TNS.2006.875130
P. Désesquelles, T. Ha, K. Hauschild, A. Korichi, F. L. Blanc, A. Lopez-Martens, A. Olariu, and C.M.Petrache, Matrix formalism and singular-value decomposition for the location of gamma interactions in segmented hpge detectors, Eur. Phys. J. A 40 (2009). https://doi.org/10.1140/epja/i2008-10749-4
P. Désesquelles, J. Bondorf, I. Mishustin, A. Botvina, Global protocol for comparison of simulated data with experimental data. Nucl. Phys. A 604, 183 (1996). https://doi.org/10.1016/0375-9474(96)00126-1
R. Hanson and C. Lawson, Solving Least Square Problems (SIAM, 1995)
P. Désesquelles, T. Ha, A. Korichi, F. L. Blanc, and C.M.Petrache, Nnlc: non-negative least chi-square minimization and application to hpge detectors, J. Phys. G 36 (2009). https://doi.org/10.1088/0954-3899/36/3/037001
P. Désesquelles, Ann. Phys. Fr. 20, 1 (1995)
E. Gatti, A. Geraci, G. Casati, S. Riboldi, G. Ripamonti, Spatial localization of multiple simultaneous hits in segmented hpge detectors: a new algorithm. Nucl. Instrum. Methods Phys. 458, 738 (2001)
F. Crespi, Radiazione gamma in rivelatori hpge segmentati. Ph.D. thesis, Universitá degli Studi di Milano (2004)
F. Crespi, F. Camera, O. Wieland, G. Benzoni, S. Brambilla, B. Million, D. Montanari, A pulse shape analysis algorithm for hpge detectors. Nucl. Instrum. Methods Phys. Res. 570(3), 459 (2007)
F. Crespi, F. Camera, A. Bracco, B. Million, O. Wieland, V. Vandone, F. Recchia, A. Gadea, T. Kröll, D. Mengoni et al., Application of the recursive subtraction pulse shape analysis algorithm to in-beam hpge signals. Nucl. Instrum. Methods Phys. Res. 604(3), 604 (2009)
T. Kröll, D. Bazzacco, R. Venturelli, M. Nespolo, B. Quintana Arnés, C. Ur, M. Bellato, R. Isocrate, C. Manea, R. Menegazzo, et al., In-beam experiment with the \(\gamma \)-ray tracking detector mars, Nucl. Instrum. Methods Phys. Res. 586(3), 421 (2008)
T. Kröll, D. Bazzacco, A genetic algorithm for the decomposition of multiple hit events in the \(\gamma \)-ray tracking detector mars. Nucl. Instrum. Methods Phys. Res. 565(2), 691 (2006)
M. Nespolo, Pulse shape analysis with germanium detectors: From mars to agata. Ph.D. thesis, Universitá degli Studi di Padova (2004)
F. Recchia, In-beam test of the agata prototype triple cluster acta, Phys. Pol. B 38 (2007)
F. Recchia, In-beam test and imaging capabilites of the AGATA prototype detector. Ph.D. thesis, Universita degli Studi di Padova (2008)
RS algorithm for 3D localization of\(\gamma \)-interactions in segmented HPGe detectors: Tests with calculated and experimental signal basis. https://doi.org/10.1109/NSSMIC.2010.5873893
T. Kröll, D. Bazzacco, A genetic algorithm for the decomposition of multiple hit events in the \(\gamma \)-ray tracking detector mars. Nucl. Instruments Methods Phys.Res.Sect.A 565(2), 691 (2006). https://doi.org/10.1016/j.nima.2006.06.036
M. Schlarb, Simulation and real-time analysis of pulse shapes from highly segmented germanium detectors. Ph.D. thesis, Technische Universität München (2008)
J. Simpson, J. Nyberg, and W. Korten. Agata technical design report (2008)
J. Johnson, M. Douze, and H. Jégou. Billion-scale similarity search with gpus (2017). https://doi.org/10.48550/ARXIV.1702.08734
F. Holloway, The development of novel pulse shape analysis algorithms for agata. Ph.D. thesis, University of Liverpool (2022). https://livrepository.liverpool.ac.uk/3150791/
S. Heil, S. Paschalis, and M. Petri, On the self-calibration capabilities of \( \gamma \) energy tracking arrays, Euro. Phys. J. A 54(7) (2018). https://doi.org/10.1140/epja/i2018-12609-0
S. Heil, S. Paschalis, M. Petri, On the self-calibration capabilities of \(\gamma \)-ray energy tracking arrays. Euro. Phys. J. A 54(10), 172 (2018). https://doi.org/10.1140/epja/i2018-12609-0
P. Luke, F. Goulding, N. Madden, R. Pehl, Low capacitance large volume shaped-field germanium detector. IEEE Trans. Nucl. Sci. 36(1), 926 (1989). https://doi.org/10.1109/23.34577
R. Cooper, D. Radford, P. Hausladen, K. Lagergren, A novel HPGe detector for gamma-ray tracking and imaging. Nucl. Instruments Methods Phys. Res. Sect. A 665, 25 (2011). https://doi.org/10.1016/j.nima.2011.10.008
M. Salathe, R. Cooper, H. Crawford, D. Radford, J. Allmond, C. Campbell, R. Clark, M. Cromaz, P. Fallon, P. Hausladen et al., Energy reconstruction of an n-type segmented inverted coaxial point-contact HPGe detector. Nucl. Instruments Methods Phys. Res. Sect. A 868, 19 (2017). https://doi.org/10.1016/j.nima.2017.06.036
J. Wright, L. Harkness-Brennan, A. Boston, D. Judson, M. Labiche, P. Nolan, R. Page, F. Pearce, D. Radford, J. Simpson, et al., 892, 84 (2018). https://doi.org/10.1016/j.nima.2018.02.106
F. Pearce, L. Harkness-Brennan, A. Alharbi, A. Boston, O. Griffiths, F. Holloway, D. Judson, M. Labiche, P. Nolan, R. Page et al., First experimental measurements with the segmented inverted-coaxial GerMAnium (SIGMA) detector. Nucl. Instruments Methods Phys. Res. Sect. A 1027, 166044 (2022). https://doi.org/10.1016/j.nima.2021.166044
Acknowledgements
This work is a result of the hard work and expertise of many people. We would like to thank all those involved, especially those in the AGATA collaboration. This work is funded by grants from the UK Science and Technology Facilities Council, including ST/F004052/1, ST/T000554/1 and ST/V001027/1. This research was supported by the German BMBF under Grants 06K-167, 06KY205I, 05P12PKFNE, 05P15PKFN9, 05P18PKFN9 and 05P21PKFN9. AGATA was supported by the European funding bodies and the EU Contract RII3-CT-2004-506065. This work has been supported by the OASIS project no. ANR-17-CE31-0026.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Nicolas Alamanos.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Boston, A.J., Crespi, F.C.L., Duchêne, G. et al. Agata characterisation and pulse shape analysis. Eur. Phys. J. A 59, 213 (2023). https://doi.org/10.1140/epja/s10050-023-01100-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epja/s10050-023-01100-w