Agata: in-beam spectroscopy with relativistic beams

Abstract

An analysis of the capabilities of AGATA for in-beam $\gamma$-ray spectroscopy at relativistic energies is presented. AGATA’s ability to determine the position of $\gamma$-ray interaction points in the Germanium crystal provides the crucial ingredient for attaining high $\gamma$-ray energy resolution when the emitting nucleus is traveling at more than half the speed of light. This is the typical velocity of exotic nuclei exiting the SuperFRS spectrometer at the future FAIR facility, where AGATA will be deployed as part of the high-resolution in-beam spectroscopy project, HISPEC. A discussion of different experimental techniques using AGATA under these conditions is presented, including analysis of the different Doppler-based methods for lifetime determination. The properties of the key reaction mechanisms expected to be applied for in-beam $\gamma$-ray spectroscopy at FAIR are discussed, along with the aspects of those reactions that can be exploited by the advanced capabilities of the AGATA array.

1 Introduction

In beam $\gamma$-ray spectroscopy with relativistic beams offers a wealth of physics opportunities through the application of specific intermediate-energy reaction mechanisms and experimental techniques made possible by the high velocity of the reaction products - see, for example, Gade and Glasmacher [1] for an extensive review. High-precision in-beam spectroscopy of exotic nuclei is significantly enhanced through the use of gamma-ray tracking arrays such as GRETINA (the early implementation of the US GRETA array [2]), and the European AGATA array. This article is part of a Topical Issue on the AGATA project, and hence AGATA and its capabilities are the principal focus. The design and concept of GRETINA are parrallel to AGATA and the two devices share common properties and capabilities. There is already considerable experience of using GRETINA using radioactive beams at energies up to $\sim 100$ MeV/u at the National Superconducting Cyclotron Laboratory – see for example Refs. [3, 4] – and is now in use at the new Facility for Rare Isotope Beams (FRIB). AGATA has, to date, only had a short period of operation using relativistic beams at GSI [5], and this article therefore focusses on future capabilities and prospects.

For the purpose of this article, we define “relativistic beams” as reactions in which the nuclei of interest, on which in-beam spectroscopy is being performed, possess energies between $100-500$ AMeV (i.e. $\beta =\frac{v}{c}\sim 0.4-0.75$). These energies are typical of those currently available with SIS18 beams using the GSI FRagment Separator (FRS) [6] and at the future Super-FRS facility [7, 8] using beams from SIS100 at FAIR – the past and future planned locations for in-beam spectroscopy with relativistic beams with AGATA [9].

Use of $\gamma$-ray tracking arrays, such as AGATA, for in-beam spectroscopy at these energies provides enormous advantages due to the exceptionally high $\gamma$-ray energy resolution, and photopeak efficiency, afforded by the combination of position sensitivity and $\gamma$-ray tracking. We describe these capabilities in this article. In Sect. 2 the use of AGATA for high-precision Doppler correction, essential for high-resolution spectroscopy, is described, and in Sect. 3 the application, using AGATA, of Doppler-based techniques for lifetime measurements is discussed. For these fast beam energies, the two principal reaction mechanisms that apply, and have been/will be exploited using AGATA, are (a) relativistic Coulomb excitation/virtual photon scattering or (b) one-(and two-) nucleon knockout. These are described in further detail in Sects. 4 and 5. When considering the wide range of secondary beam species available at fragmentation facilities, and the use of thick targets to maximise luminosity, these reactions provide essential tools for accessing specific properties of states in nuclei far from stability.

2 In-beam spectroscopy with high-velocity beams

The use of relativistic beams provides some distinct advantages in relation to in-beam spectroscopy using exotic radioactive beams. Firstly, high luminosity reactions are possible through the use of thick (e.g. several mm) targets, Secondly, the combination of thick targets and high velocity allows for a range of sophisticated Doppler-based methods for lifetime determination (these are covered in detail in Sect. 3). Thirdly, the high-velocity reactions result in forward focusing of $\gamma$-ray emission in the laboratory frame (the so-called Lorentz boost), resulting in a high effective efficiency (per unit solid angle) at forward angles. This is a useful feature that can be exploited as the AGATA array grows. Finally, the high velocity of the fragments can result in high-resolution, and highly efficient, event-by-event identification of the final nucleus of interest, especially where a downstream spectrometer is used. Hence, in-beam spectroscopy using AGATA at these energies has enormous potential for major advances in radioactive-beam physics – see Korten at al. [10] for a full discussion of physics opportunities with AGATA at HISPEC. Disadvantages for in-beam spectroscopy, using reactions at these energies, need to be borne in mind in the design of experiments with AGATA, including the presence of high levels of atomic background at low photon energies and $\gamma$-ray background from interactions of secondary high-energy particles – see e.g. [11].

The original design philosophy of the AGATA array [9], and of tracking arrays in general, was, at that time (more than two decades ago), largely focused on spectroscopy of reactions taking place at energies just above the Coulomb barrier and with high (e.g. 10–30) $\gamma$-ray multiplicity. Under these conditions, the position sensitivity (from the pulse-shape analysis approach, PSA), and the resulting $\gamma$-ray tracking capability, are both required to disentangle the multiple $\gamma$ rays and reconstruct their full energies. This is demonstrated clearly in other articles in this Topical Issue. For reactions at $>100~A$MeV, the $\gamma$-ray multiplicity is likely to be an order of magnitude lower (2–3 would be more typical) and the recoil velocity an order of magnitude higher. In these conditions, the huge advantage afforded by the exceptional position-sensitivity of AGATA comes in the area of Doppler reconstruction rather than $\gamma$-ray energy reconstruction. Gamma-ray tracking remains important for the full reconstruction of the $\gamma$ rays, to optimise efficiency and to distinguish $\gamma$ rays from the potentially high levels of background, and is also used to determine the first interaction point of the $\gamma$ ray in AGATA. However, without a position-resolution at level of a few mm (typical of the AGATA PSA), high $\gamma$-ray energy resolution in-beam spectroscopy becomes impossible due to the otherwise huge Doppler-broadening effects, and the advantage of using a high intrinsic-resolution material, such as Germanium, is nullified.

The $\gamma$-ray energy measured in the laboratory system $E_\text {lab}$ is given by

$$\begin{aligned} E_\text {lab} = E_0 \cdot \frac{\sqrt{1-\beta ^2}}{1-\beta \cos {\alpha }}. \end{aligned}$$

(1)

The transition energy $E_0$ is shifted depending on the velocity of the ejectile $\beta = v/c$ and the emission angle $\alpha$ between the ejectile and the emitted $\gamma$ ray. In terms of $\gamma$-ray energy resolution, there are two major contributions to the resolution, resulting from this Doppler shift, when performing in-beam $\gamma$-ray spectroscopy with typical targets. The first is the spread in velocities ($\varDelta \beta$) of the fragment as it passes through the target. Since $\beta =0.5$ corresponds to $v=0.15$ mm/ps, and target thicknesses are of the order of mm, then for short-lived transitions (e.g. of the order of a picosecond, or faster) the $\gamma$ decay can take place at any point in the target. This yields a spread of velocities and an uncertainty in the value of $\beta$ applied in the Doppler reconstruction. The second is the uncertainty in the emission angle ($\varDelta \alpha$), required for the Doppler reconstruction, as a result of the uncertainty in the (first) $\gamma$-ray interaction position in the Ge crystal. This is demonstrated in Fig. 1 which shows the contribution to the $\gamma$-ray energy resolution as a result of $\varDelta \beta$ and $\varDelta \alpha$ as a function of the measured emission angle with respect to the ion trajectory, $\alpha$, and assuming that all other parameters required for Doppler correction (e.g. beam tracking and identification of first interaction location in AGATA) are perfectly known. This is shown for different fragment energies in Fig. 1.

Figure 1a shows, as an example, the contribution from $\varDelta \beta$ assuming a $^{50}$Fe nucleus traversing a 1 mm thick Be target. As can be seen from the figure the contribution to the energy resolution from this effect can be severe at forward (e.g. $<30^\circ$) and backward (e.g. $>100^\circ$) laboratory angles. Figure 1a assumes a very fast (sub ps) $\gamma$-ray emission, and hence minimisation of this contribution requires careful choice of target thickness coupled to knowledge of the expected lifetimes. Figure 1b shows the contribution to the $\gamma$-ray energy resolution from the effective angle resolution, assuming $\varDelta \alpha =5^\circ$. This value is chosen as it is the approximate angle subtended by a single AGATA crystal segment at the nominal distance from the target of 23.5 cm. Hence this would be the effective angular resolution without applying PSA to determine the interaction position. Figure 1b shows the severe impact of Doppler broadening at all energies, with the effect most serious at angles around $90^\circ$ in the nuclear frame (e.g. between $30^\circ$ and $90^\circ$ in the laboratory frame at $\cos (\alpha ) = \beta$). Figure 1c shows the contributions from (a) and (b) added in quadrature. It is clear that effects of Doppler broadening are dominant, even for this fast transition with a large uncertainty in velocity ($\varDelta \beta$). The right hand two panels of Fig. 1 show the impact of PSA in this case. Figure 1d is the equivalent of (b) but with $\varDelta \alpha =1^\circ$, which is the approximate angle subtended by a typical AGATA position resolution (FWHM) of 5 mm at the nominal AGATA distance from the target. Typical Doppler broadening contributions are now between 1 and 2$\%$. Figure 1e shows the contributions from (a) and (d) added in quadrature. The total resolution is now much improved reaching values below 2% for the higher beam energies. The contributions from $\varDelta \beta$ and $\varDelta \alpha$ are of similar magnitude.

Fig. 1

The contributions to the $\gamma$-ray energy resolution as a result of velocity spread across the target ($\varDelta \beta$) and effective detector angular resolution ($\varDelta \alpha$) whilst assuming that all other parameters required for Doppler correction (e.g. beam tracking) are perfectly known. This is shown for fragment energies of 100 AMeV (blue, dot-dashed), 200 AMeV (green, solid) and 300 AMeV (red, dashed). a The contribution due to velocity changes across the target for a decay from a fast (sub ps) state in a $^{50}$Fe nucleus traversing a 1 mm thick Be target. b The contribution from the effective detector angular resolution, assuming $\varDelta \alpha = 5^\circ$. c The contributions from (a) and (b) added in quadrature. d The equivalent of (b) but with $\varDelta \alpha = \circ$, typical for AGATA PSA. e The contributions from (a) and (d) added in quadrature

Three campaigns of in-beam $\gamma$-ray spectroscopy have taken place, over the last two decades, at GSI using beams at the FRS [6], with only the most recent one deploying AGATA detectors. The $\gamma$-ray energy resolution effects demonstrated in Fig. 1 are evident from the observations in these campaigns. The first was the RISING campaign [13] in which the reaction target was deployed at the focal plane of the FRS. The $\gamma$-ray detector array included (among others) 15 Euroball Cluster detectors positioned at forward laboratory angles (between $16^\circ$ and $36^\circ$). The reaction products were identified through energy loss and time-of-flight using the FRS and CATE [14] detectors. The Cluster detectors subtended an angle of $3^\circ$, achieved by placing them 70 cm from target. Doornenbal et al. report a knockout experiment to study the first excited state in $^{36}$Ca starting from a $^{37}$Ca beam at 196 AMeV incident on a thick 3.8 mm Be target [15]. An in-beam $\gamma$-ray resolution of 5(1)$\%$ was achieved for the Cluster detectors, with contributions from both $\varDelta \beta$ and $\varDelta \alpha$. In a later campaign, the first part of the PreSPEC campaign, the Cluster detectors were again deployed, and this time the fragments were tracked and identified using the LYCCA (Lund-York-Cologne CAlorimeter) array [16]. A similar resolution of $\sim 5\%$ was found by Moschner et al. [17] in that campaign in an experiment to study $^{88}$Kr by Coulomb excitation at a beam energy of 128 AMeV.

AGATA was deployed in the final part of the PreSPEC in-beam campaign in 2012–2014 [18,19,20] as a precursor to the future HISPEC project at FAIR. Six AGATA triple clusters and two AGATA doubles were placed around the reaction target, covering the laboratory angular range $20^\circ -60^\circ$. To make the in-beam energy-resolution gains suggested by Fig. 1d and e, it is essential to accurately determine the beam properties to remove other contributions to $\varDelta \beta$ and $\varDelta \alpha$. Bracco et al. [21] suggested that to make the most of the position-sensitivity of AGATA for Doppler correction, the beam trajectory should be determined to a precision of $0.3^\circ$, the target position to a precision of 3 mm, and the $\beta$ for the beam determined, event-by-event, to a precision of better than 0.3$\%$. To achieve this in the PreSPEC campaign, the trajectory and velocity of the fragments were determined to high precision by the LYCCA detectors [16]. Only a small number of experiments were performed with AGATA, but the huge impact of PSA on the in-beam resolution was immediately obvious. In an experiment to determine lifetimes in neutron-rich Mo isotopes [22], Ralet et al. impinged a $^{109}$Tc beam at 150 AMeV on a 3.8 mm Be target, populated excited states in Mo isotopes through one-proton knockout and fragmentation reactions. A decay from a 6.8-ps state in $^{104}$Mo was reported and, even though some of the resulting decays will have taken place within the target, resulting in a velocity spread, an energy resolution of 2.1(6)$\%$ was nevertheless observed.

Fig. 2

The decay of the first-excited state in $^{46}$Ti, populated through Coulomb excitation at 170 AMeV on a 500 mg/cm$^2$ Au target, using the AGATA spectrometer as part of the PreSPEC campaign. The spectrum indicates an energy resolution (FWHM) of better than 1.5$\%$. Figure adapted from Ref. [12]

The outstanding capability of AGATA for in-beam spectroscopy with relativistic beams is perhaps best demonstrated by Coulomb excitation measurements on thin Au targets, in which the decays largely take place downstream of the target, effectively eliminating contributions from the velocity spread, $\varDelta \beta$. Pietralla et al. [18] reported on the commissioning experiment employing Coulomb excitation of a $^{80}$Kr beam at 150 AMeV on a 400 mg/cm$^2$ thick gold target (0.2 mm where the velocity $\beta$ decreases by about 5%). An energy resolution of 1.7$\%$ was reported for $^{80}$Kr. Boso et al. measured the Coulomb excitation of the mirror nuclei $^{46}$Cr and $^{46}$Ti at 170 AMeV on a 500 mg/cm$^2$ thick Au target. Figure 2, adapted from Ref. [12], shows the $^{46}$Ti spectrum reported in Boso et al. [23], but with a lesser degree of binning. Whilst Ref. [23] does not quote a resolution, Fig. 2 suggests a resolution (FWHM) better than 1.5$\%$. Both results are consistent with the “ideal” result shown in Fig. 1d.

In the following sections, we describe the different reaction mechanisms and techniques that can be applied and which exploit AGATA’s power.

3 Lifetime measurements

The fast beams available at fragmentation facilities provide access to excited state lifetimes in the range of few picoseconds to about one nanosecond.

Fig. 3

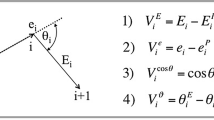
Effects of finite lifetimes on the Doppler shift of $\gamma$ rays. a Velocity effect mainly shifting the peak with $\beta _r > \beta _e(t)$ and $\alpha _r \approx \alpha _e$ b geometric effect with $\beta _e = const$ and $\alpha _e(t) > \alpha _r$, c additional degrader to change the velocity

The experimental technique makes use of the Doppler effect - see Eq. 1. Since the reaction populating the state of interest and the emission of $\gamma$ rays take place at different positions, the velocity and/or the emission angle with respect to the $\gamma$-ray detector change as a function of time. In the Doppler-reconstruction analysis procedure, Eq. 1 is inverted in order to find $E_0$. For this, one typically uses the corresponding mean reaction velocity and position for the Doppler correction. For transitions which result from the decay of states with finite lifetimes, these assumptions are not valid anymore.

Two effects can be used to determine the lifetime from the peak shape in the spectrum after Doppler correction. They are illustrated in Fig. 3. For short lifetimes, which are on the order of the time it takes for the beam to traverse the target, the decay occurs in the target and the detection angle is not affected by the lifetime, $\alpha _r \approx \alpha _e$. However, the emission happens while the nucleus is slowing down. The velocity assumed in the Doppler-correction ($\beta _\text {r}$) is larger than the velocity at emission ($\beta _\text {e}(t)$) (see Fig. 3a). For typical beam energies of several hundred AMeV, the velocities amount to $\beta \approx 0.5-0.8$ and therefore a lifetime of 1 ps corresponds to less than a mm distance, whilst typical target thicknesses are on the order of few mm to even cm for low density targets. The emission at lower velocity will then lead to a shift of the peak to lower (higher) energies in the Doppler corrected spectrum for laboratory forward (backward) detectors depending on the sign of $\cos \alpha$. If the transition energy is known, lifetimes can even be measured using a single germanium detector. The highest sensitivity is achieved for the most forward and backward angles (see also Fig. 1a). The large angular coverage of AGATA will thus enable the measurement of lifetimes and energies simultaneously.

If, on the other hand, the lifetime is longer than the traversal time of the target, the velocity $\beta _e$ is not time dependent anymore and remains constant. It can also be measured event-by-event with a spectrometer after the target. The Doppler shift is then determined by the time-dependent angle $\alpha _e(t)$ (see Fig. 3b). Emission at later times and detection at larger angles lead to a tail toward lower energies in the spectrum.

Due to the complex detector geometry, as well as effects resulting from the interaction of $\gamma$ rays with material of the beam tube, the detector housing and mounting, as well as other passive material surrounding the experiment, the extraction of lifetimes from the peak’s shape and shift is achieved through comparison with realistic simulations. Monte-Carlo simulations using the GEANT4 [24] package are employed to simulate the detector response to $\gamma$-ray events with varying transition energy and lifetime. Such an analysis was first developed for the RISING setup at GSI [25]. The enhanced position resolution of the AGATA spectrometer as well as its large angular coverage make it an ideal device for lifetime measurements. Simulations employing the $4\pi$ geometry of the device [10, 26] demonstrate this sensitivity.

The Doppler shift technique was applied in the PreSPEC in-beam campaign with the goal to measure excited state lifetimes in neutron-rich Mo isotopes [22]. A cocktail beam composed mainly of $^{109}$Tc and $^{108}$Mo ions impinged on a secondary 700-mg/cm$^2$ thick beryllium target located in the center of the AGATA array. Excited states were populated in proton and neutron removal reactions. For lifetimes in the range of a few ps, the decay occurs further downstream in the target at a lower velocity. In this case, the lifetimes have been extracted by comparing the well-known transition energy $E_0$ with the mean energy of the peak observed in the Doppler-corrected spectrum assuming a decay at the target centre for the $\gamma$-ray emission angle and the ion’s velocity as shown in Fig. 4.

Fig. 4

Doppler-corrected $\gamma$-ray energy spectrum for $^{102}$Mo. The blue curves correspond to the model fitted on the data and used to determine the mean energy of the observed transitions. The green dashed lines indicate the mean energy of the observed transition. Reprinted with permission from Ref. [22]. Copyright (2017) by the American Physical Society

Taking into account the direct and indirect feeding of states in the simulation the ratio $R = (E_0 - E_\text {lab})E_0 = 5.94(30)$ for the $2^+_1 \rightarrow 0^+_1$ in $^{102}$Mo results in $\tau =186(18)$ ps in excellent agreement with the literature value of 180(6) ps [27]. The analysis was also benchmarked on other states in the Mo isotopic chain and furthermore the lifetime of the $4^+_1$ state in $^{108}$Mo could be determined for the first time [22].

For lifetimes which are significantly longer than the target traversal time, the geometric effect of a larger $\alpha _e$ can be exploited and the line-shape method [25] can be applied to determine lifetimes. At relativistic beam energies, the lifetimes accessible by this method range from about 100 picoseconds to 1 nanosecond, corresponding to flight lengths on the order of cm and thus larger than the position uncertainties obtained from the PSA and tracking. At GSI, this method has not yet been exploited, however in a future AGATA campaign at FAIR, the enhanced $\gamma$-ray energy resolution and detection efficiency will enable such experiments. The reach and sensitivity of the method is demonstrated in Fig. 5.

Fig. 5

Doppler-corrected $\gamma$-ray energy spectrum for $^{80}$Zr. Experimental spectra are compared to simulated spectra (red) including an exponential background (dashed blue). The inset displays the $\chi ^2$ minimization as a function of the mean lifetime. Reprinted with permission from Ref. [28]. Copyright (2020) by the American Physical Society

In this experiment performed at the NSCL, the mean lifetime of the first $2^+$ state of $^{80}$Zr was determined. The state was populated in a one-neutron knockout reaction from a $^{81}$Zr beam at 77 AMeV impinging on a 188-mg/cm$^2$ thick $^{9}$Be target. GRETINA [4] was used to measure the de-excitation and through comparison with simulated response functions as shown in Fig 5, the mean lifetime of 207(19) ps was be obtained [28].

Another experimental method to determine lifetimes by Doppler effects is by using a so-called plunger device [29]. Here, a degrader is placed behind the target as shown in Fig. 3c. The emission then occurs either between the target and the degrader with high velocity, or after the degrader with a lower velocity. This leads to two peaks in the spectrum and the ratio of fast and slow decay events thus depends on the lifetime. By measuring at several distances between target and degrader, the lifetime can be extracted. Recently the technique has been extended by adding a second degrader layer [30]. This method is then sensitive to the derivative of the decay curve and therefore with only one distance setting the lifetime can be deduced.

At GSI, a similar technique was employed to study the $B(E2;\;2^+\rightarrow 0^+)$ values of $^{46}$V and $^{46}$Ti [23]. The beams impinged on a stack of Au targets with 750, 500, and 500 mg/cm$^2$ thickness separated by 1 mm. A similar idea was already employed at RISING, where a stack of Fe plates were used as target and degrader to measure lifetimes in fragmentation products of $^{37}$Ca projectiles at 200 AMeV [31]. This first application, however, showed that the resolution with the RISING array was not sufficient to derive a lifetime. However, as shown in Fig. 6, despite the three peaks being very closely spaced, the enhanced resolution of the AGATA tracking array, compared to unsegmented detectors, makes the measurement possible.

Fig. 6

Doppler-corrected $\gamma$-ray energy spectrum for $^{46}$V for the three targets. The Doppler correction is optimised for the velocity and position of the central target, the dashed line marks the known transition energy. The inset shows the $\chi ^2$ values of the fit as a function of the half-life. Figure from Ref. [23]

The lifetime of the $2^+_1$ state was then extracted using detailed GEANT4 simulations of the experimental setup and the kinematics.

All the examples above demonstrate that lifetime measurements with relativistic beams require high resolution for the $\gamma$-ray energy and interaction point position. But, as shown in Fig. 1, the in-beam energy resolution, especially at small and large emission angles depends strongly on $\varDelta \beta$. This uncertainty, which arises when the state lifetime is such that decays take place within the target volume, is linked to the beam energy and the target thickness and not the properties of the $\gamma$-ray detector. While reducing the target thickness of course improves the resolution, experiments focussing on the most exotic nuclei need substantial targets to obtain the required luminosity. A new way to maximise the luminosity while keeping the resolution of a very thin target is proposed by the LISA approach [32]. An active target will give the experimental information to obtain an event-by-event information on the velocity of the ejectile at the reaction. The target is currently under construction and will be employed for lifetime measurements with AGATA at FAIR.

4 Coulomb excitation and virtual photon scattering

Coulomb excitation (Coulex) is the excitation of a nucleus via the electromagnetic interaction with another nucleus, and is a powerful tool to provide insight in the internal structure of nuclei, as well as to establish their collective behaviour. Coulex experiments provide both the energy of the excited states and the electromagnetic matrix element ($B(E\lambda )$ and $B(M\lambda )$), through the determination of the Coulex cross section.

At relativistic beam energies electromagnetic excitation occurs only as one-step process. Consequently, only low-spin states can be excited via the absorption of virtual photons of multipolarity E1, M1, E2, or E3. In contrast, no such limitation exists with respect to the excitation energy. As a consequence, low-lying collective states are more easily excited at low incident beam energies, usually not higher than 150 AMeV, while giant resonances are best studied at beam energies of several hundred AMeV. Thus, the particular energy regime of beams at FAIR makes it one of the best suited laboratories to measure transition probabilities from the ground and isomeric states to low-lying excited states in heavy nuclei, as well as to study Giant and Pygmy resonances, i.e. collective states at excitation energies from roughly 8 to 30 MeV.

While the choice of beam energies below the Coulomb barrier excludes nuclear contributions, peripheral collisions are selected at intermediate energies to ensure that the projectile and target nuclei remain far enough apart so that nuclear contributions to the excitation process are small. The selection based on small scattering angles might not be sufficient, and an accurate study of the background originating from nuclear contributions is mandatory. In the regime of intermediate energies, FAIR will have an impact in the study of the evolution of quadrupole and octupole collectivity, in addition to help mapping the regions where triaxiality occurs. Regions of predicted quadrupole collectivity below $^{132}$Sn and $^{208}$Pb, new regions of octupole correlations, for example around $N=90$, will be explored. In addition the refractory elements which are not easily accessible at ISOL facilities, will be subjects of specific campaigns exploiting FAIR beams.

Related to the study of giant resonances, a particular emphasis is given to the study of the so-called Pygmy Dipole Resonance (PDR), the excess of dipole strength at low energies associated to a possible new collective mode. If the Giant Dipole Resonance is macroscopically depicted as the oscillating motion of neutrons against protons, this mode is described as the oscillation of a neutron skin against the core nucleons, and is expected to occur, therefore, in nuclei presenting a considerable excess of neutrons.

The PDR has already been measured in a limited number of cases, and shown to exhaust a few percent of the isovector energy-weighted sum-rule. A similar low-lying excitation is also expected for higher multipolarities, as in the case of the low-lying strength connected to quadrupole excitations, Pygmy Quadrupole resonance (PQR). Details on latest studies on PDR and PQR are found in these review papers [33, 34]. The PDR states in neutron-rich nuclei always exhibit the same peculiar features: protons and neutrons oscillate in phase inside the nucleus while in the surface region only the neutron part survives. This fact can be used as a theoretical definition of the states associated to the PDR. Since the PDR states are associated to surface oscillations, it is interesting to study them with probes interacting mainly at the surface.

Several experimental techniques have been applied to study these modes, ranging from direct nuclear resonance fluorescence, ($\gamma ,\gamma '$) excitation to inelastic scattering using isoscalar or isovector probes (($p,p'\gamma$) and ($\alpha ,\alpha ' \gamma$), ($^{17}$O,$^{17}$O$'\gamma$)) to also determine the nature of the excitation and be most sensitive to the nuclear surface.

Fig. 7

Photograph of the AGATA setup at the FRS. The secondary beam from the FRS enters the target chamber from the left. The LYCCA array [16] is used to track and identify the reaction products. In addition to the AGATA triple cluster detectors, HECTOR+ BaF$_2$ and LaBr$_3$(Ce) detectors are placed around the target to increase the efficiency and the angular coverage of the setup

At relativistic fragmentation and fission facilities, such as GSI-FAIR, it is possible to study the dipole response of nuclei thanks to Coulomb excitation performed in inverse kinematics. The radioactive beams hit a heavy target, either lead or gold, and are then excited by means of the Coulomb interaction. The de-excitation sees the competing emission of neutrons and energetic $\gamma$ rays, while states below the separation energy can only emit $\gamma$ rays, giving a complete picture of the excitations around the neutron separation energy. For such studies, owing to the large Lorentz boost caused by the relativistic energies of the incident beam, the $\gamma$ array should preferentially sit at small forward scattering angles. In particular, the use of the AGATA array, thanks to its exceptional position resolution, helps correct for the strong Doppler effect induced by the large incident energy, when used in combination with the precise scattering angle determined provided by LYCCA.

A number of experiments have already been performed at GSI using this technique, the first one aimed at the pygmy structure in $^{68}$Ni, measured with the combination of HPGe EUROBALL Cluster detectors and large-volume BaF$_2$ scintillators [35], while a second one focused on the dipole response in $^{62,64}$Fe [36], measured during the PreSPEC campaign (2012–2014), where the same scintillators were coupled to AGATA. The experimental setup with AGATA, LYCCA, and the HECTOR+, BaF$_2$ and LaBr$_3$(Ce) detectors, is shown in Fig. 7.

The latter experiment made use of $^{62,64}$Fe secondary beams at an energy of 400–440 AMeV impinging on a 1 g/cm$^2$ Au target, excited via electromagnetic excitation (via virtual photon exchange). The excitation of dipole states required the use of high bombarding energy, implying very large Doppler shift corrections ($\beta =0.72$), thus a good position resolution coupled to tracking of the $\gamma$-ray emitting particle was crucial, together with the accurate determination of the direction of the emitted $\gamma$-rays, determined thanks to the high position resolution achieved with AGATA ($\sigma \approx$ 2 mm). The incoming ions were identified and selected by standard $\varDelta E-TOF-B\rho$ technique, while the outgoing particles were identified and selected using four pieces of information: energy loss, total energy, time of flight and deflection angle, measured by LYCCA (see [36]). A careful evaluation of background and of contributions coming from reactions other than Coulomb excitation has been performed, selecting events out of the prompt coincidence window (random correlations), or occurring at very large scattering angle (accounting for nuclear excitation mainly). Despite the very large velocity, the $2^+ \rightarrow 0^+$ transitions in $^{62,64}$Fe were clearly emerging from the background and could be used as normalisation point in order to extract the E1 strength of the higher-lying states. This is visible in the insets of panels (a) and (c) of Fig. 8, for $^{64}$Fe and $^{62}$Fe respectively. The energy region where contributions from $\gamma$ rays de-exciting the PDR states is highlighted in panels (b) and (d), and insets. Short measuring time limited the statistics of the experiment, therefore the analysis of the PDR in AGATA had to be complemented with spectra from the more efficient BaF$_2$ detectors.

Fig. 8

Doppler corrected ($\beta =0.72$) spectra measured in AGATA up to 3 MeV in $^{64}$Fe (panel a) and $^{62}$Fe (panel c). In the two insets the peaks corresponding to the $2^+ \rightarrow 0^+$ in the two nuclei are highlighted. Panels b and d report AGATA spectra in the energy region above 3 MeV, which is the region of interest for E1 transitions belonging to the PDR. The shaded areas in these figures display the spectral shapes obtained with gates corresponding to events outside the Coulomb excitation conditions (red area) or out of the prompt time of flight peak (blue area). In the insets of panels b and d the counts forming peak structures at around 4.5 MeV are compared with simulations taking into account the detection conditions (Adapted from [36] under CC license)

With the upcoming higher beam intensity and energy, expected to be delivered by SIS100, one will be able to explore longer isotopic chains, thus proving the hypothesis of a marked increase of E1 strength and of its fragmentation with increasing neutron number, as seen by these exploratory studies. In particular long isotopic chains of semi-magic nuclei such as the neutron-rich Ni, Sn or Pb isotopes will be under investigation. Complementary information may be obtained from the study of deformed nuclei or those on the proton-rich side of the nuclear chart, where Pygmy strength is predicted to exist, too.

Measurements of $\gamma$-ray angular distributions allow to determine the multipolarity of the transitions, thus distinguishing E1 from E2 contributions. The continuous angular coverage of AGATA greatly enhances the sensitivity for such studies. Additionally the possibility to use liquid helium targets would allow to probe also the isoscalar component of such resonances, and compare the isovector ones extracted on standard Au or Pb targets. The fascinating idea of having PDR modes built on states other than the ground state can be proven exploiting the possibility of fragmentation reactions to populate long-living isomeric states.

An interesting application of AGATA as a Coulomb Excitation Multipolarimeter has been successfully tested in a PreSpec experiment by Napiralla et al. [37]. The idea behind this application is to measure the E2/M1 multipole mixing ratio, $\delta$, together with the lifetime of specific states. Since the ratio of Coulomb excitation cross sections between M1 and E2 excitations has a quadratic dependence on the incident beam velocity ($\beta ^2$) [38], the multipole mixing ratio $\delta$ can be accessed by the comparison of Coulomb-excitation $\gamma$-ray yields for two different well-chosen incident beam energies. In this test experiment two consecutive targets were used to simultaneously measure at two velocities.

An almost pure $^{85}$Br beam at 300 AMeV impinged on two consecutive 2 g/cm$^2$ and 1 g/cm$^2$ gold targets, placed one after the other along the beamline, reaching $\beta =0.61$ and 0.58. The direction of the outgoing particles was accurately measured by the LYCCA array. In order to reconstruct the angle between the beam direction and the emitted photon, the interaction point with the largest deposited energy in the respective detector has been selected and used as the first interaction point of the incident $\gamma$ ray. This is helped by the excellent position resolution achieved by AGATA. A careful analysis of the performances and requirements of the employed $\gamma$-ray tracking algorithms for this study is reported in Ref. [37].

5 Spectroscopy with AGATA using knockout reactions

As part of the HISPEC project at FAIR, AGATA will be deployed for high-resolution in-beam spectroscopy with relativistic beams, for which the knockout reaction will be a key mechanism for the population of excited states in exotic nuclei. Knockout reactions, principally one-proton and one-neutron knockout, with intermediate energy beams have, over the last two decades, become one of the key tools in contemporary nuclear structure physics, and have been utilised at all the major fragmentation facilities world wide - see Refs [1, 39] for comprehensive reviews. As a direct reaction, the knockout process can be used to provide a direct probe of the nuclear wave functions of the states concerned, providing a wealth of nuclear structure information in nuclei far from stability. In such experiments, a post-target spectrometer is employed to measure the parallel momentum distributions of the residues and a $\gamma$-ray array is usually placed around the reaction target to identify the specific excited states populated in the reaction, e.g. [1]. Whilst the majority of examples using knockout utilise the one-nucleon knockout reaction, increasing use is being made of two-nucleon knockout reactions. This method, first identified by Bazin et al. [40], is also considered to be a direct process, at least in exotic nuclei where the two nucleons removed are the most tightly bound ones. When coupled to predictions utilising two-nucleon knockout reaction models (e.g. [41, 42]), this provides a powerful spectroscopic and reaction tool.

When utilising knockout reactions at HISPEC, using AGATA, a magnetic spectrometer will be combined with the LYCCA detectors [16] to provide measurements of magnetic rigidity, time of flight and energy loss for complete fragment tracking and identification. The precursor to the Super-FRS, the current FRS at GSI, has been employed for knockout reactions on nuclei far from stability with the reaction target located at the intermediate focus (mid point) of the FRS, exploiting very high energy secondary beams, and using the second part of the FRS to analyse the parallel momentum distributions of the fragments. Gamma-ray arrays around the reaction target have included arrays of NaI detectors, to study (for example) excited states in $^{22}$O [43] and $^{7}$Be [44] and an array of segmented Ge detectors to perform spectroscopy of $^{55}$Ti [45]. As a precursor to HISPEC, AGATA has also been deployed at the final focus of the FRS as part of the PreSPEC campaign [18,19,20] using LYCCA [16] for particle identification. Indeed, as reported in Sect. 2, Ralet et al. [22] demonstrated the power of AGATA for high-resolution in-beam spectroscopy following knockout, in that case one-proton knockout, to study neutron-rich $^{108}$Mo.

The ability to apply high-resolution in-beam $\gamma$-ray tracking arrays, such as AGATA and GRETINA [4] to experiments that utilise knockout reactions opens a range of exciting opportunities. In particular, the high resolution provided by PSA at these very high velocities allows for the spectroscopy of more complex level schemes with multiple states, both yrast and non-yrast, populated directly in the reaction. Such complex population patterns can occur, for example, in one-nucleon knockout reactions from odd-A beams and two-nucleon knockout reactions, where selective population of a wide range of states is possible, through paths where there is significant spectroscopic overlap with the ground-state of the beam. With multiple states populated in these kinds of reactions, the vastly improved quality of $\gamma -\gamma$ coincidence spectroscopy, due to the the high in-beam $\gamma$-ray resolution and high efficiency of tracking arrays, becomes essential.

A recent example that highlights the above methods, using both one- and two-nucleon knockout, is the study of excited states in neutron rich $^{32}$Mg, populated by both one-neutron knockout from $^{33}$Mg and two-proton knockout from $^{34}$Si [46]. The in-beam spectroscopy in this case was performed at NSCL, USA, using GRETINA [4] with the secondary beam selected and identified using the A1900 spectrometer [47] with the S800 spectrograph[48] used to analyse the final reaction products. The resulting $\gamma$-ray spectra, taken from [46], are shown in Fig. 9, for both reactions. A wide range of yrast and non-yrast states were populated and identified in both reactions. Due to the selectivity of the knockout reaction process, the two reactions populate states of different nature. The one-neutron knockout from the intruder ground state of $^{33}$Mg preferentially populates negative-parity states as well as deformed intruder configurations, whilst two-proton knockout from the closed proton sub-shell in $^{34}$Si favoured population of spherical states in $^{32}$Mg.

Fig. 9

Doppler-corrected $\gamma$-ray spectra, from Ref. [46] for $^{32}$Mg produced through one-neutron knockout from $^{33}$Mg (bottom, blue) and two-proton knockout from $^{34}$Si (top, red). The spectrum was recorded using GRETINA in conjunction with the A1900/S800 spectrometers at NSCL – see [46] for details. Transitions between excited states in $^{32}$Mg are indicated by vertical dashed lines and labeled by their energies. For reference, the 885, 1437 and 1773 keV transitions de-excite the $J^\pi =2^+,4^+,6^+$ yrast states, respectively. This figure is reproduced under a CC-BY licence from Ref. [46]

In this example, 17 excited states were identified, with the scheme confirmed through $\gamma -\gamma$ coincidence measurements. The benefit of high $\gamma$-ray energy resolution, made possible by the PSA technology, is obvious from Fig. 9. Another crucial benefit of the high $\gamma$-ray energy resolution is the ability to gate on specific $\gamma$-ray transitions to determine parallel momentum distributions for the knockout-path(s) of the de-exciting state, to aid with spin-parity assignments as well as to probe the wave functions of the states concerned. This was applied in Ref. [46] for the states populated in Fig. 9, and was used to help resolve the disputed $J^\pi$ assignment of the $^{33}$Mg ground state.

It is clear from the above that AGATA will provide exceptional resolving power for in-beam spectroscopy where the spectroscopic strength in the direct process is spread over a wide rage of final states resulting in complex, or long, decay sequences. This will especially be the case where intermediate- (or even high-) spin states can be accessed, as determined by the choice of reaction. For one-nucleon knockout from odd-A beams, where there can be multiple knockout paths to each final state (through removal from more than one orbital), the coupling between the angular-momentum of the initial state and that of the removed particle allows for states of intermediate spin to be readily populated. As an example, a completely new scheme was recently established for $^{48}$Fe [49], again using GRETINA with the A1900/S800 combination at NSCL. One-neutron knockout was performed from the $J^\pi =\frac{7}{2}^-$ ground state a $^{49}$Fe secondary beam and yrast and yrare states up to $J^\pi =6^+$ were populated and identified – in this case, the yrare $J^\pi =6^+$ state was observed (and predicted) to be the most strongly populated state.

In the two-nucleon knockout process, removal of pair of high-j nucleons coupled to their maximum allowed angular momentum can, especially for removal from an odd-A nucleus, result in population of states of quite high spin. For example, states up to $J^\pi =\frac{19}{2}^-$ were observed in the $T_z=-2$ nucleus $^{51}$Co [50] using two-neutron knockout from a $^{53}$Co beam (removal of a pair of $f_\frac{7}{2}$ neutrons, coupled to $J=6$, from the $J^\pi =(\frac{7}{2}^-)$ ground state of $^{53}$Co can populate states up to $J^\pi =\frac{19}{2}^-$). Indeed the heaviest $Z>N$ nucleus studied to date through in-beam spectroscopy, $^{79}$Zr [51], was recently populated this way, through two-neutron removal from $^{81}$Zr. In that particular case, population of states up to $J^\pi =\frac{19}{2}^-$ could again, in theory, be achieved through removal of a pair of $g_\frac{9}{2}$ neutrons from the $J^\pi =(\frac{3}{2}^-)$ ground state of $^{81}$Zr. In that particular case, states up to $J^\pi =\frac{11}{2}^+$ were observed, limited by very low statistics. Finally, it is worth noting that relativistic beams produced by high-energy fragmentation at FAIR, and selected by the Super-FRS, may be expected to have significant components in isomeric states, as has been demonstrated at the current GSI facility (e.g. [52]). Knockout from isomers in fragmentation beams, e.g. Ref. [53], has the capability to populate high spin states, more so if two-nucleon knockout can be applied. It is clear that to take advantage of such opportunities, a high-resolution and high-efficiency $\gamma$-ray tracking array will be required. AGATA, as part of HISPEC, when coupled to beams from the Super-FRS, would provide an outstanding opportunity to exploit these methods.

6 Summary

In this paper, the scientific opportunities afforded by in-beam spectroscopic studies with relativistic beams using the $\gamma$-ray tracking array AGATA have been presented, along with results of past campaigns. At the future FAIR facility, AGATA will be deployed as part of HISPEC employing relativistic radioactive beams from the SIS100 and Super-FRS complex. For beam tracking and particle identification, AGATA will make use of both LYCCA [16] and a downstream magnetic spectrometer [54].

Techniques that exploit the position sensitivity, and therefore the Doppler correction capabilities, of the array have been discussed. Coulomb excitation and knock-out reactions are the preferred reaction tools, allowing for $\gamma$-ray spectroscopy of complex level schemes and precision lifetime measurements. AGATA at FAIR presents an outstanding opportunity to measure transition probabilities from the ground and isomeric states to low-lying excited states in medium and heavy nuclei, as well as high-lying collective excitations.

The article demonstrates the power of AGATA for high-resolution in-beam spectroscopy at relativistic velocities, and the requirements, in terms of beam tracking, to make the most of those capabilities.