1 Introduction

When suitably controlled, the interaction of relativistically intense laser light (\(\ge \)10\(^{18}\) Wcm\(^{-2}\) for wavelength \(\sim \)1 \(\mu \)m) with dense plasma can drive large transient electrostatic and electromagnetic (EM) fields, resulting in the generation of ultrabright pulses of energetic particles and radiation. The use of this approach to produce a compact source of energetic ions [1, 2], with wide ranging potential applications in fields as diverse as medical oncology [3,4,5,6], inertial confinement fusion [7, 8] and industrial applications [9,10,11], has motivated investigations into the interaction of intense laser pulses with thin foil targets in particular. At the peak laser intensities available to date, this primarily occurs via the formation of quasi-electrostatic sheath fields on the surfaces of the foils, via the target normal sheath acceleration (TNSA) mechanism [12, 13]. With increasing intensity, the radiation pressure of the laser pulse plays an increasingly important role and drives electrons inwards forming a strong electric field in the region of the laser focus, which gives rise to radiation pressure acceleration (RPA) of ions [14,15,16]. These mechanisms can occur in the same interaction, resulting in a TNSA-RPA hybrid ion acceleration scheme [17].

As stronger electric fields can be achieved by decreasing the thickness of the target foil, the drive to enhance the energy of the ions accelerated resulted in the introduction of ultrathin (tens-of-nanometre) targets [18, 19]. This was enabled by a combination of improvements in targetry and the temporal-intensity contrast of the laser pulses, through the introduction of techniques such as plasma mirrors [20, 21]. The use of ultrathin foils led to the demonstration of new types of ion acceleration mechanisms in targets that undergo relativistic self-induced transparency (RSIT). RSIT occurs when the relativistic mass of electrons oscillating in response to the laser light increases to the extent that the plasma frequency decreases below the laser frequency, such that an initially opaque ultrathin foil becomes transparent during the interaction, enabling the remainder of the laser light to be transmitted [22]. Plasma expansion also plays a role, decreasing the peak electron density, which also acts to decrease the plasma frequency. The transmitted laser light heats electrons over the volume of the target and enhances the sheath field, increasing the ion energies achieved, in what was termed the break-out afterburner acceleration (BOA) mechanism [23, 24]. RSIT-enhanced hybrid RPA-TNSA acceleration has also been explored [25]. As a thin foil expands to near-critical densities, and the laser propagates through the plasma, other ion acceleration schemes, such as synchronized acceleration by slow light (SASL) [26] and magnetic vortex acceleration (MVA) [27], also become feasible.

Experiments to understand the physics underpinning ion acceleration in the RSIT regime led to the discovery of the generation a relativistic plasma aperture in ultrathin foils irradiated by ultrashort (tens-of-femtoseconds) duration laser pulses [28]. This forms only at the most intense part of the laser focus where RSIT occurs. It was shown that the laser light transmitting through this self-generated aperture can diffract and moreover that the spatial-intensity distribution of the beam of directly-accelerated electrons can be tailored by controlling the polarization of the laser light [28]. The distribution in the spatial profile of the generated electron beam is effectively transferred to the ion beam profile via modification of the electric field and thus it was also shown that the resulting ion beam contains features that are laser-polarization-dependant [28, 29]. Further numerical investigation of this regime has shown that interference of the transmitted light can increase the laser intensity [30] and produce high order harmonics [31] and high order spatial modes [32] of intense light.

With the advent of multi-petawatt laser facilities (see for example [33, 34]), which promise to increase the peak intensities achievable by orders of magnitude (\(\sim \)10\(^{23}\) Wcm\(^{-2}\)), the RSIT regime will become more prevalent as the Lorentz factor of the electrons oscillating in response to the laser light will eventually become large enough that even solid density plasma will be relativistically transparent to the laser pulse. Additional high-field effects, such as non-linear Compton scattering [35, 36] and multi-photon Breit-Wheeler pair production [37], will occur at the focus of the laser pulse, leading to the onset of what is known as the QED-plasma regime [38].

In this article, the physics of laser-plasma interactions in the RSIT regime is discussed to set out areas of interest for development of experiments on current and future laser systems. The onset of relativistic transparency in an ultrathin foil, including laser energy absorption considerations and the generation of a relativistic plasma aperture along with discussion of relativistic optical phenomena, is discussed in Sect. 2. Section 3 presents an overview of the effects on electron and ion acceleration, whilst the generation of intense structured light fields is covered in Sect. 4. To provide a perspective for the future, the expected role of high-field effects is discussed in Sect. 5, and finally the new directions in laser, target and radiation source optimization is presented in Sect. 6.

The article is not intended to be a review of the body of work done on relativistic laser-plasma interaction in the RSIT regime, but a discussion of relevant new physics discovered over the years in exploring this regime, illustrated with examples from the literature and primarily from studies undertaken by our group. It is intended to provide a perspective on new physics expected and new techniques to be applied as the first experiments in this regime get underway using higher repetition rate petawatt lasers and higher intensity, multi-petawatt lasers.

2 Onset of relativistic transparency

To describe the different plasma regimes and the transition between them, we must first consider the dispersion of an electromagnetic wave in a plasma. This is given simply for unmagnetized, homogeneous plasma by,

$$\begin{aligned} \omega ^{2} = \omega _{p}^{2} + k^2c^2 \end{aligned}$$
(1)

where \(\omega \) and k are the plasma wave angular frequency and wavenumber respectively, and c is the speed of light. Here, the EM wave is cut-off at the plasma frequency and starts to evanescently decay into the plasma. This dispersion relation can be seen in blue in Fig. 1a. For a specific laser pulse frequency, this cut-off occurs when \(\omega _{L} = \omega _{p}\). As the plasma frequency is defined primarily by the electron density, this leads to the definition of the classical critical density \(n_{c} = \omega _{L}^2 \epsilon _{0} m_{e} / e^2\). However, when we consider interactions with intense laser pulses, the electrons can be accelerated to relativistic velocities within a single laser cycle. This can be quantified by the normalized laser amplitude, \(a_{0} = e{\textbf {A}}/(m_{e}c^{2})\), where \({\textbf {A}}\) is the vector potential of the wave, which can more conveniently be related to the intensity by \(a_{0} = \sqrt{I_{L}\lambda _{L}^{2}/1.37\times 10^{18}\text {\,W\,cm}^{-2}\text {\,}\mu \text {m}^{2}}\), where \(I_{L}\) is the laser intensity in Wcm\(^{-2}\) and \(\lambda _{L}\) is the laser wavelength in \(\mu \)m. For \(a_0 \ge 1\), the interacting electrons can be considered relativistic, leading to a relativistic modification of the plasma frequency,

$$\begin{aligned} \omega _{p}^{'2} = n_{e}e^{2}/(\epsilon _{0}\gamma m_{e}) \end{aligned}$$
(2)

where \(\gamma \) is the Lorentz factor of the electrons. This corresponds to a relativistically corrected critical density \(n'_{c} = \omega _{L}^2 \epsilon _{0} \gamma m_{e} / e^2\). This means that for a plasma of the same density, if the mean electron energy becomes relativistic, the plasma frequency reduces, allowing previously cut-off EM waves to propagate. This process can be seen in Fig. 1a in red and is termed relativistic induced transparency. Therefore, for a plasma that is near critical density, both the local average energy and density of electrons dictates the propagation behaviour of the laser pulse.

Fig. 1
figure 1

a The non-relativistic and relativistic dispersion relation of an electromagnetic wave in a plasma. b The variation of the relativistic plasma frequency with intensity and plasma density with the opaque region (\(\omega '_{p}>\omega _{L}\)) given in grey

Full size image

During the interaction, \(\gamma \) is related to the intensity by \(\gamma = \sqrt{1+a_0^{2}/2}\) [2], and we can see from Fig. 1b that as the laser intensity is increased, the laser can propagate in higher density plasma. For an intensity of 10\(^{22}\) Wcm\(^{-2}\), some solid density materials, such as cryogenic solid hydrogen, start to become relativistically transparent to the laser pulse, for a wavelength \(\lambda _L \sim \)1 \(\mu \)m.

Fig. 2
figure 2

a Example 2D simulation setup showing the initial longitudinal profile of \(n_{e}\) for a solid density 100 nm-thick aluminium target that would occur prior to interaction (orange) and the same target after Gaussian expansion to a peak density of 5\(n_{c}\) (black) - note the different axes. b Spatial laser intensity and \(n_{e}\) distributions for the laser propagation (in 2D) through the expanded target at t = 0 (corresponding to the peak of the laser pulse interacting with the initial target front surface position). See Supplementary Material for the simulation parameters

Full size image

Whilst 10 PW-class laser systems capable of achieving a peak focused intensity of \(\sim \)10\(^{23}\) Wcm\(^{-2}\) are becoming operational, most work to date has been done using PW class systems with a maximum of \(\sim \)10\(^{21}\) Wcm\(^{-2}\). Although available high power laser systems cannot produce relativistically transparent plasma at solid density, the RSIT regime is accessible via expanding an ultrathin (nanometre-thick) foil target. The heating and expansion results in both the peak electron density reducing and the electron temperature becoming relativistic. If the target is sufficiently thin, the peak density will drop below \(n'_c\), allowing the remainder of the laser pulse to propagate in the now relativistically underdense plasma. An example of this propagation can be seen from a 2D simulation of a longitudinally pre-expanded 100 nm aluminium target, with the longitudinal electron density profile shown before and after expansion in orange and black, respectively, in Fig. 2a. The laser intensity and electron density during the interaction with an \(a_{0}\) = 20 laser pulse is shown in Fig. 2b for time t = 0, defined as when the peak of the laser pulse temporal profile reaches X = 0. This combined expansion and heating gives rise to RSIT [22].

Prior to the onset of RSIT, the pulse will propagate up to the density of \(n'_c\). The contour corresponding to this density defines the relativistically corrected critical surface. The radiation pressure of the laser light at this surface can result in electrons being driven forward beyond the influence of the laser pulse. This can have the effect of both moving the relativistically corrected critical surface in the direction of the laser light pressure and increasing the density beyond [14]. As this density build-up depends upon the laser intensity, this leads to local higher density spatial regions within the plasma. As the plasma undergoes RSIT, these higher density perturbations lead to non-linear propagation of the laser pulse through the plasma. Likewise, within the now relativistically transparent plasma, the ponderomotive force can drive electrons out of the high intensity regions of the laser light, resulting in similar density build-up.

For sufficiently thin foil targets with the same thickness and material, the RSIT behaviour is primarily dictated by the peak intensity and spatio-temporal profile of the laser. It is therefore possible to gain a degree of control over the expansion, and ultimately the onset of RSIT. This can be achieved by using an additional laser pulse, arriving at a selected time prior to the main pulse or through careful control of the temporal-intensity contrast of the laser pulse, to induce the expansion prior to the interaction of the main pulse [39, 40]. If a target is expanded such that a large volume of plasma has a density close to that of the critical density, this is often referred to as near-critical density plasma (NCD). This can also be produced from different advanced targetry techniques, examples of which include foam or high density gas jet targets, which will be explored later in Sect. 6.1.

As the plasma transitions from opaque to relativistically underdense, a variety of effects can occur. For example, variation in laser energy absorption, plasma optical processes and the formation of a relativistic plasma aperture [28] are some of the behaviours that we have recently investigated. In the following sections, these effects are explored in more detail.

Fig. 3
figure 3

a Experimental set-up employed to determine the degree of laser energy absorbed by the target, through the use of an integrating sphere and diffuse scatter screens to quantify the the degree of unabsorbed light. b Photograph of the integrating sphere in use in an experiment. c Experiment results (black) and 2D simulation results (red) of laser energy absorption as a function of initial target thickness (prior to irradiation), together with the percentage of transmitted light (blue) in the same simulations. See reference [41] for further details

Full size image

2.1 Transition to volumetric energy absorption

In the context of expanding ultrathin foil targets that become relativistically transparent to the drive laser pulse, it is important to understand how this affects the absorption of laser energy into the plasma itself. Experimental measurements of the absorption in such targets were made by enclosing the interaction within an integrating sphere as shown in the schematic in Fig. 3a and with an example photograph of the setup in Fig. 3b [41]. This enabled the diffuse and transmitted light integrated inside the sphere to be quantified through careful calibration of optical spectrometers, with the specularly reflected light measured outside the sphere using a diffuse scatter screen. Combined, these enable the absorption into the plasma to be quantified for a range of target thicknesses. The results, along with corresponding absorption and transmitted light determined from 2D PIC simulations, are shown in Fig. 3c. As the target thickness is reduced to \(\sim \) 380 nm, the peak density approaches \(n'_{c}\) and the absorption maximizes. As the thickness is reduced further, the plasma expands and becomes relativistically transparent to the laser pulse during the interaction, resulting in a reduction in absorption as the laser light is now able to propagate. Unlike the opaque case that relies purely on surface absorption effects, such as \({\textbf {j}} \times {\textbf {B}}\) heating, volumetric heating processes within the plasma occur for the relativistically transparent case. When there is significant transmission of the laser, there is a reduction in surface absorption, and conversely there is an increase in volumetric absorption that principally takes the form of direct electron acceleration, which is discussed in Sect. 3.1. In the case of ultrathin targets, this results in an overall decrease in laser energy absorption, but a change in the partitioning of the absorbed energy from the bulk heating of electrons to the acceleration of fast electrons. This will be an important consideration when designing future experiments involving ultrathin foils.

2.2 Relativistic optical phenomena

Fig. 4
figure 4

Example 2D simulations results [42] showing the intensity profile of the laser pulse at t = 0 for an initially overdense (420\(n_c\)) 75 nm-thick plastic target, for a focal spot size of: a 1.5 \(\mu \)m; and, b 5 \(\mu \)m. The white contour indicates an electron density of \(n'_{c}\). The peak intensity as a function of time is shown for different focal spot sizes: c in vacuum; and, d for the 75 nm-thick target. The laser pulse energy is constant for all cases

Full size image

As the refractive index of plasma is related to the laser and plasma frequencies, given by \(\eta = \sqrt{1-\omega _{p}^{'2}/\omega _{L}^{2}}\), steep local refractive index variation can occur across the plasma due to both plasma depletion and buildup, as well as variation in the degree of relativistic heating of electrons. This has been reported in the case of an ultrathin foil target undergoing RSIT [42]. Figure 4a shows that for the case of a tightly focused laser pulse, with a 1.5 \(\mu \)m full-width at half-maximum (FWHM) diameter, a relativistic plasma aperture (discussed in the next section) has formed in a fully ionized, initially solid density plastic target with an initial thickness of 75 nm. In this case the focus is at the front surface of the initial target. For a larger focal spot diameter (5 \(\mu \)m) shown in Fig. 4b, the relativistic plasma aperture forms but the laser pulse then self-focuses within the plasma to a similar diameter as the 1.5 \(\mu \)m case over a distance of \(\sim \)5 \(\mu \)m. This is close to the diffraction limit of the simulated laser, meaning that the peak intensity of the interaction reaches that of the tightest focal spot without requiring a short focal length optic. The effect this has on the peak intensity of an energy-conserved pulse with different focal spot diameters is shown in Fig. 4c, d. Here, due to the conservation of energy in 2D Cartesian geometry, the intensity reduces linearly in vacuum with increasing focal spot diameter, as expected. However, in the presence of a target that has undergone RSIT, the peak intensities become comparable with the tightest focus for all focal spot diameters with the exception of the largest (10 \(\mu \)m) simulated. As these are 2D PIC simulations it is important to note that because the resultant intensity scales linearly with radius as opposed to the square, this may lead to underestimation and overestimation of certain particle dynamics at different spatial positions of the laser pulse. This occurs because the resulting intensity is lower when it focuses and higher when it defocuses when compared with the realistic 3D case. It is important that simulations and analytical models consider this behaviour and ensure that this effect is acknowledged and/or accounted for.

Depending upon the application, the potential to self-focus to the diffraction limit in targets that undergo RSIT could relax the requirement for short focal length optics on current and future laser facilities to achieve the highest intensities.

Other optical effects in the relativistic transparency regime include the potential to directly modify the polarization of the propagating laser pulse. In the case of uniform, NCD plasma extending over microns, it has been predicted that a polarization rotation can be induced in the propagating pulse when there is an anisotropic relativistic temperature in the transverse plane [43, 44]. This is attributed to asymmetrical heating resulting in an apparent variation of the critical density of the orthogonal components of the laser electric field due to the initialized counter-streaming electron population transverse to the laser-axis. The polarization can also appear to be modified by the superposition of the propagating pulse and the generation of new light at the same frequency with a different polarization state, which will be discussed in detail later.

Additionally, as overdense plasma undergoes RSIT, temporal laser pulse steepening can ensue [45, 46]. This is a consequence of relativistic self-phase modulation of the pulse [47] as it propagates in the transparent plasma, due to the intensity dependence on the refractive index of the plasma.

Fig. 5
figure 5

Example 3D simulation results, for the central plane of the laser polarization direction, showing the electron density and intensity of the laser pulse at: a \(t = -\tau _{L}\); b \(t = -\tau _{L}\)/2; and, c t = 0 (t = 0 corresponds to the peak of the laser pulse interacting with the initial front surface of the target). The target is the equivalent of a 10 nm-thick aluminium foil pre-expanded to a peak \(n_{e}\) = 30\(n_{c}\). See reference [28] for further details

Full size image

2.3 Relativistic plasma aperture formation

Due to the localized spatial-intensity profile of the focused laser pulse, heating and expansion occurs within a finite region of the target. Due to the cylindrical symmetry of the laser focus, this results in a circular area with a diameter comparable to the laser focal spot diameter where the density drops and eventually becomes relativistically transparent. The remainder of the laser pulse can propagate through this finite region that is termed a relativistic plasma aperture [28]. This formation can be observed in the time sequence shown in Fig. 5 for a laser with pulse duration \(\tau _{L}\). The laser pulse first impinges on the critical surface of the pre-expanded target shown in Fig. 5a. As the intensity rises, the relativistically corrected critical surface is driven forward, Fig. 5b. As the interaction continues, the density reduces at the centre of the pulse while the temperature becomes relativistic, leading to the onset of RSIT within the centre of the laser focus, Fig. 5c. This can lead to a complex interaction of the laser pulse with relativistically underdense plasma in the centre and overdense plasma at the edge of the laser focal spot. Note that in experiments the achieved focal spot may not necessarily be perfectly symmetric due to aberrations in the wavefront, resulting in potentially skewed aperture geometries.

The evolution of the relativistic plasma aperture diameter is related to the peak intensity, temporal profile, polarization state and focal spot size of the impinging laser pulse, as well as the initial thickness and/or density of the target. As the highest intensity occurs at the centre of the focal spot, the aperture diameter can begin small and expand. As the intensity reduces radially, the edges of the focal spot induce lower electron energies than the centre, resulting in an intensity dependence on the aperture size. As the intensity of the pulse increases with time on the pulse rising edge, the effective diameter of the focus for which the intensity is above the relativistic threshold also increases, resulting in a larger diameter aperture. As previously discussed, self-focusing can occur over \(\mu \)m-scale distances as the pulse propagates through NCD plasma. This can therefore vary both the focal spot size and the intensity at the critical surface and will depend upon the amount of expanding plasma in-front of the critical surface.

For larger NCD plasma volumes (on the order of tens of \(\mu \)m or more), such as that formed by substantially expanded solid targets, foams or gas-jets (see Sect. 6.1), this effect will also occur but is more akin to plasma channel formation [48]. This is due to the pulse propagating through significantly more plasma before reaching free-space. In this case, if the plasma is predominately below \(n'_{c}\), plasma builds up as it is expelled from the centre of the pulse and results in local overdense channel walls. This can be observed in an example 2D simulation in Fig. 6 for a 250 nm aluminium target pre-expanded with a Gaussian profile to a peak density of 2\(n_c\).

Fig. 6
figure 6

Example 2D simulation result showing the electron density (on a logarithmic scale) and longitudinal electric field contours for a 250 nm-thick aluminium target pre-expanded with a Gaussian profile to a peak density of 2\(n_c\) during interaction with a \(a_{0}\) = 20 laser pulse. This is shown when the peak of the pulse reaches X = 0. See Supplementary Material for the simulation parameters

Full size image

As the pulse propagates through the induced relativistic plasma aperture, it can undergo diffraction, producing an intense near-field diffraction pattern at the rear of the aperture [28, 29]. The near-field diffraction pattern is demonstrated from 3D PIC simulations in Fig. 5c [28]. Unlike conventional optical systems, this can be a very dynamic process due to the motion of the dense plasma over the remainder of the intense laser pulse interaction. As the aperture diameter can vary during the interaction, this can result in a temporally varying diffraction pattern over the course of the interaction. Within the near-field at the rear of the aperture, this high intensity diffraction pattern influences the plasma electrons escaping from the target and at the target rear [28]. It has been shown from 3D PIC simulations that this induces changes to the spatial profile of the beam of accelerated electrons and ions [29]. This pattern also changes with the degree of ellipticity in the polarization of the drive laser pulse and gives a potential degree of control over the resultant accelerated electron and ion beams.

As intensities are further increased, thicker targets will be able to form a relativistic plasma aperture, but may be more akin to that of a plasma channel if the thickness is significantly greater than the laser wavelength. It is therefore important to consider the effects seen in the interactions of longer plasma channels or preformed apertures, as reported in reference [49].

3 Particle acceleration in the RSIT regime

Particle acceleration is one of the primary motivations for the study of intense laser-solid interactions in the RSIT regime. In the following sections, we explore some of the recent investigations of direct electron acceleration and enhanced ion acceleration, along with potential applications.

Fig. 7
figure 7

a Experiment results showing the total energy of the electrons escaping from the rear of the target, as a function of target thickness (black). Normalized 2D simulation results for the same parameters are shown for comparison (red), together with the degree of transmission through the target (blue). b Average electron energy from a 2D simulation of a 376 nm-thick aluminium target that remains opaque. c Same, for a 40 nm-thick aluminium target that undergoes RSIT. For both cases, the pulse length is 400 fs and the results are shown 200 fs after the interaction of the peak of the pulse with the target front surface [41]

Full size image

3.1 Direct electron acceleration

During the propagation of an intense laser pulse in relativistically underdense plasma, if a relativistic plasma aperture or a longer plasma channel has formed, electrons can be accelerated and pulled inwards from the higher density walls [50, 51]. This is seeded by strong longitudinal electric fields at the edge of the laser focal spot. These exist for tightly focused laser pulses in free-space due to higher order terms in the Gaussian beam equation [52]. These longitudinal fields can accelerate electrons to relativistic velocities along the laser axis and can propagate with the laser pulse over long distances before dephasing and being decelerated. The fields responsible for the acceleration of bunches of electrons can be observed in Fig. 6. The radial motion of the electrons arises due to the transverse component of the laser electric field. This occurs at the side of the aperture edge when the transverse electric field is directed away from the laser axis. For linear polarization, this can lead to electron bunches forming at \(\omega _{L}\) at each side of the aperture/channel, whereas circular polarization leads to a continuous helical electron beam formation [28]. This can result in increased numbers of accelerated electrons that can be detected experimentally from the rear-side of the targets. This is shown in Fig. 7a for varying target thickness. The thinnest targets that have expanded and undergone relativistic transparency show the highest numbers of escaping electrons. From 2D PIC simulations, this can be verified when comparing fully opaque targets with those which undergo transparency, shown in Fig. 7a [41]. In the case of a fully opaque target, only the electrons at the front surface are accelerated by the laser before propagating through the target. This can be seen in the average electron energies 200 fs after the peak of the laser pulse has interacted with the target, shown in Fig. 7b. In contrast, the electrons in the target that undergoes RSIT are directly accelerated by the laser pulse throughout the volume, leading to high average electron energies, as shown in Fig. 7c.

Depending on the desired outcome, this change in the partitioning of energy should be considered in future experiments. For applications and/or processes that require high energy electrons, relativistically transparent targets will provide these in a larger number, whereas for improving total laser absorption, targets that are on the cusp of RSIT prove to be optimal. The specific thickness of target for optimization would need to be adjusted depending on the laser system used.

3.2 Enhanced ion acceleration

One of the main interests in the interactions of intense light with near-critical plasma is in the acceleration of ions, producing beams with both high flux and high energy. For initially opaque plasma, the main ion acceleration mechanism is TNSA [12, 13]. Here, the interaction at the critical surface of the plasma (where \(n'_{e} = n_{c}\)) produces high energy electrons, predominately via the \({\textbf {j}} \times {\textbf {B}}\) heating, resonance absorption and vacuum heating mechanisms. These hot electrons propagate through the overdense plasma and a percentage escape from the rear side. This generates a strong electrostatic sheath field that accelerates the ions at the rear surface. A divergent beam of ions with a thermal energy spectrum results, with a maximum experimentally detected energy of \(\sim \) 85 MeV [53] to date.

Fig. 8
figure 8

a Measured proton maximum energy as a function of target thickness in experiment [25]. b PIC simulation results showing the longitudinal electric field along the laser axis for a target that becomes transparent close to the peak of the interaction. The grey lines indicate the highest energy protons. The black solid line indicates the relativistically corrected critical surface and the black dashed line shows the rear proton surface [56]

Full size image

Another well studied mechanism of ion acceleration for opaque targets is radiation pressure acceleration (RPA) [14]. This relies upon the radiation pressure imparting momentum into the electrons at the target critical surface, however, if the plasma is sufficiently thin (\(\ll \lambda _{L}\)) this force can drive the entire population of plasma electrons forward, resulting in a charge separation field between the now offset electron and ion populations. It is this field that accelerates the ions. To maximize this behaviour, a circularly polarized laser pulse is typically used to reduce electron heating. The resultant ion beams are predicted to have a monoenergetic energy distribution [15]. However, as the target thickness is reduced to optimize this behaviour, instabilities such as the Weibel instability [54] and Rayleigh-Taylor-like instabilities [55] can lead to break-up of the critical surface.

Fig. 9
figure 9

2D simulation results showing electron density for a pulse with peak \(a_{0} = 20\) interacting with an initially solid density aluminium target at \(t = \tau _{L}/4\) for: a \(\tau _{L} = 100\) fs; b \(\tau _{L} = 200\) fs; c \(\tau _{L} = 400\) fs; and, d \(\tau _{L} = 600\) fs. The inset in a shows a zoomed-in region of the electron density in the region of the focal spot, corresponding to the black dashed box. The thickness of the target is adjusted such that the target undergoes RSIT at t = 0. See Supplementary Material for the simulation parameters

Full size image

In the case of an expanding foil undergoing RSIT, both processes can still take place if the plasma is locally overdense. However, when the plasma density is close to \(n_{c}\), relativistic transparency and direct electron acceleration can start to play a role. In the case of an expanding ultrathin foil undergoing RSIT, a hybrid of TNSA and RPA [17] can occur that is further enhanced by the onset of transparency.

In this case, while the plasma is overdense, a strong rear surface field forms initially accelerating ions by TNSA. As \(n_{e}\) in the focal spot region begins to reduce and approaches \(n'_{c}\), RPA begins to push the lower density population forward, setting up an additional electric field, or a second peak in the overall field distribution. When the plasma undergoes RSIT, the dual-peaked electric field is enhanced, resulting in increased acceleration of the ions. This has resulted in experimentally detected peak proton energies of near-100 MeV [25], as shown in Fig. 8a and has been found to occur when the onset time of RSIT occurs close to when the peak intensity of the laser pulse interacts with the target [56]. An example of the combining accelerating longitudinal fields, the evolution of the relativistically corrected critical surface and the position of the highest accelerated protons are shown in Fig. 8b [56] along the longitudinal laser axis, X, and as a function of time (in terms of pulse duration, \(\tau _{L}\)). The peak of the pulse is defined to interact with the target front surface at t = 0.

At the same time, direct electron acceleration from the edges of the relativistic plasma aperture increases the number of fast electrons propagating forward. As the laser pulse duration is increased to the order of hundreds of laser cycles of interaction (i.e. picosecond duration laser pulses), unstable behaviour between the formed bunches can lead to the suppression of one side of the bunches, producing a more collimated jet of electrons modulated at \(\lambda _{L}\) directed along the laser axis [39, 57]. As this propagates through the accelerated ions, the negative charge attracts the protons. The enhanced field also acts to accelerate the proton population preferentially along the laser axis. This acts to align the high energy component of the proton beam closer to the laser axis. This is more noticeable when the target normal is orientated at an angle from the laser axis [58]. The generation of this electron jet is an unstable and stochastic process [59], becoming more statistically likely as \(\tau _{L}\) is increased. This can be observed in Fig. 9a–d for \(\tau _{L}\) = 100 fs, \(\tau _{L}\) = 200 fs, \(\tau _{L}\) = 400 fs and \(\tau _{L}\) = 600 fs, respectively. The target thickness is adjusted such that the target undergoes RSIT at t = 0 and each figure is shown after RSIT at t = \(\tau _{L}\)/4. The laser \(a_0\) = 20 in all cases. As can be seen, for the smaller \(\tau _{L}\), Fig. 9a–b, the electron distribution is strongly influenced by the laser propagation through the relativistic plasma aperture, including diffraction-like effects. With increasing \(\tau _{L}\), and thus plasma expansion, as shown in Fig. 9c–d, an unstable electron jet feature is produced and extends beyond the expanded plasma.

3.3 Particle source applications

The beams of energetic particles produced by the laser-driven particle acceleration processes in the RSIT regime have the potential to be used to produce secondary sources of particles and radiation. In particular, high energy DLA electrons can scatter with high Z nuclei (such as Au) to produce gamma-rays via the bremsstrahlung emission process [60]. Similarly, high energy ions produced from targets undergoing RSIT, can be captured by a Beryllium converter to produce high numbers of energetic neutrons [61].

Another ambitious potential application of laser-driven ions is for cancer therapy. This would require selectable ion energies beyond 200 MeV for protons, with low energy spread, and produced in a stable and reproducible way [62]. At present, protons accelerated from targets undergoing RSIT have achieved energies of near-100 MeV using a high energy, low repetition rate laser [25]. Further development is required to increase the ion energies achieved with more compact, lower energy and higher repetition rate lasers, and to increase the reproducibility of the ion beams. There are also projects underway to combine laser produced protons in combination with conventional accelerators for radiobiology applications [63].

The production of jets of electrons and expansion of plasma into vacuum can also, if the scaling laws are properly accounted for, be considered as a laboratory analogue for astrophysical phenomena [64]. For example, the electrons produced via DLA during RSIT, and their associated EM fields, have been suggested as an analogue for jets produced in active galactic nuclei [28].

4 Structured light fields

Another significant discovery involving targets transitioning from opaque to relativistically transparent is the production of structured light fields [32]. The following sub-sections discuss the generation of coherent intense light with higher order mode structures, temporally varying polarization states and high harmonics.

Fig. 10
figure 10

Example 3D simulation result, showing a the generation of spatially modulated electron bunches from a relativistic plasma aperture, and b the time-integrated spatial profile of the magnitude of the parallel (top) and perpendicular (bottom) electric field components, relative to the laser polarization, detected at X = 10 \(\mu \)m. See reference [32] for further details

Full size image

4.1 Intense light in higher order modes

The interaction of an intense laser pulse with a relativistic plasma aperture or plasma channel can result in the generation of new coherent light at harmonics of the laser frequency [32]. As electrons are directly accelerated from the aperture/channel walls, they propagate through and out of the rear of the plasma where they experience the rear surface sheath field set-up by the fast electron populations. The electrons are decelerated within this field and consequently emit broadband radiation. However, as the electrons are accelerated with a longitudinal bunched structure on the order of the laser wavelength, the emitted radiation constructively interferes, resulting in coherent light at the fundamental laser frequency and higher order harmonics. For opaque targets, coherent transition radiation (CTR) is generated due to fast electrons transiting through the target rear [65]. This occurs with a frequency of 2\(\omega _{L}\) due to the electron acceleration by the \({\textbf {j}} \times {\textbf {B}}\) force, which produces CTR at 2\(\omega _{L}\) with radial polarization.

In the case of a relativistic plasma aperture, the spatial structure of the generated light is more complicated. For linearly polarized laser light, the bunches of electrons are accelerated from two opposite edges of the aperture (two poles) at \(\lambda _{L}\) where the laser polarization vector is perpendicular to the aperture, but the bunches are offset by \(\lambda _{L}\)/2 at each edge, shown in Fig. 10a. The light emitted from these offset bunches and from the interaction of the laser at the aperture surface, interferes and can produce light with a higher order spatial structure. At the fundamental laser frequency, this results in light with a TEM\(_{02}\) spatial mode polarized parallel to the laser polarization direction and TEM\(_{11}\) polarized perpendicular. As the laser propagates with the generated light it is difficult to distinguish the generated light in the same polarization direction as the laser, but the perpendicular polarized light can be detected. This can be observed from 3D PIC simulations as shown in Fig. 10b [32].

Spatial overlapping of the generated intense light at \(\omega _{L}\) with perpendicular polarization and the transmitted laser light can produce an effective rotation in polarization angle in the total measured light signal (with respect to the polarization of the incident light). As the transmitted light level is reduced to the level of the generated light, the degree of apparent polarization rotation is increased.

Fig. 11
figure 11

Example 3D simulation results [32]. a Laser energy conversion efficiency into 2\(\omega _{L}\) light, shown for the two orthogonal polarization components in absolute electric field terms. b–c Time-integrated spatial profile, in the Y–Z plane, of the intensity of 2\(\omega _{L}\) light for: b a 5 nm-thick target; and c a 20 nm-thick target, detected at X = 10 \(\mu \)m

Full size image

The generated light also occurs at harmonics of the laser frequency. The laser energy conversion efficiency to the second harmonic light (2\(\omega _{L}\)) is shown as a function of initial target thickness from 3D PIC simulations in terms of the integrated absolute electric field for both orthogonal components in Fig. 11a. The spatial structure that is produced is different from that of the fundamental. For thinner targets, the spatial structure is a TEM\(_{01}\) mode, polarized parallel to the laser polarization direction, with reduced generation in the perpendicular direction. This can be seen in Fig. 11b. For current laser systems considered, conversion efficiency into 2\(\omega _{L}\) is on the order of a few percent of the laser energy. As the target thickness is increased, the spatial mode and polarization profile reverts to the radial polarization of CTR, shown in Fig. 11c.

Based on the behaviour of targets undergoing RSIT, this generation mechanism was found to also be induced by using a target with a preformed aperture [32, 49]. This can provide a further degree of control over the produced modes and can be more readily optimized in relatively thicker targets to improve the conversion efficiency. By tailoring the target geometry it is possible to increase the conversion efficiency to 2\(\omega _{L}\) light by more than a factor of 2. Using circular polarization with such a preformed aperture can also result in higher harmonics with orbital angular momentum [31]. This can be observed in the 2\(\omega _{L}\) surface contours of the electric field components shown in Fig. 12 from the 3D simulation of a circularly polarized pulse interacting with a target with a preformed aperture diameter of 2.5 \(\mu \)m. The pulse has an intensity of 10\(^{21}\) Wcm\(^{-2}\), a duration of 40 fs, and a focal spot FWHM diameter of 3 \(\mu \)m. This produces two twisted orthogonal Laguerre-Gaussian, LG\(_{01}\) modes that are out of phase by \(\pi /2\). These distinct lobes can be readily seen in the electric field components shown in transverse plane at X = 9.4 \(\mu \)m, in Fig. 12.

Fig. 12
figure 12

Example 3D simulation results showing electric field component surface contours at ±5 TVm\(^{-1}\) filtered for 2\(\omega _{L}\), for a laser pulse interacting with a pre-formed aperture target with a 2.5 \(\mu \)m diameter and thickness of 2 \(\mu \)m. Also shown is the electric field components in the Y-Z plane at X = 9.4 \(\mu \)m [49]

Full size image

As the generation of light can begin prior to transparency, this propagates in front of the transmitted light. If these sources are of comparable intensity, they interfere and produce a detectable modulation (fringes) in the resultant spectrum [66]. This behaviour has been measured and confirmed using a frequency resolved optical gating (FROG) diagnostic. This effect can give a measure of the onset time of transparency and could be considered for future experiments.

4.2 Temporally varying polarization

Generating light with higher order spatial structure in this way can result in a temporally varying spatial structure and polarization distribution. In the case of 2\(\omega _{L}\), before the plasma becomes relativistically transparent to the laser pulse, CTR occurs producing radially polarized light with a fundamental mode structure. As the target undergoes RSIT, the direct acceleration of electrons now produces light, linearly polarized with a TEM\(_{01}\) structure. The relative strength of these light fields will vary depending upon the onset time of RSIT.

Fig. 13
figure 13

Intensity and electric field vectors in the transverse plane 10 \(\mu \)m from the rear of a 5 nm-thick target at: a 24 fs; b 40 fs; and, c 56 fs, after the peak of the pulse interacts with the front surface of the target. d–f Same, for a 20 nm-thick target [32]

Full size image

By varying the thickness of the target, the temporal delay and ratio of 2\(\omega _{L}\) CTR and generated light can be modified. As can be seen in Figs. 13a–c, for an initial target thickness of 5 nm, RSIT occurs early, and thus the generated light from the aperture dominates and the resultant observed light 10 \(\mu \)m from the target has a dominant TEM\(_{01}\) structure at times t = 24 fs, t = 40 fs and t = 56 fs. However, for a target thickness of 20 nm, the CTR can occur prior to RSIT, resulting in a radially polarized mode at t = 24 fs, shown in Fig. 13d, becoming a mixed mode at t = 40 fs (Fig. 13e) and finally a TEM\(_{01}\) structure at t = 56 fs (Fig. 13f).

This provides a potential approach to controlling the generation of a pulse of relativistically-intense 2\(\omega _{L}\) light with a temporally variable polarization and spatial-intensity distribution.

4.3 High harmonic generation

The focus so far has been on the generation of the fundamental and second-harmonic frequencies of light from a relativistic plasma aperture either pre-defined or formed by RSIT as these are the dominant frequencies. However, higher harmonics are also present during the interaction. In the case of initially opaque targets, the spectrum of generated light, detected 10 \(\mu \)m from the rear of the target, integrated across the transverse dimensions is shown in Fig. 14 for three example target thicknesses of 5 nm, 10 nm and 20 nm. The laser light is linearly polarized in all cases, with a peak intensity of 1\(\times \)10\(^{21}\) Wcm\(^{-2}\), a pulse duration of 40 fs, and focused to a FWHM diameter of 3 \(\mu \)m [32]. As can be seen, higher harmonics are produced in all cases, with the spectral power, \(E_h\), falling off with a power-law scaling of \(E_h\propto (\omega /\omega _{L})^{-1.5}\). Notably, the thinner targets show significantly higher spectral power at the fundamental frequency as more of the laser light is transmitted. As the new light can be generated just prior to RSIT, due to the DLA from the deformed relativistically corrected critical surface, and because higher frequency light can propagate through denser plasma, the higher harmonics appear at comparable spectral power even for thicker targets. Note, this is spectral power of the electric field and therefore the overall energy difference between the harmonics will be squared. For these higher harmonics, the odd and even harmonics tend to have a comparable spatial structure to the fundamental and second harmonic, respectively.

Fig. 14
figure 14

3D PIC simulation results showing the harmonic spectrum of the generated and transmitted light for: a an initially opaque target for 3 stated target thicknesses, with linearly polarized light [32]; and, b an opaque target with a pre-defined aperture of 3 \(\mu \)m diameter and 1 \(\mu \)m thickness for both linear and circular polarized light [49]. All other laser parameters are identical for all cases

Full size image

Similarly, when using a preformed aperture, the higher harmonics can also be seen. This is shown in Fig. 14b for an aperture diameter of 3 \(\mu \)m and target thickness of 1 \(\mu \)m, for both linear and circular polarization [49]. Here, the harmonic spectrum falls off with a faster power-law scaling \(E_h\propto (\omega /\omega _{L})^{-1.9}\) for both polarization cases. This is notably slower than that reported by Yi [31] of \(E_h\propto (\omega /\omega _{L})^{-3.5}\) but may be due to the finite spatial focal spot and higher \(a_0\sim 20\) used here. It is a faster fall-off compared with the initially opaque targets and is likely due to the reduced amount of plasma available at the centre of the target. The aperture targets, however, have appreciably less spectral noise compared with the initially opaque cases as there is no initial impediment to the laser pulse propagating.

4.4 Structured light applications

The possibility to generate and vary the spatio-temporal profile and polarization state of intense laser pulses opens new avenues for exploring the interactions with plasma in the RSIT regime. Investigations considering not only higher order mode structures but temporally varying mode structures may yield new insights and optimization of the processes that can occur during these interactions. The use of complex LG modes for driving wakefield acceleration in low density gas-jets [67] and circularly polarized LG modes with opaque nanometer-thick foils [68] have been considered, but there is further scope to investigate the use of temporally varying spatial structures. Additionally, it is possible to generate higher harmonics of the laser frequency. As the critical density is related to \(\omega _{L}^{2}\), by using intense pulses at 2\(\omega _{L}\) and above, it is possible to have a significantly reduced critical density, thus reducing the density requirements to undergo RSIT.

As temporally varying the polarization state is difficult to achieve with conventional optics at the intensities achievable with high power laser systems, there is significant scope for further investigation into applying this new light as a driver in laser-plasma interactions. For example, the polarization state of the laser can affect instability growth during ion acceleration mechanisms such as RPA [69], and therefore the ability to dynamically vary this state may also prove beneficial.

Fig. 15
figure 15

Schematic illustrating the feedback between quantum and relativistic plasma processes that occurs in the QED-plasma regime and the impact upon plasma dynamics and high-field mechanisms

Full size image

5 High-field effects

The multi-petawatt laser systems coming online should enable peak laser intensities on the order of 10\(^{22}\)–10\(^{23}\) Wcm\(^{-2}\). This will open up new regimes of interaction where high-field and potentially QED processes can start to play a significant role. When the plasma electrons have sufficient average momentum, emission of high energy photons can occur from deflections due to collisions (bremsstrahlung) [70, 71] and interaction with strong electric and magnetic fields (synchotron/non-linear Compton scattering) [35, 36]. An electron emitting radiation in a strong electromagnetic field is subject to the radiation reaction force, which can strongly influence its dynamics. The high-energy photons emitted can also interact with the high intensity laser pulse to produce electron-positron pairs via the non-linear Breit–Wheeler process [37]. High-field QED processes of this type change the overall plasma evolution, which in turn influences the quantum processes, as demonstrated schematically in Fig. 15 [72,73,74]. This is the QED-plasma regime [38].

Fig. 16
figure 16

2D simulation results: a The onset time of relativistic self-induced transparency as a function of target thickness; b Example electron spectra for a target thickness of 1.8 \(\mu \)m. The green and black lines indicate simulations with radiation reaction (RR) included and excluded, respectively [56]

Full size image

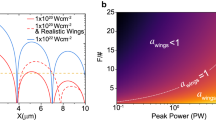
High field phenomena will affect the physics of RSIT. For example, radiation reaction is expected to delay the onset time for RSIT, \(t_{rsit}\), for a laser pulse with \(a_{0} = 310\), as shown in Fig. 16a [56]. As shown in Fig. 16b, this results from cooling of the highest energy electrons due to the emission of high energy photons [56]. While this effect can result in an overall reduction in electron energies, in the RSIT regime it can lead to increased coupling to ion energies [75]. As peak laser intensities are further increased it will also be necessary to consider the effect of spatial-intensity contrast as light in the wings outside of the main focal spot will also begin to reach relativistic intensities [76].

Photons produced via non-linear Compton scattering (NLCS)/synchrotron mechanisms are predicted to be highly energetic (\(\sim \)MeV) and with a high overall laser-to-photon energy conversion efficiency (up to tens of percent) [37, 77, 78]. This provides another potential source of usable high energy radiation. By varying the target thickness and laser intensity, the energy conversion efficiency is found to be related to the onset time of RSIT, as shown in Fig. 17 [79].

As the peak intensity is driven higher still, QED processes such as the non-linear Breit-Wheeler pair-production mechanism start to become increasingly relevant. For example, the high energy photons produced in an ultraintense laser-solid interaction can interact with a secondary high intensity laser pulse producing electron-positron pairs [80]. Similarly, by colliding two intense laser pulses within a NCD plasma, there is also the potential to produce high energy positron beams [81].

Fig. 17
figure 17

Laser-to-NLCS energy conversion efficiency (\(\eta _{sy}\)) as a function of laser intensity and target thickness, with the percentage of laser transmission shown in white contours [79]

Full size image

6 Optimization of RSIT processes

Taking full advantage of the processes and mechanisms arising from targets undergoing RSIT requires optimization of the interaction physics. This section highlights recent efforts with higher repetition rate lasers, advances in targetry design and the application of new machine learning techniques, all of which aid in optimizing the particle and radiation sources generated.

6.1 High repetition rate lasers and advanced targetry

High repetition (> 1 Hz), high power (> 100 TW) laser systems are becoming increasingly available. This provides a new paradigm in laser-plasma interactions, enabling statistically significant measurements and direct feedback. In terms of applications, sampling of high repetition X-ray generation can enable tomographic measurements [82] and ptychography imaging [83]. At present, these high repetition rate systems have been suggested for use in laser wakefield experiments with low density gas-jets [84] and could also be used with solid density tape drive targets [85]. To take full advantage of these high repetition rate laser systems, new target techniques are required to enable high repetition rate interactions in the transition of opaque to relativistically underdense plasma or the NCD plasma regime.

There have been developments in using thin liquid crystal films that can be produced in situ, creating ultrathin nanometer-thick targets [86]. This enables a layer of material to be created with variable target thickness at a current rate on the order of 0.1 Hz. Flat water jet targets could also be used at high repetition rate [87], although at present laser intensities these may not heat or expand enough to enable the RSIT regime to be accessible.

As hydrogen has the lowest ratio of electrons to ions when fully ionized, it is an ideal element to use. The high charge-to-mass ratio of the protons also produces the fastest ion response time. When the hydrogen is in solid or liquid form, the electron density is \(\sim 52 n_{c}\) or \(\sim 42 n_{c}\), respectively, for \(\lambda _L\) = 1 \(\mu \)m. While this is still classically overdense, with increasing \(a_{0}\), \(n'_c\) will begin to approach these densities. Experimental techniques for producing cryogenic hydrogen solid [88,89,90] and liquid [91] targets have been demonstrated. For interactions with currently overdense cryogenic targets, this has yielded multi-MeV proton acceleration [92,93,94].

Another technique for achieving a transition from opaque to relativistically underdense plasma is through the use of materials with low areal density. These can be materials such as carbon nanotubes [95], polymer foams [96] or aerogels [97]. Typically, these materials are made of thin, solid density filaments that lead to nanometer to micron-scale voids throughout their volume. This reduces the average density over the volume of the target. An example image of a foam structure is shown in Fig. 18a. When an intense pulse impinges on this type of target, the resultant plasma heats and expands, filling the internal voids. Ideally, this will eventually produce an approximately uniform plasma of NCD, with the average density depending on the void spacing and density of the filaments. This technique still relies upon heating the target to produce the required plasma density. This can be done with a separate, controlled pre-pulse in a dual-pulse arrangement, control of the temporal-intensity contrast or X-ray heating to induce filling of the voids. However, depending on the density and expansion time, there may still be higher density regions centred at the location of the individual filaments and significant expansion into vacuum. This can affect laser pulse propagation, as can be seen in an example 2D simulation (Fig. 18b) for a target with initially solid density filaments with an areal density of 5\(n_{c}\) across its volume interacting with an \(a_{0}\) = 20 laser pulse. The pulse can become filamented, defocused, due to Gaussian expansion, and/or refocused, due to self-focusing effects, as it propagates. Carbon nanotubes may have an advantage, compared with foam or aerogel materials, as both the filaments and the void sizes can be smaller than the typical laser wavelength (micron-scale) and may appear approximately homogeneous to the laser pulse [46]. Through interaction with these targets, layered in front of solid density foils, the laser pulse can be shaped, both spatially and temporally, and can lead to enhancement of ion acceleration mechanisms [46]. However, in order for these targets to be practical in terms of high repetition operation, developments would be required to implement them on a tape-drive or other high speed multi-target setup.

Fig. 18
figure 18

a An example picture of the physical structure of a foam target (courtesy of SciTech Precision Ltd.). b Example 2D simulation showing laser propagation through a realistic foam target with areal density of 5\(n_{c}\)

Full size image

6.2 Optimization in simulations using machine learning approaches

Simulations are necessary to elucidate the physics of intense laser-dense-plasma interactions due to the fact that the plasma cannot easily be probed, and the interaction is highly non-linear and evolves on ultra-fast timescales. As there are multiple laser and target parameters that can affect the overall behaviour of the system, optimization and the interplay between the parameters can be difficult to determine i.e. a multi-dimensional problem. To alleviate this, machine learning techniques can be applied to optimize for single or multiple interrelated output parameters, such as maximum energy or energy conversion efficiency, for a high dimensional input parameter space. Without such techniques, the computational cost of multidimensional parameter scans with the necessary precision can be prohibitive. Machine learning methods have been applied for the optimization of laser-driven ion acceleration [98, 99] and can also be used to provide direct feedback and control of experimental conditions. Such techniques have already been applied to the control and optimization of laser wake-field accelerators [84, 100, 101].

Fig. 19
figure 19

Total NLCS signal as a function of the simulation iteration number, using Bayesian optimization to determine the maximum NLCS yield when varying 5 parameters: laser incidence angle; laser pulse duration; spot size; focus position (effectively focal spot size); and, target thickness. The first 30 iterations have random inputs, to initiate the optimization algorithm, and after this, inputs are selected based on the Bayesian optimization algorithm [79]

Full size image

In a first step to apply a machine learning approach to investigate laser-plasma interactions in the transition from opaque to relativistically transparent plasma, a Bayesian optimization [102] algorithm was applied to maximize the yield of high energy photons produced via NLCS. An example of the iterative nature of this technique is shown in Fig. 19 for variation of five input parameters: laser incidence angle; pulse duration; spot size; defocus (i.e. target front surface distance from the laser focal plane); and target thickness. This was conducted for a fixed laser energy with a peak optimal (shortest pulse duration and smallest focal spot) intensity of 10\(^{22}\) Wcm\(^{-2}\). The results demonstrate that optimization of the NLCS yield for these five input parameters can be achieved within \(\sim \) 50 simulations [79]. By comparison, a systematic scan of this parameter space with the necessary resolution would require thousands of simulations. This approach can be applied to the optimization and understanding of other specific processes that have interrelated, nonlinear response to inputs, such as ion acceleration or other radiation generation mechanisms, providing a powerful tool in exploring and exploiting the RSIT regime.

It is also possible to train neural networks using data from simulations and experiments to develop models of the complex physics that is difficult to describe analytically [103]. This has the advantage of being able to determine behaviour quickly, without the need for new simulations, enabling experiment data to be analyzed in near-real-time. This can also be applied to targets that transition to relativistically transparent plasma, providing improved experimental and theoretical evaluation.

7 Summary

The interaction of ultraintense laser pulses with targets undergoing relativistic self-induced transparency has been shown to be important for laser-driven particle and radiation generation. This regime gives rise to enhancement of the TNSA mechanism and new hybrid mechanisms, the direct acceleration of electrons and the generation of structured light fields. Relativistic optical phenomena can occur in this regime, such as self-focusing, which can increase the laser intensity over short micron-scale distances, and diffraction effects as the laser propagates through a self-generated relativistic plasma aperture. At ultrahigh intensities, radiation reaction and other high field QED phenomena affects the plasma dynamics and will need to be carefully considered in experiments using multipetawatt lasers.

In terms of technology development, machine learning techniques and advanced targetry designs are being developed to optimize RSIT processes and enable them to be investigated at high-repetition rate. This will accelerate the development of particle and radiation sources for wide-ranging potential applications.