1 Introduction

The size of an atomic nucleus is one of its most fundamental properties. The charge distribution or its first moment, the charge radius, is often well known for stable nuclei from elastic electron scattering [1, 2] or the spectroscopy of normal or muonic atoms [3]. Techniques are available or are being developed to extend the reach to short-lived nuclei, e.g., laser spectroscopy [4,5,6] or electron scattering in storage rings [7,8,9]. In contrast, the matter distribution is generally not so well known, although it has significant importance to understand nuclear matter properties such as saturation and the symmetry energy. Most information on the matter distribution is extracted from elastic scattering of light hadronic probes, in particular protons, at intermediate energies of several hundred MeV on fixed targets; see e.g. [10,11,12,13,14,15,16,17,18]. Other experimental techniques such as the spectroscopy of antiprotonic atoms [19], coherent \(\pi ^0\) photo-production [20] and parity-violating electron scattering [21] are very challenging and have been applied only to very few stable nuclei. The density profile of the neutron distribution can be obtained by analyzing the data using a known charge distribution as an input.

Nuclear density distributions are sensitive observables for testing nuclear forces and their saturation properties used in ab initio theories [23] as well as for constraining the equation of state of neutron-rich matter. The difference between the root-mean-square radii of the density distributions for neutrons and protons, the neutron skin, can be directly related to the symmetry energy in the Equation-of-State (EoS) of nuclear matter [24]. The developments of experimental techniques for accurate measurements of radii of short-lived neutron-rich nuclei are of utmost importance in this context.

In this Letter, we report on the first elastic proton scattering experiment with a stored radioactive beam. \(^{56}\)Ni (\(T_{1/2} = 6.075~\textrm{d}\)) has been chosen for this first experiment. \(^{56}\)Ni is a doubly-magic self-conjugate (\(N=Z\)) nucleus and is one of only 5 isotopes of this type existing in nature: the stable \(^4\)He, \(^{16}\)O, \(^{40}\)Ca, and the radioactive \(^{56}\)Ni and \(^{100}\)Sn (the latter is out of reach for such studies because of the very low production rate). Neither the charge nor the matter radius of \(^{56}\)Ni have been measured so far.

The experiment has been carried out by the EXL (EXotic nuclei studied in Light-ion induced reactions at storage rings) [27] collaboration at the experimental storage ring ESR at GSI. The experimental technique is based on beams at energies of several 100 MeV/nucleon impinging on an internal gas-jet target in a storage ring [25, 26]. The MHz revolution frequency of the circulating beam compensates the low beam intensity typically obtained for radioactive nuclei and the low target thickness, resulting in a luminosity, which for the first time made such an experiment feasible. This approach is complementary to measurements with an active target [28,29,30,31] (target-gas volume is detector), which become technically more and more challenging for heavier nuclei [32] due to the high ionization density of the heavy beam passing the gas volume. Compared to other methods using solid targets or liquid hydrogen targets, the storage-ring approach is superior for scattering measurements at low momentum transfer, allowing for a precise measurement of low-energy recoils down to the MeV range.

2 Experiment

The use of a storage ring to perform nuclear reactions on internal targets has been considered from the very beginning of the construction of the Experimental Storage Ring (ESR) [33] at GSI. Several design studies for experimental setups at the storage rings at GSI and FAIR [34] have been performed [35,36,37,38]. However, the only earlier experimental attempt at the ESR to meassure elastic proton scattering on \(^{56}\)Ni in inverse kinematics failed, because the stored beam intensity as well as the available target technology did not allow for sufficient luminosities [39]. Only now, technical challenges for such experiments have been overcome. Meanwhile, storage-ring experiments are being developed for different reactions in a wide energy regime from few hundred MeV/nucleon as available at the ESR, the CSRe in Lanzhou [40] and at the planned future facility HIAF [41], down to Coulomb barrier energies at the CRYRING at GSI and FAIR, and at the planned TSR project [42]

The ESR [43] has a circumference of about 108 m and a maximum magnetic rigidity of \(B\rho = 10\) Tm. Excellent beam properties with an energy resolution \(\Delta E/E\) of about \(10^{-4}\) and a radial emittance of \(0.1\, \pi \, \textrm{mm} \cdot \textrm{mrad}\) are reached by both stochastic and subsequent electron cooling even for fragment beams injected with an initially large emittance of up to \(20\, \pi \, \textrm{mm} \cdot \textrm{mrad}\). Because of these unique properties, the ESR is an ideal instrument for in-ring nuclear-reaction studies at several hundred MeV/nucleon with radioactive ions.

Fig. 1
figure 1

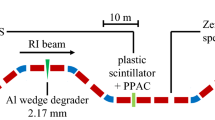
Experimental setup used in the present experiment: a Detailed exploded view of the detector telescope with the DSSD as active vacuum window in the first pocket centred at a polar scattering angle of \(80.5^\circ \). b The stored \(^{56}\)Ni beam impinges on the hydrogen target and the recoiling proton is detected by the detector telescope in the first detector pocket. c The scattering chamber is installed at the position of the internal gas-jet target at the ESR

Full size image

The \(^{56}\)Ni beam was produced by the fragmentation of a 600 MeV/nucleon \(^{58}\)Ni primary beam, selected by the Fragment Separator FRS [44] and then injected into the ESR. Each injection contained \(8 \times 10^4\) fully-stripped \(^{56}\textrm{Ni}^{28+}\) ions, an amount much too low to perform the experiment. The number of stored ions was therefore increased by beam stacking, the repetitive injection and merging of subsequent beam bunches, which was pioneered for radioactive beams in this experiment [45]. After injection, each bunch was first pre-cooled by stochastic cooling for 5 s, then moved towards its final orbit, and after 6 s of electron cooling merged with the existing orbiting bunches. This enabled almost two orders of magnitude more stored \(^{56}\)Ni ions (\(3 \times 10^6\)) in the ring. An internal window-less and pure hydrogen gas-jet target [46] was used with an effective thickness of about \(3 \times 10^{13}\) cm\(^{-2}\). Considering the revolution frequency of 1.96 MHz for the \(^{56}\)Ni ions with \(E_{kin} = 390.2\) MeV/nucleon, a luminosity of \(1.5 \times 10^{26}~\textrm{cm}^{-2}\textrm{s}^{-1}\) was achieved. The preparation of the beam and the conditions for storage in the ring resulted intrinsically in negligible beam impurities (e.g. \(^{54}\textrm{Co}^{27+}\)) of less than \(10^{-3}\). The ESR was refilled every \(\approx \)1.5 h when the luminosity had dropped to about half of its peak value because of beam losses caused mainly by recombination in the electron cooler.

The experimental setup is shown in Fig. 1. The main challenge for EXL is the compliance with the ultra-high vacuum (UHV) conditions for a storage ring (\(p=10^{-11}\) mbar). This implies that the equipment has to withstand a baking procedure at a temperature of 150 \(^\circ \)C. In combination with the need to detect low-energy reaction products this required a completely new approach. In our solution, we were employing 285 \(\mu \)m thick Double-sided Silicon-Strip Detectors (DSSDs) mounted on ceramic PCBs made of aluminium nitride (AlN) as active vacuum windows [47, 48] (Fig. 1a). They separate the UHV from the less stringent vacuum conditions (\(p=10^{-7}\) mbar) in the so-called pockets, which accommodate all non-bakeable components. Only the first pocket placed at an average angle of \(\Theta _{Lab}=80.5^\circ \) with respect to the beam was used for the investigation of elastic scattering. It housed two 6.5 mm thick Si(Li) detectors behind the DSSD in a telescope configuration capable of stopping protons with energies up to about 50 MeV. These Si(Li)s were actively cooled during bake-out as well as during normal operation. The temperature of the Si(Li)s stayed always below \(-1.8\) \(^\circ \)C.

Fig. 2
figure 2

Reconstructed energy of the scattered protons from the energy deposits measured with the individual detectors of the detector telescope as a function of the scattering angle \(\Theta _{lab}\) and a slit of 1 mm. Calculated kinematical curves for both elastic and inelastic scattering to the first-excited state of \(^{56}\)Ni are overlaid

Full size image

Elastically scattered protons are identified by the characteristic angle-energy correlation (Fig. 2). The proton energy was obtained by adding up the energy deposits in the three layers of Si detectors with an energy resolution of 300 keV fwhm for the reconstructed proton energy shown in Fig. 2. The scattering angle was reconstructed from the reaction vertex. The gas-jet target had a diameter of 6.3 mm and varied only slowly with nozzle pressure [38, 49]. The spatial extension of the gas-jet target limited the angular and, therefore, the energy resolution. In order to improve this, the acceptance was reduced by inserting a remote-controlled aperture with slits of different widths between the target and the detector (Fig. 1b). With a 1-mm slit aperture, an angular resolution of 0.22\(^{\circ }\) has been achieved resulting in a fwhm resolution of 0.18\(^{\circ }\) in the CM system, and an excitation-energy resolution of about 400 keV fwhm. The absolute target thickness was monitored with the measured pressure at the outlet of the gas target with a precision of few percent [49]. The uncertainty of the integrated luminosity for the hydrogen runs was below 10%. This value is dominated by the determination of the target density based on 4 gauge pressure meters. The intensity of the circulating beam was measured with a DC current transformer. Combining both measurements allowed for a continuous monitoring of the luminosity reaching a precision of about 15%. The cooled beam has a circular shape with a Gaussian profile [50] and a radius of about 0.3 mm which is limited by intra-beam scattering, and hence is dependent on the number of stored ions [51]. The absolute position and the size of the interaction volume has been measured. For that, the electron cooler has been turned off and the target was scanned with low-intensity beam. The beam size had a radius of about 1.2 mm at the interaction zone, measured independently. The interaction of the beam and target generate a particular shape that was used as an event generator for the simulations.

Most data have been taken with a 1-mm slit aperture allowing for a clear separation between the kinematic branches. The elastic scattering channel \(^{56}\)Ni(p, p) is clearly separated from the inelastic scattering to the first-excited state at 2.7 MeV by more than \(3\times \)fwhm (see Fig. 2). A contamination of the elastic line from the excited state can thus be safely neglected. Also, for \(^{58}\)Ni (not shown) the first-excited state at 1.4 MeV was well separated from elastic scattering. The additional particles seen in Fig. 2, which do not follow a kinematic line, originate from reactions on the aperture and on the residual gas. Their contribution to a narrow gate along the kinematic line for elastic scattering is very small around few %) and was subtracted by a gate set on the background in order to improve the data quality. The gate on the relatively uniform background has been chosen such that it contained sufficient statistics and was positioned well outside the kinematic curves (elastic and inelastic). The small tail emerging from the line of elastic scattering at an angle of about \(85^\circ \) is caused by imperfect energy reconstruction in the telescope due to a combination of angular straggling in the DSSD and acceptance in the overlap area of the subsequent detectors. The effect has been corrected using simulations and experimental data above and below that area.

Our most important observable, the differential cross section \(d\sigma /d t\) for elastic scattering as a function of the Lorentz-invariant four-momentum transfer squared, \(-t=q^2\), is shown in Fig. 3a, b. The errors reflect both statistical and systematic uncertainties (total pp an pn cross sections, ratios of the real to imaginary parts, as well as the slope parameters \(\beta p N\)) estimated from the Monte Carlo simulations. Details are given below. As a reference, the same measurement and analysis were performed with a stable \(^{58}\)Ni beam at an energy of 400.1 MeV/nucleon (Fig. 3a), where the luminosity was about 50 times higher. The \(^{58}\)Ni(p, p) cross section provides a cross-check against the most recent conventional measurement [17] at the same kinetic energy.

Fig. 3
figure 3

Differential cross sections and resulting matter distributions. a) Measured cross section for \(^{58}\)Ni(p, p) at a beam energy of 400.1 MeV/nucleon and best Glauber fit (solid line). The absolute scale of the Glauber fit has been normalised to the experimental values. Also shown is the result of a measurement in normal kinematics performed at a beam energy of 400 MeV/nucleon [17] b) Measured cross section for \(^{56}\)Ni(p, p) at a beam energy of 390.2 MeV/nucleon and best Glauber fit (solid line). c) Matter density distribution (SF) of \(^{58}\)Ni with the 1\(\sigma \)-error band obtained from our fit and experimental charge density distribution [2] (SOG) d) Matter density distribution of \(^{56}\)Ni (SF) with the 1\(\sigma \)-error band obtained from the fit

Full size image

3 Analysis

The experimental differential cross sections were analysed using the Glauber multiple-scattering theory [13]. In the eikonal and adiabatic approximations, the interaction of the proton with the nucleus is modelled by a series of intranuclear NN collisions. For the nucleus, a phenomenological density distribution was chosen given by the well-known symmetrized Fermi (SF) function normalized to unity [52],

$$\begin{aligned} \rho (r) = \frac{\textrm{sinh} \left( \frac{R_0}{r}\right) }{\textrm{cosh} \left( \frac{r}{d}\right) + \textrm{cosh} \left( \frac{R_0}{d}\right) }, \end{aligned}$$
(1)

with only two free parameters: the half-width radius \(R_0\), and the diffuseness d. It describes the key properties of the matter density distribution over a wide range of nuclei. The same density distribution is assumed for neutrons and protons. The point-matter density distributions were convoluted with the finite size of the nucleon, \(<r_{m}^{2}>^{1/2}=0.8775\) fm [53]. In the following, only convoluted distributions and corresponding radii are presented. Since our data cover the first diffraction minimum, as well as the following maximum, both \(R_0\) as well as d are well determined by the data. At energies around 400 MeV, the nucleon-nucleus central potential is at a minimum resulting in the largest possible transparency of the nuclear medium to nucleon scattering. The free pN scattering amplitudes \(f_{pN}\) were parameterized in the usual high-energy approximation using only the central amplitudes \(f_{pN}^c\) and neglecting the small spin-spin effects [13], i.e.

$$\begin{aligned} f_{pN} \approx \frac{k \sigma _{pN}}{4\pi } \left( \epsilon _{pN} + \textrm{i}\right) \textrm{exp}\!\left( \frac{-q^2\beta _{pN}}{2}\right) . \end{aligned}$$
(2)

For pp collisions, the additional scattering amplitude due to the Coulomb interaction has been added. The parameters are dependent on both the energy and the 3-momentum transfer.

For 400 MeV proton energy, the total pp and pn cross sections were set to the well-established experimental values [28, 54] of \(\sigma _{pp} = 2.6(1)~\textrm{fm}^2\) and \(\sigma _{pn} = 3.3(1)~\textrm{fm}^2\), respectively. For the ratios of the real to the imaginary parts, \(\epsilon _{pp} = 0.54(8)\) and \(\epsilon _{pn} = 0.05(2)\) were taken [28, 54].

Data for the slope parameters \(\beta _{pN}\) are scarce in literature for an energy of 400 MeV [15], where the slope parameter is expected to be close to zero. Therefore, we calculated scattering amplitudes \(f_{pN}\) by varying the slope parameters and comparing to our measured differential cross section for \(^{58}\)Ni(p, p). It should be noted that the shape of our angular distribution agrees well with the most recent data points measured in normal kinematics [17] (Fig. 3a). However, the EXL approach allows for a much better angular resolution compared to the one obtained in normal kinematics with stable beams. In this procedure of calculating the cross section, the well-measured charge density of \(^{58}\)Ni [2] was used as a reference and the neutron distribution was considered to have the same shape, in accordance with experiment [10]. We have extracted a value of \(\beta _{pp} = \beta _{pn} = 0.3(2)~\textrm{fm}^2\), which is as expected compatible with zero. In accordance with Ref. [28] a single value can be used. The large uncertainty reflects the weak sensitivity to this parameter, and has been taken into account in the following analysis.

The \(1\sigma \)-uncertainties of the slope parameter were estimated from the Monte-Carlo analysis considering the contributions from the statistical uncertainties, the acceptance correction and the errors of the other parameters for the free NN scattering amplitudes. Such an effective value for \(\beta _{pN}\) has the advantage that all effects including the spin-orbit interaction, which are not contained in the central amplitudes, are treated in a good approximation [28]. However, although the actual value of the cross section in the first diffraction minimum depends on the spin-orbit interaction, its position remains nearly unaffected [13]. The covariance matrix of the five parameters of the free pN scattering amplitudes was calculated in order to create a distribution, which was used in the analysis of \(^{56}\)Ni(p, p).

For each of these random sets of scattering amplitudes, the Glauber fits were performed varying the parameters of the phenomenological density distribution. The absolute normalization for both experimental cross sections (for \(^{56}\)Ni and \(^{58}\)Ni) was fitted to the calculated shapes of the distributions resulting in an estimated uncertainty of around 15% for the luminosity measured independently. The uncertainty was included in the chi-square analysis of the fitting procedure. The \(^{58}\)Ni(p, p) data set was analyzed in the same way as \(^{56}\)Ni(p, p) in order to check for consistency. For both data sets, a good agreement between experimental data and the Glauber fits has been achieved (see Fig. 3). The differences in the absolute scale lie well within the the normalization uncertainty.

4 Results

The corresponding matter-density distributions are shown for \(^{58}\)Ni and \(^{56}\)Ni in Fig. 3c and Fig. 3d, respectively. As our consistency check, for \(^{58}\)Ni a matter radius of \(<r_{m}^{2}>^{1/2}=3.79^{+0.01}_{-0.02}\) fm was obtained, which is in excellent agreement with previous measurements (Fig. 4) and proves the reliability of our analysis procedure. It is also in excellent agreement with the previous result of 3.78(7) fm from an analysis of \(\alpha \) scattering in the ESR by Zamora et al. [63].

For \(^{56}\)Ni, the extracted parameters are \(R_0=3.9^{+0.2}_{-0.1}\) fm and \(d=0.59^{+0.03}_{-0.04}\) fm which result in a matter radius of \(<r_{m}^{2}>^{1/2}=3.74^{+0.03}_{-0.06}\) fm. The final result for the radius presented here is in agreement with a previous analysis of preliminary data using a different approach [55].

Fig. 4
figure 4

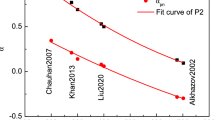
Systematics of nuclear matter radii for the even nickel isotopes. Shown are the matter radii, i.e. taking into account the radius of the proton and neutron, as a result of this work (red symbols). For comparison, previous experimental results for stable Ni isotopes (full symbols) based on different analyses of the cross section for elastic proton scattering performed at CEA Saclay [10, 11, 16] (green) (\(E_p = 1\) GeV) and at LAMPF [12, 14, 15] (blue) (\(E_p = 0.8\) GeV) are shown. Also shown are theoratical predictions [56,57,58,59,60] (open symbols). For clarity, all data points were spread along the x-axis

Full size image

The newly established matter radius of \(^{56}\)Ni follows the smooth trend of the heavier nickel isotopes (Fig. 4). The experimental values [11, 12, 14,15,16, 16] are compared to predictions by theory [56,57,58,59,60]. The older spherical Hartree-Fock (HF) calculation [56] that was predicting a dramatic shrinking of the doubly-magic \(^{56}\)Ni compared to the systematics of the heavier isotopes can clearly be ruled out. Newer deformed self-consistent mean-field Skyrme HF+BCS calculations [57] as well as non-relativistic HF-Bogoliubov (HFB) calculations [58] using a G-Matrix interaction agree well with our experimental result. The result obtained with ab initio self-consistent Green’s function (SCGF) calculations [59], which became feasible only recently in this mass region, is also in good agreement with the measurement. Latest results from In-Medium Similarity Renormalization Group calculations [60] with a family of consistent chiral Effective Field Theory (EFT) interactions up to N3LO, including estimates for the total theory uncertainties, are also in good agreement.

5 Conclusion

In conclusion, we have presented a novel approach for experiments employing nuclear reactions in a storage ring. In a first experiment using a stored radioactive beam interacting with an internal gas-jet target, elastic proton-scattering cross sections have been measured, and the matter radius of the doubly-magic self-conjugate nucleus \(^{56}\)Ni has been extracted. The developed method opens new horizons for the investigation of radioactive nuclei by direct nuclear reactions performed in storage rings, addressing open problems in nuclear structure and astrophysics [61, 62]. Future implementations of the presented experimental method at the Facility for Ion and Antiproton Research (FAIR) [34] will allow for a broad range of reaction studies formerly deemed impossible. An extended setup covering close to 2\(\pi \) is planned to be installed at the present ESR at GSI, where cooled SUPER-FRS beams could be stored and further cooled, providing two orders of magnitude more intensity compared to the pilot experiment discussed here (in addition to the intensity win of the SIS100-Super-FRS combination). This will allow, for instance, a precise measurement of the density distribution of the key nucleus \(^{132}\)Sn including three minima in the elastic proton scattering cross section. Neutron-skin thicknesses can be inferred by combing proton scattering with rms charge radii derived from laser-spectroscopy measurements, or by the combined analysis with electron-scattering data, when an electron accelerator is combined with the storage ring as proposed in the ELISe project [64].