Appendix A: Derivation of the elastic scattering amplitudes
In this section we present the detailed derivation of the \(d{-}\alpha \) elastic scattering amplitudes for all possible partial waves, \(l=0,~1,~2\).
1.1
S-wave channel
According to the Lagrangian (17), the strong interaction in the \(\xi ={^3\!S_1}\) channel of the \(d{-}\alpha \) system can be described using the up-to-NLO Lagrangian
$$\begin{aligned} {} {\mathcal {L}}^{[\xi ]}= & {} \phi ^{\dagger }\left( i\partial _0+\frac{\nabla ^2}{2m_\alpha }\right) \phi +d_i^{\dagger }\left( i\partial _0+\frac{\nabla ^2}{2m_d}\right) d_i\nonumber \\{} & {} +\,\eta ^{[\xi ]}{\bar{t}}_i^{\,\dagger }\Bigg [i\partial _0+\frac{\nabla ^2}{2m_t}-{\Delta }^{[\xi ]}\Bigg ]{\bar{t}}_i \nonumber \\{} & {} +h^{[\xi ]}{\bar{t}}_i^{\,\dagger }\Bigg [i\partial _0+\frac{\nabla ^2}{2m_t}\Bigg ]^2{\bar{t}}_i +\,g^{[\xi ]}\Big [{\bar{t}}^{\,\dagger }_i(\phi \, d_i)+h.c.\Big ],\nonumber \\ \end{aligned}$$
(A.1)
where \({\bar{t}}_i\) is the vector auxiliary field of the \({^3\!S_1}\) dimeron. According to the Feynman diagram of Fig. 2, the up-to-NLO EFT scattering amplitude in the \(^3\!S_1\) channel can be written as
$$\begin{aligned} {}{} & {} -iT_{CS}^{[\xi ]}e^{2i\sigma _0}\nonumber \\{} & {} \quad =(-ig^{[\xi ]})^2 \, \chi _{p'}^{*(-)}({\textbf{0}})\, \varepsilon _j^{d*}\,\varepsilon _j^{{\bar{t}}}\,iD^{[\xi ]}(E,{\textbf {0}})\varepsilon _i^{{\bar{t}}*}\, \varepsilon _i^d\,\chi _p^{(+)}({\textbf{0}})\nonumber \\{} & {} \quad =-ig^{[\xi ]^2}\!D^{[\xi ]}(E,{\textbf {0}})W_{0}(\eta _p)C_{0}^2(\eta _p)e^{2i\sigma _0}, \end{aligned}$$
(A.2)
where \(\varepsilon _i^{d}\) and \(\varepsilon _i^{{\bar{t}}}\) are polarization vectors of the deuteron and dimeron auxiliary fields respectively, which satisfy the relations
$$\begin{aligned} {} \varepsilon _j^{{\bar{t}}*} \,\varepsilon _i^{{\bar{t}}}= \delta _{ij},\quad \varepsilon _j^{d*} \,\varepsilon _i^{d}=\frac{1}{3}\delta _{ij}. \end{aligned}$$
(A.3)
In the last equality of Eq. (A.2) we use
$$\begin{aligned} {} \chi _{p'}^{*(-)}({\textbf{0}})\chi _p^{(+)}({\textbf{0}})=W_{0}(\eta _p)\,C_{0}^2(\eta _p) e^{2i\sigma _0}. \end{aligned}$$
(A.4)
According to the diagrams in second line of Fig. 2, The S-wave up-to-NLO full propagator is given by
$$\begin{aligned} {} D^{[\xi ]}(E,{\textbf {0}})= & {} \frac{\eta ^{[\xi ]}}{E-{\Delta }^{[\xi ]}-\eta ^{[\xi ]}g^{[\xi ]^2}J_0(E)}\nonumber \\{} & {} \times \left[ \underbrace{\,1_{_{_{_{_{_{_{_{_{}}}}}}}}}}_{\textrm{LO}}-\underbrace{\frac{\eta ^{[\xi ]}h^{[\xi ]}E^2}{E-{\Delta }^{[\xi ]}-\eta ^{[\xi ]}g^{[\xi ]^2}J_0(E)}}_{{\textrm{NLO}}~ {\textrm{correction}}}\right] ,\nonumber \\ \end{aligned}$$
(A.5)
where the fully dressed bubble \(J_{0}\), which is described the propagation of the particles from initially zero separation and back to zero separation, is written as
$$\begin{aligned} {} J_{0}(E)= & {} \lim _{{\textbf{r}}^{\prime },{\textbf{r}}\rightarrow {\textbf{0}}}\langle {\textbf{r}}^{\prime }|G_{C}^{(+)}{(E)}|{\textbf{r}}\rangle \nonumber \\= & {} 2\mu \int \frac{d^{3}q}{(2\pi )^{3}}\frac{\chi _{q}^{(+)}({\textbf{0}})\chi _{q}^{*(+)}({\textbf{0}})}{2\mu E-q^{2}+i\epsilon } \nonumber \\= & {} 2\mu \!\int \!\frac{d^{3}q}{(2\pi )^{3}}\frac{2\pi \eta _q}{e^{2\pi \eta (q)}-1}\,\frac{1}{p^2-q^{2}+i\epsilon }\nonumber \\= & {} \underbrace{2\mu \!\int \! \frac{d^{3}q}{(2\pi )^{3}}\frac{2\pi \eta _q}{e^{2\pi \eta _q}-1}\,\frac{1}{q^2}\frac{p^2}{p^2-q^{2}+i\epsilon }}_{J^{fin}_{0}}\nonumber \\{} & {} \underbrace{-2\mu \!\int \! \frac{d^{3}q}{(2\pi )^{3}}\frac{2\pi \eta _q}{e^{2\pi \eta _q}-1}\,\frac{1}{q^2}}_{J^{div}_{0}}. \end{aligned}$$
(A.6)
Calculation of the finite part of the S-wave Coulomb bubble leads to [33]
$$\begin{aligned} {} J^{fin}_0=-\frac{\mu }{\pi }k_CW_0(\eta _p)H(\eta _p)=-\frac{\mu }{2\pi }H_0(\eta _p), \end{aligned}$$
(A.7)
and taking into account the power divergence subtraction (PDS) regularization scheme, the momentum independent divergent part is obtained as [33]
$$\begin{aligned} J^{div}_0= & {} -\frac{\mu }{2\pi }\Bigg \{ \frac{\kappa }{D-3}\nonumber \\ {}{} & {} +2k_C \Bigg [\frac{1}{D-4}-\text {ln}\Bigg (\frac{\kappa \sqrt{\pi }}{2k_C}\Bigg )-1+\frac{3}{2}C_E\Bigg ]\Bigg \}, \end{aligned}$$
(A.8)
with D the dimensionality of spacetime, \(\kappa \) the renormalization mass scale and \(C_E\) Euler–Mascheroni constant. Instead of PDS regularization scheme we can use a simple momentum cutoff \({\Lambda }\) to make the divergent integral \(J^{div}_0\) finite. It then becomes [33]
$$\begin{aligned} J^{div}_0= & {} -\frac{2\mu }{\pi }\!\int _{0}^{{\Lambda }}\!dq \frac{\eta _q}{e^{2\pi \eta _q}-1}\nonumber \\= & {} -\frac{2\mu k_C}{\pi }\!\int _{ \frac{2\pi k_C}{{\Lambda }}}^{\infty }\,\! \frac{dx}{x(e^{x}-1)}\nonumber \\= & {} -\frac{2\mu k_C}{\pi }\Bigg \{\int _{0}^{\infty }\! \frac{dx}{x(e^{x}-1)}-\int _{0}^{ \frac{2\pi k_C}{{\Lambda }}}\frac{dx}{x(e^{x}-1)}\Bigg \}\nonumber \\= & {} -\frac{2\mu k_C}{\pi }\Bigg \{{\Gamma }(0)\zeta (0)-\int _{0}^{ \frac{2\pi k_C}{{\Lambda }}}dx\Bigg (\frac{1}{x^2}-\frac{1}{2x}+{\mathcal {O}}\,(x^0)\Bigg )\Bigg \}\nonumber \\= & {} -\frac{2\mu k_C}{\pi }\Bigg (\frac{1}{2}C_E+\frac{{\Lambda }}{2\pi k_C}-\frac{1}{2}\ln \frac{{\Lambda }}{k_C}+{\mathcal {O}}\,\left( \frac{2\pi k_C}{{\Lambda }}\right) \Bigg ),\nonumber \\ \end{aligned}$$
(A.9)
where in the second line we use changing integral variable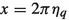 
, and in the last line we use
$$\begin{aligned} {\Gamma }(0)= & {} \lim _{\epsilon \rightarrow 0}\Bigg (\frac{1}{\epsilon }-C_E\Bigg ), \end{aligned}$$
(A.10)
$$\begin{aligned} \zeta (0)= & {} \lim _{\epsilon \rightarrow 0}\Bigg (-\frac{1}{2}(1+\epsilon \ln 2\pi )+{\mathcal {O}}\,(\epsilon ^2)\Bigg ). \end{aligned}$$
(A.11)
Thus, the up-to-NLO EFT scattering amplitude of Eq. (A.2) is rewritten
$$\begin{aligned}{} & {} T^{[\xi ]}_{CS}=-\frac{2\pi }{\mu }\frac{C_{0}^2(\eta _p)W_{0}(\eta _p)}{\left( \frac{2\pi {\Delta }^{[\xi ]}}{\eta ^{[\xi ]}g^{[\xi ]^2}\!\mu }+\frac{2\pi }{\mu }J^{div}_0\right) -\frac{1}{2}\left( \frac{2\pi }{\eta ^{[\xi ]}g^{[\xi ]^2}\!\mu ^2}\right) p^2-H_0(\eta _p)} \nonumber \\{} & {} \quad \times \left[ \underbrace{\,1_{_{_{_{_{_{_{_{_{_{_{_{_{_{}}}}}}}}}}}}}}}_{\mathrm {\!\!LO}}\!\!\!+\underbrace{\frac{1}{4}\frac{\left( \frac{2\pi h^{[\xi ]}}{g^{[\xi ]^2}\!\mu ^3}\right) }{\left( \frac{2\pi {\Delta }^{[\xi ]}}{\eta ^{[\xi ]}g^{[\xi ]^2}\mu }+\frac{2\pi }{\mu }J^{div}_0\right) -\frac{1}{2}\left( \frac{2\pi }{\eta ^{[\xi ]}g^{[\xi ]^2}\!\mu ^2}\right) p^2-H_0(\eta _p)}p^4\,\,}_{\textrm{NLO}~\textrm{correction}}\!\!\!\!\right] \!.\nonumber \\ \end{aligned}$$
(A.12)
Regardless of which renormalization scheme we use to calculate the divergent integral \(J^{div}_0\), this momentum independent divergence part is absorbed by the parameter \({\Delta }^{[\xi ]}\) via introducing the renormalized parameter \({\Delta }^{[\xi ]}_R\) as [40]
$$\begin{aligned} {\Delta }^{[\xi ]}_R={\Delta }^{[\xi ]}+\eta ^{[\xi ]}g^{[\xi ]^2}J^{div}_0. \end{aligned}$$
(A.13)
Finally, the up-to-NLO scattering amplitude for \(\xi ={^3\!S_1}\) partial wave is expressed as
$$\begin{aligned} T^{[\xi ]}_{CS}= & {} \frac{2\pi }{\mu }\frac{C_{0}^2(\eta _p)W_{0}(\eta _p)}{\frac{2\pi {\Delta }_R^{[\xi ]}}{\eta ^{[\xi ]}g^{[\xi ]^2}\!\mu }-\frac{1}{2}\left( \frac{2\pi }{\eta ^{[\xi ]}g^{[\xi ]^2}\!\mu ^2}\right) p^2-H_0(\eta _p)}\nonumber \\ {}{} & {} \times \left[ \underbrace{\,\,1_{_{_{_{_{_{_{_{_{_{_{_{_{_{_{_{}}}}}}}}}}}}}}}}}_{\textrm{LO}}+\!\underbrace{\frac{1}{4}\frac{\left( \frac{2\pi h^{[\xi ]}}{g^{[\xi ]^2}\!\mu ^3}\right) }{\frac{2\pi {\Delta }_R^{[\xi ]}}{\eta ^{[\xi ]}g^{[\xi ]^2}\!\mu }-\frac{1}{2}\left( \frac{2\pi }{\eta ^{[\xi ]}g^{[\xi ]^2}\!\mu ^2}\right) p^2-H_0(\eta _p)}p^4\,\,}_{\textrm{NLO}~\textrm{correction}}\!\!\right] .\nonumber \\ \end{aligned}$$
(A.14)
1.2
P-wave channels
The up-to-NLO Lagrangian for the strong interaction in the \(\xi =\) \({^3\!P_0}\) channel of the \(d{-}\alpha \) system can be written as
$$\begin{aligned} {} {\mathcal {L}}^{[\xi ]}= & {} \phi ^{\dagger }\left( i\partial _0+\frac{\nabla ^2}{2m_\alpha }\right) \phi +d_i^{\dagger }\left( i\partial _0+\frac{\nabla ^2}{2m_d}\right) d_i \nonumber \\{} & {} +\,\eta ^{[{\xi }]}t^\dagger \Bigg [i\partial _0 +\frac{\nabla ^2}{2m_t}-{\Delta }^{[{\xi }]}\Bigg ]t +h^{[{\xi }]}t^{\dagger }\Bigg [i\partial _0+\frac{\nabla ^2}{2m_t}\Bigg ]^2t\nonumber \\{} & {} +\sqrt{3}\,g^{[{\xi }]}\Big [t^{\dagger }(\phi {\mathcal {P}} _i d_i)+h.c.\Big ], \end{aligned}$$
(A.15)
where t is the scaler auxiliary field of the \(^3\!P_0\) dimeron. According to the Feynman diagrams of Fig. 2 we have
$$\begin{aligned}{} & {} -i3T^{[\xi ]}_{CS}P_1(\hat{{{\textbf {p}}}}'\cdot \hat{{{\textbf {p}}}})e^{2i\sigma _1}\nonumber \\{} & {} \quad =3(-ig^{[\xi ]})^2[{\mathcal {P}}^*_j\chi _{p'}^{*(-)}({\textbf{0}})] \varepsilon _j^{d*} iD^{[\xi ]}(E,{\textbf {0}})\,\varepsilon _i^{d}\,[{\mathcal {P}}_i\chi _p^{(+)}({\textbf{0}})]\nonumber \\{} & {} \quad =-3ig^{[\xi ]^2}D^{[\xi ]}(E,{\textbf {0}}) \varepsilon _j^{d*}\,\varepsilon _i^{d*}[\nabla _j\chi _{p'}^{*(-)}({\textbf{0}})][\nabla _i\chi _p^{(+)}({\textbf{0}})]\nonumber \\{} & {} \quad =-ig^{[\xi ]^2}D^{[\xi ]}(E,{\textbf {0}}) C_0^2(\eta _p) W_1(\eta _p) P_1(\hat{{{\textbf {p}}}}'\cdot \hat{{{\textbf {p}}}}) e^{2i\sigma _1}, \end{aligned}$$
(A.16)
where in the last line, the following relation is used
$$\begin{aligned} {}{} & {} [\nabla _i \chi _{p'}^{*(-)}({\textbf{0}})][\nabla _i \chi _p^{(+)}({\textbf{0}})]=C^2_0(\eta _p)\, p'_ip_{i}\,(1+\eta _p^2)e^{2i\sigma _1}\nonumber \\{} & {} \quad =C^2_0(\eta _p)\, W_1(\eta _p) P_1(\hat{{{\textbf {p}}}}'\cdot \hat{{{\textbf {p}}}})e^{2i\sigma _1}. \end{aligned}$$
(A.17)
The up-to-NLO strong interaction Lagrangian in the \(\xi ={^3\!P_1}\) channel is introduced as
$$\begin{aligned} {} {\mathcal {L}}^{[\xi ]}= & {} \phi ^{\dagger }\left( i\partial _0+\frac{\nabla ^2}{2m_\alpha }\right) \phi +d_i^{\dagger }\left( i\partial _0+\frac{\nabla ^2}{2m_d}\right) d_i\nonumber \\{} & {} +\,\eta ^{[\xi ]}t_i^\dagger \Bigg [i\partial _0+\frac{\nabla ^2}{2m_t}-{\Delta }^{[\xi ]}\Bigg ]t_i+h^{[\xi ]}t_i^{\dagger }\Bigg [i\partial _0+\frac{\nabla ^2}{2m_t}\Bigg ]^2t_i\nonumber \\{} & {} +\sqrt{\frac{3}{2}}\epsilon _{kji}\, g^{[\xi ]}\Big [t_k^{\dagger }(\phi {\mathcal {P}}_j d_i)+h.c.\Big ], \end{aligned}$$
(A.18)
where \(t_i\) denotes the vector field of the \(^3\!P_1\) dimeron. So, the scattering amplitude in the \(^3\!P_1\) channel is written as
$$\begin{aligned} {}{} & {} -i3T^{[\xi ]}_{CS}P_1(\hat{{{\textbf {p}}}}'\cdot \hat{{{\textbf {p}}}})e^{2i\sigma _1}\nonumber \\{} & {} \quad =\frac{3}{2}(-ig^{[\xi ]})^2\, [{\mathcal {P}}^*_m\chi _{p'}^{*(-)}({\textbf{0}})] \epsilon _{lmj} \varepsilon _j^{d*}\,\varepsilon ^{t}_l\nonumber \\{} & {} \qquad \times iD^{[\xi ]}(E,{\textbf {0}})\epsilon _{ksi}\varepsilon _{k}^{t*}\,\varepsilon _i^{d}\,[{\mathcal {P}}_s\chi _p^{(+)}({\textbf{0}})]\nonumber \\{} & {} \quad =-\frac{1}{2}\,ig^{[\xi ]^2}\, D^{[\xi ]}(E,{\textbf {0}})\,\epsilon _{kmi}\,\epsilon _{ksi} [\nabla _m\chi _{p'}^{*(-)}({\textbf{0}})]\,[\nabla _s\chi _p^{(+)}({\textbf{0}})]\nonumber \\{} & {} \quad =-ig^{[\xi ]^2}D^{[\xi ]}(E,{\textbf {0}}) C_0^2(\eta _p) W_1(\eta _p) P_1(\hat{{{\textbf {p}}}}'\cdot \hat{{{\textbf {p}}}}) e^{2i\sigma _1}, \end{aligned}$$
(A.19)
with \(\varepsilon _i^{t}\) as the polarization vector of the \(^3\!P_1\) dimeron auxiliary field. Also, the strong interaction Lagrangian for the \(d{-}\alpha \) system in the \(\xi ={^3\!P_2}\) channel can be written as
$$\begin{aligned} {} {\mathcal {L}}^{[\xi ]}= & {} \phi ^{\dagger }\left( i\partial _0+\frac{\nabla ^2}{2m_\alpha }\right) \phi +d_i^{\dagger }\left( i\partial _0+\frac{\nabla ^2}{2m_d}\right) d_i \nonumber \\{} & {} +\,\eta ^{[\xi ]}t_{ij}^\dagger \Bigg [i\partial _0+\frac{\nabla ^2}{2m_t}-{\Delta }^{[\xi ]}\Bigg ]t_{ij}\nonumber \\{} & {} +h^{[\xi ]}t_{ij}^\dagger \Bigg [i\partial _0+\frac{\nabla ^2}{2m_t}\Bigg ]^2\!t_{ij}\nonumber \\ {}{} & {} +\frac{3}{\sqrt{5}} g^{[\xi ]}\Big [t_{ij}^{\dagger }(\phi {\mathcal {P}} _j d_i)+h.c.\Big ], \end{aligned}$$
(A.20)
where \(t_{ij}\) is the auxiliary tensor field of the \(^3\!P_2\) dimeron. Therefore, the scattering amplitude in the \(^3\!P_2\) channel is obtained as
$$\begin{aligned} {}{} & {} -3iT^{[\xi ]}_{CS}P_1(\hat{{{\textbf {p}}}}'\cdot \hat{{{\textbf {p}}}})e^{2i\sigma _1}\nonumber \\{} & {} \quad =\frac{9}{5}(-ig^{[\xi ]})^2\,[{\mathcal {P}}^*_m\chi _{p'}^{*(-)}({\textbf{0}})] \varepsilon _j^{d*}\,\varepsilon _{jm}^t\nonumber \\{} & {} \qquad \times iD^{[\xi ]}(E,{\textbf {0}}) \varepsilon _{si}^{t*}\,\varepsilon _i^{d}\,[{\mathcal {P}}_s\chi _p^{(+)}({\textbf{0}})]\nonumber \\{} & {} \quad =-ig^{[\xi ]^2}\!D^{[\xi ]}(E,{\textbf {0}}) C_0^2(\eta _p) W_1(\eta _p) P_1(\hat{{{\textbf {p}}}}'\cdot \hat{{{\textbf {p}}}}) e^{2i\sigma _1},\nonumber \\ \end{aligned}$$
(A.21)
with \(\varepsilon _{ij}\) as the polarization tensor of the \(^3\!P_2\) dimeron auxiliary field which satisfies the expression
$$\begin{aligned} {} \varepsilon _{jm}^t\,\varepsilon _{si}^{t*}=\frac{1}{2}\left( \delta _{js}\delta _{mi}+\delta _{ji}\delta _{ms}-\frac{2}{3}\delta _{jm}\delta _{si}\right) . \end{aligned}$$
(A.22)
The up-to-NLO full propagator for the \(^3\!P_0\), \(^3\!P_1\) and \(^3\!P_2\) channels is given by
$$\begin{aligned} {} D^{[\xi ]}(E,{\textbf {0}})= & {} \frac{\eta ^{[\xi ]}}{E-{\Delta }^{[\xi ]}-\frac{1}{3}\eta ^{[\xi ]}g^{[\xi ]^2}J_1(E)}\nonumber \\{} & {} \times \left[ \underbrace{1_{_{_{_{_{_{_{_{_{_{_{}}}}}}}}}}}}_{\textrm{LO}}-\underbrace{\frac{\eta ^{[\xi ]}h^{[\xi ]}E^2}{E\!-{\Delta }^{[\xi ]}\!-\frac{1}{3}\eta ^{[\xi ]}g^{[\xi ]^2}J_1(E)}}_{\mathrm {NLO~corection}}\!\right] \!.\nonumber \\ \end{aligned}$$
(A.23)
The function \(J_1(E)\) is given by
$$\begin{aligned} J_1(E)= & {} 2\mu \!\!\int \! \!\frac{d^3 q}{(2 \pi )^3}\frac{[\nabla _i\chi _{{q}}^{(+)}({\textbf{0}})] [\nabla _i\chi _{{q}}^{*(+)}({\textbf{0}})]}{2\mu E -{q}^2+i\epsilon } \nonumber \\= & {} 2\mu \!\!\int \! \!\frac{d^3 q}{(2 \pi )^3}\frac{q^2 +k_C^2}{p^2-{q}^2+i\epsilon }\,\frac{2 \pi \eta _q }{e^{2 \pi \eta _q}-1}\nonumber \\= & {} 2\mu \!\!\int \!\! \frac{d^3 q}{(2 \pi )^3}\frac{q^2 }{p^2-{q}^2+i\epsilon }\,\frac{2 \pi \eta _q }{e^{2 \pi \eta _q}-1}+k_C^2J_0(E)\nonumber \\= & {} 2\mu \!\!\int \!\!\frac{d^3 q}{(2 \pi )^3}\frac{q^2-p^2 }{p^2-{q}^2+i\epsilon }\,\frac{2 \pi \eta _q }{e^{2 \pi \eta _q}-1}+(p^2+k_C^2)J_0(E)\nonumber \\= & {} W_1(\eta _p)J_0(E)\underbrace{-2\mu \int \frac{d^3 q}{(2 \pi )^3}\,\frac{2 \pi \eta _q }{e^{2 \pi \eta _q}-1}}_{J}. \end{aligned}$$
(A.24)
In the second line of Eq. (A.24) we use
$$\begin{aligned}{}[\nabla _i \chi _{q}^{(+)}({\textbf{0}})][\nabla _i \chi _q^{*(+)}({\textbf{0}})]=C^2_0(\eta _q)W_1(\eta _q). \end{aligned}$$
(A.25)
The integral J is divergent and independent of the external momentum p. According to the PDS regularization scheme it takes the form [40]
$$\begin{aligned} J=-4\pi \mu k_C^2 \Bigg ( k_C\zeta '(-2)+\frac{\kappa }{24}\Bigg ), \end{aligned}$$
(A.26)
where \(\zeta '\) is derivative of the Riemann zeta function and \(\zeta '(-2)\approx -0.0304\). If we use the cutoff regularization scheme the integral J takes the form
$$\begin{aligned} J= & {} -\frac{2\mu }{\pi }\!\int _{0}^{{\Lambda }}\!dq q^2 \frac{\eta _q}{e^{2\pi \eta _q}-1}\nonumber \\= & {} -8\pi \mu k^3_C\!\int _{\frac{2\pi k_C}{{\Lambda }}}^{\infty }\, \frac{dx}{x^3(e^{x}-1)} \nonumber \\= & {} -8\pi \mu k^3_C\Bigg \{\int _{0}^{\infty }\! \frac{dx}{x^3(e^{x}-1)}-\int _{0}^{\frac{2\pi k_C}{{\Lambda }}}\frac{dx}{x^3(e^{x}-1)}\Bigg \}\nonumber \\= & {} -8\pi \mu k^3_C\Bigg \{{\Gamma }(-2)\zeta (-2)\nonumber \\{} & {} -\int _{0}^{ \frac{2\pi k_C}{{\Lambda }}}dx\Bigg (\frac{1}{x^4}-\frac{1}{2x^3}+\frac{1}{12x^2}+{\mathcal {O}}\,(x^0)\Bigg )\Bigg \}\nonumber \\= & {} -8\pi \mu k^3_C\Bigg \{ 2\pi ^2C_E \,\zeta '(-2) +\frac{1}{3}\Bigg (\frac{{\Lambda }}{2\pi k_C }\Bigg )^{\!3}-\frac{1}{4}\Bigg (\frac{ {\Lambda }}{2\pi k_C}\Bigg )^{\!2}\nonumber \\{} & {} +\frac{1}{12}\Bigg (\frac{{\Lambda }}{2\pi k_C}\Bigg )+{\mathcal {O}}\left( \frac{2\pi k_C}{{\Lambda }}\right) \Bigg \}, \end{aligned}$$
(A.27)
where in the second line we use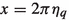 
. Thus, \(J_1\) can be divided as \(J_1=J_1^{fin}+J_1^{div}\) with
$$\begin{aligned} J^{fin}_1= & {} W_1(\eta _p)J^{fin}_0=-\frac{\mu }{2\pi }H_1(\eta _p),\end{aligned}$$
(A.28)
$$\begin{aligned} J^{div}_1= & {} W_1(\eta _p)J^{div}_0+J=p^2J^{div}_0+(k_C^2J^{div}_0+J).\nonumber \\ \end{aligned}$$
(A.29)
Consequently, the up-to-NLO EFT scattering amplitude of Eqs. (A.16), (A.19) and (A.21) is rewritten as
$$\begin{aligned} T^{[\xi ]}_{CS}= & {} -\frac{2\pi }{\mu }\frac{C_{0}^2(\eta _p)W_{1}(\eta _p)}{\left( \frac{6\pi {\Delta }^{[\xi ]}}{\eta ^{[\xi ]}g^{[\xi ]^2}\mu }+\frac{2\pi }{\mu }(k_C^2J^{div}_0+J)\right) -\frac{1}{2}\left( \frac{6\pi }{\eta ^{[\xi ]}g^{[\xi ]^2}\mu ^2}+\frac{2\pi }{\mu }J^{div}_0\right) p^2-H_1(\eta _p)} \nonumber \\{} & {} \times \left[ \underbrace{\,\,1_{_{_{_{_{_{_{_{_{_{_{_{_{}}}}}}}}}}}}}}_{\textrm{LO}}+\!\underbrace{\frac{1}{4}\frac{\left( \frac{6\pi h^{[\xi ]}}{g^{[\xi ]^2}\mu ^3}\right) }{\left( \frac{6\pi {\Delta }^{[\xi ]}}{\eta ^{[\xi ]}g^{[\xi ]^2}\mu }+\frac{2\pi }{\mu }(k_C^2J^{div}_0+J)\right) -\frac{1}{2}\left( \frac{6\pi }{\eta ^{[\xi ]}g^{[\xi ]^2}\mu ^2}+\frac{2\pi }{\mu }J^{div}_0\right) p^2-H_1(\eta _p)}p^4\,\,}_{\textrm{NLO}~\textrm{correction}}\!\!\right] . \end{aligned}$$
(A.30)
The function \(J_1^{div}\) has two divergences, momentum independent and momentum-squared. Regardless of PDS or cutoff renormalization scheme are used to calculate the divergent integrals \(J_0^{div}\) and J, these momentum independent and momentum-squared divergence parts are absorbed by the parameters \({\Delta }^{[\xi ]}\), \(g^{[\xi ]}\) and \(h^{[\xi ]}\) via introducing the renormalized parameters \({\Delta }_R^{[\xi ]}\), \(g_R^{[\xi ]}\) and \(h_R^{[\xi ]}\) as
$$\begin{aligned} {\Delta }^{[\xi ]}_R&=\frac{{\Delta }^{[\xi ]}+\frac{1}{3}\eta ^{[\xi ]}g^{[\xi ]^2} (k_C^2J^{div}_0+J)}{1+\frac{1}{3}\eta ^{[\xi ]}g^{[\xi ]^2}\mu J^{div}_0}, \end{aligned}$$
(A.31)
$$\begin{aligned} \frac{1}{g_R^{[\xi ]^2}}&=\frac{1}{g^{[\xi ]^2}}+\frac{1}{3}\eta ^{[\xi ]}\mu J^{div}_0, \end{aligned}$$
(A.32)
$$\begin{aligned} h_R^{[\xi ]}&=\frac{h^{[\xi ]}}{1+\frac{1}{3}\eta ^{[\xi ]}g^{[\xi ]^2}\mu J^{div}_0}. \end{aligned}$$
(A.33)
Finally, the up-to-NLO Coulomb-subtracted EFT scattering amplitude for \(^3\!P_0\), \(^3\!P_1\) and \(^3\!P_2\) channels are obtained
$$\begin{aligned} {} T^{[\xi ]}_{CS}= & {} -\frac{2\pi }{\mu }\frac{ C_0^2(\eta _p)W_1(\eta _p) }{\frac{6\pi {\Delta }_{\!R}^{[\xi ]}}{\eta ^{[\xi ]}g_{\!R}^{[\xi ]^2}\mu }-\frac{1}{2}\left( \frac{6\pi }{\eta ^{[\xi ]}g_{\!R}^{[\xi ]^2}\mu ^2}\right) p^2-H_1(\eta _p)} \!\nonumber \\{} & {} \times \left[ \underbrace{\,\,1_{_{_{_{_{_{_{_{_{_{_{_{_{_{_{_{_{_{}}}}}}}}}}}}}}}}}}}_{\textrm{LO}}+\underbrace{\frac{1}{4}\frac{\left( \frac{6\pi h_{\!R}^{[\xi ]}}{g_{\!R}^{[\xi ]^2}\mu ^3}\right) }{\frac{6\pi {\Delta }_{\!R}^{[\xi ]}}{\eta ^{[\xi ]}g_{\!R}^{[\xi ]^2}\mu }-\frac{1}{2}\left( \frac{6\pi }{\eta ^{[\xi ]}g_{\!R}^{[\xi ]^2}\mu ^2}\right) p^2-H_1(\eta _p)}p^4\,}_{\mathrm {NLO~corection}}\!\!\right] \!,\nonumber \\ \end{aligned}$$
(A.34)
1.3
D-wave channels
The Lagrangian for the strong \(d{-}\alpha \) interaction in the \(\xi =\) \({^3D_1}\) channel is written as
$$\begin{aligned} {} {\mathcal {L}}^{[\xi ]}= & {} \phi ^{\dagger }\left( i\partial _0+\frac{\nabla ^2}{2m_\alpha }\right) \phi +d_i^{\dagger }\left( i\partial _0+\frac{\nabla ^2}{2m_d}\right) d_i\nonumber \\{} & {} +\,{\tilde{t}}_{i}^{\,\dagger }\Bigg [\eta ^{[\xi ]}\left( i\partial _0+\frac{\nabla ^2}{2m_t}-{\Delta }^{[\xi ]}\right) \Bigg ]{\tilde{t}}_{i}\nonumber \\ 3{} & {} +{\tilde{t}}_{i}^{\,\dagger }\Bigg [h^{[\xi ]}\left( i\partial _0+\frac{\nabla ^2}{2m_t}\right) ^2\Bigg ]{\tilde{t}}_{i}\nonumber \\{} & {} +\frac{3}{\sqrt{2}}\,g^{[\xi ]}\Big [{\tilde{t}}_{j}^{\,\dagger }(\phi \,\tau _{ji} d_i)+h.c.\Big ], \end{aligned}$$
(A.35)
where \({\tilde{t}}_i\) is the vector field of the \({^3\!D_1}\) dimeron. Using the Lagrangian (A.35), the Coulomb-subtracted amplitude in \({^3\!D_1}\) partial wave is evaluated by
$$\begin{aligned} {}{} & {} -i5T^{[\xi ]}_{CS}P_2(\hat{{{\textbf {p}}}}'\cdot \hat{{{\textbf {p}}}})e^{2i\sigma _2}\nonumber \\{} & {} \quad =\frac{9}{2}(-ig^{[\xi ]})^2[\tau ^*_{jl}\chi _{p'}^{*(-)}\!({\textbf{0}})] \varepsilon _j^{d*}\varepsilon ^{{\tilde{t}}}_l iD^{[\xi ]}(E,{\textbf {0}})\varepsilon _{k}^{{\tilde{t}}*}\varepsilon _i^{d}[\tau _{ki}\chi _p^{(+)}\!({\textbf{0}})]\nonumber \\{} & {} \quad =-\frac{3}{2}ig^{[\xi ]^2} D^{[\xi ]}(E,{\textbf {0}}) [\tau ^*_{ki}\chi _{p'}^{*(-)}({\textbf{0}})]\,[\tau _{ki}\chi _p^{(+)}({\textbf{0}})]\nonumber \\{} & {} \quad =-ig^{[\xi ]^2} D^{[\xi ]}(E,{\textbf {0}})\,C_0^2(\eta _p)W_2(p) P_2(\hat{{{\textbf {p}}}}'\cdot \hat{{{\textbf {p}}}})e^{2i\sigma _2}, \end{aligned}$$
(A.36)
where \(\varepsilon ^{{\tilde{t}}}_i\) is the vector auxiliary field of the \({^3\!D_1}\) dimeron and in the last equality we use
$$\begin{aligned}{} & {} [\tau ^*_{ki}\chi _{p'}^{*(-)}\!({\textbf{0}})][\tau _{ki}\chi _p^{(+)}\!({\textbf{0}})]\nonumber \\{} & {} \quad =\frac{1}{4}(p'_k p_k \,p'_ip_i-\frac{1}{3}p'^{2}p^2\delta _{ki}) C^2_0(\eta _p)(1+\eta _p^2)(4+\eta _p^2)e^{2i\sigma _2}\nonumber \\{} & {} \quad =\frac{1}{6}C^2_0(\eta _p)p^4(1+\eta _p^2)(4+\eta _p^2)P_2(\hat{{{\textbf {p}}}}'\cdot \hat{{{\textbf {p}}}})e^{2i\sigma _2}\nonumber \\{} & {} \quad =\frac{2}{3}W_2(p)P_2(\hat{{{\textbf {p}}}}'\cdot \hat{{{\textbf {p}}}})e^{2i\sigma _2}. \end{aligned}$$
(A.37)
In order to calculate the Coulomb-subtracted EFT amplitude of \(d{-}\alpha \) scattering in the \(\xi ={^3\!D_2}\) channel, we introduce the strong interaction in this channel using the Lagrangian
$$\begin{aligned} {} {\mathcal {L}}^{[\xi ]}= & {} \phi ^{\dagger }\left( i\partial _0+\frac{\nabla ^2}{2m_\alpha }\right) \phi +d_i^{\dagger }\left( i\partial _0+\frac{\nabla ^2}{2m_d}\right) d_i\nonumber \\{} & {} +\,{\tilde{t}}_{ij}^{\,\dagger }\Bigg [\eta ^{[\xi ]}\left( i\partial _0+\frac{{\nabla } ^2}{2m_t}-{\Delta }^{[\xi ]}\right) +h^{[\xi ]} \left( i\partial _0+\frac{\nabla ^2}{2m_t}\right) ^2\Bigg ]{\tilde{t}}_{ij}\nonumber \\{} & {} +\sqrt{\frac{3}{2}}\epsilon _{lji} \,g^{[\xi ]}[{\tilde{t}}_{kl}^{\,\dagger }(\phi \,\tau _{kj} d_i)+h.c.], \end{aligned}$$
(A.38)
with \({\tilde{t}}_{ij}\) as the \({^3\!D_2}\) tensor auxiliary field. So, we have
$$\begin{aligned} {}{} & {} -i5T^{[\xi ]}_{CS}P_2(\hat{{{\textbf {p}}}}'\cdot \hat{{{\textbf {p}}}})e^{2i\sigma _2}\nonumber \\{} & {} \quad =\frac{3}{2}(\!-ig^{[\xi ]})^2[\tau ^*_{mn} \chi _{p'}^{*(-)}({\textbf{0}})] \varepsilon _j^{*d}\epsilon _{snj}\varepsilon _{ms}^{{\tilde{t}}}\nonumber \\{} & {} \qquad \times iD^{[\xi ]}(E,{\textbf {0}}) \varepsilon _{kp}^{*{\tilde{t}}}\,\epsilon _{pli} \,\varepsilon _i^{d}\,[\tau _{kl}\chi _p^{(+)}({\textbf{0}})]\nonumber \\{} & {} \quad =-\frac{3}{2}ig^{[\xi ]^2}D^{[\xi ]}(E,{\textbf {0}}) [\tau ^*_{ki}\chi _{p'}^{*(-)}({\textbf{0}})][\tau _{ki}\chi _p^{(+)}({\textbf{0}})]\nonumber \\{} & {} \quad =-ig^{[\xi ]^2} D^{[\xi ]}(E,{\textbf {0}})\,C_0^2(\eta _p) W_2(p) P_2(\hat{{{\textbf {p}}}}'\cdot \hat{{{\textbf {p}}}})e^{2i\sigma _2},\nonumber \\ \end{aligned}$$
(A.39)
Also, the strong interaction Lagrangian of the \(d{-}\alpha \) system in the \(\xi ={^3\!D_3}\) channel can be described as
$$\begin{aligned} {} {\mathcal {L}}^{[\xi ]}= & {} \phi ^{\dagger }\left( i\partial _0+\frac{\nabla ^2}{2m_\alpha }\right) \phi +d_i^{\dagger }\left( i\partial _0+\frac{\nabla ^2}{2m_d}\right) d_i\nonumber \\{} & {} +\sqrt{\frac{45}{8}} g^{[\xi ]}[{\tilde{t}}_{ijk}^{\,\dagger }(\phi \tau _{ij} d_k)+h.c.]\nonumber \\{} & {} +\,{\tilde{t}}_{ijk}^{\,\dagger }\Bigg [\eta ^{[\xi ]}\left( i\partial _0+\frac{\nabla ^2}{2m_t}-{\Delta }^{[\xi ]}\right) \Bigg ]{\tilde{t}}_{ijk}\nonumber \\{} & {} +\,h^{[\xi ]} \left( i\partial _0+\frac{\nabla ^2}{2m_t}\right) ^2\Bigg ]{\tilde{t}}_{ijk}, \end{aligned}$$
(A.40)
where \(t_{ijk}\) indicates the auxiliary tensor field of the \(^3\!D_3\) dimeron. According to the Feynman diagram of Fig. 2, we have
$$\begin{aligned} {}{} & {} -i5T^{[\xi ]}_{CS}P_2(\hat{{{\textbf {p}}}}'\cdot \hat{{{\textbf {p}}}})e^{2i\sigma _2}\nonumber \\{} & {} \quad =\frac{45}{8}(-ig^{[\xi ]})^2 [\tau ^*_{kl}\chi _{p'}^{(-)*}({\textbf{0}})] \varepsilon ^{*d}_{j}\varepsilon _i^{d} iD^{[\xi ]}(E,{\textbf {0}})\nonumber \\{} & {} \qquad \times \,\varepsilon ^{{\tilde{t}}}_{klj} \varepsilon _{mni}^{*{\tilde{t}}}\,[\tau _{mn}\chi _p^{(+)}({\textbf{0}})]\nonumber \\{} & {} \quad = -ig^{[\xi ]^2} D^{[\xi ]}(E,{\textbf {0}})\,C_0^2(\eta _p) W_2(p) P_2(\hat{{{\textbf {p}}}}'\cdot \hat{{{\textbf {p}}}})e^{2i\sigma _2},\nonumber \\ \end{aligned}$$
(A.41)
where \(\varepsilon _{ijk}\) denotes the tensor polarization of \(^3\!D_3\) auxiliary field which satisfies the following relation
$$\begin{aligned} \varepsilon ^{{\tilde{t}}}_{klj} \varepsilon _{mni}^{*{\tilde{t}}}= & {} \frac{1}{6}\bigg [\!-\frac{2}{5}\bigg \{\delta _{mn}(\delta _{ij}\delta _{kl}+\delta _{ik}\delta _{jl}+\delta _{il}\delta _{jk})\nonumber \\{} & {} +(m\! \leftrightarrow \!l )+(n \!\leftrightarrow \!l )\bigg \} +(\delta _{il}\delta _{jm}\delta _{kn} +\delta _{il}\delta _{jn}\delta _{km})\nonumber \\{} & {} +(i \rightarrow \! j\rightarrow \!k\rightarrow \! i)+(i \rightarrow k\rightarrow j \rightarrow i)\bigg ].\nonumber \\ \end{aligned}$$
(A.42)
The full propagator for D waves is expressed by
$$\begin{aligned} {} D^{[\xi ]}(E,{\textbf {0}})=\frac{\eta ^{[\xi ]}}{E-{\Delta }^{[\xi ]}+h^{[\xi ]}E^2-\frac{1}{5}\eta ^{[\xi ]}g^{[\xi ]^2}J_2(E)}, \end{aligned}$$
(A.43)
with
$$\begin{aligned} J_2(E)= & {} \frac{3}{2}\Bigg \{2\mu \int \frac{d^3 q}{(2 \pi )^3}\frac{[\tau _{ij}\chi _{{q}}^{(+)}({\textbf{0}})] [\tau _{ij}\chi _{{q}}^{*(+)}({\textbf{0}})]}{2\mu E -{q}^2+i\epsilon }\Bigg \} \nonumber \\= & {} \frac{\mu }{2} \int \frac{d^3 q}{(2 \pi )^3}\frac{4q^4 +5q^2k_C^2+k_C^4}{p^2-{q}^2+i\epsilon }\frac{2 \pi \eta _q }{e^{2 \pi \eta _q}-1}\nonumber \\= & {} \frac{5}{4}k_C^2J_1(p)+(p^4-k_C^4)J_0(p)\nonumber \\{} & {} +2\mu \int \frac{d^3 q}{(2 \pi )^3}\frac{q^4-p^4 }{p^2-{q}^2+i\epsilon }\,\frac{2 \pi \eta _q }{e^{2 \pi \eta _q}-1}\nonumber \\= & {} \frac{5}{4}k_C^2J_1(p)+(p^4-k_C^4)J_0(p)+p^2J\nonumber \\{} & {} -2\mu \int \frac{d^3 q}{(2 \pi )^3}q^2\,\frac{2 \pi \eta _q }{e^{2 \pi \eta _q}-1}\nonumber \\= & {} W_2(p)J_0(p)-(p^2+\frac{5}{4}k_C^2)J\nonumber \\{} & {} \underbrace{-2\mu \int \frac{d^3 q}{(2 \pi )^3}q^2\,\frac{2 \pi \eta _q }{e^{2 \pi \eta _q}-1}}_{I}. \end{aligned}$$
(A.44)
The integral I is divergent and independent of the external momentum p. According to the PDS regularization scheme takes the form [57]
$$\begin{aligned} I=\frac{4}{3}\pi ^3\mu k_C^4\Bigg ( k_C \zeta '(-4)-\frac{\kappa }{120}\Bigg ), \end{aligned}$$
(A.45)
with \(\zeta '(-4)\approx 0.00798\). If we use the cutoff regularization scheme the integral J takes the form
$$\begin{aligned} I= & {} -\frac{2\mu }{\pi }\!\int _{0}^{{\Lambda }}\!dq q^4 \frac{\eta _q}{e^{2\pi \eta _q}-1}\nonumber \\= & {} -32\pi ^3 \mu k^5_C\!\int _{\frac{2\pi k_C}{{\Lambda }}}^{\infty }\frac{dx}{x^5(e^{x}-1)}\nonumber \\= & {} -32\pi ^3 \mu k^5_C\Bigg \{\int _{0}^{\infty }\frac{dx}{x^5(e^{x}-1)}-\int _{0}^{\frac{2\pi k_C}{{\Lambda }}}\frac{dx}{x^5(e^{x}-1)}\Bigg \}\nonumber \\= & {} -32\pi ^3\mu k^5_C\Bigg \{{\Gamma }(-4)\zeta (-4)\nonumber \\{} & {} -\int _{0}^{\frac{2\pi k_C}{{\Lambda }}}dx\Bigg (\frac{1}{x^6}-\frac{1}{2x^5}+\frac{1}{12x^4}-\frac{1}{720x^2}+{\mathcal {O}}\,(x^0)\!\Bigg )\Bigg \}\nonumber \\= & {} -32\pi ^3\mu k^5_C\Bigg \{-\frac{1}{18}\pi ^2C_E \,\zeta '(-4)+\frac{1}{5}\Bigg (\frac{{\Lambda }}{2\pi k_C }\Bigg )^{\!5}\nonumber \\{} & {} -\frac{1}{8}\Bigg (\frac{ {\Lambda }}{2\pi k_C}\Bigg )^{\!4}+\frac{1}{36}\Bigg (\frac{{\Lambda }}{2\pi k_C}\Bigg )^{\!3}-\frac{1}{720}\Bigg (\frac{{\Lambda }}{2\pi k_C}\Bigg )\nonumber \\{} & {} +\,{\mathcal {O}}\,\left( \frac{2\pi k_C}{{\Lambda }}\right) \Bigg \}, \end{aligned}$$
(A.46)
where in the second line we use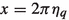 
. Consequently, separating the integrals \(J_2\) into the finite and divergent part leads to
$$\begin{aligned} {} J^{fin}_2= & {} W_2(p)J^{fin}_0=-\frac{\mu }{2\pi }H_2(\eta _p),\end{aligned}$$
(A.47)
$$\begin{aligned} J^{div}_2= & {} W_2(p)J^{div}_0-\left( p^2+\frac{5}{4}k_C^2\right) J+I \nonumber \\= & {} p^4J^{div}_0+p^2\left( \frac{5}{4}k_C^2J^{div}_0-J\right) \nonumber \\{} & {} +\left( \frac{1}{4}k_C^4J^{div}_0-\frac{5}{4}k_C^2J+I\right) . \end{aligned}$$
(A.48)
Thus the up-to-NLO EFT scattering amplitude for D waves is written as
$$\begin{aligned} T^{[\xi ]}_{CS}= & {} -\frac{2\pi }{\mu }\frac{C_{0}^2(\eta _p)W_{2}(\eta _p)}{(\frac{10\pi {\Delta }^{[\xi ]}}{\eta ^{[\xi ]}g^{[\xi ]^2}\!\mu }+\frac{2\pi }{\mu }(\frac{1}{4}k_C^4J^{div}_0-\frac{5}{4}k_C^2J+I)-\frac{1}{2}(\frac{10\pi }{\eta ^{[\xi ]}g^{[\xi ]^2}\!\mu ^2}+\frac{2\pi }{\mu }(\frac{5}{4}k_C^2J^{div}_0-J)p^2-\frac{1}{4}(\!\frac{10\pi h^{[\xi ]}}{g^{[\xi ]^2}\!\mu ^3}\!+\frac{2\pi }{\mu }J^{div}_0)p^4-H_2(\eta _p)}. \end{aligned}$$
(A.49)
The function \(J_2^{div}\) has three divergences, momentum independent, momentum-squared and momentum-cubed which are absorbed by the parameters \({\Delta }^{[\xi ]}\), \(g^{[\xi ]}\) and \(h^{[\xi ]}\) via introducing the renormalized parameters \({\Delta }_R^{[\xi ]}\), \(g_R^{[\xi ]}\) and \(h_R^{[\xi ]}\) as
$$\begin{aligned} {} {\Delta }_{\!R}^{[\xi ]}= & {} \frac{{\Delta }^{[\xi ]}+\frac{1}{5}\eta ^{[\xi ]}g^{[\xi ]^2}\mu \left( \frac{1}{4}k_C^4J^{div}_0-\frac{5}{4}k_C^2J+I\right) }{1+\frac{1}{5}\eta ^{[\xi ]}g^{[\xi ]^2}\mu \left( \frac{5}{4}k_C^2J^{div}_0-J\right) }, \nonumber \\\end{aligned}$$
(A.50)
$$\begin{aligned} \frac{1}{g_R^{[\xi ]^2}}= & {} \frac{1}{g^{[\xi ]^2}}+\frac{1}{5}\eta ^{[\xi ]}\mu \left( \frac{5}{4}k_C^2J^{div}_0-J\right) , \end{aligned}$$
(A.51)
$$\begin{aligned} h_{\!R}^{[\xi ]}= & {} \frac{h^{[\xi ]}+\frac{1}{5}g^{[\xi ]^2}\mu J_0^{div}}{1+\frac{1}{5}\eta ^{[\xi ]}g^{[\xi ]^2}\mu \left( \frac{5}{4}k_C^2J^{div}_0-J\right) }. \end{aligned}$$
(A.52)
Finally, the Coulomb-subtracted EFT scattering amplitude for all possible D waves are written as
$$\begin{aligned}{} & {} T^{[\xi ]}_{CS}=\nonumber \\ {}{} & {} -\frac{2\pi }{\mu }\frac{ C_0^2(\eta _p)W_2(p)}{\frac{10\pi {\Delta }_{\!R}^{[\xi ]}}{\eta ^{[\xi ]}g_{\!R}^{[\xi ]^2}\!\mu }-\frac{1}{2}\left( \frac{10\pi }{\eta ^{[\xi ]}g_{\!R}^{[\xi ]^2}\!\mu ^2}\right) p^2-\frac{1}{4}\left( \frac{10\pi h_{\!R}^{[\xi ]}}{g_{\!R}^{[\xi ]^2}\!\mu ^3}\right) p^4-H_2(\eta _p)}.\nonumber \\ \end{aligned}$$
(A.53)
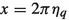, and in the last line we use
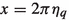. Thus, \(J_1\) can be divided as \(J_1=J_1^{fin}+J_1^{div}\) with
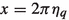. Consequently, separating the integrals \(J_2\) into the finite and divergent part leads to