1 Introduction

The theoretical determination of the QCD phase diagram as a function of temperature T and baryon chemical potential \(\mu _B\) remains a challenging task. Despite the persistent sign problem, combining increasingly detailed lattice information on baryon number fluctuations [1,2,3] and their modeling [4], the chiral transition in the massless limit [5, 6] and its relation to the physical point [7, 8], as well as improved reweighted calculations checked against imaginary chemical potential [9], one may bound the critical endpoint of a possible chiral phase transition at finite density by \(\mu _B\gtrsim 2.5T\) and \(T\lesssim 135\) MeV. Critical endpoint candidates predicted by functional methods are consistent with and well beyond these bounds in a region, where the current truncations require further stability checks [10,11,12]. For recent reviews and further references, see [10, 13, 14].

On the other hand, an unexpected new symmetry was discovered to emerge at zero density, where there is no sign problem. Lattice simulations with \(N_F=2\) flavors of chiral fermions show approximate \(SU(2)_{CS}\) chiral spin and \(SU(2N_F)\) symmetries for both spatial and temporal \(J=0,1\) meson correlators in a temperature range \(T_\textrm{ch}\lesssim T \lesssim 3T_\textrm{ch}\) above the chiral crossover, \(T_\textrm{ch}\) [15, 16]. This symmetry is larger than the \(SU(2)_L\times SU(2)_R\times U(1)_A\) chiral symmetry of the QCD Lagrangian, which it contains as a subgroup. It is a symmetry of the color charge, but not of the QCD Lagrangian, and can only be realized in the quantum effective action when color-electric quark gluon interactions dynamically dominate over color-magnetic interactions and kinetic terms. This suggests that chiral quarks are bound by color-electric flux tubes in such a regime, which thus has been dubbed a “stringy liquid” [15, 16]. When temperature increases beyond \(T_s\sim 3T_\textrm{ch}\), the color-electric interactions between quarks get screened and the symmetry reduces to the expected chiral symmetry corresponding to a quark gluon plasma.

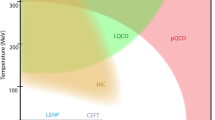
In this work, we elaborate on a suggestion [17] that the chiral spin symmetric temperature range observed at zero density continues as a band across the QCD phase diagram, sketched in Fig. 1. To render this paper self-contained, we begin with a brief summary of chiral spin symmetry in Sec. 2 and its observation in finite temperature lattice QCD, Sect. 3. In Sect. 4 we show that all known results on screening masses are fully consistent with such an intermediate temperature range between broken chiral symmetry and a partonic quark gluon plasma. Using quark hadron duality of screening masses to identify the onset of the plasma regime, we derive how the upper boundary of the chiral spin symmetric band curves away from the T-axis in Sect. 5. In Sect. 6 we identify parity doubled baryon matter as a candidate for a chiral spin symmetric regime of cold and dense QCD, which can be naturally embedded into quarkyonic matter. Finally, we discuss the prospects and limitations of dilepton spectra to probe matter in the chiral spin symmetric regime, Sect. 7.

2 Chiral spin symmetry of the color charge and its implications

The Banks-Casher relation [18] connects the quark condensate of the QCD vacuum with the density of the near-zero modes \(\lambda _n\) of the Dirac operator,

$$\begin{aligned} \langle \bar{\psi }\psi \rangle= & {} \pi \rho (0)\;,\\ \rho (0)= & {} { \lim _{\lambda \rightarrow 0} \lim _{m \rightarrow 0} \lim _{V\rightarrow \infty } \frac{1}{\pi V} \int d \lambda \sum _n \frac{\delta (\lambda -\lambda _n)}{m + i\lambda }\;.\nonumber } \end{aligned}$$
(1)

An artificial truncation of the near-zero modes on the lattice at \(T=0\) may then be expected to restore the \(SU(N_F)_L \times SU(N_F)_R\) and possibly the \(U(1)_A\) chiral symmetry of the QCD Lagrangian. For example, the instanton liquid model [19, 20] suggests that both \(SU(N_F)_L \times SU(N_F)_R\) and \(U(1)_A\) breakings are due to the ’t Hooft determinant induced by the instanton fluctuations of the QCD vacuum at sufficiently strong coupling [21].

Fig. 1
figure 1

Qualitative sketch of a possible QCD phase diagram with a band of approximate chiral spin symmetry. At zero density, both transitions between the regimes are smooth crossovers. The lower boundary corresponds to full chiral symmetry restoration, which could be a true phase transition at larger density. Beyond the upper boundary, light quark meson correlators are consistent with a partonic description

Full size image

A spectrum calculation based on such truncated Dirac operators has revealed a larger degeneracy pattern than expected, both for mesons [22,23,24] and baryons [25]. From the quantum numbers of the degenerate states the symmetry groups responsible for this large degeneracy, the chiral spin \(SU(2)_{CS}\) and \(SU(2N_F)\), were reconstructed in Refs. [26, 27]. An \(SU(2)_{CS}\) chiral spin transformation acting on Dirac spinors can be defined as

$$\begin{aligned} \psi \rightarrow \psi ^\prime = \exp \left( i \frac{\varepsilon ^n \varSigma ^n}{2}\right) \psi \;, \end{aligned}$$
(2)

where the generators \(\varSigma ^n/2\) of the four-dimensional reducible representation are

$$\begin{aligned} \varSigma ^n = \{\gamma _0,-i \gamma _5\gamma _0,\gamma _5\} \end{aligned}$$
(3)

and satisfy the su(2) algebra. This transformation rotates in the space of right- and left-handed Weyl spinors R, L, and an equivalent representation of Eq. (2) is

$$\begin{aligned} \left( \begin{array}{c} R\\ L \end{array}\right) \; \rightarrow \left( \begin{array}{c} R'\\ L' \end{array}\right) = \exp \left( i \frac{\varepsilon ^n \sigma ^n}{2}\right) \left( \begin{array}{c} R\\ L \end{array}\right) \; . \end{aligned}$$
(4)

In Euclidean spacetime with its O(4) symmetry, all four directions are equivalent and one can use any Euclidean hermitian \(\gamma \)-matrix \(\gamma _k\), \(k=1,2,3,4\) to replace the Minkowskian \(\gamma _0\),

$$\begin{aligned}{} & {} \varSigma ^n = \{\gamma _k,-i \gamma _5\gamma _k,\gamma _5\}, \end{aligned}$$
(5)
$$\begin{aligned}{} & {} \gamma _i\gamma _j + \gamma _j \gamma _i = 2\delta ^{ij}; \qquad \gamma _5 = \gamma _1\gamma _2\gamma _3\gamma _4. \end{aligned}$$
(6)

The su(2) algebra is satisfied for any \(k=1,2,3,4\), so any choice is permitted that does not mix operators with different spatial O(3) spins. Note that \(SU(2)_{CS}\) contains \(U(1)_A\) as a subgroup. The direct product of the \(SU(2)_{CS}\) group with the flavor group \(SU(N_F)\) can be embedded into a \(SU(2N_F)\) group, which includes the chiral symmetry as a subgroup,

$$\begin{aligned} SU(2N_F)\supset SU(N_F)_L \times SU(N_F)_R \times U(1)_A \;. \end{aligned}$$
(7)

The multiplets of the \(SU(2)_{CS}\) and SU(4) groups have been worked out in Refs. [26, 27]. In particular, these symmetries require the degeneracy of all isovector \(J=1\) mesons, including the \(a_1\) and \(b_1\), which are not degenerate under chiral symmetry.

The \(SU(2)_{CS}\) and \(SU(2N_F)\) groups are not symmetries of the massless Dirac part of the QCD Lagrangian. In a fixed Lorentz frame we can split the latter in color-electric (temporal) and color-magnetic (spatial) parts,

$$\begin{aligned} \bar{\psi }\gamma ^\mu D_\mu \psi = \bar{\psi }\gamma ^0 D_0 \psi + \bar{\psi }\gamma ^i D_i\psi \;, \end{aligned}$$
(8)

where the first term is invariant under \(SU(2)_{CS}\) and \(SU(2N_F)\), while the second term is not. At the same time these are symmetries of the Lorentz-invariant color charge

$$\begin{aligned} Q^a = \int d^3x \;\; \psi ^\dagger (x) T^a \psi (x)\;, \end{aligned}$$
(9)

with \(T^a\) the SU(3) color generators. This feature allows for the \(SU(2)_{CS}\) and \(SU(2N_F)\) symmetries to distinguish between the chromoelectric and chromomagnetic interactions in a given reference frame. The chromoelectric gauge field couples to the color charge, consequently the chromoelectric interaction of quarks and gauge fields is \(SU(2)_{CS}\) and \(SU(2N_F)\) symmetric. The chromomagnetic gauge fields couple to a current, which is not \(SU(2)_{CS}\) and \(SU(2N_F)\) symmetric. Thus, the symmetry of the electric part of the QCD Lagrangian is larger than the symmetry of the QCD Lagrangian as a whole.

The observation of the \(SU(2)_{CS}, SU(2N_F)\) symmetries in the hadron spectrum upon truncation of the near-zero modes of the Dirac operator then implies that the magnetic interaction at zero temperature is located mostly in those near-zero modes, whereas a confining electric interaction is distributed among all Dirac modes. Hence, confinement and chiral symmetry breaking in QCD are not directly related phenomena. Based on this observation it was predicted that, for finite temperature QCD without any truncations, where the rest frame of the medium constitutes a preferred reference frame, the chiral spin and \(SU(2N_F)\) symmetries should emerge above the chiral symmetry restoring crossover [28].

3 Chiral spin symmetry at finite temperature

Fig. 2
figure 2

Temporal correlation functions for \(N_F=2\) QCD with chiral fermions on \(12 \times 48^3\) lattices. Left: Full QCD results at \(T=220\) MeV, representing multiplets of all groups, \(U(1)_A\), \(SU(2)_L \times SU(2)_R\), \(SU(2)_{CS}\) and SU(4). Right: Correlators calculated with free quarks with manifest \(U(1)_A\) and \(SU(2)_L \times SU(2)_R\) symmetries. From [16]

Full size image

At finite temperature, the chiral condensate decreases significantly through a smooth crossover between \(T\approx \) 100–200 MeV. The pseudo-critical temperature for chiral symmetry restoration is usually defined by the peak of the chiral susceptibility, and for \(N_F=2+1\) QCD at the physical point in the continuum is \(T_\textrm{pc} =157(2)\) MeV [29, 30]. Above this temperature, one a priori expects observables to exhibit a \(SU(2)_L \times SU(2)_R\) chiral symmetry. The effects of the axial anomaly are determined by the topological charge density. There are strong indications from the lattice that the \(U(1)_A\) symmetry is approximately restored above \(T_\textrm{ch} \approx 200\) MeV [31,32,33,34], which suggests that the topological fluctuations at these temperatures are strongly suppressed. This effective symmetry restoration is visible by the degeneracy of all correlators (obtained with a chirally symmetric Dirac operator) connected by the \(U(1)_A\) transformation [15, 16], and the degeneracy of scalar and pseudo-scalar susceptibilities in particular. Closer to \(T_\textrm{pc}\), the quark condensate becomes appreciable and should provide a splitting of the respective correlators, as is also observed [33, 35]. For the following, mostly qualitative, considerations, we take \(T_\textrm{ch}\approx T_\textrm{pc}\) approximately, without loss of generality.

Detailed lattice studies of spatial [15] and temporal [16] meson correlators at \(T\gtrsim T_\textrm{ch}\), calculated in \(N_F=2\) QCD with a chirally symmetric Dirac operator at physical quark masses, exhibit approximate multiplets of both \(SU(2)_{CS}\) and \(SU(2N_F)\) groups, i.e. they display a symmetry larger than the chiral symmetry of the QCD Lagrangian. As an example and for later reference, we reproduce the temporal correlators from [16] in Fig. 2. Correlators of the isovector scalar (S) and isovector pseudo-scalar (PS) operators are connected by the \(U(1)_A\) transformation and their degeneracy indicates an effective restoration of this symmetry. If there is a tiny splitting of the S and PS correlators, it is too small to be seen in the present lattice data. As per Eq. (7), this symmetry is necessary, but not sufficient to demonstrate realisation of the larger chiral spin symmetry. An approximate degeneracy of the \(a_1\), \(b_1\), \(\rho (1,0)+(0,1)\) and \(\rho (1/2,1/2)_b\) correlators indicates emergent approximate \(SU(2)_{CS}\) and SU(4) symmetries. This larger symmetry disappears again once temperatures exceed \(T\gtrsim 3 T_\textrm{ch}\) [15, 16]. Let us assess the implications of this observation in some detail.

For any meson operator \(O_\varGamma (\tau ,\varvec{x})=\bar{\psi }(\tau ,\varvec{x})\varGamma \frac{\varvec{\tau }}{2}\psi (\tau ,\varvec{x})\) with \(\varGamma \in \{1,\gamma _5,\gamma _\mu ,\gamma _5\gamma _\mu ,\sigma _{\mu \nu },\gamma _5\sigma _{\mu \nu }\}\), the Euclidean correlation functions,

$$\begin{aligned} C_\varGamma (\tau ,\varvec{x})=\langle O_\varGamma (\tau ,\varvec{x})\,O_\varGamma ^\dag (0,\textbf{0})\rangle \;, \end{aligned}$$
(10)

carry the full spectral information of all excitations with \(J=0,1\) in their associated spectral functions \(\rho _\varGamma (\omega ,\varvec{p})\),

$$\begin{aligned} C_\varGamma (\tau ,\varvec{p})= & {} \int _0^\infty \frac{d\omega }{2\pi }\;K(\tau ,\omega )\rho _\varGamma (\omega ,\varvec{p})\;, \nonumber \\ K(\tau ,\omega )= & {} \frac{\cosh (\omega (\tau -1/2T))}{\sinh (\omega /2T)}\;. \end{aligned}$$
(11)

The spatial and temporal correlators probed in [15, 16],

$$\begin{aligned}{} & {} C_\varGamma ^s(z)=\sum _{x,y,\tau } C_\varGamma (\tau ,\varvec{x})\;, \end{aligned}$$
(12)
$$\begin{aligned}{} & {} C_\varGamma ^\tau (\tau )=\sum _{x,y,z}C_\varGamma (\tau ,\varvec{x})\;, \end{aligned}$$
(13)

collect the spectral information projected on the \((p_x=p_y=\omega =0)\) and \((p_x=p_y=p_z=0)\) axes, respectively. In thermal equilibrium the system is isotropic and the momentum distribution is the same in all directions, \(\rho _\varGamma (\omega ,\varvec{p})=\rho _\varGamma (\omega ,|\varvec{p}|)\). Observing approximate chiral spin symmetry both in the frequency and one momentum direction is therefore sufficient to conclude that it is also approximately realized in the full spectral functions \(\rho _\varGamma (\omega ,\varvec{p})\). Finally, since different quantum number channels are evaluated with the same action, one must conclude that the observed degeneracy patterns reflect an approximate symmetry of the non-perturbative effective action, and hence the thermal partition function of QCD.

Finite temperature chiral spin symmetry is thus an example of an emergent symmetry. Similar to the synthetic vacuum situation described in the last section, for this to happen the chromoelectric sector of the effective quark action must dominate over the chromomagnetic sector. Moreover, the chromoelectric interaction has to dominate over the spatial kinetic terms, which implies that the effective action is far from that of a weakly interacting system. Indeed, meson correlators evaluated in a free quark gas are even qualitatively incompatible with the observed multiplet structure [15, 16], as Fig. 2 demonstrates. This suggests that the degrees of freedom of QCD in the chiral spin symmetric regime, \(T_\textrm{ch}\lesssim T \lesssim 3 T_\textrm{ch}\), are chirally symmetric quarks bound to color singlet objects by the chromoelectric field.

Disappearance of these symmetries for \(T\gtrsim 3 T_\textrm{ch}\) indicates that the chromoelectric interactions between light quarks get screened, and one observes a smooth crossover to a quark gluon plasma with quasiquarks and quasigluons being effective degrees of freedom. The latter picture is supported by the success of the hard thermal loop approach [36] at these temperatures.

At zero density, there are then three temperature regimes in QCD with clearly distinguishable symmetries: the low temperature regime with spontaneously broken chiral symmetry, an intermediate regime with approximate chiral spin and \(SU(2N_F)\) symmetries, and a high temperature regime with chiral symmetryFootnote 1.

4 Screening masses

Ultimately, the nature of the degrees of freedom composing the thermal system in its different regimes is encoded in the spectral functions. At present, these are not yet available fully non-perturbatively. However, we have increasingly detailed, non-perturbative knowledge of screening masses, which govern the exponential decay of spatial correlators, Eq. (12). For the following it is useful to recall that, on a Euclidean space time lattice, the thermal partition function can be represented equivalently by two different Hamiltonians,

$$\begin{aligned} e^{pV/T}= & {} Z=\textrm{Tr}(e^{-aHN_\tau })=\sum _{n}e^{-aE_nN_\tau } \nonumber \\= & {} \textrm{Tr}(e^{-aH_zN_z})=\sum _{n_z}e^{-aE_{n_z}N_z}\;. \end{aligned}$$
(14)

Here, H is the usual QCD Hamiltonian translating states by one lattice spacing in Euclidean time, whereas \(H_z\) is the analogous operator translating states in the z-direction,

$$\begin{aligned}{} & {} |\psi (\tau +1;\varvec{x})\rangle =\exp (-aH)|\psi (\tau ;\varvec{x})\rangle \;,\nonumber \\{} & {} |\psi (\tau ; x,y,z+1)\rangle =\exp (-aH_z)|\psi (\tau ;\varvec{x})\rangle \;. \end{aligned}$$
(15)

On the lattice, both are straightforwardly defined without gauge fixing via the lattice action between adjacent \(\tau \)- or z-slices, respectively [42].

The thermodynamic limit (\(N_{x,y,z}\rightarrow \infty \) with \(T^{-1}=aN_\tau \) finite) formally represents the “vacuum” physics of \(H_z\), whose spectrum is sensitive to the ”finite volume effect” of the compactified \(\tau \)-direction, i.e. \(T^{-1}\). The screening masses are the corresponding ground state energies in each quantum number channel. Obviously, in the limit \(T=0\) the spectrum is identical to that of H, while for \(T\rightarrow \infty \) it reduces to the spectrum of 3d QCD, which is known as dimensional reduction. Evidently, screening masses are directly related to the equation of state, which is completely determined by the full spectrum of \(H_z\).

In order to characterize the dominant dynamical degrees of freedom, it is natural to proceed in analogy to vacuum QCD, where rarely any confusion arises between hadronic physics and quark gluon physics. While experimental initial and final states are ever exclusively hadronic, one may speak of parton physics driving the dynamics whenever quark hadron duality holds [43], i.e. the hadronic observables follow perturbative predictions for partonic (sub- ) processes. This is also the terminology adopted in some discussions of experimental results, see e.g. [44]. For a thermal equilibrium system, screening masses are accessible by perturbative and non-perturbative calculations, thus providing a viable theoretical testing ground.

4.1 Chromoelectric vs. chromomagnetic fields

Thermal QCD generates three parametrically distinguished scales, the hard scale of the non-zero Matsubara modes, \(\sim \pi T\), the intermediate scale of the color-electric fields, \(\sim gT\), and the fully non-perturbative soft scale \(\sim g^2T\) of the color-magnetic fields [45, 46]. For sufficiently small gauge coupling, the scales are separated and the harder modes can be integrated out to successively produce the effective theories EQCD, describing the gauge fields \(A_0,A_i\) on scales \(\lesssim gT\), and MQCD for \(A_i\) on scales \(\lesssim g^2T\). The latter is equivalent to three-dimensional Yang-Mills theory and fully non-perturbative.

The balance between color-electric and color-magnetic fields was studied on the lattice by a mixing analysis of correlation matrices of gauge invariant gluonic operators within EQCD [47]. At \(T\approx 2T_\textrm{ch}\) the lowest screening mass is associated with the operator \(\textrm{Tr}(A_0^2)\), whereas the one pertaining to \(\textrm{Tr} (F_{ij}^2)\) is more than twice as large. Hence, the dynamical ordering of “soft” and “ultra-soft” scales is opposite to the perturbative expectation. The color-electric fields cannot be integrated out, but rather give the largest contributions to the EQCD partition function at this temperature. This demonstrates their dynamical dominance in this regime, and fully supports the emergence of chiral spin symmetry as a consequence of non-perturbative gauge field dynamics.

4.2 The Debye mass

According to a non-perturbative definition of the Debye mass based on Euclidean time reflection of gauge invariant operators [48], lattice evaluations at \(T\approx 2T_\textrm{ch}\) give \(m_D^\textrm{gi}\approx 7.5 T\) [47, 49, 50], which amounts to a Debye radius of \(r_D\approx 0.09\) fm. Defining the Debye mass instead as the matching coefficient of the \(A_0^2\)-term in EQCD, which to leading order corresponds to the propagator pole mass, one obtains \(m_D^\textrm{pole}\approx 2.5 T\) [51] or \(r_D\approx 0.27\) fm. While rather different, both definitions result in a screening length smaller than a typical hadron size. A chiral spin symmetric regime composed of hadron-like objects thus appears to contradict the common picture of Debye screening [52], as was also pointed out in [53].

However, both definitions of the Debye mass are based on pure gauge quantities and related to the screening of static charges. Even for heavy quarks the dynamical picture is more complicated, with mass values differing widely between quantum number channels, and the precise connection between the Debye mass and the dissociation of bound states remains far from clear, for a review see [54]. In the context of chiral spin symmetry we are interested in the fate of the light quarks and mesons, which also give the dominant contribution to the equation of state. But relativistic quarks have no associated potentials in the first place, and chromoelectric flux distributions within light mesons will depend on all quantum numbers and behave quite differently from those between static quarks.

Moreover, restricting QCD to \(N_f=2+1\) light flavors, as is done in most lattice simulations at the physical point, neither propagator poles nor heavy quarkonium screening masses enter the partition function Eq. (14) at all. Only \(m^\textrm{gi}_D\) can possibly appear as screening mass pertaining to the purely gluonic \(J^{PC}=0^{-+}\) operator \(\textrm{Tr} (F_{ij}A_0)\) [47]. This represents one single term, which is subdominant since its screening mass value is larger than those of all twelve flavor non-singlet \(J=0,1\) mesons to be discussed below. The Debye mass therefore has little influence on the thermodynamics of light quarks.

4.3 Meson screening masses

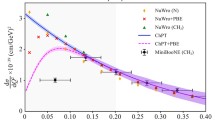
What we need to do instead is to study meson screening masses in the light quark sector. A lot of progress has been made, both analytically and numerically, towards an increasingly precise evaluation over a wide temperature range. In Fig. 3 we reprint a recent lattice determination of the scalar and vector screening masses composed of \(\bar{u}d\) quarks [33]. Also shown is the leading perturbative result \(\sim 2\pi T\), corresponding to the Matsubara modes of two free quarks, and the first correction \(\sim g^2\) evaluated within EQCD [55]. Note that this includes an all-loop-order HTL resummation of soft contributions from the scale \(\sim gT\). One observes the screening masses in both vector and scalar channels to overshoot the \(\sim 2\pi T\) level and to slowly approach the \(O(g^2)\) prediction, while spin dependence enters the perturbative series at \(O(g^4)\) only [56, 57].

Fig. 3
figure 3

Screening masses of the lightest \(\bar{u}d\) mesons, evaluated in simulations using HISQ fermions, from [33]

Full size image

Lattice calculations of pseudo-scalar and vector meson screening masses have recently been extended with unprecedented precision to the high temperature range \(T=\)1–160 GeV [58], permitting a detailed analysis of their perturbative behavior. In particular, over all three orders of magnitude in temperature, the lattice data are well described by a fit to

$$\begin{aligned} \frac{m_{PS}}{2\pi T}= & {} 1+p_2 \,\hat{g}^2(T) + p_3 \, \hat{g}^3(T)+p_4 \,\hat{g}^4(T)\;,\nonumber \\ \frac{m_{V}}{2\pi T}= & {} \frac{m_{PS}}{2\pi T} + s_4\, \hat{g}^4(T)\;, \end{aligned}$$
(16)

where \(\hat{g}^2(T)\) denotes the temperature-dependent running coupling renormalized in the \(\overline{\textrm{MS}}\)-scheme at \(\mu =2\pi T\). The perturbative value of \(p_2\) from [55] is fully confirmed, while \(p_3,p_4,s_4\) are not yet available analytically. Note that all coefficients are numbers, and the only temperature dependence of Eq. (16) resides in the coupling, whose logarithmically slow running is responsible for the flat behavior observed for \(T\gtrsim 1\) GeV in Fig. 3. The spin dependence is found to be consistent with a single \(O(\hat{g}^4)\) term \(s_4\) over the entire temperature range down to 1 GeV, and vanishes only for \(T\rightarrow \infty \) with the running coupling. Thus, (neglecting the wiggles within errors) all structure of the lattice data above \(T\gtrsim 1\) GeV in Fig. 3 can be described by a sufficiently deep, resummed perturbative expansion about partonic degrees of freedom, and is therefore characteristic of a quark gluon plasma.

What has remained entirely uncommented in the literature so far is the rapid bending of the curves within \(T\approx \) 0.5–0.7 GeV, from a steep increase with temperature to an entirely flat behavior. The nearly vertical portions of the plot cannot possibly be accounted for by series like Eqs. (16), since their temperature dependence resides in the coupling only. The same bending is observed in the same temperature range for all \(J=0,1\) mesons composed of \(\bar{u}s\) and \(\bar{s}s\) quarks as well [33]. That is, altogether this abruptly bending structure is present across 12 different quantum number channels! Since these constitute the dominant contributions to the partition function Eq. (14), an apparent change of dynamics takes place for the entire system, signalled by the complete breakdown of resummed perturbation theory at the “knee” of those curves. At the temperatures in question, this cannot be caused by chiral symmetry breaking. Rather, when decreasing temperature from the plasma regime, at the “knee” of the screening masses the chiral spin symmetric regime is entered, which a perturbative calculation about partons cannot reproduce to any order.

Conversely, increasing temperature from the hadronic regime, each meson screening mass \(m_\varGamma \) enters the perturbative regime at some individual screening temperature \(T_\textrm{s}(\varGamma )\), which one may define by, e.g., the most negative curvature of \(m_\varGamma /T\) (the location of the bend),

$$\begin{aligned} T_\textrm{s}(\varGamma ):\quad \min _{T}\left\{ \frac{d^2}{dT^2}\frac{m_\varGamma }{T}\right\} \;. \end{aligned}$$
(17)

Thus, for \(T\gtrsim T_\textrm{s}(\varGamma )\) quark hadron duality is realized in that quantum number channelFootnote 2. We may then conclude that the bound states have released their quark gluon content, i.e., their chromoelectric interaction is screened. Once this happens in sufficiently many quantum number channels, chiral spin symmetry is broken as expected for a quark gluon plasma. Note that the resulting value of \(T_s\), where this happens, depends on the precise flavor and mass content of the theory, as well as on the definition of \(T_\textrm{s}(\varGamma )\), as expected for a crossover.

We conclude that the behavior of meson screening masses from 12 different quantum number channels in \(N_f=2+1\) QCD provides an independent demonstration of the existence of a temperature window \(T_\textrm{ch}\lesssim T\lesssim T_\textrm{s}\), in which chiral symmetry is restored but the dynamics is inconsistent with a partonic description. By Eq. (14), it is then equally impossible to describe the equation of state in this regime by parton dynamics.

By contrast, Fig. 3 (left) shows chiral symmetry restoration to be achieved by the initially heavier chiral partners of the lowest screening masses dropping abruptly around \(T_\textrm{ch}\), and the same is true for all other flavour combinations [33]. Then Eq. (14) implies growing pressure around \(T_\textrm{ch}\), also in the absence of parton dynamics. The same observation was made for chiral multiplets of baryons extracted from temporal lattice correlators. When used in a hadron resonance gas calculation, these equally lead to growing pressure [59] at and above \(T_\textrm{ch}\).

5 Chiral spin symmetry at finite temperature and density

Having discussed the chiral spin symmetric temperature range \(T_\textrm{ch}\lesssim T\lesssim T_\textrm{s}\) at zero density, what are the nature and values of its boundaries at \(T_\textrm{ch},T_\textrm{s}\)? It is well-known that chiral symmetry restoration, marking \(T_\textrm{ch}\), proceeds gradually by an analytic crossover. On the other hand, very little attention has been paid to the temperature range around \(T_\textrm{s}\) so far. The screening mass data of Fig. 3 suggest a smooth crossover as well. In order to rule out a non-analytic phase transition, a finite size scaling study would be necessary to demonstrate that no discontinuity develops in the thermodynamic limit. It is well known that in the case of crossovers there are no sharp phase boundaries, and thus the numerical values for \(T_\textrm{ch},T_\textrm{s}\) necessarily vary with their definition. So far these are based on degeneracy patterns of meson correlators with fairly coarse temperature resolution, which is confirmed by the qualitative behavior of screening masses, as discussed in the last section. In addition, \(T_\textrm{ch},T_\textrm{s}\) depend on the number of quark flavors and their precise masses. For these reasons, accurate numbers for physical QCD are not available at present. But they can be obtained straightforwardly, from standard lattice simulations of meson correlators, with high precision and temperature resolution at the physical point in the future.

The next question is what happens with this regime at non-vanishing baryon chemical potential. The quark chemical potential term in the QCD action is manifestly \(SU(2)_{CS}\) and \(SU(2N_F)\) symmetric [60]. This suggests that both symmetries observed at \(\mu =0\) should also persist at finite chemical potential.

It is well known from lattice simulations how the chiral crossover temperature, which constitutes a lower bound for and is close to the chiral spin symmetric regime, behaves for small \(\mu _B\lesssim 3T\). Several consistent evaluations give

$$\begin{aligned} \frac{T_\textrm{pc}(\mu _B)}{T_\textrm{pc}(0)}= & {} 1-0.016(5)\left( \frac{\mu _B}{T_\textrm{pc}(0)}\right) ^2+\ldots \;,\nonumber \\\approx & {} \frac{T_\textrm{ch}(\mu _B)}{T_\textrm{ch}(0)} \end{aligned}$$
(18)

with the subleading term not yet statistically significant [29, 61,62,63,64]. The approximation in the second line is due to \(T_\textrm{ch}\) being somewhat larger than \(T_\textrm{ps}\), as discussed in Sect. 3 and visible in Fig. 3. It can be improved upon by a suitable definition and quantitative evaluation of \(T_\textrm{ch}\), e.g. by \(U(1)_A\) restoration.

The qualitative behavior of the upper boundary can be inferred from the value of a chosen meson screening mass at the temperature \(T_\textrm{s}\). Here we choose vector mesons as they show the most pronounced bend across all flavor channels. The screening mass at the bend corresponds to an inverse screening radius,

$$\begin{aligned} r_V^{-1}\equiv m_V(\mu _B=0, T_\textrm{s})=C_0T_\textrm{s}\;. \end{aligned}$$
(19)

Beyond this length scale the corresponding screening mass behaves perturbatively, i.e., for zero density the chromoelectric interaction is screened once \(T>T_\textrm{s}\). Then, by CP-symmetry we know that mesonic screening masses are even functions of \(\mu _B/T\), and therefore

$$\begin{aligned} \frac{m_V(\mu _B)}{T}=C_0+C_2\left( \frac{\mu _B}{T}\right) ^2+\ldots \;. \end{aligned}$$
(20)

Keeping \(r_V^{-1}\) constant as chemical potential is varied, \(dm_V{\mathop {=}\limits ^{!}}0\), one finds

$$\begin{aligned} \frac{dT_\textrm{s}}{d\mu _B}=-\frac{2C_2}{C_0}\frac{\mu _B}{T}-\frac{2C_2^2}{C_0^2}\left( \frac{\mu _B}{T}\right) ^3+\ldots \;. \end{aligned}$$
(21)

Since we know from analytic calculations [65] as well as lattice simulations [66, 67] that \(C_2>0\), the upper boundary of the chiral spin symmetric regime leaves the temperature axis with zero slope and negative curvature. We then conclude that the QCD phase diagram shows a chiral spin symmetric band that bends downwards with chemical potential, as sketched in Fig. 1. This can be checked straightforwardly by repeating the analysis of meson correlators from [15, 16] with imaginary chemical potential. Since the chemical potential term is invariant under chiral spin symmetry, screening masses and correlators will be shifted differently for real and imaginary chemical potentials, cf. Eq. (20), but the degeneracy patterns should be the same in both cases.

Finally, we stress that these expectations concerning the shape of the chiral spin symmetric band hold for sufficiently small \(\mu _B/T\). The further qualitative behavior depends on the relative size of the curvatures \(d^2T_\textrm{ch}/d\mu _B^2\) and \(d^2T_\textrm{s}/d\mu _B^2\) with growing chemical potential. If the latter is sufficiently much larger than the former, then the boundaries of the band merge at some non-vanishing temperature. This might in particular be expected to happen at the critical endpoint of a possible first-order chiral phase transition, as sketched in Fig. 4. In this case the steeply rising part of the screening masses \(m_\varGamma /T\), Fig. 3 right, would move towards \(T_\textrm{ch}(\mu _B)\) and evolve into a discontinuous jump as \(\mu _B\) approaches the critical endpoint, where the scalar screening masses have to vanish and display a kink. Again, at least a trend towards one or another behavior can be determined by screening mass studies at imaginary chemical potential.

Fig. 4
figure 4

Qualitative sketch of a possible QCD phase diagram with a band of approximate chiral spin symmetry terminating at the critical end point of a non-analytic chiral phase transition

Full size image

6 Baryonic parity doublet matter and its symmetries

As chemical potential gets larger, we have no more reliable information from the lattice. We now discuss on a merely qualitative level, how a chiral spin symmetric regime can exist in the baryon rich region at reasonably large chemical potentials, as would be the case in a scenario like Fig. 1.

It has been known for a long time that one can construct a manifestly chirally symmetric Lagrangian with massive fermions if there are degenerate fermions of opposite parity [68], the so called parity doublet Lagrangian. Indeed, parity doubling of the light baryons is clearly observed on the lattice above \(T_\textrm{ch}\) at zero density [59, 69], as a consequence of chiral symmetry restoration.

Consider a pair of isodoublet fermion fields

$$\begin{aligned} \varPsi = \left( \begin{array}{c} \varPsi _+\\ \varPsi _- \end{array} \right) , \end{aligned}$$
(22)

where the independent Dirac spinors \(\varPsi _+\) and \(\varPsi _-\) have positive and negative parity, respectively. Note that there is in addition an isospin index which is suppressed. The right- and left-handed fields are directly connected with the opposite parity fields

$$\begin{aligned} \varPsi _R = \frac{1}{\sqrt{2}}\left( \varPsi _+ + \varPsi _-\right) ;~~ \varPsi _L = \frac{1}{\sqrt{2}}\left( \varPsi _+ - \varPsi _-\right) . \end{aligned}$$
(23)

The vectorial and axial parts of the chiral transformation under the \((0,1/2) \oplus (1/2,0)\) representation of \(SU(2)_L \times SU(2)_R\) are

$$\begin{aligned} \varPsi\rightarrow & {} \exp \left( \imath \frac{\theta ^a_V \tau ^a}{2} \otimes \mathbbm {1}\right) \varPsi \;, \nonumber \\ \varPsi\rightarrow & {} \exp \left( \imath \frac{\theta ^a_A\tau ^a}{2}\otimes \sigma _1 \right) \varPsi \;. \end{aligned}$$
(24)

Here \(\tau _j, \sigma _k\) are Pauli matrices that act in the spaces of isopsin and the parity doublets, respectively. In the chiral transformation law the axial rotation mixes two independent fields \(\varPsi _+\) and \(\varPsi _-\). The chirally invariant Lagrangian of the free parity doublet is then given as

$$\begin{aligned} \mathcal {L}= & {} i \bar{\varPsi }_+ \gamma ^\mu \partial _\mu \varPsi _+ + i \bar{\varPsi }_- \gamma ^\mu \partial _\mu \varPsi _- \nonumber \\{} & {} - m \bar{\varPsi }_+ \varPsi _+ - m \bar{\varPsi }_- \varPsi _-\;. \end{aligned}$$
(25)

The equivalence of the present form of the Lagrangian [68] with those used in [70, 71] was demonstrated in [72] and the chiral transformation law Eq. (24) corresponds to the “mirror” assignment of [71]. In terms of the right- and left-handed fields of Eq. (23), we have

$$\begin{aligned} \mathcal {L}= & {} i \bar{\varPsi }_L \gamma ^\mu \partial _\mu \varPsi _L + i \bar{\varPsi }_R \gamma ^\mu \partial _\mu \varPsi _R \nonumber \\{} & {} - m \bar{\varPsi }_L \varPsi _L - m \bar{\varPsi }_R \varPsi _R\;. \end{aligned}$$
(26)

The latter form demonstrates that the right- and left-handed degrees of freedom are decoupled and the Lagrangian with massive fermions is chirally invariant.

A crucial property of the Lagrangian (25,26) is that the fermions \(\varPsi _+\) and \(\varPsi _-\) are degenerate and have a nonzero chiral-invariant mass m. The diagonal axial charge of the fermions \(\varPsi _-\) and \(\varPsi _+\) vanishes, while the off-diagonal axial charge is 1.

This Lagrangian can be supplemented by the pion and sigma-fields of the linear sigma model [70, 71]. Chiral symmetry breaking, \(\langle 0|\sigma |0\rangle \ne 0\), generates a mass splitting of the positive and negative parity baryons. I.e. the chiral symmetry of the Lagrangian (25–26) is lifted. This regime can be associated with nuclear matter, where physics is guided by a coupling of nucleons of positive parity with \(\pi ,\sigma \) fields [73,74,75]. The combined Lagrangian has sometimes been used in baryon spectroscopy [76, 77] and as a model for chiral symmetry restoration scenario at high temperature or density, where baryons with non-zero mass do not vanish upon a chiral restoration, see e.g. [78,79,80,81] and references therein. Depending on the parameters the chiral restoration transition can be either of first or second oder [78].

It turned out, however, that the free parity doublet Lagrangian (25–26) has a larger symmetry than the \(SU(2)_L \times SU(2)_R\) symmetry. It is in addition manifestly \(SU(2)_{CS}\) and \(SU(2N_F)\) symmetric [72]. Indeed, given Eq. (23), the parity doublet (22) can be unitarily transformed into a doublet

$$\begin{aligned} \tilde{\varPsi } = \left( \begin{array}{c} \varPsi _R\\ \varPsi _L \end{array} \right) \;, \end{aligned}$$
(27)

which is a two-component spinor composed of Dirac bi-spinors \(\varPsi _R\) and \(\varPsi _L\) (i.e., altogether there are eight components).

The Lagrangian (25–26) is obviously invariant under the \(SU(2)_{CS}\) rotations (4),

$$\begin{aligned} \left( \begin{array}{c} \varPsi _R\\ \varPsi _L \end{array}\right) \; \rightarrow \exp \left( i \frac{\varepsilon ^n \sigma ^n}{2}\right) \left( \begin{array}{c} \varPsi _R\\ \varPsi _L \end{array}\right) \; . \end{aligned}$$
(28)

Then it follows that the parity doublet Lagrangian is not only chirally invariant under the transformation (24), but also \(SU(2)_{CS}\)- and \(SU(2N_F)\)-invariant with the generators of \(SU(2N_F)\) being

$$\begin{aligned} \{ (\tau ^a \otimes \mathbbm {1}), (\mathbbm {1} \otimes \sigma ^n), (\tau ^a \otimes \sigma ^n) \}. \end{aligned}$$
(29)

We then conclude that baryonic parity doublet matter is a very natural candidate for a chiral spin symmetric regime at low temperatures.

It is important to stress that a coupling of pions and sigmas to the parity doublets lifts the SU(4) symmetry of the free parity doublet Lagrangian because the \(\pi -\sigma \)-Lagrangian, while chirally invariant, is not a SU(4) singlet. If one insists on the SU(4) symmetry, then the usual pion-sigma Lagrangian must approximately decouple from the parity doubled baryons. The \(J=0\) mesons then reflect the usual chiral symmetry, but do not mix with the proper SU(4) multiplets to leading order, similar to the situation at \(\mu _B=0\). In summary, if parity doubled baryons decouple to leading order from \(\pi ,\sigma \), they are chiral spin and SU(4)-symmetric. This corresponds to Fig. 1. Parity doublets strongly coupled to \(\pi ,\sigma \) are chiral invariant but not chiral spin and SU(4) symmetric., this corresponds to Fig. 4.

SU(4)-symmetric parity doubled baryon matter is fully consistent with the concept of quarkyonic matter, which was proposed in [82] based on large \(N_c\) arguments. It characterizes the cold and dense regime of QCD and features the possibility of chirally symmetric but confined baryonic matter. Its defining features are the pressure scaling as \(p\sim N_c\) (for large \(N_c\)) and a Fermi sphere in momentum space, Fig. 5, consisting of quark matter surrounded by a shell of baryons with thickness \(\sim \varLambda _{QCD}\). Since the Fermi momentum is set by the baryon chemical potential, \(p_F\sim \mu _B\), quarkyonic matter interpolates between purely baryonic matter for \(\mu _B\sim \varLambda _{QCD}\), and quark matter for \(\mu _B\gg \varLambda _{QCD}\). The pressure scaling as well as the possibility of such a shell structure were verified for lattice QCD with heavy quarks by a combined strong coupling and hopping expansion [83], with the onset transition to baryon matter identified as the lower boundary of this regimeFootnote 3. Note also, that recent model investigations suggest neutron star data to be well described by baryonic matter up to six times nuclear density [75]. In principle, this baryonic matter could then be either chirally broken or symmetric.

Cold baryon matter can then appear in two different forms: ordinary nuclear matter with broken chiral symmetry, and baryon parity doublet matter with restored chiral and approximate chiral spin symmetry, as sketched in Fig. 1. These are separated by the chiral phase transition or crossover. As the chemical potential increases, a growing fraction of the Fermi sea consists of quark matter and chiral spin symmetry is lost again. Beyond this density, the system is dominated by parton dynamics, i.e., quark matter. Currently, based on QCD nothing can be said about either the location or the width of the chiral spin symmetric band in the cold and dense regime, except that it can exist by continuation from the thermal regime.

7 Dileptons and the chiral spin symmetric band

Dileptons have been used for a long time as a diagnostic tool to study the nature of hadronic matter. In vacuum the electron – positron annihilation into hadrons shows a powerful resonance peak related to the existence of \(\rho \)- and \(\omega \)-mesons, which reflects the confining and chiral symmetry breaking properties of the QCD vacuum. These properties persist also in a hadron resonance gas or in a sufficiently dilute baryonic medium. Hence, experimental studies in heavy ion collisions at different temperatures and chemical potentials employ the inverse process, with the final state being the electron-positron pair, to shed light on the question to what extent a hot or dense medium differs from the vacuum.

Fig. 5
figure 5

Qualitative sketch of the Fermi sphere of quarkyonic matter. The Fermi momentum is set by the chemical potential, \(p_F\sim \mu _B\). Quark matter inside is surrounded by a shell of baryon matter of thickness \(\sim \varLambda _\textrm{QCD}\), with a smooth, gradual transition between the two

Full size image

The differential dilepton production rate is determined by the spectral function of the electromagnetic current in the medium, expressed by its self-energy [45],

$$\begin{aligned} \frac{dN}{d^4q d^4x}= - \frac{\alpha ^2}{\pi ^3 M^2} f^{B}(q_0,T) \textrm{Im} [\varPi _\textrm{em}(M,q;T,\mu _B)],\nonumber \\ \end{aligned}$$
(30)

where M is the invariant mass of the \(e^+e^-\) pair with the four-momentum \( q= (q_0, \varvec{q})\), \(f^{B}(q_0,T)\) is the Bose–Einstein distribution characterizing the thermalized medium and \(\alpha \) the fine structure constant.

The absence of resonance peaks is usually taken as a signal of chiral symmetry restoration and deconfinement. For a detailed interpretation, however, some care is in order. For example, the perturbative description of the electron-positron annihilation into hadrons in vacuum via \(e^+ + e^- \rightarrow {\bar{q}} + q\) above the \( \rho , \omega , \phi \) resonance peaks receives so-called duality violating corrections. These are due to the very broad and overlapping \(\rho ', \rho '', ...\) resonances and/or instanton effects, which violate a purely partonic description and lead to the observed oscillating behaviour of the corresponding spectral function [43].

Via Eq. (11), the finite temperature \(\rho \)- and \(\omega \)-meson spectral functions are also encoded in the Euclidean correlators of the vector currents \(\rho _{(1,0)+(0,1)}\) and \(\omega _{(0,0)}\) of Fig. 2. Their extraction from a Euclidean correlator with a finite number of lattice points is an ill-defined problem. However, if a Euclidean correlator evaluated in full QCD is very different from that calculated with non-interacting quarks, one can safely state that the spectral density will not be dual to a perturbative description, but should contain some remnant resonance structure. According to Fig. 2, we expect this to be the case for the spectral functions of \(J=0\) operators. On the other hand, the electromagnetic current correlator \(\rho _{(1,0)+(0,1)}\) turns out to be close, but not equal, to the correlator calculated with free quarks. This could be caused by a fast decay of the \(J=1\) excitation into \(J=0\) excitations, \(\rho \rightarrow \pi +\pi \). Hence, in this case the spectral density might not show an obvious resonance structure, and the dilepton production should be close to the perturbative \( {\bar{q}} + q \rightarrow e^+ + e^-\) processes. This is consistent with the less pronounced or absent \(\rho \)-peaks in the spectral function representing the fireball above the chiral restoration temperature, as observed at RHIC [84, 85], SPS [86, 87] and LHC [88]. We thus conclude that the absence of \(\rho \) and \(\omega \) peaks in high temperature dilepton spectra is entirely consistent with the chiral spin and SU(4) symmetry above the chiral restoration. Approximate SU(4) symmetry requires the isoscalar \(\omega _{(0,0)}\) correlator to be very close to the isovector correlator \(\rho _{(1,0)+(0,1)}\). Hence, what was said about the absence of the \(\rho \) peak above chiral restoration line, should also be true with respect to the \(\omega \) peak.

A remarkable piece of information about the phase structure at large chemical potentials and low temperatures is delivered by recent experimental results from the HADES collaboration [89]. HADES measured the dielectron production in Au–Au collisions at \(\sqrt{s_{NN}}=2.42\) GeV. The excess yield extracted by subtracting the \(\eta , \omega \) contributions, which are produced beyond the fireball, is shownFootnote 4 in Fig. 6. It exhibits a nearly exponential fall-off. A fit of the black-body spectral distribution

$$\begin{aligned} \frac{dN}{dM} \sim M^{3/2} e^{-M/T} \end{aligned}$$
(31)

to the data (red curve) yields \(T \sim 72\) MeV. No pronounced \(\rho \)-structure is visible, and the data are well described by the leading order \( {\bar{q}} + q \rightarrow e^+ + e^-\) diagram (blue curve). A slight oscillation about the perturbative curve seems apparent in Fig. 6, hinting at hadronic duality violations. Such violations can appear both in the chirally broken and in the chirally symmetric phase.

Fig. 6
figure 6

Acceptance-corrected dilepton excess yield obtained in Au–Au collisions at \(\sqrt{s_{NN}}=2.42\) GeV [89]

Full size image

The HADES result is also consistent with the in-medium broadening of \(\rho \)-mesons (for the corresponding curves, see Ref. [89]). The Rapp–Wambach model [90] describes coupling of pions with the nucleon–nucleon-hole excitations in the baryon medium (including also different baryon resonances). The \(\rho \rightarrow \pi + \pi \) width then becomes very broad because of the additional couplings of the \(\rho \)-meson to these collective excitations. This mechanism implicitly relies on spontaneous breaking of chiral symmetry, since its parameters are extracted from the elementary processes in vacuum.

A third possibility for the disappearance of the \(\rho \)-peak in a dense chirally symmetric baryonic medium is provided by chiral spin and SU(4) symmetric parity doublet matter. When chiral symmetry is restored, the baryons of positive and negative parity to leading order decouple from pions and sigmas. Hence a baryonic medium becomes a true Fermi gas. An electromagnetic coupling of baryon–baryon hole transitions to photons guarantees an equilibrium between the baryonic Fermi gas and the photonic Bose gas. Photons can be converted into electron-positron pairs. This is consistent with the black-body radiation description of the excess shown in Fig. 6. The dilepton production of baryonic parity doublet matter is hence very similar to that of thermalized quark matter. This suggests that the HADES point at \(T \sim 72\) MeV, \(\mu _B \sim 900\) MeV is just above the chiral restoration line, \(T_\textrm{ch}(\mu _B)\), and could possibly be within the chiral spin and SU(4) symmetric band. It would be most interesting to further assess whether there is a fine structure in the dilepton data allowing to further distinguish between scenarios such as those sketched in Figs. 1 and 4.

8 Conclusions

Based on recent lattice studies of meson correlators with chiral fermions, we must take approximate \(SU(2)_{CS}\) and SU(4) symmetries of QCD, as well as its associated dominance of color-electric interactions between light quarks, as a matter of fact in a temperature range above the chiral crossover. In this work we have collected already published spectra of screening masses, and employed their direct relation to the QCD partition function to confirm the existence of such an intermediate temperature regime independent of symmetry arguments.

In particular, there is non-perturbative evidence that color-electric fields are dynamically enhanced over color-magnetic ones for the temperatures in question. Debye screening is a non-relativistic concept which applies to heavy quarks, but its associated Debye mass does not enter the partition function for \(N_f=2+1\) QCD with relativistic quarks. We then applied quark hadron duality as a criterion for screening: once a hadron screening mass in a given quantum number channel becomes amenable to a perturbative description, the color-electric interaction between quarks is sufficiently screened to allow for parton dynamics. Recent lattice results show this to happen in a narrow temperature window \(T\sim \) 0.45–0.75 GeV across 12 different quantum number channels of \(J=0,1\) mesons, with partonic behavior for higher and non-perturbative behavior for lower temperatures.

From the known behavior of meson screening masses with small baryon chemical potential, we then conjectured the chiral spin symmetric band to extend downwards across the QCD phase diagram. At least the behavior for small baryon densities can be fully determined by future studies of spatial correlation functions at imaginary chemical potential with known techniques. Baryonic parity doublet matter satisfies both chiral spin and SU(4) symmetries, and is a candidate for the form of nuclear matter beyond the chiral crossover/phase transition at \(T=0\). In the cold and dense regime however, the location and width of a chiral spin symmetric regime is not yet constrained from QCD. High precision dilepton spectra with fine resolution, combined with theoretical efforts towards QCD spectral functions, should be a promising tool to unravel the nature of the degrees of freedom in the chiral spin symmetric regime.

Note added: After completion of our manuscript an analysis of the pseudo-scalar spectral function at temperatures above the chiral crossover appeared [91]. It shows resonance-like peaks for the pion and its first excitation which only gradually disappear, consistent with the non-perturbative dynamics of the chiral-spin-symmetric band, as desribed here.