⁹⁹Tc in stars, reactors, and nuclear medicine

Abstract

The roles of ^99gTc in stars and in nuclear fission reactors and that of ^99mTc in nuclear medicine that were studied using neutrons provided from accelerators are reported. In addition to the critical role of ^99gTc in stars, we also describe the roles of related light nuclei such as ¹⁶O, and experimental studies on keV-neutron capture cross sections of these light nuclei that were performed using keV neutrons provided from a 3.2-MV Pelletron accelerator are reported. The keV-neutron capture cross section of ^99gTc, that is important in studies on the nucleosynthesis of ⁹⁹Tc in stars and on the nuclear transmutation of long-lived nuclear wastes produced in fission reactors, were measured. The cross sections of both light nuclei and ^99gTc were measured using a neutron time-of-flight method with a ns-pulsed neutron source from the ⁷Li(p,n)⁷Be reaction and with an anti-Compton γ-ray NaI(Tl) spectrometer. The measurements reported here were compared with the values of recent worldwide evaluated nuclear data libraries.

We proposed a method of producing ^99mTc from the ¹⁰⁰Mo(n,2n)⁹⁹Mo reaction, and performed a ^99mTc production experiment using a ^natMo sample and MeV neutrons from the ^natC(d,n) reaction by 40 MeV deuterons at a cyclotron. Calculations for the ^99mTc production with an enriched ¹⁰⁰Mo sample were also performed, and calculated results were compared with the experimental results. Moreover, the thermoseparation of ^99mTc from ⁹⁹Mo was discussed. As a result, it was shown that ^99mTc prepared by the thermoseparation using ⁹⁹Mo produced by the ¹⁰⁰Mo(n,2n)⁹⁹Mo reaction can be a promising substitute for the fission product ⁹⁹Mo.

1 Introduction

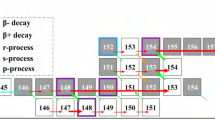
Technetium (Tc) is one of two elements with an atomic number less than 83 that have no stable isotopes. In 1937, Perrier and Segré discovered Tc in a sample obtained by bombarding a Mo sample with deuterons in the 37-inch cyclotron of the Berkeley Radiation Laboratory [1]. They asked Lawrence, who invented a cyclotron in 1929 [2], to do the bombardment. In 1938, Segré and Seaborg discovered the metastable state of ⁹⁹Tc (^99mTc) [3]. A partial decay scheme of ⁹⁹Mo (T_1/2 = 66 h) to excited states in ⁹⁹Tc currently proposed is shown in Fig. 1. [4].

Fig. 1

A partial decay scheme of ⁹⁹Mo (T_1/2 = 66 h) to excited states in ⁹⁹Tc. The half-life of ^99mTc and ⁹⁹Tc is 6 h and 211,100 years, respectively

In 1952, Merrill discovered Tc, presumably ⁹⁹Tc, at the surface of red giant stars [5]. The observation of Tc provided the first powerful evidence that Tc has been synthesized recently within stars and contributed to our understanding of the origins of elements heavier than iron observed in stars [6]. Since then, the spectral observations of peculiar red giants turned out to be a prolific source of information on s-processes during the He burning stage of stellar evolution [7]. As for ^99gTc, it is one of long-lived fission products (LLFPs) produced in fission reactors. LLFPs will remain as radioactive wastes for a long period if they are not transmuted into stable or short-lived nuclides. From this viewpoint, recently, much interest is paid to the nuclear transmutation studies, for which the neutron capture cross sections of individual LLFPs are the most important physical quantities. Since both the fission yield and hazard index of ^99gTc are large, ^99gTc is one of the most important LLFPs and its neutron capture cross section is very important.

On the other hand, among the medical radioisotopes (RIs), ^99mTc (T_1/2 = 6 h), the decay product of ⁹⁹Mo (T_1/2 = 66 h), is the most widely used diagnostic nuclear medicine RI [8] that is usually obtained from a ⁹⁹Mo/^99mTc generator. Because of the short half-life of ⁹⁹Mo, a constant supply of ⁹⁹Mo is a key issue for ensuring the routine application of ^99mTc. However, the supply chain of ⁹⁹Mo that is mostly produced by the fission reaction of ²³⁵U in a limited number of research reactors operating over 50 years around the world is vulnerable since 2008 [9]. The vulnerable situation of the supply chain of ⁹⁹Mo is the impetus to study alternative methods for producing ⁹⁹Mo and/or ^99mTc in reactors or accelerators [10].

2 ⁹⁹Tc in stars

2.1 Background

When we began our experimental study in nuclear astrophysics in 1989, using fast neutrons that were provided from an accelerator at the Tokyo Institute of Technology, there was great interest in the abundance of s-process isotopes for various metallicity stars in order to construct models of the chemical evolution of the Galaxy [11, 12]. Indeed, efforts involving observations and yields estimations of these s-process isotopes were being made for a wide range of metallicities and stellar masses to compare the chemical evolution models with the observational data [13]. In the models of the chemical evolution of the s-process isotopes for low-metallicity massive stars, it was necessary to clarify the relation between the yields of the s-process isotopes versus the abundance of ⁵⁶Fe (seed) nucleus and/or of ¹⁶O (source) nucleus. In the weak s-process nucleosynthesis theory, neutrons from the ²²Ne(α,n)²⁵ Mg reaction are used to produce s-process isotopes [14, 15]. Hence, if the neutron capture cross sections of abundant light nuclei, such as ¹²C and ¹⁶O, direct products of He burning, would be large, the yields of heavier s-process isotopes would decrease; the releationship of the yields versus the abundance of either ⁵⁶Fe and/or ¹⁶O becomes nonlinear. Therefore, in order to construct a model that predicts s-process istope production as a function of metalllicity and stellar mass, it was necessary to know the neutron capture cross sections of these light nuclei at stellar neutron energy. However, these cross sections were rarely measured compared to the extensive measurements of capture cross sections of intermediate- and heavy-mass nuclei that were needed to interpret the various mechanisms of stellar nucleosynthesis [16, 17].

Based on the experimental status of neutron capture cross sections for light nuclei at that time, we challenged the measurement of neutron capture reaction cross sections for ¹²C [18] and ¹⁶O [19] at stellar neutron energies by combining a pulsed neutron beam and a prompt discrete γ-ray detection method. Among a variety of neutron sources [7], we used a pulsed neutron beam produced by the ⁷Li(p,n)⁷Be reaction in a small accelerator, as in the case of Franz Käppeler’s Karlsruhe group at KfK. For the neutron capture γ-ray detection, our discrete γ-ray detection method was complementary to the detection method of the energy sum of the γ-ray cascade emitted in the decay of the compound nucleus, used in Karlsruhe and elsewhere. Here, it is worth-mentioning that the level density of excited states in light-mass isotopes that are populated by the keV-neutron capture reaction is low. We would therefore observe discrete γ rays emitted from the neutron capture states to the low-lying states of residual nucleus with specific spin-parity, excitation energies, and spectroscopic factors.

2.2 Experimental method: pulsed neutrons and discrete γ-ray detection

The pulsed neutrons were produced by the ⁷Li(p,n)⁷Be reaction at the 3.2-MV Pelletron Accelerator of the Research Laboratory for Nuclear Reactors at the Tokyo Institute of Technology [20]. Neutron energy spectra were measured by a ⁶Li-glass scintillation detector by a time-of-flight (TOF) method. Discrete prompt γ rays emitted in the transition from a capture state of residual nucleus to low-lying states were measured by an anti-Compton NaI(Tl) spectrometer that was heavily shielded from backgrounds with ⁶LiH, borated paraffin, Cd sheet, and Pb [18,19,20]. In this type of setup, background events could be due to γ rays from the ⁷Li(p,γ)⁸Be reaction, γ rays from the ¹²⁷I(n,γ)¹²⁸I reaction occurring in the NaI(Tl) spectrometer, γ and β rays from the decay of ¹²⁸I with T_1/2 = 25 m, and γ rays from the decay of ambient natural radioactivity, such as ⁴⁰ K and ²⁰⁸Tl. Using the spectrometer together with the pulsed neutron beam we could measure discrete γ rays emitted after neutron capture reactions, even for small cross sections of about 10 µb at a neutron energy (E_n) of 30 keV. The relationship between a γ-ray pulse height (PH), taken by the central NaI(Tl) detector in the NaI(Tl) spectrometer, and neutron energy was determined by obtaining a TOF spectrum by using signals from the NaI(Tl) detector and the pulsed proton beams from the accelerator. The NaI(Tl) spectrometer was set at 125.3° with respect to the proton beam direction, where the second Legendre polynomial is zero and thus the γ-ray intensity measured at this angle provides the angle-integrated value for a dipole radiation emitted in the capture events. One set of each experimental run was composed of individual measurements for one of two oxygen compound samples of ⁷Li₂O or ²H₂O, Au, and blank samples. Each experimental run was carried out by cyclically changing these samples to mitigate systematic uncertainties in the measurement. The blank run was performed to monitor any change in the primary neutron energy, to derive the thickness of the ^natLi neutron production target during each set of experimental runs, and to determine the background without sample.

2.3 Experimental results

A typical TOF spectrum for an Au sample used to normalize the absolute capture cross section of the ¹⁶O(n,γ)¹⁷O reaction at E_n = 398 keV taken by the NaI(Tl) spectrometer is shown in Fig. 2 [21]. The sharp peak in channel 600 and the broad peak in channel 490 were attributed to the ⁷Li(p,γ)⁸Be and ¹⁹⁷Au(n,γ)¹⁹⁸Au reactions, respectively.

Fig. 2

Typical TOF spectrum for an Au sample used to normalize the absolute capture cross section of the ¹⁶O(n,γ)¹⁷O reaction at E_n = 398 keV taken by the NaI(Tl) spectrometer. Here, the dashed and solid lines indicate the TOF spectra for the Au and ²H₂O samples, respectively

Typical foreground (Fore) and background (Back) PH spectra for the ¹⁶O(n,γ)¹⁷O reaction that were obtained by putting the gates on Fore- and Back-ground regions indicated in Fig. 2, are shown in Fig. 3. Note that, as shown in a net spectrum in Fig. 4, the discrete γ rays at 3.65 and 4.52 MeV corresponding to the γ rays emitted from the neutron capture state of ¹⁷O to the first excited (J^π = 1/2⁺) and the ground (J^π = 5/2⁺) states of ¹⁷O were clearly observed. The partial cross sections from the neutron capture state of ¹⁷O to these lower-lying states of ¹⁷O were determined by analyzing the intensities of these γ rays.

Fig. 3

γ-ray PH spectra from the ¹⁶O(n,γ)¹⁷O reaction at the neutron energy of 398 keV. Typical foreground and background spectra are respectively shown as solid and dashed lines. The background γ-ray peaks other than ⁴⁰ K are from the ¹H(n,γ)²H (filled square), ⁵⁶F(n,γ)⁵⁷Fe (down filled triangles), and ¹²⁷I(n,γ)¹²⁸I (filled circle) reactions

Fig. 4

Net γ-ray PH spectrum for the ¹⁶O(n,γ)¹⁷O reaction at the neutron energy of 468 keV

The γ-ray relative intensities thus obtained for 157 keV neutrons are compared with those generated by thermal neutrons [22] in Fig. 5. The γ-ray strength from the capture state of ¹⁷O feeding directly to the first-excited state (J^π = 1/2⁺) in ¹⁷O is large for 157 keV neutrons, whereas the largest γ-ray strength is observed for the transition leading directly to the second-excited state (J^π = 1/2⁻) for thermal neutrons. Since the thermal neutron capture proceeds only by s-wave neutrons, the strongest transition from the capture state of ¹⁷O to the second-excited state is an E1 transition. Hence, assuming the same E1 character for the transition leading to the first-excited state (J^π = 1/2⁺) also for 157 keV neutrons, the keV neutron capture process on ¹⁶O was found to be dominated by a non-resonant direct p-wave capture process. Note that such a non-resonant direct p-wave neutron reaction process was also observed in the measurement of the ¹²C(n,γ)¹³C reaction cross sections at neutron energies from 10 to 530 keV [23].

Fig. 5

γ-ray relative intensities for thermal neutrons (left) [22] are compared with those obtained by 157 keV neutrons (right) [21]

By the way, the excited state of ¹⁷O has a resonance state (J^π = 3/2⁻) with the total width of about 40 keV at 4554 keV, corresponding to the neutron energy of 411 keV in the center-of-mass system. The resonance state can provide a great opportunity to study an interference between a non-resonant p-wave neutron capture process and a resonance neutron capture process in the ¹⁶O(n,γ)¹⁷O reaction in a relevant neutron energy region for astrophysical importance. Note that the excited state of ¹³C populated by the ¹²C(n,γ)¹³C reaction at E_n < 1 MeV does not have such a resonance state. Hence, we extended the energy range of neutrons in the cross-section measurement of the ¹⁶O(n,γ)¹⁷O reaction at average neutron energies of 157, 349, 398, 427, 468, 498, and 556 keV to investigate the possibility of the aforementioned interference [21]. In the study, we prepared thin ^natLi metal targets to cover the cross section measurements in the region of the 3/2⁻ resonance state with an energy resolution of about 50 keV full width at half maximum. Meanwhile, a thick ^natLi metal target was used for the off-resonance region, because the cross section is considered to change smoothly with neutron energy.

The partial neutron capture cross section σ_γ,i, corresponding to the i-th γ-ray transition with energy E_γ,i from the neutron capture state of ¹⁷O to the low-lying state i, was obtained by using the γ-ray yield Y_γ,i (¹⁷O) as given in Eq. (1):

$${\sigma }_{\gamma ,i}=\frac{{T}_{\mathrm{O}}}{{T}_{\mathrm{Au}}} \frac{{P}_{\mathrm{Au}}}{{P}_{\mathrm{O}}} \frac{{C}_{\mathrm{Au}}}{{C}_{\mathrm{O}}} \frac{{{(r}^{2}n)}_{\mathrm{Au}}}{{{(r}^{2}n)}_{\mathrm{O}}} \frac{{Y}_{\gamma ,i}\left({}^{17}\mathrm{O}\right)}{{Y}_{\gamma }\left(\mathrm{Au}\right)}{\sigma }_{\gamma }\left(\mathrm{Au}\right)$$

(1)

Here, O and Au refer to ¹⁶O and ¹⁹⁷Au, respectively. P_s and T_s are the number of the neutron counts measured by the ⁶Li-glass detector and the neutron transmission of a sample s = {O, Au}, respectively. r and n are the radius and the thickness (atoms/barn) of sample s. Y_γ(Au) and σ_γ(Au) are the γ-ray yield and the absolute capture cross section for ¹⁹⁷Au, respectively. Y_γ(Au) and Y_γ,i(¹⁷O) were obtained by using the response function of the NaI(Tl) spectrometer [24]. C_Au and C_O are correction factors for ¹⁹⁷Au and ¹⁶O samples that are defined as the product of four factors. Namely, the factors to correct the γ-ray yield for multiple-scattering and self-shielding effects of the incident neutrons in the sample s, γ-ray absorption by the sample, and the finite size of the sample. Note that both the elastic and capture reaction processes were considered as main sources of neutron attenuation. The measured partial as well as the total cross sections of the ¹⁶O(n,γ)¹⁷O reaction are given in Table 1.

Table 1 Measured partial and total cross sections of the ¹⁶O(n,γ)¹⁷O reaction

2.4 Conclusion

Model calculations of the (n,γ) cross section were performed to be compared with the measured results by using a theoretical approach based on a direct radiative capture (DRC) process coupled to a single-level Breit-Wigner (SLBW) resonance model [21, 25]. The results [21] are shown in Fig. 6, where very good agreement is found between the model calculations and the present experimental results, both for the transitions leading to the ground state as well as for those leading to the first-excited state in ¹⁷O. The interference effect is clearly visible, for both transitions leading to the ground state as well as to the first-excited state in ¹⁷O.

Fig. 6

Neutron capture cross section in the energy range up to 800 keV, fully covering the region of the p-wave resonance at 437 keV. The interference effect is clearly visible, for both transitions leading to the ground state as well as to the first-excited state in ¹⁷O

Finally, a numerically integrated neutron capture reaction rate for the ¹⁶O(n,γ)¹⁷O reaction, N_A < σv > , is calculated for the various components of the capture process, as given Eq. (2).

$$ N_{{\text{A}}} \, < \,\sigma v\, > \,\, = \,a_{0} \, + \,a_{{1}} T_{{9}} \, + \,a_{{2}} /\left\{ {\left( {T_{{9}} } \right)^{{{3}/{2}}} } \right\}\, \times \,{\text{exp}}( - \,{2}.{225}/T_{{9}} ) $$

(2)

where σ is the Maxwellian-averaged capture cross section (MACS), T₉ is the temperature in 10⁹ K. Here, the first term is determined by the thermal capture cross section, ${\sigma }_{\gamma }$= 0.173 ± 0.006 mb [26], the second term is a good approximation of the p-wave DRC component, and the last term is the resonance term. The rate is in cm³ s⁻¹ mol⁻¹ when the parameters are a₀ = 26.5 (± 3.5%), a₁ = 12,434 ( + 10%−15%) and a₂ = 56,820 (± 20%). In the present study, we confirmed that a non-resonant p-wave direct capture process plays a dominant role in the reaction at the neutron energy between 10 and about 300 keV. Furthermore, we found that the interference effect between the 3/2⁻ resonance state with the total width of 40 keV at E_n = 411 keV and a non-resonant p-wave direct contribution significantly dominates the reaction cross section at E_n > 300 keV. Based on the present results we determined the Maxwellian-averaged capture cross section for thermal energies between kT = 5 and 100 keV. Since we solved a longstanding problem of the ¹⁶O(n,γ)¹⁷O reaction cross section, we expect that the present results could contribute to the progress on the various astrophysical phenomena, as given in [27,28,29,30], as well as a neutron capture reaction process.

3 ⁹⁹Tc in reactors

3.1 Background

As aforementioned, ^99gTc is one of the most important LLFPs for the study on the transmutation of nuclear wastes. However, experimental data for the capture cross sections of LLFPs are very poor both in quality and in quantity. As for ^99gTc, there exist three sets [31,32,33] of capture cross sections in the keV region before starting the present study [34], but large discrepancies exist among the previous data.

One of the main reasons for the discrepant results is due to LLFP difficulties in sample preparation: it is not easy to prepare enough amount of high purity sample of LLFPs to perform ordinary keV neutron capture experiments. Another reason is due to the radioactivity of LLFP sample: the accurate measurement of capture γ rays from the radioactive sample is not easy. Therefore, we have developed a capture γ-ray spectrometer with high sensitivity [35] and it has become possible to perform the keV-neutron capture experiment with a small amount (less than 1 g) of sample.

3.2 Experimental procedure and data processing

The experimental procedure and data processing are briefly described, as follows. The capture cross sections of ^99gTc were measured in the incident neutron energy region from 8 to 90 keV and at 190, 330, and 540 keV, using the same neutron source as that described in the previous section.

The ^99gTc sample was oxide powder (^99gTcO₂) sealed in an aluminum case of the inner diameter of 20.0 mm. The net weight of ^99gTc was 1.026 g (about 700 MBq) and the chemical purity of ^99gTc was 99.6%. A ¹⁹⁷Au sample with a diameter of 20.0 mm and a thickness of 1.0 or 2.0 mm was used as a standard.

Capture γ rays were detected with a large anti-Compton NaI(Tl) spectrometer with a heavy shield [20] by means of TOF method. Capture events detected by the spectrometer were stored in a workstation as two-dimensional data of TOF and PH. On the other hand, the energy spectrum of neutrons incident on each sample was measured by a TOF method with a ⁶Li-glass detector.

The measurements with and without the ^99gTc sample, with the ¹⁹⁷Au sample, and with a ²⁷Al sample (corresponding to the aluminum case of the ^99gTc sample) were made cyclically to average out changes in experimental conditions such as the incident neutron energy spectrum.

The γ-ray PH spectra for the ^99gTc or ¹⁹⁷Au sample in the Fore- and Back-ground regions were extracted by analyzing the two-dimensional data of the γ-ray spectrometer. Then, the net capture γ-ray PH spectrum of the ^99gTc or ¹⁹⁷Au sample was obtained by subtracting the Back-ground PH spectrum from the Fore-ground PH spectrum for each incident neutron energy spectrum.

A PH weighting technique [36] with the weighting function of the γ-ray spectrometer was applied to the net capture γ-ray PH spectra of the ^99gTc and ¹⁹⁷Au samples to obtain the capture yields, i.e., the numbers of capture events. Finally, the capture cross section of ^99gTc was derived by using the standard capture cross sections of ¹⁹⁷Au taken from ENDF/B-VI [37]. Corrections were made for the self-shielding and multiple-scattering of neutrons in the sample, the absorption and/or scattering of γ rays in the sample, the dead time, and others such as the effect of impurities in the ^99gTc sample. In addition to the statistical error (1–4%), the following nonstatistical errors were taken into account for those of capture cross sections: the errors due to the standard capture cross sections of ¹⁹⁷Au (3%), the weighting function of the γ-ray spectrometer (1%), the extrapolation of PH spectrum below the discrimination level of 0.6 MeV (2%), and the neutron self-shielding and multiple-scattering correction factors (1–2%). The total uncertainty of about 5% was evaluated by taking the square root of a quadratic sum of the statistical and nonstatistical errors.

3.3 Results and discussion

The capture cross sections of ^99gTc were derived with the error of about 5% in the neutron energy region from 8 to 90 keV and at 190, 330, and 540 keV. The present results are shown in Fig. 7, and compared with other measurements [31,32,33, 38, 39] and the evaluated values in JENDL-5 [40], ENDF/B-VIII.0 [41], and JEFF-3.3 [42].

Fig. 7

Neutron capture cross sections of ^99gTc in the keV region. Previous measurements and recent evaluated values are also shown

Chou and Werle [31] measured the capture cross sections in the neutron energy region from 1 eV to 50 keV, using a lead slowing-down spectrometer with a 14 MeV neutron source at Karlsruhe. Their results from 10 to 50 keV are smaller than the present ones by about 30%. Little and Block [32] measured the capture cross sections up to 80 keV, using a photo-neutron source by the electron linear accelerator of the Rensselaer Polytechnic Institute. Their results from 10 to 80 keV agree with the present ones within the experimental errors. Macklin [33] measured the capture cross sections in the energy region of 2.65 to 2000 keV, using the Oak Ridge Electron Linear Accelerator (ORELA). His results from 10 to 80 keV are smaller than the present ones by 15–20%, but his results from about 150–600 keV are in good agreement with the present ones. After starting the present measurements, Gunsing et al. [38] reported their results from 3 to 90 keV, which were obtained from the measurement with the pulsed white neutron source GELINA at Geel. Their results seem to support the present results, although they did not give the errors of their results. Kobayashi et al. [39] measured the capture cross sections in the energy region of 0.005 eV to 47 keV, using the 46-MeV electron linear accelerator at the Kyoto University, Research Reactor Institute. Their results above 10 keV are in good agreement with the present ones.

The evaluated values of JENDL-5 are in excellent agreement with the present measurements in the whole energy region. The evaluations of ENDF/B-VIII.0 around 10 keV are smaller than the present result at 12 keV by about 10%, but the evaluations around 70 keV are larger than the present result at 69 keV by about 15%. Namely, the energy dependence of ENDF/B-VIII.0 evaluations is gentle compared to that of the present measurements in the neutron energy region from about 10 to 100 keV. On the other hand, above 190 keV, the ENDF/B-VIII.0 evaluations are in good agreement with the present measurements. As for the evaluations of JEFF-3.3, those below 70 keV are smaller than the present results by 5−20%, but those above 190 keV are larger than the present results by 5−10%.

3.4 Conclusion

The capture cross sections of ^99gTc were measured in the incident neutron energy region from 8 to 90 keV and at 190, 330, and 540 keV, using a 1.5 ns pulsed neutron source by the ⁷Li(p,n)⁷Be reaction and a large anti-Compton NaI(Tl) γ-ray spectrometer. The errors of the present capture cross sections were about 5%. In the 8–90 keV region, the present measurements were larger than those of Macklin by 15–20% and those of Chou and Werle by about 30%, but agreed with those of Little and Block, those of Gunsing et al. and those of Kobayashi et al. On the other hand, the present results at 190, 330, and 540 keV were in good agreement with those of Macklin. The present accurate data on the neutron capture cross sections of ^99gTc that were obtained using an unconventional and unique experimental method also contribute to improve its evaluated cross sections, as shown below. The evaluations of JENDL-5 were in excellent agreement with the present results. On the other hand, there existed discrepancies between the present results and the evaluations of ENDF/B-VIII.0 and JEFF-3.3.

4 ^99mTc in nuclear medicine

4.1 Background

Medical radioisotopes (RIs) have been used for diagnostic imaging studies of diseases and therapeutic applications in cancer treatments [43]. Among the medical RIs, ^99mTc (T_1/2 = 6 h), the decay product of ⁹⁹Mo (T_1/2 = 66 h), is the most widely used diagnostic nuclear medicine RI that is usually obtained from a ⁹⁹Mo/^99mTc generator [8]. Because of the short half-life of ⁹⁹Mo a constant supply of ⁹⁹Mo is a key issue for ensuring the routine application of ^99mTc. Typical proposed reactions are the ⁹⁸Mo(n,γ)⁹⁹Mo reaction in reactors and the ¹⁰⁰Mo(p,pn)⁹⁹Mo, ¹⁰⁰Mo(p,2n)^99mTc, ²³⁵U(n,fission)⁹⁹Mo, ²³⁸U(γ,fission)⁹⁹Mo, and ¹⁰⁰Mo(γ,n)⁹⁹Mo reactions in accelerators [10]. Here, it should be mentioned that all alternative ⁹⁹Mo production routes would face the challenges of lower reaction rates and lower specific activity. In fact, the current route of fission-⁹⁹Mo provides a large amount of ⁹⁹Mo with a high specific activity of ~ 370 TBq/(g ⁹⁹Mo) in a reactor. On the other hand, a specific activity of ⁹⁹Mo based on any alternative routes, other than that of fission-⁹⁹Mo, is as low as about 1/5000 of the fission-⁹⁹Mo production [44].

In 2009, we proposed a new route to produce ⁹⁹Mo by the ¹⁰⁰Mo(n,2n)⁹⁹Mo reaction using fast neutrons from an accelerator (Hereinafter referred to as accelerator neutrons) [45]. Here, we discuss important physical parameters in the ¹⁰⁰Mo(n,2n)⁹⁹Mo reaction to produce a large amount of ⁹⁹Mo that can mitigate the aforementioned challenges. They are the cross section of the reaction, accelerator neutron beam flux, and number of ¹⁰⁰Mo sample nuclei. Firstly, that cross section has been evaluated based on the measurement and is as large as about 1.5 barn in the neutron energy (E_n) range between 12 and 20 MeV, as shown in Fig. 8 [46]. On the other hand, the cross sections of the ¹⁰⁰Mo(n,α), ¹⁰⁰Mo(n,3n), and ¹⁰⁰Mo(n,p) reactions that produce impurity radioisotopes other than ⁹⁹Mo are less than a few mb at E_n ~ 14 MeV. Hence, we could expect to obtain a high radionuclide purity of ⁹⁹Mo. Secondly, an intense accelerator neutron flux of 10¹⁵ n/s that has a most probable E_n of 14 MeV is produced by the ^natC(d,n) reaction using 40 MeV, 5 mA deuterons [47]. The neutron spectrum is advantageous for producing ⁹⁹Mo (see Fig. 8). The neutrons are mostly emitted in the forward-direction with respect to the deuteron beam direction. Hence, a ¹⁰⁰Mo sample placed at the forward-direction is effectively irradiated with the neutrons to produce ⁹⁹Mo. A quantity of ¹⁰⁰Mo samples of over 100 g mass can be used, because the neutron has no charge, and therefore the traveling range in a sample is much longer than that of a charged particle that is demonstrated in the measurement of the ⁹⁹Mo yield using a thick ^natMo sample in the next section.

Fig. 8

Neutron-induced reaction cross sections on.¹⁰⁰Mo [46]

4.2 ⁹⁹Mo yield studied by using neutrons from the C(d,n) reaction

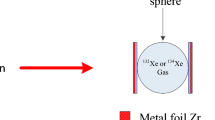
Next, in order to estimate an available production yield of ⁹⁹Mo on the basis of the proposed route we made a rigorous test of the measured energy and angular distributions of the accelerator neutrons, including the evaluated cross section of the ¹⁰⁰Mo(n,2n)⁹⁹Mo reaction. The test was made by measuring the yield of ⁹⁹Mo produced by the ^natMo(n,2n)⁹⁹Mo reaction [48]. We used four pellet ^natMoO₃ samples of 25.869, 25.868, 25.483 and 25.220 g mass with dimensions of 30 mmϕ × 11.6 mm (total length 46.4 mm), as shown in Fig. 9. The accelerator neutrons were provided by the ^natC(d,n) reaction using 40 MeV deuterons at the cyclotron at Cyclotron and Radioisotope Center (CYRIC), Tohoku University [49].

Fig. 9

Schematic view of the experimental setup at the ^natMoO₃ sample position. Sample numbers are indicated in parentheses. [48]

We estimated the yield of ⁹⁹Mo by numerical calculations for a comparison with the measured yield, as follows. We used the neutron-nucleus reaction cross sections given in JENDL-4.0 [46] for molybdenum and oxygen in the ^natMoO₃ sample. In calculating the neutron flux we used the latest data of the cross section, which was obtained by irradiating a 15-mm-thick carbon target with 40 MeV deuteron beams [50]. The estimated yield of ⁹⁹Mo for each set of the ^natMo samples is in good agreement with the measured yield, as given in Table 2.

Table 2 Measured ⁹⁹Mo yield (⁹⁹Mo_meas.) at the EOI compared with the calculated yield (⁹⁹Mo_cal.). The number in brackets in the first line is the number of the sample shown in Fig. 9

Based on the good agreement between the measured ⁹⁹Mo yield and the calculated yield, we calculated the activities of ⁹⁹Mo at the end of irradiation (EOI), produced by the ¹⁰⁰Mo(n,2n)⁹⁹Mo reaction for an enriched ¹⁰⁰MoO₃ sample. In the calculation, we used the latest data on the angular and energy distributions of neutrons from ^natC(d,n) at E_d = 40 MeV (assuming a beam intensity of 2 mA) and evaluated cross sections given in JENDL-4.0. We obtained the calculated yield of 700 GBq ⁹⁹Mo using a ¹⁰⁰MoO₃ sample of 100 g produced every day by the ¹⁰⁰Mo(n,2n)⁹⁹Mo reaction with 40 MeV, 2 mA deuteron beams (24 h irradiation) [48]. If 700 GBq of ⁹⁹Mo is produced daily, 6 days a week, the daily production of ⁹⁹Mo is stockpiled, so that an average of 2.44 TBq of ⁹⁹Mo per day [48] is used to obtain ^99mTc, which is discussed in subsection 4.3. A detailed discussion of average ⁹⁹Mo yields can be found in Ref. 51 (Fig. 3).

4.3 Thermoseparation of ^99mTc from ⁹⁹Mo with a low specific activity

First, it should be noted that the typical radioactivity of ^99mTc radiopharmaceutical solutions administered to patients is as high as about 740 MBq/(several ml). In order to recover ^99mTc with such high specific activity from ⁹⁹Mo with aforementioned low specific activity, various method, such as chromatographic, solvent extraction, and thermoseparation methods, have been developed.

We employed the thermoseparation procedure, which utilizes the different volatility of technetium oxide and ¹⁰⁰MoO₃ to separate ^99mTc from ⁹⁹Mo. We developed newly a home-made thermochromatography system shown in Fig. 10 to achieve a higher separation efficiency of ^99mTc over 90% for an irradiated ¹⁰⁰MoO₃ sample of about 100 g [52], a high capability of nearly 100% recovery of irradiated enriched ¹⁰⁰MoO₃ sample [53]. Note that it is important to recycle an enriched (expensive) ¹⁰⁰Mo sample irradiated by neutrons.

Fig. 10

Schematic view of thermochromatography system. 1, Electric furnace (three individual heating zones); 2, Crucibles for MoO₃ samples; 3, MoO₃ needle crystal holder; 4, Quartz wool; 5, ^99mTc condensation region; 6, CZT detector; 7, Moist oxygen inlet

The ^99mTc activity that can be obtained from the aforementioned 2.44 TBq ⁹⁹Mo using the thermochromatography system was evaluated as follows. First, the irradiated ¹⁰⁰MoO₃ sample containing the ⁹⁹Mo is placed in a thermochromatography apparatus to separate ^99mTc twice a day from the ⁹⁹Mo. The ^99mTc activity immediately after separating ^99mTc from the ⁹⁹Mo was evaluated to be 2.35 TBq in which the separation efficiency of 80% and the decay loss of ^99mTc during the separation procedure for about 2 h were considered.

Next, quality control testing of ^99mTc-radiopharmaceuticals using the ^99mTc thus obtained is described. Note that the current United States Pharmacopeia (USP) contains regulatory requirements concerning the radionuclidc purity and the radiochemical purity of ^99mTc. The USP sets those pharmacopeia standards for ^99mTcO₄⁻ obtained from a ⁹⁹Mo/^99mTc generator. We have tested the pharmaceutical equivalence of ^99mTcO₄⁻ obtained by ^99mTc from the thermochromatographic separation procedure to that obtained from the alumina-based ⁹⁹Mo/^99mTc generator. We have also studied quality-control tests of ^99mTc-radiopharmaceuticals commonly used for the imaging of brain perfusion (^99mTc-ECD), myocardial perfusion (^99mTc-MIBI), and kidney (^99mTc-MAG3), to ensure the safe clinical use of ^99mTc obtained by the ¹⁰⁰Mo(n,2n)⁹⁹Mo reaction. The results of the quality assessments of the ^99mTcO₄⁻ saline solution and ^99mTc-radiopharmaceuticals were shown to satisfy the USP requirements. These results provide the important evidence that ^99mTc prepared by thermochromatographic separation using ⁹⁹Mo produced by the ¹⁰⁰Mo(n,2n)⁹⁹Mo reaction can be a promising substitute for the fission product ⁹⁹Mo [52].

4.4 ⁹⁹Mo demand in Japan and conclusion

Next, we will examine the extent to which 2.35 GBq of ^99mTc can be covered in the nuclear medicine diagnosis of ^99mTc performed in Japan. About 0.9 million diagnostic procedures (2750 procedures/day) have been performed every year using ^99mTc radiopharmaceuticals with an average dose of about 740 MBq (20 mCi) at the time of injection to a patient: 2.05 TBq (55 Ci) of ^99mTc is used every day. By considering the decay losses associated with transporting ^99mTc from radiopharmaceutical companies to hospitals, a total of 4.10 TBq (110 Ci) of ^99mTc is needed daily in Japan [48]. As discussed above, 2.35 TBq of ^99mTc is obtained at the end of the separation of ^99mTc, i.e., immediately before forming the ^99mTc radiopharmaceuticals at a radiopharmaceutical company. When one can inject the ^99mTc radiopharmaceuticals prepared by using the 2.35 TBq ^99mTc within 6 h to a patient, about 57% of the daily procedures using ^99mTc radiopharmaceuticals can be performed in Japan. In fact, because about 35% of Japan’s population live in the capital-area (a region within about 150 km radius from the center of Tokyo), and the number of people who live in the capital-area, Kansai-area, and Chukyo-area is about 60% of the total population of Japan, ^99mTc radiopharmaceuticals can be delivered from a radiopharmaceutical company to those who live there within 6 h. The proposed delivery of ^99mTc would be possible by using the current delivery system of ¹⁸F-FDG, a radiopharmaceutical fluorodeoxyglucose containing ¹⁸F with a half-life of 1.8 h, shorter than ^99mTc (T_1/2 = 6 h). In Japan, deliveries of ¹⁸F-FDG are being carried out three times per day by road transport from the ¹⁸F-FDG-producing radiopharmaceutical company to hospitals about 200 km away within 3 h [54]. The activity of ¹⁸F prepared at the radiopharmaceutical company is three times stronger than that needed for the injection into a patient at the hospital by considering the decay loss of 68% during the transportation of ¹⁸F in 3 h. Note that the ^99mTc activity needed at hospitals for the ^99mTc procedures to satisfy 50% of the demand in Japan is 1.03 TBq (28 Ci). The decay loss of ^99mTc activity in transportation for 3 h is 30%. Hence, the ^99mTc activity of 2.35 TBq (64 Ci) obtained at a radiopharmaceutical company would be enough to perform the procedures mentioned.

Based on these results and the results of the quality assessment of ^99mTc radiopharmaceuticals, it can be concluded that ⁹⁹Mo produced by the ¹⁰⁰Mo(n,2n)⁹⁹Mo reaction is a promising alternative to fission-⁹⁹Mo for domestic use [52].

5 Summary

The discovery of ⁹⁹Tc has opened up new research area, s-process nucleosynthesis in stars, nuclear transmutation of long-lived nuclear waste produced in fission reactors, and diagnosis in nuclear medicine, that were unforeseen at the time of its discovery. The present paper summarizes the results of our studies on ^99gTc and ^99mTc using an accelerator-based neutron source that have been performed based on either by developing a neutron time-of-flight method combined with a discrete γ-ray detection technique using an anti-Compton NaI(Tl) spectrometer having high sensitivity or by proposing a new production scheme of medical radioisotope of ^99mTc. A non-resonant p-wave direct capture process observed in the ¹⁶O(n,γ)¹⁷O reaction is shown to play a dominant role in the reaction at the neutron energy between 10 and about 300 keV, and in addition the interference effect between the 3/2⁻ resonance state in ¹⁷O at E_n = 411 keV and a non-resonant p-wave direct contribution significantly dominates the reaction cross section at E_n > 300 keV. The resulting Maxwellian-averaged capture cross section for thermal energies between kT = 5 and 100 keV is expected to contribute to the progress on the various astrophysical phenomena as well as a neutron capture reaction process. The capture cross sections of ^99gTc were measured in the incident neutron energy region between 8 and 540 keV accurately with an uncertainty of about 5% that provides valuable information on the nuclear transmutation of ^99gTc and the s-process nucleosynthesis. The quality assessments of ^99mTc-radiopharmaceuticals prepared using ⁹⁹Mo produced by the ¹⁰⁰Mo(n,2n)⁹⁹Mo reaction were shown to satisfy the quality control test of USP requirements that can be a promising substitute for the fission product ⁹⁹Mo for domestic use. We are pleased to have been involved in different aspects of the ⁹⁹Tc research activities, pioneered by our colleague and friend Franz Käppeler and to have made the contributions described here.