Validation of an optical potential for incident and emitted low-energy $\alpha$–particles in the $A$ $\sim$60 mass range

Abstract

The assessment of an $\alpha$-particle optical model potential for nucleon–induced $\alpha$-emission within the $A$ $\sim$60 mass-number range [Avrigeanu and Avrigeanu (Eur. Phys. J. A 57:54, 2021)] is completed by analysis of neutron–induced reactions on stable Ni isotopes. The same consistent set of nuclear–model input parameters as well as first uncertainty analysis of calculated cross sections related to the accuracy of independent data formerly used within parameter setting up have been concerned. Description of absorption and emission of $\alpha$-particles by the same potential is validated, while the pickup direct reaction and Giant Quadrupole Resonance (GQR) $\alpha$-emission beyond the statistical predictions are confirmed by recent data around the GQR energies.

1 Introduction

An $\alpha$-particle optical model potential (OMP) established previously by analysis of $\alpha$-particle elastic scattering as well as induced reactions on $A$ $\approx$45–209 nuclei, at energies $\le$50 MeV [1], has lately been proved able to describe also the $\alpha$–emission from excited nuclei in nucleon-induced reactions within the $A$ $\sim$60 mass-number range [2]. The description in terms of the statistical Hauser-Feshbach (HF) [3] and pre-equilibrium emission (PE) [4] models made use of consistent parameter sets formerly validated by analysis of other independent data (e.g. [5]). An alternate solution of so-called $\alpha$-potential mystery [6] concerning the account of both $\alpha$-emission and absorption was thus provided too, of equal interest for astrophysics and fusion technology.

Actually, further consideration given to the pickup direct reaction (DR) increasing the $\alpha$-emission beyond the HF+PE results, set off the above conclusion. A suitable account of the measured $\alpha$-emission cross sections at the Giant Quadrupole Resonance (GQR) energies of $^{55,57,58}$Fe excited nuclei, in addition to HF+PE results, has also been attributed to a like–GQR component. While the previous $\alpha$–emission analysis [2] took the advantage of recent data of low-lying states feeding in $(n,\alpha )$ reaction on Fe, Co, Cu, and Zn nuclei, further new data around the GQR energies of nuclei excited by neutrons incident on $^{58,60,61}$Ni [7, 8] have triggered a similar interest for their account.

In fact, the $\alpha$–emission in neutron–induced reactions on $^{59}$Co and stable Ni isotopes up to 20 MeV made also the object of an earlier systematic investigation [9]. The use of an OMP [10] set up to describe the $\alpha$-particle emission in neutron-induced reactions, with distinct predictions from potentials for incident $\alpha$ particles [11], provided however large overestimation of $(n,\alpha )$ reaction data. Further experimental and theoretical progress related particularly to neutrons incident on more abundant $^{58,60}$Ni (e.g., [12, 13] and Refs. therein) as well as latter studies [7, 8, 14, 15] pointed out still open questions of the $\alpha$–emission insight.

A proper account of all available data for competitive reaction channels, beyond the $\alpha$–emission of interest for this work, is also concerned to avoid compensation effects of rough model parameters. A latest conclusive remark in this respect has underlined that ’simplistic or arbitrary parameter adjustments, tuned to provide a better fit for a singular reaction channel of interest, are nonunique and may not hold a global physical basis because neighboring reaction channels can suffer from the fit choice’ [16].

Table 1 Low-lying levels [17] used in HF calculations and fitted (with uncertainty in units of the last digit, in parentheses) at once with $D_0^{exp}$ data$^a$ in one or more (separated by slash) energy ranges $\Delta$ $E$ above S, for target g.s. spin $I_0$, to obtain a and $\Delta$ parameters [18] with uncertainties related firstly to those of fitted $D_0^{ exp}$ and then in addition to those of fitted $N_d$

The present work as well as the related OMP setting up [1, 20,21,22] and support [2, 23, 24] have become possible since no empirical rescaling factors of the $\gamma$ and/or neutron widths were concerned. Thus, the effective presentation of the consistent input parameter set is mandatory, particularly before the uncertainty analysis of calculated cross sections just due to error bars of independent data formerly used for parameters validation. However, because this work is an extension of Ref. [2], only the additional issues concerning particularly the Ni isotopes are given in Sect. 2. The PE+HF results for all reaction channels are shown in Sect. 3, including the $\alpha$-emission, while its further DR analysis within the distorted-wave Born approximation (DWBA) method and the code FRESCO [25], are given in Sect. 4 at once with the GQR consideration.

Table 2 Comparison of experimental [19] and calculated s- and p-wave strength functions $S_0$ and $S_1$ (in units of 10$^{-4}$), and potential scattering radius $R'$ of $^{58,60,61,62,64}$Ni isotopes at neutron energies of $\sim$0.4, $\sim$0.2, 0.034, $\sim$0.28, and 0.3 MeV [28], respectively, and (bottom) the changes of the corresponding global parameters [29] (with [29] notations, energies in MeV and geometry parameters in fm) which provide best results cf. Delaroche et al. [30]

2 Compound and pre-equilibrium parameters

The following calculated results have been obtained by using the same nuclear models, codes and local approach as previously [2]. Thus, typical direct inelastic–scattering cross sections, e.g. for neutrons on $^{58,60}$Ni, grow up from $\sim$1.5% and $\sim$4%, respectively, to $\sim$4% and $\sim$9% of the reaction cross section $\sigma _R$ for incident energies from 2 to 7 MeV, and then decrease slightly below 4% and $\sim$7%, respectively, at energy of $\sim$25 MeV.

The low-lying levels and nuclear level density (NLD) parameters of the back-shifted Fermi gas (BSFG) model [18] are given in Table 1 for all nuclei involved in this work, to be available at once. Fit of the error-bar limits of s-wave nucleon–resonance spacings $D_0^{ exp}$ data has also been used to provide limits of the fitted a-parameters. These limits have also been used within HF calculations to illustrate the NLD effects on the calculated cross-section uncertainty bands (Sect. 3). The uncertainties of the averaged a-values are given also in Table 1 for nuclei without resonance data, following the spread of the fitted a parameters. They could be larger than those of the a-values obtained by fit of more accurate $D_0^{ exp}$ while their use in HF calculations leads to increased calculated cross-section uncertainty bands. Assumption of an additional uncertainty of the fitted $N_d$ has led to increased NLD parameter uncertainties as given in a second pair of brackets in Table 1. Better choice of the fitted $N_d$ or data becoming available in the meantime (e.g. for $^{57}$Fe nucleus [26, 27]) led for several nuclei to eventual differences between the NLD parameters in this table and Refs. [2, 23] but still within their uncertainties.

Fig. 1

Comparison of neutron total cross sections for $^{58,60,61,62,64}$Ni measured [31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52] and calculated using either the global (dash-dotted curves, thin dash-dotted for $^{64}$Ni) or local (dashed) OMP parameters sets of Koning and Delaroche [29], and the energy-dependent changes of the global geometry parameters given in Table 2 (solid, thin solid for $^{64}$Ni). Broad energy–averages over 50, 100, and 200 keV of several measured data sets were used for comparison with the OMP results

Fig. 2

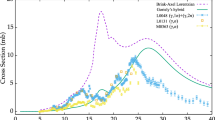
Comparison of a measured [53, 54] and sum of calculated M1-radiation SLO model (dotted curve) with E1-radiation SLO (dash-dot-dotted), GLO (dash-dotted), and EGLO (dashed) RSFs, as well as the sum (solid) of the upbend–including M1 component (short dotted) and EGLO, for $^{60}$Ni nucleus, b $^{59}$Co$(p,\gamma )^{60}$Ni and $^{59}$Co$(p,n)^{59}$Ni reaction cross sections measured [55,56,57,58,59,60,61,62], evaluated [63] ($+$), and calculated using either the proton OMP of this work and the above RSF models (similar curves), or the potential [29] and sum of EGLO and upbend–including M1-radiation RSFs (short dot-dashed), and c proton–reaction cross sections measured [64] and calculated with the OMPs of Ref. [29] (short dot-dashed) and this work (solid). Uncertainty bands correspond to GDR peak cross sections [65] (light-gray) and the M1-radiation upbend (gray), while there are also shown the average s-wave radiation width $\Gamma _{\gamma }$ (in meV) measured [19] and related to above RSFs

The neutron OMP of Koning and Delaroche [29] has been the subject of an additional analysis [30] similar to that for $^{54,56}$Fe nuclei [2]. Thus, we found that the energy–dependent geometry parameters of their global parameter sets given in Table 2 describe fairly well the neutron total cross–section $\sigma _T (E)$ minimum around 1 MeV in Fig. 1. Its account seems to be even better as one provided by renewed coupled-channels (CC) analyses at an incident energy not less than of $\sim$2 MeV (Fig. 1 of Ref. [66]). At the same time, $\sigma _T (E)$ decrease below 1 MeV is at least similar to the CC results, while the calculated s- and p-wave neutron strength functions $S_0$ and $S_1$, respectively, and potential scattering radius $R'$ [19] are either comparable or improved. One may note the neutron energies given in Table 2 for this comparison, quite different by 10 keV involved within the CC analysis [66]. Except $^{61}$Ni (Fig. 1c), the adopted energy dependence of the geometry parameters [29] avoids an overestimation even $\ge$20% at the neutron energies around 1 MeV, of obvious importance for competition of neutron evaporation and charged–particle emission from excited compound nuclei (CN).

The proton OMP of Koning and Delaroche [29] used within HF analysis of proton–induced reaction on $^{59}$Co and incident energies below $\sim$6 MeV has led to an underestimation $\ge$50% of the $(p,\gamma )$ data below the (p, n) reaction effective threshold, and an overestimation $\ge$50% of the (p, n) data around 4 MeV (Fig. 2b). Actually, the proton OMP fully constrains the calculated $(p,\gamma )$ cross sections below the proton energy of $\sim$2 MeV, where they are closest to $\sigma _R$. The same is true for the (p, n) reaction at energies higher than 3 MeV, where this becomes the dominant reaction channel with cross sections also close to $\sigma _R$.

The due account of the corresponding $(p,\gamma )$ and (p, n) data at lower energies as well as $\sigma _R$ data between 9 and 50 MeV (Fig. 2c) has been achieved by replacing the constant real potential radius $r_V$=1.998 fm [29] with the energy–dependent form 1.29-0.03E up to 2 MeV, 1.35-0.06E up to 5 MeV, 0.9+0.03E up to 10 MeV, and 1.225-0.0025E up to 50 MeV.

Moreover, only the discrete low-lying levels of the residual nucleus $^{59}$Ni (Table 1) have been excited for incident energies up to 5 MeV. Thus, there were no NLD but only proton OMP constraints on calculated (p, n) results at low proton energies so important also for statistical emission from excited nuclei.

The radiative strength functions (RSF) for Ni isotopes have not yet had an unique parametrization despite the M1 low–energy enhancement was formerly observed for $^{60,64,65}$Ni isotopes by the Oslo method, in proton–capture [67], $(p,p'\gamma )$ [54], and $(d,p\gamma )$ [68] reactions, consistently with the hypothesis of the independence by initial excitation energy [69]. Moreover, measured photoneutron cross sections of $^{58,60,61,64}$Ni were used to extract complementary RSFs above threshold as well as reliable limits of the M1 upbend [70], lastly observed for the first time down to $\gamma$-ray energies of $\approx$ 0.2 MeV [71].

Therefore, firstly, we have adopted the recently–compiled [65] giant dipole resonance (GDR) parameters within the former Lorentzian (SLO) [72], generalized Lorentzian (GLO) [73], and enhanced generalized Lorentzian (EGLO) [74] models for the electric-dipole RSF. The constant nuclear temperature $T_f$ = 1.2 MeV of the final states [54] was particularly assumed within the EGLO model.

The global [19] GDR energy and width of SLO model has also been used for M1 radiation, i.e. $E_0$ = 41/$A^{1/3}$ MeV and $\Gamma _0$ = 4 MeV. On the other hand, a related peak cross section $\sigma _0$ = 4 mb has been assumed at once with the above-mentioned $T_f$ value in order to describe the only RSF data [53, 54] available for $^{64}$Ni (Fig. 2a). The additional M1 upbend to zero energy has been described by the same function $f_{up}(E_{\gamma })$ = Cexp$(-{\eta }E_{\gamma })$ but with the parameter value $\eta$=0.8 MeV$^{-1}$ and limits C = (0.3–1)$\times$10$^{-7}$ MeV$^{-3}$ [70]. The uncertainty band related to these limits is obviously essential below $E_{\gamma }$ $\sim$5 MeV while the upper limit 10$^{-7}$ MeV$^{-3}$ led to a good agreement with the corresponding measured RSFs not only for $^{64}$Ni but the systematic description for all Ni isotopes shown in Fig. 4 of Ref. [70]. At the same time, the uncertainty of the two–component GDR peak cross–sections [65, 75] becomes important mainly above the nucleon binding energy and even beyond the E1 model assumption. Nevertheless, the E1–radiation EGLO model provides a better RSF energy dependence in comparison with the sum of the SLO for M1 radiation and either SLO or GLO models. Unfortunately, the large limits of the compiled $\Gamma _{\gamma }$ [19] are not contributing additionally to RSF approach validation.

On the other hand, the final propagation of the RSF uncertainty on the calculated $(p,\gamma )$ reaction cross sections (Fig. 2b) shows no effect below the neutron threshold, and a lower one in comparison with various electric-dipole RSF models at higher proton energies. Therefore, the $(p,\gamma )$ data analysis has also provided a meaningful check of the proton OMP while, more generally, the suitable RSF account has increased the confidence on calculated cross sections just above the particle–emission thresholds.

3 Compound and pre-equilibrium results

The model analysis of the measured cross sections of neutron–induced reactions on Ni stable isotopes, using the above consistent parameter set, are displayed hereafter with a particular attention paid to recent data [7, 8, 14, 15]. The aim is to ascertain either the account of the $\alpha$-particle emission by the $\alpha$-particle OMP [1] or eventual questions that may still need further consideration, while all competing reaction channels are also properly described.

Fig. 3

Comparison of measured [8, 9, 12, 14, 15, 76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109], evaluated [63] (short–dashed curves), and calculated TALYS-1.95 (short–dotted) and this work (solid; also thin–solid and dash–dot–dotted for $(n,\alpha )$ and $(n,n'\alpha )$ reactions, respectively) cross sections of neutron–induced reactions on $^{58}$Ni, with alternate use of neutron (dashed) or proton (dash–dotted) OMPs [29], d $\alpha$-particle OMP [10] within HF (thin dash-dotted) and both HF+GDH (thin dashed) calculations. Uncertainty bands correspond to NLD-parameter error bars (Table 1) of $^{58}$Ni (gray bands), $^{58}$Co and $^{55}$Fe (light–gray), and GDH parameter $\varphi$ (yellow)

3.1 $^{58}$Ni(n, x) reactions

The (n, p) reaction large cross sections of the lightest stable Ni isotope provide, in a similar way to the case of the also semi–magic nucleus $^{54}$Fe [2], an useful check of the proton OMP. The NLD effects, existing only above an incident energy of $\sim$6 MeV (Fig. 3a), should be also noted. On the other hand, the broad plateau of the (n, p) excitation function makes visible the distinct NLD uncertainties for the residual nuclei $^{58}$Ni and $^{58}$Co within neutron– and proton–emission channels, respectively. The average values of their level density parameter a are smaller due to magic number Z = 28, so that we have assumed uncertainties for them only related to larger values (Table 1). Consequently, the corresponding effects as well as uncertainty bands of the calculated (n, p) excitation function are opposite. They are larger even than 10% between 10 and 12 MeV but lower at higher energies, where the PE contribution increases. However, because the PE cross sections also depend by a values through the related PLDs [110, 111], the good agreement of our calculated results and the available data does support the present approach.

It should be noted that use of the unchanged neutron and proton OMPs [29], both of them corresponding to higher transmission coefficients, may have also opposite effects for this reaction (Fig. 3a). These effects have rather similar size and however may not change the plateau slope but its height by up to $\sim$23%. The OMP effects are therefore rather equal to the NLD ones but around a lower incident energy of 7 MeV. There is thus a sound explanation for so different various evaluations of this excitation function.

The (n, 2n) reaction excitation function has been affected similarly by the NLD of the residual nuclei $^{58}$Ni and $^{58}$Co but leading to calculated total uncertainties even larger than 30% (Fig. 3b). Other, still larger uncertainties may have arisen from the use of either neutron or proton global OMPs [29], with the results also shown in Fig. 3b. Unfortunately, the various data sets are spread over these uncertainty bands. Nevertheless, the results of the present work are just between the more recently measured cross sections [14, 15] of both (n, 2n) and (n, p) reactions, providing confidence in them.

The $^{58}$Ni$(n,x)^{57}$Co reaction excitation function (Fig. 3c) has been obtained by adding the calculated results of this work for $(n,n'p+pn)$ reaction, and that of TALYS-1.95 [112] for (n, d) reaction with $\sim$4% weighting. The agreement between the measured and presently calculated cross sections is only in the limit of twice the data standard deviation. At the same time, the uncertainty bands corresponding to the above–mentioned NLD effects are only within $\sim$2%. The same is true for the case of using either the neutron or proton unchanged OMPs [29]. These findings may follow the compensation of the above–mentioned NLD and OMP uncertainties related to the neutron and proton emission. On the other hand, while the TALYS-1.95 default results have provided a much better overall agreement with the data, the further TENDL-2019 [63] evaluation aimed an increased account of the excitation–function maximum at the price of worse overestimation of the main body of data around the incident energy of 14 MeV.

The $(n,\alpha )$ reaction analysis first proves a suitable account of recent data [8, 12] except an obvious underestimation at the incident energies between $\sim$5 MeV and 10–11 MeV (Fig. 3d). The uncertainty band of the calculated $(n,\alpha )$ cross sections related to limits of the s-wave resonance spacing $D_0^{ exp}$ of residual nucleus $^{55}$Fe and consequent ones for its LD parameter a (Table 1), becomes significant from incident energies higher than 9–10 MeV. It increases up to $\sim$14% due to $D_0^{ exp}$ enlarged limits for this nucleus, but at neutron energy around 15 MeV. On the other hand, the uncertainty band mainly corresponding to the LD parameter a of the residual nucleus $^{58}$Ni, may additionally decrease by up to $\sim$15% the $(n,\alpha )$ reaction cross section above the neutron energy of $\sim$6 MeV. A decrease would correspond also to the use of either the neutron or proton unchanged OMPs [29], eventually from 3–4 MeV (Fig. 3d). Finally, a GDH $\alpha$-particle pre-formation probability $\varphi$ = 0.08 has been used following the $\alpha$-emission spectra analysis for $^{60}$Ni target nucleus within Sect. 4. Its assumed limits of ±0.02 lead to an uncertainty band yet within 5–8%, and becoming visible only from $\sim$10 MeV.

It results that no NLD, OMP, and PE effect may enlighten the underestimation of the $(n,\alpha )$ cross sections between $\sim$5–11 MeV, where the $\alpha$-particle OMP is thus the main HF parameter. Moreover, alternate use of the $\alpha$-particle OMP [10] has concerned, first, the $\alpha$-particle transmission coefficients involved in HF calculations, and then also the corresponding PE intranuclear transition rate [113]. The former replacement provides an overestimation from $\sim$50% at the incident energy of $\sim$2 MeV, to $\sim$25% at 7 MeV, while the latter brings an additional increase of up to 60%. Obviously, it can not be compensated by the above–mentioned NLD and PE effects.

3.2 $^{60}$Ni(n, x) reactions

Fig. 4

As Fig. 3 but for $^{60}$Ni, additional measured data [7, 114,115,116,117,118,119,120,121,122,123,124,125,126], and d comparison of measured $\alpha$-emission spectra from 14.1–14.8 MeV neutron–induced reactions on $^{60}$Ni [12, 76, 124], and calculated DR pickup (dash-dotted curve), PE (dashed), CN first– (short–dash) and second–emission (dotted) components at 14.3 MeV, respectively, and their sum (solid). Uncertainty bands related to NLD-parameter error bars (Table 1) are for residual nuclei $^{60}$Ni (light-gray bands), $^{60}$Co and $^{57}$Fe (gray)

The (n, p) reaction excitation function (Fig. 4a) is also of particular interest for model validation being so different from that of $^{58}$Ni. Its analysis should take the advantage of LD parameter a-values obtained by fit of $D_0^{ exp}$ data for the residual nuclei following the neutron and proton emission (Table 1). However, the accuracy of these data is quite different, being 3 times better for the odd–odd nucleus $^{60}$Co than for the even-even $^{60}$Ni. Consequently, the uncertainty bands corresponding to them are in a similar ratio, so that the former has a width rather close to error bars of measured data while the latter includes even rather disparate (n, p) reaction cross sections at incident energies $\ge$17 MeV. It is thus pointed out the usefulness of newer accurate data for both average s-wave nucleon–resonance spacings and reaction cross sections, for a better understanding of the latter ones.

However, while the NLD effects become obvious at higher incident energies (>7 MeV), the use of unchanged nucleon OMPs [29] may alter the calculated cross sections from lower energies. Additionally, one may note that use of this proton OMP would increase the (n, p) cross sections by more than twice the decrease related to the neutron OMP [29]. The latter effect is even larger than the one due to the less accurate $D_0^{ exp}$ value for $^{60}$Ni, at lower incident energies. Then it becomes rather similar around the excitation function maximum, but decreases much more with the energy increase.

The (n, 2n) reaction excitation function (Fig. 4b) proves good agreement with the newer measured data except that at the incident energy of 19 MeV. The above–mentioned NLD effects of the residual nuclei $^{60}$Ni and $^{60}$Co are similar to the (n, p) reaction, including their size, as well as the ones possible due to the use of the unchanged nucleon OMPs [29].

The $(n,x\alpha )$ excitation function analysis (Fig. 4c) should take the advantage of the recent Refs. [7, 8] for incident energies <12 MeV. However, a large underestimation of the experimental data at neutron energies of 6–12 MeV is again obvious.

The first point in order to avoid this underestimation, may concern the low–lying levels and NLD of the residual nucleus $^{57}$Fe. Thus, its number of levels in a complete level scheme has been taken into account based on the most recent studies [26, 27] (Table 1), with only an upper limit of 10 levels in agreement with [19]. On the other hand, the discrepant $D_0^{ exp}$ values [18, 19] have also contributed to an enlarged NLD uncertainty band up to $\sim$30% at the excitation function maximum. However, obviously it matters only above the neutron energy of 9 MeV.

At the same time, only an uncertainty band related to the above–mentioned NLD parameters of $^{60}$Ni is effective at lower incident energies. It becomes similar to the measured–data error bars from neutron energies of 7–8 MeV, while the present results are also supported by the suitable account shown above for the main reaction channels. It may yet be noted that the use of the neutron unchanged OMP [29] would provide a larger underestimation at incident energies <10 MeV, unlike the similar proton OMP.

The PE assumptions have no effect at incident energies below 11 MeV, too. An uncertainty band is shown in Fig. 4c, corresponding to the pre-formation probability $\varphi$ = 0.08$~\pm$ 0.04. This $\varphi$-value has been proved by the analysis of the $\alpha$-emission angle-integrated spectra around the incident energy of 14.3 MeV [12, 76, 124] (Fig. 4d). Nevertheless, this component becomes significant only for neutron energies above 15–20 MeV, where there is already a suitable data account.

It thus results again that the $\alpha$-particle OMP is the main HF parameter at incident energies $\le$ 8 MeV where the most recent and precise $(n,\alpha )$ data above $\sim$5 MeV remain underestimated. Moreover, the replacement of the $\alpha$-particle OMP [1] by the earlier one [10] provides an overestimation similar to the case of $^{58}$Ni target nucleus. Once more, its compensation can not be expected by neither NLD nor OMP effects within consistent limits.

3.3 $^{61,62,64}$Ni(n, x) reactions

Fig. 5

As Fig. 4 but for $^{61,62,64}$Ni target nuclei, additional measured data [127,128,129,130,131,132,133,134,135,136,137,138,139,140], and c population of the 5$^+$ isomeric state of $^{62}$Co (thin–solid curve). Uncertainty bands corresponding to NLD-parameter error bars (Table 1) are for residual nuclei $^{61,62,64}$Ni (gray bands), $^{61,62,64}$Co and $^{58,59,61}$Fe (light–gray)

Measured neutron–activation data of heavier $^{61,62,64}$Ni stable isotopes are available only for the (n, p) and $(n,x\alpha )$ reactions. Several common features motivate the following concurrent discussion.

The (n, p) reaction analysis for $^{61,62}$Ni target nuclei may benefit from $D_0^{ exp}$ values available for these nuclei, at variance with the case of the residual nuclei $^{61,62}$Co. This fact is well reflected by the uncertainty bands related to the $D_0^{ exp}$ error bars, for the former nuclei, and the estimated accuracy of the LD a-parameter values for the latter ones (Fig. 5a, c). Their ratio around 0.3 proves once more the usefulness of accurate resonance data.

On the other hand, these uncertainty bands illustrate the lack of NLD effects below incident energies of 8–9 MeV. It results that the measured data in this energy range could be useful for validation of the proton OMP, provided that the neutron OMP is particularly well-suited. Otherwise, the cross-section changes following, e.g. the nucleon OMPs [29], would act against each other. The outcome of such a case could be (i) their complete compensation, as for (n, p) reaction on $^{61}$Ni at incident energies below 5–6 MeV (Fig. 5a), (ii) a partial compensation overall of the neutron OMP overprediction, as for $^{62}$Ni (Fig. 5b), or (iii) even partial compensation of each one below and above $\sim$15 MeV, respectively, as for $^{61}$Ni.

The case is much more serious if there are available only several and also discrepant data sets including newer ones, as for $^{61}$Ni (Fig. 5a). Consideration of the isomeric–state cross sections may be of additional help, as for $^{62}$Ni (Fig. 5c).

Very few and earlier data have been present also for $^{64}$Ni (Fig. 5e), at once with no residual–nuclei resonance data, i.e. large uncertainty bands for the NLD effects of both residual nuclei $^{64}$Ni and $^{64}$Co. Nevertheless, more recent data within the low incident–energy range, particularly for $^{61}$Ni, have been well described and provide confidence in the present model approach.

The $(n,\alpha )$ reaction analysis for $^{61,62,64}$Ni nuclei is essential due to the data available below the neutron energy of 10 MeV, including the newest ones for $^{61}$Ni [8]. However, the HF+PE results of this work have provided a less suitable account of the data at these energies, from an underestimation beyond 2$\sigma$ of the data for $^{61}$Ni [8] and particularly $^{64}$Ni [128] (Figs. 5b, f), to only the average trend for $^{62}$Ni (Fig. 5d).

The model analysis of the data below 10 MeV has the advantage of only low–lying discrete levels population, with no further NLD effects. Thus, there are cross–section uncertainty bands corresponding to either $D_0^{ exp}$ error bars for $^{58,59}$Fe nuclei, or the estimated accuracy of the a-parameter value for $^{61}$Fe, only above the incident energy of 10 MeV. There is a significant uncertainty band for $^{64}$Ni, but due to NLD effects related to the target nucleus. Nevertheless, even taking it into account, the $(n,\alpha )$ calculated cross sections are lower than the data available below $\sim$9 MeV by one order of magnitude.

The $\alpha$–emission PE component has been related to a pre-formation probability $\varphi$ around the value of 0.08, that was provided by the above–mentioned analysis of the $\alpha$-emission angle–integrated spectra of $^{60}$Ni. Actually, we have found that the $\varphi$-values of 0.1, 0.06, and 0.08 correspond to a suitable agreement with the measured data yet available around 14 MeV for $^{61,62,64}$Ni nuclei, respectively. Therefore, we have assumed a common $\varphi$-uncertainty of 0.02 for these heavier nuclei (Figs. 5b, d, f).

A final remark may concern the additional effect of the neutron unchanged OMP [29], which would decrease the calculated cross sections given by the $\alpha$-particle OMP [1]. On the other hand, the calculation results using the OMP [10] are obviously twice than the ones related to the potential [1]. It thus results again that an additional attention should concern the $\alpha$–emission new data at incident energies below 14 MeV.

4 Direct reaction and like–GQR processes

Fig. 6

As Fig. 3d but for $^{58,60,62,64}$Ni target nuclei, and only PE+CN calculated results (dashed curves) using the $\alpha$-particle OMP [1], uncertainty bands (light-gray) related to NLD of residual Fe isotopes, and additionally DR pickup (dash–dotted) and like–GQR (dotted) components, as well as the sum of all contributions (solid)

The pickup contributions to the low–lying levels in $(n,\alpha )$ reactions [4, 141, 142] have also been determined within the DWBA formalism using the code FRESCO [25], the same OMP parameters given above, and the approach outlined in Ref. [2]. However, no measured angular distribution of $\alpha$ particles from pickup processes has been found for the $(n,\alpha )$ reactions on stable Ni isotopes. Thus, we have carried out the pickup $(n,\alpha )$ cross-sections calculations on the ground of the spectator proton–pair [143] spectroscopic factor given by Glendenning (Table II of Ref. [144]). Then, the spectroscopic factors for the picked neutron, that becomes thus responsible for the angular-momentum transfer, have been obtained by angular–distribution analysis of neutron pickup processes, as $(^3He,\alpha )$, (d, t), and (p, d), populating the same residual nuclei. Obviously, only qualitative conclusions about the importance of the pickup mechanism in $(n,\alpha )$ reactions may be thus obtained. The related references are given in the following for each target nucleus.

$^{58}$Ni$(n,\alpha )^{55}$Fe reaction pickup cross sections have been obtained using the neutron spectroscopic factors reported by Zaman et al. [145] from analysis of $^{56}$Fe$(^3He,\alpha )^{55}$Fe pickup reaction, and Glendenning spectroscopic factor [144] corresponding to the transferred spectator proton pair from $1f_{7/2}$ subshell. A number of 26 excited states with well-known $J^{\pi }$ and transferred orbital angular momentum [17, 19], until 9.115 MeV excitation energy, was considered in this respect.

The corresponding pickup excitation function shown in Fig. 6a is increasing effectively from 4–5 MeV, and has a maximum around the incident energy of 12 MeV. Thus, it brings $\sim$6% in addition to the above–mentioned CN+PE cross sections and the $\alpha$-particle OMP [1] (Fig. 3d). Hence, a good agreement with the measured data above 12 MeV results besides the one already proved below $\sim$5 MeV.

However, there is yet an underestimated $\sim$5% increase of the more recent data [8, 12] around the neutron energy of 8 MeV, where neither the NLD nor PE contributions are present. Because the centroid of the apparent enhancement beyond the DR+PE+CN cross sections coincides with the GQR energy $E_{GQR}$=$65A^{-1/3}$ MeV [146] of 16.70 MeV for $^{59}$Ni excited nucleus, it seems that a decay from giant resonances populated via neutron capture may be assumed again [2]. We have obtained a fit of this extra yield by addition of a Gaussian distribution at $E_{GQR}$, with FWHM width of 3.54 MeV, and peak cross section of 8 mb (Fig. 6a).

$^{60}$Ni$(n,\alpha )^{57}$Fe reaction pickup cross sections could be obtained only using the picked–neutron spectroscopic factors from analysis of $^{58}$Fe$(p,d)^{57}$Fe for 5 excited states until 2.21 MeV excitation energy [17]. Therefore the corresponding pickup component, only around of 1% of the PE+CN sum (Fig. 6c), should be considered only as a lower limit based on actual knowledge.

On the other hand, the DR pickup contribution on low–lying states is confirmed by the comparison of measured and calculated $\alpha$–emission spectra in Fig. 4d. This analysis provides a support also for the pre-formation probability $\varphi$-value of 0.08. One may also note, concerning an underestimation of the spectrum low-energy side, the question marks pointed out by Fischer et al. [124] at $\alpha$–particle energies below $\sim$6 MeV.

Thus, the only available lower limit of the DR pickup contribution may account for the calculated $(n,\alpha )$ cross sections being smaller but yet within the measured–data errors, around the neutron energy of 14 MeV. Moreover, concerning the obvious underestimation in the energy range between 6–12 MeV, the uncertainty bands related to residual–nucleus NLD and PE parameters have already shown that none of these effects are present. A fit of the extra yield by addition of a Gaussian distribution at $E_{GQR}$ energy of 16.51 MeV, with FWHM width of 4.37 MeV, and peak cross section of 8 mb (Fig. 6a) has also provided finally a suitable agreement with most recent data [7, 8].

Fig. 7

As Fig. 6 but for $^{61}$Ni target nucleus and like-GQR, PE, and CN contributions (solid)

$^{61}$Ni$(n,\alpha )^{58}$Fe reaction pickup cross sections could not be obtained due to missing of any angular–distribution and spectroscopic data to be used in this respect. However, we may consider the already proved minor pickup contribution to $(n,\alpha )$ reaction on $^{58}$Ni as well as suitable PE+CN description of the available data around the neutron energies of 10 and 15 MeV (Fig. 7). Therefore, we have focused on significant underestimation several times the error bars of the newest data around 5 MeV [8]. We found again that this can be removed by addition of a Gaussian distribution at $E_{GQR}$ energy of 16.42 MeV, with FWHM width of 4.47 MeV, and peak cross section of 3 mb (Fig. 7). A little bit better agreement with an earlier data measured around 10 MeV [31] has also been obtained.

$^{62}$Ni$(n,\alpha )^{57}$Fe reaction DR assessment faced the same missing of any neutron hole–state spectroscopic data corresponding to $(n,\alpha )$, (p, d), (d, t), or $(^3He,\alpha )$ pickup reactions. However, a qualitative estimation of the related pickup $(n,\alpha )$ cross sections was possible by the groundless use of particle–state spectroscopic factors obtained from the stripping $^{58}$Fe$(d,p)^{59}$Fe reaction analysis [147], and Glendenning spectroscopic factor [144] for the transferred spectator proton pair from $1f_{7/2}$ subshell. This approach was involved for 16 excited states until 2.856 MeV excitation energy [17]. The consequently obtained pickup cross sections have been yet bellow the PE+CN contributions by more than one order of magnitude (Fig. 6b). Unfortunately, less confident data even around the neutron energy of 14 MeV [31] make difficult a certain evaluation of this excitation function.

A definite feature of these calculated cross sections is the much smaller results at the lowest incident energies. The corresponding measured cross sections can be described however by addition of a Gaussian distribution at $E_{GQR}$ energy of 16.34 MeV, with FWHM width of 4.37 MeV and a peak cross section of 0.8 mb. Actually, while the FWHM width is the same as for $^{61}$Ni, the peak cross section has been considered following the subsequent similar analysis for $^{64}$Ni. At the same time, one may note for this nucleus, as well as for $^{58}$Ni, the rather similar like-GDR and pickup cross–section maximum values at the specific energies.

$^{64}$Ni$(n,\alpha )^{59}$Fe reaction DR assessment encounters the same problem of no neutron hole–state spectroscopic data corresponding to pickup reactions. Thus, the qualitative estimation of the pickup $(n,\alpha )$ cross sections was obtained using particle–state spectroscopic factors obtained from the stripping $^2$H$(^{60}Fe,p)^{61}$Fe reaction analysis [148], and Glendenning spectroscopic factor [144] for the transferred spectator proton pair from $1f_{7/2}$ subshell. Only 4 excited states until 0.862 MeV excitation energy [17] have been involved in this respect, so that we may consider again the present results as a lower limit of the corresponding pickup cross sections.

Despite the order of magnitude between the PE+CN and DR pickup contributions, a slightly improved agreement is yet provided with the more consistent data around the neutron energy of 14 MeV (Fig. 6d). On the other hand, an underestimation even larger than an order of magnitude there is for a data set at the lowest energies. Nevertheless, these data have been well described by a Gaussian distribution at $E_{GQR}$ energy of 16.17 MeV of the excited $^{65}$Ni nucleus, with a FWHM width of 4.37 MeV, and a peak cross section of 0.8 mb. It should be underlined the similar like-GQR cross sections for $^{62,64}$Ni nuclei while the same related width works well also for $^{61}$Ni and is quite close to that of $^{58,60}$Ni nuclei. Their sound evidence for $^{64}$Ni is obviously due to the isotopic effect triggered by reaction Q-values, i.e. the CN cross–section decrease with the isotope mass increase [127].

5 Conclusions

The former validation of an optical potential established previously [1] and then checked [23, 24] by analysis of $\alpha$-particle elastic–scattering and induced reactions, as well as finally also for $\alpha$-emission in reactions induced by nucleons on $A$ $\sim$60 nuclei [2], is confirmed for neutron–induced $\alpha$-emission on $^{58,60,61,62,64}$Ni nuclei, too. The same consistent set of formerly–endorsed input parameters has been used, with increased consideration given to questionable low-lying level scheme of residual Fe nuclei, and additional analysis for OMPs of neutrons on Ni stable isotopes as well as of protons on Co. Concurrently, an earlier but distinct $\alpha$-particle OMP [10] is proved again [9] not suitable for $(n,\alpha )$ reaction analysis for Ni isotopes, despite its setting particularly for $\alpha$-emission account but for incident energies up to $\sim$10 MeV.

At the same time, the consistent parameter set has been additionally supported by similar consideration of all competing reaction channels and their available data. Moreover, sensitivity of calculated $\alpha$-emission cross sections to main parameters of other reaction channels has also been concerned in order to point out finally the incident energies where the $\alpha$-particle potential has the primary role for data accounting (eventually at the level of the nucleon–emission data). The advantage of rather recent data at quite low neutron energies has been essential. On the other hand, is has been shown that further accurate data of average s-wave nucleon–resonance spacings are needed for an increased accuracy of calculated cross sections.

The suitable account of additional reaction channels in order to increase the $\alpha$-emission cross sections beyond the statistical predictions [2], has again been proved essential. However, the assessment of $(n,\alpha )$ pickup cross sections has been possible even for the most investigated nucleus $^{58}$Ni only by using neutron hole–state spectroscopic data corresponding to $(^3He,\alpha )$ pickup reactions. Actually just a qualitative estimation has been possible using similar data available for much fewer excited states, as for $^{60}$Ni, or absent and having to be replaced by particle–state spectroscopic factors obtained from the stripping (d, p) reaction analysis for $^{62,64}$Ni target nuclei. Thus, only $\sim$6% DR pickup contributions have now been found, as for Fe nuclei, and at variance with the four times higher ones for protons incident on $^{64}$Ni [2].

Nevertheless, a comparable contribution at the GQR energies of Ni excited nuclei has been needed for a suitable account of the measured $\alpha$-emission cross sections at these energies. This issue is proved particularly for $^{64}$Ni target nucleus due to the isotopic effect of the $(n,\alpha )$ reaction cross sections [127]. On the other hand, because the corresponding Gaussian distributions added in this respect have widths which are rather lower than the systematic ’best’ values [146], we still may call these components only like–GQR components. More similar analyses may enlighten also the understanding of these particular processes.