1 Introduction

There is growing interest in the study of nuclear processes and phenomena including hyperons, as these have important influences on the properties of finite nuclei and infinite nuclear matter [1,2,3,4]. The development of an ab initio formalism to study hypernuclear physics is an important step along this direction. The auxiliary-field quantum Monte Carlo (AFQMC) method is particularly well-suited to study the properties of finite nuclei and nuclear matter. This holds in particular for Wigner’s SU(4) symmetry [5] where the interaction is independent of spin and isospin. Then, the AFQMC method becomes very powerful as it is free of the fermion sign problem [6, 7]. However, when hyperons are included in AFQMC simulations, the sign problem resurfaces since there is no longer an approximate symmetry for the interactions [8]. Therefore, hypernuclear physics requires an alternative approach such as the so-called the impurity lattice Monte Carlo (ILMC) method, which is the subject of this paper.

ILMC is a “hybrid” algorithm, in the sense that it combines AFQMC with worldline MC simulations, and provides a powerful means to study non-relativistic, strongly coupled systems, such as polarons in various dimensions, or hypernuclei. The basic assumption is that the minority species of impurities, such as hyperons in a nucleus, is treated differently than the majority species of particles, which are filling the background in a medium. In the case of hypernuclei, the majority particles are nucleons. The ILMC method has been introduced in Ref. [9] in the context of a Hamiltonian theory of spin-up and spin-down fermions, and applied to the intrinsically non-perturbative physics of Fermi polarons in two dimensions in Ref. [10].

The ILMC method has proven to be successful for the case in which only one fermion (of a given species) is immersed in a sea of particles from one or more other species. ILMC leads to a formalism in which only the majority species fermions appear as explicit degrees of freedom, while the minority fermion is represented by a worldline in Euclidean projection time. The spatial position of this worldline is updated using Metropolis moves, while the interactions between the majority fermions are described by auxiliary fields. The efficient performance of ILMC was explicitly demonstrated in Ref. [10] for a calculation with 10 spin-up fermions (the sea of majority particles) and one spin-down impurity. The first application of ILMC to the inclusion of hyperons into Nuclear Lattice Effective Field Theory (NLEFT) simulations [11, 12, 20] was performed in Ref. [13]. In that work, the \(\Lambda \) hyperon was considered as the minority species and represented by a worldline in Euclidean time. This \(\Lambda \) worldline was then immersed in a medium consisting of an arbitrary number of nucleons N. With simple spin- and isospin-independent hyperon-nucleon and nucleon-nucleon interactions, the binding energies of the hypertriton, \(^4_\Lambda \)H/He, and \(^5_\Lambda \)He were calculated, leading to a qualitative agreement with experiment. Most importantly, the computational effort for ILMC was found to scale approximately linearly with the number of nucleons. This paves the way for the calculation of light, medium-mass and heavy hypernuclei.

Here, we extend ILMC to the case of two interacting, distinguishable impurities represented by worldlines. Besides applications in atomic physics, this extension is necessary if one wants to consider double-\(\Lambda \) hypernuclei within NLEFT, see [14, 15] for recent reviews. In this work, we consider two distinguishable impurities immersed in a sea of polarized fermions of the same species. For convenience of notation, we refer to the two impurities as spin-up fermions (\(\uparrow _a\) and \(\uparrow _b\)), while the majority background particles will be labeled as spin-down fermions, \(\downarrow \).

For simplicity, we take the masses of all particles to be the same. We take the interactions between each impurity and the background particles to be a zero-range attractive interaction with the same strength for \(\uparrow _a+\downarrow \) and \(\uparrow _b+\downarrow \). We take the impurity–impurity interaction \(\uparrow _a+\uparrow _b\) to also have zero range, but we consider both the attractive and repulsive cases. Our aim is to calculate the binding energies of these N-body systems and draw some conclusions for the fate of double-\(\Lambda \) hypernuclei from such a simplified scenario.

This paper is organized as follows: In Sect. 2, we present the Hamiltonian used for this study. In Sect. 3, we extend the impurity worldline formalism to the case of two impurities, and focus mostly on the differences to the one-worldline case developed and described in Ref. [9]. In Sect. 4, we present our results for the binding energies of the systems made from two impurities and an arbitrary number of background particles. In Sect. 5, we conclude by a discussion of future directions and applications of the impurity Monte Carlo method to the problem of hypernuclei in NLEFT. In the Appendix, we benchmark our approach by calculating the triton binding energy for an interaction that is independent of spin and isospin.

2 Lattice Hamiltonian

We consider systems of two distinguishable impurity particles labeled a and b, interacting with a background sea of indistinguishable spin-down fermions. For simplicity, we assume that impurities and spin-down fermions have equal mass m. A lattice Hamiltonian can then be constructed in the following way. We start with the non-relativistic Hamiltonian of the free theory,

$$\begin{aligned} {\hat{H}}_0 = \frac{1}{2m}\sum _{s=\uparrow _a,\uparrow _b,\downarrow }\int \,{\mathrm{d}}^{3}{\varvec{r}} \varvec{\nabla } a_s^\dagger \left( \varvec{r}\right) \varvec{\nabla }a_s^{}\left( \varvec{r}\right) , \end{aligned}$$
(1)

in which \(a_s\) and \(a_s^\dagger \) represent annihilation and creation operators, and \(i \in {\mathbb {N}}\) is the labeling index for the background particles. The zero-range interaction between the impurities and background particles is controlled by the coupling constant \(C_{IB}\). This corresponds to the low-energy limit of a theory in which the scattering length \(a_{\text {scatt}}\) is large compared to the effective range \(r_{\text {eff}}\). In a similar fashion, we introduce a contact interaction between the two impurities \(C_{II}\). The interaction Hamiltonian is given by

$$\begin{aligned} {\hat{H}}_I = \,&C_{II}\int \,{\mathrm{d}}^{3}{\varvec{r}}{\hat{\rho }}_{\uparrow _b}\left( \varvec{r}\right) {\hat{\rho }}_{\uparrow _a} \left( \varvec{r}\right) \nonumber \\&+ C_{IB}\int \,{\mathrm{d}}^{3}{\varvec{r}}\, \bigg [ {\hat{\rho }}_{\uparrow _a}\left( \varvec{r}\right) {\hat{\rho }}_{\downarrow }\left( \varvec{r}\right) +{\hat{\rho }}_{\uparrow _b}\left( \varvec{r}\right) {\hat{\rho }}_{\downarrow } \left( \varvec{r}\right) \bigg ], \end{aligned}$$
(2)

where \({\hat{\rho }}_{s}\left( \varvec{r}\right) \) are density operators given by

$$\begin{aligned} {\hat{\rho }}_{s}\left( \varvec{r}\right) = a_s^\dagger \left( \varvec{r}\right) a_s^{}\left( \varvec{r}\right) . \end{aligned}$$
(3)

As in all lattice calculations, the ultraviolet physics of the zero-range interactions are regulated by the lattice spacing. We denote the spatial lattice spacing by a, and the temporal lattice spacing (due to the Trotter decomposition of the Euclidean time evolution) by \(a_t\). We express all physical quantities in lattice units by multiplying them with corresponding powers of a, so as to form dimensionless combinations. We also define the lattice spacing ratio \(\alpha = a_t/a\). The free lattice Hamiltonian is

$$\begin{aligned} {\hat{H}}_0={\hat{H}}_0^{\uparrow _a}+{\hat{H}}_0^{\uparrow _b}+{\hat{H}}_0^{\downarrow }, \end{aligned}$$
(4)

with

$$\begin{aligned} H_0^s = \,&\frac{1}{2m}\sum _{\varvec{n}}\sum _{i=1}^3a^\dagger _s\left( \varvec{n}\right) \nonumber \\&\times \left[ 2a_s\left( \varvec{n}\right) -a_s\left( \varvec{n}+{\hat{l}}_i\right) -a_s\left( \varvec{n}-{\hat{l}}_i\right) \right] , \end{aligned}$$
(5)

where the \({\hat{l}}_i, i\in {1,2,3}\) are unit vectors in the spatial dimensions. We express the various lattice interaction terms in a compact form, as

$$\begin{aligned} H_{s's} = C_{s's}\sum _{\varvec{n}}{\hat{\rho }}_{s'}\left( \varvec{n}\right) {\hat{\rho }}_{s}\left( \varvec{n}\right) , \end{aligned}$$
(6)

where the couplings \(C_{s's}\) can be tuned in such a way as to either produce specific dimer binding energies, or scattering lengths via Lüscher’s formula [16,17,18].

3 Impurity lattice Monte Carlo: extension to two impurities

The ILMC method for a single impurity has already been treated in the literature [9, 10, 13]. We now extend the formalism to systems with two impurities. As in the single impurity case, the goal is to integrate out all impurities from the lattice action and to reduce the explicit degrees of freedom in the Monte Carlo simulation. We also derive the transfer matrix formalism for two impurities in a sea of an arbitrary number of spin-down particles. This can be achieved using the exact correspondence between the Grassmann path integral and the normal-ordered transfer matrix formalisms [12].

We define our system in a three-dimensional periodic cubic box of length L in the spatial directions and \(L_{t}\) in the temporal direction. We denote anti-commuting Grassmann variables by \(\theta ^{\,}_{s}\) and \(\theta ^{*}_{s}\) and choose the Grassmann variables to be periodic in the spatial directions and anti-periodic in the temporal direction. The path integral formula for the Grassmann variables is

$$\begin{aligned} {\mathcal {Z}} = \int \left[ \prod _{\begin{array}{c} n_{t}, \varvec{n} \\ s = {\uparrow _a},{\uparrow _b},\downarrow \end{array}} d\theta ^{\,}_{s}\left( n_{t},\varvec{n}\right) d\theta ^{*}_{s}\left( n_{t},\varvec{n}\right) \right] e^{-S\left[ \theta ,\theta ^*\right] }, \end{aligned}$$
(7)

where \(S\left[ \theta ,\theta ^*\right] \) is the lattice action in terms of the Grassmann variables, given by

$$\begin{aligned} S\left[ \theta ,\theta ^*\right] =&\sum _{n_{t}}\bigg \{ S_{t}\left[ \theta ,\theta ^*,n_{t}\right] + S_{H_0}\left[ \theta ,\theta ^*,n_{t}\right] \nonumber \\&+ S_{H_{SI}}\left[ \theta ,\theta ^*,n_{t}\right] + S_{H_{II}}\left[ \theta ,\theta ^*,n_{t}\right] \bigg \}, \end{aligned}$$
(8)

with

$$\begin{aligned} S_{t}\left[ \theta ,\theta ^*,n_{t}\right] =&\!\! \sum _{s = {\uparrow _a},{\uparrow _b},\downarrow } \sum _{\varvec{n}} \left[ \theta ^{*}_{s}{\left( n_{t}+{\hat{0}},\varvec{n}\right) } -\theta ^{*}_s\left( n_t,\varvec{n}\right) \right] \nonumber \\&\times \theta ^{\,}_s\left( n_t,\varvec{n}\right) \,, \end{aligned}$$
(9)

and

$$\begin{aligned}&S_{H_0} \left[ \theta ,\theta ^*,n_{t}\right] = W_h \!\! \sum _{s = {\uparrow _a},{\uparrow _b},\downarrow } \sum _{\varvec{n}}\sum _{i=1}^3\theta ^*_s{\left( n_{t},\varvec{n}\right) } \nonumber \\&\quad \times \bigg [2\theta ^{\,}_{s}{\left( n_{t},\varvec{n}\right) } -\theta ^{\,}_s\left( n_t,\varvec{n}+{\hat{l}}_i\right) -\theta ^{\,}_s\left( n_t,\varvec{n}-{\hat{l}}_i\right) \bigg ], \end{aligned}$$
(10)

where \(W_h\) is given by Eq. (21). For the interaction terms, we find

$$\begin{aligned} S_{H_{SI}}\left[ \theta ,\theta ^*,n_{t}\right] =&\, \alpha \, C_{IB} \sum _{\varvec{n}} \sum _{s = \uparrow _a,\uparrow _b} \theta ^*_s{\left( n_{t},\varvec{n}\right) } \theta ^{\,}_s{\left( n_{t},\varvec{n}\right) } \nonumber \\&\times \theta ^*_{\downarrow }{\left( n_{t},\varvec{n}\right) } \theta ^{\,}_{\downarrow }{\left( n_{t},\varvec{n}\right) }, \end{aligned}$$
(11)

and

$$\begin{aligned} S_{H_{II}}\left[ \theta ,\theta ^*,n_{t}\right] =&\, \alpha \, C_{II} \sum _{\varvec{n}} \theta ^*_{\uparrow _a}{\left( n_{t},\varvec{n}\right) } \theta ^{\,}_{\uparrow _a}{\left( n_{t},\varvec{n}\right) } \nonumber \\&\times \theta ^*_{\uparrow _b}{\left( n_{t},\varvec{n}\right) } \theta ^{\,}_{\uparrow _b}{\left( n_{t},\varvec{n}\right) }. \end{aligned}$$
(12)

While Eq. (7) is convenient for deriving lattice Feynman rules, the transfer matrix operator formalism is more amenable to lattice MC simulations. For a detailed derivation of the exact relation between the Grassmann path integral formula and the normal-ordered transfer matrix formalism, we refer the reader to Refs. [11, 12]. We can write the amplitude \({\mathcal {Z}}\) as

$$\begin{aligned} {\mathcal {Z}} = \hbox {tr} \, {\hat{M}}^{L_{t}} \,, \end{aligned}$$
(13)

where \({\hat{M}}\) is the normal-ordered transfer matrix.

We start from the occupation number basis [9]. With \(\chi ^s_{n_t}\left( \varvec{n}\right) \) counting the occupation number on each lattice site for any particle species, we can write any configuration as

$$\begin{aligned}&\left| \chi _{n_{t}}^\downarrow ,\chi _{n_{t}}^{\uparrow _a},\chi _{n_{t}}^{\uparrow _b}\right\rangle \nonumber \\&\quad =\prod _{\varvec{n}}\left[ a_\downarrow ^\dagger \left( \varvec{n}\right) \right] ^{\chi _{n_t}^\downarrow \left( \varvec{n}\right) }\left[ a_{\uparrow _a}^\dagger \left( \varvec{n}\right) \right] ^{\chi _{n_t}^{\uparrow _a} \left( \varvec{n}\right) }\left[ a_{\uparrow _b}^\dagger \left( \varvec{n}\right) \right] ^{\chi _{n_t}^{\uparrow _b}\left( \varvec{n}\right) }\!\left| 0\right\rangle . \end{aligned}$$
(14)

Without loss of generality, we can take all of the particles to be fermions, including the two distinguishable impurities. Thus the occupation numbers can assume the values 0 or 1. We shall use this property to determine the transfer matrix elements between two successive time steps \(n_t\) and \(n_{t+1}\) from the lattice Grassmann functions,

$$\begin{aligned}&\left\langle \chi _{n_{t+1}}^{\downarrow },\chi _{n_{t+1}}^{\uparrow _a}, \chi _{n_{t+1}}^{\uparrow _b}\right| { \, {\hat{M}}\, } \left| \chi _{n_{t}}^{\downarrow },\chi _{n_{t}}^{\uparrow _a},\chi _{n_{t}}^{\uparrow _b}\right\rangle \nonumber \\&\quad =\prod _{\varvec{n}}\left( \left[ \frac{\overrightarrow{\partial }}{\partial \theta _{\uparrow _b}^*{\left( n_{t},\varvec{n}\right) }}\right] ^{\chi _{n_{t+1}}^{\uparrow _b}\left( \varvec{n}\right) } \left[ \frac{\overrightarrow{\partial }}{\partial \theta _{\uparrow _a}^*{\left( n_{t},\varvec{n}\right) }}\right] ^{\chi _{n_{t+1}}^{\uparrow _a}\left( \varvec{n}\right) }\right. \nonumber \\&\qquad \left. \times \left[ {\frac{\overrightarrow{\partial }}{\partial \theta _\downarrow ^*{\left( n_{t},\varvec{n}\right) }}}\right] ^{\chi _{n_{t+1}}^{\downarrow }\left( \varvec{n}\right) }\right) \times X\left( \varvec{n}\right) M\left( n_t\right) \nonumber \\&\qquad \times \prod _{\varvec{n}'}\left( \left[ \frac{\overleftarrow{\partial }}{\partial \theta _{\downarrow }{\left( n_{t},\varvec{n}'\right) }}\right] ^{\chi _{n_{t}}^{\downarrow }\left( \varvec{n}'\right) }\left[ {\frac{\overleftarrow{\partial }}{\partial \theta _{\uparrow _a}{\left( n_{t},\varvec{n}'\right) }}}\right] ^{\chi _{n_{t}}^{\uparrow _a}\left( \varvec{n'}\right) }\right. \nonumber \\&\qquad \left. \left. \times \left[ {\frac{\overleftarrow{\partial }}{\partial \theta _{\uparrow _b}{\left( n_{t},\varvec{n}'\right) }}}\right] ^{\chi _{n_{t}}^{\uparrow _b}\left( \varvec{n}'\right) }\right) \right| _{\begin{array}{l} \theta _\downarrow =\theta _{\uparrow _a}=\theta _{\uparrow _b}=0 \\ \theta ^*_\downarrow =\theta ^*_{\uparrow _a}=\theta ^*_{\uparrow _b}=0 \\ \end{array}} \,, \end{aligned}$$
(15)

where the  :  :  represent the normal ordering of operators. Here, \(X\left( \varvec{n}\right) \) and \(M\left( n_t\right) \) are the Grassmann functions

$$\begin{aligned} X\left( \varvec{n}\right) =&\prod _{\varvec{n}} e^{\theta ^*_\downarrow \left[ n_t,\varvec{n}\right] \theta _\downarrow \left[ n_t,\varvec{n}\right] } e^{\theta ^*_{\uparrow _a}\left[ n_t,\varvec{n}\right] \theta _{\uparrow _a}\left[ n_t,\varvec{n}\right] }\nonumber \\&\times e^{\theta ^*_{\uparrow _b}\left[ n_t,\varvec{n}\right] \theta _{\uparrow _b}\left[ n_t,\varvec{n}\right] }, \end{aligned}$$
(16)

and

$$\begin{aligned} M\left( n_t\right) = \exp \left( -S_{H_0}\right) \exp \left( -S_{H_{SI}}\right) \exp \left( -S_{H_{II}}\right) . \end{aligned}$$
(17)

The above matrix elements of the transfer matrix operator are non-zero only if

$$\begin{aligned} \sum _{\varvec{n}}\chi _{n_{t}}^{\uparrow _a}(\varvec{n}) = \sum _{\varvec{n}} \chi _{n_{t+1}}^{\uparrow _a}(\varvec{n}) = 1, \end{aligned}$$
(18)

and

$$\begin{aligned} \sum _{\varvec{n}}\chi _{n_{t}}^{\uparrow _b}(\varvec{n}) = \sum _{\varvec{n}} \chi _{n_{t+1}}^{\uparrow _b}(\varvec{n}) = 1. \end{aligned}$$
(19)

We now treat the impurities as fixed worldlines and integrate them out from the lattice action. This leads to the “reduced” transfer matrix given in Eq. (20), which is acting on the wave functions of the majority particles only,

(20)

where

We consider the reduced transfer matrix between two successive Euclidean time steps \(n_t\) and \(n_{t+1}\), and this corresponds to three different cases.

The first case is when both impurities hop from lattice sites \((\varvec{n},\varvec{n}')\) to nearest neighbor sites \((\varvec{n}\pm {\hat{l}},\varvec{n}'\pm {\hat{l}}')\). The amplitude for one worldline to hop to a neighboring lattice site is

$$\begin{aligned} W_h=\frac{\alpha }{2m}, \end{aligned}$$
(21)

while the amplitude to stay on the same lattice site is given by

$$\begin{aligned} W_s=1-6W_h. \end{aligned}$$
(22)

When this is applied to Eq. (20), the reduced transfer matrix reads

(23)

where the upper set of indices of refers to the new and old position of worldline a while the lower set of indices refers to the positions of worldline b.

The second case results when one of the impurities (either worldline a or worldline b) hops to some nearest neighbor site while the other one remains stationary. The corresponding transfer matrix elements for \((\varvec{n},\varvec{n}') \rightarrow (\varvec{n},\varvec{n}'\pm {\hat{l}}')\) and \((\varvec{n},\varvec{n}') \rightarrow (\varvec{n}\pm {\hat{l}},\varvec{n})\) are equivalent,

(24)

We can then write

(25)

From this result, we find that only the worldline that does not hop between time steps \(n_t\) and \(n_{t+1}\) can interact with the background particles.

The third and last case is where both worldlines remain stationary between time steps \(n_t\) and \(n_{t+1}\), \((\varvec{n},\varvec{n}') \rightarrow (\varvec{n},\varvec{n}')\), and the reduced transfer matrix is

(26)

As can be seen from Eq. (26), the stationary worldlines do interact with the background particles. If the worldlines are occupying the same spatial lattice site between time steps \(n_t\) and \(n_{t+1}\), then they can also can interact with each other. Therefore, by considering all possible configurations of the worldlines, we obtain the reduced transfer matrix elements to be used in our MC calculations. In Eqs. (23–26) all expressions multiplied with \(e^{-\alpha H_0^\downarrow }\) can be viewed as local auxiliary fields felt by the background particles.

Fig. 1
figure 1

Illustration of a representative worldline configuration. When the two worldlines (solid and dashed) stay at the same lattice site for one Euclidean time step, they interact with the interaction strength \(C_{II}\)

Full size image

From the scenarios discussed above, we obtain the reduced transfer matrix operators

(27)
(28)
(29)

These operators are only acting on the spin-down background particles. One example configuration for two worldlines is depicted in Fig. 1. In comparison with the one impurity case, the evaluation of Eq. (20) gives rise to an additional term associated with the impurity–impurity interaction term \(C_{II}\). In order to illustrate this behaviour we consider the case where both worldlines stay on the same lattice side (\(\varvec{n}=\varvec{n}'\)). After expanding the exponentials, the expression for the matrix element reads

(30)

In contrast to the one-impurity case, the term proportional to \(C_{II}\) is an interacting term that is not proportional to the background field \(\theta _\downarrow \). It can be therefore combined with fields coming from \(H_0^\downarrow \) or . This leads to a contribution of the form

$$\begin{aligned} \begin{aligned}&\left\langle \chi _{n_{t+1}}^{\downarrow },\chi _{n_{t+1}}^{\uparrow _a},\chi _{n_{t+1}}^{\uparrow _b}\right| { {\hat{M}} } \left| \chi _{n_{t}}^{\downarrow },\chi _{n_{t}}^{\uparrow _a},\chi _{n_{t}}^{\uparrow _b}\right\rangle \\&\quad = W_s^2\left( W_s-\alpha \frac{C_{II}}{W_s}-2\alpha \frac{C_{IB}}{W_s}\right) . \end{aligned} \end{aligned}$$
(31)

4 Results

In our numerical ILMC calculations, we set the spatial lattice spacing to \(1/a = 100\) MeV, and the temporal lattice spacing to \(1/a_t = 300\) MeV, and thus \(\alpha = a_t/a = 1/3\). We use a periodic cubic lattice with length \(L = 10\) (in units of a). We use the average nucleon mass \(m=938.92\) MeV for the mass of the fermions. The impurity–background interaction \(C_{IB}\) is taken to be attractive and tuned to give a natural-sized scattering length, in this case 3 fm. This is comparable to the hyperon-nucleon interaction scattering length, see e.g. the recent chiral EFT work in Ref. [19]. As a check and benchmark of our formalism, we also calculate the triton binding energy for a Wigner SU(4) symmetric interaction adopting the AFMC code used in Ref. [6]. For further details, see the Appendix.

4.1 Repulsive impurity–impurity interaction

We first consider the case where impurity–impurity interaction is repulsive and vary the interaction strength \(C_{II}\) to investigate the formation or disintegration of N-body bound states for \(N=3,4,6,8\). In Fig. 2, we show the ILMC results for a periodic box with length \(L = 10\) lattice units. The dashed lines in Fig. 2 represent the one- and two-dimer thresholds at infinite volume.

We note that the \(N=3\) ground state lies below the one-dimer threshold even for very repulsive \(C_{II}\), suggesting that the trimer bound state remains bound even for strongly repulsive impurity–impurity interactions. Meanwhile, the \(N=4\) ground state quickly moves to a position slightly above the two-dimer threshold for repulsive \(C_{II}\), indicating that the ground state of the four-body system consists of two dimers. A finite-volume analysis of the offset relative to the two-dimer threshold would extract the properties of the dimer-dimer interaction.

Such re-configuration of the two impurity particles is rather interesting. The two impurities are bound together into a trimer when there is only one background particle. But when there are two background particles, the two impurities prefer to separate and form two dimers. For \(N=6\) and \(N=8\) we find that the extra background fermions do not provide additional binding energy. Instead, they are filling the Fermi sea of our periodic box.

Fig. 2
figure 2

Energy for \(N_{BG}=1,2,4\) and 6 background particles. The dotted lines are extrapolations to infinite repulsion, while the dashed lines represent the one- and two-dimer thresholds

Full size image

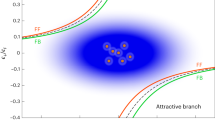
4.2 Attractive impurity–impurity interaction

In similar fashion as in the repulsive case, we perform an analysis for the attractive impurity–impurity interaction. We vary the coupling constant \(C_{II}\) in order to study the appearance of N-body states for \(N=3,4,6,8\). The ILMC results are shown in Fig. 3. We see that the \(N=4\) ground state energy drops below the \(N=3\) ground state at around \(C_{II}\approx 0.02\). In fact, \(C_{II}\approx 0.02\) is also where the \(N=6\) ground state drops below the \(N=4\) ground state and where the \(N=8\) ground state drops below the \(N=6\) ground state. This crossing of several energy levels at the same point is reminiscent of a quantum phase transition. In this case, however, we are considering a finite system with relatively few particles. This rich phase structure will be explored in a future publication. We note another recent study that considered the properties of two heavy impurities in a Fermi bath which also found similar bound states [21].

While the system we study here does not directly correspond to double \(\Lambda \) hypernuclei, there are some interesting parallels worth noting. The attractive \(\Lambda \Lambda \) interaction is not strong enough to to produce a \(\Lambda \Lambda \) bound state, see e.g. Ref. [14]. However, the attraction is sufficient to help in the binding of hypernuclei.

Fig. 3
figure 3

Energy for attractive impurity impurity interaction for different numbers of background particles \(N_{BG}=1,2,4\) and 6

Full size image

5 Discussion

We have shown, as a proof of principle, that a two-impurity Monte Carlo approach is suitable to describe systems with more than one impurity, immersed in a sea of majority particles. While the majority particles have no direct interactions with each other, an effective interaction is mediated by interactions with the impurities. Such a mediated interaction through impurities was extracted for a slightly different scenario in one dimension in Ref. [22]. Moreover, we have observed the expected disappearance of complex bound states into dimers, for a sufficiently strong and repulsive impurity–impurity interaction. For an attractive impurity–impurity interaction, we have observed the expected formation of bound states when we increase the interaction strength, which we expect to give rise to a rich and complex phase diagram.

We recall that the scenario studied here is formulated in terms of an impurity–impurity interaction similar to a hyperon-hyperon interaction, which allows for a straightforward application to \(\Lambda \Lambda \) nuclei. In addition, it would be worthwhile to study the emergence of few-body states in the context of ultra-cold gases, as particle mixtures could be treated as impurities. In such a case, the couplings can be tuned such that one is at (or close to) unitarity, in order to map out the universal features of such systems, see e.g. Ref. [23].