Analyzing powers at low nucleon–nucleon relative energies in proton–deuteron breakup reaction

Abstract

Vector analyzing powers for the $d(\vec {p},pp)n$ reaction have been measured at KVI for different kinematical configurations using a polarized proton beam with an energy of 190 MeV. We compared our data with different theoretical calculations at extremely low relative energies of the proton–proton and proton–neutron systems in the final state. For the proton–neutron case, we used the information of the two detected protons in the final state in which one of them scattered to an angle smaller than $40^{\circ }$ and the other one to an angle larger than $100^{\circ }$ in the laboratory frame. We extrapolated our measurements towards a kinematical configuration to a vanishing relative energy. Our results show that none of the theoretical models presented here is able to reproduce experimental data for the proton–proton case at very low relative energies. For the proton–neutron case, we were not able to provide a reliable extrapolation to small relative energies of less than 1 MeV. Present results are the basis for future investigations of spin-isospin dependencies in the nuclear many-body force.

1 Introduction

A lot of effort has been made to build a framework for describing the nuclear force since Chadwick discovered the neutron as a building block of atomic nuclei [1]. The first systematic approach for describing the nucleon–nucleon (NN) interaction in analogy to the electromagnetic interaction was proposed in 1935 by Yukawa [2]. The potentials based on Yukawa’s model solely take the nucleons and mesons as degrees of freedom in the nuclei. Based on these degrees of freedom, different NN potentials have been developed in the past decades. They usually carry the name of the group which developed them such as AV18 [3], CD-Bonn [4], etc.. Each of these models has different parameters and they are fitted to the empirical pp and np scattering database. While these models do a great job in describing two-nucleon systems below the pion-production threshold energy, they fail to describe systems which have more than two nucleons. There is lots of evidence for this by comparing data and theory for both the nuclear binding energies [5,6,7] and various scattering observables [8,9,10,11]. It became clear that there are additional underlying dynamics, beyond the NN interaction, playing a role in the nuclear force which are referred to as many-body force effects. We expect that the three-nucleon forces (3NFs) is the leading term in the hierarchy of many-body force effects [12]. In the past decades, several phenomenological 3NF models such as Urbana-Illinois (UIX) [13, 14] and CD-Bonn+$\varDelta$ [15,16,17] have been developed based on the works by Fujita and Miyazawa [18], and Brown and Green [19] to implement 3NFs in the interaction of nucleons. However, different studies have shown that the inclusion of current models of 3NFs do not completely fill the gap between data and calculations. For a detailed discussion of the progress of the field at intermediate energies, see Refs. [20, 21]. Also, a fundamental approach for nucleonic systems known as Chiral Perturbation Theory (ChPT) [22] has been developed based on QCD principles. This approach has been discussed in details in Refs. [12, 23,24,25,26]. Presently, there are no ChPT predictions suitable for comparison with the data shown in this paper. For a proton beam energy of 190 MeV, interaction at orders higher than available today should be included in the calculations before an accurate comparison can be made.

In the past decades, the elastic channel in Nd scattering has been investigated experimentally at different beam energies below the pion-production threshold. The results showed that the current 3NF models are not able to describe the discrepancy between measurements and calculations particularly at higher beam energies and at the minimum of the differential cross section as well as at backward angles [11, 27]. In particular, the spin-related parts of nuclear force reveal deficiencies when comparing the results of theoretical calculations based on modern potentials with measured spin observables. It was shown that 3NFs incorporated within Faddeev calculations fail to describe the analyzing power $A_{y}$ at low energies, an effect known in literature as the $A_{y}$-puzzle [28, 29]. The elastic channel has a limited kinematical phase space and one cannot test all the aspects of the theoretical models. To have a systematic and a detailed investigation of 3NFs, the three-body breakup channel is a suitable candidate because of its rich kinematical phase space yielding various degrees of sensitivity to the underlying nucleon–nucleon and three-nucleon forces.

A systematic investigation of 3NFs through the elastic and the breakup reactions was initiated at KVI in a common effort between the Dutch and the Polish groups since the end of the 90s by developing various experimental setups and exploiting high-quality polarized beams [27, 30,31,32,33,34]. BINA (Big Instrument for Nuclear-polarization Analysis) is the latest experimental setup which was exploited at KVI for few-nucleon scattering experiments. This detection system is capable of measuring the energy and the scattering angles of all the reaction yields of three and four-body final states in coincidence. A series of experiments has been conducted using BINA to study the deuteron breakup channel using polarized proton and deuteron beams in a wide range of energies between 50 and 190 MeV/nucleon [35,36,37,38,39]. Recent analysis of the data taken with BINA provided new insights by investigating different aspects of the nuclear force at different kinematics and reaction channels[40,41,42,43,44].

We present here the results of measurements of the analyzing power $A_{y}$ of the proton–deuteron breakup reaction obtained with a polarized proton–beam with an energy of 190 MeV. In this work, we focus on the breakup kinematics in which the relative energy of the pair of nucleons is close to zero. Therefore, we are able to investigate the state with isospin 1 for the proton–proton case and the states with isospin 0 and 1 for the proton–neutron case. The results of the proton–proton case have been already published and it was shown that there are serious disagreements between data and theoretical predictions [45]. Furthermore, similar disagreements were shown for the proton–proton case using a proton beam with an energy of 135 MeV [46]. Since our detection system BINA has a large angular acceptance, it is possible to extract analyzing powers for many configurations within the breakup phase space. A new aspect and part of this publication is the extraction of analyzing powers of the proton–neutron case at low relative energies. In Sect. 2 the experimental setup will be described. The analysis method is presented in Sect. 3 and the results are shown in Sect. 4 along with a discussion of the results.

2 Experimental setup

The present experiment was conducted utilizing the AGOR (Accélérateur Groningen-ORsay) cyclotron at KVI delivering a high-quality polarized-proton beam with an energy of 190 MeV. The polarized beam was created in the POLarized Ion Source (POLIS) [47] with the beam polarization value, $p_{Z}$, of around $\pm 0.5$–0.7. During and after the acceleration of the beam in AGOR, the quantization axis of the beam polarization (y direction) was perpendicular to the beam momentum, defining the z direction in the laboratory frame. For details about the experimental setup, see Refs. [35, 48]. BINA, is a specially-designed 4$\pi$ detection system with which 3NF effects could be studied through the elastic and the breakup reactions of three- and four-nucleon systems. The detection system consists of different components which make it capable of measuring energies up to 140 MeV per nucleon, scattering angles between $10^{\circ }$ and $160^{\circ }$ in the laboratory system, and almost a full coverage of azimuthal angles. There are two features that make BINA unique among other detection systems in the field of few-nucleon scattering:

• Detection of all the charged particles (and neutrons with lower efficiencies) in the final-state of the three-body and the four-body reactions in coincidence;

• The almost 4$\pi$ angular coverage which can probe a large part of the phase space of the breakup reactions.

In general, BINA has two main parts, the forward-wall and the backward-ball. The left panel of Fig. 1 displays the main components of BINA. The forward-wall consists of a cylindrically-shaped array of 10 scintillators (E-detectors) to measure the energy of charged particles, a MWPC to measure their scattering angles, and a vertical array of $\varDelta E$-detectors that is used in combination with E-detectors for particle identification. The forward-wall covers angles which are in the range of $10^{\circ }<\theta <35^{\circ }$. The backward-ball is a ball-shape scattering chamber which consists of 149 pyramid-shaped plastic scintillators. The geometrical design of the backward-ball and its building blocks are similar to the classic football ball. The position of each backward-ball scintillator is labeled with a specific $\theta$ and $\phi$ in the laboratory coordinate system. The backward-ball can measure the scattering angles of the particles with a precision of about $\pm 10^{\circ }$. The right panels of Fig. 1 demonstrates the structure of the backward-ball and the positioning of the detector elements. This part of BINA is capable of measuring the energy and the scattering angles of the particles in the range of $35^{\circ }<\theta <160^{\circ }$ except where the target holder is attached to the scattering chamber at $80^{\circ }<\theta <120^{\circ }$ and $60^{\circ }<\phi <120^{\circ }$. The analyzing powers $A_{y}$ of the proton–deuteron breakup reaction have been measured for the available kinematics at small, medium, and large scattering angles of the outgoing proton [41, 48]. In the present analysis, we exploited the measured analyzing powers for two regions of the reaction $d(\vec {p},pp)n$ corresponding to small relative energies of $'\text {pp}'$ and $'\text {pn}'$. The $'\text {pp}'$ case refers to the kinematics that two protons are observed in the final state. The $'\text {pn}'$ case refers to the proton–neutron kinematics in which the proton is detected and the neutron information is obtained from a missing momentum reconstruction.

Fig. 1

Figure a shows the structure of BINA together with the angular coverage of each part. The figure b shows the partly assembled backward-ball. The figure c illustrates the angular positions of the detector elements of the backward-ball. The centroid of each detector element is considered as the angular position of that detector; see the black points in figure (c)

3 Analysis method

In the proton–deuteron breakup reaction, there are three particles in the final state, two protons and one neutron. From the kinematics point of view, there are 9 variables $(\theta _{i},\phi _{i}, E_{i})$ for this reaction channel which can be measured. Applying energy and momenta conservation reduces the number of degrees of freedom to 5. It is, therefore, sufficient to measure 5 of the 9 variables to have all the kinematic information of the reaction. BINA is able to measure the energy and the scattering angles of two protons in coincidence which provides an extra redundancy of one degree of freedom. However, we did not use this redundancy in the present analysis. Conventionally, in the three-body breakup reaction, each configuration is defined with $(\theta _{1}, \theta _{2}, \phi _{12}=|\phi _{2}-\phi _{1}|)$ which represents the polar scattering angles of protons 1 and 2 and the relative azimuthal angle between them. Figure 2 shows the definition of the scattering angles of two protons in the p-d breakup reaction. There are two conventions for defining the y-axis [49]. In this paper, we use the asymmetric choice for the azimuthal angles, where $\vec {k}_{1}$ lies in the xz plane, and therefore $\phi _{1}=0$, see Fig. 2. Here, $\vec {k}_{1}$ is the momentum of the outgoing proton which scattered to smaller polar angle $\theta _{1}$. For each kinematical configuration, the energy correlation of the two protons is referred to as the S-curve. By employing the S-curve, a variable S is defined as the arc length of the curve with a starting point at the minimum energy of one of the protons. Here, we used a convention in which the starting point of S is the minimum value of $E_{2}$ and it increases counter-clockwise as shown in the left panel of Fig. 3. Here, $E_{1}$ and $E_{2}$ related to $\vec {k}_{1}$ and $\vec {k}_{2}$, respectively. Traditionally, the three-body breakup observables are presented as a function of the S-value.

Fig. 2

The scattering diagram of a three-body final-state reaction. $\vec {k}$ $_1$ and $\vec {k}_2$ are the momenta of the two detected particles with scattering angels $\theta _{1}$ and $\theta _{2}$, respectively. $\phi _{2}$ is the angle between the projection of $\vec {k}_2$ on the $x-y$ plane and the x-axis. $\hat{s}$ denotes the direction of spin of the projectile. $\phi$ is the angle between the projection of $\hat{s}$ on the $x-y$ plane and the y-axis. $\beta$ is the angle between the spin of the projectile and its momentum direction (z-axis). In the present experiment, the polarization of the beam is perpendicular to the direction of the beam momentum and, therefore $\beta =90^{\circ }$

Fig. 3

The solid line on the left panel shows the kinematically-allowed relation of the energies of the two protons of the three-body breakup reaction, the so-called S-curve, for the indicated configuration along with the experimental data. The protons which have energies $E_{1}>140$ MeV punch through the E-detectors of the forward-wall resulting in a kink in the spectrum. The dashed lines marks a typical S-bin. The right panel shows the reconstructed missing-mass of the neutron for the indicated S-bin. The peak position is around the expected missing-mass of the neutron. The interval of $\pm 3\sigma$ was used to obtain the number of breakup events under the peak after subtracting the background. The blue line shows the total missing-mass spectrum. The red line represents the estimated background. The green histogram shows the missing-mass spectrum after background subtraction. The vertical black dashed lines illustrate the integration window of $\pm 3\sigma$ wide

To investigate spin effects in the nuclear force, one measures various spin-related observables such as analyzing powers. The polarized beam (or target) imposes an asymmetry on the cross section of the breakup reaction. In this article, we present a study of the vector analyzing power $A_{y}$ in the proton–deuteron breakup reaction. $A_{x}$ is odd and $A_{y}$ is even under the parity inversion. Here, the parity inversion corresponds to changing the sign of the azimuthal scattering angle of the two outgoing protons. By exploiting the formulation taken from Ref. [49] for spin-$\frac{1}{2}$ protons, the following expressions can be derived for the two parity modes:

$$\begin{aligned} \varUpsilon ^{+}(\xi ,\phi )= & {} \frac{N_{p}^{\uparrow }-N_{p}^{\downarrow }}{N_{p}^{\downarrow }p_{Z}^{\uparrow }-N_{p}^{\uparrow }p_{Z}^{\downarrow }}= A_{y}(\xi )\cos \phi -A_{x}(\xi )\sin \phi ,\nonumber \\ \end{aligned}$$

(1)

$$\begin{aligned} \varUpsilon ^{-}(\xi ,\phi )= & {} \frac{N_{m}^{\uparrow }-N_{m}^{\downarrow }}{N_{m}^{\downarrow }p_{Z}^{\uparrow }-N_{m}^{\uparrow }p_{Z}^{\downarrow }}= A_{y}(\xi )\cos \phi +A_{x}(\xi )\sin \phi ,\nonumber \\ \end{aligned}$$

(2)

where $\varUpsilon ^{+}(\xi ,\phi )$ and $\varUpsilon ^{-}(\xi ,\phi )$ are the asymmetry terms for the two parity modes and $\xi$ represents any appropriate set of kinematical variables. $N_{p}^{\uparrow }$ ($N_{p}^{\downarrow }$) is the number of events for up (down) polarization modes of a particular $\phi _{2}$. Similarly, $N_{m}^{\uparrow }$ ($N_{m}^{\downarrow }$) is the number of events for up (down) polarization modes of $-\phi _{2}$. $p_{Z}^{\uparrow }$ and $p_{Z}^{\downarrow }$ are the polarization degrees of up and down modes, respectively. $A_{x}(\xi )$ and $A_{y}(\xi )$ are the two components of the vector analyzing power and $\phi$ is the azimuthal angle of the reaction plane. The asymmetry component $h(\xi ,\phi )$ can be constructed from $\varUpsilon ^{+}(\phi )$ and $\varUpsilon ^{-}(\phi )$ to extract $A_{y}(\xi )$:

$$\begin{aligned} h(\xi ,\phi )=\frac{\varUpsilon ^{-}(\xi ,\phi )+\varUpsilon ^{+}(\xi ,\phi )}{2}=A_{y}(\xi )\cos \phi . \end{aligned}$$

(3)

Fig. 4

The results of $A_{y}$ as a function of S for several breakup configurations which are labeled as ($\theta _{1}, \theta _{2}, \phi _{12}$) on the top-left of each pad. Each line represents the results of a theoretical calculation as mentioned in the legend. The gray band shows the systematic uncertainty ($2\sigma$) of the experimental results

   Two different approaches were applied for energy calibration of the forward-wall and the backward-ball detectors [48]. The protons with energies larger than 140 MeV ($E_{1}>140$ MeV) punch through the E-detectors of the forward-wall and, consequently, deposit part of their energies in the detectors, see the left panel of Fig. 3. The points corresponding to the region of punch through are excluded in the final spectrum. For every configuration of ($\theta _{1}, \theta _{2}, \phi _{12}$) the angular bins of $\pm 2.5^{\circ }$ and $\sim \pm 10^{\circ }$(angular resolutions of the detector part) are taken for selecting an event for polar angle $\theta$ in the forward-wall and the backward-ball, respectively. For each kinematic, the S-curve is divided into equally-sized bins and the events within each S-bin are used to construct the asymmetry distributions as a function of $\phi$ for each parity mode and spin state. The background for those configurations in which both protons scatter to the forward-wall was significantly suppressed using the time (TDC) information. The ball detectors were not equipped with TDC, therefore configurations in which one of the outgoing protons scatters to the backward angles ($\theta >40^{\circ }$) suffers from a background that mainly stems from uncorrelated protons from two different reactions, either elastically scattered or from a breakup reaction. To subtract this background, the missing-mass of the neutron was reconstructed for each S-bin. The number of counts was obtained for each missing-mass spectrum after subtracting the background, see the right panel of Fig. 3. The cut on the S-curve induces an artificial correlation between the two time-uncorrelated hits. As a consequence, a peaking structure of the background is observed. The location of this peak depends upon S and is well understood. To account for the background including the one from the elastic channel, we used a method that is described in Ref. [50]. For a complete discussion of applying this method in this analysis, including computing the systematic uncertainty ($\sigma$) shown in Fig. 4, we refer to Refs. [41, 48]. To extract the analyzing power $A_{y}$ from Eq. 3, the number of counts for each polarization and parity modes are extracted and normalized with the integrated charge from the Faraday cup. $h(\xi ,\phi )$ is constructed using the normalized counts as a function of $\phi$. To measure the values of analyzing power $A_{y}$, the function $A\cos \phi +B$ is fitted to the $h(\xi ,\phi )$ distribution. The parameter A represents the analyzing power $A_{y}$. The parameter B is a free parameter to correct for a possible offset in the charge measurement and other normalization factors which were missing during the analysis. The quality of the fits for all configurations has been found to be good and an average $\chi ^{2}/$ndf$\sim 1$ was obtained for the ndf values ranging from 8 to 36. Note that the discrepancy between the theoretical calculations and the experimental data has been observed in the symmetric configurations ($\theta _1=\theta _2$) and $\phi _{12}<40^{\circ }$ in the proton–deuteron breakup reaction at different energies and it is still an unsolved puzzle; see Refs. [45, 46].

The analyzing powers $A_{y}$ have been measured for 193 breakup configurations at small and large scattering angles of protons. Figure 4 shows the results of our measurements of $A_{y}$ as a function of S for some configurations at small and large polar scattering angle of proton together with the results of different theoretical calculations using NN and NN+3NF models. With these configurations, we are able to investigate the isospin effects using the results of the kinematics which are close to the $'\text {pp}'$ and $'\text {pn}'$ systems. These kinematics can be identified using the relative energy (${E_{\mathrm {rel}}}$) between two of the three outgoing particles. The relative energy between two outgoing particles for the pd breakup reaction is defined as:

$$\begin{aligned} \begin{aligned}&P_{12}=(P_{1}+P_{2})^{2};\\&{E_{\mathrm {rel}}}=\sqrt{P_{12}}-m_{1}-m_{2}, \end{aligned} \end{aligned}$$

(4)

Fig. 5

An illustration of the scattering angles of the quasi-elastic channel of the three-body break-up reaction. The left figure shows the scattering process in the laboratory frame and the right one shows the corresponding center-of-mass frame. The two outgoing particles that scatter together with a small relative energy are labeled with $\vec {p}_{3}$

Fig. 6

Center-of-mass angle distributions of the data for different ${E_{\mathrm {rel}}}$ intervals. The yellow and magenta colors show data for the $'\text {pp}'$ and the $'\text {pn}'$ cases, respectively

Fig. 7

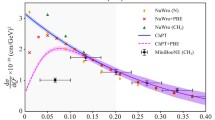
The top panel shows the results of theoretical predictions of CDB$+\varDelta$ for $A_{y}$ as a function of S for low relative energies of the $'\text {pn}'$ case. The solid black line (left axis) represents $A_{y}$ and the red dashed line (right axis) shows the variation of ${E_{\mathrm {rel}}}$ as a function of the S-value. It is clear that the $A_{y}$ rapidly changes as ${E_{\mathrm {rel}}}$ reaches its minimum. The lower panel shows the results for the same configuration as the top panel but for the $'\text {pp}'$ case. Here, the variation of $A_{y}$ is very small as ${E_{\mathrm {rel}}}$ reaches to its minimum

Fig. 8

The left panel shows the extrapolation of the theoretical results of CDB$+\varDelta$ for the $'\text {pn}'$ case in which the ${E_{\mathrm {rel}}}=0.5$ MeV was used as the lowest value of relative energy for the extrapolation. The dashed line shows the results of the extrapolation at ${E_{\mathrm {rel}}}=0$ MeV. The right panel is the same as the left panel except for the fact that ${E_{\mathrm {rel}}}=0.1$ MeV was used as the lowest value of relative energy for the extrapolation. It shows that including ${E_{\mathrm {rel}}}=0.1$ MeV makes the extrapolation result closer to the results at ${E_{\mathrm {rel}}}=0$ MeV but it is not sufficient

where $P_{12}$ is the total 4-momenta of the two outgoing particles. $P_{1}$ and $P_{2}$ are the 4-momenta of the two particles. $m_{1}$ and $m_{2}$ are the masses of the two particles and ${E_{\mathrm {rel}}}$ is the relative energy between them. For the $'\text {pp}'$ case, we have to take the relative energy between the two outgoing protons in the forward angles as a reference. For the other reaction, we used the information of the two outgoing protons in which one of them scattered to the backward angles ($\theta >100^{\circ }$) to construct the 4-momentum of the neutron. Then, we extracted the relative energy between the proton and the neutron in the forward angles. Part of the data in which ${E_{\mathrm {rel}}}<12$ MeV was selected and divided into three groups: 1–4 MeV, 4–8 MeV, and 8–12 MeV. We considered the $'\text {pp}'$ and $'\text {pn}'$ as one body as illustrated in Fig. 5. Figure 6 depicts the distributions of $\theta _{CM}$ for different ${E_{\mathrm {rel}}}$ intervals. For each $\theta _{CM}$ in which there are data for the $'\text {pn}'$ case, we put a gate of $\pm 2^{\circ }$ around the mean value of the $\theta _{CM}$ of $'\text {pn}'$ case to select the corresponding data of the $'\text {pp}'$ case. Therefore, we have three $\theta _{CM}$ candidates for $1<{E_{\mathrm {rel}}}<4$ and four candidates for each of the two other relative energy intervals. For each $\theta _{CM}$, the weighted average of the $A_{y}$ values were obtained for all the data within that $\theta _{CM}$ bin. The weighting factor is ($1/\sigma ^{2}$) where $\sigma$ is the statistical uncertainty of each measured value. This procedure was performed for averaging of the corresponding theoretical calculation (CDB, AV18, etc.) with the same weighting factor taken from each data point. As a result, we converted the data and the results of the theoretical calculations as a function of $\theta _{CM}$ for three different intervals of ${E_{\mathrm {rel}}}$. Then, a polynomial of order two was fitted to the data points to extract $A_{y}$ at the same $\theta _{CM}$ angles for all the intervals of ${E_{\mathrm {rel}}}$; see the gray line at the third column of Fig. 9. The $A_{y}$ values are extracted using the fitted function for $\theta _{CM}$ between $135^{\circ }$ and $160^{\circ }$ in steps of $5^{\circ }$. For each $\theta _{CM}$ candidate, the data were obtained as a function of ${E_{\mathrm {rel}}}$ and a polynomial of order two was fitted to the data to extrapolate $A_{y}$-values at ${E_{\mathrm {rel}}}=0$. For $A_{x}$, it was already shown that measured values of $A_{x}$ are very close to zero as required for a two-body reaction [46] and we do not considered $A_{x}$ in the present analysis.

4 Results and discussion

Fig. 9

The results of analyzing power $A_{y}$ as a function of the center-of-mass scattering angle for the $'\text {pp}'$ and the $'\text {pn}'$ cases. The three rows on the bottom show the results for different intervals of ${E_{\mathrm {rel}}}$. The first three panels of the first row show the results at very low relative energy (${E_{\mathrm {rel}}}=0$ MeV) and the last panel shows the results of the proton–deuteron elastic reaction. The first two columns in the left are the results of the $'\text {pn}'$ case for $E_{p}>E_{n}$ and $E_{p}<E_{n}$, respectively. The third column represents the results of the $'\text {pp}'$ case at different ${E_{\mathrm {rel}}}$ intervals. The solid black circles and triangles represent the breakup data and the extrapolated values at ${E_{\mathrm {rel}}}=0$ MeV, respectively. Each line represents a different theoretical calculations of CDB, CDB$+\varDelta$, AV18, and AV18+UI; see the legend. The gray band shows the systematic uncertainty ($2\sigma$)

The extrapolated $A_{y}$ values for the $'\text {pp}'$ and the $'\text {pn}'$ cases correspond to the $d(\vec {p},pp)n$ and $d(\vec {p},pn)p$ reactions, respectively. For the interpolated and the extrapolated points, the statistical uncertainty was obtained from the propagation of the statistical uncertainties of the initial data points using the variance-covariance matrices resulting from the fitted functions. We investigated the analyzing power $A_{y}$ of the proton–deuteron breakup reaction at 190 MeV proton beam energy for the $'\text {pp}'$ and $'\text {pn}'$ channels. In the extrapolation procedure, it became clear that for the $'\text {pn}'$ case the theoretical $A_{y}$ value rapidly changes as a function of ${E_{\mathrm {rel}}}$ for the relative energies lower than 0.5 MeV, see the top panel of Fig. 7. To investigate it further, we performed an extrapolation test on theoretical results of CDB+$\varDelta$. The $A_{y}$ values are extracted using the spline for $\theta _{CM}$ between $130^{\circ }$ and $160^{\circ }$ in steps of $2^{\circ }$ for calculations at ${E_{\mathrm {rel}}}=10,6,2$, and 0.5 MeV. The result of extrapolation is shown in Fig. 8 for two different lowest values of ${E_{\mathrm {rel}}}$. One can see that even by including ${E_{\mathrm {rel}}}=0.1$ MeV as the lowest value, the extrapolation result at ${E_{\mathrm {rel}}}=0$ MeV is not in agreement with the result of exact theoretical calculation at ${E_{\mathrm {rel}}}=0$ MeV, see the right panel of Fig. 8. Therefore, the extrapolation does not give accurate results when no data is available for ${E_{\mathrm {rel}}}<1$ MeV in the $'\text {pn}'$ case, and we decided not to present the results of the extrapolation for the $'\text {pn}'$ case. On the other hand, the variation of $A_{y}$ for the $'\text {pp}'$ case is very small for ${E_{\mathrm {rel}}}<1$ MeV as shown in the bottom panel of Fig. 7. Therefore, the extrapolation towards the minimum of the ${E_{\mathrm {rel}}}$ is accurate for this case.

Figure 9 presents the results for $A_{y}$ at three different ${E_{\mathrm {rel}}}$ intervals for the $'\text {pp}'$ and the $'\text {pn}'$ systems as a function of $\theta _{CM}$, and the extrapolation results of the $'\text {pp}'$ channel at vanishing relative energy. Results of different theoretical calculations from CDB, CDB$+\varDelta$, AV18, and AV18$+$UIX are compared with the data. It was already shown that the Coulomb effect is negligible in the analyzing powers [48]. Therefore, the results of CDB+$\varDelta$+C are not included for ease of comparison with the other calculations. Each of the three bottom rows shows the results at a different ${E_{\mathrm {rel}}}$ value. The first and the second columns show the results of the $'\text {pn}'$ case for $E_{p}>E_{n}$ and $E_{p}<E_{n}$, respectively. The third column shows the results of the $'\text {pp}'$ case. Also, the $A_{y}$ measurements of the proton–deuteron elastic reaction at proton beam energy of 190 MeV from Ref. [27] are shown for comparison at the top-right panel of Fig. 9.

The gray band in each figure represents the systematic uncertainty which consists of three parts. The polarization of the beam was measured by analyzing the elastic proton–deuteron channel with BINA and by using the measurements of the In-Beam Polarimeter (IBP). The associated relative uncertainties of the polarization values are $6\%$ statistical and $3\%$ systematical [35]. This uncertainty in the polarization causes a systematic error of $\sigma _{pol}\,{\sim }7\%$ in the analyzing power measurement. Another source of systematic uncertainty is identified to be from residual and unknown asymmetries caused by efficiency variations between the up and down polarization states of the beam, error in charge normalization, etc.. All of these will distort the distribution and the model presented in Eq. 3 will not be valid. This source of systematic uncertainty was investigated through comparing the results with and without the free parameters of the fitted functions on the asymmetry distributions. The total systematic uncertainty for the corresponding $'\text {pp}'$ configurations was obtained from a quadratic sum of the two sources of systematic errors. For the configurations of the $'\text {pn}'$ case, the systematic uncertainty comes from the shape of the background. This part of the systematic uncertainty consists of two components. The first one is the difference between results of full and limited ranges of the background estimation, see the right panel of Fig. 3. To do this, we keep the polynomial order to be the same but decrease the range of the background estimation. The other component of the error in the shape of the background was obtained using the difference between the results of the background estimation using two different polynomial orders (6 and 8) but keeping the full range. The total systematic uncertainty was obtained by a quadratic sum of the systematic errors, assuming them to be independent. For the results of the extrapolation of the $'\text {pp}'$ case, we used a different approach to identify the systematic error. The systematic error of each data point was either added or subtracted from the values and then for each set of the data we applied the extrapolation procedure to both cases. The difference between the results was taken as the first part of the systematic error. Moreover, we applied the extrapolation procedure for the theoretical results of CDB+$\varDelta$. The difference between the extrapolated values at ${E_{\mathrm {rel}}}=0$ MeV and the exact theoretical results at this relative energy was taken as the second part of the systematic error. The total systematic uncertainty for the extrapolated values was obtained by a quadratic sum of the two systematic errors.

As it is shown in the third column of Fig. 9, even with addition of 3NFs none of the models is able to reproduce data. The largest discrepancy is observed for AV18+UIX, especially at the lower values of relative energies. This might indicate that the isospin components in UIX three-nucleon correction is not modeled properly. These kinds of the disagreements between theoretical calculations and data were reported at different proton beam energy and center-of-mass angles[46]. For the $'\text {pn}'$ case at very low relative energies there is a disagreement between the theoretical models at $\theta _{CM}>140^{\circ }$.

5 Summary and conclusion

The 3NFs have major impact on the nuclear force and the prediction of the properties of the nuclear systems. It depends on different properties of the nucleons such as spin and isospin. In the present work, the effects of the spin-isospin properties of the proton–deuteron breakup reaction were studied for very low relative energies of nucleons using an incident proton beam with an energy of 190 MeV. Extrapolation techniques were used to reach kinematics with vanishing relative energies.

We aimed to extract the $A_{y}$ values for both $'\text {pp}'$ and $'\text {pn}'$ cases from proton–deuteron breakup data. For the first reaction channel, one can only investigate isospin $I=1$ whereas the second one has two possible isospin states, $I=0$ and $I=1$. Therefore, $'\text {pn}'$ has more isospin information and it is the only reaction which can be used to make a comparison with the pd elastic data where $I=0$. We showed that for extracting the results of the $'\text {pn}'$ case from the $d(\vec {p},pp)n$ breakup data, due to the large variation of $A_{y}$ at ${E_{\mathrm {rel}}}<1$ MeV, one cannot use the extrapolation approach for this case. For the $'\text {pp}'$ case, analyzing powers $A_{y}$ at ${E_{\mathrm {rel}}}=0$ were extracted. Although the theoretical results are not in satisfactory agreement with our data at larger values of relative energies they show a relatively better agreement at ${E_{\mathrm {rel}}}=0$ in the investigated range of $\theta _{CM}$. However, the shapes of the data and the theoretical predictions are not compatible with each other at ${E_{\mathrm {rel}}}=0$. Furthermore, for $\theta _{CM}<135^{\circ }$, as it was shown in Refs. [45, 46], the discrepancy between data and theory is significant and it needs further investigations.