First trap-assisted decay spectroscopy of the $^{81}$Ge ground state

Abstract

The $\beta$-delayed $\gamma$ spectroscopy of $^{81}$As has been performed using a purified beam of $^{81}$Ge $(9/2^+)$ ground state at the Ion Guide Isotope Separator On-Line facility (IGISOL). The $^{81}$Ge$^+$ ions were produced using proton-induced fission of $^{232}$Th and selected with the double Penning trap JYFLTRAP for the post-trap decay spectroscopy measurements. The low-spin $(1/2^+)$ isomeric-state ions $^{81m}\hbox {Ge}^+$ were not observed in the fission products. The intrinsic half-life of the $^{81}$Ge ground state has been determined as $T_{1/2}=6.4(2)~\hbox {s}$, which is significantly shorter than the literature value. A new level scheme of $^{81}$As has been built and is compared to shell-model calculations.

1 Introduction

The $^{78}$Ni ($Z=28, N=50$) region has been one of the main focus points in nuclear structure studies during the last decades. Measured nuclear masses [1, 2] and spectroscopy experiments (e.g. Refs. [3,4,5,6,7]) on nearby nuclei, as well as large-scale shell-model calculations (e.g. [8, 9]) have indicated that the $Z=28$ and $N=50$ shell closures remain persistent even far from stability. The recently measured $2^+$ excitation energy of $^{78}$Ni, $E_x(2^+_1)=2.6$ MeV [9] has been interpreted as a indication of its doubly magic nature.

Despite this remarkable result, the nuclear structure in the region is far from fully understood. Shape coexistence phenomena observed in the $N=40$ region seem to extend to the $N=50$ region and result in a new island of inversion [8,9,10,11,12,13]. Coexisting shapes can also lead to isomeric states which complicate the studies of these nuclei. $\beta$-decaying isomers are widespread in this region, just before the $N=50$ shell closure. For example the odd-A $N=49$ isotones between $^{83}$Se and $^{93}$Ru ($Z=34{-}44$) all have a $(9/2^+)$ ground state and an isomeric state with a spin-parity $(1/2^-)$ originating from a neutron hole configuration $\nu g_{9/2}^{-1}$ and $\nu p_{1/2}^{-1}$, respectively [14]. The situation changes closer to the $Z=28$ shell closure. Both $^{81}$Ge ($Z=32$) and $^{79}$Zn ($Z=30$) have an isomeric $(1/2^+)$ state mainly originating from a $1p-2h$ $\nu g_{9/2}^{-2}s_{1/2}^1$ intruder configuration produced by a neutron excitation across the $N=50$ shell gap [12]. Although the existence of shape coexistence in these nuclei was proposed a long time ago [15] direct experimental evidence has long remained scarce. The recent observation of a large mean squared charge radius difference between the $(9/2^+)$ ground and the $(1/2^+)$ isomer states of $^{79}$Zn from laser spectroscopy measurements at ISOLDE [12] is the most direct indication we have so far of a noticeable shape difference between the two. So far there is no information on the nature of the $(1/2^+)$ supposed intruder state in $^{81}$Ge.

In this work, we re-investigate the $^{81}$As level scheme populated in the $\beta$-decay of $^{81}$Ge in a systematic attempt to improve spectroscopy knowledge in this region of suspected shape coexistence. This is in continuation of the work performed in Ref. [16], where intruder configurations in the neighbouring odd-odd nucleus $^{82}$As have been identified. Up to now, the $\beta$-decay studies of the $N=49$ isotones for $Z\le 32$ have not been performed with an unambiguous ground state and isomer separation. In this work, we have utilized the JYFLTRAP Penning trap and selected the $(9/2^+)$ ground state of $^{81}$Ge ($Z=32$) for detailed studies at a post-trap decay spectroscopy setup. This is a clear improvement compared to the previous spectroscopy study of the decay of $^{81}$Ge [14] which utilized a mass-separated $A=81$ beam consisting mainly of $^{81}$Ga. Since the $\beta$-decay of $^{81}$Ga populates both isomeric states in $^{81}$Ge and because their half-lives could not be differentiated in [14], the $\beta$-delayed $\gamma$ transitions in $^{81}$As have been assigned to the decay of the ground state or the isomeric state based on indirect arguments. Additional information on (near) Yrast spectroscopy was also obtained via fusion-fission reactions using the Euroball array [17].

In addition to their nuclear structure interest, the neutron-rich nuclei in the $A=80$ region play an essential role in astrophysics. The first abundance peak in the astrophysical rapid neutron capture (r) process [18] forms at $A\approx 80$ with the radioactive neutron-rich nuclei acting as progenitors for the final abundances. These lighter r-process nuclei and their decays contributed to the blue kilonova [19,20,21] observed after the binary neutron star merger event GW170817 [22]. Their presence is also evidenced by the strong strontium lines observed from the kilonova [23]. Precise knowledge of $\beta$-decay half-lives and $\beta$-delayed neutron emissions in the $A\approx 80$ region are relevant inputs for the r-process calculations modelling the final abundances and the features of the resulting kilonova [24], while isomeric states can also impact the calculations [25]. A large fraction of the r-process flow to stability proceeds via the $\beta$-decay of $^{81}$Ge [24], resulting in a high final abundance at $A=81$. In this work we provide a new and more precise $\beta$-decay half-life for the $^{81}$Ge ground state, a necessary step toward more precise astrophysical calculations.

The paper is outlined in the following way. The experimental method and in particular the isomeric separation are presented in Sect. 2. Then, the half-life measurement and the level scheme are presented in Sect. 3. Finally, results are discussed in comparison with shell-model calculations in Sect. 4.

2 Experimental method

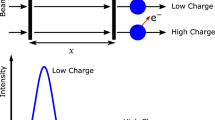
The $^{81}$Ge nuclei were produced at the Ion Guide Isotope Separator On-Line (IGISOL) [26] facility at the Accelerator Laboratory of the University of Jyväskylä. A 15 mg/cm$^{2}$ $^{232}$Th target inside the fission ion guide [27, 28] was exposed to a 35-MeV proton beam from the K-130 cyclotron with an average intensity of 10 $\upmu$A. The fission fragments were thermalized in helium buffer gas and extracted from the gas cell with a typical charge state of $q=+e$ using a radio-frequency sextupole ion guide [29]. Subsequently, the ions were accelerated to 30 keV before mass separation with a dipole magnet set at $A/q=81$. The continuous beam was then cooled and bunched in a radio-frequency quadrupole cooler buncher [30] prior to injection into the double Penning-trap mass spectrometer JYFLTRAP [31]. $^{81}$Ge$^+$ ions were selected from the $A/q=81$ ions using the mass-selective buffer gas cooling method [32] in the first trap, the so called purification trap, see Fig. 1 (top). Only the $J^{\pi }=(9/2^+)$ ground state of $^{81}$Ge was observed as confirmed by a Time-of-Flight Ion Cyclotron Resonance (ToF-ICR) [33, 34] measurement in a second, so-called measurement trap, see Fig. 1 (middle). This suggests that the direct population of the low-spin isomer with $J^{\pi }=(1/2^+)$ and an excitation energy $E_x(1/2^+)=619.14(4)$ keV, is negligible as compared to the $(9/2^+)$ ground state in proton-induced fission of $^{232}$Th or that the $(1/2^+)$ isomer has much lower excitation energy.

As the half-lives of the $(9/2^+)$ and $(1/2^+)$ $\beta$-decaying states could not be distinguished in previous studies [35], the values quoted in literature are exactly identical ($T_{1/2}=7.6(6)$ s). In order to confirm the excitation energy (and the negligible yield in $^{232}$Th proton induced fission) of this low-spin isomer the study of the decay of a $^{81}$Ga population inside the trap was undertaken. First, the mass-selective buffer-gas cooling technique [32] was used to select $^{81}$Ga$^+$ ($T_{1/2}=1.217(5)$ s, $J^{\pi }=(5/2^-)$) ions in the purification trap. The $^{81}$Ga$^+$ ions were then allowed to $\beta ^-$ decay to $^{81}$Ge$^{2+}$ in the purification trap by trapping them for 530 ms. The produced $^{81}$Ge ions are doubly-charged due to the increase in the proton number, and therefore, their cyclotron resonance frequency $\nu _c=qB/(2\pi m)$ is twice the frequency for a singly-charged ion. This makes it easier to resolve the ground and isomeric states. The buffer-gas cooling technique was reapplied to select $^{81}$Ge$^{2+}$ ions which were further sent to the second trap for a ToF-ICR measurement using a 100-ms quadrupolar excitation. The $\beta$-decay of $^{81}$Ga $(5/2^-)$ feeds both the ground and isomeric states in $^{81}$Ge [14, 35], and clearly, two states are visible in the ToF-ICR spectrum shown in Fig. 1 (bottom).

To perform $\beta$-delayed spectroscopy of $^{81}$As, the sources were constituted by the interception of the first-trap-selected $^{81gs}$Ge$^+$ ion bunches by a Mylar movable tape at the center of the decay station. An ion bunch was released from the Penning trap to the tape every 133 ms. In order to limit long-lived activities, the tape was moved every $t_a=60.6$ s after a $t_0=0.5$ s background measurement, a $t_c=30.6$ s build-in (230 bunches) followed by a $t_d=30$ s decay time, see Fig. 2.

Fig. 1

(Top) A quadrupole excitation frequency scan in the first trap of JYFLTRAP showing the isobaric distribution at $A=81$. (middle) A ToF-ICR spectrum for $^{81}$Ge$^+$ ions using 200 ms quadrupolar excitation in the second trap of JYFLTRAP. (Bottom) A ToF-ICR spectrum with 100 ms quadrupolar excitation in the second trap for $^{81}$Ge$^{2+}$ ions after the in-trap $\beta$-decay of $^{81}$Ga. The ground- and isomeric-state frequencies are indicated with dashed lines in (middle) and (bottom). Blue shaded points are the actual data points, black points represent their mean value with a 1$\sigma$ error bar

The source was surrounded by a cylindrical 2-mm-thick plastic detector in order to register electrons from $\beta$-decay. This detector was itself surrounded by a set of five HPGe detectors for $\gamma$ spectroscopy placed at right angles to each other (for a total $\gamma$-ray efficiency of $2.9(2)\%$ at 1 MeV) comprising :

• Two coaxial detectors GC7020;

• Two EUROGAM-2-like CLOVER detectors;

• A BEGe2020 detector with a Be entrance window.

The timing signals for the tape movement and the ion bunch ejection were produced by the JYFLTRAP timing card. These timing signals, together with all detector signals, were sent to a 16-channel Nutaq numerical acquisition card with a 105 MHz sample rate [36]. The data were recorded triggerlessly and the $\beta -\gamma$ and $\beta -\gamma -\gamma$ events were then reconstructed offline.

3 Results

3.1 Half-life of the $(9/2^+)$ ground state of $^{81}$Ge

As already mentionned, prior to this experiment, the half-lives for the $(9/2^+)$ ground and $(1/2^+)$ isomeric states in $^{81}$Ge had not been separately determined, and an identical half-life of 7.6(6) s had been adopted for both states [14, 35]. In the present work, the ions belonging to the ground state of $^{81}$Ge could be exclusively selected for the $\beta$-decay studies for the first time. Therefore, the ground-state half-life could also be unambiguously determined for the first time. The half-life was determined using the time distribution of $\gamma$ events corresponding to the most intense transitions in $^{81}$As following the $\beta$-decay of $^{81}$Ge. The half-lives of $^{81}$As excited states are negligible compared to $^{81gs}$Ge, therefore their measured apparent half-lives are assumed to be the intrinsic $\beta$-decay half-life of $^{81gs}$Ge.

The obtained time distribution of $\gamma$-ray events corresponding to the selected transitions (see Fig. 2) were fitted using the Bateman equations (1):

$$\begin{aligned} N(t) = \left\{ \begin{array}{lcl} \overline{\phi }(1-e^{-\lambda t}) &{} \text {if} &{} t_0\le t\le t_c \\ \overline{\phi }(1-e^{-\lambda t_c})e^{-\lambda (t-t_c)} &{} \text {if} &{} t_c\le t\le t_a \end{array}\right. \end{aligned}$$

(1)

where $\overline{\phi }$ is the average number of ions collected on the tape per second.

Fig. 2

Time distribution of the background-subtracted $\gamma$-ray events corresponding to the 335.9(2)-keV transition in $^{81}$As. The Bateman equation fit is shown in red

The final half-life value for the $^{81}$Ge ground state, $T_{1/2}(^{81gs}\text {Ge})=6.4(2)$ s, was obtained as a weighted mean over all measured half-lives (see Fig. 3). A systematic uncertainty of 0.133 s is considered as the beam was bunched with a frequency of a bunch every 133 ms.

Fig. 3

The determined half-lives for the studied $\gamma$-ray transitions as a function of the $\gamma$-ray energy $E_\gamma$ (in black). The weighted mean and its error band including both systematic and statistical uncertainties is shown in red

This value shows that the value previously reported using a mixture of the ground and isomeric states of $^{81}$Ge [14] is overestimated leading to assume that $T_{1/2}(^{81m}\text {Ge})\ge 7.6(6)$ s.

Fig. 4

Trap assisted experimental $\beta$-gated $\gamma$-ray spectrum at $\nu _c=1327846.166$ Hz. a–d Represent subsequent energy ranges 0–700, 700–1400, 1400–2100, and 2100–2800 keV, respectively. Red circles indicate transitions attributed to $^{81}$As and black squares, transitions in $^{81}$Se. Peaks indicated with X are considered as pollutant as their time distribution is not correlated to the beam. Finally, ? shows unindentified peaks (no coincidence, unclear time distribution)

Table 1 $\gamma -\gamma$ coincidences in $^{81}$Ge $\beta$-decay. $\gamma -\gamma$ indicates the transition energy observed in the spectrum obtained by making a gate at $E_{\gamma }$. $I_{\gamma }$ is the relative intensity of the transition at $E_{\gamma }$ compared to the 336-keV one and $T_{1/2}$ is the $^{81gs}$Ge half-life obtained by fitting the time distribution of events corresponding to the transition $E_{\gamma }$, see Fig 2. *Indicates that intensity has been corrected by conversion coefficient assuming M1 multipolarity. # indicates existence of a doublet and their $\gamma -\gamma$ coincidences are given as a whole. Continues in Table 2

Table 2 Same as Table 1

Table 3 The table presents possible spin and parity assignments for the excited levels in $^{81}$As populated in the decay of the $^{81}$Ge ground state. The propositions are based on the relative branching ratios and calculated log ft values as well as systematics. $^u$ Indicates that the given value is calculated assuming a 1$^{\text {st}}$-unique transition (or used as a lower limit for higher $\Delta L$). When several possibilities remain, bold numbers show the preferred ones after comparison with shell-model calculations (see Sec. 4)

3.2 Level scheme of $^{81}$As

The total $\beta$-gated $\gamma$-ray spectrum obtained in this experiment is shown in Fig. 4 and was accumulated over 3170 iterations of the tape motion (about 53 hours of beam on tape). All the observed activity can be attributed to $^{81gs}$Ge decay and its daughter $^{81}$As. $\gamma$-ray transitions were attributed to $^{81}$As based on the half-life measurements of the corresponding $\beta$-delayed $\gamma$-rays and the $\gamma -\gamma$ coincidence measurements. The most intense $\gamma$-line is at 336 keV as measured in [14], and is indeed mainly populated by the de-excitation of states at higher energy. We mainly confirm the tentative level scheme which was based on systematics in Ref. [14]. Nevertheless, a few $\gamma$ transitions attributed earlier to the $^{81m}$Ge decay have now been associated with the ground-state $\beta$-decay of $^{81}$Ge.

Absolute intensities (see Tables 1 and 2) were estimated using the absolute intensity of the 491.4-keV transition in $^{81}$As decay using the corresponding set of Bateman equations describing the $A=81$ decay chain. The obtained coefficient of conversion between absolute and relative intensities is $I_{abs}/I_{rel}=0.54(9)$. All identified excited states as well as their $\beta$-decay branching ratios and the corresponding $\log ft$ value are given in Table 3. The sum of $I_{\beta }$ is found to be $108(13)\%$.

The level scheme (Fig. 5) was built based on the observed $\beta$-delayed $\gamma$-rays and $\gamma -\gamma$ coincidences (see Tables 1 and 2). Here we focus our discussion on four transitions that were considered as doublets at 666 and 793 keV in Ref. [14]. These doublets were unambiguously resolved thanks to $\gamma -\gamma$ coincidence data.

Firstly, a gate on the full peak at 793 keV results in a strong coincidence with both the 290-keV and 336-keV transitions which are not connected at all in the level scheme. Placing the 793-keV transition at higher energy was overruled due to intensity matching (it is the second most intense transition). The existence of a 46-keV transition between 336 and 290-keV states was excluded because such a transition in this mass region cannot be fully converted and was not observed on the low energy part of our BEGe spectra (threshold $\sim 10$ keV). A gate placed either on the lower or the higher energy part of the 793-keV peak reveals a very different I(290 keV)/I(336 keV) ratio, see Fig. 6, strongly suggesting a doublet. Using the reverse gates, the energy difference between the two components of this doublet is measured to be 0.1(3) keV. We suggest then that the higher-energy transition of the doublet is feeding the 290-keV state whereas the lower-energy transition is feeding the 336-keV state in order to match the $I_{\gamma }$ ratios observed in Fig. 6.

Concerning the 666-keV doublet the situation is similar to the one of the 793-keV transition but the suspicion of the doublet nature of the peak comes from less intense transitions. Firstly, a gate on the full peak at 666 keV suggests a strong coincidence with both the 1156-keV and 1495-keV transitions which are not connected in the level scheme. Secondly, by using the same trick as for the 793-keV doublet, we observed that the I(93 keV)/I(336 keV) ratio almost doubles if we gate either on the lower energy or higher energy half of the peak, see Fig. 7. Using the reverse gates, the energy difference between the two components of this doublet is measured to be 0.4(4) keV. Taking into account this fact, it is proposed that the higher-energy transition of the doublet is placed at higher energy feeding the 2625-keV state in order to take into account the coincidence with 1495-keV transition whereas the lower-energy one is directly feeding the 93-keV state.

3.3 Spin-parity suggestions for the $^{81}$As excited states

The ground state of all $N=49$ isotones has been assumed to be $J^{\pi }=9/2^+$ originating from their neutron hole $\nu 1g_{9/2}^{-1}$ nature [14]. Therefore, $^{81}$As excited state spin-parity restrictions and/or suggestions can be made using $\beta$-decay selection rules with the help of odd-A As systematics presented in Fig. 8.

The observed strong $\beta$-feedings and low $\log ft$ values to the states at 2625 keV, 2758 keV, 2966 keV and 3368 keV indicate that they are populated by allowed Gamow-Teller $\beta$-transitions from the $(9/2^+)$ ground state of $^{81}$Ge. Therefore, their spin-parities should be $J^\pi =7/2^+$, $9/2^+$ or $11/2^+$. Further hypotheses on spin-parity assignments are based on the assumption that all transitions connecting two opposite-parity state are either of E1 or M2 nature, whereas the transitions connecting two identical-parity states are either M1 or E2 nature. Available literature has also been considered in the spin-parity assignments, in particular for the lowest lying levels [14, 37,38,39,40].

The ground state of $^{81}$As has a spin-parity $3/2^-$ based on the observed $L=1$ transfer in the pick-up reaction $^{82}$Se$(d,^3$He) [37]. This is similar to every odd-A $N\le 40$ As isotopes and also compatible with the absence of direct ground state $\beta$ feeding from the $^{81gs}$Ge decay, which would be 3$^{\text {rd}}$ forbidden Gamow-Teller $\beta$ transition. Moreover, the same pick-up reaction study indicates that the 336-keV state is populated in the (d,$^3$He) reaction with a transferred orbital momentum $\ell =3$ suggesting a $(5/2)^-$ state [37].

Fig. 5

81gsGe $\beta$-decay scheme. Levels and transitions shown in black (blue) were already attributed to the $^{81}$Ge ground state (isomer) decay in Ref. [14], respectively. Levels and transitions shown in red are those newly proposed from the present work. * Indicates that intensity has been corrected by conversion coefficient assuming M1 multipolarity. ** Indicates that intensity has been corrected taking into account the $^{81}$Se transition. # are indicating intensities estimated using $\gamma -\gamma$ coincidences for the doublets. Spin-parity notation $(1/,3/,5/2^-)$ stands for $(1/2^-)$, $(3/2^-)$ or $(5/2^-)$

The 336-keV state de-excites by two $\gamma$-ray transitions. The very intense 336-keV transition has been assigned as a mixed M1+E2 transition based on $\gamma$-ray angular distributions in [17], confirming $(5/2)^-$ as its spin-parity. The 336-keV state decays by two $\gamma$-ray transitions: one going directly to the ground state and a second one to the first excited state, by a 243-keV gamma-ray emission. The decay is by far dominated by the 336-keV ground-state transition (intensity ratio 100:5.3) which has been assigned a mixed M1+E2 nature from angular distributions in Ref. [17] strongly favoring a $5/2^-$ spin-parity assignment for this 336-keV level. The strong suppression of the second decay channel that feeds the first excited state suggests a higher multipolarity for the associated 243-keV transition, typically E2. Since the populated 93-keV state is not fed by the $^{81gs}$Ge $\beta$-decay, a spin-parity of $(1/2)^-$ is proposed for it as it fits the $1/2^-$ states systematic in As isotopes, see Fig. 8. This is also consistent with the $\beta$-feeding observed from the $(1/2^+)$ isomer to this level in [14].

The state at 290 keV de-excites mainly to the supposed $(1/2^-)$ state at 93 keV. The 290-keV state was proposed to be either $(3/2)^-$ or $(7/2)^-$ in Ref.  [37]. Here we prefer to suggest $(3/2)^-$, compatible with a M1 transition. A M3 transition from a $7/2^-$ state would preferentially decay to the $3/2^-$ state rather than the $(1/2)^-$ state. However, we note here that the observed $I_\beta =9(5)$ % from the $(9/2^+)$ state to the 290-keV level is not compatible with the forbidden decay to a $(3/2)^-$ state.

Concerning the state at 737 keV, it was populated by the $(t,\alpha )$ pick-up reaction with a $\ell =3$ orbital momentum transfer [40]. The spin-parity is then $(5/2^-)$ or $(7/2^-)$. As it is populating both $(5/2)^-$ and $3/2^-$ states but not the $(1/2)^-$ state, the spin-parity $(7/2^-)$ is preferred. This assignment confirms the one obtained by angular distribution in in-flight $\gamma$-ray spectroscopy [17].

The 758-keV state was attributed $\ell =4$ $(9/2^+)$ from pick-up reaction data [40]. This is not confirmed by our data as the log ft value indicates a first-forbidden $\beta$-transition. Moreover, this state decays to a low-spin negative parity state rather favouring a $(5/2^-)$ spin-parity.

The 864-keV state decays only to the 93-keV, $(1/2)^-$ state. Furthermore, the $\log ft$ value suggests a first-forbidden $\beta$ transition, which leads to a $(5/2^-)$ spin-parity proposition for this state. However, due to the compatible-to-zero $\beta$-branching ratio, $(1/2^-)$ and $(3/2^-)$ cannot be ruled out.

The 1129-keV state de-excites through two different transitions. The first, strong 792-keV transition feeds the $(5/2)^-$ state at 336 keV and could be of E2 character. The weaker 391-keV transition populating the $(7/2^-)$ state at 738 keV could be a mixed M1+E2 transition. The $\log ft$ value suggests a first-forbidden $\beta$ population of the 1129-keV state. As a result, the most probable assignment is $(9/2^-)$ for this level. This is also supported by the $\gamma$-ray angular distributions given in Ref. [17].

The 1195-keV state does not seem to be directly populated by the $\beta$-decay from the $(9/2^+)$ ground state, therefore suggesting a spin-parity $(1/2^-)$ or $(3/2^-)$ as higher spin (like 13/2 or more) seems unlikely at this energy from a nuclear structure point of view. This state is moreover fed by the 1430-keV transition which is either E1 or M2 as the 2624-keV state has a positive parity as shown by the low $\log ft$ value. In order to match all these conditions, we suggest a spin-parity $(3/2^-)$ for the 1195-keV state and $(7/2^+)$ for the 2625-keV one. A E3 nature to a $(1/2^-)$ 1195-keV state hypothesis is rejected as a $1/2^-$ state would have preferentially decayed to lower energy and lower spin states.

The state at 1614 keV decays solely to the supposed $(7/2^-)$ state at 738 keV and not to lower spin ones. Moreover, its $\log ft$ value suggests a first-forbidden $\beta$ transition leading to a supposed $(11/2^-)$ spin-parity for the 1614-keV state and an E2 nature for the 876-keV transition. However, there are good arguments from angular correlation data in Ref. [17] for a 9/2 assignment. In that case our data would suggest a positive parity as it decays only to a $(7/2^-)$ state and not to a lower spin negative parity state. That hypothesis would imply that the 876-keV transition is of E1 nature. The $\log ft$ to this state obtained in our work is rather large for a $9/2^+\rightarrow 9/2^+$ $\beta$ transition. This may be related to nuclear structure effects related to the supposed deformation of $^{81}$As [17].

The 2142-keV level has a $\log ft$ value indicating a non-unique first forbidden Gamow-Teller transition. It is connected to the supposed $(7/2^+)$ state at 2625-keV by the 483-keV transition. Moreover, it decays through the 1013-keV transition to the 1129-keV state supposed to have a $(7/2^-)$ spin-parity. Therefore, we suggest a $(7/2^-)$ or $(9/2^-)$ spin-parity for the 2142-keV state. In addition, the 2142-keV state decays to a low spin $(1/2^-)$ or $(3/2^-)$ state at 1083-keV (indicated by the absence of $\beta$-feeding), therefore the $(7/2^-)$ spin-parity for the 2142-keV state and a $(3/2^-)$ spin-parity for the 1083-keV one are the privileged hypotheses.

Fig. 6

Normalised $\gamma$ spectra obtained by gating on the lower (black) or higher (red) energy part of the 793-keV peak in the $\beta$-gated $\gamma -\gamma$ coincidence matrix with identical background subtraction. I(290 keV)/I(336 keV)$\, =0.02$(2) for lower energy gate and I(290 keV)/I(336 keV)$\, = 0.12$(3) for higher energy part

Fig. 7

Normalised $\gamma$ spectra obtained by gating on the lower (black) or higher (red) energy part of the 666-keV peak in the $\beta$-gated $\gamma -\gamma$ coincidence matrix with identical background subtraction. I(93 keV)/I(336 keV)$\, =2.2$(9) for lower energy gate and I(93 keV)/I(336 keV)$\, =0.9$(2) for higher energy part

The state at 2758 keV decays to the state located at 2625-keV by a low energy transition which is strong compared to the other transitions depopulating this state, thus suggesting a M1 nature. Then, we suggest a spin-parity $(7/2^+)$ or $(9/2^+)$ as it has a $\log ft$ corresponding to an allowed $\beta$ transition.

Several states identified in this work are common to the work of Ref. [17] where they were populated by fusion-fission processes (favoring Yrast and near Yrast states). Below 1 MeV, our spin assignments are agreeing with those proposed in Ref. [17] from $\gamma -\gamma$ angular correlation measurements, some discrepancies appear above this excitation energy. For instance, the state located at 737.7(2) keV has been populated in the direct reaction $^{82}$Se(d,$^3$He)$^{81}$As [37] with a mixture of $\ell =3$ and $\ell =4$ transferred momentum. Both Ref. [17] and the present work suggest a $(7/2^-)$ assignment for this state. However, the 1195-keV state was suggested with a (7/2) spin where our results rather suggest a $(3/2^-)$ spin parity. If this last assignment is adopted then one must also revise the spin-parity assignments of states located in the 2.6–2.9 MeV energy region taking into account angular correlations performed in [17]. Therefore, a new $(7/2^+)$ spin parity can be proposed for the 2625 keV state. Similarly, the previous $J^\pi =(11/2^+)$ proposition for the 2758-keV state could be revised to $J^\pi =(9/2^+)$. As can be seen in Fig. 9 these two states at 1614-keV and 2758-keV excitation energy fall nicely into the $9/2^+_{1,2}$ systematics of the As isotope chain.

Fig. 8

Level systematics of odd-mass As isotopes. Data are taken from [35]. Circles indicate levels with a strong single-particle component seen in one-proton pick-up [37] and/or stripping [38, 39] reactions

Fig. 9

Systematics of the energy of $9/2^+_1$ (full symbols) and $9/2^+_2$ (open symbols) state energy in odd-A Rb, Br and As isotopes as a function of Z [35]

4 Discussion

Experimental results were compared with shell-model calculations performed with the m-scheme antoine [41, 42] and j-coupled scheme nathan codes using an effective interaction with a $^{56}$Ni core and a valence space composed of $2p_{3/2}$, $1f_{5/2}$, $2p_{1/2}$, $1g_{9/2}$ orbits for both protons and neutrons. In this interaction the effective two-body matrix elements (TBMEs) were obtained from either JJ44B or JUN45 [43] interactions. These interactions were chosen because they include the proton $1g_{9/2}$ state which is most probably necessary to correctly describe the positive parity system populated by Gamow-Teller allowed transitions. The main limitation of this approach is that it does not include neutron excitations across the $N=50$ gap even though they are known to play a significant role in the neighboring isotope $^{82}$As [16].

Fig. 10

Comparison between experimental (EXP.) and calculated level schemes for $^{81}$As obtained with two different shell-model interactions (JJ44B and JUN45). Negative parity states are represented on the left hand side and positive parity ones are on the right hand side. Indicated EXP. values are those for which the $J^{\pi }$ assignment hypotheses are best established. Green ellipses indicate most probable theory-experiment correspondences

The results of the shell-model calculations for $^{81}$As are given in Fig. 10. The first remark is that negative-parity states are very well reproduced, in particular using the JJ44B interaction. This fact encourages us to propose a one to one correspondence between a subset of calculated and observed states. These proposed correspondences are indicated by bold numbers in Table 3. For the positive-parity states the situation is more involved and only the $7/2^+_1$ state finds a natural theoretical counterpart. The energy of the $9/2^+_1$ state is overestimated by more than 500 keV by the calculations in the best case. Such a discrepancy was already noted in Ref. [43] in the case of several isotopes of Cu, Ga and As, explained by the deformation expected at mid-occupation of the neutron subshells. The lower panel of Fig. 11 shows the difference between the experimental $9/2^+_1$ energy and the one obtained in Ref. [43] for several As isotopes. The largest difference is found for $N=40$, however there is no noticeable effect related to a neutron-shell mid occupation, and the discrepancy at $\hbox {N}=48$ is one of the worse. It seems that one should look for another explanation.

Fig. 11

Upper panel : comparison between experimental (green) and calculated $3^-_1$ (square, full lines) and $5^-_1$ (diamond, dashed lines) states obtained with two different shell-model interactions JJ44B (red) and JUN45 (black). Lower panel : difference between the experimental and (JUN45) shell model excitation energies of the $9/2^+_1$ states for As isotopes

It is because of this difficulty with the shell-model reproduction of the positive parity states that Porquet et al. used a rotor+quasi-particle coupling model in Ref. [17]. By doing so the agreement for the sequence of negative parity states was significantly worsened. It seems to have escaped these authors that this strongly resembles an indirect evidence of shape coexistence. The almost perfectly parabolic shape of the $9/2^+_1$ experimental systematics for As and Br isotopes, well visible in Fig. 9, is a further argument that these states belong to a distinct structure, characterized by a larger deformation, or at least very sensitive to quadrupole correlations. The collective origin of the low lying positive parity structure in the odd-proton nuclei of this region has been discussed since very long [44, 45]. On the contrary, the $9/2^+_2$ experimental systematics is more erratic, and, as can be seen in Fig. 10, the $9/2^+_2$ of $^{81}$As has an easily found theoretical counterpart within the present shell model approach (as do the the $7/2^+_1$ and $11/2^+_1$ states). This would mean that this $9/2^+_2$ has a more standard, vibrational structure.

This last hypothesis can be further explored by noting that, according to Fig. 8, the trend of $9/2^+_2$ states along the As isotopic chain seems to follow the one of the $3^-$ states in the Ge isotopic chain (with only one exception at $N=42$). In their $\beta$-delayed $\gamma$ spectroscopy investigation of $^{80}$Ge Verney et al. [46] suggested that the two excited states located at 2852 and 3424 keV could have negative parity with spin $(5^-)$ and $(3^-)$, respectively. A coupling of these core excitations with the valence proton occupying the $\pi f_{5/2}$ single-particle state would create six states in $^{81}$As with suitable spin-parity for allowed Gamow-Teller (GT) population from the $9/2^+$ $^{81}$Ge ground state decay. Using a simple particle-octupolar vibration coupling interaction [47] given by the Eq. 2 with $\lambda =3$, we obtained the following order ($7/2^+,9/2^+,11/2^+$) which corresponds to the ordering of the levels observed experimentally and we reproduce the energy difference with $\frac{\langle j_1|k(r)|J\rangle }{(2C_{\lambda })^{1/2}}\simeq 400$ MeV$^{1/2}$.

$$\begin{aligned} \langle (j_1\lambda )J|H|J\rangle = \langle j_1|k(r)|J\rangle \langle j_1||Y_{\lambda }||J\rangle (2J+1)^{-1/2} \left( \frac{\hbar \omega _{\lambda }}{2C_{\lambda }}\right) ^{1/2}\nonumber \\\ \end{aligned}$$

(2)

The energy of the $3^-_1$ and $5^-_1$ excitations of $^{80}$Ge are very well reproduced by the shell model calculations as can be seen in Fig. 11 which contains also the results for lighter isotopes, even if part of this agreement might look accidental in view of the somewhat worse agreement with the experimental values in that last case. Anyway, one can conclude that, contrary to the $9/2^+_1$ case, the degrees of freedom available in the ($2p_{3/2}$, $1f_{5/2}$, $2p_{1/2}$, $1g_{9/2}$) valence space are sufficient to describe the positive parity triplet ($7/2^+_1,9/2^+_2,11/2^+_1$) which can be interpreted as originating from a proton particle to octupole vibration coupling.

Fig. 12

Upper panel : theoretical B(GT) distribution obtained with JUN45 shell-model calculation for $^{81}$As. Bottom panel : experimental results from this work for $^{81}$As, the red vertical bars represent the B(GT) for allowed transitions, while the green discontinuous line represents cumulative $\beta$ strength as a function of the energy

Fig. 13

Schematic representation of the doorway configurations involved in the $9/2^+\rightarrow 7/2^+,9/2^+,11/2^+$, $^{81gs}\text {Ge}\rightarrow ^{81}\text {As}$ Gamow-Teller decay

One can investigate if the $\beta$ strength received by the positive parity level system is compatible with this interpretation. Fig. 12 shows a comparison between the B(GT) extracted from the experimental data for allowed $\beta$ transitions. For the ($7/2^+_1,9/2^+_2,11/2^+_1$) region, just below 3 MeV excitation energy, the agreement is fair. This provides a nice further internal coherence argument confirming our previous interpretation for the structure of this triplet of states. However the calculations also predict a significant GT strength around 3.5 MeV which is barely noticeable in our data. It is difficult to conclude about this apparent disagreement in an energy region where the $\beta$ transitions are strongly suppressed by the phase-space factor. They would be revealed in any case by very weak $\gamma$ transitions which may have escaped our observational capabilities.

One experimental fact is striking and will deserve further comment : the B(GT) value for the transition to the $9/2^+_1$ is extremely small compared to those populating the “normal” positive parity states. To try and understand the origin of this phenomenon one may use the concept of GT doorway state in the spirit of Ref. [48]. Figure 13 shows schematically the doorway configurations through which the allowed GT population must proceed due to the valence topology. The doorway configuration a) is the one that opens on the $\{ 3^-,5^-\otimes \pi f_{5/2} \}_{7/2^+,9/2^+,11/2^+}$ “normal” core-couple states. Using the model of Ref. [48] one finds an associated total GT strength of $B(GT)\simeq 0.1$ associated to this doorway configuration, which compares favorably to the total of $B(GT)\simeq 0.15$ for the group of states located just below 3 MeV. In contrast, due to its supposedly more “collective” nature, the population of the lowest lying $9/2^+$ state (and that of other states originating from the same structure) must necessarily proceed through another doorway which can easily mix with configurations lying outside the natural valence space. The simplest configuration which meet this criteria is configuration b) in Fig. 13, involving a $\nu g_{9/2} \rightarrow \pi g_{9/2}$ single particle GT transition. Once a $\nu g_{9/2}$ pair is formed correlations are triggered that lead to a typical intruder, collective state, similar to the one described in Ref. [11], thus leading to a high fragmentation of the initial doorway GT strength.

5 Conclusion

$^{81}$As has been studied using $\beta$-delayed $\gamma$ spectroscopy at IGISOL, University of Jyvaskyla. Thanks to the high selectivity of the double Penning trap JYFLTRAP, the $^{81gs}$Ge beam obtained by proton-induced fission of $^{232}$Th was isomerically purified which allowed to determine unambiguously the half-life of the ground state [$T_{1/2}(^{81gs} \text {Ge})=6.4(2)$ s]. Moreover, as the spin-parity of the ground state of the mother nucleus can be reasonably assumed to be $(9/2^+)$, suggestions on the spin-parity of excited states of $^{81}$As have been improved allowing to the completion of the $9/2^+$ states systematics in odd-proton nuclei of this mass region. Whereas the understanding of the negative-parity states is quite trivial within the natural valence space of the region $Z>28$, $N<50$, the understanding of the positive-parity states is more challenging. This shows that positive-parity states contain correlations coming from outside the valence space either through the coupling to the core $3^-$ excitation with a proton structure involving protons from the $\pi f_{7/2}$ single-particle state under $Z=28$ , or from neutron $\nu d_{5/2}$ and $\nu s_{1/2}$ single-particle states that have an important role in this region as it is suggested by recent results [11, 12]. In the future, a study of the decay of $^{81m}$Ge ($E_{\text {ex}}=679.14(4)$ keV, $J^{\pi }=1/2^+$) using an isomerically pure beam would be welcome in order to go further in the understanding of $^{81}$As and constrain the role of isomeric states in the r process [49].