Fission resonances observed in the $^{237}$Np(d,pf) reaction and the fission barrier topology of $^{238}$Np

Abstract

The fission probability of $^{238}$Np was measured as a function of the excitation energy in the energy range of E$^* = 5.4 - 6.2$ MeV in order to search for transmission fission resonances. A radioactive $^{237}$Np target was bombarded with deuterons of E$_d$ = 12 MeV, whereas the energy of the protons was analyzed with a superior resolution of $\varDelta$E = 8 keV. The experiment was performed at the Tandem accelerator of the Maier-Leibnitz Laboratory in Garching employing the $^{237}$Np(d,pf) reaction. A group of fission resonances has been observed at excitation energies between E$^* = 5.5 - 5.8$ MeV, which could be ordered into three (superdeformed) rotational bands with a rotational parameter of $\hbar ^2/2\varTheta = 3.507$ keV, and identified as the first direct observation of transition states composing rotational bands in an odd-odd nucleus as they appear above the top of the outer fission barrier. Nuclear reaction code (talys1.95) calculations were also performed to extract the multi-humped fission barrier parameters of $^{238}$Np by fitting them to the experimental data of the present (d,pf) and previous (n,f) experiments. The extracted barrier parameters also support the above interpretation of the observed resonances.

1 Introduction

Shape isomerism has been a well-established phenomenon in the region of the actinides since the early 1960 s [1], which could be successfully explained by a double-humped fission barrier with a second minimum in the potential energy surface (PES). The second minimum appears due to strong nuclear shell effects on top of the liquid drop energy [2]. In such a model, the second potential minimum explains the stability of the isomeric state, which has a strong quadrupole deformation ($\beta _2\approx 0.6-0.7$). Since its discovery, a whole “island” of fission isomers has been identified in the actinide region with Z = 92–97 and N = 141–151 including 35 experimentally observed fission isomeric states [3]. Half-lives spread from 5 ps to 14 ms, covering a very extended timescale, but being still several orders of magnitude shorter than the half lives of spontaneous fission from their nuclear ground state.

However, shape isomers in odd-N uranium and neptunium isotopes have not yet been observed despite the large number (n=17) of isomeric states identified in the neighboring Pu isotopes. Only one experiment, reported by Oberstedt and co-workers in 2007 [4], claimed the observation of the isomeric fission decay of $^{235}$U with an unexpectedly long isomeric half life of $3.6\pm 1.8$ ms, recently in a re-analysis extended to 11±3 ms [5], populated in the (n,f) reaction, which is in apparent contradiction with theoretical expectations as well as half-life systematics [6]. In this regard, $^{238}$Np is of great interest, as a good odd–odd candidate for observing an isomeric state among the Np isotopes. Such isomeric state can decay with $\gamma$ emission and fission as competing processes. The branching ratio and the half life of an isomeric state are primarily determined by the structure of the double-humped fission barrier. In particular, the height and the penetrability (curvature parameter) of the first and the second potential barrier, which can be experimentally explored by the analysis of the measured sub-barrier fission cross sections. Experimental fission barrier parameters of $^{238}$Np, thus, would directly induce and justify the search for fission isomers of this nucleus.

In recent years, large efforts have been devoted to calculate the potential energy surfaces of the actinides, and to provide a comprehensive set of fission barrier heights and excitation energies of potential minima. These calculations employed a variety of theoretical approaches, such as microscopic-macroscopic models with different parametrization [7,8,9,10,11] as well as relativistic mean-field calculations [12, 13]. Most of these calculations resulted in a significant deviation with 0.5–1.5 MeV, furthermore they were inconsistent with the experimental values as well. As an outstanding case, predictions on the first (E$_A$) and second fission barrier (E$_B$) heights of $^{238}$Np spread from $\hbox {E}_A=5.3$ to 7.4 MeV, and $\hbox {E}_B=5.2$ to 7.0 MeV, respectively. In such cases, the experimental fission barriers represent a solid basis for model development and parameter tuning.

Another very characteristic consequence of the second potential minimum is the appearance of an intermediate fine structure in the sub-threshold fission cross sections observed in high-resolution experiments due to the coupling to the so-called superdeformed (SD) or class-II states [6, 14]. The fine structure manifests as resonances in the fission cross sections, which are caused by resonant tunneling through these excited class-II states. These high-lying resonances then can reveal the level structure of the SD states, moreover, the observed states could often be ordered into rotational bands [15]. Ultimately, the moments of inertia of these bands can characterize and prove the underlying superdeformed nuclear shape. In addition, the triple-humped fission barrier and the corresponding hyperdeformed (HD) or class-III states in the third minimum of the fission barrier were established both experimentally and theoretically in the region of the light, even–even actinides [16,17,18]. However, no such systematics has been established for the odd-odd actinides. In a recent experiment, we found conclusive evidence on the existence of HD bands in an odd–odd nucleus ($^{232}$Pa) [19], which initiated an experimental campaign on the systematic investigation of the odd–odd actinides. $^{238}$Np is an interesting isotope regarding hyperdeformation: it is an isobar of $^{238}$U, where a hyperdeformed third minimum has already been indicated [20]. In a previous $^{237}$Np(n,f) experiment, Fubini and co-workers [21] found indications for an intermediate structure at a neutron energy around E$_n$=40 eV, which leads to excitations close to the top of the fission barrier. However, no direct evidence on SD or HD states was claimed.

In this paper, we present the results of an experiment dedicated to search for fission resonances and to explore the topology of the fission barrier landscape of $^{238}$Np using the (d,pf) reaction at sub-barrier excitation energies.

2 Experimental setup

The measurement was carried out at the Tandem accelerator of the Maier-Leibnitz Laboratory (Garching, Germany) employing the $^{237}$Np(d,pf) reaction with a bombarding energy of E$_d$ = 12 MeV. The fission probability of $^{238}$Np was measured in the excitation energy region of E$^*$ = 5.4–6.2 MeV. An enriched (99%), 200 $\upmu$g/cm$^2$ thick, radioactive target of $^{237}$Np was used on a 25 $\upmu$g/cm$^2$ thick carbon backing. The $\alpha$ activity of the target was approximately 1.05 kBq. The ground-state Q-value for the reaction is 3.264 MeV, which was calculated using the NNDC Q-value calculator. The excitation energy of the compound nucleus was derived from the kinetic energy of the outgoing protons, that was measured by a Q3D magnetic spectrograph set at $\varTheta _{lab}$=139.4$^{\circ }$ relative to the deuteron beam direction. The well-known lines of the $^{208}$Pb(d,p) reaction were applied to perform the energy calibration of the focal plane detector [22]. The experimental energy resolution was deduced to be $\varDelta$E = 8 keV (FWHM) in the energy region of our interest. The potential effect of target radioactivity on the proton detection was considered, which was found insignificant due to the well-defined setting of the Q3D magnetic field to focus the outgoing protons with a kinetic energy between E$_p$ = 9–10 MeV on the focal plane. Such a setting filters out any low energy alpha particles by their significantly different magnetic rigidity. In addition, the focal plane detector of the Q3D is designed to be capable of particle identification as a further possibility to filter out any undesired particle type (eg. scattered deuterons). Kinematically broadened proton groups from reactions of the target backing ($^{12,13}$C) or the $^{16}$O contamination of the target material can be avoided by setting a proper proton detection. Eventually, we did not observe proton groups in the focal plane, only a structure-less continuum.

Fission fragments were detected in coincidence with the outgoing protons by two position sensitive avalanche detectors (PSAD) placed at ±70 degrees relative to the beam direction. The angular coverage was 20–170 degree with respect to the recoil axis ($\varTheta =15^{\circ }$ with respect to the beam direction). With a PSAD sensitive area of $10\times 10$ cm$^2$ and a detector-target distance of 5 cm, the solid angle coverage was 20% of 4$\pi$. Owing to the low pressure of the filling gas (p = 5 mbar), the PSAD detectors were not sensitive to any scattered light particles nor to the $\alpha$ particles from the radioactive target promoting this type of detector to be an ideal choice for heavy ion detection.

To determine the fission probability, the energy distribution of the outgoing protons was measured both in coincidence with the fission detectors and in a configuration where no coincidence was required (singles spectrum). Taking the solid angle of the PSAD detectors ($\varOmega _f$), the ratio of coincidence (N$_c$) to singles (N$_s$) spectra gave the distribution of fission probability (P$_f$) as follows:

$$\begin{aligned} P_f = \frac{4\pi }{2\varOmega _f}\cdot \frac{N_c}{N_s}. \end{aligned}$$

(1)

Here, we considered the fact, that the angular anisotropy of the coincident fission fragments is small for the present reaction ($W(0^{\circ })/W(90^{\circ })\approx 1.05-1.1$) [23, 24], and it was assumed to be negligible considering the large solid angle of the PSADs.

Fig. 1

a High resolution excitation energy spectrum of the $^{237}$Np(d,pf) reaction below the fission threshold. The contribution of the dominant, non-resonant processes (referred to as a continuous fission background) is indicated by the red spectrum. The insert shows the singles proton spectrum. No contamination proton groups were observed in this energy region. b The result of a Markov-chain peak searching algorithm applied to the background-free excitation energy spectrum. In the probability distribution, a resonance group could be clearly identified between E$^* = 5.5 - 5.8$ MeV. As a result of the fitting procedure, these resonances could be ordered into three rotational bands with K = 4 and with $\hbar ^2/2\varTheta$ = 3.507 keV as shown by its picket fence structure. The reduced $\chi ^2$ value of the fit was $\chi ^2$/F = 1.27

3 Fission resonances in $^{237}$Np(d,pf)

Fission resonances have already been observed in numerous high resolution fission experiments, in $^{230}$Th(n,f) [25], $^{233}$U(d,pf) [16], $^{231}$Pa(d,pf) [19], and in $^{231}$Pa($^3$He,df) [18] reaction studies. In most of these cases, the observed resonances could be ordered into rotational bands with moments of inertia characterizing the underlying deformation of the particular compound nucleus.

Figure 1a shows the measured high resolution ($\varDelta E/E \approx 0.1$%) excitation energy spectrum in coincidence with the fission of $^{238}$Np between E$^*$ = 5.4 and 6.2 MeV. The contribution of random coincidences was subtracted by gating on the flight time difference between the protons and fission fragments. As expected due to the very high level density of the odd-odd $^{238}$Np [$\rho (S_n)\approx 43\cdot 10^6$ MeV$^{-1}$], a very complex resonance region was observed below the fission threshold. The high resolution (n,f) experiment [21] showed similar complexity of intermediate structure, but did not allow for the identification of any rotational sequences due to the very limited momentum transfer ($l\le 1\hbar$) by s-wave neutron capture in thermal neutron induced reactions.

Owing to the rather low neutron separation energy of $^{238}$Np (S$_n = 5.488$ MeV), neutron evaporation competes with the fission process and thus the fission probability is rather small. Together with the exponential dependency of the quantum-mechanical tunneling, it results in a very limited fission yield at deep sub-barrier energies. Therefore, we applied a widely-used, very sensitive peak-searching method, the so-called Markov- chain algorithm [26] to the data to suppress the statistical fluctuations of the excitation energy spectrum and to identify any significant resonances. This method can also be used to determine and subtract the continuous, exponentially rising fission background (indicated by the red spectrum in Fig. 1a) emerging from the non-resonant tunneling process through the fission barrier. In the generated probability spectrum (Fig. 1b), a number of overlapping fission resonances could be clearly identified between E$^* = 5.5$ and 5.8 MeV. To allow for an interpretation of the underlying structure, the observed fission resonances have been fitted with overlapping rotational bands. Gaussians were used to describe the different band members assuming a dominant convolution with $\varDelta$E = 8 keV. In the fitting procedure, the energy of the band heads and the intensity of the band members were treated as free parameters, whereas a common rotational parameter was adopted for all three bands. Since the population of the different spins varies only slightly with excitation energy, the intensity ratios of the band members were also set to common values. The goodness of the fit was $\chi ^2/F$ = 1.27. In a preliminary analysis [27], we interpreted these resonances as members of a hyperdeformed rotational band, but the revised analysis with the above improved background suppression suggests that the fine structure of the observed resonances can be most convincingly described with three rotational bands with K = 4 as indicated in the figure with its picket fence structure and with a rotational parameter ($\hbar ^2/2\varTheta =3.507\pm 0.250$ keV) characteristic to an SD-like nuclear configuration. Here we mention that the angular data of the PSADs could not be applied to extract the spin information of the bands due to the very limited statistics and to the governing non-resonant background. Nevertheless, the K-values and spin assignments of the three bands are constrained by the ground state spin and parity of the $^{237}$Np target nucleus (I$^{\pi }$=$\frac{5}{2}^{+}$) and by the distribution of the transferred angular momentum in the (d,p) reaction at E$_d = 12$ MeV estimated by DWBA calculations [28, 29]. An average transfer angular momentum is inferred to be ${\overline{l}} = 2.9 \hbar$.

We also tested the assumption of an underlying HD rotational band configuration generating the observed resonance structure. In this scenario (Fig. 2), our data could be best described by three K = 3 rotational bands. The third band is indicated by dashed line due to its low significance and missing high-spin band members. The rotational parameter of the bands was fitted to be $\hbar ^2/2\varTheta =1.898\pm 0.272$ keV. The goodness of the fit was $\chi ^{2}$/F = 1.703. In addition to the worse fit, the missing band members also disfavor this interpretation as one can see in Fig. 2. Expected resonances assigned to the J = 4 and J = 6 states of the first and second band, respectively, were not observed as indicated by the question marks.

Fig. 2

The fission resonance group of Fig. 1b with the result of the fitting procedure (solid line) assuming HD rotational bands. The picket fence structure and the K values of the bands are indicated. The question marks represent the missing members of the bands. The quality of the fit (the reduced $\chi ^{2}$ value) is $\chi ^{2}$/F = 1.703

4 On the fission barrier of $^{238}$Np

In order to extract the fission barrier parameters of $^{238}$Np, we performed cross section calculations on neutron- and deuteron-induced reactions of $^{237}$Np employing the talys1.95 nuclear reaction code [30].

The physical models implemented in talys1.95 have been validated for the calculations of nuclear reactions that involve neutrons, $\gamma$ rays and light charged particles in a very wide bombarding energy range of 1 keV–200 MeV and for target nuclei with A $\ge$ 19 [30]. Therefore, it represents a perfect playground to understand and to describe the measured fission cross sections of $^{238}$Np near and below the fission threshold. The code also has some well-known limitations. Such limitations are the absence of a well-accepted model for $\gamma$ transitions in the region of neutron resonances and of an explicit treatment of break-up reactions leading to discrete states. However, in our case, none of these limitations are disturbing due to the energy region of our interest. On the other hand, the strength of the code is based on the standard nuclear reaction models it uses, applying a balanced combination of microscopic nuclear structure ingredients and phenomenological model parameters in order to achieve a solid description of the nuclear data.

In the reaction code, the fission transmission coefficients are calculated following the concept of the Hill-Wheeler formalism, which then enter the Hauser-Feshbach statistical model to compete with the particle (here primarily neutron) and photon emission. The fission barrier parameters, such as the barrier heights (E$_{A,B}$) and the curvature ($\hbar \omega _{A,B}$) of the double- or even triple-humped fission barrier, are given as input parameters. An important ingredient of the cross section calculations is the nuclear level density (NLD) both at the equilibrium and the saddle points of the deformation potential landscape. The NLD is given as a combination of the Constant Temperature (CT) and Back-Shifted Fermi Gas (BSFG) formulas, and has to be defined not only for the target nucleus, but also for the compound nucleus and for all residual nuclei that are involved in the calculation. This means typically a large set of parameters, usually 3 or 4 parameters for each isotope: the level density parameter a, the spin cut-off parameter $\sigma$, and the pairing shift P (or E0 and T in the CT formula.). The effect of nuclear deformation on the level density is taken into account by extra parameters that explicitly describe this collective enhancement. The ground state NLD parameters were taken from the RIPL-3 database [31] and from Ref. [32], while the level densities at the saddle point deformations (T$_{A,B}$ and E0$_{A,B}$) were taken from systematics and varied to fit the experimental data of the reaction channels competing with fission, e.g. (n,$\gamma$) and (n,tot) since no direct experimental information is available on the NLD at the saddle points. With this procedure, the NLD parameters of the saddle points were fixed to the values summarized in Table 2.

Another essential ingredient of the reaction calculations is the $\gamma$-ray strength function that drives the competition of the photon decay channel with other particle decay channels through the Hauser-Feshbach model. The most important parameters are the height, width, and energy centroid of the Giant Dipole Resonances (GDR) and the possible Pygmy Resonances (PR). The resonance parameters of any other transitions (typically M1,E2,M2) are usually taken from systematics. In the present case, the GDR and PR parameters were taken from Ref. [32]. The NLD and the GDR input parameters are summarized in Table 1.

Table 1 Input parameters used in the TALYS1.95 calculations: neutron separation energy (S$_{n}$), asymptotic level density parameter (${\bar{a}}$), damping parameter ($\gamma$), nuclear temperature (T), energy shift (E0), shell correction energy (dW), and the parameters of the giant dipole resonances; the peak cross section ($\sigma _{E1}$), the energy ($\omega _{E1}$) and the FWHM ($\varGamma _{E1}$) of the two GDRs. The NLD and the GDR input parameters were adpoted from Refs. [31, 32]

Table 2 Saddle point level density parameters of the first (T$_A$ and E0$_A$) and the second barrier (T$_B$ and E0$_B$) fixed by the cross section calculations of the (n,$\gamma$) and (n,tot) reactions. Estimated uncertainties are also indicated

The analysis of deuteron-induced reactions is complicated by its weak binding energy of 2.224 MeV resulting from the deuteron breakup process as described in Ref. [33]. A new model has been implemented in talys since version 1.7 enabling an improved treatment of the deuteron breakup, which has a significant effect on the calculated cross sections at the energy range of interest compared to previous models.

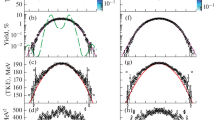
As described above, a large input parameter set is applied in these reaction code calculations. Some parameter values are well-established, evaluated and can be taken from the RIPL-3 database [31], while other parameters are hardly known, or not settled at all, and have to be adjusted by fitting them with the experimental cross section data. Thus, we performed calculations not only on the $^{237}$Np(d,pf) reaction, which was the goal of the present work, but also on previously measured neutron induced reactions, $^{237}$Np(n,$\gamma$), $^{237}$Np(n,tot), and finally on $^{237}$Np(n,f) in order to constrain the possible values of indefinite parameters, such as the NLD parameters at the saddle points. The experimental data, taken from the Experimental Nuclear Reaction Data (EXFOR) database [34], and the results of the calculations for the $^{237}$Np(n,$\gamma$) and $^{237}$Np(n,tot) reactions are presented in Fig. 3a and b in the relevant neutron energy region, respectively. A good agreement between the calculated and the experimental data is apparent.

Fig. 3

Experimental cross sections of the a) $^{237}$Np(n,$\gamma$) and b) $^{237}$Np(n,tot) reactions together with the results of the corresponding talys1.95 reaction code calculations (solid red lines)

The measured high-resolution fission probability spectrum of $^{238}$Np is shown in Fig. 4 as a function of the excitation energy of the compound nucleus in the energy region of E$^* = 5.4 - 6.5$ MeV. The experimental data of a previous, low-resolution ($\varDelta$E = 150 keV) experiment measured by Back and co-workers [35] is also presented. In the present experiment, we could reduce the uncertainty of the P$_f$ values by an order of magnitude at the low-energy side of the spectrum, which is the most crucial region for the exact determination of the fission barrier parameters.

The experimental data reduction of (d,p) reactions are always complicated by the deuteron breakup process. The contribution of this deuteron breakup to the (d,p) data cannot be separated experimentally, and thus, can only be estimated by the approach of Refs. [24, 29] which can be made by comparing the fission probabilities in different reactions leading to the same compound system. In the present study, we took the measured fission probability data of the $^{238}$U($^{3}$He,tf) [36] reaction. However, this correction can be considered only as a rough and qualitative estimate, since different reactions, such as (d,p) and ($^{3}$He,t) reactions in the present case, leads to different distributions of angular momentum states in the compound nucleus due to the different angular momentum transfer. In addition, we measured the fission probability in the excitation energy range of E = 5.4–6.2 MeV, below the range of the measurement of Ref. [36], so the direct comparison of the two reactions was not possible. Therefore, we used the experimental data of Ref. [35] to normalize our fission probability. Since we measured only the low-energy side of the fission probability, and only in a 800 keV wide range, we regarded it as a good assumption. We also remark, that the break-up contribution has only a slight variation with energy in this energy range without a significant influence on the fission barrier parameters, but only on the $\gamma$ and neutron-decay channel normalization factors (g$_{\gamma }$ and g$_n$ in talys1.95) used in the reaction code calculations.

Fig. 4

a The measured experimental fission probability of $^{238}$Np in the excitation energy range of E$^* = 5.4 - 6.5$ MeV (full red circles) together with the result of the reaction code calculation (solid red line). The experimental data of a previous, low-resolution experiment [35] is also shown by full blue circles. Underestimated values below 5.6 MeV are due to the resonances displayed in Fig. 1b. b Experimental cross section of the $^{237}$Np(n,f) reaction and the result of the talys1.95 calculation. All nuclear structure parameters (level density, fission barrier, etc) are identical to the (d,pf) case

In order to simulate the fission probability distribution, the total (d,p) and the inclusive (d,pf) cross sections were calculated as the function of the outgoing proton energy. The fission barrier parameters (E and $\hbar \omega$) were varied to achieve a good match between the calculation and experimental data, while all other input parameters were treated as fix parameters as taken from the result of the (n,tot) and (n,$\gamma$) analysis. The result of the talys1.95 calculation on the (d,pf) reaction is shown in Fig. 4a (solid line). The fission barrier parameters were deduced to be $\hbox {E}_A = 6.05 \pm 0.15$ MeV, $\hbox {E}_{B} = 5.35 \pm 0.15$ MeV, $\hbar \omega _A = 0.65$ MeV and $\hbar \omega _B = 0.45$ MeV, slightly different from the values of the RIPL-3 database (E$_A$ = 6.50 MeV, E$_{B}$ = 5.75 MeV, $\hbar \omega _A$ = 0.60 MeV and $\hbar \omega _B$ = 0.40 MeV), but in a better agreement with other experimental barrier systematics of the light actinides [36]. On the other hand, the present barrier parameters are inconsistent with the PES obtained in the most recent Woods-Saxon microscopic-macroscopic calculations [8]. Other evaluated theoretical results [9, 10] show better agreement with our experimental data. A significant difference in the second barrier heights was found in comparison with the data published by Back and co-workers [35] and by Bjørnholm and Lynn [6]. The later has long been considered as a unique reference since more than four decades already. However, the present reaction code calculations with the most recent experimental results on key input parameters of $^{237}$Np(d,pf), such as the ground state level density parameters and the $\gamma$-ray strength function suggest the revision of this picture of this particular nucleus.

The quoted errors of our experimental values on E$_{A,B}$ are estimates. Since we used the smallest possible set of input parameters in our reaction calculations, and beside the fission barrier parameters only the saddle point NLDs were not provided by direct measurements, the main uncertainties of the barrier parameters should originate from the uncertainty of the saddle point NLDs. Thus, we checked the sensitivity of the fission barrier parameters by varying the saddle point NLDs, and we concluded an upper limit on the errors of the fission barrier parameters.

To support the above results on the fission barrier parameters of $^{238}$Np, we performed calculations also on the $^{237}$Np(n,f) reaction. Experimental data were taken from Ref. [34]. The result of the calculation is shown in Fig. 4b. The same fission barrier and NLD parameters were applied as for (d,pf), only the value of the $\gamma$ decay normalization factor (g$_{\gamma }$) was modified.

Table 3 Experimental fission barrier parameters, the barrier heights and widths (in MeV) of the present study and the parameters reported by Refs. [6, 34,35,36]. Uncertainties are indicated if available

It is also worth mentioning, that the surprisingly low values of the barrier widths may suggest the reconsideration of the widely-accepted approximation of the fission barrier with a harmonic oscillator potential curve in fission models. An an-harmonic, “tower-like” potential originally suggested by Bowman and co-workers [37] decades ago in their low-energy photofission studies would better describe the potential curve determined from the current data.

Given the above results on the fission barrier parameters, the observed fission resonances in Fig. 1b could be a nice signature of the so-called transition states, which are assigned to states built on top of the second potential barrier (E$_B = 5.35$ MeV). According to the transition state concept introduced by Bohr [38], most of the nuclear excitation energy is transformed into deformation energy when the nucleus is passing over the saddle point. Thus, at this high deformation, the compound nucleus is thermodynamically cold, resulting in a discrete spectrum of low-lying collective excitations, like rotational bands in this case. Following Bohr’s concept, the near-barrier fission proceeds through these discrete transition states. The direct observation of such states is difficult and could so far only be concluded in a few cases of (n,f) and ($\gamma$,f) experiments [39] through the observation of characteristic fission fragment angular distributions. However, the rotational behavior of such states has not been unambiguously observed so far, while we identified for the first time such candidates in an odd-odd nucleus.

We emphasize that the present results could give a consistent picture as a combination of a more microscopic approach of nuclear spectroscopy and the rather phenomenological approach of nuclear reaction code simulations. As a conclusion, all measured and analyzed data could be nicely described by a double-humped fission barrier, while the observed resonances could be attributed to transition states on top of the second potential barrier.

5 Summary and outlook

We measured the fission probability of $^{238}$Np as a function of the excitation energy in the energy range of E$^*=5.4 - 6.2$ MeV in order to search for transmission fission resonances using the (d,pf) transfer reaction on a radioactive $^{237}$Np target. A group of fission resonances has been observed at excitation energies between E$^*=5.5 - 5.8$ MeV, which could be ordered into three rotational bands with a rotational parameter of $\hbar ^2/2\varTheta$ = 3.507 keV. Nuclear reaction code (talys1.95) calculations were performed to extract the multi-humped fission barrier parameters for $^{238}$Np. The fission barrier parameters were deduced to be E$_A = 6.05$ MeV and E$_{B} = 5.35$ MeV, sightly different from the evaluated RIPL-3 values, but in a good agreement with the systematics for the light actinides. Given the fission barrier topology, the above fission resonances were identified as rotational sequences of transition states of Bohr’s fission concept, the first time for an odd-odd nucleus. From the present experiment and analysis, there is no clear indication for hyperdeformation in $^{238}$Np, however, further high resolution investigations, in particular the identification of any fission isomeric state in $^{238}$Np and measuring its branching to $\gamma$ and fission decay could shed new light upon such a scenario.