Radiative corrections to the lepton current in unpolarized elastic lp-interaction for fixed $Q^2$ and scattering angle

Abstract

The kinematical difference between the description of radiative effects for fixed $Q^2$ vs a fixed scattering angle in the elastic lepton–proton (lp)-scattering is discussed. The technique of calculation as well as explicit expressions for radiative corrections to the lepton current in unpolarized elastic lp-scattering for these two cases are presented without using an ultrarelativistic approximation. A comparative numerical analysis within kinematic conditions of Jefferson Lab measurements and MUSE experiment in PSI is performed.

Appendices

Appendix A: Calculation of $\delta _S$ and $\delta _H$

For calculation of $\delta _S$ in the dimensional regularization

$$\begin{aligned} \frac{d^3k^\prime }{k^\prime _0}\rightarrow & {} \frac{d^{n-1}k^\prime }{(2\pi \mu )^{n-4}k_0} \nonumber \\= & {} \frac{2\pi ^{n/2-1}k_0^{\prime n-3}dk_0(1-x^2)^{n/2-2} dx }{(2\pi \mu )^{n-4}\varGamma (n/2-1)}, \end{aligned}$$

(A.1)

where $x=\cos \theta$ ($\theta$ is defined as the spatial angle between the photon three-momentum and $\mathbf{k}^\prime _i$ ($i=1-3$) that are introduced below) and $\mu$ is an arbitrary parameter of the dimension of a mass the reference system $\mathbf{p}_1+\mathbf{q}=\mathbf{0}$ is used.

The Feynman parameterization of (59) gives

$$\begin{aligned} \mathcal{F_{IR}}= & {} \frac{1}{4k_0^{\prime 2}}\int \limits _0^1dy \Biggl [ \frac{m^2}{k_{10}^{\prime 2}(1-x\beta _1)^2} +\frac{m^2}{k_{20}^{\prime 2}(1-x\beta _2)^2} \nonumber \\&-\frac{Q^2+2m^2}{k_{30}^{\prime 2}(1-x\beta _3)^2} \Biggr ] =\frac{1}{4k_0^{\prime 2}}\int \limits _0^1dy \mathcal{F}(x,y). \end{aligned}$$

(A.2)

Here $\beta _i=|\mathbf{k^\prime }_i|/k^\prime _{i0}$ for $i=1,2,3$ and $k_3=y k_1+(1-y)k_2$.

After the substitution of Eqs. (A.1) and (A.2) into the definition of $\delta _S$ by Eq. (62) and, using $\delta$-function, integrated over the photon energy $k_0$ one can find that

$$\begin{aligned} \delta _S= & {} -\frac{1}{2(4\mu \sqrt{\pi })^{n-4}\varGamma (n/2-2)}\int \limits _{-1}^1dx(1-x^2)^{n/2-2} \nonumber \\&\times \int \limits _0^1dy\mathcal{F}(x,y)\int \limits _0^{\bar{v}}\frac{dv}{v}\left( \frac{v}{M}\right) ^{n-4}. \end{aligned}$$

(A.3)

The integration over v and the expansion of the obtained expression into the Laurent series around $n=4$ result in

$$\begin{aligned} \delta _S= & {} \delta _S^{IR}+\delta _S^1, \end{aligned}$$

(A.4)

where

$$\begin{aligned} \delta _S^{IR}= & {} -\frac{1}{2}\biggl [P_{IR}+\log \frac{\bar{v}}{\mu M }\biggr ] \int \limits _0^1dy \int \limits _{-1}^1dx {\mathcal F}(x,y) \end{aligned}$$

(A.5)

and

$$\begin{aligned} \delta _S^1= & {} -\frac{1}{4} \int \limits _0^1dy \int \limits _{-1}^1dx\log \biggl [\frac{1}{4}(1-x^2)\biggr ] {\mathcal F}(x,y). \end{aligned}$$

(A.6)

Here $P_{IR}$ is the infrared divergent term defined by Eq. (43). Taking into account that $k_3^2=y(1-y)Q^2+m^2$ the integration over x and y variables in $\delta _S^{IR}$ is simple:

$$\begin{aligned} \delta _S^{IR}= & {} J_0\biggl [P_{IR}+\log \frac{\bar{v}}{\mu M }\biggr ], \end{aligned}$$

(A.7)

where $J_0$ is defined by Eq. (42).

For the calculation of $\delta _S^1$ we note that in the system $\mathbf{p}_1+\mathbf{q}=\mathbf{0}$ the energies of the initial and scattering lepton through the invariants:

$$\begin{aligned} k_{10}^\prime =\frac{X}{2M^2},\qquad k_{20}^\prime =\frac{S}{2M^2}. \end{aligned}$$

(A.8)

As a result,

$$\begin{aligned} \delta _S^1= & {} \frac{1}{2} SL_S+\frac{1}{2} XL_X+S_\phi (k_1,k_2,p_2), \end{aligned}$$

(A.9)

where

$$\begin{aligned} L_S= & {} \frac{1}{\sqrt{\lambda _S}}\log \frac{S+\sqrt{\lambda _S}}{S-\sqrt{\lambda _S}}, \nonumber \\ L_X= & {} \frac{1}{\sqrt{\lambda _X}}\log \frac{X+\sqrt{\lambda _X}}{X-\sqrt{\lambda _X}}, \end{aligned}$$

(A.10)

and

$$\begin{aligned} S_\phi (k_1,k_2,p_2)= & {} \frac{Q^2+2m^2}{4}\int \limits _{-1}^1dx\int \limits _0^1dy \frac{\log [(1-x^2)/4]}{k^{\prime 2}_{30}(1-x \beta _3)^2}. \nonumber \\ \end{aligned}$$

(A.11)

Notice that the standard expressions for $S_\phi$ are rather cumbersome, see for example Eqs. (35) and (A.14) of work [17]. In Appendix B we present a more compact analytical expression for this quantity.

For the calculation of $\delta _H$ the straightforward integration is used. Taking into account (60), one can find that

$$\begin{aligned} \delta _H= & {} -\int \limits _{\bar{v}}^{v_{cut}}\frac{dv}{v} \int \limits _{\tau _{min}}^{\tau _{max}}d\tau F_{IR} =J_0\log \frac{v_{cut}}{\bar{v}}. \end{aligned}$$

(A.12)

Appendix B: Calculation of $S_\phi$

Here we present a general approach suggested by ’t Hooft and Veltman in their work [28] for a compact representation of the $S_\phi$-function introduced by Bardin and Shumeiko in [16]. Let us consider a real photon with a momentum k and three other time-like four-momenta $a_i$ ($i=1,2,3$) with masses $m_i^2=a_i^2$. The basic idea consists in Feynman parameterization. Instead of usual approach used in the standard Bardin-Shumeiko technique with two fermionic propagator presented in previous appendix, taken in the system $\mathbf{a}_3=0$:

$$\begin{aligned} \frac{1}{a_1k}\frac{1}{ a_2k}=\gamma \frac{1}{a_1k} \frac{1}{\gamma a_2k}=\frac{\gamma }{k_0^2}\int \limits _0^1\frac{dy}{a_{40}^2(1-x\beta )^2}. \end{aligned}$$

(B.1)

Here, as in the previous appendix $x=\cos \theta$, a new four-vector $a_4=y a_1+(1-y)\gamma a_2$, and $\beta =|\mathbf{a}_4|/a_{40}$. The quantity $\gamma$ is choosing in such a way, that $(a_1-\gamma a_2)^2=0$, i.e. $a_1-\gamma a_2$ is lightlike vector.

Now introduce the following invariants:

$$\begin{aligned} s_1= & {} 2a_1a_3,\; \lambda _1=s_1^2-4m_1^2m_3^2, \nonumber \\ s_2= & {} 2a_2a_3,\; \lambda _2=s_2^2-4m_2^2m_3^2, \nonumber \\ s_3= & {} 2a_1a_2,\; \lambda _3=s_3^2-4m_1^2m_2^2. \end{aligned}$$

(B.2)

Then equation $(a_1-\gamma a_2)^2=0$ has the following two solutions:

$$\begin{aligned} \gamma _1=\frac{2m_1^2}{s_3+\sqrt{\lambda _3}},\qquad \gamma _2=\frac{s_3+\sqrt{\lambda _3}}{2m_2^2}, \end{aligned}$$

(B.3)

and the generalized form of $S_\phi$ looks as (A.11):

$$\begin{aligned} S_\phi =\frac{1}{4}\gamma s_3\int \limits _{0}^1\frac{dy}{a_{40}^2}\int \limits _{-1}^1dx \frac{\log [(1-x^2)/4]}{(1-x\beta )^2}. \end{aligned}$$

(B.4)

The first integration over x is straightforward

$$\begin{aligned} S_\phi =\frac{1}{2}\gamma s_3\int \limits _{0}^1\frac{dy}{m_4^2\beta } \log \frac{1-\beta }{1+\beta }, \end{aligned}$$

(B.5)

where $m_4^2=a_4^2=ym_1^2+(1-y)\gamma ^2 m_2^2$. The second integration has to be performed after the standard substitutions, while taking into account that for the first two momenta $a_{i0}=s_i/(2m_3)$.

Finally, we can find that for the general case $S_\phi$ depends on six variables and for $\gamma =\gamma _1$ it has the following structure:

$$\begin{aligned} S_\phi (a_1,a_2,a_3)= & {} \frac{s_3}{\sqrt{\lambda _3}} \Biggl ( \log ^2\frac{s_1+\sqrt{\lambda _1}}{2m_1m_3} -\log ^2\frac{s_2+\sqrt{\lambda _2}}{2m_2m_3} \nonumber \\&+ \, \mathrm{Li}_2\biggl [1-\frac{(s_1+\sqrt{\lambda _1})\rho }{8m_1^2m_3^2}\biggr ] \nonumber \\&+ \, \mathrm{Li}_2\biggl [1-\frac{\rho }{2(s_1+\sqrt{\lambda _1})}\biggr ] \nonumber \\&-\,\mathrm{Li}_2\biggl [1-\frac{(s_2+\sqrt{\lambda _2})\rho }{4m_3^2(s_3+\sqrt{\lambda _3})}\biggr ] \nonumber \\&-\,\mathrm{Li}_2\biggl [1-\frac{m_2^2\rho }{(s_2+\sqrt{\lambda _2})(s_3+\sqrt{\lambda _3})}\biggr ], \nonumber \\ \end{aligned}$$

(B.6)

where $\rho =(2s_1(s_3+\sqrt{\lambda _3})-4m_1^2s_2)/\sqrt{\lambda _3}$.

It should be noted that

$$\begin{aligned} S_\phi (a_1,a_2,a_3)= S_\phi (a_2,a_1,a_3) \end{aligned}$$

(B.7)

The r.h.s. of this equation corresponds $\gamma =\gamma _2$.

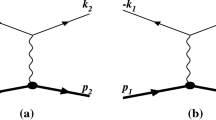
In our case $a_1=k_1$, $a_2=k_2$, $a_3=p_2$, and $s_1=X$, $s_2=S$, $s_3=Q^2+2m^2$, $m_1=m_2=m$, $m_3=M$.