Abstract
A software package for modeling segmented High-Purity Segmented Germanium detectors, AGATAGeFEM, is presented. The choices made for geometry implementation and the calculations of the electric and weighting fields are discussed and models used for charge-carrier velocities are described. Numerical integration of the charge-carrier transport equation is explained. The impact of noise and crosstalk on the achieved position resolution in AGATA detectors is investigated. The results suggest that crosstalk, as seen in the AGATA detectors, is of minor importance for the position resolution. The sensitivity of the pulse shapes to the parameters in the pulse-shape calculations is determined as a function of position in the detectors. Finally, AGATAGeFEM has been used to produce pulse-shape data bases for pulse-shape analyses of experimental data. The results with the new data base indicate improvement with respect to those with the standard AGATA data base. The AGATAGeFEM package sets itself apart with its high precision of the detector geometry description. This lends itself to numerical studies of the impact of segmentation lines and charge diffusion in the next step of code development.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Gamma-ray spectroscopy is one the most powerful techniques to study atomic nuclei, often combined with in-beam production of the species of interest. Its technical development has often been followed by new discoveries in the field of nuclear structure physics [1]. The development and construction of new advanced radioactive-beam and stable-beam facilities has prompted the development and construction of a new generation of \(\gamma \)-ray spectrometers. The last before present generation of \(\gamma \)-ray spectrometers, such as EUROBALL [2] and GAMMASPHERE [3], has limitations in terms of efficiency, resolving power, and maximum counting-rate capabilities. A way to improve the performance is to use fully digital electronics combined with highly segmented High-Purity Germanium detectors and perform the so-called \(\gamma \)-ray tracking [4]. Two large projects have been developed and are presently in the construction phase. In Europe the Advanced GAmma-ray Tracking Array (AGATA) [5] and in the USA the Gamma-Ray Energy Tracking Array (GRETA) [6]. For a more complete discussion on \(\gamma \)-ray spectrometers and their development over time see, e.g., Eberth and Simpson [1]. A recent discussion on the current performance of AGATA can be found in [7,8,9].
The main characteristic of \(\gamma \)-ray tracking spectrometers is the lack of Compton suppression shields. These shields, made of dense scintillator material such as BGO, act to veto \(\gamma \) rays which scatter and fail to deposit their full photo-peak energy in the germanium crystal and are crucial for a high peak-to-total in a standard \(\gamma \)-ray spectroscopy array. In \(\gamma \)-ray tracking the shields are removed allowing an increase of the solid angle covered by germanium, with a corresponding increase in efficiency. A high peak-to-total ratio is achieved by comparing the interaction positions of the scattering \(\gamma \) rays in the germanium with the Compton scattering formula and rejecting not fully absorbed \(\gamma \) rays. For tracking it is crucial that the PSA gives the interaction positions with high accuracy (i.e. less than 5 mm FWHM at 1 MeV) to achieve high performance . The accuracy of the PSA depends on how well the detector response is known, and to a lesser degree, the algorithm used for the PSA. Characterisation of the HPGe detectors, and associated electronics, is hence of great importance.
Extensive work has been carried out to model the response of the highly segmented germanium detectors used by AGATA and GRETA. Over the years, several software packages have been developed within the AGATA collaboration to model the pulse shapes from segmented detectors [10,11,12,13,14]. At the same time extensive efforts have been made to provide these codes with accurate input in terms of impurity concentrations [15, 16], crosstalk and electronics response [17,18,19], and charge-carrier mobility [20]. Within the AGATA community it is presently the ADL [14] package that is used to produce the data bases of pulse shapes needed for pulse-shape analysis. For the corresponding work related to GRETA and GRETINA see [21, 22] and the references therein.
The large volume HPGe crystals developed for \(\gamma \)-ray spectroscopy have also found use in other scientific fields such as the search for WIMPs [23] and neutrino-less double beta decay [24, 25]. These applications share with \(\gamma \)-ray tracking the need to accurately know the response of the detectors and tools developed for HPGe \(\gamma \)-ray detectors are used within the neutrino-less double beta decay community [24, 26].
In this paper a software package written to model the segmented HPGe germanium detectors used in AGATA is described. It has been under development and used for investigating different aspects of the pulse-shape analysis and \(\gamma \)-ray tracking procedure for more than a decade. The main intended use of this package is PSA development. However, it can also be used for detector characterization or pulse-shape data bases production. A short introduction to pulse-shape calculations in semiconductor detectors is given in Sect. 2. The AGATAGeFEM package together with models and assumptions made are described in Sect. 3. An effort to characterize where in the detector volume the calculated pulse-shape parameters have the largest influence is presented in Sect. 4. How a poorly known crystal geometry might affect pulse-shape analysis is investigated in Sect. 5. The use of the software package to benchmark the effect of crosstalk and noise on the two pulse-shape algorithms Extensive Grid Search (EGS) and Singular Value Decomposition (SVD) is covered in Sect. 6. To validate the pulse shapes calculated by the AGATAGeFEM package pulse-shape data bases used for PSA have been calculated. Results using the AGATAGeFEM bases are compared to results produced with bases calculated with the ADL [14] and presented in Sect. 7. Conclusions are given in Sect. 8.
2 A short introduction to signal generation in semiconductor detectors
The signal generation (referred to as “pulse shapes” in this work) in all detectors is based on the motion and collection of charge carriers and is calculated using the Shockley-Ramo theorem [27, 28]. The theorem states that the induced charge on an electrode due to moving charges is
where \(\mathbf {W}(\mathbf {r}_{e,h})=-\nabla \varPhi _W(\mathbf {r}_{e,h})\) is the weighting field, \(N_{e,h}\) the number of charge carriers for electrons and holes, respectively, and \(\mathbf {v_{e,h}}(\mathbf {r_{e,h}})\) are the charge-carrier velocities. The charge carrier velocities are functions of the electric field \(\mathbf {E}(\mathbf {r})\). The electric field is calculated from the electric potential as \(\mathbf {E}(\mathbf {r})=-\nabla \varPhi (\mathbf {r})\).
The calculation of pulse shapes for a semiconductor detector begins with solving the two partial differential equations (PDE)
and
known as the Poisson and Laplace equations, respectively. It is hence formulated as an electrostatic problem imposing the approximation that leakage currents in the detectors are too small to influence the electric field. Together with appropriate boundary conditions they describe the electric (Poisson) and weighting (Laplace) potentials. In Eq. 2, \(\rho (\mathbf {r})\) is the space charge distribution in the detector and \(\epsilon _{Ge}\) the dielectric constant for germanium. Boundary conditions for the electric potential are the applied detector bias and 0 V on the conducting surfaces. For surfaces requiring passivation the boundary condition should include possible charges, as they potentially changes the electric field close to them. As the charges are unknown the approximation of natural boundary conditionsFootnote 1 is used in this work. The weighting potential \(\varPhi _{W}(\mathbf {r})\) is calculated by setting the potential on the electrode of interest to 1 and to 0 on all other conducting surfaces.
One of the major difficulties when integrating Eq. 1 is to find the correct function for the charge-carrier velocities \(\mathbf {v_{e,h}}(\mathbf {r_{e,h}})\). The physics and the models used in this work is discussed in Sect. 2.1.
To reproduce realistic pulse shapes for a given detector the effects of the limited bandwidth of the electronics have to be included. The effect of the bandwidth can in principle be measured for a system using a pulse generator. However, the approximation using an analytical function is usually sufficient and is more practical. The crosstalk between different segments has to be modeled. Typically a difference is made between so-called linear and derivative crosstalks. The former originates mainly from the capacitive coupling of the electrodes whereas the later has originates in the front-end electronics. The AGATAGeFEM package models both types of crosstalk.
2.1 Charge-carrier motion in High-Purity Germanium detectors
For all pulse-shape calculations the models used to describe the charge-carrier mobilities are of crucial importance. A commonly used function [29] to describe the charge-carrier velocity is
where \(E_0\), \(\beta \), \(\mu _{n}\), and \(\mu \) are experimentally adjusted parameters. Here \(\mu \) is the low-field mobility, \(E_{0}\) is the critical field above which the velocity starts to saturate. The parameters \(\mu _n\) and \(\beta \) allows a better fit to experimental data. This parameterization is valid when the electric field is parallel to one of the symmetry axes of the germanium crystal (\(<100>\), \(<110>\), or \(<111>\)). The charge-carrier velocity is only parallel to the electric field when the electric field is parallel to a symmetry axes. For germanium crystals cooled down to liquid nitrogen temperatures (\(\approx -175^{\,\circ }\)C) several models have been developed for the electron mobilities. For AGATAGeFEM the model of Nathan [30] is used. It treats the anisotropy of the electron drift velocity observed in germanium with high accuracy with the formalism described in Mihailescu et al. [31].
For the hole mobility Bruyneel et al. [20] have developed a model based on the so-called “streaming motion” concept. The holes are accelerated to a threshold energy, they emit an optical phonon losing most of their energy, are re-accelerated in the applied electric field to the threshold energy, and so on. In this work a different approach has been used, this to investigate the validity of the approach in the context of large volume HPGe detectors. The model used in this work assumes that the variation in carrier velocity as a function of the electric field can be described by the fraction of holes populating the light-hole band and the heavy-hole band with a field-dependent relaxation time. The term light(heavy)-hole band refers to the effective mass (see Eq. 6) of the hole in the conduction band in question [32]. The anisotropy is given by the effective masses of the second derivative of the energy of the hole bands. Despite the much higher energy of the light-hole band as compared to the heavy-hole band the model reproduces experimental data for hole drift velocities [33]. For the holes the surfaces of equal energy in the conduction bands are not ellipsoids, which means that the reciprocal effective mass tensor will depend on the direction of the wavevector \(\mathbf {k}\). Here the assumption is made that the wavevector is parallel to the applied electric field. The hole energy functions read [32].
where the positive (negative) sign is for the light (heavy)-hole band. Using equation
to calculate the reciprocal effective mass tensor, we have
In Eq. 7 the factor \(\mathcal {T}(E)\) is considered an electric-field-dependent relaxation time and \(\mathcal {F}\left( E\right) \) is the fraction of the holes moving in the heavy-hole band and is also field dependent. As in the case of electrons, Eq. 4 can now be used to calculate the hole drift velocities in the \(<100>\) and \(<111>\) directions. Using these velocities \(\mathcal {T}\left( E\right) \) and \(\mathcal {F}\left( E\right) \) are obtained at the electric-field strength for which the velocity is calculated. A big difference for holes as compared to electrons is that the reciprocal effective mass tensor changes with the direction of the electric field. In Fig. 1 the anisotropy of charge carrier transport is illustrated. Without anisotropy the top row would show perfect spheres in one color and the second and third rows would show zero velocities. The deficiency of the model can be noted from the \(v^{h}_{\varphi }\) shown in the bottom right corner. There should be no anisotropy in any of the \(<100>\), \(<110>\), or \(<111>\) directions as these are symmetry axes in germanium. This is different for the electrons shown in the left column.
Neither the drift model for electrons nor for holes takes into account the effects of crystal temperature or impurity concentrations on the charge-carrier drift velocities although these effects modify the drift velocities [34]. The effect of varying the hole-drift velocity was studied within the GRETINA [22] and AGATA collaborations [35]. In these works it is concluded that the position resolution is not limited by the hole mobility models. When the hole mobility is varied within reasonable limits it is difficult to separate the effects from those coming from the front-end electronics. Numerical values used in this work for the mobility parameters are presented in Table 1.
3 The AGATAGeFEM software package
Several software packages have been developed to calculate pulse shapes from the High-Purity Germanium detectors used in AGATA. Examples from the AGATA collaboration are MGS [13, 36], JASS [12, 12, 19] and ADL [14, 20]. Although differing in details, they have in common the use of finite difference PDEs solvers for the electric field and the weighting potentials in the detector. However, the complex shapes of the AGATA crystals can only be accurately described using a finite difference scheme with very dense rectangular grids. One way of improving the approximation without needing the very dense grids is to use finite element methods (FEM), especially when combined with adaptive mesh refinement. While it is beyond the scope of the present work to describe FEM (the interested reader is referred to [37] and references therein) the method solves partial differential equations by reformulating them into integral equations, the so-called weak formulation. The domain of integration can then be subdivided into smaller domains and for each domain the integration can be performed using a predefined function. Domain and/or function is commonly refereed to as the “element”. It is the possibility to subdivide any integration domain into smaller domains that makes it easier to implement complex geometries in FEM as compared to finite difference schemes and gives natural inclusion of boundary conditions. For the finite difference schemes a spatial resolution of typically 0.5 mm is used, whereas in AGATAGeFEM it varies from several millimeters in regions of weak fields to tens of micrometers where the combination of strong field gradients and complex geometry are combined. Another strong point of FEM is that the solution is an approximation of a function describing the electric potential and not the electric potential at the grid points. This removes possible ambiguities when calculating the electric field in the detector volume. The program written for the MARS project [10] uses FEM for calculating the fields and was used to optmize the electrical segmentation of the AGATA detectors. The development of this code seems however to have stopped.
The AGATAGeFEM package, written in C++, uses high-quality open-source FEM software to calculate the electric and weighting potentials of AGATA type germanium detectors. For the charge-carrier transport the ordinary differential equation solvers of the Gnu Scientific Library [38] are used. The geometry is described to within \(10^{-6}\) mm for charge transport and mesh generation. Earlier versions of the program used mainly the FEM library dealII [39, 40]. This is a very flexible code that allows an iterative refinement of the FEM mesh in a very simple way. However, the mesh cell geometry is limited to quadrilaterals and hexahedra. From the point of view of solving the partial differential equations this is a good choice. However, in AGATAGeFEM the solutions of the Poisson and Laplace equations are not projected down to a regular grid when used in the charge carrier-transport process. This is also the case for calculations of the induced signals via the Shockley-Ramo theorem. The fundamental idea is that the mesh refinement procedure tells where a high granularity is needed and all projection onto a regular grid deteriorates this information. The problem is then to find the correct cell in an irregular mesh. The curved boundaries of hexahedra cells make these calculations complicated. As a result the first version of AGATAGeFEM was capable of calculating about 2–3 pulse shapes/s. Although this is sufficient to calculate a basis for PSA it is far from what is required when using AGATAGeFEM to fit parameters in the pulse-shape calculations or for use in a complete Monte Carlo simulation chain. The FEM part of the program was therefore changed to the libmesh library [41]. It uses tetrahedra with each side defined by three points, which allows quicker finding of the correct mesh cell. The AGATAGeFEM is further constrained to use only linear bases functions in the solution. This allows an increase in calculation speed by a factor of almost 100 while still reproducing the results using dealII.
AGATAGeFEM is fully parallelized with threads and the MPI interface. This applies to the field calculations and the pulse-shape calculations. Parallelism is also used while fitting the pulse-shape parameters. To minimize the \(\chi ^2\) Minuit and Minuit2 [42] are employed. AGATAGeFEM further has interfaces allowing calculating and displaying fields and pulses from the ROOT [43] interpreter interface. This can be performed inside the chosen detector geometry if needed. Furthermore, a very simple server client mechanism allows other programs to ask the server to calculate pulse shapes.
The AGATAGeFEM package also contains miscellaneous codes for
-
applying pre-amplifier response
-
crosstalk
-
re-sample pulse shapes
-
compare pulse shapes
-
calculate pulse shapes from the output of the AGATA geant4 MC [44]
-
create data bases for PSA.
3.1 AGATA Detector model
3.1.1 Geometry
The AGATA crystals are \(90\) mm long and have an diameter of \(80\) mm and were produced in four different shapes. A symmetric hexagonal shape for three prototypes and three different non-symmetric hexagonal shapes for use in the AGATA [5]. For the generation of the FEM mesh OpenCASCADE models of the detectors are generated. For the charge transportation the detector geometries are implemented in C++ as the union of a cylinder and six planes or using the CSG geometry of geant4 [45]. The hole corresponding to the central contact has several parameters allowing it shape and orientation to be varied. These are the radius of the hole, the radius at the bottom of the hole joining the side of the bore hole with the bottom part, and translation and rotation of the axes of the hole. The two different geometrical models of the detectors are equivalent. Examples of the geometries are shown in Fig. 2, where the crystal-fix coordinate system used in this paper also is shown. For details on the segmentation and crystal-fix coordinate system see [5].
3.1.2 Calculations of the electric fields and weighting fields
AGATAGeFEM uses a total of 40 fields for calculating the pulse shapes. Thirty seven of these are the weighting fields for the 36 segments and the central contact. These are defined either using the limiting depth values and start and stop angles of a segment or using the intersection between the detector surface and four planes, excluding the central cotact which is trivial. The segments do not have to cover the entire surface of the detector. This is intended for modeling the gaps between the segment contacts on the outer surface [46]. Presently no implementation of suitable boundary conditions for the electric field exists in AGATAGeFEM limiting the value of this option, so in this work the outer segmentation covers the whole outer surface without overlap.
When solving the charge-transport equations, AGATAGeFEM uses three fields to calculate the electric field. The first is the solution to the Poisson equation with \(0\) V on the surface of the detector and \(V_{bias}\) on the central contact, and the nominal impurity concentration. The choice to include charge impurities here was made to maximize the benefits of mesh refinement. Representative values for the charge impurities are presented in Table 3. The second field is the solution of the Poisson equation assuming \(0\) V on both the surface and the central contact but with an impurity contribution of \(10^{10}\)/cm\(^3\) at the front of the detector that decreases linearly as a function of depth to the back of the detector where it is \(0\). The third and final field is similar to the second but has an impurity concentration with reversed slope. The use of three fields allows variation of the effective impurity concentration and its effect on the electric field in the detector without recalculating the electric field, this by adding field two and three to the first field with varying weights. Solving the Poisson equation when varying the impurity concentration is too computationally intensive to allow the fitting of detector parameters to experimental signals.
To solve the Laplace equation and the Poisson equation AGATAGeFEM uses the libmesh library [41], with the meshes generated with gmsh [47]. As a first step the Laplace or the Poisson equation is solved using a uniform mesh with an average cell size of 2 mm. This solution is then used to estimate the largest acceptable geometrical approximation of the mesh in order to ensure an error on the field of less than one per mil of the maximum value of the field. This step is then followed by repeated local refinement of the mesh based on an estimate of the local error of the solution [48] until the field is described by at least \(2.5*10^{5}\) degrees of freedom. A limit that gives a good approximation of the fields as shown in Sect. 7. The final step for each of the 40 fields is to create look-up tables on a 2 \(\times \) 2 \(\times \) 2 mm\(^3\) grid over the detector volume to allow fast access to the correct mesh cell when evaluating the fields.
3.1.3 Solving the charge transport equation
The detector pulses are calculated by first transporting the point representing electrons and the point representing holes from the point of the \(\gamma \)-ray interaction until they reach the boundary of the detector volume using
The equations are solved separately for the holes and the electrons using a solver algorithm with an adaptive time step. AGATAGeFEM allows the user to choose between any of the possible algorithms provided by GSL, but the default choice is the embedded Runge-Kutta-Prince-Dormand method [49]. The paths of the charge carriers are calculated with an adaptive time step and sampled at a chosen frequency, by default 100 MHz. As the charge carriers approach the boundary of the detector the sampling frequency is adapted to allow an accurate description of the pulse shape as a \(10\) ns time step typically gives a path that ends outside the detector.
In the next step the charge on electrode \(i\) is calculated using
for all \(37\) signals.
3.1.4 Convolution of the signals with the transfer function of the electronics
The signals can be convoluted with the response of the electronics. This is not done when generating a basis for PSA. In this work the response of the electronics have been modeled by the function [11, 12] shown in Fig. 3. A convolution (in time-domain) is made for all 37 calculated signals. A possible improvement is to use a function with a slower rise time for the central contact. However, the convolution is mainly used for PSA development where AGATAGeFEM is used both for generating the bases and the signals that are analyzed so the exact form of the function is of minor importance.
Left: Example of a front segment weighting field. The field strength goes from 0 (blue) to 1 (red). Shown is also the mesh used for solving the Poisson equation. Right: Examples of net-charge signals and transient signals with and without convolution with the transfer function. The modulating effect of the response of the electronics is clearly seen (red shape). The effect of linear (green shape) and derivative (blue shape) crosstalk is also shown. For the net-charge segment the effect of the derivative crosstalk is too small to be seen
The effect of both linear and derivative crosstalk can be included in the transfer function. Here the linear crosstalk is applied as
where i and j are the index of the electrodes and \(C_{ij}\) the fitted crosstalk coefficients, and the derivative crosstalk is applied using
where \(C_{der}\) is a common factor. Typical values for \(C_{ij}\) are less than one per mil (for segment to segment) to a few per mil (core to segment). The \(C_{der}\) coefficient is about 1/ns, i.e. 10 in absolute numbers with a 100 MHz sampling ratio. The linear crosstalk is applied before the convolution with the response function shown in Fig. 3 whereas the derivative crosstalk is applied afterwards. For in-depth discussion concerning crosstalk in segmented germanium detectors, see [17, 50]. An example of the signals calculated with and without response function is given in Fig. 4. The effects of linear and derivative crosstalks are also shown.
4 Investigation of the sensitivity of signal shapes to detector parameters
To understand the influence of the different parameters in the calculations of charge-carrier velocities on the shape of the signals the sensitivity of the pulse shapes to each such parameter is calculated for a large number of points inside a detector of symmetric type. As the absolute value of the different parameters varies over many orders of magnitude normalized dimensionless parameters were used to estimate this sensitivity. The sensitivity is evaluated as the second derivative of a \(\chi ^2\) at zero fractional variation of the parameter in question. It is extracted by fitting a second degree polynomial and is hence the curvature of the \(\chi ^2\) function. The \(\chi ^2\) is calculated using the original pulse shape and a pulse shape calculated using the changed parameter. In Fig. 5 the extraction of the sensitivity is shown for the hole mobility in the \(<111>\) direction.
The number of positions in the detector of the pulse shapes that are most sensitive to each parameter are shown in Fig. 6. The parameters that control the velocity of the charge carriers in the \(<100>\) direction are dominating at most points. This is not surprising since in the coaxial part of the detector the charge transport is never in a \(<111>\) direction. It is worth noting that the hole mobility parameters for the \(<111>\) direction have a large impact at more positions than the \(<111>\) direction parameters for the electrons. This can also be understood geometrically as the paths close to the \(<111>\) direction with an overlapping large weighting potential are dominated by hole transport occurring at the corners of the front face of the detector. Crystal orientation only dominates at one position, a consequence of the definition and its evaluation at zero change.
Figure 7 shows the average sensitivity of the pulse shapes to a parameter at the positions dominated by the parameter. One can notice that the highest average sensitivity is found for the crystal orientation followed by the parameterization of the hole mobility in the \(<111>\) direction. This is understandable since these parameters are the most likely to change in which segment the charges are collected. To give an idea of what the curvature represents the pulse shapes corresponding to the five points used to fit the curvature for the position − 15,10,70 in the crystal and the \(E_{0h}^{<111>}\) parameter are shown (in black) in Fig. 8. At this point the curvature is about \(9*10^{5}\). Also shown are the pulse shapes (in grey) generated when moving away from the original position \(\pm 1\) mm along all three axes. This illustrates that the parameter space searched when determining the curvature does not modify the pulse shapes beyond the present achieved position resolution. This explains why different choices of parameter values give comparable results when used for calculating bases used for PSA (see Sect. 7).
Example of pulse shape (black) from a position where the variation of the \(E_{0h}^{<111>}\) parameter generated a curvature of \(9*10^{5}\). Also shown, as a reference, are the variations of the pulse shapes as steps of \(\pm 1\) mm are taken in the x (red curves), y (green curves), or z (blue curves) directions
In Fig. 9 the relative sensitivity as a function of position in the detector volume is shown for the \(\mu _e^{<100>}\) parameter. It is homogeneous inside the volume although the projection on the XY plane shows that, apart from the volume effect, there is an increase in sensitivity close to the \(<100>\) directions. This is expected as the charge carrier velocity mainly depends on parameters for that crystal axes at these positions.
The sensitivity of the pulse shapes to the \(\mu _{e,h}^{<100>,<111>}\) parameters as a function of position. The size of the cubes are proportional to the sensitivity. Note that the cube sizes are not comparable between the figures. Top left: \(\mu _{e}^{<100>}\) Top right: \(\mu _{h}^{<100>}\) Bottom row left: \(\mu _{e}^{<111>}\) Bottom right: \(\mu _{h}^{<111>}\)
A similar pattern can be seen for the \(\mu _h^{<100>}\) parameter in Fig. 9, but with the maximum shifted towards lower radii corresponding to pulses in which the hole drift contributes more to the pulse shapes. The situation is different for the parameters \(\mu _e^{<111>}\) and \(\mu _h^{<111>}\), also shown in Fig. 9. For the electrons the pattern is easily understood, i.e. parameters concerning the \(<111>\) direction show sensitivity in the region where charge transport is parallel to the \(<111>\) direction.
For the holes the pattern is not reflecting the \(<111>\) direction in the crystal. This is not imposed by the model, unlike for the model of the electrons. When the electric field is parallel to a symmetry axis of the crystal the charge carriers move, by symmetry arguments, parallel to the field and the axis. This can also be seen in Fig. 1 where the \(\varphi \) component of the hole velocity is non zero in the xy-plane \(<100>\) directions. Imposing this symmetry on the hole velocity model is planned for future work, but as shown in Sect. 7 this deficiency does not seem to degrade the results.
5 Impact of imperfectly known crystal geometry on PSA
As the geometry (including contact thickness dead layers etc.) is not perfectly known, it is interesting to investigate its possible impact on the pulse shapes. A different geometry was used to generate the basis for PSA. The influence of an imperfect geometry has been investigated for three different cases, ranging from an extreme (unrealistic) case to a small error on the front-face segmentation.
The three different geometries used for investigating the impact of an imperfect geometry on the pulse-shape data bases. In picture a, the nominal geometry of a capsule type A is shown. In b the bore hole for the central contact has been displace 5 mm and with an angle of \(\varphi =0.2\) radians and \(\theta =0.1\) radians. In figure c the radius of the bore hole has been enlarged with 3 mm, this as an (extreme) example of the lithium drifted central contact
Using the nominal geometry of an A type crystal with a representative impurity concentration a pulse-shape basis for PSA with a grid size of 1 \(\times \) 1 \(\times \) 1 mm\(^3\) and a sample rate of 100 MHz was first calculated. Using three differently modified geometries the same 1 \(\times \) 1 \(\times \) 1 mm\(^3\) grid of points were used to calculate pulse shapes for each of those. The following geometry modifications were used: (1) An incorrect front-face segmentation. (2) A displaced and tilted borehole for the central contact. (3) An enlarged bore hole for the central contact. The nominal geometry and geometries 2 and 3 are shown in Fig. 10 whereas the difference in front segmentation is shown in Fig. 11. The pulse-shape basis of the nominal geometry was then used for PSA on the three different pulse-shape sets corresponding to each geometry variation and on itself as a reference. The used PSA is a simple extensive grid search using the full length of the traces (50 samples/500 ns in this case) for the net-charge segment and its four (three in case of an A or F net-charge segment) neighbouring segments to calculate the \(\chi ^2\). For these tests 5 keV (RMS) Gaussian noise was added to the pulses from the data bases that were compared to the data base for the reference geometry. An interaction energy of 1 MeV was used. In Fig. 12 the reduced \(\chi ^2\) for the four different cases are shown. It can be seen that for all of the geometries it is impossible to use the \(\chi ^2\) distribution to make a statement on whether the geometry used to produce the basis is good or bad - all four distributions are reasonable.
The average error on the determined positions (Fig. 13 shows this for the x coordinate) is the most important parameter to evaluate the performance of a pulse-shape basis. The incorrect segmentation lines do not produce an error that is significant as compared to the experimentally determined values (\(\sigma \approx 1.7\) mm [51]). The two other geometries give an error in the determination of the actual position that is larger than the experimental result. A tentative conclusion is that the geometries of actual AGATA crystals are better known than the two rather extreme cases used for this test. These results also show that the geometry of a crystal should be determined by 3D scanning.
Examination of the scatter plots of the determined interaction positions, see Fig. 14, shows no clustering effects for the case where PSA is performed on pulses belonging to the reference basis (i.e. on itself) nor with a small error on the front segmentation. However, when the basis is made with a geometry that deviates from the geometry of the detector, one of the effects is clustering of events. The origin of this clustering is that the rise times contain most of the information in the pulse shapes and all pulses with extreme rise times will be clustered towards the position in the basis with the closest rise time. The empty voids are a combination of this rise-time mismatch and the union of the central contacts of the nominal geometry and that of the two variations of the bore hole geometry.
Scatter plots of positions determined with PSA using a basis calculated with the nominal AGATA A type detector. From left, PSA performed with the basis on itself with noise added, PSA performed on signals calculated with an incorrect front-face segmentation, PSA performed with signals calculated using a too large central contact diameter, and finally, to the extreme right, PSA performed using signals calculated with a bore hole for the central contact off center and tilted. The scale to the right applies to each row. The projection and position of the projected slice is given to the left of each row
6 Evaluation of the impact on pulse-shape analyses of crosstalk and noise
The resolution for Extensive Grid Search (EGS) and the Singular Value Decomposition matrix inversion (SVD) [52] as a function of noise level and the inclusion of derivative and linear crosstalk has been investigated using the AGATAGeFEM package. It is of high interest to characterise the difference at small signal-to-noise ratios for the two algorithms as the grid search presently used for PSA does not give meaningful results for signals smaller than about 50 keV. The amount of linear crosstalk used for this investigation is typical for AGATA crystals when mounted in AGATA triple cryostats [17, 18] and is about one part per mil. The derivative crosstalk is assumed to be proportional to the linear crosstalk with the proportionality factor taken as that used in the AGATA online PSA (a factor of 10).
Assuming that the physics of a segmented germanium detector is well known, the possibility to determine the coordinates of a \(\gamma \)-ray interaction in a large volume HPGe detector is limited by the knowledge of the response of the electronics and by the signal-to-noise ratio. These two aspects have been studied by performing PSA on a data set of pulse shapes calculated using the AGATAGeFEM with exactly the same parameters as the basis used by the PSA code. The data set consisted of 2700 shapes corresponding to interactions randomly distributed in the detector volume. Each pulse shape in the data set was analysed for 6 different levels of noise (ranging from 0.6 to 37% rms) and using EGS and SVD. This was performed with or without linear and derivative crosstalk for a total of 48 different combinations. Each pulse was analyzed 20 times with noise regenerated for each time. For both PSA methods linear and derivative crosstalks were added to the analyzed pulses but not to the pulse-shape basis used for the PSA. The results are summarized in Table 2. Note that the distributions are not Gaussian (see, e.g., Siciliano et al. [53]) and a FWHM comparable to the segment size is therefor possible. According to this work the crosstalks have a very limited influence on the resolution. In non of the cases shown in Table 2 was the average found position different from the actual position showing that crosstalks do not introduce any systemtic errors. In Figs. 15 and 16 two-dimensional projections of interaction positions as determined by the two different PSA algorithms are shown. A striking difference appears for large noises in Figs. 15 and 16. The EGS tends to cluster points towards the segment boundaries whereas the SVD seems to move the points towards the barycenter of the segment.
Data from Söderström et al. [51] is presented together with the result from present work in figure 17. One notes that the EGS is better on simulated data than what has been experimentally measured for energies above about 50 keV. The Matrix inversion using SVD decomposition to increase the signal-to-noise ratio is better at very low interaction energies. It is hence of interest to try SVD on low-energy experimental data even though the method in its present implementation is too slow for online PSA.
7 Pulse-shape analysis on experimental data
One of the objectives of the AGATAGeFEM package is to produce pulse-shape bases used for the PSA of experimental data. In the AGATA collaboration an adaptive grid search algorithm is presently used [56]. The validation of bases calculated with AGATAGeFEM for the AGATA PSA is presented in this section. This step also validates the AGATAGeFEM package for use in the development of pulse-shape analyses by proving that the pulse shapes are realistic. Pulse-shape data bases have been calculated for 6 AGATA crystals. These crystals were previously used to estimate the position resolution achieved [9, 57] employing bases calculated with ADL [14]. An optimistion of some of the parameters that enter into the pulse-shape bases calucations is also performed. The reader is cautioned that this is a pragmatic effort to see if it is possible to improve a basis using in-beam data for an experiment, i.e. as a part of analysing data. The parameter values as determined from this optimisation are therefor not to be seen as “more correct” but as a set of parameters giving the best result on the data used. There is no guarantee that the adjusted parameters have not compensated for some other parameter not optimised that is slightly wrong, and with only the FWHM of a \(\gamma \)-ray peak as metric the disentanglement is not feasible.
The space charge is an important parameter when calculating the electric fields inside the fully depleted detectors. Space charges come from impurities in the Germanium crystals. For the AGATA crystals they have been measured using techniques based on the capacity of the crystal [15, 16] and are used as input here with numerical values presented in table 3. The parameters for the electron and hole mobility are taken from [33]. They differ slightly from values used in ADL [14] and are presented in Table 1 appendix 2.1.
The addition of electronics transfer-function and crosstalk to the pulse-shape data bases is performed by the standard AGATA PSA codes. For crosstalk, the values measured during each experiment for each crystal are used (for typical values see Bruyneel at al. [17, 18]). In the AGATA PSA codes the differential crosstalk is modeled as a constant times the linear crosstalk coefficient for the segment in question, and is not measured for the crystals. The response function of the electronics is modeled as an exponential with a rise time of 35 ns, the default used for PSA in AGATA.
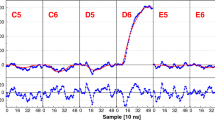
Variation in rise time and shape of transient signals as a function of central contact radius (black = 5mm, red = 6mm, blue = 7 mm), and scaled charge-carrier velocities (thin = 0.8, thicker = 1.0, thickest = 1.1), respectively. This is shown for interaction at three different radii (solid = 8 mm, dotted = 20mm, dashed-dotted = 36 mm)
To optimize the calculated bases, the parameters controlling the direction of the \(<100>\) crystal axis, the radius assumed for the central contact, and the scaling of the hole and electron velocities, were varied. The best results for the PSA was sought in this parameter space for each crystal. The orientation of crystal lattice was varied by rotating the lattice around the \(<100>\) crystal axis assumed parallel to the bore hole for the central contact. Rotations in steps of 5 degrees until 90 degrees were performed. For the bore hole, three different radii were used: 5 mm (nominal), 6 mm, and 7mm. The charge carrier velocities were scaled from \(0.8\) to \(1.1\) is steps of \(0.1\) of their nominal values. In Fig. 18 and 19 the variation of the pulse shapes over the used parameter space is illustrated. As can be seen in Fig. 18 the lattice orientation has a noticeable impact on the pulse shapes. The varied parameters with the largest impact are the 10 % step scaling of the charge-carrier velocities, clearly seen in Fig. 19. This is coherent with what was shown in Sect. 4. Evaluation of the performance of the PSA was performed using the peak width of the 1221 keV \(\gamma \)-ray transition in \(^{98}\)Zr. Doppler correction was performed using first interaction point as defined by the \(\gamma \)-ray tracking and the recoil velocity of the nucleus given by the VAMOS spectrometer (for details see Li et al. [57]). An automatic fit procedure was chosen to exclude biases for one or the other set of bases. A Gaussian peak plus a linear background were fitted. The background was determined on the intervall 1180 keV to 1250 keV exluding the region 1200–1235 keV. An estimate of the peak position and standard devition were then performed and used to limit the range of the fit to include about \(1\sigma \) to the left of the maxium to 1250 keV. Examples of fits are shown in Fig. 25. The experimental data were processed, with the exception of choice of pulse-shape data bases, exactly as described in Ljungvall et al. [9]. For the detectors used in this work neutron-damage correction was not needed. Similar efforts to optimize the results of PSA using ADL have recently been published by Lewandowski et al. [35]. It is important to note that due to strong correlations between different parameters entering in the calculation of pulse shapes and in the PSA it is difficult to compare individual parameters, especially as different figures of merits are used.
A first optimisation varying only the lattice orientation and the central contact hole radius was performed. Pulse-shape analyses were done using a total of 72 different bases for each crystal followed by \(\gamma \)-ray tracking. The resulting spectra were fitted by an automatic routine and the FWHM were extracted for each crystal and for the total spectrum. The results, for each crystal and for the sum of the crystals, are presented in Fig. 20. The minimum FWHM is achieved close to the nominal orientation for most of the crystals. However, the minimum of the sum is close to a lattice rotation of 30\(^{\circ }\) and with an assumed core radius of 6 mm. This seems to be driven by crystal A007. The nominal direction of the lattice is 45\(^{\circ }\). In figure 20 the results obtained with the data bases calculated using ADL are also shown as a reference.
A second minimisation was performed on a parameter space including the three different central contact radii, 5 different crystal lattice orientations and 16 different scalings of the charge carrier velocities. In Fig. 21 the variation of the FWHM for crystal A002 is shown for the three different central contact radii and as a function of the scale of the electron and hole velocities. For each data point a crystal lattice orientation of 45\(^{\circ }\) was chosen. A correlation between the central contact radius and the best scale factor for the electron velocity can be clearly seen. It is reasonable that it is the electron velocity that can be used to compensate for changes in the central contact radius as they are (mainly) responsible for the generation of the signal on the central contact. Furthermore, the change of the central contact radius generates the strongest change in the electric field in the regions where the largest contribution from the electrons to the signal is created. From this optimisation it is also clear that different parameters for the pulse-shape calculations are strongly correlated and that it is difficult, if not impossible, to determine individual parameters using only the width of a \(\gamma \)-ray peak (or any other single figure of merit).
Full Width at Half Maximum of the 1221 keV \(\gamma \)-ray peak in \(^{98}\)Zr as a function of crystal lattice orientation for the set of charge carrier velocity scaling giving the smallest FWHM for each crystal used for evaluating the PSA performance. The best combination for each crystal is marked with a circle. Results using the ADL bases are given as reference
From the second minimisation the bases that produce the smallest FWHM of the 1221 keV peak were chosen for each crystal. In Fig. 22 the lowest FWHM for each crystal is marked with a circle. It seems as if a slight increase of the hole mobilities, reflected by the scaling factor \(S_h\), improves the performance on average, except for the C001 crystal. This is not a general statement about hole mobilities when modeling HPGe detectors and only applies to this work. For the bore hole radius, 6 mm seems to be preferred , with C001 again in disagreement. Possible reasons for the different behaviour of the C001 crystal will be discussed later in this section.
Full Width at Half Maximum of the 1221 keV \(\gamma \)-ray peak in \(^{98}\)Zr as a function of the exponential \(p\) in the metric used to compare entries in the pulse-shape bases with experimental pulse shapes. The test was performed with the bases selected to be the best according to the FWHM for each crystal. The best value of \(0.3\) is in accordance with earlier results. A range of 0.1–3 in steps of 0.1 was scanned but as the results grow worse as the metric increases beyond \(0.3\) results are only shown up to \(1.5\). Results from using the ADL bases and with AGATAGeFEM bases assuming a central contact radius of 6 mm and a crystal lattice rotation of 45\(^{\circ }\) are given as reference (shown as grey circles and blue rectangles, respectively). On the lower panel an approximate conversion to position resolution (FWHM) is given (see [57])
The most important parameter in the adaptive grid search PSA algorithm used within the AGATA collaboration [56] is the power used to calculate the figure of merit (FOM) for a pulse shape in the basis when compared to the experimental signal. A minimum is sought for the expression
which for \(p=2\) is the typical square sum FOM and i is the index of the samples points. Using the ADL bases it was shown that \(p=0.3\) gives the best result [58] (for a recent in-depth discussion of the impact of the distance metric on PSA, see Lewandowski et al. [35]). A scan of \(p\)’s were performed using the six selected AGATAGeFEM bases, and the resulting FWHM are presented in Fig. 23. For reference the FWHM achieved using the ADL bases and the AGATAGeFEM are also shown. The AGATAGeFEM bases were calculated with a central contact radius of 6 mm and a lattice orientation of 45\(^{\circ }\). This is the final result of the optimisations made in this work. On the lower panel in Fig. 23 an approximate conversion to position resolution is shown (for details see Li et al. [57]) allowing to estimate the improvements made. Looking at the lower panel in Fig. 23 an improved position resolution of a few tens of millimeters is suggested by comparing the points using the ADL bases and the optimised AGATAGeFEM bases (at 0.3 on the x-axis). The corresponding \(\gamma \)-ray spectra are shown in Fig. 24. An alternative fit approach was therefore used to fit the individual spectra for each of the six crystals and the three pulse-shape bases. For the second fit a fit function including a left tail was used. The chosen functional form was
Final spectra for the three different bases and the six crystals. In the left column spectra using the final AGATAGeFEM bases (grey), the ADL bases (green), and the AGATAGeFEM bases generated using a 6 mm core radious and the \(<100>\) axis oriented at 45 degrees (blue) are overlayed. Also shown in black are the differences between the spectra produced using the optimized AGATAGeFEM bases and ADL bases. Column two to four show the fits of the two used functions to extract the FWHM. The black solid line is a simple Gaussian with a linear background wheras the dashed red line also has left tail component (see text for details)
The parameter \(A_{Skewed}\) was fixed to 21 % of \(A_{Gaus}\) and the decay parameter of the left tail, \(\beta \), was fixed to 4.4 keV. The background was determined by fitting a straight line between 1180 keV and 1250 keV excluding the region between 1200 keV and 1235 keV for both functions used for fitting the peaks. The fits are shown in Fig. 25. In Table 4 the FWHM of the fits are given together with the reduced \(\chi ^2\) of each fit. The fits using a left tail give FWHM’s that are a few tens of keV’s smaller, with the exception of detector C001 where the inverse situation is found. This is related to the worse resolution found in this detector and the fixed parametrisation of the tail on the \(\gamma \)-ray peaks. As for the comparisons between different pulse-shape bases the ordering remains the same where the optimised AGATAGeFEM bases give the smallest FWHM in 6 and 5 cases for fitting without and with the left tail, respectively. This is unlikely to be a statistical fluctuation although the differences are never significant beyond one sigma. These results therefor state that the bases generated with AGATAGeFEM perform as well or slightly better than the standard ADL bases. It is the authors conviction that for the present data the fitting of a Gaussian peak using mainly the high-energy part of the \(\gamma \)-ray peaks provides the best estimates of the variation of the Doppler Correction component of the FHWM and is the better choice for evaluating the actual achieved position resolution.
Gamma-ray interaction points as determined with the ADL, AGATAGeFEM core radius 6 mm, and AGATAGeFEM final pulse-shape data bases. For crystal C001 the regions used to create averaged traces when investigating the origins of “hot spots” are found inside the red circle and are marked in white for events belonging to the “hot spot” and in green for reference events, respectively (for details see text) in the ADL column
An homogeneous \(\gamma \)-ray flux over the solid angle covered by one AGATA crystal is an excellent approximation of the situation in real experiments. A consequence of this approximation is that the \(\gamma \)-ray interaction points should be homogeneously distributed on planes parallel to front face of the detector. The small effect coming from slight surface sphericity is ignored. Examination of projections of \(\gamma \)-ray interaction points onto the plane parallel to the front face is therefore an indicator of how well the PSA is performing. In the Fig. 26 projections of \(\gamma \)-ray interaction points are shown for the six crystals and three different sets of bases, respectively. For all bases similar features can be seen. With the exception of crystal C001 the intensity of \(\gamma \)-ray interactions is clearly seen to be lower at segment boundaries. This is interpreted as originating from the one-interaction per segment approximation used in the PSA and supported by the results of performing PSA on calculated signals as previously shown in Figs. 15 and 16. Based on the number of counts in the maximum bin, the quality of the PSA improves when moving from ADL bases to optimized AGATAGeFEM bases for four out of six detectors. This is seen when comparing the scales between columns in Fig. 26. However, the “hot spots” seen for crystal C001 remain pronounced for all bases. These are located at the corners of the front face and for depths in the crystal that is smaller than 4 mm (as determined using the ADL bases). To investigate these events closer an average of all traces belonging to the hot spot close to \(x\approx -30\) mm, \(y\approx 0\) mm, and \(z<4\) mm was produced together with an average of events that gave x and y coordinates next to the hot spot (the two regions are marked in Fig. 26). On the events used for averaging the condition of only one net-charge segment was also required. In Fig. 27 the resulting averages are shown together with the pulse shapes from the ADL and optimized AGATAGeFEM bases coming from positions in the bases corresponding to the hot spot. The average trace for events ending up at the hot spot is seen not to reach its full value. This is most likely related to an incorrect determination of the start time for these events. (In Fig. 27 the traces have been aligned for clarity). When trying to fit the time-misaligned traces the PSA algorithm always finds the same best position as the time alignment can be compensated by choosing an extreme rise time in the pulse-shape data basis. Note that it is the error in timing, exaggerated by the slow pulses in this region of the crystal, that drives the PSA to a specific solution, and not a position dependant timing error. It is interesting to note that the C001 crystal has an inverted impurity concentration profile and hence lower electric field strength in the front of the crystal as compared to the other crystals. This might contribute to large differences in timing characteristics between the front segments and the bulk of the crystal, complicating the time calibration procedure. When comparing the traces from the ADL bases and the optimized AGATAGeFEM bases an explanation to why the C001 hot spots are “less hot” for the AGATAGeFEM bases is given. The start of the signal for the AGATAGeFEM bases is different, allowing for more positions to reproduce the “false” rise time of the time-misaligned traces. However, it is difficult to state if one basis is more realistic than the other as the “hot spot” is related to the preprocessing of the traces performed before the PSA or to the time-pickup made in the digitizers of AGATA. This underlines the importance of preprocessing for successful PSA.
Signals from the net-charge segment for one-segment events coming from the “hot spot” seen for crystal C001 (for the ADL bases, see Fig. 26)
8 Conclusions
The C++ based software package AGATAGeFEM that models segmented High-Purity Germanium detectors is described. This software allows the implementation of detector geometry and segmentation schemes to within \(10^{-6}\) mm and uses Finite Element Methods to solve the Laplace and Poisson equations. The resulting fields are calculated using the basis functions and support points of the actual FEM grid, i.e. using function evaluation rather than interpolation.
The charge-transport equations are solved using time adaptive Runge-Kutta methods from the GNU Scientific Library. Linear and derivative crosstalk is added to the induced charge signals together with the transfer function of the electronics. Convolution is made in the time domain. The model used in AGATAGeFEM for hole-charge carrier velocity is shown to give good results for PSA but still has room for improvements.
In this work AGATAGeFEM has been used to investigate the impact of crosstalk and noise for the EGS PSA and for the SVD PSA. The result suggests that crosstalk at the level of what is found in AGATA has a small impact on the resolution of the PSA. Furthermore the influence of an imperfectly known crystal geometry has been investigated. It was found that a \(\chi ^2\) figure-of-merit stating on how good the experimental signals could be fitted using the pulse-shape basis is not a good indicator for the precision of the geometry. In extreme cases the measured position resolution using in-beam methods can give indications. These results point to the importance of having well-defined crystal geometries when modeling pulse shapes.
As a validation of the pulse shapes calculated using AGATAGeFEM pulse-shape data bases for PSA on AGATA data have been produced and optimized. The resulting bases allow for analysis of data with results that are as good as the other state-of-the-art pulse-shape data bases. This demonstrates that the concepts and models used in AGATAGeFEM produce pulse shapes which are as realistic as the ADL presently used within the AGATA collaboration. It has also been shown that “hot spots” seen in the distribution of \(\gamma \)-ray interaction points from the AGATA PSA can be linked to problems in the data treatment prior to PSA, e.g. the time alignment of the traces.
The intended use of AGATAGeFEM is that of pulse-shape analysis development but as has been showed in this paper it is also an attractive alternative for producing data bases for PSA. To calculate a data base starting from the beginning takes a few hours per field (can be calculated in parallel) and an hour for the calculations of the pulse shapes and requires the editing of a few lines in two text files. The package contains code both to generate the input files for a basis and to verify that the pulses from all points are indeed correct (one net-charge segment etc.). The ease with which the geometry of the crystals can be varied in detail makes AGATAGeFEM an excellent choice as a companion when performing 3D scans of crystals.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: The experimental data is handled under the AGATA data policy and will be made public at some point on a decision taken by the Agata Collaboration Council. For the code and calculated data the author plan to make the code available via a the in2p3 github.]
Notes
A boundary condition automatically satisfied by the variational formulation used in the Finite Element Method. Here it corresponds to demanding that the component of the field that is orthogonal to the surface is zero.
References
J. Eberth, J. Simpson, From ge(li) detectors to gamma-ray tracking arrays-50 years of gamma spectroscopy with germanium detectors. Progress Particle Nucl. Phys. 60(2), 283–337 (2008). https://doi.org/10.1016/j.ppnp.2007.09.001, http://www.sciencedirect.com/science/article/pii/S0146641007000828
J. Simpson, The euroball spectrometer. Zeitschr. Phys. A Hadrons Nucl. 358(2), 139–143 (1997). https://doi.org/10.1007/s002180050290
M.A. Deleplanque, R.M.E. Diamond, 1987 gammasphere proposal preprint lbnl-5202, Tech. rep., LBNL (1987)
I. Lee, Gamma-ray tracking detectors. Nucl. Instr. Methods Phys. Res. Sect. A: Acceler. Spectrom. Detect. Assoc. Equip. 422(1–3), 195–200 (1999). https://doi.org/10.1016/S0168-9002(98)01093-6, http://www.sciencedirect.com/science/article/pii/S0168900298010936
S. Akkoyun, A. Algora, B. Alikhani, F. Ameil, G. de Angelis, L. Arnold, A. Astier, A. Ataç, Y. Aubert, C. Aufranc, A. Austin, S. Aydin, F. Azaiez, S. Badoer, D. Balabanski, D. Barrientos, G. Baulieu, R. Baumann, D. Bazzacco, F. Beck, T. Beck, P. Bednarczyk, M. Bellato, M. Bentley, G. Benzoni, R. Berthier, L. Berti, R. Beunard, G. L. Bianco, B. Birkenbach, P. Bizzeti, A. Bizzeti-Sona, F. L. Blanc, J. Blasco, N. Blasi, D. Bloor, C. Boiano, M. Borsato, D. Bortolato, A. Boston, H. Boston, P. Bourgault, P. Boutachkov, A. Bouty, A. Bracco, S. Brambilla, I. Brawn, A. Brondi, S. Broussard, B. Bruyneel, D. Bucurescu, I. Burrows, A. Bürger, S. Cabaret, B. Cahan, E. Calore, F. Camera, A. Capsoni, F. Carrió, G. Casati, M. Castoldi, B. Cederwall, J.-L. Cercus, V. Chambert, M. E. Chambit, R. Chapman, L. Charles, J. Chavas, E. Clément, P. Cocconi, S. Coelli, P. Coleman-Smith, A. Colombo, S. Colosimo, C. Commeaux, D. Conventi, R. Cooper, A. Corsi, A. Cortesi, L. Costa, F. Crespi, J. Cresswell, D. Cullen, D. Curien, A. Czermak, D. Delbourg, R. Depalo, T. Descombes, P. Désesquelles, P. Detistov, C. Diarra, F. Didierjean, M. Dimmock, Q. Doan, C. Domingo-Pardo, M. Doncel, F. Dorangeville, N. Dosme, Y. Drouen, G. Duchêne, B. Dulny, J. Eberth, P. Edelbruck, J. Egea, T. Engert, M. Erduran, S. Ertürk, C. Fanin, S. Fantinel, E. Farnea, T. Faul, M. Filliger, F. Filmer, C. Finck, G. de France, A. Gadea, W. Gast, A. Geraci, J. Gerl, R. Gernhäuser, A. Giannatiempo, A. Giaz, L. Gibelin, A. Givechev, N. Goel, V. González, A. Gottardo, X. Grave, J. Grebosz, R. Griffiths, A. Grint, P. Gros, L. Guevara, M. Gulmini, A. Görgen, H. Ha, T. Habermann, L. Harkness, H. Harroch, K. Hauschild, C. He, A. Hernández-Prieto, B. Hervieu, H. Hess, T. Hüyük, E. Ince, R. Isocrate, G. Jaworski, A. Johnson, J. Jolie, P. Jones, B. Jonson, P. Joshi, D. Judson, A. Jungclaus, M. Kaci, N. Karkour, M. Karolak, A. Kas̨kas̨, M. Kebbiri, R. Kempley, A. Khaplanov, S. Klupp, M. Kogimtzis, I. Kojouharov, A. Korichi, W. Korten, T. Kröll, R. Krücken, N. Kurz, B. Ky, M. Labiche, X. Lafay, L. Lavergne, I. Lazarus, S. Leboutelier, F. Lefebvre, E. Legay, L. Legeard, F. Lelli, S. Lenzi, S. Leoni, A. Lermitage, D. Lersch, J. Leske, S. Letts, S. Lhenoret, R. Lieder, D. Linget, J. Ljungvall, A. Lopez-Martens, A. Lotodé, S. Lunardi, A. Maj, J. van der Marel, Y. Mariette, N. Marginean, R. Marginean, G. Maron, A. Mather, W. Meczyński, V. Mendéz, P. Medina, B. Melon, R. Menegazzo, D. Mengoni, E. Merchan, L. Mihailescu, C. Michelagnoli, J. Mierzejewski, L. Milechina, B. Million, K. Mitev, P. Molini, D. Montanari, S. Moon, F. Morbiducci, R. Moro, P. Morrall, O. Möller, A. Nannini, D. Napoli, L. Nelson, M. Nespolo, V. Ngo, M. Nicoletto, R. Nicolini, Y. L. Noa, P. Nolan, M. Norman, J. Nyberg, A. Obertelli, A. Olariu, R. Orlandi, D. Oxley, C. Özben, M. Ozille, C. Oziol, E. Pachoud, M. Palacz, J. Palin, J. Pancin, C. Parisel, P. Pariset, G. Pascovici, R. Peghin, L. Pellegri, A. Perego, S. Perrier, M. Petcu, P. Petkov, C. Petrache, E. Pierre, N. Pietralla, S. Pietri, M. Pignanelli, I. Piqueras, Z. Podolyak, P. L. Pouhalec, J. Pouthas, D. Pugnére, V. Pucknell, A. Pullia, B. Quintana, R. Raine, G. Rainovski, L. Ramina, G. Rampazzo, G. L. Rana, M. Rebeschini, F. Recchia, N. Redon, M. Reese, P. Reiter, P. Regan, S. Riboldi, M. Richer, M. Rigato, S. Rigby, G. Ripamonti, A. Robinson, J. Robin, J. Roccaz, J.-A. Ropert, B. Rossé, C. R. Alvarez, D. Rosso, B. Rubio, D. Rudolph, F. Saillant, E. Sahin, F. Salomon, M.-D. Salsac, J. Salt, G. Salvato, J. Sampson, E. Sanchis, C. Santos, H. Schaffner, M. Schlarb, D. Scraggs, D. Seddon, M. enyiĝit, M.-H. Sigward, G. Simpson, J. Simpson, M. Slee, J. Smith, P. Sona, B. Sowicki, P. Spolaore, C. Stahl, T. Stanios, E. Stefanova, O. Stézowski, J. Strachan, G. Suliman, P.-A. Söderström, J. Tain, S. Tanguy, S. Tashenov, C. Theisen, J. Thornhill, F. Tomasi, N. Toniolo, R. Touzery, B. Travers, A. Triossi, M. Tripon, K. Tun-Lanoë, M. Turcato, C. Unsworth, C. Ur, J. Valiente-Dobon, V. Vandone, E. Vardaci, R. Venturelli, F. Veronese, C. Veyssiere, E. Viscione, R. Wadsworth, P. Walker, N. Warr, C. Weber, D. Weisshaar, D. Wells, O. Wieland, A. Wiens, G. Wittwer, H. Wollersheim, F. Zocca, N. Zamfir, M. Ziebliński, A. Zucchiatti, Agata-advanced {GAmma} tracking array, Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 668 (2012) 26 – 58. https://doi.org/10.1016/j.nima.2011.11.081. http://www.sciencedirect.com/science/article/pii/S0168900211021516
I.Y. Lee, M.A. Deleplanque, K. Vetter, Developments in large gamma-ray detector arrays. Rep. Progress Phys. 66(7), 1095 (2003). http://stacks.iop.org/0034-4885/66/i=7/a=201
D. Weisshaar, D. Bazin, P. Bender, C. Campbell, F. Recchia, V. Bader, T. Baugher, J. Belarge, M. Carpenter, H. Crawford, M. Cromaz, B. Elman, P. Fallon, A. Forney, A. Gade, J. Harker, N. Kobayashi, C. Langer, T. Lauritsen, I. Lee, A. Lemasson, B. Longfellow, E. Lunderberg, A. Macchiavelli, K. Miki, S. Momiyama, S. Noji, D. Radford, M. Scott, J. Sethi, S. Stroberg, C. Sullivan, R. Titus, A. Wiens, S. Williams, K. Wimmer, S. Zhu, The performance of the \(\gamma \)-ray tracking array gretina for \(\gamma \)-ray spectroscopy with fast beams of rare isotopes. Nucl. Instrum. Methods Phys. Res. Sect. A Acceler. Spectrom. Detect. Assoc. Equip. 847, 187–198 (2017). https://doi.org/10.1016/j.nima.2016.12.001http://www.sciencedirect.com/science/article/pii/S0168900216312402
A. Korichi, T. Lauritsen, Tracking \(\gamma \) rays in highly segmented hpge detectors: a review of agata and gretina. Eur. Phys. J. A 55(7), 121 (2019). https://doi.org/10.1140/epja/i2019-12787-1
J. Ljungvall, R. Pérez-Vidal, A. Lopez-Martens, C. Michelagnoli, E. Clément, J. Dudouet, A. Gadea, H. Hess, A. Korichi, M. Labiche, N. Lalović, H. Li, F. Recchia, Performance of the advanced gamma tracking array at ganil. Nucl. Instrum. Methods Phys. Res. Sect. A Acceler. Spectrom. Detect. Assoc. Equip. 955, 5 (2020). https://doi.org/10.1016/j.nima.2019.163297, http://www.sciencedirect.com/science/article/pii/S0168900219315475
T. Kröll, D. Bazzacco, Simulation and analysis of pulse shapes from highly segmented hpge detectors for the \(\gamma \)-ray tracking array mars. Nucl. Instrum. Methods Phys. Res. Sect. A Acceler. Spectrom. Detect. Assoc. Equip. 463(1), 227–249 (2001). https://doi.org/10.1016/S0168-9002(01)00208-X, http://www.sciencedirect.com/science/article/pii/S016890020100208X
M. Schlarb, R. Gernhäuser, S. Klupp, R. Krücken, Pulse shape analysis for \(\gamma \)-ray tracking (part ii): Fully informed particle swarm algorithm applied to agata. Eur. Phys. J. A 47(10), 1–9 (2011). https://doi.org/10.1140/epja/i2011-11131-3
M. Schlarb, R. Gernhäuser, S. Klupp, R. Krücken, Pulse shape analysis for \(\gamma \)-ray tracking (part i): pulse shape simulation with JASS. Eur. Phys. J. A 47(10), 132 (2011). https://doi.org/10.1140/epja/i2011-11132-2
I. Mateu, P. Medina, J. Roques, E. Jourdain, Simulation of the charge collection and signal response of a hpge double sided strip detector using mgs. Nucl. Instr. Methods Phys. Res. A 735, 574–583 (2014). https://doi.org/10.1016/j.nima.2013.09.069
B. Bruyneel, B. Birkenbach, P. Reiter, Pulse shape analysis and position determination in segmented hpge detectors: the agata detector library. Eur. Phys. J. A 52(3), 70 (2016). https://doi.org/10.1140/epja/i2016-16070-9
B. Birkenbach, B. Bruyneel, G. Pascovici, J. Eberth, H. Hess, D. Lersch, P. Reiter, A. Wiens, Determination of space charge distributions in highly segmented large volume hpge detectors from capacitance–voltage measurements. Nucl. Instrum. Methods Phys. Res. Sect. A Acceler. Spectrom. Detect. Assoc. Equip. 640(1), 176–184 (2011). https://doi.org/10.1016/j.nima.2011.02.109, http://www.sciencedirect.com/science/article/pii/S0168900211005912
B. Bruyneel, B. Birkenbach, P. Reiter, Space charge reconstruction in highly segmented hpge detectors through capacitance-voltage measurements. Nucl. Instrum. Methods Phys. Res. Sect. A Acceler. Spectrom. Detect. Assoc. Equip. 641(1), 92–100 (2011). https://doi.org/10.1016/j.nima.2011.02.110, http://www.sciencedirect.com/science/article/pii/S0168900211006085
B. Bruyneel, P. Reiter, A. Wiens, J. Eberth, H. Hess, G. Pascovici, N. Warr, D. Weisshaar, Crosstalk properties of 36-fold segmented symmetric hexagonal HPGe detectors. Nucl. Instrum. Methods Phys. Res. Sect. A Acceler. Spectrom. Detect. Assoc. Equip. 599(2–3), 196–208 (2009). https://doi.org/10.1016/j.nima.2008.11.011, http://www.sciencedirect.com/science/article/pii/S0168900208015921
B. Bruyneel, P. Reiter, A. Wiens, J. Eberth, H. Hess, G. Pascovici, N. Warr, S. Aydin, D. Bazzacco, F. Recchia, Crosstalk corrections for improved energy resolution with highly segmented hpge-detectors. Nucl. Instrum. Methods Phys. Res. Sect. A Acceler. Spectrom. Detect. Assoc. Equip. 608(1), 99–106 (2009). https://doi.org/10.1016/j.nima.2009.06.037, http://www.sciencedirect.com/science/article/pii/S0168900209012455
M. Schlarb, R. Gernhäuser, R. Krücken, Simulation and real-time analysis of pulse shapes from hpge detectors, Tech. rep. (2008)
B. Bruyneel, P. Reiter, G. Pascovici, Characterization of large volume HPGe detectors. part i: Electron and hole mobility parameterization. Nucl. Instrum. Methods Phys. Res. Sect. A Acceler. Spectrom. Detect. Assoc. Equip. 569(3): 764 – 773 (2006). https://doi.org/10.1016/j.nima.2006.08.130, http://www.sciencedirect.com/science/article/pii/S0168900206015166
...S. Paschalis, I. Lee, A. Macchiavelli, C. Campbell, M. Cromaz, S. Gros, J. Pavan, J. Qian, R. Clark, H. Crawford, D. Doering, P. Fallon, C. Lionberger, T. Loew, M. Petri, T. Stezelberger, S. Zimmermann, D. Radford, K. Lagergren, D. Weisshaar, R. Winkler, T. Glasmacher, J. Anderson, C. Beausang, The performance of the gamma-ray energy tracking in-beam nuclear array gretina. Nucl. Instrum. Methods Phys. Res. Sect. A Acceler. Spectrom. Detect. Assoc. Equip. 709, 44–55 (2013). https://doi.org/10.1016/j.nima.2013.01.009, http://www.sciencedirect.com/science/article/pii/S0168900213000508
V. Prasher, M. Cromaz, E. Merchan, P. Chowdhury, H. Crawford, C. Lister, C. Campbell, I. Lee, A. Macchiavelli, D. Radford, A. Wiens, Sensitivity of gretina position resolution to hole mobility. Nucl. Instrum. Methods Phys. Res. Sect. A Acceler. Spectrom. Detect. Assoc. Equip. 846, 50–55 (2017). https://doi.org/10.1016/j.nima.2016.11.038, http://www.sciencedirect.com/science/article/pii/S0168900216311925
Q. Arnaud, E. Armengaud, C. Augier, A. Benoît, L. Bergé, J. Billard, A. Broniatowski, P. Camus, A. Cazes, M. Chapellier, F. Charlieux, M. De Jésus, L. Dumoulin, K. Eitel, E. Elkhoury, J.-B. Fillipini, D. Filosofov, J. Gascon, A. Giuliani, M. Gros, Y. Jin, A. Juillard, M. Kleifges, H. Lattaud, S. Marnieros, D. Misiak, X.-F. Navick, C. Nones, E. Olivieri, C. Oriol, P. Pari, B. Paul, D. Poda, S. Rozov, T. Salagnac, V. Sanglard, B. Siebenborn, L. Vagneron, M. Weber, E. Yakushev, A. Zolotarova, First germanium-based constraints on sub-mev dark matter with the edelweiss experiment. Phys. Rev. Lett. 125, 141301 (2020). https://doi.org/10.1103/PhysRevLett.125.141301
M. Agostini, M. Allardt, A.M. Bakalyarov, M. Balata, I. Barabanov, L. Baudis, C. Bauer, E. Bellotti, S. Belogurov, S.T. Belyaev, G. Benato, A. Bettini, L. Bezrukov, T. Bode, D. Borowicz, V. Brudanin, R. Brugnera, A. Caldwell, C. Cattadori, A. Chernogorov, V. D’Andrea, E.V. Demidova, N. Di Marco, A. di Vacri, A. Domula, E. Doroshkevich, V. Egorov, R. Falkenstein, O. Fedorova, K. Freund, N. Frodyma, A. Gangapshev, A. Garfagnini, C. Gooch, P. Grabmayr, V. Gurentsov, K. Gusev, J. Hakenmüller, A. Hegai, M. Heisel, S. Hemmer, W. Hofmann, M. Hult, L .V. Inzhechik, J. Janicskó Csáthy, J. Jochum, M. Junker, V. Kazalov, T. Kihm, I .V. Kirpichnikov, A. Kirsch, A. Kish, A. Klimenko, R. Kneißl, K .T. Knöpfle, O. Kochetov, V .N. Kornoukhov, V .V. Kuzminov, M. Laubenstein, A. Lazzaro, V .I. Lebedev, B. Lehnert, H .Y. Liao, M. Lindner, I. Lippi, A. Lubashevskiy, B. Lubsandorzhiev, G. Lutter, C. Macolino, B. Majorovits, W. Maneschg, E. Medinaceli, M. Miloradovic, R. Mingazheva, M. Misiaszek, P. Moseev, I. Nemchenok, D. Palioselitis, K. Panas, L. Pandola, K. Pelczar, A. Pullia, S. Riboldi, N. Rumyantseva, C. Sada, F. Salamida, M. Salathe, C. Schmitt, B. Schneider, S. Schönert, J. Schreiner, O. Schulz, A.-K. Schütz, B. Schwingenheuer, O. Selivanenko, E. Shevchik, M. Shirchenko, H. Simgen, A. Smolnikov, L. Stanco, L. Vanhoefer, A .A. Vasenko, A. Veresnikova, K. von Sturm, V. Wagner, M. Walter, A. Wegmann, T. Wester, C. Wiesinger, M. Wojcik, E. Yanovich, I. Zhitnikov, S .V. Zhukov, D. Zinatulina, K. Zuber, G. Zuzel, T .G. Collaboration, Background-free search for neutrinoless double-\(\beta \) decay of 76ge with gerda. Nature 544(7648), 47–52 (2017). https://doi.org/10.1038/nature21717
C.E. Aalseth, N. Abgrall, E. Aguayo, S.I. Alvis, M. Amman, I.J. Arnquist, F.T. Avignone, H.O. Back, A.S. Barabash, P.S. Barbeau, C.J. Barton, P.J. Barton, F.E. Bertrand, T. Bode, B. Bos, M. Boswell, A.W. Bradley, R.L. Brodzinski, V. Brudanin, M. Busch, M. Buuck, A.S. Caldwell, T.S. Caldwell, Y.-D. Chan, C.D. Christofferson, P.-H. Chu, J.I. Collar, D.C. Combs, R.J. Cooper, C. Cuesta, J.A. Detwiler, P.J. Doe, J.A. Dunmore, Y. Efremenko, H. Ejiri, S.R. Elliott, J.E. Fast, P. Finnerty, F.M. Fraenkle, Z. Fu, B.K. Fujikawa, E. Fuller, A. Galindo-Uribarri, V.M. Gehman, T. Gilliss, G.K. Giovanetti, J. Goett, M.P. Green, J. Gruszko, I.S. Guinn, V.E. Guiseppe, A.L. Hallin, C.R. Haufe, L. Hehn, R. Henning, E.W. Hoppe, T.W. Hossbach, M.A. Howe, B.R. Jasinski, R.A. Johnson, K.J. Keeter, J.D. Kephart, M.F. Kidd, A. Knecht, S.I. Konovalov, R.T. Kouzes, B.D. LaFerriere, J. Leon, K.T. Lesko, L.E. Leviner, J.C. Loach, A.M. Lopez, P.N. Luke, J. MacMullin, S. MacMullin, M.G. Marino, R.D. Martin, R. Massarczyk, A.B. McDonald, D.-M. Mei, S.J. Meijer, J.H. Merriman, S. Mertens, H.S. Miley, M.L. Miller, J. Myslik, J.L. Orrell, C. O’Shaughnessy, G. Othman, N.R. Overman, G. Perumpilly, W. Pettus, D.G. Phillips, A.W.P. Poon, K. Pushkin, D.C. Radford, J. Rager, J.H. Reeves, A.L. Reine, K. Rielage, R.G.H. Robertson, M.C. Ronquest, N.W. Ruof, A.G. Schubert, B. Shanks, M. Shirchenko, K.J. Snavely, N. Snyder, D. Steele, A.M. Suriano, D. Tedeschi, W. Tornow, J.E. Trimble, R.L. Varner, S. Vasilyev, K. Vetter, K. Vorren, B.R. White, J.F. Wilkerson, C. Wiseman, W. Xu, E. Yakushev, H. Yaver, A.R. Young, C.H. Yu, V. Yumatov, I. Zhitnikov, B.X. Zhu, S. Zimmermann, Search for neutrinoless double-\(\beta \) decay in \(^{76}{\rm Ge}\) with the majorana demonstrator. Phys. Rev. Lett. 120, 132502 (2018). https://doi.org/10.1103/PhysRevLett.120.132502
N. Abgrall, E. Aguayo, F.T. Avignone, A.S. Barabash, F.E. Bertrand, M. Boswell, V. Brudanin, M. Busch, A.S. Caldwell, Y.-D. Chan, C.D. Christofferson, D.C. Combs, J.A. Detwiler, P.J. Doe, Y. Efremenko, V. Egorov, H. Ejiri, S.R. Elliott, J. Esterline, J.E. Fast, P. Finnerty, F.M. Fraenkle, A. Galindo-Uribarri, G.K. Giovanetti, J. Goett, M.P. Green, J. Gruszko, V.E. Guiseppe, K. Gusev, A.L. Hallin, R. Hazama, A. Hegai, R. Henning, E.W. Hoppe, S. Howard, M.A. Howe, K.J. Keeter, M.F. Kidd, A. Knecht, O. Kochetov, S.I. Konovalov, R.T. Kouzes, B.D. LaFerriere, J. Leon, L.E. Leviner, J.C. Loach, P.N. Luke, S. MacMullin, R.D. Martin, S. Mertens, L. Mizouni, M. Nomachi, J.L. Orrell, C. O’Shaughnessy, N.R. Overman, D. Phillips, A.W.P. Poon, K. Pushkin, D.C. Radford, K. Rielage, R.G.H. Robertson, M.C. Ronquest, A.G. Schubert, B. Shanks, T. Shima, M. Shirchenko, K.J. Snavely, N. Snyder, D. Steele, J. Strain, A.M. Suriano, J. Thompson, V. Timkin, W. Tornow, R.L. Varner, S. Vasilyev, K. Vetter, K. Vorren, B.R. White, J.F. Wilkerson, T. Williams, W. Xu, E. Yakushev, A.R. Young, C.-H. Yu, V. Yumatov, The majorana demonstrator neutrinoless double-beta decay experiment. Adv. High Energy Phys. 2014, 365432 (2014). https://doi.org/10.1155/2014/365432
S. Ramo, Proc. IRE 27, 584 (1939)
W. Shockley, J. Appl. Phys. 9, 635 (1938)
G. Knoll, Radiation Detection and Measurement (Wiley, Hoboken, 2000)
M.I. Nathan, Anisotropy of the conductivity of \(n\)-type germanium at high electric fields. Phys. Rev. 130, 2201–2204 (1963). https://doi.org/10.1103/PhysRev.130.2201
L. Mihailescu, W. Gast, R. Lieder, H. Brands, H. Jäger, The influence of anisotropic electron drift velocity on the signal shapes of closed-end HPGe detectors. Nucl. Instrum. Methods Phys. Res. Sect. A Acceler. Spectrom. Detect. Assoc. Equip. 447(3), 350–360 (2000). https://doi.org/10.1016/S0168-9002(99)01286-3, http://www.sciencedirect.com/science/article/pii/S0168900299012863
C. Kittel, Introduction to Solid State Physics. (Wiley, Hoboken, 1996). https://books.google.fr/books?id=1X8pAQAAMAAJ
J. Ljungvall, Ph.D. thesis, Uppsala Universitet, Institutionen För Kärn-och Partikelfysik, Tekniska Naturvetenskapliga Vetenskapsområdet (2005)
H. Mei, D.-M. Mei, G.-J. Wang, G. Yang, The impact of neutral impurity concentration on charge drift mobility in p-type germanium. J. Instrum. 11(12), P12021–P12021 (2016). https://doi.org/10.1088/1748-0221/11/12/p12021
L. Lewandowski, P. Reiter, B. Birkenbach, B. Bruyneel, E. Clement, J. Eberth, H. Hess, C. Michelagnoli, H. Li, R.M. Perez-Vidal, M. Zielinska, Pulse-shape analysis and position resolution in highly segmented hpge agata detectors. Eur. Phys. J. A 55(5), 81 (2019). https://doi.org/10.1140/epja/i2019-12752-0
S.C. Brenner, L.R. Scott, The Mathematical Theory of Finite Element Methods, 2nd Edition, Vol. 15 of Texts in Applied Mathematics. (Springer, Berlin, 2002)
G.P. Contributors, GSL - GNU scientific library - GNU project - free software foundation (FSF), (2010), http://www.gnu.org/software/gsl/. Accessed 20 Jun 2010
W. Bangerth, R. Hartmann, G. Kanschat, deal.II—a general purpose object oriented finite element library. ACM Trans. Math. Softw. 33(4), 24/1–24/27 (2007)
G. Alzetta, D. Arndt, W. Bangerth, V. Boddu, B. Brands, D. Davydov, R. Gassmoeller, T. Heister, L. Heltai, K. Kormann, M. Kronbichler, M. Maier, J.-P. Pelteret, B. Turcksin, D. Wells, The deal.II library, version 9.0. J. Numer. Math. 26(4), 173–183 (2018). https://doi.org/10.1515/jnma-2018-0054
B.S. Kirk, J.W. Peterson, R.H. Stogner, G.F. Carey, libMesh: a C++ library for parallel adaptive mesh refinement/coarsening simulations. Eng. Comput. 22(3–4), 237–254 (2006)
M. Hatlo, F. James, P. Mato, L. Moneta, M. Winkler, A. Zsenei, Developments of mathematical software libraries for the lhc experiments. IEEE Trans. Nucl. Sci. 52(6), 2818–2822 (2005). https://doi.org/10.1109/TNS.2005.860152
I. Antcheva, M. Ballintijn, B. Bellenot, M. Biskup, R. Brun, N. Buncic, P. Canal, D. Casadei, O. Couet, V. Fine, L. Franco, G. Ganis, A. Gheata, D. G. Maline, M. Goto, J. Iwaszkiewicz, A. Kreshuk, D. M. Segura, R. Maunder, L. Moneta, A. Naumann, E. Offermann, V. Onuchin, S. Panacek, F. Rademakers, P. Russo, M. Tadel, Root—a c++ framework for petabyte data storage, statistical analysis and visualization, 40 YEARS OF CPC: a celebratory issue focused on quality software for high performance, grid and novel computing architectures. Comput. Phys. Commun. 180(12), 2499 – 2512 (2009). https://doi.org/10.1016/j.cpc.2009.08.005, http://www.sciencedirect.com/science/article/pii/S0010465509002550
E. Farnea, F. Recchia, D. Bazzacco, T. Kröll, Z. Podolyák, B. Quintana, A. Gadea, Conceptual design and monte carlo simulations of the AGATA array. Nucl. Instrum. Methods Phys. Res. Sect. A: Acceler. Spectrom. Detect. Assoc. Equip. 621(1–3), 331–343 (2010). https://doi.org/10.1016/j.nima.2010.04.043, http://www.sciencedirect.com/science/article/pii/S0168900210008922
S. Agostinelli, J. Allison, K. Amako, J. Apostolakis, H. Araujo, P. Arce, M. Asai, D. Axen, S. Banerjee, G. Barrand, F. Behner, L. Bellagamba, J. Boudreau, L. Broglia, A. Brunengo, H. Burkhardt, S. Chauvie, J. Chuma, R. Chytracek, G. Cooperman, G. Cosmo, P. Degtyarenko, A. Dell’Acqua, G. Depaola, D. Dietrich, R. Enami, A. Feliciello, C. Ferguson, H. Fesefeldt, G. Folger, F. Foppiano, A. Forti, S. Garelli, S. Giani, R. Giannitrapani, D. Gibin, J.G. Cadenas, I. González, G.G. Abril, G. Greeniaus, W. Greiner, V. Grichine, A. Grossheim, S. Guatelli, P. Gumplinger, R. Hamatsu, K. Hashimoto, H. Hasui, A. Heikkinen, A. Howard, V. Ivanchenko, A. Johnson, F. Jones, J. Kallenbach, N. Kanaya, M. Kawabata, Y. Kawabata, M. Kawaguti, S. Kelner, P. Kent, A. Kimura, T. Kodama, R. Kokoulin, M. Kossov, H. Kurashige, E. Lamanna, T. Lampén, V. Lara, V. Lefebure, F. Lei, M. Liendl, W. Lockman, F. Longo, S. Magni, M. Maire, E. Medernach, K. Minamimoto, P.M. de Freitas, Y. Morita, K. Murakami, M. Nagamatu, R. Nartallo, P. Nieminen, T. Nishimura, K. Ohtsubo, M. Okamura, S. O’Neale, Y. Oohata, K. Paech, J. Perl, A. Pfeiffer, M. Pia, F. Ranjard, A. Rybin, S. Sadilov, E.D. Salvo, G. Santin, T. Sasaki, N. Savvas, Y. Sawada, S. Scherer, S. Sei, V. Sirotenko, D. Smith, N. Starkov, H. Stoecker, J. Sulkimo, M. Takahata, S. Tanaka, E. Tcherniaev, E.S. Tehrani, M. Tropeano, P. Truscott, H. Uno, L. Urban, P. Urban, M. Verderi, A. Walkden, W. Wander, H. Weber, J. Wellisch, T. Wenaus, D. Williams, D. Wright, T. Yamada, H. Yoshida, D. Zschiesche, Geant4-a simulation toolkit. Nucl. Instrum. Methods Phys. Res. Sect. A: Acceler. Spectrom. Detect. Assoc. Equip. 506(3), 250–303 (2003). https://doi.org/10.1016/S0168-9002(03)01368-8, http://www.sciencedirect.com/science/article/pii/S0168900203013688
S. Aydin, F. Recchia, D. Bazzacco, E. Farnea, C. Ur, Effective size of segmentation lines of an agata crystal, in Laboratori Nazionali di Legnaro, Annual Report, p. 195–196 (2007). http://www.lnl.infn.it/~annrep/read_ar/2007/contributions/pdfs/195_FA_103_FAA098.pdf
C. Geuzaine, J.-F. Remacle, Gmsh: a 3-D finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Methods Eng. 79, 1309–1331 (2009)
D. W. Kelly, J. P. De S. R. Gago, O.C. Zienkiewicz, I. Babuska, A posteriori error analysis and adaptive processes in the finite element method: part i–error analysis. Int. J. Numer. Methods Eng. 19(11), 1593–1619 (1983) . arXiv:https://onlinelibrary.wiley.com/doi/pdf/10.1002/nme.1620191103, https://doi.org/10.1002/nme.1620191103, https://onlinelibrary.wiley.com/doi/abs/10.1002/nme.1620191103
J. Dormand, P. Prince, A family of embedded runge-kutta formulae. J. Comput. Appl. Math. 6(1), 19–26 (1980). https://doi.org/10.1016/0771-050X(80)90013-3, http://www.sciencedirect.com/science/article/pii/0771050X80900133
A. Wiens, H. Hess, B. Birkenbach, B. Bruyneel, J. Eberth, D. Lersch, G. Pascovici, P. Reiter, H.-G. Thomas, The AGATA triple cluster detector. Nucl. Instrum. Methods Phys. Res. Sect. A Acceler. Spectrom. Detect. Assoc. Equip. 618(1–3), 223–233 (2010). https://doi.org/10.1016/j.nima.2010.02.102, http://www.sciencedirect.com/science/article/pii/S0168900210003384
P.-A. Söderström, F. Recchia, J. Nyberg, A. Al-Adili, A. Ataç, S. Aydin, D. Bazzacco, P. Bednarczyk, B. Birkenbach, D. Bortolato, A. Boston, H. Boston, B. Bruyneel, D. Bucurescu, E. Calore, S. Colosimo, F. Crespi, N. Dosme, J. Eberth, E. Farnea, F. Filmer, A. Gadea, A. Gottardo, X. Grave, J. Grebosz, R. Griffiths, M. Gulmini, T. Habermann, H. Hess, G. Jaworski, P. Jones, P. Joshi, D. Judson, R. Kempley, A. Khaplanov, E. Legay, D. Lersch, J. Ljungvall, A. Lopez-Martens, W. Meczynski, D. Mengoni, C. Michelagnoli, P. Molini, D. Napoli, R. Orlandi, G. Pascovici, A. Pullia, P. Reiter, E. Sahin, J. Smith, J. Strachan, D. Tonev, C. Unsworth, C. Ur, J. Valiente-Dobón, C. Veyssiere, A. Wiens, Interaction position resolution simulations and in-beam measurements of the AGATA HPGe detectors. Nucl. Instrum. Methods Phys. Res. Sect. A Acceler. Spectrom. Detect. Assoc. Equip. 638(1), 96–109 (2011). https://doi.org/10.1016/j.nima.2011.02.089, http://www.sciencedirect.com/science/article/pii/S016890021100489X
P. Désesquelles, T.M.H. Ha, K. Hauschild, A. Korichi, F. Le Blanc, A. Lopez-Martens, A. Olariu, C.M. Petrache, Matrix formalism and singular-value decomposition for the location of gamma interactions in segmented hpge detectors. Eur. Phys. J. A 40(2), 237–248 (2009). https://doi.org/10.1140/epja/i2008-10749-4
M. Siciliano, J. Ljungvall, A. Goasduff, A. Lopez-Martens, M. Zielińska, AGATA, O. collaborations, Position uncertainties of agata pulse-shape analysis estimated via the bootstrapping method. Eur. Phys. J. A 57(2), 64 (2021). https://doi.org/10.1140/epja/s10050-021-00385-z
M.R. Dimmock, A.J. Boston, H.C. Boston, J.R. Cresswell, L. Nelson, P.J. Nolan, C. Unsworth, I.H. Lazarus, J. Simpson, Characterisation results from an agata prototype detector. IEEE Trans. Nucl. Sci. 56(3), 1593–1599 (2009). https://doi.org/10.1109/TNS.2009.2019103
M.R. Dimmock, A.J. Boston, J.R. Cresswell, I. Lazarus, P. Medina, P. Nolan, C. Parisel, C. Santos, J. Simpson, C. Unsworth, Validation of pulse shape simulations for an agata prototype detector. IEEE Trans. Nucl. Sci. 56(4), 2415–2425 (2009). https://doi.org/10.1109/TNS.2009.2021842
D.B.R. Venturelli, Adaptive Grid Search as Pulse Shape Analysis Algorithm for \(\gamma \)-Tracking and Results (Tech. rep, LNL, 2004)
H.J. Li, J. Ljungvall, C. Michelagnoli, E. Clément, J. Dudouet, P. Désesquelles, A. Lopez-Martens, G. de France, Experimental determination of reference pulses for highly segmented hpge detectors and application to pulse shape analysis used in \(\gamma \)-ray tracking arrays. Eur. Phys. J. A 54(11), 198 (2018). https://doi.org/10.1140/epja/i2018-12636-9
F. Recchia, Ph.D. thesis, Università degli Studi di Padova (2008)
Acknowledgements
The author would like to thank the AGATA collaboration and the GANIL technical staff. Gilbert Duchêne is thanked for providing the in-beam data set used to extract the position resolution of the pulse-shape analysis. R.M. Pérez-Vidal, A. Lopez-Martens, C. Michelagnoli, E. Clément, J. Dudouet, and H. J. Li are thanked for their contribution given via the work performed in the scope of earlier publications. The excellent performance of the AGATA detectors is assured by the AGATA Detector Working group. The AGATA project is supported in France by the CNRS and the CEA. This work has been supported by the OASIS project no. ANR-17-CE31-0026.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Wolfram Korten
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ljungvall, J. Pulse-shape calculations and applications using the AGATAGeFEM software package. Eur. Phys. J. A 57, 198 (2021). https://doi.org/10.1140/epja/s10050-021-00512-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epja/s10050-021-00512-w