Lifetime measurements in $^{182}\hbox {Pt}$ using $\gamma$–$\gamma$ fast-timing

Abstract

The level lifetimes of the $2_1^+$ and $4_1^+$ states in $^{182}\hbox {Pt}$ have been re-measured employing the $\gamma$–$\gamma$ fast-timing technique using fast $\hbox {LaBr}_3$(Ce) scintillators. Excited states in the nucleus of interest were populated by the fusion-evaporation reaction $^{170}\hbox {Yb}(^{16}\hbox {O},\hbox {4n})^{182}\hbox {Pt}$ at a beam energy of 87 MeV provided by the FN Tandem accelerator of the University of Cologne. The lifetime of the $2_1^+$ state was re-measured with high accuracy to be $\tau = 563(12)~$ps and resolves inconsistencies from previous measurements. Experimental results are compared to theoretical calculations in the framework of the sd-IBM with and without configuration mixing.

1 Introduction

Neutron-deficient Pt ($Z=78$) isotopes have attracted great interest due to coexisting shapes [1] originating from intruder states and core excitations above the $Z=82$ shell gap [2]. Around ${}^{208}\hbox {Pb}$, an increase of quadrupole collectivity of proton particle-hole excitations results in the appearance of a deformed band on top of the near-spherical ground-state band [1,2,3]. For light Pb and Hg isotopes, the deformed $0^+$ intruder state approaches the spherical ground state which results in an excitation energy below the $2_1^+$ energy around the mid-shell region [4, 5]. For light Pt isotopes, the 2p-6h intruder configuration crosses the spherical configuration and becomes the ground state [2, 6,7,8]. Interacting boson model (IBM) calculations without configuration mixing describe the Pt nuclei as a transition from spherical to deformed nuclei with increasingly $\gamma$-soft energy surfaces as N increases [9]. In a more recent study, configuration mixing was established to be important when describing the spectroscopic properties of the Pt isotopes [10, 11].

${}^{182}\hbox {Pt}$ is the mid-shell nucleus with 104 neutrons and lifetimes of low-lying yrast states were measured previously employing the recoil distance Doppler-shift (RDDS) technique [12, 13]. Two inconsistent results for the $2_1^+$ state, namely 590(102) [12] and 709(43) ps [13], were obtained. The values for the $4_1^+$ state are consistent and the adopted value is 47(3) ps [14]. The nucleus ${}^{182}\hbox {Pt}$ was interpreted as a good candidate for a X(5) nucleus based on the reduced transition probabilities deduced from lifetimes measured in Ref. [12]. The interpretation relies on the correct determination of the $B(E2;2_1^+\rightarrow 0_1^+)$ value. In order to shed light on the experimental discrepancy, the nucleus ${}^{182}\hbox {Pt}$ is re-investigated in terms of the lifetimes of the low-lying yrast states. These lifetimes are in the range of the electronic timing measurement using fast $\hbox {LaBr}_3$(Ce) scintillation detectors. The fast-timing technique allows for the elimination of side-feeding problems by gating on transitions directly above and below the state of interest. In addition, small Doppler shifts for ${}^{182}\hbox {Pt}$ nuclei were observed which can lead to larger systematic uncertainties.

2 Experimental details

The nucleus of interest was populated using the

$$\begin{aligned} {}^{170}\hbox {Yb}({}^{16}\hbox {O},\hbox {4n}){}^{182}\hbox {Pt} \end{aligned}$$

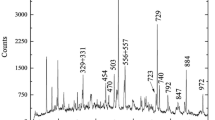
fusion-evaporation reaction at a beam energy of 87 MeV provided by the 10 MV FN Tandem accelerator of the Institute for Nuclear Physics of the University of Cologne. The $\gamma$ rays were detected using the HORUS spectrometer [15] equipped with eight high-purity germanium (HPGe) detectors and eight $1.5^{\prime \prime }~\times ~1.5^{\prime \prime }$ $\hbox {LaBr}_3\hbox {(Ce)}$ scintillation detectors (LaBr). The anode signals of the LaBr detectors were connected to constant-fraction discriminators which minimize the energy-dependent time-walk and deliver start and stop signals for the time-to-amplitude converters (TAC). The HPGe and LaBr energy signals are connected together with the TAC outputs to digital gamma finder (DGF) modules by XIA. For details regarding the electronic circuit and its modules the reader is referred to Ref. [16].

Lifetimes of excited states in ${}^{182}\hbox {Pt}$ are determined using the convolution and the Generalized Centroid Difference (GCD) method [16] which rely on the direct measurement of the time difference between $\gamma$ rays feeding and de-populating a particular state. If the start (stop) signal of the TAC is provided by the feeding (decaying) $\gamma$ ray, the so-called delayed (anti-delayed) time distribution is generated. It is described by a convolution of the prompt-response function (PRF) and an exponential decay [17]:

$$\begin{aligned} D(t) = n\lambda \int _{-\infty }^{t}PRF(t'-t_0)e^{-\lambda (t-t')dt'} + n_r, ~~ \lambda = 1/\tau , \end{aligned}$$

(1)

where n is the number of coincidences in the time distribution, $n_r$ is the number of random counts and $\tau$ is the mean lifetime of the state connected by the feeder-decay cascade. If the start (stop) signal is provided by the depopulating (feeding) $\gamma$ ray, the so-called anti-delayed time distribution is obtained. In the case where the lifetime of a given state is larger than the width of the PRF, an exponential slope can be seen in the delayed time spectrum which is directly linked to the decay constant $\lambda$. However, if the lifetime is shorter and no exponential tail is visible, it can be measured by the shift of the centroid of the PRF. The GCD method utilizes both delayed and anti-delayed time distribution and the lifetime can be measured via [16]:

$$\begin{aligned} 2\tau = \varDelta C(E_{feeder},E_{decay}) - \text {PRD}(E_{feeder},E_{decay}). \end{aligned}$$

(2)

In Eq. (2), $\varDelta C$ is the difference of centroid from the delayed and anti-delayed distribution and the prompt response difference (PRD) describes the $\gamma$–$\gamma$ time response of the system. The PRD has to be calibrated which is done using known lifetimes from excited states following the decay of a ${}^{152}\hbox {Eu}$ source. Figure 1 shows the calibration curve obtained in the present experiment and the fit corresponds to an empirical function [18]. The uncertainty is determined from the statistical fluctuations of the fit and amounts to 5 ps. Furthermore, the data has to be corrected for unaccounted (Compton) background contributions which is done by interpolating the time behavior at the feeding and decaying energy and weighting it with the peak-to-background ratio. For details on the fast-timing background correction the reader is referred to Ref. [19] and recent examples of its application can be found in Refs. [20,21,22,23].

Fig. 1

Calibrated PRD curve with reference energy $E_{ref} = 344~\hbox {keV}$. The data points obtained with other reference energies are shifted in parallel. The standard deviation results in a PRD uncertainty of 5 ps

Fig. 2

Time distribution for all LaBr detectors obtained using a $6_1^+\rightarrow 4_1^+$ (355 keV) HPGe gate and LaBr gates on the $2_1^+\rightarrow 0_1^+$ (155 keV) and the $4_1^+\rightarrow 2_1^+$ (264 keV) transitions. Gates are given in keV. An convolution fit of a Gaussian and an exponential to the data with constant background is shown as a solid blue line. Delayed and anti-delayed distributions are summed

Fig. 3

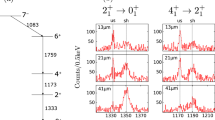
Delayed (blue) and anti-delayed (red) time distributions to measure a the $2_1^+$ and b the $4_1^+$ state in ${}^{182}\hbox {Pt}$. The spectra include all LaBr detectors and are labeled with their respective HPGe and LaBr gates in keV as well as the experimentally determined centroid difference. The centroids of each time distribution are highlighted by dashed lines

Fig. 4

Example of the background analysis for the $2^+_1$ state gated on its a decaying transition (155 keV) and b feeding transition (264 keV). Each spectrum shows the HPGe–LaBr gated HPGe (blue histogram) and LaBr (gray histogram) spectrum for all detectors, respectively. Additionally, the centroid difference measured at the full-energy peak (red square) and of the Compton background around the peak (purple crosses) is plotted. The solid green line shows the interpolation for the time behavior of the background. Each background panel is labeled with their respective LaBr and HPGe gates in keV

3 Results

The lifetime of the $2_1^+$ state is measured by looking at the time difference of the 155 keV $2_1^+\rightarrow 0_1^+$ decaying and the 264 keV $4_1^+\rightarrow 2_1^+$ feeding transition, i.e. $dT(155,264) =t(155)-t(264)$. The lifetime value is comparable with the width of the PRF which makes it well-suited for both, slope and GCD method. In both cases, a HPGe gate on the 355 keV $6_1^+\rightarrow 4_1^+$ transition is mainly used to select the $\gamma$-ray cascade of interest. Figure 2 shows the sum of delayed time distribution and (mirrored) anti-delayed spectrum where a slope on the right side is clearly visible. A convolution of a Gaussian and an exponential with constant background is fitted to the data and results in a lifetime of $\tau = 509(40)~\hbox {ps}$. The uncertainty is determined by variation of fit region, width of the Gaussian and background component which is added in quadrature to obtain the final error.

Table 1 Comparison of lifetimes and reduced transition probabilities of low-lying yrast states in ${}^{182}\hbox {Pt}$. Unless denoted otherwise, lifetimes are from this work. Adopted values from this work are highlighted in bold. Reduced transition probabilities are corrected for internal conversion calculated using the code BrICC [24]

Fig. 5

Comparison of experimental and theoretical a excitation energies and b reduced transition probabilities B(E2) as a function of spin. The experimental values are connected with solid lines to guide the eye. See text for details on the discussion of the different theoretical values. The B(E2) values for $I=2,4$ are the adopted ones from this work. Excitation energies and B(E2) values for $I>4$ are taken from the evaluated nuclear data file [14]

To further support this result, the GCD method has been applied to the delayed and anti-delayed time distribution shown in Fig. 3a. A centroid difference of $\varDelta C_{exp} = 586(9)~\hbox {ps}$ is measured. This value has to be corrected for unaccounted background contributions and the procedure is described in Ref. [19]. The background correction for the $2_1^+$ state is shown in Fig. 4 for the (a) feeding and (b) decaying transition. In Fig. 4, both LaBr and HPGe energy spectra are presented which are generated from HPGe-LaBr-LaBr and HPGe-LaBr-HPGe coincidence events, respectively. Those events require the condition that exactly 2 LaBr (HPGe) detectors and 1 HPGe (LaBr) detector fired within the coincidence window. Both event types are used to ensure that there are no other peaks contaminating the peak of interest in the LaBr spectrum with worse energy resolution. Additionally, Fig. 4 shows the centroid difference of surrounding background events and the interpolated time characteristics at the respective peaks. The values are $t_{cor}(E_f) = 424(5)~\hbox {ps}$ and $t_{cor}(E_d) = 71(4)~\hbox {ps}$ with their respective peak-to-background ratios, $p/b(E_f) = 1.14(11)$ and $p/b(E_d) = 1.31(10)$. The PRD($E_f , E_d$) value amounts to $-16(5)$ ps and together with Eq. 19 from Ref. [19] this results in a corrected value for the lifetime of $\tau = 563(12)~\hbox {ps}$. This value is in accordance with the lifetime obtained using the convolution method and supports the quality of the result. For the $2_1^+$ lifetime, the measurement of the GCD method is adopted due to its smaller uncertainty.

The same procedure is applied to determine the lifetime of the $4_1^+$ state. A HPGe gate on the 430 keV $8_1^+\rightarrow 6_1^+$ transition is used to select the yrast cascade in ${}^{182}\hbox {Pt}$. The time difference spectra are shown in Fig. 3b. The same procedure for the background correction is applied to the $4_1^+$ state and results in a final lifetime of $\tau = 41(5)~$ps which is consistent with both previously reported values. A summary of the results and a comparison to both previous RDDS measurements is given in Table 1.

4 Discussion and summary

The lifetimes of the $2_1^+$ and $4_1^+$ states were measured using electronic $\gamma$–$\gamma$ timing. The adopted value of $\tau (2_1^+)=563(12)~\hbox {ps}$ resolves the previous inconsistent results while significantly improving the uncertainty. The lifetime of the $4_1^+$ state was re-measured with similar precision. In the following, these new experimental findings are compared to theoretical calculations.

Having an excitation energy ratio of $R_{4/2} = 2.71$, ${}^{182}\hbox {Pt}$ is located in the symmetry triangle between O(6) ($\gamma$-soft) and SU(3) (rigid rotor) [25]. sd-IBM-1 [26] calculations in the extended consistent-Q formalism (ECQF) [27] were performed using the following Hamiltonian:

$$\begin{aligned} H(\zeta ,\chi ) = c \left[ (1-\zeta )\hat{n}_d - \dfrac{\zeta }{N_B}\hat{Q}^{\chi }\hat{Q}^{\chi }\right] , \end{aligned}$$

(3)

where $\hat{n}_d = d^{\dagger }\cdot \tilde{d}$ is the d-boson number operator, $N_B=14$ the boson number and $\hat{Q}^{\chi }$ the quadrupole operator given by:

$$\begin{aligned} \hat{Q}^{\chi } = \left( s^{\dagger }\tilde{d} + d^{\dagger }\tilde{s}\right) + \chi (d^{\dagger }\tilde{d})^{(2)}. \end{aligned}$$

(4)

From the quadrupole operator defined in Eq. (4), the transition probability T(E2) can be calculated via the effective boson charge $e_B$, i.e., $T(E2)=e_BQ$. Excitation energies from the yrast and $\gamma$-band and reduced transition probabilities were used to scan for optimal parameters $\zeta$ and $\chi$. From that, $\zeta = 0.57$ and $\chi = -0.85$ were obtained, similar to a study performed in Refs. [9, 10]. Together with the scaling factors of $c=1.19$ and $e_B=0.187~e^2\hbox {b}^2$, the results are compared to experimental values in Fig. 5 in a similar way as in Ref. [12].

Excitation energies are very well reproduced by the IBM-1 calculations, showing a similar trend and deviations below 100 keV for $I\le 10$. The B(E2) values are well reproduced for $I = 2,4$ but the experimental increase for $I >4$ is not fully accounted for in the IBM-1 calculation. Furthermore, the SU(3) and X(5) limits are also presented for comparison. The X(5) interpretation of this nucleus describes the evolution of the reduced transition probabilities while slightly overestimating the values for $I=8,10$. Note that the IBM calculation includes excited states $\gamma$ band in the optimization which comes at the cost of the description of yrast transition probabilities, see Fig. 5b. We further compare the results with a configuration mixing (CM) IBM-1 calculation taken from Refs. [10, 28]. These calculations reproduce well the B(E2) values at higher spins after increasing the boson charges for the N and $N+2$ configurations mentioned in Ref. [10] by 5%. Despite a slight underestimation of the $B(E2;2_1^+\rightarrow 0_1^+)$ strength, these calculations reproduce all other B(E2) values very well.

While the evolution of yrast B(E2) strengths support the X(5) character of ${}^{182}\hbox {Pt}$, non-yrast energies and transition probabilities have to be taken into account. As pointed out by the authors in Ref. [12], the main discrepancy is the excitation energy of the $0_2^+$ state. This state is related to shape coexistence and configuration mixing and the fact that the simple X(5) model cannot account for its energy shows that ${}^{182}\hbox {Pt}$ shows general features of an X(5) candidate with coexisting excitations belonging to different nuclear shapes.

In summary, lifetimes of the $2_1^+$ and $4_1^+$ states in ${}^{182}\hbox {Pt}$ were re-measured. For this purpose, the electronic $\gamma$–$\gamma$ fast-timing technique using $\hbox {LaBr}_3\hbox {(Ce)}$ scintillators has been employed to resolve previous ambiguities from RDDS measurements. The lifetime of the $2_1^+$ state was measured using both the slope and the GCD method which results in a self-consistent way and the adopted value amounts to $\tau = 563(12)~\hbox {ps}$. From this new data, the suggested X(5) signatures of ${}^{182}\hbox {Pt}$ from Ref. [12] could be confirmed from the B(E2) values.