Influence of halo single-neutron transfer on near barrier $^{15}$C + $^{12}$C total fusion

Abstract

A recent comparison of the average fusion cross section, $\left\langle \sigma _\mathrm {F}\right\rangle$, for energies just above the Coulomb barrier for the $^{12-15}$C + $^{12}$C systems found that the behaviour as a function of projectile neutron excess could not be satisfactorily explained by static barrier penetration model calculations and suggested that the neutron dynamics plays an important rôle. In this work we demonstrate that the ($^{15}$C,$^{14}$C) single neutron transfer has a significant influence on the above barrier $^{15}$C + $^{12}$C total fusion, although not quite in the way expected since it leads to a reduction in the cross section, contrary to the trend in the measured $\left\langle \sigma _\mathrm {F}\right\rangle$. However, this result underlines the danger of ignoring the effect of neutron transfer reactions on fusion in systems involving neutron halo nuclei.

In a recent article deSouza et al. [1] make a systematic comparison of measurements [2, 3] of the fusion excitation functions for the $^{12-15}$C + $^{12}$C systems at energies just above the respective Coulomb barriers. They find that the average fusion cross section, $\left\langle \sigma _F\right\rangle$, shows a more rapid increase with increasing projectile neutron number than can be accounted for by static barrier penetration models using potentials based on calculated nuclear matter densities. It is suggested that the failure of the static models adequately to describe the dependence of the average fusion cross sections on neutron excess could be interpreted as due to the importance of neutron dynamics. However, time-dependent Hartree-Fock model calculations also failed to reproduce the behaviour of the fusion cross sections. In this brief note we wish to point out that in the $^{15}$C + $^{12}$C system coupling to the ($^{15}$C,$^{14}$C) single-neutron transfer reaction has a significant influence on the fusion cross section excitation function and that while this coupling does not explain the observed dependence of $\left\langle \sigma _F\right\rangle$ on neutron excess—it significantly reduces the fusion cross section over the measured range of incident energies—its influence is sufficiently important that it must be included in any attempt at understanding the fusion of this neutron-rich system. By contrast, the single-nucleon transfer reactions have a negligible effect on the fusion cross sections for the other systems.

The most important structural particularity of $^{15}$C compared to the other carbon isotopes considered by deSouza et al. [1], $^{12}$C, $^{13}$C and $^{14}$C, is the halo nature of its $1/2^+$ ground state. Not only is this state weakly bound, $S_n = 1.2$ MeV, but its wave function is an almost pure $2s_{1/2}$ neutron coupled to the $^{14}$C core in its $0^+$ ground state. This suggests that, in addition to the expected significance of breakup effects, stripping of the valence neutron should also play an important rôle in reactions involving $^{15}$C, since the tail of its wave function extends to a considerable distance beyond the $^{14}$C core.

The weak binding of the valence neutron in $^{15}$C is also reflected in the reaction Q value for one-neutron removal compared to the other carbon isotopes considered in Ref. [1]. The relevant Q values for single-nucleon transfers are listed in Table 1.

It can immediately be seen that single-nucleon transfers may be ruled out as a significant influence on the $^{12}$C + $^{12}$C system in the energy region under consideration since the reaction Q values are large and negative. Similar considerations apply to the other systems for both single-neutron addition and single-proton removal from the projectile. Of the other transfer processes listed in Table 1 the $^{12}$C($^{13}$C,$^{12}$C)$^{13}$C “elastic transfer” (and, by extension, its “inelastic transfer” counterparts) and the $^{12}$C($^{14}$C,$^{13}$C)$^{13}$C single-neutron removal reaction could possibly influence the fusion cross section at the energies under consideration here, with the $^{12}$C($^{15}$C,$^{16}$N)$^{11}$B, $^{12}$C($^{14}$C,$^{15}$N)$^{11}$B and $^{12}$C($^{13}$C,$^{14}$N)$^{11}$B proton transfer reactions becoming progressively less likely, judging by the reaction Q values.

In this work we are not concerned with attempting to fit the measured fusion excitation functions for the systems investigated by deSouza et al., we merely wish to establish the exceptional nature of the influence of the ($^{15}$C,$^{14}$C) single-neutron transfer reaction on the fusion of the $^{15}$C + $^{12}$C system. Therefore, we only consider couplings to inelastic excitations of the target and projectile nuclei and single-nucleon transfer reactions. Following the kinematic considerations discussed in the preceding paragraph, in addition to $^{15}$C + $^{12}$C we limit our analysis to the $^{12}$C + $^{13,14}$C systems to provide benchmarks for the influence of single-nucleon transfer reactions on the fusion cross section.

Table 1 Reaction Q values (in MeV) for single-nucleon transfers in each of the systems considered by deSouza et al. [1]. The target nucleus is $^{12}$C in all cases

Within these limits relatively full coupling schemes were included in calculations of the fusion excitation functions using the code fresco [5]. We begin by considering inelastic excitations of both target and projectile nuclei. In all three systems coupling to the 4.44-MeV $2^+$ excited state of the $^{12}$C target was included, with the B(E2) taken from Raman et al. [6] and the nuclear deformation length, $\delta _2 = -1.40$ fm, from Ref. [7]. For the $^{15}$C + $^{12}$C system, coupling to the 0.74-MeV $5/2^+$ bound excited state of $^{15}$C was included using the B(E2) of Ref. [8], with the corresponding nuclear deformation length $\delta _2 = 0.52$ fm derived from the B(E2) assuming the rotational model and a radius of $1.2 \times 15^{1/3}$ fm. In the $^{14}$C + $^{12}$C system coupling to the 7.01-MeV $2^+$ excited state of $^{14}$C was included using the B(E2) of Raman et al. [6] and a nuclear deformation length $\delta _2 = -0.60$ fm, taken from Ref. [10]. We have followed Ref. [10] in assuming a slight oblate deformation for $^{14}$C, although this does not affect the results for the fusion cross section. In the $^{13}$C + $^{12}$C system couplings to the 3.09-MeV $1/2^+$, 3.68-MeV $3/2^-$ and 3.85-MeV $5/2^+$ states were included. Although these are not considered to be collective states they were treated as such for the sake of simplicity. The respective B(E1), B(E2) and B(E3) values were taken from Ref. [8] and the corresponding nuclear deformation lengths from Ref. [9]. While the use of standard collective model form factors for these states is questionable, Peterson et al. [9] note that for $^{13}$C($\alpha$,$\alpha ^\prime$) inelastic scattering the results do not differ greatly from those using more realistic form factors and the inelastic scattering data, including that for the $\Delta L = 1$ transition to the 3.09-MeV $1/2^+$ level, are rather well reproduced. Thus, collective model form factors should be adequate for our purposes. No mutual excitation was included in any of the three systems studied. Coulomb multipoles were of the standard form for a deformed charged sphere while nuclear multipoles were calculated by numerically deforming the radius of the diagonal potential and projecting by Gaussian quadrature onto the appropriate multipole.

The following single-neutron transfer couplings were also investigated: $^{12}$C($^{15}$C,$^{14}$C)$^{13}$C, $^{12}$C($^{14}$C,$^{13}$C)$^{13}$C, and $^{12}$C($^{13}$C,$^{12}$C)$^{13}$C. The various overlaps, together with the spectroscopic amplitudes used are listed in Table 2.

Table 2 Overlaps plus corresponding spectroscopic amplitudes (S) and shell model level ($n\ell _j$) included in the full CRC calculations. The signs of the spectroscopic amplitudes are consistent with the phase convention used in fresco

Due to the special nature of the $^{13}$C + $^{12}$C system with “elastic transfer” and “inelastic transfer” of the single neutron between the two $^{12}$C cores the various $\left\langle ^{13}\mathrm {C} \mid {^{12}\mathrm {C}} + n \right\rangle$ overlaps were implemented as both “projectile-like” and “target-like” and the same inelastic couplings were included in the “exit” partition as for the entrance. Inelastic couplings were also included in the $^{13}$C + $^{13}$C exit partition of the $^{14}$C + $^{12}$C system for both projectile-like and target-like $^{13}$C nuclei.

The real parts of the input optical model potentials were calculated within the double-folding framework with the M3Y nucleon-nucleon effective interaction [16] using the code dfpot [17]. The required $^{12}$C, $^{14}$C and $^{15}$C nuclear matter densities were taken from Dobrovolsky et al. [18], and the $^{13}$C density from Ahmad et al. [19]. The imaginary parts of the optical potentials were of Woods-Saxon squared form, with depth $W = 50$ MeV, radius $R_W = 1.0 \times (\mathrm {A}_p^{1/3} + \mathrm {A}_t^{1/3})$ fm and diffuseness $a_W = 0.3$ fm, effectively reproducing the incoming wave boundary condition [20]. In this model the total fusion cross section is defined as the sum of the absorption by the imaginary parts of the potentials in all channels and is thus the difference between the reaction cross section and the sum of the integrated cross sections for all channels included in the coupling scheme. While the total fusion calculated in this way is complete within the model space used since it sums over the absorption in all channels explicitly included in the coupling scheme, it should be noted that the measured total fusion cross section may contain contributions from other processes.

Fig. 1

Fusion excitation functions for: a $^{13}$C + $^{12}$C, b $^{14}$C + $^{12}$C and c $^{15}$C + $^{12}$C. Calculations are compared with the data of Refs. [2, 3] (filled circles) and Kovar et al. [4] (open circles), see text for details

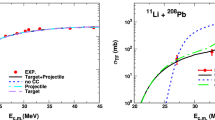
The calculations are compared with the data in Fig. 1. The results of three calculations are plotted for each system: the bare, no coupling result (denoted by the dotted curves), calculations including coupling to inelastic excitations of the projectile and target only (denoted by the dashed curves) and calculations including couplings to both inelastic excitations and neutron transfers (the solid curves). In all three systems the inelastic excitations have a negligible effect on the fusion excitation function, as do the single-neutron transfer couplings in the $^{13}$C + $^{12}$C and $^{14}$C + $^{12}$C systems. In the $^{15}$C + $^{12}$C system the single-neutron transfer does have a visible effect, reducing the calculated fusion cross section, and while this is only of the order of 10% or so for the incident energies where there are data, the size of the effect is comparable with the differences discussed by deSouza et al. [1], so must be regarded as significant. A similar reduction of the total fusion cross section at energies just above the Coulomb barrier due to coupling to the ($^{15}$C,$^{14}$C) single-neutron transfer reaction was also predicted for the $^{15}$C + $^{208}$Pb system [21]. Test calculations for the $^{14}$C + $^{12}$C and $^{13}$C + $^{12}$C systems additionally including the $^{12}$C($^{14}$C,$^{15}$N)$^{11}$B and $^{12}$C($^{13}$C,$^{14}$N)$^{11}$B single proton transfers respectively found a negligible influence of these reactions on the corresponding above barrier total fusion cross sections. A meaningful test of the effect of coupling to the $^{12}$C($^{15}$C,$^{16}$N)$^{11}$B single proton transfer on the $^{15}$C + $^{12}$C total fusion cross section could not be performed due to a lack of available spectroscopic amplitudes for the $\left\langle ^{16}\mathrm {N} \mid {^{15}\mathrm {C}} + p \right\rangle$ overlaps, although the results of the similar calculations for the $^{14}$C + $^{12}$C and $^{13}$C + $^{12}$C systems suggest that it does not play an important rôle.

The $^{13}$C + $^{12}$C fusion excitation function is reasonably well described for energies up to approximately $E_\mathrm {c.m.} = 13$ MeV; thereafter it is increasingly over-predicted by the calculations. The $^{14}$C + $^{12}$C fusion excitation function is well described over the whole range of available data, the slight over-prediction at the lowest $E_\mathrm {c.m.}$ value being within the effect of different choices of nuclear matter density as input to the calculation of the double-folded potential. By contrast, the $^{15}$C + $^{12}$C fusion excitation function is well described by the no-coupling barrier penetration calculation and while the introduction of target and projectile inelastic couplings does not affect this good agreement, the single-neutron transfer coupling worsens it, leading to significant under-prediction of the cross section at the two lowest available $E_\mathrm {c.m.}$ values.

A more global presentation of the dependence of the above barrier fusion on neutron excess is provided by the average fusion cross section, $\left\langle \sigma _\mathrm {F}\right\rangle$. This is illustrated in Fig. 2 where we compare the $\left\langle \sigma _\mathrm {F}\right\rangle$ values of deSouza et al. [1], obtained by averaging Wong model fits to the experimental fusion cross sections over the interval $10 \le E_\mathrm {c.m} \le 18$ MeV, with the equivalent quantities derived from the present calculations.

Fig. 2

Experimental average above barrier fusion cross sections $\left\langle \sigma _\mathrm {F}\right\rangle$ (filled triangles [1]) as a function of projectile neutron excess. The lines denote the equivalent quantities obtained from the present calculations with no coupling (dotted), inelastic coupling only (dashed) and both inelastic and single-neutron transfer couplings (solid). The dot-dashed line denotes the results of the RMF-SP(NL3) calculation of Ref. [1]

Also plotted on Fig. 2 are the $\left\langle \sigma _\mathrm {F}\right\rangle$ values extracted by deSouza et al. [1] from their barrier penetration model calculations with potentials calculated using nuclear matter densities from relativistic mean field (RMF) calculations employing the NL3 interaction and the Sao Paulo potential as effective interaction. The slope of the present no-coupling results is almost identical, although the $\left\langle \sigma _\mathrm {F}\right\rangle$ values are approximately 5% larger. However, this is within the spread of values obtained with different choices of nuclear matter densities. The behaviour of $\left\langle \sigma _\mathrm {F}\right\rangle$ as a function of neutron excess is not affected by the inclusion of inelastic couplings, neither do the ($^{13}$C,$^{12}$C) and ($^{14}$C,$^{13}$C) neutron transfer couplings have a significant influence. By contrast, the ($^{15}$C,$^{14}$C) single-neutron transfer coupling acts in the opposite sense to the trend of the measured $\left\langle \sigma _\mathrm {F}\right\rangle$ values as a function of neutron excess, i.e. it reduces $\left\langle \sigma _\mathrm {F}\right\rangle$ for $^{15}$C + $^{12}$C to the extent that it is slightly smaller than for $^{14}$C + $^{12}$C.

It is thus apparent that while the ($^{15}$C,$^{14}$C) single-neutron transfer reaction has a significant effect on the total fusion in the $^{15}$C + $^{12}$C system, it does not explain the discrepancy between the trend of the measured and calculated values of $\left\langle \sigma _\mathrm {F}\right\rangle$ as a function of neutron excess, rather, it increases it. However, it is equally clear that any attempt at understanding the observed behaviour must include this process. Some other process, not included in the calculations presented here, must act to compensate for the effect of the single-neutron transfer coupling if the observed increase in $\left\langle \sigma _\mathrm {F}\right\rangle$ for the $^{15}$C + $^{12}$C system beyond the trend as a function of neutron excess expected from “geometric” considerations is to be explained. The most likely candidate is coupling to the $^{15}\mathrm {C} \rightarrow {^{14}\mathrm {C}} + n$ breakup, although this is difficult to demonstrate in a consistent manner with currently available models. However, the coupled discretised continuum channels (CDCC) calculations presented in Ref. [22] found that for the $^6$He + $^{208}$Pb system coupling to the $^6\mathrm {He} \rightarrow \alpha + {^2n}$ breakup did increase the total fusion cross section at similar incident energies with respect to the Coulomb barrier, and test CDCC calculations for the $^{15}$C + $^{12}$C system including coupling to the $^{15}\mathrm {C} \rightarrow {^{14}\mathrm {C}} + n$ breakup show a similar effect. Whatever the additional coupling may be, without taking into account the ($^{15}$C,$^{14}$C) single-neutron transfer the good agreement of the no coupling calculation with the data would have led to the—erroneous—conclusion that the influence of coupling in general was negligible in this energy regime.

In summary, the present work provides evidence for the suggested importance of neutron dynamics in explaining the evolution of $\left\langle \sigma _\mathrm {F}\right\rangle$ as a function of neutron excess in the $^{12-15}$C + $^{12}$C systems [1], although perhaps not quite in the way expected. The CRC calculations presented here suggest that some other process, most likely the $^{15}\mathrm {C} \rightarrow {^{14}\mathrm {C}} + n$ breakup, must affect the total fusion cross section in such a way as to compensate for, or even somewhat exceed, the influence of the ($^{15}$C,$^{14}$C) single-neutron transfer reaction in the $^{15}$C + $^{12}$C system in the energy regime discussed here. There is also some evidence for a slight, $\sim 5$%, reduction of the above-barrier fusion cross section in the $^{13}$C + $^{12}$C system compared to our CRC calculations, possibly due to the formation of molecular orbitals by the single neutron between the two $^{12}$C cores, see, e.g., Ref. [23]. The main conclusion is therefore that in systems involving neutron-rich and neutron halo nuclei the influence of neutron transfer reactions on the total fusion cross section should not be ignored.