Models of breakup: a final state interaction problem

Abstract

In this paper, we discuss the evolution of breakup models from fully quantum mechanical, such as the Ichimura–Austern–Vincent model to semiclassical, to eikonal approximations following the insight on the mechanism first proposed by Hussein and McVoy (HM) for the presently called stripping term. In particular we concentrate on, and stress that, the correct implementation of a quantum mechanical model of breakup requires the use of energy dependent interactions and the energy averaging procedure is a key point to understand the difference among models. On the other hand using fixed energy potentials is one of the steps towards the high energy eikonal limit first proposed by HM. However the intermediate semiclassical transfer to the continuum model of Bonaccorso and Brink does use an energy dependent nucleon–target optical potential, while fixing the core–target interaction at the incident energy. The relationship between these methods is clarified.

Appendices

A Reminder of eikonal formulae

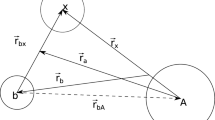
Following Refs. [26,27,28, 81] we consider a single-particle model for a halo nucleus and introduce the eikonal approximation to study its scattering on another target nucleus. The ground state is described by a wave function $\phi _{0}(\mathbf {r}_{\mathbf{Cn}})$ which depends on the relative coordinate $\mathbf {r}_{\mathbf{Cn}}$, Fig. 1. between the nucleon and the core. After interacting with the target the eikonal wave-function of the halo nucleus in its rest frame has the form

$$\begin{aligned} \varPsi \left( \mathbf {r}_{Cn}, \mathbf {r}_{\mathbf{P}}\right) =S_{n}\left( \mathbf {b}_{n}\right) S_{CT}\left( \mathbf {b}_{c}\right) \phi _{0}\left( \mathbf {r}_{Cn}\right) \end{aligned}$$

(17)

where $\mathbf {r_P}$ and $\mathbf {r}_{\mathbf{Cn}}$ are the coordinates of the center-of-mass of the projectile consisting of the core plus one nucleon, and of the nucleon with respect to the core respectively, see Fig. 1. The vectors

$$\begin{aligned} \mathbf {b}_{n}=\mathbf {r_P}_{\perp }+\beta _{2}\mathbf {r}_{\mathbf{Cn} \perp }\qquad \mathrm {and}\qquad \mathbf {b}_{c}=\mathbf {r_P}_{\perp }-\beta _{1}\mathbf {r}_{\mathbf{Cn}\perp } \end{aligned}$$

(18)

are the impact parameters of the nucleon and the core with respect to the target nucleus. Thus $\beta _{1}=m_{n}/m_{p}$, $\beta _{2}=m_{c}/m_{p} =1-\beta _{1}$, where $m_{n}$ is the nucleon mass, $m_{c}$ is the mass of the projectile core and m$_{p}=m_{n}+m_{c}$ is the projectile mass. The two profile functions $S_{n}$ and $S_{CT}$ are defined in terms of the corresponding potentials by

$$\begin{aligned} S\left( \mathbf {b}\right) =\exp \left( -\frac{i}{\hbar v}\int dzV\left( \mathbf {b,}z\right) \right) \end{aligned}$$

(19)

where v is the beam velocity. The breakup amplitude generated from the eikonal wave function (17) has a direct contribution from the nucleon–target optical potential $V_{nT}$ represented by nucleon–target profile function $S_{n}$ and a core-recoil contribution from the core–target interaction $V_{CT}$ represented by the profile function $S_{CT}$ [63, 64]. The recoil contribution depends on the ratio $\beta _{1}$ of the nucleon mass to the projectile mass and goes to zero in the limit $\beta _{1}\rightarrow 0$. The potential $V_{CT}$ includes the core–target Coulomb potential and the real and imaginary parts of the nuclear potential. The Coulomb part of $V_{CT}$ is responsible for Coulomb breakup. Using the approximate form of the wave function (17) with (19) implies the “frozen halo” approximation; the nucleon velocity relative to the core in the projectile and in the final state is slow compared with the incident velocity v.

The eikonal breakup amplitude is defined by [28]

$$\begin{aligned} A\left( \mathbf {K,k}\right)&=\int d^{2}\mathbf {r_P}_{\perp }~e^{-i\mathbf {K_{\perp }\cdot r_P} _{\perp }}\nonumber \\&\quad \times \int d^{3}\mathbf {r}_{\mathbf{Cn}}~\phi _{\mathbf {k}}^{*}\left( \mathbf {r}_{Cn} \right) \left( S_{CT}\left( \mathbf {b}_{C}\right) S_{n}(\mathbf {b} _{n})-1\right) \phi _{0}\left( \mathbf {r}_{\mathbf{Cn}}\right) . \nonumber \\ \end{aligned}$$

(20)

The impact parameters $\mathbf {b}_{n}$ and $\mathbf {b}_{C}=\mathbf {b} _{n}+\mathbf {r}_{\perp }$ are defined in Eq. (18). The quantities $\left( \mathbf {K,k}\right)$ are the momenta conjugate to the coordinates $\left( \mathbf {r_P,r_{Cn}}\right) .$ They are related to the final momenta of the core, nucleon and target by

$$\begin{aligned} \mathbf {k}_{C}=-\mathbf {k}+\beta _{2}\mathbf {K},\qquad \mathbf {k}_{n} =\mathbf {k}+\beta _{1}\mathbf {K,}\qquad \mathbf {k}_{T}=-\mathbf {K.} \end{aligned}$$

(21)

The wave function $\phi _{\mathbf {k}}\left( \mathbf {r}_{Cn}\right)$ is the final continuum wave function of the nucleon relative to the core. The complete differential cross-section is

$$\begin{aligned} \frac{d\sigma }{d^{2}\mathbf {K}d^{3}\mathbf {k}}=\frac{1}{\left( 2\pi \right) ^{5}}\left| A\left( \mathbf {K,k}\right) \right| ^{2} \end{aligned}$$

(22)

Equation (20) can also be written as

$$\begin{aligned} A\left( \mathbf {K,k}\right)&=\int d^{2}\mathbf {r_P}_{\perp }~e^{-i\mathbf {K_{\perp }\cdot r_P} _{\perp }}\nonumber \\&\quad \times \int d^{3}\mathbf {r}_{\mathbf{Cn}}~\phi _{\mathbf {k}}^{*}\left( \mathbf {r}_{Cn} \right) S_{CT}\left( \mathbf {b}_{C}\right) S_{n}(\mathbf {b} _{n}) \phi _{0}\left( \mathbf {r}_{Cn}\right) . \nonumber \\ \end{aligned}$$

(23)

because of the orthogonality of $\phi _{\mathbf {k}}\left( \mathbf {r}_{Cn}\right)$ and $\phi _{0}\left( \mathbf {r}_{Cn}\right)$ (cf. Eq. (8) of Ref. [28]). Equations (23) is a general eikonal expression which has been used in [28] and by many other authors.

Finally following the derivation in [74] the EBU eikonal cross section in the no-recoil approximation is

$$\begin{aligned} \frac{d\sigma _{EBU}}{dk_1}&=\int d^{2}\mathbf {b}_{C}~|S_{CT}\left( \mathbf {b}_{C}\right) |^2\nonumber \\&\quad \times \int d^{2}\mathbf {r}_{{Cn}_{\perp }}~\left| 1-S_{n}\left( \mathbf {b} _{n} \right) \right| ^2 |{\tilde{\phi }}_{0}\left( \mathbf {r}_{{Cn}_{\perp }},k_1\right) |^2, \nonumber \\ \end{aligned}$$

(24)

and the NEB formula [27, 28]

$$\begin{aligned} \frac{d\sigma _{NEB}}{dk_1}&=\int d^{2}\mathbf {b}_{C}~|S_{CT}\left( \mathbf {b}_{C}\right) |^2 \nonumber \\&\quad \times \int d^{2}\mathbf {r}_{{Cn}_{\perp }}~\left( 1-|S_{n}\left( \mathbf {b} _{n}\right) |^2\right) |{\tilde{\phi }}_{0}\left( \mathbf {r}_{{Cn}_{\perp }},k_1\right) |^2. \nonumber \\ \end{aligned}$$

(25)

B Derivation of the STC transfer amplitude

The derivations of Eq. (9) is given in these appendices in a systematic approach which is useful for making different approximations to the FSI. The core spectator model is at the basis of semiclassical methods of breakup and transfer as shown by Eq. (15). To simplify the notation in this section the coordinate $\mathbf{r}$ and $\mathbf{R}$ are used instead of $\mathbf{r}_n$ and $\mathbf{r}_p$ of Eqs. (9, 10) and Fig. 1.

Semi-classical formulae for transfer amplitudes in heavy ion transfer reactions which incorporate the kinematical conditions are developed following the approach of Brink [46], Hasan and Brink [47, 48], Lo Monaco and Brink [49] and Bonaccorso et al. [3, 50]. The method of Broglia et al. [51, 52] is very similar to ours. The theory is semi-classical in the sense that the nuclei involved in the reaction are assumed to follow classical trajectories but the transfer is calculated by quantum mechanics. The wave function $\psi$ of the transferred particle satisfies a time-dependent Schrödinger equation

$$\begin{aligned} { i }\hbar {\partial \psi \over \partial t} = (T + V_1(\mathbf{r_1},t) +V_2(\mathbf{r_2},t))\psi . \end{aligned}$$

(26)

Here $T=-(\hbar ^2/2m) \nabla ^2$ is the kinetic energy operator for the transferred particle, while the potentials $V_1$ and $V_2$ represent its interaction with the projectile and target. The potentials are time dependent and move along classical trajectories $\mathbf{s}_1(t)$ and $\mathbf{s}_2(t)$ describing the motion of the projectile and target during the collision.

$$\begin{aligned} V_1({\mathbf{r}}_1,t)=V_1({\mathbf{r}} - \mathbf{s_1}(t)), \qquad V_2({\mathbf{r}}_2,t) = V_2({\mathbf{r}} - \mathbf{s_2}(t)). \end{aligned}$$

(27)

The initial state $\psi _1(\mathbf{r},t)$ of the transferred particle satisfies the time-dependent Schrödinger equation for the potential $V_1$ with a correction $\varDelta V_2$ which takes into account some of the effects of $V_2$a

$$\begin{aligned} { i} \hbar {{\partial }\psi _1\over {\partial }t} = (T + V_1(\mathbf{r},t) +\varDelta V_2(\mathbf{r},t))\psi _1. \end{aligned}$$

(28)

In the case of neutron transfer we can choose $\varDelta V_2 =0$, but for charged particle transfer it is non zero and takes into account the long range effects of the Coulomb field. The exact form of $\varDelta V_2$ will be specified later. The final state wave-function satisfies a similar equation

$$\begin{aligned} { i}\hbar {{\partial }\psi _2\over {\partial }t} = (T + V_2(\mathbf{r},t) +\varDelta V_1(\mathbf{r},t))\psi _2. \end{aligned}$$

(29)

A very similar starting point as the present one was used in Ref. [26] where however the eikonal formalism was eventually followed. During transfer the particle is affected by both the potentials $V_1$ and $V_2$ and a perturbation formula [46, 51] can be derived for the transfer amplitude $A_{21}$ between the initial state of the particle $\psi _1$ in the projectile and the final state $\psi _2$ in the target. The amplitude is

$$\begin{aligned} A_{21} \approx {1 \over {i \hbar }} \int d t \int d \mathbf{r}\psi _2^\star (\mathbf{r},t) (V_1(\mathbf{r})- \varDelta V_1(\mathbf{r})) \psi _1 (\mathbf{r},t). \end{aligned}$$

(30)

Equation (30) can be obtained from the following argument. From Eqs. (26) and and (29) we have

$$\begin{aligned}&{ i}\hbar {{\partial }\over {\partial }t}\langle \psi _2(t)|\psi (t)\rangle \nonumber \\&\quad = \langle \psi _2| (T + V_1 +V_2 -(T +V_2 +\varDelta V_1))|\psi \rangle \nonumber \\&\quad = \langle \psi _2|(V_1 -\varDelta V_1) |\psi \rangle . \end{aligned}$$

(31)

The state $\psi (t)$ satisfies the initial condition $\psi (t) \rightarrow \psi _1(t)$ as $t \rightarrow -\infty$. Integrating both sides of Eq. (31) gives

$$\begin{aligned} A_{21}= & {} \lim _{t\rightarrow \infty } \langle \psi _2(t)|\psi (t)\rangle \nonumber \\= & {} {1\over { i}\hbar } \int _{-\infty }^{\infty }d t \langle \psi _2(t)|(V_1 -\varDelta V_1) |\psi (t)\rangle . \end{aligned}$$

(32)

Equation (30) is obtained by making the approximation $\psi (t) \approx \psi _1(t)$ in the integral on the right hand side of Eq. (32). An alternative derivation of Eq. (30) is given in the following.

It was shown by Lo Monaco and Brink [49] and Stancu and Brink [82] that this perturbation integral can be transformed to a surface integral over a surface $\varSigma$ drawn between the two nuclei perpendicular to the line joining their centers at the point of closest approach. This surface is at a distance $d_1$ from the center of the first nucleus and $d_2$ from the second and $d_1 + d_2 = d$. The surface integral formula is

$$\begin{aligned} A_{21} = {\hbar \over 2m i } \int d t \int d \mathbf{S} \cdot (\psi _2^\star (\mathbf{r},t)\nabla \psi _1( \mathbf{r},t) - \psi _1(\mathbf{r},t)\nabla \psi _2^\star ( \mathbf{r},t)).\nonumber \\ \end{aligned}$$

(33)

Equation (33) is derived from Eq. (30) in Appendix C. The two equations are exactly equivalent if $V_2 -\varDelta V_2=0$ in the region $R_1$ above the surface $\varSigma$ and $V_1 -\varDelta V_1 =0$ in $R_2$ below $\varSigma$. Otherwise Eq. (33) is an approximation to Eq. (30).

We want to evaluate the amplitude Eq. (33) when the relative motion of the two nuclei is a Coulomb orbit. If the scattering angle is small then such an orbit can be replaced by a constant velocity orbit tangential to it at the point of closest approach. This is a reasonable approximation because the transfer takes place near the point of closest approach and because the acceleration in the Rutherford orbit is small. It would not be a good approximation for large-angle scattering. The transfer amplitude depends only on the relative velocity so we can assume that $V_2$ is at rest and $V_1$ has a velocity $\mathbf{v}$ which is the tangential relative velocity in the Rutherford orbit at the distance of closest approach d. We write the equation of the orbit relative to the center of $V_2$ as

$$\begin{aligned} \mathbf{R}(t) = \mathbf{d} + \mathbf{v}t. \end{aligned}$$

(34)

We will choose a cordinate system so that, at the point of closest approach between the two nuclei, the z-axis is parallel to the velocity of the first nucleus relative to the second and the x-axis is in the reaction plane directed from the center of second nucleus towards the center of the first. The y-axis is perpendicular to the reaction plane.

C Green’s function formalism

We consider the unitary time dependent propagator $G(t_2,t_1)$ which transforms the solution of the Schrödinger Eq. (26) at time $t_1$ into the solution at time $t_2$,

$$\begin{aligned} \psi (t_2)=G(t_2,t_1)\psi (t_1). \end{aligned}$$

(35)

This propagator satisfies the integral equation

$$\begin{aligned} G(t_2,t_1)= & {} G_0(t_2,t_1)+{1\over i\hbar }\int _{t_1}^{t_2}dt ~G_0(t_2,t)\nonumber \\&\times (V_1(t)+V_2(t))G(t,t_1) \end{aligned}$$

(36)

which we abbreviate by

$$\begin{aligned} G=G_0+G_0(V_1+V_2)G. \end{aligned}$$

In Eqs. (36) and (37) $G_0$ is the free propagator. Both G and $G_0$ satisfy the boundary condition

$$\begin{aligned} G(t,t)=G_0(t,t)=1. \end{aligned}$$

(37)

First we consider the case of a transition from an initial state $\psi (t_1)$ which is a bound state in the potential $V_1$ to a final state $\psi (t_2)$ which is a bound state in $V_2$. The transition amplitude is given by the matrix element

$$\begin{aligned} A= \lim _{\begin{array}{c} t_2\rightarrow \infty \\ t_1\rightarrow -\infty \end{array}} \langle \psi _2(t_2)|G(t_2,t_1)|\psi _1(t_1)\rangle \end{aligned}$$

(38)

where $\psi _1(t)$ and $\psi _2(t)$ propagate in time according to the Schrödinger equations (28) and (29) with potentials $V_1 +\varDelta V_2$ and $V_2 + \varDelta V_1$ respectively. All the multiple scattering effects are included in the propagator G. The integral equation (36) can be solved by iteration to give a multiple scattering series. Various partial summations can be made by introducing the propagators $G_1$ and $G_2$ for the potentials $V_1 +\varDelta V_2$ and $V_2+\varDelta V_1$ respectively.

$$\begin{aligned} G_1= & {} G_0+G_0(V_1 +\varDelta V_2)G_1=G_0+G_0(V_1+\varDelta V_2)G_0 \nonumber \\&+ G_0(V_1+\varDelta V_2)G_0(V_1+\varDelta V_2)G_0+\cdots \end{aligned}$$

(39)

$$\begin{aligned} G_2= & {} G_0+G_0(V_2+\varDelta V_1)G_2 =G_0+G_0(V_2+\varDelta V_1)G_0\nonumber \\&+ G_0(V_2+\varDelta V_1)G_0(V_2+\varDelta V_1)G_0+\cdots \end{aligned}$$

(40)

The operator $G_1$ is the exact propagator for a nucleon interacting with the potential $V_1+\varDelta V_2$ and similarly for $G_2$. Thus

$$\begin{aligned} \psi _1(t_2) = G_1(t_2,t_1)\psi _1(t_1);~~ \psi _2(t_2) = G_2(t_2,t_1)\psi _2(t_1). \end{aligned}$$

(41)

The exact propagator G can be written in terms of $G_2$ or $G_1$ as

$$\begin{aligned} G= & {} G_2+G_2(V_1-\varDelta V_1)G=G_2+G(V_1-\varDelta V_1)G_2, \end{aligned}$$

(42)

$$\begin{aligned} G= & {} G_1+G_1(V_2-\varDelta V_2)G=G_1+G(V_2-\varDelta V_2)G_1.\nonumber \\ \end{aligned}$$

(43)

The transition amplitude equation (38) can be calculated in different approximations. Using Eqs. (41) and (43) we get

$$\begin{aligned} A= & {} \langle \psi _2(t_2)|G_2(t_2,t_1)|\psi _1(t_1)\rangle \nonumber \\&+\langle \psi _2(t_2) |G_2(V_1-\varDelta V_1)G|\psi _1(t_1)\rangle . \end{aligned}$$

(44)

The first term in Eq. (44) tends to zero as $t_2 \rightarrow \infty$ because of Eq. (41). In fact using Eq. (41) the first term in Eq. (44) can be written as $\langle \psi _2(t_2)|\psi _1(t_2)\rangle .$ This tends to zero as $t_2 \rightarrow \infty$ because $\psi _1$ is a bound state in the potential $V_1$ which moves away from the target as t increases. In the second term in Eq. (44) G can be written in terms of its multiple scattering series. Each partial summation represents an approximation to Eq. (44). The simplest approximation is obtained by replacing G by $G_1$

$$\begin{aligned} A_{21}=\langle \psi _2(t_2)|G_2(V_1-\varDelta V_1)G_1|\psi _1(t_1)\rangle , \end{aligned}$$

(45)

using Eq. (41) this can be written as

$$\begin{aligned} A_{21}={1\over 2\hbar }\int _{-\infty }^{\infty }~dt~ \langle \psi _2(t)|(V_1-\varDelta V_1)|\psi (t)\rangle . \end{aligned}$$

(46)

This is the same as Eq. (30) above. An equivalent formula can be obtained by using Eq. (42) and approximating G by $G_2$

$$\begin{aligned} A_{21}={1\over 2\hbar }\int _{-\infty }^{\infty }~dt~ \langle \psi _2(t)|(V_2-\varDelta V_2)|\psi (t)\rangle . \end{aligned}$$

(47)

The argument is slightly different if the final state is a continuum state. We introduce an asymptotic wave function $\psi _{2out}(t)$ which propagates in time according to the free particle Schrödinger equation (Newton [83]) and satisfies the boundary condition $\psi _{2out}(t)\rightarrow \psi _{2}(t)$ as $t\rightarrow \infty$. The transition amplitude (38) can be written in terms of the asymptotic wave function as

$$\begin{aligned} A=\lim _{\begin{array}{c} t_2\rightarrow \infty \\ t_1\rightarrow -\infty \end{array}}\langle \psi _{2out}(t_2)|G(t_2,t_1)| \psi _{1i}(t_1)\rangle \end{aligned}$$

(48)

It is important to note that $\psi _{2out}(t)$ is a free nucleon wave function. All the FSI of the nucleon are included in the propagator G.

The transition amplitude equation (48) can be calculated in different approximations. Using Eqs. (41) and (43) we get

$$\begin{aligned} A= & {} \langle \psi _{2out}(t_2)|G_1(t_2,t_1)|\psi _{1i}(t_1)\rangle \nonumber \\&+\langle \psi _{2out}(t_2) |GV_2G_1|\psi _{1i}(t_1)\rangle \end{aligned}$$

(49)

As in the case of Eq. (44) the first term in equation (49) tends to zero as $t_2 \rightarrow \infty$. In the second term in Eq. (49) G can be written in terms of its multiple scattering series. Each partial summation represents an approximation to Eq. (49). We consider two cases for the purpose of studying transfer to the continuum.

• i. The propagator G in Eq. (49) is approximated by $G_2$. Then the transition amplitude can be written as

  $$\begin{aligned} A_{21}=\langle \psi _{2out}(t_2)|G_2(V_2-\varDelta V_2)G_1|\psi _{1i}(t_1)\rangle \end{aligned}$$

  (50)

  when $t_2 \rightarrow \infty$. In this matrix element the propagator $G_2$ acting on $\psi _{2out}$ introduces FSI with $V_2 +\varDelta V_1$. The combination

  $$\begin{aligned} \langle \psi _{2out}(t_2)|G_2(t_2,t)=\langle \psi _{2}^{\prime }(t)| \end{aligned}$$

  (51)

  is a time dependent wave function for a nucleon propagating in the potential $V_2+\varDelta V_1$ of the target. Using Eqs. (41) and (51) and (50) can be written as

  $$\begin{aligned} A_{21}={1\over 2\hbar }\int _{-\infty }^{\infty }~dt~\langle \psi _{2}^{\prime }(t)|V_2|\psi _{1i}(t )\rangle . \end{aligned}$$

  (52)

  This is the case discussed by Bonaccorso and Brink [3].

• ii. The propagator G in Eq. (49) is approximated by $G_1$. Then the transition amplitude can be written as

  $$\begin{aligned} A_{21}=\langle \psi _{2out}(t_2)|G_1(V_2-\varDelta V_2)G_1|\psi _{1i}(t_1)\rangle . \end{aligned}$$

  (53)

  This case corresponds to inelastic excitations of the projectile.

• iii. The propagator G is approximated by the free particle propagator $G_0$, then one would calculate

  $$\begin{aligned} A_{11}=\langle \psi _{2out}(t_2)|G_0V_2G_1|\psi _{1i}(t_1)\rangle . \end{aligned}$$

  (54)

  Written more explicitly this is

  $$\begin{aligned} A_{01}= \int _{-\infty }^{\infty }d t \langle \psi _0|(V_2 -\varDelta V_2)|\psi _1 \rangle . \end{aligned}$$

  (55)

  This form corresponds to the break-up of the nucleon in the projectile due to the interaction with the target.

Case i) includes the FSI of the nucleon with the potential $V_2$. It can be used to study the influence of nucleon resonances in the target nucleus. Similarly case ii) includes the final state interaction of the neutron with the potential of the projectile and can be used to study effect of resonances in the projectile. There are no FSI in approximation iii).

Equation (46) can be transformed into a simpler form in the case of a peripheral collision. Let $\varSigma$ be a surface which lies between the two potentials $V_1$ and $V_2$ and which divides the space into regions $R_1$ and $R_2$. In the following we assume that

$$\begin{aligned} V_1 -\varDelta V_1 =0 \quad \mathrm{in}~R_2;\qquad V_2 -\varDelta V_2 =0 \quad \mathrm{in}~R_1. \end{aligned}$$

(56)

Then the matrix element $\langle \psi _2 |(V_1 -\varDelta V_1)|\psi _1 \rangle$ in Eq. (46) can be written as a sum of integrals over the regions $R_1$ and $R_2$. The integral over $R_2$ is zero if $V_1 -\varDelta V_1 =0$ in $R_2$. Using Eq. (28) the first integral can be written as

$$\begin{aligned}&\int _{R_1} \psi _2^* (V_1 - \varDelta V_1)\psi _1 d^3 \mathbf{r}\nonumber \\&\quad = \int _{R_1} \psi _2^* \Bigl ({ i}\hbar {{\partial }\over {\partial }t} +{\hbar ^2 \over 2m} \nabla ^2 -\varDelta V_2 - \varDelta V_1\Bigr )\psi _1 d^3 \mathbf{r}. \end{aligned}$$

(57)

Applying Green’s theorem reduces this to

$$\begin{aligned}&\int _{R_1} \psi _2^* (V_1 - \varDelta V_1)\psi _1 d^3 \mathbf{r}\nonumber \\&\quad ={\hbar ^2 \over 2m}\int _{\varSigma }d \mathbf{S}\cdot (\psi _2^*\nabla \psi _1 - \psi _1 \nabla \psi _2^*)+ { i}\hbar {{\partial }\over {\partial }t}\int _{R_1} \psi _2^* \psi _1 d^3 \mathbf{r}\nonumber \\&\qquad + \int _{R_1} \Bigl ({ i}\hbar {{\partial }\psi _2 \over {\partial }t}+{\hbar ^2 \over 2m} \nabla ^2 \psi _2 -\varDelta V_2 \psi _2 - \varDelta V_1 \psi _2\Bigr )^*\psi _1 d^3 \mathbf{r}.\nonumber \\ \end{aligned}$$

(58)

where $d \mathbf{S}$ is a surface element normal to $\varSigma$ directed out of $R_1$. If Eq. (58) is integrated over time between $t=-\infty$ and $t=\infty$ the second term vanishes because the potentials $V_1$ and $V_2$ are very far away from each other as $t \rightarrow \pm \infty$ and $\psi _1$ and $\psi _2$ have no overlap in that limit. If $V_2 -\varDelta V_2=0$ in $R_1$ then the third term in Eq. (58) is zero because $\psi _2$ satisfies the Schrödinger equation (29). This proves Eq. (33). The next step is to obtain our final formula Eq. (63) from (33).

First the wave functions $\psi _1$ and $\psi _2$ are expressed in terms of $\phi _1$ and $\phi _2$ using Eq. (10). They can be written as inverse transforms of momentum distributions

$$\begin{aligned} \phi _1(x,y,z) ={1\over (2\pi )^2}\int \int d k_{1y} d k_{1z} \exp ^{{ i}( y k_{1y} +z k_{1z})}\tilde{\phi }(x,k_{1y},k_{1z}),\nonumber \\ \end{aligned}$$

(59)

and similarly for $\phi _2(x,y,z)$. Substituting into Eq. (33) yields a 7-dimensional integral over y,  z,  t and $k_{1y},~k_{1z},~k_{2y},~k_{2z}$. This integral contains a phase factor

$$\begin{aligned}&\exp \Big [mvz/\hbar + \left( \varepsilon _2 -\varepsilon _1 -{1\over 2}m v^2\right) t /\hbar \nonumber \\&\quad +(z-vt)k_{1z} +y k_{1y}-zk_{2z} -yk_{2y} \Big ] \end{aligned}$$

(60)

which contains all the dependence on y, z and t. Hence the integration over those variables gives a product of three $\delta$-functions

$$\begin{aligned}&{(2\pi )^3 \over v}\delta (k_{1z} -k_{2z}\nonumber \\&\quad +mv/\hbar ) \delta \left( k_{1z} - \left( \varepsilon _2 -\varepsilon _1 -{1\over 2}m v^2\right) /\hbar v\right) \delta (k_{1y} - k_{2y}).\nonumber \\ \end{aligned}$$

(61)

Finally Eq. (33) reduces to a 1-dimensional integral over $k_y = k_{1y} = k_{2y}$. The remaining two $\delta$-functions in (61) give

$$\begin{aligned} k_{1z}= & {} k_1 = \left( \varepsilon _2-\varepsilon _1 -{1\over 2}m v^2\right) /\hbar v,\nonumber \\ k_{2z}= & {} k_2 = \left( \varepsilon _2-\varepsilon _1 +{1\over 2}m v^2\right) /\hbar v. \end{aligned}$$

(62)

These are the values of $k_1$ and $k_2$ used in the text following Eqs. (9) and (16). After evaluation the derivatives normal to the surface $\varSigma$ in (33) one obtains a factor ${ i}(\gamma _{1x} +\gamma _{2x}) = 2{ i}\sqrt{\eta ^2 + k_z^2}$. When these results are collected the final form of the transfer (breakup) amplitude is obtained as

$$\begin{aligned} A_{21} = {\hbar \over 2\pi mv}\int d k_y \sqrt{\eta ^2 +k_y^2} \tilde{\phi }_2^\star (d_2, k_y, k_2) \tilde{\phi }_1(-d_1, k_y, k_1). \end{aligned}$$

(63)

Note that the amplitude $A_{21}$ of this section was indicated as $A_{fi}$ in the main text.