Precision branching-ratio measurements in $^{18}$O

Abstract

An experiment has been performed utilising the $^{12}$C($^{7}$Li,p)$^{18}$O reaction to populate high-energy states in $^{18}$O. Using the Munich Q3D magnetic spectrograph in conjunction with the Birmingham large-angular-coverage DSSD array, branching ratios have been measured for over fifty states in $^{18}$O, investigating the $\alpha$-decay, n-decay, 2n-decay and $\gamma$-decay branches. In tandem, Monte-Carlo techniques have been used to identify and separate features.

1 Introduction

The measurement and study of the nuclear force is important to increasing our understanding of nature, playing a substantial role in the formation and interactions of almost all everyday matter. To test the behaviour of this force, information regarding the existence and properties of excited states is required in order for a complete model to be formed and tested. The $^{18}$O nucleus provides an excellent opportunity to extract such information, as the relatively low number of nucleons reduces the complexity of modelling the nucleus. This complexity could be further reduced due to its theoretical propensity towards $\alpha$-clustering [1,2,3], with particular interest in the possibility of nuclear molecular formations based on carbon and $\alpha$ cores. However, information regarding absolute branching ratios of high-energy excited states of the nucleus is limited for some states and non-existent for others.

Fig. 1

Examples of particle identification provided by the focal plane detector. The y-axes shows the energy loss measured by the anode wires, plotted against scintillator energy (a) and focal plane position (b). The distinct loci can be seen for protons and deuterons in panel (a) and in panel (b) the states in the recoil $^{18}$O can be seen as expected, due to the increase in cross section of populating an excited state

Direct measurement of branching ratios, in particular concurrent measurement of varying decay paths (i.e. $\alpha$-decay, n-decay and $\gamma$-decay), can be difficult due to differing requirements for the detection of final state particles. A method presented here utilising Double-sided Silicon Strip Detectors (DSSDs) to measure charged decay products in conjunction with the Munich Q3D magnetic spectrograph and extensive Monte-Carlo simulations enables the identification of multiple decay channels. This allows for a more complete determination of the branching ratios for the excited states. The Monte-Carlo simulations also provided a way to establish the geometric efficiency of the detectors for a specific decay path, in order to calculate the total number of decays from those detected. A value of $\nicefrac {\Gamma _i}{\Gamma _{tot}}$ could then be extracted for each available decay path by normalising to the total number of decays from all decay paths that had occurred. The excitation range investigated in this work was 7 MeV to 16 MeV.

2 Experimental method

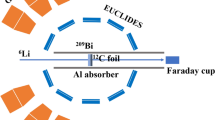
The experiment was performed utilizing the $^{12}$C($^{7}$Li,p)$^{18}$O reaction, with a 44 MeV $^{7}$Li beam, provided by the tandem Van de Graaff accelerator at the Maier-Leibnitz Laboratory (MLL) in Munich, incident on a 110 $\mu$g/cm$^2$ $^{nat.}$C target. The proton ejectile was measured through use of the Q3D magnetic spectrograph at the facility, providing particle identification through measurement by the focal plane detector. More detail on the Q3D magnetic spectrograph can be found in Refs. [4, 5]. This particular reaction has previously been performed by von Oertzen et al. [6], resulting in the measurement of many previously discovered and undiscovered states. The focal plane detector consisted of two cathode foils, on either side of a pair of anode wires, resulting in a charge avalanche as a charged particle passes through the gas volume between the foils. The charge registered on the anode wires enabled a measurement of the energy loss of the particle. The second cathode foil (furthest downstream of the Q3D) was segmented into 255 strips (3.5 mm wide), enabling a position measurement of the charged particle. This was achieved by performing a Gaussian fit to the charge distribution measured on the strips, the centroid of which corresponded to the position of the particle. The measured position of the proton ejectiles was proportional to the excitation energy of the residual $^{18}$O nucleus [7]. After this cathode foil, a scintillator detector measured the total remaining energy of the particle, enabling identification of the species. More detail on the focal plane detector is given in Ref. [8]. Examples of the particle identification are shown in Fig. 1, utilising the various stages of the focal plane detector.

As well as the Q3D magnetic spectrograph and focal plane detector, the Birmingham large-angular-coverage DSSD array was set up in order to detect any charged products arising from the decay of $^{18}\hbox {O}^*$. This comprised four 500 $\mu$ m thick 50$\times$50 mm$^2$ DSSDs [9], with 16 strips on each side and orthogonal, resulting in a total 256 pseudo-pixels (each with an area of $\approx$ 9.5 mm$^2$). The angular coverage of the array was 14$^{\circ }\rightarrow$ 92$^\circ$ in-plane and −36$^{\circ }\rightarrow$ 40$^\circ$ out-of-plane, placed such as to detect the majority of decay products coincident to a proton measured in the Q3D, which was set in-plane at an angle of $-\,39^\circ$. The in-plane and out-of-plane angular acceptances of the Q3D were ± 3.0$^\circ$ and ± 2.0$^\circ$ respectively.

The Q3D was calibrated by using the known energy levels in $^{18}$O, which appeared in the energy distribution of the recoil proton, of which examples can be seen in Fig. 1b. The DSSD array was calibrated through use of a triple-$\alpha$ source consisting of $^{239}$Pu, $^{241}$Am and $^{244}$Cm — this source was also used to determine the thickness of the $^{nat.}$C target by calculating the energy loss of these $\alpha$-particles through the target. Particles incident on the DSSD array had their position determined by overlapping vertical and horizontal strips — the position of each detection was smeared across the appropriate pseudopixel.

Read-out of the experimental set-up was triggered by either a Q3D event or a DSSD event. The latter condition was with a 1/25,000 scale-down factor due to the high rate of incident particles (this was useful for monitoring the health of the DSSDs via using elastically scattered beam particles).

Fig. 2

A Cartesian view of the DSSD array for states around 13.2 MeV for real data (a) and simulated data (b). The centres of the pseudopixels are shown by the grid of dots

3 Monte-Carlo simulations

Monte-Carlo simulations used in this work were performed using Resolution8.1, in-house software written and used by the Nuclear Physics group at the University of Birmingham. This code simulates nuclear reactions as a series of sequential two-body interactions, able to produce events for elastic scattering, inelastic scattering, break-up and compound nucleus production reactions. The software also includes a variety of smearing functions to match experimental effects accurately, such as beam divergence and energy loss of particles through the target. More detail about the software is given in Refs. [10,11,12].

These simulations were used in order to identify features of spectra and to calculate the expected geometric efficiencies of the $^{18}$O break-ups for the various excitation energies investigated. For each energy level, all available decay paths were simulated using 10$^7$ events in order to determine an accurate geometric efficiency for each type of event. Other experimental smearing, such as the energy and position resolutions of the DSSD array and Q3D, were taken into account. Features such as dead strips were also included, due to the large effect this could have on geometric efficiency. A comparison between real data and simulated data is shown in Fig. 2 for states around 13.2 MeV, showing the agreement between the Gaussian profiles from different decay paths. Here, in-plane angle is plotted against out-of-plane angle. The simulated data have a pronounced cut-off across the right-hand detectors due to these DSSDs being blocked by the target mount in the real data.

4 Identification of decay products

Though measurement of the correct reaction could be confirmed by identification of the proton measured by the Q3D, the determination of which decay mode the $^{18}\hbox {O}^*$ had undergone required the employment of the kinematic technique known as a Catania plot (also known as a Romano plot) [13, 14]. This technique enables the identification of the species of a particle, providing the other final state products are all measured. If the $^{18}\hbox {O}^{*}$ decays into particles A and B, the total Q-value of the reaction can be expressed as

$$\begin{aligned} Q = E_A + E_B + E_{\text {proton}} - 44.0~\text {MeV}, \end{aligned}$$

(1)

where E refers to the kinetic energy of the associated particle and 44.0 MeV is the beam energy.

Fig. 3

Catania plots generated for states in the 13.2 MeV region assuming the decay of $^{18}\hbox {O}^*$ into $^{14}$C (detected) $+ \alpha$ for real data (a) and simulated data (b). The detected particle is given second in each locus label

If a detection occurs in the DSSD array in coincidence with a proton measured in the Q3D, a guess can be made about the species of the particle, and hence its mass. Assuming that an $^{18}$O nucleus has decayed into particles A and B, and that particle A (with mass $m_A$) is subsequently detected by the DSSD array, the position and energy information from the DSSD array can be used to calculate total momentum p of particle A, and thus the momenta of the particle in each Cartesian direction:

$$\begin{aligned} p_{A}= & {} \sqrt{2E_{A}m_{A}},\nonumber \\ {p_{A}}_x= & {} p_{A}\sin {\theta _x}\cos {\theta _y}, \nonumber \\ {p_{A}}_y= & {} p_{A}\sin {\theta _y} \, ~\text {and} \nonumber \\ {p_{A}}_z= & {} p_{A}\cos {\theta _x}\cos {\theta _y}, \end{aligned}$$

(2)

where $\theta _x$ and $\theta _y$ correspond to the in-plane and out-of-plane angles of detection of the particle. The three latter equations can then be used to determine the corresponding Cartesian momenta for particle B through conservation of linear momentum, as the position (and hence momentum) of the proton is known (taken as the centre of the Q3D angular acceptance), which is the only other final state particle.

With the momentum of the undetected particle, $p_B$, calculated, the energy can also be calculated through $E_B = \nicefrac {p^2_B}{2m_B}$. The energy of B can hence be substituted in to give

$$\begin{aligned} 44.0~\text {MeV} - E_A - E_{\text {proton}} = \frac{p_B^2}{2m_B} - Q. \end{aligned}$$

(3)

This is a linear equation in the form $y = mx + c$, in which the quantities $44.0~\text {MeV} - E_A - E_{\text {proton}}$ and $\nicefrac {p_B^2}{2}$ are known by either detection or calculation. Plotting these quantities against one another would give a straight line of gradient $\nicefrac {1}{m_B}$ and intercept $-Q$ if the correct mass was assumed in Eq. 2. If the assumed mass was incorrect, the events would not lie on this line but could be identified through use of Monte-Carlo simulations. An example of this is shown in Fig. 3 for states around 13.2 MeV, assuming an $^{12}$C($^{7}$Li,p)$\alpha +^{14}$C break-up event ($Q = 2.173$ MeV) in which the $^{14}$C is detected in the DSSD array. This locus can be seen in the red region, lying on the dashed line representing a gradient of $\nicefrac {1}{4}$ (as the value plotted on the x-axis is $\nicefrac {p_B^2}{2u}$, where u is the atomic mass unit) and a y-intercept of $-2.173$. The other loci, which are labelled by the particles the $^{18}$O decays into (with the detected species last), are distinct and can be identified with Monte-Carlo simulation.

4.1 States below the n-threshold

The available particle decay paths (excluding $\beta$-decay) for $^{18}$O over the excitation range investigated become possible at the following energies: $S_{\alpha }=$ 6.227 MeV, $S_n=$ 8.045 MeV, $S_{2n}=$ 12.188 MeV, $S_{n\alpha }=$ 14.404 MeV and $S_p=$ 15.942 MeV. As some of the states investigated lie below 8.045 MeV, $\gamma$-decay was an important consideration due to some states potentially having an unnatural parity (and hence being unable to $\alpha$-decay), and some states would possibly $\gamma$-decay and $\alpha$-decay. It is important to consider the $\gamma$-decay path, in which an $^{18}$O nucleus was detected in the DSSD array. This is because events corresponding to a $\gamma$-decay can lie across loci belonging to other decay paths on the Catania plot. Thus, these $\gamma$-decay events would be incorrectly assigned to other decay paths, producing inaccurate branching ratios.

To overcome this, the method described in Ref. [15] was utilised. To be coincident with a proton measured by the Q3D, a $\gamma$-decaying $^{18}$O has a very limited associated kinematic cone. The radius of the kinematic cone is determined almost entirely by the angular acceptance of the Q3D for measuring the coincident proton, because the $^{18}$O was significantly more focused than the protons due to the large mass difference. Therefore, the pseudopixels that these events were incident on could be isolated by identifying them through Monte-Carlo simulation. This can be seen in Fig. 4, in which the bright spot due to $^{18}$O events is highlighted in red and compared with Monte-Carlo simulation.

Fig. 4

Cartesian detector view of states around 7.8 MeV for real data (a) and simulated data (b). There are 4 pseudopixels in which events arising from the $\gamma$-decay and subsequent detection of an $^{18}$O nucleus were found to be detected from the Monte-Carlo simulations, shown by the red rectangle

Once the pseudopixels that had $^{18}$O nuclei incident upon them were identified, events that were detected on these were removed from the Catania plot in order to prevent contamination of the other decay path loci. The Monte-Carlo simulations were then used to establish the percentage of total detected events from the particle decay paths incident on these pixels and correct both the $\alpha$-decay and $\gamma$-decay branches accordingly. No obvious $\gamma$-decay features were present on the Catania plot for excitations higher than 8 MeV, whereas below 8 MeV these features were clear in comparison to Monte Carlo simulated events (in particular the 7.117 MeV and 7.969 MeV states). Between $7\rightarrow 8$ MeV the amount of $\alpha$-decay events incident on the pseudopixels ranged from 8$\rightarrow$1%, so the uncertainty on the correction was relatively small, while above 8 MeV this was not a concern due to lack of $\gamma$-decay events.

Just above the n-decay threshold of $S_n = 8.045$ MeV, it is very difficult to distinguish between $\gamma$-decay and n-decay events due to the limited kinetic energy available to product $^{17}$O nuclei. As $\gamma$-decay becomes suppressed above particle decay thresholds, it is very unlikely to find a significant value of $\nicefrac {\Gamma _{\gamma }}{\Gamma _{tot}}$ for high-lying excitations, however, the states at 8126(3) MeV, 8219(1) MeV and 8280(1) MeV have been previously determined to $\gamma$-decay [16]. In the current work, events corresponding to $\gamma$-decay and n-decay are difficult to distinguish to a reasonable certainty due to the similarity of detection position of the respective $^{18}$O and $^{17}$O nuclei, though loci on the Catania plot corresponding to $\gamma$-decay and n-decay were not identical. No obvious features from $\gamma$-decay of these states were observed on the Catania plot, implying the relative percentage of these $\gamma$-events was low compared to that of n-decay. Due to the difficulty in quantitatively distinguishing between the two (and lack of qualitative evidence of significant $\gamma$-decay branches), all events corresponding to either branch were assigned as n-decay events.

Fig. 5

Catania plots generated for the 15825(2) keV excitation in $^{18}$O, assuming the decay of $^{18}\hbox {O}^*$ into $^{14}$C (detected) $+ \alpha$ for real data (a) and simulated data (b). The different decay paths are labelled and coloured to indicate the different loci

4.2 Events above the 2n-decay threshold

Decays that arise from an excited state above the 2n-decay threshold in $^{18}$O, $S_{2n} = 12.188$ MeV, can n-decay sequentially through an excited state in $^{17}$O. This raises a problem, as the geometric efficiencies can be very different for n-decay and 2n-decay for the same excitation (particularly close to the 2n-decay threshold, due to the large difference in available kinetic energy), but due to the similarity of the decay paths, the loci formed by these two processes greatly overlap. In order to overcome this, gates were placed on the Catania plots and across pseudopixels on the DSSD array containing $>99$% of 2n-events from the Monte-Carlo simulations — this was done for all excitations above the $S_{2n}$ threshold. By comparing the amount of n-events in the real data that lay within these gates to the expected number from the simulation, the number of events from both decay paths could be established. More detail on this is given in Ref. [17].

The population of specific energy levels in the daughter $^{17}$O could not be disentangled due to the high level density of states and the limited resolution of reconstruction, as in the case of 2n-decay two final state particles are undetected. To overcome this, all possible daughter nucleus states were simulated and a corresponding geometric efficiency calculated, all of which were averaged to give the final geometric efficiency for this branch. As the geometric efficiency typically differed $<\,5\%$ across all potential populated states, and it is likely that there would be mixed population of these states during decays, this did not impact the uncertainty significantly. If the spin-parity of the parent state and daughter states are known, the daughter states can be preferentially selected in cases where the n would carry low amounts of angular momentum, however, in high-energy excited states of $^{18}$O there is limited spin-parity information and as such this was not an option.

4.3 Excited levels in daughter nuclei

As with excited states in the daughter $^{17}$O, it is possible for the population of excited states in all daughter nuclei. If the population of the excited state results in a further particle decay, this can be established by comparison with Monte-Carlo events; other than 2n-decay, no sequential particle decay features were observed in the current work. It is also possible for bound states in daughter nuclei to be populated. For example, it is possible for unnatural parity states to decay via $\alpha$-decay as long as the decay is to a similarly unnatural parity state in the daughter nucleus [18] — in the case of ($^{18}\hbox {O}^*$,$\alpha$)$^{14}$C ($Q = -6.227$ MeV), the first level with an unnatural parity in $^{14}$C has an energy of 6902.6 MeV, while the first excited state of the $\alpha$-particle sits at 20.210 MeV. Therefore, in the range of excitations measured in this work only excited states in $^{14}$C need be considered. In the case of $\alpha$-decay, both product nuclei can be detected by the DSSD array, meaning it is much more likely to have features on the Catania plot uncontaminated by other loci.

The only state observed in this work to decay through an excited level in $^{14}$C was the state at 15825(2) keV, which had a large branch passing to a state at roughly $\approx$7 MeV. Figure 5 shows the experimental data compared with Monte-Carlo simulation, in which these events can be seen clearly in the region shown in blue. As this region overlapped the other loci, only events that did not lie in other regions were used. Monte-Carlo simulation was then used to establish the number of these events in the other regions such that they could be appropriately extracted. In Table 1, this value is presented together with decays to the ground state of $^{14}$C as a total value of $\nicefrac {\Gamma _\alpha }{\Gamma _{tot}}$. Due to this extra source of uncertainty, it was difficult to also distinguish between n-decay and 2n-decay for this state, and hence these values are also presented together in Table 1.

5 Results

The results are summarised in Table 1, with measured centroid values, widths and branching ratio values compared with previous literature values. Values given in bold are previously published and discussed in Ref. [19] in the context of $\alpha$-cluster bands. The work in Ref. [19] found no consistent cluster structure across any of the proposed cluster bands, but did observe potential $\alpha$-cluster structure in both the 11696(1) keV $J^{\pi }=6^+$ and 12557(2) keV $J^{\pi }=6^+$ states. The $\theta ^2_{\alpha }$ values are provided for states that have known or tentative spin-parity assignments in the literature, calculated assuming a spherical geometry. These were calculated using $E_{level}$ and $\Gamma _{tot}$ values measured in this work, in conjunction with values of $\nicefrac {\Gamma _{\alpha }}{\Gamma _{tot}}$, except in cases in which a lower upper limit value of $\Gamma _{tot}$ was present in the literature than that measured in the current work. Values of $\nicefrac {\Gamma _i}{\Gamma _{tot}}$ within $2\sigma$ of 0 are presented as an upper limit value, determined to be one standard deviation above the measured value. The standard deviation for a particular branch is equal to the standard deviation for all other branches for each excitation.

Branching ratio results are compared with several previous works. One such work is that of Avila et al. [20], in which states in $^{18}$O from 8.0 MeV to 15.0 MeV were fit using an R-Matrix approach following a resonant scattering reaction ($^{14}$C + $\alpha$ using the Thick Target Inverse Kinematics (TTIK) technique). This was done for $\Gamma _{tot}$, $\Gamma _\alpha$ and $\Gamma _n$ from which values of $\nicefrac {\Gamma _\alpha }{\Gamma _{tot}}$ and $\nicefrac {\Gamma _n}{\Gamma _{tot}}$ can be calculated. Another is the work of Yang et al. [21] in which states from 10.3 MeV to 15.9 MeV were populated, through use of the $^{9}$Be($^{13}$C,$^{18}$O)$\alpha$ reaction, and lower limit values of $\nicefrac {\Gamma _\alpha }{\Gamma _{tot}}$ were extracted. Also used in comparison is the work of Goldberg et al. [22] which investigated a wide range of states, from 9.0 MeV to 21.3 MeV, using the same reaction as that of Ref. [20].

Table 1 Results produced in the current work, presenting energies, widths and branching ratios for all observed states between 7 MeV and 16 MeV. Errors presented represent statistical errors only in the case of energy and width, whereas the values of $\nicefrac {\Gamma _i}{\Gamma _{tot}}$ also include errors arising geometry efficiency correction. Where not otherwise stated, literature values are taken from Ref. [16]. Values of $\theta ^2_{\alpha }$ are calculated using $\Gamma _{tot}$ measured in this work, except in cases ($^*$) where the literature value of $\Gamma _{tot}$ is significantly smaller than a measured upper limit. Values given in bold are previously published and discussed in Ref. [19]

5.1 7.0 MeV to 9.4 MeV

The first Q3D setting investigated lay between 7.0 MeV and 9.4 MeV, above the $\alpha$-decay threshold of 6.227 MeV. During this excitation region, the n-decay channel becomes possible ($S_n = 8.045$ MeV). States below this energy are given a value of $\nicefrac {\Gamma _\gamma }{\Gamma _{tot}}$ using the method detailed in Sect. 4.1 and Ref. [15]. There has been little work done in determining particle-decay branches relative to $\gamma$-decay branches for states in $^{18}$O, so these values represent a first measurement of both $\nicefrac {\Gamma _\gamma }{\Gamma _{tot}}$ and $\nicefrac {\Gamma _\alpha }{\Gamma _{tot}}$ for these resonances. The value of $\nicefrac {\Gamma _\alpha }{\Gamma _{tot}}$ for the 7969(3) keV state is consistent with 0, supporting the tentative unnatural parity $3^+$ or $4^-$ assignments. The value of $\theta ^2_{\alpha }<0.5$ in Table 1 was calculated assuming $J=4$, but it should be noted that $\theta ^2_{\alpha }<0.07$ assuming $J=3$. The excitation spectra acquired while gating on the different decay paths are shown in Fig. 6.

Fig. 6

Q3D spectra obtained for states between 7.0 and 9.4 MeV for Q3D singles data (a), $\alpha$-decay events (b), n-decay events (c) and $\gamma$-decay events (d). The fitted background (dashed magenta line) is constant at just above 0 until the n-decay threshold, at which point the background becomes due to the two-body ($^{17}$O,n) phase space

Above the n-decay threshold, several states have been observed with no prior measurement of $\nicefrac {\Gamma _\alpha }{\Gamma _{tot}}$ and $\nicefrac {\Gamma _n}{\Gamma _{tot}}$. The $J^{\pi }=3^-$ state at 8280(1) keV has been previously measured in Ref. [20] to have values of 0.34(4) and 0.66(10) for $\nicefrac {\Gamma _\alpha }{\Gamma _{tot}}$ and $\nicefrac {\Gamma _n}{\Gamma _{tot}}$ respectively. This value of $\nicefrac {\Gamma _n}{\Gamma _{tot}}$ is in agreement with the value of 0.52(4) obtained here, while the value of $\nicefrac {\Gamma _\alpha }{\Gamma _{tot}}$, 0.48(4), lies a little over 2$\sigma$ away. This state has a calculated value of $\theta ^2_{\alpha }=0.1$ using the literature value of $\Gamma _{tot}=8(1)$ keV from Ref. [16], which is often the typical $\theta ^2_\alpha$ boundary at which excitations might be considered clustered.

The state at 8843(14) keV has a similar energy to that measured by Avila et al. [20] of 8.82(3) MeV, but the value of $\nicefrac {\Gamma _n}{\Gamma _{tot}}$ obtained is $\approx$100%, significantly different to the value of 0.68(10) measured in the current work. This could imply that a different state has been observed in this work.

The 9238(16) keV state is proposed in the literature [16] to have possible spin assignments of $0^-$, $1^-$ and $2^-$. Based on the value $\nicefrac {\Gamma _\alpha }{\Gamma _{tot}} = 0.9(3)$ obtained in the current work, the only possible assignment of these three is the natural parity $1^-$, due to angular momentum selection rules for $\alpha$-decay. The large error on this value is due to the weak population of the state.

The tentative assignment of $J^{\pi }=2^-$ (unnatural parity) for the 8409(11) keV state [16] is consistent with the results obtained in this work, as the value of $\nicefrac {\Gamma _\alpha }{\Gamma _{tot}}$ is within 2$\sigma$ of 0. For the state at 8514(5) keV, the non-zero value of $\nicefrac {\Gamma _\alpha }{\Gamma _{tot}} = 0.19(5)$ contradicts the tentative $J^{\pi }=4^-$ assignment in Ref. [16].

The states at 7861(1) keV and 8126(3) keV have upper limit values of $\theta ^2_{\alpha }$ presented in Table 1 of <170 and <50 respectively, which gives potential for these states to display cluster structure. This largely depends on their widths, which are too narrow to be measured in the current work—in the case of the 7861(1) keV state, this could be as narrow as 10 eV and still be above the typical cluster threshold of $\theta ^2_{\alpha }=$0.1. Other than these two states and the 8280(1) keV state, the values of $\theta ^2_{\alpha }$ obtained do not suggest $\alpha$-cluster structure in the measured states in this excitation region.

5.2 9.6 MeV to 11.9 MeV

The states in the excitation range of 9.6 MeV to 11.9 MeV are shown in Fig. 7, along with the spectra obtained when the available decay paths in the Catania plot are gated on.

The $J^{\pi }=3^-$ state at 10106(11) keV has been measured to have $\nicefrac {\Gamma _\alpha }{\Gamma _{tot}} = 0.44(18)$ by Avila et al. [20], within 1$\sigma$ of the value 0.55(10) obtained in the current work, and $\nicefrac {\Gamma _\alpha }{\Gamma _{tot}}= 0.35(7)$ by Goldberg et al. [22], within 2$\sigma$. The value of $\nicefrac {\Gamma _\alpha }{\Gamma _{tot}}$ obtained in this work, 0.45(10), is also in agreement with that of Avila et al. [20] of 0.6(3).

Fig. 7

Q3D spectra obtained for states between 9.6 and 11.9 MeV for Q3D singles data (a), $\alpha$-decay events (b) and n-decay events (c). The fitted background (dashed magenta line) is due to the two-body ($^{17}$O,n) phase space

Regarding the $J^{\pi }=3^-$ 10386(7) keV state, the value of $\nicefrac {\Gamma _n}{\Gamma _{tot}} = 0.61(7)$ is in agreement with that obtained by Avila et al. [20] of 0.7(4), while the value of $\nicefrac {\Gamma _\alpha }{\Gamma _{tot}} = 0.39(7)$ is within 2$\sigma$ agreement of the previous value of 0.7(2).

A previous measurement by Goldberg et al. [22] of the 10774(9) keV state received a value of $\nicefrac {\Gamma _\alpha }{\Gamma _{tot}}= 0.45(15)$, and agreement with the value of $\nicefrac {\Gamma _\alpha }{\Gamma _{tot}} < 0.32$ obtained in the current work.

Measurement of the 10997(16) keV state yielded values of $\nicefrac {\Gamma _\alpha }{\Gamma _{tot}} < 0.11$ and $\nicefrac {\Gamma _n}{\Gamma _{tot}}= 0.94(5)$, in excellent agreement with the values of < 0.12 and 0.9(6) obtained by Avila et al. These values are also consistent with the tentative assignment of this state as a $J^{\pi }=2^-$ [16].

The value of $\nicefrac {\Gamma _\alpha }{\Gamma _{tot}}= 0.68(6)$ measured for the 11127(4) state is in good agreement with that measured by Yang et al. [21] of > 0.65(3), and is within 2$\sigma$ of the value of 0.80 published by Goldberg et al. [22] without an uncertainty.

The tentatively assigned $J^{\pi }=4^+$ [16] 11419(4) state was measured to have a value of $\nicefrac {\Gamma _\alpha }{\Gamma _{tot}}= 0.74(6)$, in excellent agreement with the results of Avila et al. (0.8(3)), Yang et al. (>0.23(1)) and Goldberg et al. (0.90(10)), while improving upon the uncertainty provided by the other absolute measurements. The value of $\nicefrac {\Gamma _n}{\Gamma _{tot}}= 0.26(6)$ is likewise in good agreement with the value of 0.25(14) measured by Avila et al. [20].

Aside from the 11696(1) keV state discussed in Ref. [19], there is no evidence of cluster structure for any states in this region with prior spin-parity information. All calculated $\theta ^2_{\alpha }$ values are significantly under 0.1, suggesting typical shell-model behaviour of states in this region.

5.3 12.4 MeV to 14.5 MeV

The Q3D excitation spectra for energies ranging from 12.4 to 14.5 MeV is shown in Fig. 8, with the Q3D singles spectrum as well as spectra arising from $\alpha$-decay and n-decay events.

Fig. 8

Q3D spectra obtained for states between 12.4 and 14.5 MeV for Q3D singles data (a), $\alpha$-decay events (b) and n-decay events (c). The fitted background (dashed magenta line) is due to the combination of the two-body $^{17}$O+n and three-body ($^{16}$O,2n) phase spaces

At 12188 keV, the 2n-decay channel opens and excited $^{18}$O nuclei have enough energy to decay sequentially to $^{16}$O. As described previously in Sect. 4.2, this can have a significant effect on the geometric efficiency and as such must be taken into account to produce accurate branching ratios. Results in this region have the total n-decay branch split into decays that proceed via single n-emission and double n-emission.

The levels at 12680(3) keV and 12764(3) keV provide a challenge to fit, especially as there is evidence of wide, $\alpha$-decaying states around this region [20, 22]. Despite this, the value of $\nicefrac {\Gamma _\alpha }{\Gamma _{tot}}= 0.53(7)$ for the 12680(3) is in good agreement with the value obtained by Avila et al. [20] of 0.40(5), perhaps being slightly higher due to the presence of these wide states.

The 13005(3) keV state has a measured $\nicefrac {\Gamma _\alpha }{\Gamma _{tot}}$ of 0.49(16), over 3$\sigma$ from 0. This suggests that the tentative $J^{\pi }=4^-$ assignment is incorrect, as no evidence is seen of decays through an excited state of $^{14}$C for $\alpha$-decays from this level.

The value of $\nicefrac {\Gamma _\alpha }{\Gamma _{tot}}= 0.18(4)$ for the 13614(2) keV state is consistent with that measured by Yang et al. [21] of >0.07(1). Consistency is also seen for the states at 13972(8) keV, 14138(4) keV and 14410(12) keV, all lying within $1\sigma$ of the results from Avila et al. [20], or consistent with the lower limits measured by Yang et al. [21]. The 14138(4) keV state is also seen to be inconsistent with the tentative $J^{\pi }=6^-$ spin-parity assignment.

No states in this region, aside from the $J^{\pi }=6^+$ state at 12557(2) keV, display cluster structure based on the values of $\theta ^2_{\alpha }$. This again suggests population of mostly shell-model states in this region, though there is potential for cluster structure in the states at 12764(3) keV and 12893(7) keV if these states were determined to have sufficiently-high spin ($J\ge {6}$).

5.4 14.5 MeV to 16.3 MeV

The Q3D excitation spectra for singles, $\alpha$-decay-gated and n-decay-gated events in shown in Fig. 9. The 14410(12) keV state is seen on the far left of the spectra, though with considerably lower statistics than in Fig. 8. The width for this state is fixed to that measured in the previous excitation region when fitting this excitation region, as lower statistics in this region and a possible artificial decrease in counts at the edge of the focal plane acceptance can cause fitting difficulties. The value of $\Gamma _{tot}$ given in Table 1 for this state is thus that measured in Figure 8. The branching ratios extracted using the data in this region are $\nicefrac {\Gamma _\alpha }{\Gamma _{tot}}= 0.17(7)$, $\nicefrac {\Gamma _n}{\Gamma _{tot}}= 0.38(7)$ and $\nicefrac {\Gamma _{2n}}{\Gamma _{tot}}= 0.45(7)$, which all lie within 1$\sigma$ of the same results from the lower excitation range measurement.

Fig. 9

Q3D spectra obtained for states between 14.5 and 16.3 MeV for Q3D singles data (a), $\alpha$-decay events (b) and n-decay events (c). The fitted background (dashed magenta line) is due to the combination of the two-body ($^{17}$O,n) and three-body ($^{16}$O,2n) phase spaces

There is literature information on values of $\nicefrac {\Gamma _i}{\Gamma _{tot}}$ for states in the range of 14.5 to 15.0 MeV from Avila et al. [20], though the largely different widths and values of $\nicefrac {\Gamma _i}{\Gamma _{tot}}$ compared with states measured in the current work suggest that different states are observed across both works, which is likely due to the typical increase of level density as a function of excitation energy.

Three further states at 15970(8) keV ($\Gamma _{tot}$=90(30) keV), 16112(16) keV ($\Gamma _{tot}$=90(40) keV) and 16324(16) keV ($\Gamma _{tot}>$126 keV) are observed, which have previously been seen in the work of von Oertzen et al. [6] at energies of 15981(9) keV, 16111(8) keV and 16333(7) keV respectively. These centroid energies lie above the p-decay threshold, $S_{p} =$ 15.942 MeV, the branching ratio for which was unable to be determined in the current work due to contamination of this locus. The contamination arises from pile-up events — events in which there are multiple hits in a DSSD detector, of which some are random (do not originate from the reaction which produced the recoil proton incident on the Q3D). Reconstruction of the unrelated hits causes a region on the Catania plot that lies across the p-decay locus. As such, values of branching ratios for these states have not been presented.

The results from the current work represent the first comprehensive branching-ratio measurements of $^{18}$O below 16 MeV. Where previous results exist, these are generally in good agreement to the current work. In some instances, the branching ratios have provided additional constraints and allow unnatural spin-parity assignments to be ruled out.

6 Conclusions

Branching ratio measurements have been performed for over fifty high-energy states in $^{18}$O, ranging from 7.0 MeV to 16.0 MeV, utilising Monte-Carlo techniques to distinguish between the various decay paths and establish branching ratios across all of them. This was achieved by measuring decay products from $^{18}$O using the Birmingham large-angular-coverage DSSD array in coincidence with a recoil proton, from the ($^{12}$C($^{7}$Li,p)$^{18}\hbox {O}^*$) reaction, measured using the Q3D magnetic spectrograph. These have been compared with previous data from resonant scattering techniques [20, 22] and from lower-limit branching ratio measurements [21]. Generally, good agreement is seen for results across the excitation ranges, showing the viability of the method for comparing $\gamma$-decays with particle-decays, as well as determining population of excited levels in the daughter nuclei and if, as a result, further sequential decay had occurred from these levels in the daughter nucleus.

No states determined to display cluster structure based on $\theta ^2_{\alpha }$ were measured in the current work apart from the 11696(1) keV and 12557(2) keV $J^\pi =6^+$ states. The $J^{\pi }=3^-$ excitation at 8280(1) keV had a measured $\theta ^2_{\alpha }$ value of 0.1, which while at the typical threshold for clustering is too low to be conclusive. The states at 7861(1) keV and 8126(3) keV are too narrow for their widths to be precisely measured via the Q3D magnetic spectrograph (energy resolution $\approx$ 65 keV for states measured at −39$^\circ$), but could potentially be shown to display cluster structure if precision width measurements were made which found the widths to be sufficiently large. In some cases, lack of spin-parity information also hinders the ability to determine propensity towards cluster structure. For the majority of states measured in this work with prior (tentative or confirmed) spin-parity information, $\theta ^2_{\alpha }$ was determined to be < 0.1, suggesting that these states may be typical shell model excitations.