Abstract
The dipole response of the proton-magic nucleus \({}^{124}\hbox {Sn}\) was previously investigated with electromagnetic and hadronic probes. Different responses were observed revealing the so-called isospin splitting of the Pygmy Dipole Resonance (PDR). Here we present the results of a new study of \({}^{124}\hbox {Sn}\) using inelastic proton scattering at low energies to test an additional probe possibly exciting states of the PDR. The response to the new probe as well as the \(\gamma \)-decay behavior of excited states were studied. The \({}^{124}\hbox {Sn}\)(p,p’\(\gamma \)) experiment was performed at \(E_p = {15}\,\,\hbox {MeV}\) using the combined spectroscopy setup SONIC@HORUS at the Tandem accelerator of the University of Cologne. Proton-\(\gamma \) coincidences were recorded, enabling a state-to-state analysis due to the excellent energy resolution for both particles and \(\gamma \) rays. \( J=1 \) states in the PDR region were populated in the present inelastic proton scattering experiment. Many \(\gamma \)-decay branching ratios could be determined.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
1 Introduction
In nuclear physics, different experimental probes and techniques are utilized to investigate structure phenomena and to understand their microscopic origins. This approach has been applied to study the low-lying electric dipole strength – often denoted as Pygmy Dipole Resonance (PDR) – in atomic nuclei during the last two decades. This excitation mode is located around and below the particle emission thresholds [1, 2].
Although the PDR exhausts only a marginal fraction of the isovector dipole energy-weighted sum rule in stable or modestly neutron-rich nuclei, its strength is important to precisely determine the electric dipole polarizability \( \alpha _D \). The value of \( \alpha _D \) has been shown to be correlated with different isovector properties related to the nuclear equation of state, e.g., the neutron-skin thickness. The precise determination of these properties is crucial to also describe highly asymmetric matter such as neutron stars [3,4,5,6,7,8]. The PDR strength itself might also strongly correlate with the neutron-skin thickness which might be understood in terms of the macroscopic interpretation of this mode as originating from a dipole-type oscillation of the neutron skin against the proton-neutron core [1,2,3, 6, 9, 10].
Due to its selectivity to E1 excitations, the isovector PDR strength is studied intensively via the nuclear resonance fluorescence (NRF) method using quasi mono-energetic photon beams and/or bremsstrahlung [1, 2, 11]. However, the continuous beam profile of bremsstrahlung and the strongly increasing background at lower energies complicates the investigation of \(\gamma \)-decay branchings [12]. The B(E1) transition strengths extracted from such experiments need to be corrected for unobserved \(\gamma \)-decay branchings which are typically studied using mono-energetic \(\gamma \)-ray beams.
To gain structural insights, probes where the hadronic interaction dominates (“hadronic probes”) such as \(\alpha \) particles, \({}^{17}\hbox {O}\) and protons at intermediate energies of around \(20~\,\,\hbox {MeV}/\hbox {A}\) to \(80~\,\,\hbox {MeV}/\hbox {A}\) are used. The comparison of the responses to the different probes revealed a possible isospin splitting in \({}^{124}\hbox {Sn}\) [13, 14], among the N=82 isotones \({}^{140}\hbox {Ce}\) [15,16,17] and \({}^{138}\hbox {Ba}\) [15, 16]. The isospin splitting is not completely understood. Current explanations include different isospin characters of the states as well as different radial transition densities at the nuclear surface [2, 14, 18].
To understand the PDR in \({}^{124}\hbox {Sn}\) in more detail, an inelastic proton scattering experiment at low energies of \(E_p={15}\,\,\hbox {MeV}\) was performed at the Institute for Nuclear Physics of the University of Cologne. Up to now, the PDR in \({}^{124}\hbox {Sn}\) was investigated via \(\alpha \) particles (\( E_\alpha = {136}\,\,\hbox {MeV} \)) [13, 14], \({}^{17}\hbox {O}\) (\( E_{^{17}O} = {340}\,\,\hbox {MeV} \)) [19] and bremsstrahlung (\( E_{e^-} = 7.5, 7.8, {10}\,\,\hbox {MeV} \)) [20, 21]. Furthermore, a (p,p’) Coulomb excitation experiment, performed at the RCNP in Osaka with \(E_p={295}\,\,\hbox {MeV}\), was recently published by Bassauer et al. [22, 23].
In this paper, dipole excitations observed in the PDR region in our experiment will be presented and compared to existing experimental data on \({}^{124}\hbox {Sn}\) with special regard to the isospin splitting. \(\gamma \)-decay branchings of lower energetic states to excited states below about 5 MeV, were investigated and the results compared to already existing values, obtained from (n,n’\(\gamma \)) [24,25,26] and (\(\alpha \),\(\alpha \)’\(\gamma \)) [27] experiments as well as from studies of the \(\beta \) decay of \({}^{124}\hbox {In}\) [28].
2 Experimental setup
The \({}^{124}\hbox {Sn}\)(p,p’\(\gamma \)) experiment was performed at the Institute for Nuclear Physics of the University of Cologne. The 15 MeV proton beam was provided by the 10 MV FN Tandem accelerator and directed to the combined spectroscopy setup SONIC@HORUS [29].
The \({}^{124}\hbox {Sn}\) target, enriched to 95.3%, was positioned at the center of the SONIC array, which also acts as target chamber. To detect the scattered protons, twelve PIPS (Passivated Implanted Planar Silicon) detectors were mounted inside the SONIC chamber using a modular holding frame. Azimuthal angles of \({45}^{\circ }\), \({135}^{\circ }\), \({225}^{\circ }\), and \({315}^{\circ }\) are covered for polar angles of \({107}^{\circ }\) and \({145}^{\circ }\) while the azimuthal angles of \({0}^{\circ }\), \({90}^{\circ }\), \({180}^{\circ }\), and \({270}^{\circ }\) are covered for a polar angle of \({123}^{\circ }\) [29]. For the present experiment, HORUS consisted of thirteen high-purity germanium (HPGe) detectors of which six were additionally equipped with BGO shields for active Compton suppression. In addition, lead and copper absorbers were installed at the entrance windows of all HPGe detectors in order to reduce the contribution of \(\gamma \) rays with energies below about 1 MeV. Out of the twelve mounted silicon detectors, eleven were functioning properly, i.e., 143 proton-\(\gamma \) detector combinations could be analyzed. The data acquisition combining the two spectroscopic systems, consisting of DGF-4C Rev. F modules from XIA [29, 30], recorded all hits seen by the detectors, i.e., no trigger was applied. For the analysis, the particle-\(\gamma \) coincidence window was chosen to be 250 ns which could be achieved after correcting the timing data for time walk effects. For the determination of \(\gamma \)-decay branchings below excitation energies of 4 MeV, only seven silicon detectors were taken into account. The silicon detectors positioned at a polar angle of \({145}^{\circ }\) have a shallower thickness compared to the rest of the detectors. This results in an incomplete energy deposition of the protons with increasing energy [29]. According to calculations using LISE [31], the energy deposition of the protons drops below 100% below excitation energies of approximately 3.3 MeV. Consequently, the affected excitations are distorted and shifted towards lower energies in the proton spectra resulting in a worsened peak-to-background ratio in the \(\gamma \)-ray spectra for the given energy range while increasing the background in the low-energy regime.
The summed FEP efficiency for all detectors is shown in the energy region of interest. In gray, the experimental data of the \({}^{226}\hbox {Ra}\) and \({}^{56}\hbox {Co}\) measurements are displayed. The fit function corresponds to the Wiedenhöver function [32]
The full-energy peak (FEP) efficiencies of the HPGe detectors were determined experimentally. For this, two radiation sources, \({}^{226}\hbox {Ra}\) and \({}^{56}\hbox {Co}\), were used. The summed efficiency curve for \(\gamma \)-ray energies below 4.5 MeV is shown in Fig. 1 and is well described by a Wiedenhöver function [32]. To determine the FEP efficiency at higher energies, the decay of \({}^{26}\hbox {Al}\) was measured which was produced via the \({}^{26}\hbox {Mg}\)(p,n) reaction. Further details on this method can be gathered from Ref. [29]. The experimentally determined efficiencies were confirmed by Geant4 [33,34,35] simulations. At \(E_\gamma = {1131.7}\,\,\hbox {keV}\) a summed FEP efficiency of 1.26% was achieved. The resulting energy resolution in the summed spectra, taking into account 143 detector combinations, amounts to a full width at half maximum (FWHM) of \( FWHM_\gamma = {2.6}\,\,\hbox {keV} \) at \( E_\gamma = {1120}\,\,\hbox {keV} \) and \( FWHM_x \approx {90}\,\,\hbox {keV} \). For the excitation/ proton spectra the \(FWHM_x\) does not alter significantly with energy. Besides the Doppler correction, the events were also corrected for differential non-linearities (DNL) representing inconsistencies in the digital sampling of the incoming analog signal within the analog-to-digital converters. As a result, the energy assignment of the signal is affected leading to a worse peak shape and a decreased peak-to-background ratio. Since the DNL occur at fixed channel numbers they can be identified, and hence corrected as stated in Ref. [36].
3 Analysis
Starting from the p-\(\gamma \) coincidence data, a time-background subtraction was performed. The sorting of the proton-\(\gamma \) coincidences itself was performed with the computer program SOCOv2 [37]. Figure 2 shows the resulting p-\(\gamma \) coincidence matrix. On the x axis, the excitation energy is displayed which was derived from the proton energy deposited in the silicon detectors. The \(\gamma \)-ray energy, i.e., transition energy is depicted on the y axis and a Doppler correction has already been performed. The diagonal band structures, highlighted with colored lines in Fig. 2, correspond to \(\gamma \) decays to different final states. Furthermore, strong excitations at energies around \(E_x \approx {3}\,\,\hbox {MeV}\) and \(E_x \gtrsim {7}\,\,\hbox {MeV}\) are visible. These excitations can be assigned to the target contaminants \({}^{12}\hbox {C}\) and \({}^{16}\hbox {O}\) which are shifted on the \( E_x \) axis due to different reaction kinematics. These contaminants contributed to the overall count rate in the detectors, but did not significantly affect the analysis of \(\gamma \) decays to the first excited states of \({}^{124}\hbox {Sn}\) (compare Fig. 2).
Projections of the p-\(\gamma \) coincidence matrix onto the \(\gamma \)-ray energy axis. The red histograms a and c show ground-state decays and the \(\gamma \) decays leading to the \( 2_1^+ \) state are shown in blue b and d. Note that instead of the \(\gamma \)-ray energy (transition energy) the excitation energy \( E_x = E_{\gamma } + E_x^f \) is given on the x axis, where \( E_x^f = \) \({0}\,\,\hbox {keV}\) or \({1132}\,\,\hbox {keV}\), respectively. Decays of states mentioned in the text are marked with an asterisk
For the data analysis, diagonal and excitation-energy gates were applied to the p-\(\gamma \) coincidence matrix. While diagonal gates fix the final state of the decay, excitation-energy gates fix the excited state. The projections of the ground-state diagonal (red) and the \( 2^+_1 \)-state diagonal (gray) onto the \( E_\gamma \) axis are shown in Fig. 3. Note that the excitation energy and not the transition energy is given on the x axis of Fig. 3. The neutron-separation threshold, \( S_n \), of \({}^{124}\hbox {Sn}\) lies at \({8489.33(239)}\,\,\hbox {keV}\) [38]. In the projected ground-state diagonal, the \( 2^+\) states at \({1132}\,\,\hbox {keV}\), \({2426}\,\,\hbox {keV}\), \({3214}\,\,\hbox {keV}\), \({4228}\,\,\hbox {keV}\) and \({4605}\,\,\hbox {keV}\) can be clearly identified. In the PDR region, between \(5\,\,\hbox {MeV}\) and \(8\,\,\hbox {MeV}\), an accumulation of resolved and unresolved strength is visible (compare Fig. 3a, c). In the projected \( 2^+_1 \)-state diagonal (Fig. 3b, d), many distinct peaks are observed below \({5.5}\,\,\hbox {MeV}\). Between \(2\,\,\hbox {MeV}\) and \(4.5\,\,\hbox {MeV}\), all observed decays can be assigned to known states with a spin of \( J=2 \) or higher in \({}^{124}\hbox {Sn}\). The lines observed above 4.5 MeV excitation energy seem to correspond to unknown excited states. The broad peak structure around 8 MeV corresponds to the \( 3^- \) state in \({}^{16}\hbox {O}\) which is shifted towards higher energies as discussed earlier.
The number of detected \(\gamma \) rays of energy \( E_\gamma \) is given by the peak area A in the summed spectrum. To obtain \(\gamma \)-ray yields, the peak area has to be corrected for the efficiency \( \epsilon \) of the setup, the dead time \( \tau \) of the detectors and possible \(\gamma \)-decay branchings. The \(\gamma \)-ray yield I is then derived via:
where \( \epsilon _{ij} \equiv \epsilon _{\mathrm {Si}i}\epsilon _{\mathrm {Ge}j} \) and \( \tau _{ij} \equiv \tau _{\mathrm {Si}i}\tau _{\mathrm {Ge}j} \). The probability that a proton tunnels through the Coulomb barrier after exciting the target nucleus is given by \( \xi _T \) and is described in detail later in this section. The last term considers \(\gamma \)-decay branchings, where \( \varGamma \) is the total decay width and \( \varGamma _0 \) is the partial decay width with respect to the ground state. Proton-\(\gamma \) angular correlations were not considered. Since the beam current was not measured during the experiment, no absolute differential cross sections could be determined. Due to the comparably low beam energy and the Coulomb barrier of approximately \( V_C = {9.6}\,\,\hbox {MeV} \), additional corrections have to be considered. The corresponding correction factor \( \xi _T(E) \) (see Eq. 1) considers the tunneling of the ejectile through the Coulomb barrier after populating an excited state. It is given by the product of energy and the inverse Gamow factor [39]:
where \(\eta \) is the Sommerfeld parameter and Z is the charge of the target nucleus. Its dependency on E can be expressed as \( E=E_{beam}-E_x \) for \( E_{p'}<V_C \) and \( E=V_C \) for \( E_{p'}>V_C \) where the latter is a constant used for normalization. Equation 2 has been adopted for protons as ejectiles. For simplicity, the angular momentum barrier is neglected. The effect of the decreasing tunneling probability will be discussed in Sect. 4.1. However, the tunneling correction cancels out for the determination of branching ratios. Nevertheless, the proton tunneling affects the detection of low-energetic protons and, therefore, excitations above a certain excitation energy cannot be analyzed. In general, the branching ratio of decays into states 1 and 2 of energies \( E_1 \) and \( E_2 \), respectively, is given in terms of their transition widths \( \varGamma _i \):
For unobserved transitions a sensitivity limit has been considered. According to Ref. [13], peaks of area A which fulfill the following relation should be observed:
where B describes the background area below the peak. The relative uncertainty p of the unobserved peak is fixed to 30% or smaller in accordance with Ref. [13].
4 Results
4.1 Dipole excitations
\(\gamma \)-ray yields determined for \( J = 1 \) states excited in the \({}^{124}\hbox {Sn}\)(p,p’\(\gamma \)) reaction at \( E_p={15}\,\,\hbox {MeV} \). Yields corrected for the effect of the Coulomb barrier (see text) are shown in a and yields without this particular correction are shown in b. The excitation energy \( E_x(V_C) \) beyond which protons have to tunnel through the Coulomb barrier is given by the gray line and the orange line represents the sensitivity limit according to Eq. (4). Upper limits are also given for individual excited states that were observed but could not be clearly separated from neighboring peaks in the \(\gamma \)-ray spectrum
Comparison of dipole excitations observed in a \({}^{124}\hbox {Sn}\)(\(\alpha \),\(\alpha \)’\(\gamma \)) [13], b \({}^{124}\hbox {Sn}\)(p,p’\(\gamma \)) (this work) and c \({}^{124}\hbox {Sn}\)(\(\gamma \),\(\gamma \)’) [20, 21] experiments. The solid lines represent the total strength decaying to the ground state considering unresolved strength. The (p,p’\(\gamma \)) data is corrected for the proton tunneling probability, leading to a possible large amount of hidden strength above 7 MeV. The binning is chosen to be \({100}\,\,\hbox {keV}\) and the color code of the middle panel is adopted from Fig. 4
In total, 44 tentative J = 1 states have been assigned from the present experiment as shown in Fig. 4. Since no angular correlations are studied in this work only excitations that were identified at the same energy as \( J=1 \) states in NRF experiments [13, 20, 21] were analyzed in the present (p,p’\(\gamma \)) experiment. Furthermore, \( J=1 \) states of unknown parity are assumed to be of negative parity. Figure 4 also presents the effect of the Coulomb barrier which becomes significant for excitation energies above \({5378}\,\,\hbox {keV}\), indicated by the gray line. The lower panel shows the results without considering the tunneling of the protons through the Coulomb barrier after excitation. Most of the excited states are observed in the energy region between \(5.5\,\,\hbox {MeV}\) and \(7\,\,\hbox {MeV}\). According to the sensitivity limit given by the solid line, only weak excitations are missing for energies above 7 MeV. This appearance changes when taking the influence of the Coulomb barrier into account, as depicted in the upper panel of Fig. 4. At energies below \( E_x(V_C) \), the protons have enough energy to overcome the barrier. However, protons with an energy lower than \( V_C \) have to tunnel through the barrier. This clearly limits the experimental sensitivity at higher excitation energies. The comparison of \( J=1 \) states excited in the present work with the differential cross section of PDR states observed via (\(\alpha \),\(\alpha \)’\(\gamma \)) [13, 14] and the energy-integrated cross section extracted from bremsstrahlung experiments [13, 20] is shown in Fig. 5. The unresolved strength has been determined by integrating over the ground-state decay spectrum in bins of \({100}\,\,\hbox {keV}\) after time background subtraction and efficiency correction. To allow for a better comparison, both the resolved and unresolved \(\gamma \)-ray yields have been corrected for the tunneling effect (see Eq. 1). The unresolved strength is thus highly affected by low statistics at high energies and does not provide a precise measure. Similar to the inelastic \(\alpha \)-particle scattering, most of the resolved excitation strength is located below 7 MeV. In contrast to the (\(\gamma \),\(\gamma \)’) measurements, the intensity drops at higher energies, also visible in the ground-state spectrum (cf. Fig. 3c), indicating a behavior similar to the splitting observed in Ref. [13, 14]. However, due to the decreasing tunneling probability, the experimental sensitivity limit is strongly affected with increasing excitation energy (cf. Fig. 5a). Thus, the present data do not allow for detailed conclusions about a possible observation of the isospin splitting in \({}^{124}\hbox {Sn}\). At lower energies, the unresolved strength pattern resembles the (\(\gamma \),\(\gamma \)’) pattern more than the (\(\alpha \), \(\alpha \)’\(\gamma \)) pattern. However, a close correlation between \(I_{(p,p'\gamma )}\) and \(I_S\) was not observed, as is shown in Fig. 6. The ratio of the observed strengths varies by an order of magnitude among the states and demonstrates how the \((p,p'\gamma )\) reaction at low energies seems to be sensitive to underlying structures in each of the excited states.
Recent results from high energy proton scattering on several Sn isotopes show the importance of the complete knowledge of the decay behavior [22]. The strong difference between the extracted dipole strengths from \((\gamma ,\gamma ')\) using bremsstrahlung and \((p,p')\) using virtual photons was explained by the strong decay branching to higher excited states in the energy region above 7 MeV. A precise determination of the complete decay behavior is experimentally not observable in \((\gamma ,\gamma ')\) using bremsstrahlung. For the neighboring isotope \({}^{120}\hbox {Sn}\), a recent bremsstrahlung measurement has been corrected for statistical \(\gamma \) decay and unresolved strength [40]. It was reported that the corrected strengths suddenly exceed the high energy \((p,p')\) data by approx. a factor of two for higher excitation energies. This underlines the importance of the complete knowledge of the decay behavior when comparing these two types of measurements. In the high energy \((p,p')\) experiment, virtual photons were used to excite the target nuclei, similar to real-photon scattering, and the measured excitation cross sections were then converted to an electric dipole strength \(B(E1,\uparrow )\), independent of the specific decay behavior. While the tunneling-corrected \(\gamma \)-ray yields determined in the present work do depend on the individual \(\gamma \)-decay behavior, similar to NRF, the ratios shown in Fig. 6 indicate that also the excitation of individual states depends strongly on the used probe and on the structure of the excited states. This results in the largely varying response to the low energy protons, being a dominantly hadronic probe instead of a purely electromagnetic one. A better understanding of the reaction mechanism and of the nature of the individual states is needed to further investigate the observed differences. An example can be found in Ref. [41], where the single particle character of \(J=1\) states in \({}^{208}\hbox {Pb}\) was investigated via the excitation of isobaric analog resonances with low energy protons in conjunction with a (d, p) neutron-transfer reaction.
4.2 \(\gamma \)-decay branching
The \(\gamma \)-decay branching behavior of several low-energy states in \({}^{124}\hbox {Sn}\) was also studied and compared to literature values if available. Due to the increasing background at lower \(\gamma \)-ray energies, resulting from the missing energy deposition of the protons, the entire statistics, i.e., 143 Si-HPGe detector combinations were investigated only for \( E_\gamma \ge {4}\,\,\hbox {MeV} \). Unfortunately, the investigation of branching ratios of higher-lying states in the PDR region is hindered by decreasing sensitivity, as discussed in the previous subsection.
The results are listed in the supplemental material. Furthermore, literature values are listed that were obtained in (n,n’\(\gamma \)) [24,25,26] and (\(\alpha \),\(\alpha \)’\(\gamma \)) [27] experiments and by the \(\beta \) decay of \({}^{124}\hbox {In}\) [28]. Branching ratios that were preliminarily introduced by Färber et al. [42] could not be confirmed unambiguously, therefore they are not listed in the table. The uncertainties of the branching ratios were all determined via the propagation of error. Most of the determined branching ratios are in good agreement with the literature values. In addition, some branching ratios could be further restricted as, for example, the \( \varGamma _{2^+_1}/\varGamma _{4^+_1} \) ratio of the excited state at \({3346}\,\,\hbox {keV}\). However, discrepancies occur, which will be discussed in the following for a few excited states.
2875 keV and 2879 keV levels. The \( 2^+ \) states at the given energies were observed in the experiment but could not be clearly separated in the spectra. Hence, information on their branching behavior is not listed in the supplemental material.
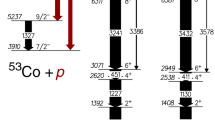
3144 keV level. The \( 4^+ \) state at \(E_x={3144}\,\,\hbox {keV}\) has two known \(\gamma \)-decay branchings of same strength leading to the lower lying \( 2^+_1 \) state and \( 2^+_3 \) state at \({2426}\,\,\hbox {keV}\). However, the transition with \( E_\gamma ={718}\,\,\hbox {keV} \) to the \( 2^+_3 \) state was not observed while the one leading to the \( 2^+_1 \) state was (cf. Fig. 7). From the experiment’s point of view, this mismatch in intensities cannot be understood since the detection efficiency of the setup is determined to be higher for the unobserved than for the observed transition due to the lower \(\gamma \)-ray energy (cf. Fig. 1).
An explanation might be found in the \( (6^+)({2819}\,\,\hbox {keV})\,\rightarrow 4^+_1({2101}\,\,\hbox {keV}) \) transition having the same energy as the transition from the \( 4^+({3144}\,\,\hbox {keV})\) state to the \(2^+_3 \) state, namely \( E_\gamma ={718}\,\,\hbox {keV} \). The mentioned \( (6^+) \) state, introduced by Bandyopadhyay et al. [26], has not been known by Demidov and Mikhail, hence, a false assignment of this transition cannot be excluded in their work.
3214 keV level. A similar observation was made for the \( 2^+({3214}\,\,\hbox {keV})\rightarrow 2^+_2 \) transition at \( E_\gamma ={1085}\,\,\hbox {keV} \). The transition to the \( 2^+_1 \) state with an energy \(E_\gamma ={2083}\,\,\hbox {keV}\) has nearly the same branching ratio, but was observed while the \({1085}\,\,\hbox {keV}\) transition was not (cf. Fig. 7).
3697 keV level. The \(J=1\) state at \({3697}\,\,\hbox {keV}\) and its decay to the \( 2_1^+ \) state at \({1132}\,\,\hbox {keV}\) were investigated in the full statistics data, including all eleven silicon detectors. Both transitions could not be clearly resolved otherwise. Analysis of full statistics yields a branching ratio of 41(9)%. Compared to the expected value of 17(5)%, obtained by Demidov and Mikhailov [24, 25], the newly determined branching ratio is larger by a factor of about 2.5.
4331 keV level. The \(\gamma \)-decay branching to three lower-lying excited states is known for the \( 2^+ \) state at 4331 keV. Transitions going to the ground state and the \( 2^+_1 \) state were observed and the branching ratios agree within the uncertainties with literature values determined by Spieker et al. [27]. However, the transition leading to the \( 2^+_3 \) state was not observed and the branching ratio is estimated to be below 14%. This is in contradiction to the literature value of 80(30)% [27]. Furthermore, the missing observation of the transition cannot be explained by experimental properties because the efficiency of the setup is determined to be higher for the unobserved transition as for the observed ones (cf. Fig. 1).
5 Summary and Conclusions
The proton-magic nucleus \({}^{124}\hbox {Sn}\) was investigated via inelastic proton scattering and \(\gamma \) spectroscopy at energies of \(E_p = {15}\,\,\hbox {MeV}\). A proton-\(\gamma \) coincidence analysis was performed, enabling a state-to-state analysis. Hence, excitation via protons and de-excitation via \(\gamma \) rays could be investigated.
In total, 44 PDR candidates were observed, mainly below 7 MeV. Although similar states were excited as in the (\(\alpha \), \(\alpha \)’\(\gamma \)) experiment, the strength pattern of the present (p,p’\(\gamma \)) experiment rather resembles the dipole response extracted in the (\(\gamma \),\(\gamma \)’) measurements. Above 7 MeV, a comparison of the (p,p’\(\gamma \)) results with the dipole response observed in the bremsstrahlung experiments is hindered due to the tremendous influence of the decreasing probability of proton tunneling through the Coulomb barrier. Thus, it remains an open question whether or not the isospin splitting found in inter-mediate-energy \(\alpha \) scattering can also be observed in low-energy inelastic proton scattering on \({}^{124}\hbox {Sn}\). In the present experiment, \(\gamma \)-decay branchings of low-lying excited states could be determined. One hiterto unknown branching was observed. Unobserved transitions are taken into account by considering the sensitivity limit of the experiment, yielding upper limits for the corresponding branching ratios. A good agreement with the existing branching ratios was observed in most cases. However, some discrepancies appear which are partly not understood. A false assignment of the transition with an energy of \({718}\,\,\hbox {keV}\) was identified. Instead of the original assignment to the \( 4^+ \) state at \({3144}\,\,\hbox {keV}\) it may be the \({718}\,\,\hbox {keV}\) transition decaying from the \( J^\pi = (6^+) \) state at \({2819}\hbox { keV}\) observed by Bandyopadhyay et al. [26].
The approach of determining branching ratios using SONIC@HORUS as well as the excitation of PDR states was successful. By choosing a higher beam energy, the proton tunneling can be shifted towards higher excitation energies such that the dipole response can be investigated without loosing too much sensitivity up to the neutron separation threshold. Furthermore, the required coincidence between the scattered proton and the \(\gamma \) rays allowed to investigate even weak \(\gamma \)-decay branchings due to the better peak-to-background ratio.
Data Availability Statement
This manuscript has data included as electronic supplementary material.
References
D. Savran, T. Aumann, A. Zilges, Prog. Part. Nucl. Phys. 70, 210 (2013)
A. Bracco, E. Lanza, A. Tamii, Prog. Part. Nucl. Phys. 106, 360 (2019)
J. Piekarewicz, Phys. Rev. C 83, 034319 (2011)
C. Horowitz, J. Piekarewicz, Phys. Rev. Lett. 86, 25 (2001)
J. Piekarewicz, M. Centelles, Phys. Rev. C 79, 054311 (2009)
A. Klimkiewicz, N. Paar, P. Adrich, M. Fallot, K. Boretzky, T. Aumann, D. Cortina-Gil, U. Datta Pramanik, T. W. Elze, H. Emling, et al., Phys. Rev. C 76, 051603(R) (2007)
J. Piekarewicz, B.K. Agrawal, G. Colò, W. Nazarewicz, N. Paar, P.G. Reinhard, X. Roca-Maza, D. Vretenar, Phys. Rev. C 85, 041302 (2012)
J. Piekarewicz, J. Phys. Conf. Ser. 420, 012143 (2013)
P.G. Reinhard, W. Nazarewicz, Phys. Rev. C 81, 051303(R) (2010)
N. Tsoneva, H. Lenske, Phys. Rev. C 77, 024321 (2008)
U. Kneissl, N. Pietralla, A. Zilges, J. Phys. G Nucl. Part. Phys. 32, R217 (2006)
U. Kneissl, H. Pitz, A. Zilges, Prog. Part. Nucl. Phys. 37, 349 (1996)
J. Endres, D. Savran, P. Butler, M. Harakeh, S. Harissopulos, R.D. Herzberg, R. Krücken, A. Lagoyannis, E. Litvinova, N. Pietralla et al., Phys. Rev. C 85, 064331 (2012)
J. Endres, E. Litvinova, D. Savran, P.A. Butler, M.N. Harakeh, S. Harissopulos, R.D. Herzberg, R. Krücken, A. Lagoyannis, N. Pietralla et al., Phys. Rev. Lett. 105, 212503 (2010)
J. Endres, D. Savran, A. van den Berg, P. Dendooven, M. Fritzsche, M.N. Harakeh, J. Hasper, H. Wörtche, A. Zilges, Phys. Rev. C 80, 034302 (2009)
V. Derya, J. Endres, M.N. Harakeh, D. Savran, H.J. Wörtche, A. Zilges, J. Phys. Conf. Ser. 366, 012012 (2012)
D. Savran, M. Babilon, A.M. van den Berg, M.N. Harakeh, J. Hasper, A. Matic, H.J. Wörtche, A. Zilges, Phys. Rev. Lett. 97, 172502 (2006)
N. Paar, Y.F. Niu, D. Vretenar, J. Meng, Phys. Rev. Lett. 103, 032502 (2009)
L. Pellegri, A. Bracco, F. Crespi, S. Leoni, F. Camera, E. Lanza, M. Kmiecik, A. Maj, R. Avigo, G. Benzoni et al., Phys. Lett. B 738, 519 (2014)
K. Govaert, F. Bauwens, J. Bryssinck, D. De Frenne, E. Jacobs, W. Mondelaers, L. Govor, V. Ponomarev, Phys. Rev. C 57, 2229 (1998)
F. Schlüter, Diploma thesis (2011)
S. Bassauer, P. von Neumann-Cosel, P.G. Reinhard, A. Tamii, S. Adachi, C.A. Bertulani, P.Y. Chan, A. D’Alessio, H. Fujioka, H. Fujita et al., Phys. Rev. C 102, 034327 (2020)
S. Bassauer, P. von Neumann-Cosel, P.G. Reinhard, A. Tamii, S. Adachi, C.A. Bertulani, P.Y. Chan, G. Colò, A. D’Alessio, H. Fujioka, H. Fujita, Y. Fujita, G. Gey, M. Hilcker, T.H. Hoang, A. Inoue, J. Isaak, C. Iwamoto, T. Klaus, N. Kobayashi, Y. Maeda, M. Matsuda, N. Nakatsuka, S. Noji, H.J. Ong, I. Ou, N. Paar, N. Pietralla, V.Y. Ponomarev, M.S. Reen, A. Richter, X. Roca-Maza, M. Singer, G. Steinhilber, T. Sudo, Y. Togano, M. Tsumura, Y. Watanabe, V. Werner, Phys. Lett. B 810 (2020)
I.M.A.M. Demidov, Bull. Acad. Sci. USSR Phys. Ser. 54, 41 (1990)
I.M. A.M. Demidov, Izv. Akad. Nauk SSSR, Ser. Fiz. 54, 2126 (1990)
D. Bandyopadhyay, N. Warr, C. Fransen, N. Boukharouba, V. Werner, S. Yates, J. Weil, M. McEllistrem, Nucl. Phys. A 747, 206 (2005)
M. Spieker, N. Tsoneva, V. Derya, J. Endres, D. Savran, M. Harakeh, S. Harissopulos, R.D. Herzberg, A. Lagoyannis, H. Lenske et al., Phys. Lett. B 752, 102 (2016)
B. Fogelberg, P. Carlé, Nucl. Phys. A 323, 205 (1979)
S. Pickstone, M. Weinert, M. Färber, F. Heim, E. Hoemann, J. Mayer, M. Müscher, S. Prill, P. Scholz, M. Spieker, et al., Nucl. Inst. Meth. Phys. Res. Sec. A 875, 104 (2017)
B. Hubbard-Nelson, M. Momayezi, W.K. Warburton, Nucl. Inst. Meth. Phys. Res. A 422, 411 (1999)
O. Tarasov, D. Bazin, Nucl. Inst. Meth. Phys. Res. Sec. B 376, 185 (2016)
I. Wiedenhöver, Dissertation thesis (1994)
S. Agostinelli, J. Allison, K. Amako, J. Apostolakis, H. Araujo, P. Arce, M. Asai, D. Axen, S. Banerjee, G. Barrand, et al., Nucl. Inst. Meth. Phys. Res. Sec. A 506, 250 (2003)
J. Allison, K. Amako, J. Apostolakis, H. Araujo, P. Arce, M. Asai, G. Barrand, R. Capra, S. Chauvie, R. Chytracek et al., IEEE Trans. Nucl. Sci. 53, 270 (2006)
J. Mayer, E. Hoemann, M. Müllenmeister, P. Scholz, A. Zilges, Nucl. Inst. Meth. Phys. Res. Sec. A 972, 164102 (2020)
A. Hennig, C. Fransen, W. Hennig, G. Pascovici, N. Warr, M. Weinert, A. Zilges, Nucl. Inst. Meth. Phys. Res. A 758, 69 (2014)
N. Saed-Samii, SOCOv2 (Accessed March 2019). https://gitlab.ikp.uni-koeln.de/nima/soco-v2
M. Wang, G. Audi, F. Kondev, W. Huang, S. Naimi, X. Xu, Chin. Phys. C 41, 030003 (2017)
W. Gibson, The physics of nuclear reactions. Pergamon International Library of Science, Technology, Engineering, and Social Studies (Elsevier Science & Technology Books, 1980)
M. Müscher, J. Wilhelmy, R. Massarczyk, R. Schwengner, M. Grieger, J. Isaak, A.R. Junghans, T. Kögler, F. Ludwig, D. Savran, D. Symochko, M.P. Takács, M. Tamkas, A. Wagner, A. Zilges, Phys. Rev. C 102(1), 1 (2020)
M. Spieker, A. Heusler, B.A. Brown, T. Faestermann, R. Hertenberger, G. Potel, M. Scheck, N. Tsoneva, M. Weinert, H.F. Wirth, A. Zilges, Phys. Rev. Lett. 125(10), 102503 (2020)
M. Färber, A. Bohn, V. Everwyn, M. Müscher, S. Pickstone, S. Prill, P. Scholz, M. Spieker, M. Weinert, J. Wilhelmy, A. Zilges, Acta Phys. Pol. B 50, 475 (2019)
Acknowledgements
The authors thank the accelerator and local staff at the Institute for Nuclear Physics, University of Cologne, for their support during the measurement. This work was supported by the Deutsche Forschungsgemeinschaft under Contract No. ZI 510/7-1.
Funding
Open Access funding enabled and organized by Projekt DEAL
Author information
Authors and Affiliations
Corresponding author
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Färber, M., Weinert, M., Müscher, M. et al. Low-energy excitations and \(\gamma \)-decay branchings in \(^{124}\)Sn via (p,p’\(\gamma \)) at \(E_p={15}\,\,\hbox {MeV}\). Eur. Phys. J. A 57, 191 (2021). https://doi.org/10.1140/epja/s10050-021-00422-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epja/s10050-021-00422-x