1 Introduction

Although the nucleon-nucleon (2N) interaction has been studied extensively in the past using proton–proton and proton–neutron scattering data, the role of higher-order forces, such as the three-nucleon force (3NF) remains mysterious. The need for an additional three-nucleon potential became evident when comparing three-body scattering observables [1, 2] and binding energies of light nuclei [3] with state-of-the-art calculations [1,2,3]. The two nucleon force models such as CD Bonn, Argonn V18, Reid93, Nijmegen I and Nijmegen II [4,5,6] are able to describe the two nucleon systems very well below the pion-production threshold. The next step would be to significantly extend the world database in the three-nucleon scattering system as a benchmark to eventually have a better understanding of the structure of the three-nucleon interaction. For almost all observables in nucleon–deuteron elastic scattering, the calculations which only include two nucleon forces (2NFs) fail to a large extent to describe the data, in particular at energies above 60 MeV and at large center-of-mass scattering angles. In addition to the elastic channel, the deuteron break-up reaction offers a rich spectrum of kinematical configurations and as such provides a good testing ground for understanding the structure of the nuclear force [7].

Fujita and Miyazawa described the 3NF with two-pion exchange (TPE) between three nucleons with an intermediate excitation of one nucleon into its first excited state, the \(\varDelta \)-isobar [8]. Later, more refined ingredients have been added leading to the Tucson-Melbourne (TM) [9] and corrected Tucson–Melbourne (TM\('\) or TM99) 3NFs [10, 11] allowing for additional processes contributing to the re-scattering of the mesons. In addition to this, other 3NF models such as Urbana IX were developed [12]. One could also treat the intermediate \( \varDelta \) as a dynamic state to create an effective 3NF [13, 14]. These theoretical approaches have been embedded within rigorous calculations using the Faddeev-type equations by, for example, Bochum–Kraków [15,16,17,18] and Hannover–Lisbon [13, 14, 19, 20] groups. Besides these phenomenological approaches, also two- and three-nucleon forces 3NF have been constructed from chiral perturbation theory (ChPT). The leading 3NF in ChPT shows significant contributions to the nuclear force [21], but the most advanced nowadays complete and consist chiral calculations at the third order of chiral expansion [22] give a description of three-nucleon data with similar quality as the one provided by semi-phenomenological models.

In the non-relativistic limit and in the center-of-mass frame, the dynamics of the wave function before scattering is the solution of the Schrödinger equation. As soon as the wave packet approaches the interaction region, the time evolution of the state is given by the Hamiltonian of \(H = H_0+ V\), where \(H_{0}\) is the Hamiltonian of a freely moving particle and V is the interaction potential. In the three-body system the Hamiltonian can be decomposed as

$$\begin{aligned} H=H_{0}+V_{i}+V^{i} \equiv H_{i}+V^{i}, \end{aligned}$$
(1)

where \(H_{0}\) is the kinetic energy, \(H_{i}\) the so-called channel Hamiltonian with one pair interaction \(V_{i} \equiv V_{jk}\) (\(j \ne i\), \(k \ne i\)) and \(V^{i}\) the sum of the remaining two interactions with the \(i^\mathrm{th}\) particle. We shall use this convenient notation to denote a pair by the number of the third particle. Obviously \(\phi _{i}\) is an eigenstate of \(H_{i}\) with the eigen energy, E. Now, using the resolvent identities, we obtain

$$\begin{aligned} G_{\pm } = G_0 + G_0V^{i}G, \end{aligned}$$
(2)

for \(i=1, 2, 3\), where \(G_0= (E -H_0 \pm i\epsilon )^{-1}\) is the free-particle propagator. We can define \(G_{\pm } =(E-H\pm i\epsilon )^{-1}\) as the resolvent or Green’s function for the Helmholtz equation. In the scattering process, we are interested in the transition of the initial state to a final state via the intermediate state, \(|\psi ^+\rangle \). The transmutation operator, t, is defined by

$$\begin{aligned} V|\psi ^+\rangle \equiv t|\phi \rangle . \end{aligned}$$
(3)

Multiplying the Lippmann-Schwinger Equation (LSE) by V from the left results in

$$\begin{aligned} t= V + VG_0t. \end{aligned}$$
(4)

The t-matrix can be evaluated iteratively (Born series) by

$$\begin{aligned} \begin{aligned} t&= V + VG_0(V + VG_0t) \\&= V + VG_0V + VG_0VG_0V + VG_0VG_0VG_0V +\cdots \end{aligned} \end{aligned}$$
(5)

The matrix elements of the transition operator in the momentum space are used to obtain the cross section. Nowadays, exact theoretical descriptions for the 3N system can be obtained by using the Faddeev equations with realistic potentials and with model 3NF interactions. The non-uniqueness of the Lippmann–Schwinger equation (LSE) has been pointed out by Faddeev and he could overcome this problem by splitting up the LSE to three equations with a unique solution [23].

The proton–deuteron break-up is a suitable reaction to study three nucleon systems since one can measure various observables in a large part of the available phase space of this reaction. In this paper, cross sections and vector analyzing powers, \(A_{x}\) and \(A_{y}\), for the \(d(\vec {p}, pp)n\) reaction at 135 MeV are extracted from configurations whereby the two final-state protons scatter at small polar angles between \(14^{\circ }\)-\(30^{\circ }\) . The data taken at other scattering angles have been reported in Refs. [24,25,26].

2 Experimental setup

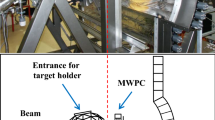
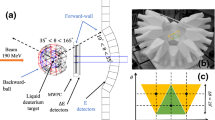
The \(\vec {p}{d}\) break-up reaction was studied using a polarized proton beam of 135 MeV impinging on a liquid deuterium target which was located at the center of BINA (Big Instrument for Nuclear-polarization Analysis). The polarized beam is provided with POLIS (POLarized Ion Source) [27]. The beams of (polarized) protons and deuterons are accelerated by AGOR (Accelerateur Groningen ORsay) [28] at KVI, the Netherlands. The proton-deuteron break-up reaction was studied with BINA. The BINA detector is particularly suited to study the elastic and break-up reactions at intermediate energies. BINA is composed of two major parts, the forward-wall and the backward-ball. The forward-wall measures the energy and scattering angles of final-state particles in the range \(10^{\circ }\)–\(37^{\circ }\). The forward-wall is composed of three main parts, Energy scintillators (E-scintillators), \(\varDelta E\)-scintillators, and a Multi-Wire Proportional Chamber (MWPC). The \(\varDelta E\)-scintillators are used in combination with the E-scintillators to identify the type of particle. The backward-ball is made of 149 small cut pyramid-shaped scintillator detectors by a ball-shaped detector which covers the rest of the polar angles up to \(165^{\circ }\). Therefore, the BINA detector covers almost the complete phase space of the break-up and elastic reactions. For a more detailed description of the detector, we refer to [23, 29]. In this work, we present the results of break-up configurations in which the final-state protons are registered in coincidence by the forward-wall.

3 Data analysis

The data analysis of \(\vec {p}{d}\) break-up reaction, taken with a proton-beam energy of 135 MeV, was performed with the goal of measuring the vector analyzing powers, \(A_{x}\) and \(A_{y}\), and the differential cross sections.

Events of the break-up reaction are identified by reconstructing the scattering angles and energies of the two final-state protons. During data taking, a hardware trigger was used requiring at least two of the ten E-scintillators to give a signal above the threshold (\(\sim \)1 MeV). These events were further processed offline by combining the information of the MWPC with the corresponding E-scintillators. In this way, two proton candidate tracks were reconstructed for further analysis. The E-scintillators were calibrated by matching their raw charge-to-digital converter (QDC) information with the expected energy correlation of break-up events.

The two dominant channels in \(\vec {p}{d}\) scattering are the elastic and break-up reactions. The phase space of the break-up reaction is significantly larger than that of the elastic channel. With the high event rate, there is a large probability for receiving, within the coincidence window of the hardware trigger, two uncorrelated events. The proton track with the largest scattering angle is labeled as particle 1 and the other as particle 2. In the case the two reconstructed proton tracks fall within the same bin in scattering angle, we randomly label one of the tracks as particle 1 and the other as particle 2.

Fig. 1
figure 1

The left panel shows \(E_{2}\) versus \(E_{1}\), kinetic energies of the two outgoing protons at the lab reference with (\(\theta _{1}\), \(\theta _{2}\), \(\phi _{12})=(24^{\circ }\pm 2^{\circ }\), \(24^{\circ }\pm 2^{\circ }\), \(180^{\circ }\pm 5^{\circ }\)). The solid line shows the kinematical S-curve calculated for the central values of the experimental angular ranges. The right panel is the projection of events along the D-axis for one slice shown in the left panel

Full size image

To reduce the time-uncorrelated background, we exploit the relative time-of-flight information (TOF\(_{1}\)–TOF\(_{2}\)) induced by the two coincidence particles. Here, TOF\(_{1}\) and TOF\(_{2}\) refer to the sum of the TDC values of the discriminated signals of the left and right PMTs of the E-scintillators for two particle tracks (1 and 2), respectively. The TOFs are measured with respect to the radio frequency (RF) of the accelerator. Details of the analysis can be found in Ref. [23].

The energy correlation between the two outgoing protons, \(E_{2}\) versus \(E_{1}\), after the calibration for a particular configuration \((\theta _{1}, \theta _{2}, \phi _{12})=(24^{\circ }\pm 2^{\circ }, 24^{\circ }\pm 2^{\circ }, 180^{\circ }\pm 5^{\circ })\) is shown in the left panel of Fig. 1, whereby \(\theta _{1}\) and \(\theta _{2}\) are the polar angles of two outgoing protons and \(\phi _{12}\) is their relative azimuthal angle (\(\phi _{12}=\phi _{1}-\phi _{2}\)). The solid line shows the kinematical S-curve calculated for the central values of the angular bins. The kinematic variable S corresponds to the arc-length along the kinematic curve with \(S=0\) at the point wherby \(E_{2}\) is at its minimum. To measure the break-up observables, at the first step, we make several slices along the kinematical S-curve with a window of \(\sim \)9.5 MeV. We note that the energy resolution, \(\sim \)4 MeV, is significantly smaller than this window size. The projection of the indicated region on the line perpendicular to the S-curve (D-axis) is shown in the right panel of Fig. 1. The peak around zero corresponds to break-up events. Most of the events on the left-hand side of the peak are also due to break-up events. In these cases, the protons have lost energy due to hadronic interactions inside the detector. The amount of accidental background is small as can been seen from the small amount of events on the right-hand side of the peak. We fit this spectrum by using a third-order polynomial, representing the hadronic interactions and the accidental background, and a Gaussian function, representing the signal. The extracted number of signal events was corrected by the data-acquisition dead-time and the down-scaling factor. This number is subsequently used to measure the cross sections and vector analyzing powers.

The cross section of the break-up reaction can be obtained by:

$$\begin{aligned} \frac{d^5\sigma }{d\Omega _{1}d\Omega _{2}dS}=\frac{N}{\frac{Q}{Z}t\epsilon \varDelta \Omega _{1}\varDelta \Omega _{2}\varDelta S}, \end{aligned}$$
(6)

whereby N is, the number of break-up events in each slice along the S-curve corrected for the down-scaling factor and the dead-time, Q is the total integrated charge, Z is the projectile charge (here \(Z=\)1), t is the number of the scattering centers, \(\epsilon \) is the multiplication of all the efficiencies including the MWPC efficiency, hadronic correction and geometrical efficiency, \(\varDelta \Omega \)s are the solid angles for the two outgoing protons and \(\varDelta S\) is, the width of the selected window in each slice along S-curve [23]. We studied various sources that we identified as the main contributors to the systematic uncertainty in the cross section measurements. In the following, we briefly summarize each of them and we give a description on how magnitudes of corresponding errors have been estimated.

The first source we identified as a contributor to the systematic error is related to uncertainties in the determination of the effective target thickness. Taking into account the bulging of the target, we estimated an effective target thickness of \(3.85\pm 0.20\) mm. The resulting error in this measurement (5%) is assigned as a systematic error in the cross section measurements. This value has been estimated by earlier cross section studies of the elastic proton–proton scattering process using similar targets by comparing data with precision calculations of this reaction [30].

The second systematic uncertainty that we considered is related to the error in estimating the fraction of events that suffered from a hadronic interaction in the scintillators of BINA. Since in the calculation of the number of break-up events, we only account for those events for which the energy of both protons are well reconstructed, one needs to correct for the hadronic interaction effect. To determine this effect, we used Monte Carlo studies that are based on the interaction models provided by the GEANT-3 simulation package [31]. Typically, we found that about 12% of all break-up events suffered from hadronic interactions. The uncertainty of this value (6%) is assigned as a source of systematic uncertainty. It has been estimated by taking the difference between the number of hadronic background events derived from simulations with the value estimated from a fit of the measured D spectrum (right panel of Fig. 1) [32,33,34].

The third source of systematic uncertainty is associated with the trigger efficiency. This efficiency has been studied using Monte Carlo simulations based on GEANT-3. It was found that for break-up events whereby \(\phi _{12}\) is larger than 20\(^\circ \), the trigger efficiency is about 98% and that it drops to 88% for selected events associated with \(\phi _{12}\)=20\(^\circ \). To be conservative, we assigned a systematic error due to the trigger efficiency by taking the observed inefficiencies using the Monte Carlo results, therefore 2% for \(\phi _{12}>20^\circ \) and 12% for \(\phi _{12}=20^\circ \) [35].

The fourth source of systematic error is due to uncertainties in the efficiency determination of the MWPC. Proton tracks from the elastic proton–deuteron scattering process were identified using the information of the E and \(\varDelta \) \(E\) detectors. The \(E-\varDelta \) \(E\) hodoscope provides a surface grid that is used to map onto the MWPC. This allows us to measure the MWPC efficiency for protons at various locations corresponding to every \(E-\varDelta \) \(E\) hodoscop. Typically, we found an efficiency of about (92±1)% for each proton, whereby the error corresponds to statistical fluctuations of the unbiased data sample that is used in this study. We associated a systematic error due to uncertainties of the MWPC efficiency for the cross section measurements by summing up the efficiency errors of the two final-state protons, i.e. 2% [35].

The total systematic uncertainties for the cross sections at small relative azimuthal angles (\(\le 20^{\circ }\)) are about 14% and for the larger relative azimuthal angles (\(> 20^{\circ }\)) is about 9%. For this, we added up, quadratically, the systematic errors of the various sources assuming them to be independent.

To measure the vector analyzing powers, the number of break-up events were normalized to the collected beam charge for the two polarization states (up and down). The relation between the normalized number of events with the polarized beam, \(N_{\xi ,\phi _{12}}^{s}(\phi )\), and unpolarized beam, \(N_{\xi ,\phi _{12}}^{0}\), is given by [36]:

$$\begin{aligned} N_{\xi ,\phi _{12}}^{s}(\phi )= & {} N_{\xi ,\phi _{12}}^{0}(1+p_{z}^{s}A_{y}(\xi ,\phi _{12})\cos \phi \nonumber \\&-p_{z}^{s}A_{x}(\xi ,\phi _{12})\sin \phi ), \end{aligned}$$
(7)

whereby s indicates the spin of the beam. \(\xi \) defines a given kinematical point (\(\theta _{1}\), \(\theta _{2}\), S). The component of the vector polarization of the beam is given by \(p_{z}^{s}\) and the vector analyzing powers are indicated by \(A_{x}\) and \(A_{y}\). Here, \(\phi \) is the angle between quantization axis for the polarization and the normal to the scattering plane in the laboratory frame of reference shown in Fig. 2. \(\phi _{12}\) is the relative azimuthal opening angle of the two protons.

The polarization of the proton beam is defined as:

$$\begin{aligned} p_{z} = \frac{N^{+}-N^{-}}{N^{+}+N^{-}}, \end{aligned}$$
(8)

whereby \(N^{+,-}\) are the number of particles with a particular spin (up or down). The beam polarization has been determined using the in-Beam Polarimeter (IBP) [37] that was installed at the high-energy beam at KVI. The IBP measured regularly the beam polarization by recording the azimuthal asymmetries of the H\((\vec {p}, pp)\) reaction. The vector analyzing power of the proton-proton scattering process was used as input to the polarization measurements and its uncertainty is the main source of error.

Fig. 2
figure 2

Definition of the coordinate systems for the break-up reaction with transversally-polarized beam. The laboratory system (\({x}^\prime \), \(y^\prime \), \(z^\prime \)), with \(z^\prime \) along the beam-momentum direction and \(y^\prime \) vertically upward, is used to define the angular configuration of the outgoing protons (with momenta \(p_{1}\) and \(p_{2}\)). The reaction coordinate system is defined with z along the beam-momentum direction and x obtained by projection of \(p_{1}\) onto the plane perpendicular to z. The angle \(\phi \) is defined as the angle between the y axis and the spin quantization axis s, which, in the present case, is vertical (parallel to \(y^\prime \)) [36, 38, 39]

Full size image

Since the statistics obtained with an unpolarized beam for \(d(\vec {p}, pp)n\) reaction was limited, we extracted the spin observables by solely using \(N_{\xi , \phi _{12}}^{{\uparrow }}(\phi )\) and \(N_{\xi , \phi _{12}}^{{\downarrow }}(\phi )\), corresponding to the normalized number of events for the spin-up and spin-down polarized beams, respectively. The analyzing powers \(A_{x}\) and \(A_{y}\) are extracted using the following relation:

$$\begin{aligned} \begin{aligned} f_{\xi ,\phi _{12}}(\phi )&= \frac{N_{\xi ,\phi _{12}}^{{\uparrow }}(\phi )-N_{\xi ,\phi _{12}}^{{\downarrow }}(\phi )}{N_{\xi ,\phi _{12}}^{{\uparrow }}(\phi )p_{z}^{\downarrow }-N_{\xi ,\phi _{12}}^{{\downarrow }}(\phi )p_{z}^{\uparrow }} \\&=A_{y}(\xi ,\phi _{12})\cos \phi -A_{x}(\xi ,\phi _{12})\sin \phi , \end{aligned} \end{aligned}$$
(9)

whereby \(p_{z}^{\uparrow }\) and \(p_{z}^{\downarrow }\) are the values of up (\(0.57\,\pm \,0.03\)) and down (\(-0.70\,\pm \,0.04\)) beam polarizations. Parity conservation imposes the following restrictions on the components of the vector analyzing powers [36]:

$$\begin{aligned} \begin{aligned} A_{x}(\xi ,-\phi _{12})= -A_{x}(\xi ,\phi _{12}); \\ A_{y}(\xi ,-\phi _{12})= A_{y}(\xi ,\phi _{12}), \end{aligned} \end{aligned}$$
(10)

whereby for \(\phi _{12}=180^{\circ }\), we expect \(A_{x}=0\). By taking the sum and difference of \(f_{\xi , \phi _{12}}(\phi )\) and \(f_{\xi ,-\phi _{12}}(\phi )\) in combination with the results of Eq. 10, the following combination of asymmetries for mirror configurations (\(\xi \),\(\phi _{12}\)) and (\(\xi \),\(-\phi _{12}\)) can be obtained [29]:

$$\begin{aligned} \begin{aligned} g_{\xi ,\phi _{12}}(\phi )&= \frac{f_{\xi ,\phi _{12}}(\phi )+f_{\xi ,-\phi _{12}}(\phi )}{2}, \\&=A_{y}(\xi ,\phi _{12})\cos \phi ;\\ h_{\xi ,\phi _{12}}(\phi )&= \frac{f_{\xi ,\phi _{12}}(\phi )-f_{\xi ,-\phi _{12}}(\phi )}{2}, \\&=-A_{x}(\xi ,\phi _{12})\sin \phi .\\ \end{aligned} \end{aligned}$$
(11)

The components of vector analyzing-power values, \(A_{x}\) and \(A_{y}\), are obtained from the fits of Eq. 11 for various kinematical configurations.

The error of the beam polarization is about 6%. For instance, the beam polarization for the down-mode has been measured at a value of \(0.70\,\pm \,0.04\), which gives rise to 6% systematic uncertainty in the beam polarization. We estimated the impact of the polarization uncertainty on the analyzing powers by recalculating both analyzing powers with an input polarization that differs by \(+\)6% (−6%) for the spin-up (down) mode. The difference with the results using the nominal values of the beam polarizations is used as an estimate of the corresponding systematic error. We also considered a systematic error due to asymmetries that are induced by rate- or polarization-dependent differences in detection efficiencies that do not cancel in Eq. 9. This uncertainty has been estimated by exploiting data at particular kinematical configurations for which the vector analyzing powers are known or constrained. For \(A_y\), we have analyzed various symmetric configurations for which both protons scatter to the same polar angle with a relative azimuthal angle of 180\(^{\circ }\). By taking the average vector analyzing power for the covered S-range, one expects a value of zero. We have performed a fit with a free offset value to the data and we used the corresponding offset as a measure of the systematic uncertainty for \(A_y\). To estimate the systematic error for \(A_x\), we analyzed the data for a relative azimuthal angle of 180\(^{\circ }\) for which \(A_x\) should be zero, and extracted the corresponding value for \(A_x\) as a function of S. Subsequently, these results are fitted with a zeroth-order polynomial and its value is used as an estimate for the corresponding systematic error. This error and the error in the polarization are added in quadrature assuming them to be independent, to form the total systematic uncertainty.

Figures 3, 4, 5 show the cross-sections and vector analyzing powers as a function of S for symmetric and asymmetric configurations at small, intermediate and large relative azimuthal angles. The results of our analysis are indicated as black dots. The error bars indicate statistical uncertainties which are in some cases smaller than the symbol sizes. The cyan bands depict the systematical uncertainty whereby the width corresponds to 2\(\sigma \). The various lines present the results of Faddeev calculations using 2NF and 2N+3NF models. The results show a different behavior between the data and theoretical calculations at small and large relative azimuthal angles.

The results of the cross sections and vector analyzing powers as a function of S for about hundred configurations (with \(14^{\circ }<\theta _1<30^{\circ }\), \(14^{\circ }<\theta _2<30^{\circ }\) and \(0^{\circ }<\phi _{12}<180^{\circ }\)) for incident proton energy of 135 MeV were extracted. A small subset of vector analyzing power data for selected symmetric configurations was presented in Ref. [29]. An extensive overview of all the results can be found in the supplementary material associated with this paper [43].

For most of the configurations, the results at small and large relative azimuthal angles show a similar behavior when compared to the ones shown in Figs. 3, 4, 5. Similar behaviours were also observed in the measurements of the same observables at 190 MeV [44].

To have a more efficient study and to compare globally the theoretical predictions with the complete data set, a global analysis is performed with averages of observables [23, 24]. For this purpose, we follow the same procedure as presented in earlier work [45] whereby we analyzed the average difference between data and the available theoretical calculations in units of the experimental uncertainties. The quantity \(\chi ^2\) per degree of freedom is defined by

$$\begin{aligned} \chi _{m}^{2}/d.o.f.=\frac{1}{N-1} \sum \limits _{i=1}^{N}\Big \{ \frac{O_{i}-T_{i}^{m}}{\sigma _{i}}\Big \} ^2, \end{aligned}$$
(12)

whereby N is the number of specific configuration in (S, \(\theta _{1}\), \(\theta _{2}\), \(\phi _{12}\)), \(O_{i}\) is one of the observables (\(A_{x}\), \(A_{y}\), or \(d^{5}\sigma /d\Omega _{1}d\Omega _{2}dS\)), \(\sigma _{i}\) is the measured statistical error of a data point and \(T_{i}^{m}\) is the results of the theoretical calculation whereby m refers to a specific model, namely, CDB, CDB+TM\('\), CDB\(+\varDelta \) and CDB\(+\varDelta +\)Coulomb. The subindex i refers to a specific configuration in (S, \(\theta _{1}\), \(\theta _{2}\), \(\phi _{12}\)) and N is the number of specific configuration in (S, \(\theta _{1}\), \(\theta _{2}\)) as presented in the right panels of Figs. 6 and 7 or the number of specific configuration in (S, \(\phi _{12}\)) as shown in the left panels of Figs. 6 and 7. We note that we do not minimize the chi-square variable by performing a fit. Hence, the chi-square value is merely a quality measure of the theoretical results with respect to the data taking into account the experimental errors. Figures 6 and 7 show the results of \(\chi ^{2}\)/d.o.f. for sum over (S, \(\phi _{12}\)) for specific (\(\theta _{1}\), \(\theta _{2}\)) versus the angular combination (\(\theta _{1}\) and \(\theta _{2}\)) (left panels) and for sum over (S, \(\theta _{1}\), \(\theta _{2}\)) for specific \(\phi _{12}\) versus \(\phi _{12}\) (right panels) for different observables (\(A_{x}\), \(A_{y}\) and \(d^{5}\sigma /d\Omega _{1}d\Omega _{2}dS\)) for data taken with a proton-beam energy of 135 MeV and 190 MeV [46], respectively. The asymmetric error bars reflect the systematic uncertainty of the data with respect to one of the theoretical calculations, namely CDB\(+\varDelta +\)Coulomb. These errors were obtained by rescaling the measured observable within the range corresponding to twice the estimated systematic uncertainty, i.e. \(\pm \sigma \). The smallest and largest chi-square values found within this range correspond to the two outer edges of the depicted error bars.

Fig. 3
figure 3

Cross sections at \((20^{\circ }\),\(16^{\circ })\) (left) and \((28^{\circ }\),\(28^{\circ })\) (right) as a function of S at small, intermediate and large relative azimuthal angles for data taken with a proton beam of 135 MeV. Error bars show the statistical uncertainties for the data points. The red (dotted-dashed), blue (dotted), black (solid) and green (double dotted-dashed) lines show predictions of Faddeev calculations using CD-Bonn, CDB\(+\varDelta \), and CDB\(+\varDelta +\)Coulomb and CDB+TM\('\) calculations [15,16,17,18, 20, 40,41,42], respectively. The cyan bands depict the systematic uncertainties (2\(\sigma \))

Full size image
Fig. 4
figure 4

The same as in Fig. 3 but for \(A_{x}\). The red lines in the bottom panels correspond to a zero line

Full size image
Fig. 5
figure 5

The same as in Fig. 3 but for \(A_{y}\)

Full size image
Fig. 6
figure 6

The results of \(\chi ^{2}/\)d.o.f. versus (\(\theta _{1}\) and \(\theta _{2}\)) (left panels) and versus \(\phi _{12}\) (right panels) for different observables (\(A_{x}\), \(A_{y}\) and \(d^{5}\sigma /d\Omega _{1}d\Omega _{2}dS\)) for data taken with a proton-beam energy of 135 MeV. The symbols show the theoretical calculations such as CDB (squares), CDB\(+\varDelta \) (open circles) and CDB\(+\varDelta +\)Coulomb (solid circles) and CDB+TM\('\) (triangles). The error bars reflect the systematic uncertainty. For details, see text

Full size image
Fig. 7
figure 7

Same as Fig. 6 except for 190 MeV

Full size image

4 Discussion

As observed in Fig. 3, at small azimuthal opening angles the results are closer to the predictions of the theoretical approach that the CDB\(+\varDelta +\)Coulomb potential. This demonstrates the Coulomb effect is sizeable for this observable at these configurations. Note that in this case the relative energy between the two protons is small. For large relative azimuthal angles, the model based on the CDB+TM\('\) potential appears to be the closest to the experimental data, albeit that the differences between the various models are in general small. For intermediate values of \(\phi _{12}\), the predicted shape of the cross sections differ significantly with the data. In Figs. 4 and 5, the measurements of \(A_{x}\) for relative azimuthal angles of \(180^{\circ }\) is found to be consistent with zero as expected from Eq. 10. This demonstrates that our procedure to extract the analyzing powers does not suffer from experimental asymmetries. This is also confirmed by our estimate of the systematic uncertainty, which is found to be small. Our polarization observables are reasonably well described by the calculations for kinematical configurations with intermediate and large \(\phi _{12}\) that the three-nucleon force effect is predicted to be small. However, striking discrepancies are observed at specific configurations, in particular in cases whereby the relative azimuthal angle between the two outgoing protons becomes small. In this range, the measured values of \(A_{y}\) are close to the results of the 2NF calculation. Although, the disagreement is still significant, the effects of the Coulomb force are very small. The addition of the TM\('\) 3NF makes the agreement even worse. Therefore, the origin of this discrepancy must lie in the treatment of 3NFs. The same behavior was observed for the data taken at a beam energy of 190 MeV [46]. Based on this observation, we suggest to improve the short-range part of the 3NF for which the data presented n this paper and those in Ref. [46] can be used as a benchmark.

The results of the analyzing powers for different combinations of (\(\theta _{1}=\theta _{2}\), \(\phi _{12}\)) for small \(\phi _{12}\) which corresponds to \(d(\vec {p},\mathrm{{^{2}He}})n\) for 135 MeV proton beam energy were also compared to the results using a proton beam with an energy of 190 MeV [47] to study the spin-isospin sensitivity of the 3NF models [29, 48, 49].

By inspecting Fig. 6, we note that the absolute values of the \(\chi ^{2}/\)d.o.f. for the analyzing powers \(A_{x}\) and \(A_{y}\) appear to behave better than the ones for the cross section. However, also for analyzing powers, there are clear trends to be observed in which all the model predictions deviate, beyond statistical and systematic uncertainties, from the data. For \(A_{y}\), the trend observed in the plots as a function of polar angle combination looks similar to what is observed for the cross section. The models show a larger discrepancy towards larger angles. The trends as a function of \(\phi _{12}\) are vastly different compared to the ones observed in the cross section. Although \(A_{y}\) features a worse agreement towards small \(\phi _{12}\) (and partly large \(\phi _{12}\)), the observable \(A_{x}\) is well predicted at small \(\phi _{12}\) except for CDB+TM\('\). By comparing all the model predictions, the calculation based on the CDB\(+\varDelta +\)Coulomb model is the most compatible with the data. By comparing the results between the two energies, see Figs. 6 and 7, in general, similar trends as a function of \(\phi _{12}\) are observed for the cross section and \(A_{y}\). For the cross section data taken at 190 MeV, the calculation that is based on CDB\(+\varDelta +\)Coulomb potentials shows the worst agreement, in particular for large values of \(\phi _{12}\). The sensitivity to 3NF effects appears to be larger at the higher energy. For both energies, it is clear that the inclusion of the TM\('\) 3NF is by far not sufficient to remedy the observed discrepancies. We also note that the Coulomb effect is very small for both spin observables. By globally reviewing the chi-square data, we note that CDB+TM\('\) gives the worst description of the data for analyzing powers.

5 Summary and conclusions

Finding a suitable theory of nuclear forces is one of the main challenges in nuclear physics. To study the three nucleon systems, the reaction \(d(\vec {p}, pp)n\) was studied at KVI using a polarized proton beam. In this paper, the results of the vector analyzing powers, \(A_{x}\) and \(A_{y}\), and the cross section for data taken with a proton-beam energy of 135 MeV are presented. Moreover, we performed a global review of a rich set of cross section and vector analyzing-power data taken with proton-beam energies of 135 MeV and 190 MeV. The results were compared with theoretical Faddeev calculations using 2N and 2N+3NF models such as CD-Bonn, CDB\(+\varDelta \), CDB\(+\varDelta +\)Coulomb and CDB\(+\)TM\('\) [15,16,17,18, 20, 40,41,42] for the kinematics in which both protons scatter to polar angles smaller than \(30^{\circ }\) and with a relative azimuthal opening angle varying between \(20^{\circ }\) and \(180^{\circ }\). The results of cross sections and analyzing powers, \(A_{x}\) ans \(A_{y}\), as a function of S for different configurations (\(\theta _{1}\), \(\theta _{2}\), \(\phi _{12}\)) are shown in Figs. 3, 4, 5. At small azimuthal opening angles, the calculation, which is based on the extended CDB+\(\varDelta \) and with Coulomb corrections, CDB+\(\varDelta +\)Coulomb, shows a smaller discrepancy with the data than the other calculations. The results show that there is a general disagreement between the data and the calculations using two- and three-nucleon forces. In particular, predictions for the vector analyzing powers show a systematic deficiency at small relative azimuthal angles, which corresponds to small relative energies. In this range, the data for \(A_{y}\) are closest to the three-body calculation that is based on a 2N potential. The addition of 3NF makes the agreement even worse.

The results of the global review show very large values of \(\chi ^{2}\)/d.o.f. for the cross sections at specific scattering and relative azimuthal angles. The deviations, independent of the model and beam energy, appear to increase towards large values of \(\phi _{12}\). This implies that the present models are not able to provide a reasonable description of the data. The absolute \(\chi ^2\)/d.o.f. for the analyzing powers \(A_{x}\) and \(A_{y}\) are much closer to unity than the ones observed for the cross sections. However, also for these observables no satisfactory agreement is found for all the angular combinations (\(\theta _{1}\), \(\theta _{1}\)) and \(\phi _{12}\).