Abstract
Activation cross sections of the \(^{\mathrm {nat}}\hbox {Rb (d,xn)}^{87\mathrm {m,85m,85g,83,82}}\hbox {Sr}\), \(^{\mathrm {nat}}\hbox {Rb(d,x)}^{\mathrm {86,84,83,82m}}\hbox {Rb}\) and \(^{\mathrm {nat}}\hbox {Rb(d,x)}^{85\mathrm {m}}\hbox {Kr}\) nuclear reactions have been measured for the first time through an activation method combining the stacked foil irradiation technique and gamma-ray spectrometry. The provided cross sections from the present investigation are all new, in such a way contribute to the completeness of the experimental database. The experimental cross sections were compared with the theoretical prediction in the TENDL-2019 TALYS based library and with our calculation using ALICE-D and EMPIRE-D model codes in order the improve their predictivity. Thick target production yields were calculated form the new cross sections for all investigated radioisotopes. Practical applications of the results are shortly discussed.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
1 Introduction
Integral excitation functions for the production of residual nuclides through light charged particle activation constitute basic data for various applications. Nowadays, deuteron induced reactions start to play an important role as the stripping process generates high production yields and the stopping power for deuterons is relatively low. Some years ago, to meet requirements of practical applications, we started to establish an experimental activation database by performing new experiments and a systematic survey of existing data of deuteron induced cross-sections up to 50 MeV. This database is essential for accelerator and target technology to produce high-energy, high-intensity neutron fluxes, wear and material studies through TLA (Thin Layer Activation), medical radioisotope production, space applications (resistance of electronics, shielding, etc.), monitoring of deuteron beam intensities and energies, etc.
Unlike for proton induced reactions, the status (reliability and completeness) of the experimental data for deuteron induced reactions was rather poor, especially above 15–20 MeV. We embarked hence on a systematic program of extending the study to more targets and up to 50 MeV incident deuteron energy. In this work we present the excitation functions for reactions on rubidium (stable isotopes \(^{{85}}\hbox {Rb}\) and \(^{{87}}\hbox {Rb}\)) leading to radionuclides of Sr, Rb and Kr.
The measured excitation functions are compared with the results of three nuclear reaction model codes. These comparisons can show the present status of the predictivity of these codes and contribute to their development. The reliability of the presently used theoretical codes for deuteron induced reactions is low, compared to proton and alpha particle induced reactions, due to the modeling problems of the deuteron stripping and pickup.
Concerning activation cross sections of deuteron induced reactions on Rb, no experimental data were found in the literature. Only integral physical yields at 22 MeV deuteron energy were reported by Dmitriev et al. [1] for production of \(^{{84,86}}\hbox {Rb}\) and \(^{{85}}\hbox {Sr}\).
2 Experiments and data evaluation
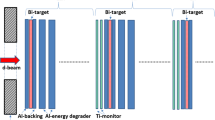
The main experimental parameters and data evaluation methods used in this work are shown in Table 1. The cross section data were measured by using the activation method, stacked foil irradiation technique and high resolution gamma-ray spectrometry. Beam current and energy scale are based on monitor reactions, re-measured simultaneously over the whole covered energy range (Fig. 1).
The Rb-targets were obtained by deposition of \(\hbox {Rb}_{{2}} \hbox {SO}_{{4}}\) (99.8%, Sigma Aldrich) using a sedimentation method [2] on a \(50 ~\upmu \hbox {m}\) thick, high purity Al backing in an 11 mm diameter spot. Actual thickness of the layer was determined by measuring the area and differential weighing of the material deposited on the Al backing. The pellets were covered by a \(10 ~\upmu \hbox {m}\) Al foil for protection. The metal foils were high purity products from Goodfellow.
The stack was irradiated with deuterons of 50 MeV incident energy at an external beam line of the Cyclone 110 cyclotron of the Université Catholique in Louvain la Neuve (LLN): (protons 20–80 MeV; d, \(\upalpha \) 2.3–27 MeV/nucleon; heavy ions, radioactive ions).
The present stack contained 19 blocks of \(\hbox {Al--Rb}_{{2}} \hbox {SO}_{{4}}\)–Al targets alternated with \(\hbox {Al--RuCl}_{{2}}\)–Al targets and further 6 blocks of \(\hbox {Al--Rb}_{{2}} \hbox {SO}_{{4}}\)–Al targets alternated with \(\hbox {Al--RuCl}_{{2}}\)–Al targets combined with \(20 ~\upmu \hbox {m}\) Ti monitors. The nominal current during the 40 min irradiation was 27 nA. The targets were mounted in a target holder (Faraday cup like) provided with a long collimator defining a 5 mm beam diameter.
Gamma-spectra were measured with Canberra GX1520 HPGe detectors of 15% efficiency and 1.9 keV resolution at the 1332 keV \(^{{60}}\hbox {Co}\) peak at the VUB (Free University of Brussels) laboratory. The detectors were vertically arranged with adjustable distance sample holders from the detector surface to several meters. The detector head was put into 10 cm lead shielding with 2 mm copper internal lining. The individual foils or a group of target foils were measured in such a distance that the dead time was always under 5%. To make the evaluation easier not more than 5 distances were selected. The samples were measured first after a short cooling time of several hours for the short-lived components up to after several months for the longer-lived radioisotopes. The measuring time was chosen to acquire good statistics for the expected gamma-peaks, but of course it cannot be optimized for every radioisotope in question. The used decay data, taken from the online version of NUDAT 2.6 [3], and the energy threshold values in MeV, obtained from the Q-value calculator [4], are presented in Table 1.
The median beam energies in the individual targets were preliminarily determined by a degradation calculation (see [5]) and were corrected on the basis of the fitted monitor reaction [6]. The activities of the individual radioisotopes were determined from the measurement of the corresponding gamma-peaks (Eq. 1):
where \(A_{EOB} \) is the activity at the End of Bombardment, T is the net area of the gamma-peak, \(\uplambda \) is the decay constant, \( t_{real}{, t}_{live}\) and \(t_{c}\) are the real-time, live-time of the measurement and the cooling time, \(I_{\gamma }\) is the gamma-line abundance (intensity) and \(\upvarepsilon \) is the detector efficiency. From the measured activities the corresponding cross section was calculated according to Eq. 2.
where z is the projectile charge, I(A) is beam current, \(N_{A} \) is Avogadro’s number (\(6.02214\times 10^{{23}}\, \hbox {mol}^{{-1}}\)), M (g/mol) should be molar mass of the chemical compound used as the target material, e is the electron charge (\(1.6\hbox {x}10^{{-19}}\hbox { C}\)), \(\rho \) (g/cm\(^{2}\)) is the mass density of the target material, s (cm) is the thickness of the measured target foil, \(\nu \) is the number of the particular element atoms in the compound molecule and f is the abundance of the particular isotope (entering the particular nuclear reaction) in the element. \(\sigma \textit{(E) (cm}^{2}) \) is the cross section at bombarding energy E, where E is the median energy in the measured foil of the stack. By using both Eqs. 1 and 2 one must take care of the measuring units. Equation 2 is valid for isotopic cross sections. In our case mainly elemental cross sections were determined, where \(f=\textit{1}\).
Uncertainties of the median energies were obtained taking into account cumulative effects of possible uncertainties (primary energy, target thickness, energy straggling, correction to monitor reaction). Uncertainty of cross-sections was determined by considering the sum in quadrature of all independent contributions following the ISO recommendations (cf. [7]): beam current (7 %), target thickness (6 %), detector efficiency (5 %), nuclear decay data (3 %), full energy peak area determination and counting statistics (1-20 %).
Natural Rb has two stable isotopes: \(^{{85}}\hbox {Rb}\) (72.17 %) and \(^{{87}}\hbox {Rb}\) (27.83 %). The experimental parameters and the data evaluation methods are summarized in Table 1.
3 Nuclear model calculation
The cross sections of the investigated reactions were calculated using the pre-compound model codes ALICE-IPPE [13] and EMPIRE-II [14]. The experimental data are also compared with the cross section data in the TENDL-2019 on-line library [15]. The TENDL-2019 library contains the results of the blind and adjusted calculations on the basis of the latest version (1.6) of the TALYS nuclear model code system [16]. For showing the evolution of this code and database also the results of the TENDL-2017 version are indicated and nearly no or only marginal changes in the results can be noticed.
In our previous works ALICE-IPPE and EMPIRE-II were used successfully for the description of a large amount of reaction cross sections induced by light charged particles. However, during the recent analyses of the (d,p) reactions on the isotopes, \(^{{114}}\hbox {Cd}\) [17]; \(^{{169}}\hbox {Tm}\) [18]; \(^{{ 192}}\hbox {Os}\) [19] and some others, we were confronted with a large underestimation of the measured cross sections. We come to the conclusion that the experimentally observed cross sections of the (d,p) reaction cannot be reproduced below 20–30 MeV with the available statistical model codes. To achieve a better description of available data for (d,p) reactions with the ALICE and EMPIRE a phenomenological simulation of direct (d,p) and (d,t) transitions were introduced to the above-mentioned codes. A phenomenological enhancement factor K in these relations was taken as energy dependent and estimated to describe the whole set of the observed (d,p) cross sections for medium and heavy nuclei. By this improvement, in the ALICE IPPE-D and EMPIRE-D code versions for the deuteron induced reactions, the direct (d,p) channel is increased strongly and this is reflected in changes for all other reaction channels in both codes. As ALICE-IPPE calculates only the total cross section, for estimation of isomeric states from the ALICE code the isomeric ratios calculated by EMPIRE-D were applied.
4 Results and discussion
Formation cross sections for the \(^{\mathrm {nat}}\hbox {Rb}\hbox {(d,xn)}^{87\mathrm {m}}\hbox {Sr}\), \(^{\mathrm {nat}}\hbox {Rb}\hbox {(d,xn)}^{85\mathrm {m}}\hbox {Sr}\), \(^{\mathrm {nat}}\hbox {Rb}\hbox {(d,xn)}^{85\mathrm {g}}\hbox {Sr}(\hbox {m}+)\), \(^{\mathrm {at}}\hbox {Rb}\hbox {(d,xn)}^{\mathrm {83g}}\hbox {Sr}(\hbox {m}+)\), \(^{\mathrm {nat}}\hbox {Rb}\hbox {(d,xn)}^{{82}}\hbox {Sr}\), \(^{\mathrm {nat}}\hbox {Rb}\hbox {(d,x)}^{\mathrm {86g}}\hbox {Rb}(\hbox {m}+)\), \(^{\mathrm {nat}}\hbox {Rb}\hbox {(d,x)}^{\mathrm {84g}}\hbox {Rb}(\hbox {m}+)\), \(^{\mathrm {nat}}\hbox {Rb}\hbox {(d,x)}^{{83}}\hbox {Rb}\)(cum), \(^{\mathrm {nat}}\hbox {Rb}\hbox {(d,x)}^{\mathrm {82m}}\hbox {Rb}\) and \(^{\mathrm {nat}}\hbox {Rb}\hbox {(d,x)}^{85\mathrm {m}}\hbox {Kr}\) reactions are presented in Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10 and 11 in comparison with the TALYS predictions in TENDL-2019 (and TENDL-2017) and with our calculation using the ALICE-D and EMPIRE-D model codes.
4.1 Cross sections for production of strontium radioisotopes
The radioisotopes of strontium are produced via direct (d,xn) reactions on one or both of the stable Rb isotopes.
4.1.1 \(^{\mathrm{nat}}\)Rb(d,xn)\(^{87\hbox {m}}\)Sr
The isotope \(^{{87}}\hbox {Sr}\) has a stable ground state and a rather short-lived isomeric state \(^{87\mathrm {m}}\hbox {Sr}\) (\(\hbox {T}_{{1/2 }}= 2.815\) h) that was measured with poor statistics because of the long cooling time. It is produced in our experimental circumstances only through the \(^{{87}}\hbox {Rb}\)(d,2n) reaction. The agreement of our indicative results (large uncertainties, huge difference in decay corrections between different target foils) with predictions of the theoretical codes is acceptable (Fig. 2). There is no visible difference between the two versions of TENDL.
4.1.2 \(^{\mathrm{nat}}\)Rb(d,xn)\(^{85\mathrm{m}}\)Sr
The radionuclide \(^{{85}}\hbox {Sr}\) has a longer-lived ground state (\(\hbox {T}_{{1/2}}= 64.849\) d) and a shorter-lived isomeric state (\(\hbox {T}_{{1/2}}= 67.63\) min) decaying partly to the ground state. The excitation function for production of the metastable state is shown in Fig. 3. There is a good agreement with the TENDL-2019 (TENDL-2017) predictions at lower energies, representing the \(^{{85}}\hbox {Rb}\)(d,2n) contribution. But around the weak maximum of the \(^{{87}}\hbox {Rb}\)(d,4n) reaction the predictions of the three codes are significantly different. The both versions of the TENDL gave the same results.
4.1.3 \(^{\mathrm{nat}}\)Rb(d,xn)\(^{85\mathrm{g}}\)Sr (m\(+\))
To determine the activity of \(^{85\mathrm {g}}\hbox {Sr}\) (\(\hbox {T}_{{1/2}}= 64.849\) d) with gamma-spectrometry, it is necessary to separate the 514 keV gamma-line from the strong annihilation peak. The measured cross sections include the complete decay contribution from the short-lived metastable state (\(\hbox {T}_{{1/2}}= 67.63\) min, IT 83.6 %) (see above). Comparing with code results the magnitudes are similar, but the shapes differ significantly (Fig. 4).
4.1.4 \(^{\mathrm{nat}}\)Rb(d,xn)\(^{83\mathrm{g}}\)Sr(m\(+\))
As it is obvious from Table 2, the very short-lived isomeric state of \(^{{83}}\hbox {Sr}\) (\(\hbox {T}_{{1/2}}= 4.95\) s, IT: 100 %) decayed completely to the ground state (\(\hbox {T}_{{1/2}}= 32.41\) h) before the spectra measurements started. The experimental and theoretical data for the excitation curve of \(^{83\mathrm {g}}\hbox {Sr}(\hbox {m}+)\) are systematically shifted in energy and differ in maximum cross section value (Fig. 5).
4.1.5 \(^{\mathrm{nat}}\)Rb(d,xn)\(^{82}\)Sr
The longer-lived radionuclide \(^{{82}}\hbox {Sr}\) (\(\hbox {T}_{{1/2}}= 25.35\) d) has no gamma-lines. The activity was measured through the 776 keV gamma-line of its daughter \(^{82\mathrm {g}}\hbox {Rb}\) (\(\hbox {T}_{{1/2}}= 1.2375\) min). The comparison of the experimental and the theoretical data (in our experimental conditions only contribution of \(^{{85}}\hbox {Rb}\)(d,5n)\(^{{82}}\hbox {Sr}\)) are presented in Fig. 6, showing an excellent agreement with EMPIRE-D while an energy shift with the other codes appear.
4.1.6 Calculations for strontium isotopes
The statistical codes EMPIRE-D and TALYS describe rather well the near-threshold parts of the neutron emission reactions. The ALICE-D results are less satisfactory for this region through overly simplified modeling of the low-lying discrete levels of the considered nuclei. For calculations of the cross sections in the region of maximums, a ratio of the level densities of competing reaction channels is crucial. The existing differences in calculations reflect differences of the default level-density parameters of the corresponding codes. Discrepancies between calculations with experiment can be eliminated by the appropriate adjustments of parameters. For the \(^{\mathrm {nat}}\hbox {Rb}\hbox {(d,xn)}^{\mathrm {83g}}\hbox {Sr}(\hbox {m}+)\) and \(^{\mathrm {nat}}\hbox {Rb}\hbox {(d,xn)}^{{82}}\hbox {Sr}\) reactions the EMPIRE-D results look preferable over other ones.
4.2 Excitation functions for production of rubidium radioisotopes
The radioisotopes of rubidium are produced via direct (d,pxn) reactions and through the \(\upvarepsilon \) and/or \(\upbeta ^{{+}}\) decay of Sr parent radioisotopes.
4.2.1 \(^{\mathrm{nat}}\)Rb(d,x)\(^{86\mathrm{g}}\)Rb (m\(+\))
The longer-lived ground state \(^{{86}}\hbox {Rb}\) (\(\hbox {T}_{{1/2}}= 18.642\) d) is produced via direct (d,pxn) reaction on \(^{{85,87}}\hbox {Rb}\). The measured data are so called \((\hbox {m}+)\), including the complete decay of the isomeric state (\(\hbox {T}_{{1/2}}= 1.017\) min, IT 100 %) (Fig. 7). The description of \(^{{87}}\hbox {Rb}\)(d,p) part is not satisfactory in all model codes. The experimental data are in good agreement with the systematics for a (d,p) reaction in this mass region [20].
4.2.2 \(^{\mathrm{nat}}\)Rb(d,x)\(^{84\mathrm{g}}\)Rb(m\(+\))
The \(^{\mathrm {84g}}\hbox {Rb}\) (\(\hbox {T}_{{1/2}}= 32.82\) d) and \(^{\mathrm {84m}}\hbox {Rb}\) (\(\hbox {T}_{{1/2}}= 20.26\) min, IT 100 %) isomers are produced only directly on \(^{\mathrm {nat}}\hbox {Rb}\) targets via \(^{{85}}\hbox {Rb(d,p2n)}\) and \(^{{87}}\hbox {Rb(d,p4n)}\) reactions. The cross sections for production of \(^{\mathrm {84g}}\hbox {Rb}\) were deduced from spectra measured after complete isomeric decay of the short-lived metastable state. Among the model predictions only the EMPIRE-D descriptions are acceptable over the energy region studied (Fig. 8).
4.2.3 \(^{\mathrm{nat}}\)Rb(d,x)\(^{83}\)Rb(cum)
The measured production cross section of \(^{{83}}\hbox {Rb}\) (\(\hbox {T}_{{1/2}}= 86.2\) d) are cumulative. It contains the complete decay of its \(^{{83}}\hbox {Sr}\) (\(\hbox {T}_{{1/2}}= 32.41\) h, \(\upvarepsilon :100\) %) parent isotope (Fig. 9). The model predictions are very different and cannot even describe rather well the cumulative maximum. EMPIRE-D is acceptable up to 38 MeV, and the cumulative TENDL version give the better results above this energy.
4.2.4 \(^{\mathrm{nat}}\)Rb(d,p4n)\(^{82\mathrm{m}}\)Rb
The metastable state \(^{\mathrm {82m}}\hbox {Rb}\) (\(\hbox {T}_{{1/2}}=\) 6.472 h) is produced here directly only via the \(^{{85}}\hbox {Rb}\)(d,p4n) reaction (\(\hbox {Q} = --\,32.41\) MeV). The experimental data, with high practical threshold, are described more satisfactory by the ALICE-D prediction (Fig. 10).
4.2.5 Calculations for rubidium isotopes
The general comments on the (d, pxn) reactions are the same as those discussed in Sect. 4.1.6 above. However, a special consideration is required for the (d, p) reaction. It is well known that this reaction is dominated by the mechanism of a direct breakup without the formation of any intermediate pre-equilibrium state of the nucleus. A satisfactory description of the experimental data on this reaction can be achieved only on the basis of the phenomenological systematics proposed in [21]. For the \(^{\mathrm {nat}}\hbox {Rb}\hbox {(d,x)}^{\mathrm {84g}}\hbox {Rb}(\hbox {m}+)\) reaction the TENDL-2019 results look a little preferable over the EMPIRE-D ones and for the \(^{\mathrm {nat}}\hbox {Rb}\hbox {(d,xn)}^{{83}}\hbox {Rb}\)(cum) reaction we observed an inverse case. For the \(^{\mathrm {nat}}\hbox {Rb}\hbox {(d,xn)}^{82\mathrm {m}}\hbox {Rb}\) reaction the ALICE-D results are certainly preferable, but that seems rather accidental result. Description of experimental data can be surely improved for each reaction by the appropriate adjustments of the nuclear level density parameters.
4.3 Excitation functions for production of krypton radioisotopes
4.3.1 \(^{\mathrm{nat}}\)Rb(d,x)\(^{85\mathrm{m}}\)Kr
The metastable state \(^{85\mathrm {m}}\hbox {Kr}\) (\(\hbox {T}_{{1/2}}= 4.480\) h) is produced directly by \(^{{85}}\hbox {Rb(d,2p)}\) and \(^{{87}}\hbox {Rb}(\hbox {d},\upalpha )\) reactions, both with low thresholds. The \(^{85\mathrm {m}}\hbox {Kr}\) has common gamma-lines with \(^{{85}}\hbox {Sr}\) (both decay to stable \(^{{85}}\hbox {Rb}\)). The presented data were corrected for contribution of the \(^{{85}}\hbox {Sr}\) in the measured gamma-spectra. The 151 keV gamma-line was present only in the first(early) series of gamma spectra measurements and with low statistics. We had possibility to deduce the cross section data for \(^{85\mathrm {m}}\hbox {Kr}\) via subtracting the contribution of the \(^{85\mathrm {m}}\hbox {Sr}\). The contribution was significant and taking into account that the cross section of the \(^{85\mathrm {m}}\hbox {Kr}\) is low, the statistics of the separated 151 of the \(^{85\mathrm {m}}\hbox {Kr}\) was poor. The experimental data, slowly rising as a result of the combination of the two contributing reactions without pronounced maximum in the studied energy region, and their curve is described acceptable well by the used model codes (Fig. 11).
4.4 The thick target and integral yields of the investigated radioisotopes
The thick target yields as a function of the bombarding energy, calculated from integration of a fit to our experimental excitation functions (Eq. 3), are shown in Figs. 12 and 13 compared to values obtained in direct thick target measurements [1]. All thick target and integral yields are deduced for metallic Rb targets of natural composition. The integral yields represent so called physical yields (see [11] and [12]). The only experimental values are for \(^{85\mathrm {g}}\hbox {Sr}\) and \(^{86\mathrm {g},84\mathrm {g}}\hbox {Rb}\) available [1] and shows acceptable agreement with our curve at 22 MeV deuteron energy.
Where \(E_{th} \) is the threshold energy of the nuclear reaction in question, and F is the conversion constant, which contains all the constants as density, molar weight, decay constant, electron charge, Avogadro’s number, etc. and the conversion factors necessary to get the integral yield (Y(E)) in proper units. Instead of integral along a numerical integration was performed along depth with \(\varDelta \textit{x(E,dE)}\), where dE is equidistant, and in such a way \(\varDelta x\) is not.
5 Applications of deuteron induced reactions on rubidium for nuclear medicine
Many investigated activation products are relevant for nuclear medicine (\(^{87\mathrm {m}}\hbox {Sr}\), \(^{85\mathrm {g}}\hbox {Sr}\), \(^{\mathrm {83g}}\hbox {Sr}\), \(^{{82}}\hbox {Sr}\) (\(^{{82}}\hbox {Rb}\)), \(^{\mathrm {82m}}\hbox {Rb}\), \(^{85\mathrm {m}}\hbox {Kr}\)). Through the presently investigated reactions, the production of \(^{\mathrm {82m}}\hbox {Rb}\) is carrier added and the production yields of \(^{85\mathrm {m}}\hbox {Kr}\) and \(^{{82}}\hbox {Sr}\) (in the investigated energy range) are very low. Only production of the \(^{87\mathrm {m}}\hbox {Sr}\), \(^{{85}}\hbox {Sr}\), \(^{{83}}\hbox {Sr}\) and \(^{{82}}\hbox {Sr}\) radioisotopes are hence discussed shortly in more detail. More detailed discussion, including production parameters (yield, impurities, targetry, etc.) will be prepared and published in a dedicated journal.
6 Production of \(^{{{87\mathrm{m}}}}\)Sr
\(^{87\mathrm {m}}\hbox {Sr}\) (2.815 h) is used in skeletal SPECT (Single Photon Emission Computer Tomography) imaging for diagnosis of diseases. This radionuclide can be produced directly: by proton and deuteron induced reaction on rubidium: \(^{\mathrm {nat}}\hbox {Rb}\hbox {(p,x)}^{87\mathrm {m}}\hbox {Sr}\) [22], \(^{{87}}\hbox {Rb}\hbox {(p,x)}^{87\mathrm {m}}\hbox {Sr}\) [23,24,25], \(^{\mathrm {nat}}\hbox {Rb}\hbox {(d,x)}^{87\mathrm {m}}\hbox {Sr}\) (this work) or by alpha and \(^{{3}}\hbox {He}\) induced reactions on krypton: \(^{\mathrm {nat}}\hbox {Kr}(\upalpha ,\hbox {x})^{87\mathrm {m}}\hbox {Sr}\) [26], \(^{\mathrm {nat}}\hbox {Kr}(^{{3}}\hbox {He},\hbox {n})^{87\mathrm {m}}\hbox {Sr}\) [26], or indirectly: through \(^{{87}}\hbox {Y}\) (13.37 h)/\(^{87\mathrm {m}}\hbox {Sr}\) generator by alpha and \(^{{3}}\hbox {He}\) induced reactions on rubidium: \(^{\mathrm {nat}}\hbox {Rb}(\upalpha ,\hbox {x})^{87\mathrm {m}}\hbox {Y}\) [27, 28], \(^{{85}}\hbox {Rb}(\upalpha ,\hbox {x})^{87\mathrm {m}}\hbox {Y}\) [29, 30], \(^{{85}}\hbox {Rb}(\upalpha ,\hbox {x})^{87\mathrm {g}}\hbox {Y}\) [29, 30], \(^{{85}}\hbox {Rb}(\upalpha ,\hbox {x})^{{87}}\hbox {Y}\) [28, 30,31,32,33], \(^{\mathrm {nat}}\hbox {Rb}(^{{3}}\hbox {He},\hbox {x})^{87\mathrm {m}}\hbox {Y}\) [2, 27], \(^{\mathrm {nat}}\hbox {Rb}(^{{3}}\hbox {He},\hbox {x})^{87\mathrm {g}}\hbox {Y}\) [2] or proton induced reaction on enriched \(^{{87}}\hbox {Sr}\) target [29, 34,35,36,37], proton induced reaction on \(^{{88}}\hbox {Sr}\) target [29, 38,39,40] or proton induced reaction on natural strontium target [41,42,43] or deuteron induced reactions on \(^{\mathrm {nat}}\hbox {Sr}\) [44, 45]. In practical medical isotope production, the role of the \(^{{3}}\hbox {He}\) induced reaction is minimal due to lack of accelerator and high price of \(^{{3}}\hbox {He}\) and the high stopping power. The situation is practically same in case of alpha particle induced reactions, except the price of \(^{{4}}\hbox {He}\) gas. Alpha particles are used only when no low energy possibility with protons and deuterons is available (\(^{{211}}\hbox {At}\)). In practice proton induced reactions are the favorites due to the large cross sections, availability of high intensity beams, and lower stopping power. But during our systematic study of deuteron induced reactions it was shown that some isotopes cannot be produced by protons, but they are available with deuterons via (d,n) and (d,p) reactions, and at medium and heavy mass targets the production yields of (d,2n) are significantly higher comparing to (p,n).
6.1 Production of \(^{{{85}}}\)Sr
The \(^{85\mathrm {g}}\hbox {Sr}\) (\(\hbox {T}_{{1/2}}= 64.849\) d) had importance in nuclear medicine as diagnostic radioisotope, later it was proposed to use it for the endotherapy and as important disturbing impurity in the application of the \(^{{82}}\hbox {Sr}\) and \(^{\mathrm {83g}}\hbox {Sr}\). It can be produced directly or indirectly through \(^{{85}}\hbox {Y}\) parent. In the literature the following direct and indirect production routes have been found. Direct production routes: \(^{{85}}\hbox {Rb}\hbox {(p,n)}^{{85}}\hbox {Sr}\) [29, 46,47,48], \(^{\mathrm {nat}}\hbox {Rb}\hbox {(p,xn)}^{\mathrm { 85}}\hbox {Sr}\) [22, 24, 49,50,51,52,53], \(^{\mathrm {nat}}\hbox {Rb}\hbox {(d,xn)}^{{85}}\hbox {Sr}\) (this work), \(^{\mathrm {nat}}\hbox {Kr}(\upalpha ,\hbox {n})^{85\mathrm {m}}\hbox {Sr}\) [26, 54], \(^{\mathrm {nat}}\hbox {Kr}(\upalpha ,\hbox {n})^{85\mathrm {g}}\hbox {Sr}\) [26, 54], \(^{\mathrm {nat}}\hbox {Kr}(^{{3}}\hbox {He},\hbox {n})^{85\mathrm {m}}\hbox {Sr}\) [26, 54], \(^{\mathrm {nat}}\hbox {Kr}(^{{3}}\hbox {He},\hbox {n})^{85\mathrm {g}}\hbox {Sr}\) [26, 54]. Indirect production routes: \(^{{86}}\hbox {Sr}\hbox {(p,2n)}^{{85}}\hbox {Y}\) [2, 29], \(^{\mathrm {nat}}\hbox {Sr}\hbox {(d,xn)}^{{85}}\hbox {Y}\) [45].
6.2 Production of \(^{{{83}}}\)Sr
The \(^{\mathrm {83g}}\hbox {Sr}\) is a positron emitter analog of the \(\upbeta ^{-}\) emitting \(^{{89}}\hbox {Sr}\) (\(\hbox {T}_{{1/2}}= 50.5\) d) used for endotherapy.
The following production routes have been investigated in the literature: \(^{\mathrm {nat}}\hbox {Rb}\hbox {(p,xn)}^{{83}}\hbox {Sr}\) [22, 24, 49], \(^{{85}}\hbox {Rb}\hbox {(p,3n)}^{{83}}\hbox {Sr}\) [29, 48, 55], \(^{\mathrm {nat}}\hbox {Rb}\hbox {(d,xn)}^{{83}}\hbox {Sr}\) [this work], \(^{{82}}\hbox {Kr}(^{{3}}\hbox {He}\),n)\(^{{83}}\hbox {Sr}\) [26, 54], \(^{\mathrm {nat}}\hbox {Kr}(\upalpha ,\hbox {xn})^{{83}}\hbox {Sr}\) [26, 54], \(^{\mathrm {nat}}\hbox {Kr}(^{{3}}\hbox {He},3\hbox {n})^{{83}}\hbox {Sr}\) [26, 54].
6.3 \(^{{{82}}}\) Sr production
\(^{{82}}\hbox {Sr}(^{{82}}\hbox {Rb}\)) is widely used in myocardial perfusion imaging in Positron Emission Tomography (PET). The following production routes have been investigated: \(^{{85}}\hbox {Rb}\hbox {(p,4n)}^{{82}}\hbox {Sr}\) [22, 48, 49, 53, 56], \(^{\mathrm {nat}}\hbox {Rb}\hbox {(p,xn)}^{{82}}\hbox {Sr}\) [22, 48, 49, 52, 53, 55,56,57], \(^{\mathrm {nat}}\hbox {Rb}\hbox {(d,xn)}^{{82}}\hbox {Sr}\) [this work], \(^{{82}}\hbox {Kr}(\upalpha ,4\hbox {n})^{{82}}\hbox {Sr}\) [26], \(^{{83}}\hbox {Kr} (\upalpha ,\hbox {5n})^{{82}}\hbox {Sr}\) [58], \(^{{82}}\hbox {Kr}(^{{3}}\hbox {He},3\hbox {n})^{{82}}\hbox {Sr}\) [26], \(^{{83}}\hbox {Kr}(^{{3}}\hbox {He},4\hbox {n})^{{82}}\hbox {Sr}\) [26], \(^{\mathrm {nat}}\hbox {Kr}(^{{3}}\hbox {He},\hbox {xn})^{{82}}\hbox {Sr}\) [26, 54], \(^{\mathrm {nat}}\hbox {Kr}(\upalpha ,\hbox {xn})^{{82}}\hbox {Sr}\) [26, 54].
7 Summary and conclusions
Activation cross sections of the \(^{\mathrm {nat}}\hbox {Rb}\hbox {(d,xn)}^{87\mathrm {m},85\mathrm {m},85\mathrm {g},83,82}\hbox {Sr}\), \(^{\mathrm {nat}}\hbox {Rb}\hbox {(d,x)}^{86,84,83,82\mathrm {m}}\hbox {Rb}\) and \(^{\mathrm {nat}}\hbox {Rb}\hbox {(d,x)}^{85\mathrm {m}}\hbox {Kr}\) nuclear reactions were measured for the first time up to 50 MeV relative to well documented \(^{{27}}\hbox {Al(d,x)}^{{22,24}}\)Na monitor reactions. Model calculations were done with the ALICE-IPPE-D and EMPIRE D code and completed with the TALYS results from TENDL-2019 library. The model calculations predict with varying success the shape and the absolute values of the experimental data. Physical integral yields were deduced for every studied radioisotope and compared with the literature data for production of \(^{{84,86}}\hbox {Rb}\) and \(^{{85}}\hbox {Sr}\). The status of cross section and yield data for production of some medically important radioisotopes is also discussed.
The obtained experimental data also provide a basis for improved model calculations and for applications in radioisotope production.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: Cross section data is given in the manuscript in table form, both cross section and yield data will be deposited in the IAEA EXFOR database after publication, but is a question of time.]
References
P.P. Dmitriev, N.N. Krasnov, G.A. Molin, Yields of radioactive nuclides formed by bombardment of a thick target with 22-MeV deuterons. in INDC(CCP)-210/L, (1983)
F. Rosch, S.M. Qaim, G. Stocklin, Nuclear-data relevant to the production of the positron emitting radioisotope Y-86 Via the Sr-86(P, N)-processes and (Nat)Rb(He-3, Xn)-processes. Radiochim. Acta 61, 1–8 (1993)
NuDat, NuDat2 database (2.6), in National Nuclear Data Center, Brookhaven National Laboratory, (2014)
B. Pritychenko, A. Sonzogni, Q-value calculator, in NNDC, Brookhaven National Laboratory, (2003)
H.H. Andersen, J.F. Ziegler, Hydrogen Stopping Powers and Ranges in All Elements. The Stopping and Ranges of Ions in Matter, vol. 3 (Pergamon Press, New York, 1977)
F. Tárkányi, S. Takács, K. Gul, A. Hermanne, M.G. Mustafa, M. Nortier, P. Oblozinsky, S.M. Qaim, B. Scholten, Y.N. Shubin, Z. Youxiang, Beam monitor reactions (Chapter 4). Charged particle cross-section database for medical radioisotope production: diagnostic radioisotopes and monitor reactions, in TECDOC 1211, IAEA, pp. 49, (2001)
International-Bureau-of-Weights-and-Measures, Guide to the Expression of Uncertainty in Measurement, 1st ed., (International Organization for Standardization, Genève, 1993)
Canberra, 2000. http://www.canberra.com/products/radiochemistry_lab/genie-2000-software.asp. Accessed July 2020
G. Székely, Fgm—a flexible gamma-spectrum analysis program for a small computer. Comput. Phys. Commun. 34, 313–324 (1985)
F. Tárkányi, F. Szelecsényi, S. Takács, Determination of effective bombarding energies and fluxes using improved stacked-foil technique. Acta Radiol., Suppl. 376, 72 (1991)
M. Bonardi, The contribution to nuclear data for biomedical radioisotope production from the Milan cyclotron facility, in Consultants Meeting on Data Requirements for Medical Radioisotope Production, IAEA, INDC(NDS)-195 (1988), ed. by K. Okamoto (Japan, Tokyo, 1987), pp. 98–112
N. Otuka, S. Takacs, Definitions of radioisotope thick target yields. Radiochim. Acta 103, 1–6 (2015)
A.I. Dityuk, A.Y. Konobeyev, V.P. Lunev, Y.N. Shubin, New version of the advanced computer code ALICE-IPPE, in INDC (CCP)-410, IAEA, Vienna, (1998)
M. Herman, R. Capote, B.V. Carlson, P. Oblozinsky, M. Sin, A. Trkov, H. Wienke, V. Zerkin, EMPIRE: nuclear reaction model code system for data evaluation. Nucl. Data Sheets 108, 2655–2715 (2007)
A.J. Koning, D. Rochman, J.C. Sublet, N. Dzysiuk, M. Fleming, S. van der Marck, TENDL-2019, in, https://tendl.web.psi.ch/tendl_2019/tendl2019.html (2019). Accessed July 2020
A.J. Koning, D. Rochman, Modern nuclear data evaluation with the TALYS code system. Nucl. Data Sheets 113, 2841–3172 (2012)
F. Tárkányi, S. Takács, A. Hermanne, P. Van den Winkel, R. Van der Zwart, Y.A. Skakun, Y.N. Shubin, S.F. Kovalev, Investigation of the production of the therapeutic radioisotope \(^{\rm 114m}\)In through proton and deuteron induced nuclear reactions on cadmium. Radiochim. Acta 93, 561–569 (2005)
F. Tárkányi, A. Hermanne, S. Takács, F. Ditrói, I. Spahn, S.F. Kovalev, A.V. Ignatyuk, S.M. Qaim, Activation cross sections of the Tm-169(d,2n) reaction for production of the therapeutic radionuclide Yb-169. Appl. Radiat. Isot. 65, 663–668 (2007)
F. Tárkányi, A. Hermanne, S. Takács, K. Hilgers, S.F. Kovalev, A.V. Ignatyuk, S.M. Qaim, Study of the \(^{{192}}\)Os(d,2n) reaction for, production of the therapeutic radionuclide \(^{{192}}\)Ir in no-carrier added form. Appl. Radiat. Isot. 65, 1215–1220 (2007)
A.V. Ignatyuk, Phenomenological systematics of the (d,p) cross sections, in: IAEA (Ed.), Vienna (2011), http://www-nds.iaea.org/fendl3/000pages/RCM3/slides//Ignatyuk_FENDL-3%20presentation.pdf. Accessed July 2020
A.V. Ignatyuk, Evaluations of (d,p) crosssections. In: Final Report of the Coordinated Research Project on Nuclear Data Libraries for Advanced Systems: Fusion Devices, IAEA, Vienna, pp. 56–64, (2013)
T. Ido, A. Hermanne, F. Ditrói, Z. Szucs, I. Mahunka, F. Tárkányi, Excitation functions of proton induced nuclear reactions on Rb-nat from 30 to 70 MeV. Implication for the production of Sr-82 and other medically important Rb and Sr radioisotopes. Nucl. Instrum. Methods Phys. Res., Sect. B 194, 369–388 (2002)
H.G. Blosser, T.H. Handley, Survey of (p, n) reactions at 12 MeV. Phys. Rev. 100, 1340–1344 (1955)
K. Sakamoto, M. Dohniwa, K. Okada, Excitation functions for (p, xn) and (p, pxn) reactions on natural 79 \(+\) 81Br, 85 \(+\) 87Rb, 127I and 133Cs upto \(\text{ Ep }=52\) MeV. Int. J. Appl. Radiat. Isot. 36, 481–488 (1985)
K. Miyano, H. Ohnuma, H. Morinaga, Compound-nucleus cross sections far below the Coulomb barrier. J. Phys. Soc. Jpn. 23, 895–895 (1967)
F. Tárkányi, S.M. Qaim, G. Stöcklin, Excitation-functions of \(^{{3}}\text{ He }\) particle and alpha-particle induced nuclear-reactions on natural krypton–production of \(^{{82}}\text{ Sr }\) at a compact cyclotron. Appl. Radiat. Isot. 39, 135–143 (1988)
Y. Homma, M. Ishii, Y. Murase, Excitation functions and yields for the production of 87mY and preparation of a 87mSr generator. Int. J. Appl. Radiat. Isot. 31, 399–403 (1980)
S.A. Kandil, I. Spahn, B. Scholten, Z.A. Saleh, S.M. Saad, H.H. Coenen, S.M. Qaim, Excitation functions of (alpha, xn) reactions on (nat)Rb and (nat)Sr from threshold up to 26 MeV: possibility of production of (87)Y, (88)Y and (89)Zr. Appl. Radiat. Isot. 65, 561–568 (2007)
V.N. Levkovskii, The Cross-Sections of Activation of Nuclides of Middle-Range Mass (A=40-100) by Protons and Alpha Particles of Middle Range Energies (E=10-50 MeV) (Inter-Vesy, Moscow, 1991)
A. Demeyer, N. Chevarier, A. Chevarier, T. Duc, Reculs Moyens. Rapports isomeriques et fonctions d’excitation pour les reactions induites par des particules alpha sur le rubidium (1971). https://doi.org/10.1051/jphys:01971003208-9058300, 32
R. Guin, S.K. Das, S.K. Saha, Cross-sections and linear momentum transfer in \(\upalpha \)-induced reactions on 85Rb. Radiochim. Acta 88, 435–438 (2000)
A. Agarwal, M.K. Bhardwaj, I. Rizvi, A.K. Chaubey, Measurement and analysis of excitation functions for alpha induced reactions with rubidium. Indian J. Pure Appl. Phys. 41, 829–832 (2003)
S. Iwata, Isomeric cross section ratios in alpha-particle reactions. J. Phys. Soc. Jpn. 17, 1323–1333 (1962)
J.F. Allen, J.J. Pinajian, A Sr87m generator for medical applications. Int. J. Appl. Radiat. Isot. 16, 319–325 (1965)
J. Kutzner, K. Hahn, G.J. Beyer, W. Grimm, A. Bockisch, H.P. Rösler, Scintigraphic use of 87Y during 90Y therapy of bone metastases. Nuklearmedizin 31, 53–56 (1992)
E.A. Skakun, V.G. Batij, Level density parameters from excitation cross-sections of isomeric states. Z. Phys. a-Hadron Nucl. 344, 13–16 (1992)
J.P. Blaser, F. Boehm, P. Marmier, P. Scherrer, Excitation functions and cross sections of the (p,n) reaction. II, Helv. Phys. Acta (Switzerland), 24, 441 (1951)
A.G.M. Janssen, R.A.M.J. Claessens, R. Vandenbosch, J. Degoeij, A rapid and high-yield preparation method for 87Y/87mSr generators, using the 88Sr(p,2n) reaction, International Journal of Radiation Applications and Instrumentation. Int. J. Radiat. Appl. Instrum. Part A Appl. Radiat. Isot. 37, 297–303 (1986)
R.A.M.J. Claessens, A.G.M. Janssen, R.L.P. van den Bosch, J.J.M. de Goeij, The Y87 / Sr87m Generator: a new approach to its preparation. in Progress in Radiopharmacy. Developments in Nuclear Medicine, vol. 10, ed. by P.H. Cox, S.J. Mather, C.B. Sampson, C.R. Lazarus (Springer, Dordrecht, 1986). https://doi.org/10.1007/978-94-009-4297-4_4
D. Sachdev, N. Porile, L. Yaffe, Reactions of 88Sr with protons of energies 7-85 MeV. Can. J. Chem. 45, 1149–1160 (2011)
K. Kettern, K.H. Linse, S. Spellerberg, H. Coenen, S. Qaim, Radiochemical studies relevant to the production of 86 Y and 88 Y at a small-sized cyclotron. Radiochim. Acta 90, 845–849 (2002)
A. Elbinawi, M. Al-abyad, I. Bashter, U. Seddik, F. Ditrói, Excitation function of proton induced nuclear reaction on strontium: Special relevance to the production of 88Y. Appl. Radiat. Isot. 140, 272–277 (2018)
R. Michel, R. Bodemann, H. Busemann, R. Daunke, M. Gloris, H.J. Lange, B. Klug, A. Krins, I. Leya, M. Lüpke, S. Neumann, H. Reinhardt, M. Schnatz-Büttgen, U. Herpers, T. Schiekel, F. Sudbrock, B. Holmqvist, H. Condé, P. Malmborg, M. Suter, B. Dittrich-Hannen, P.W. Kubik, H.A. Synal, D. Filges, Cross sections for the production of residual nuclides by low- and medium-energy protons from the target elements C, N, O, Mg, Al, Si, Ca, Ti, V, Mn, Fe, Co, Ni, Cu, Sr, Y, Zr, Nb, Ba and Au. Nucl. Instrum. Methods Phys. Res., Sect. B 129, 153–193 (1997)
A. Hermanne, F. Tárkányi, S. Takács, Production of medically relevant radionuclides with medium energy deuterons, in International Conference on Nuclear Data for Science and Technology, ed. by O. Bersillon, F. Gunsing, E. Bange EDP Sciences Nice, France, April 22-27. 2007, pp. 1355-1358 (2008)
F. Tárkányi, A. Hermanne, F. Ditrói, S. Takács, Z. Szücs, K. Brezovcsik, Investigation of activation cross sections for deuteron induced reactions on strontium up to 50MeV. Appl. Radiat. Isot. 127, 16–25 (2017)
G. Kiss, T. Rauscher, G. Gyürky, A. Simon, Z. Fülöp, E. Somorjai, Coulomb suppression of the stellar enhancement factor. Phys. Rev. Lett. 101, 191101 (2008)
T. Rauscher, G.G. Kiss, G. Gyürky, A. Simon, Z. Fülöp, E. Somorjai, Suppression of the stellar enhancement factor and the reaction \(^{85} \rm Rb\mathit{ \text{(p, n) }^{85} \rm Sr}\). Phys. Rev. C 80, 035801 (2009)
S. Kastleiner, S.M. Qaim, F.M. Nortier, G. Blessing, T.N. van der Walt, H.H. Coenen, Excitation functions of 85Rb(p, xn)85m, g,83,82,81Sr reactions up to 100MeV: integral tests of cross section data, comparison of production routes of 83Sr and thick target yield of 82Sr. Appl. Radiat. Isot. 56, 685–695 (2002)
M.C. Lagunas-Solar, Radionuclide production with \(\%3e\)70-MeV proton accelerators: current and future prospects. Nucl. Instrum. Methods Phys. Res. Sect. B 69, 452–462 (1992)
A. Grütter, Cross sections for reactions with 593 and 540 MeV protons in aluminium, arsenic, bromine, rubidium and yttrium. Int. J. Appl. Radiat. Isot. 33, 725–732 (1982)
S.M. Qaim, G.F. Steyn, I. Spahn, S. Spellerberg, T.N. van der Walt, H.H. Coenen, Yield and purity of 82Sr produced via the natRb(p, xn)82Sr process. Appl. Radiat. Isot. 65, 247–252 (2007)
E. Gilabert, B. Lavielle, S. Neumann, M. Gloris, R. Michel, T. Schiekel, F. Sudbrock, U. Herpers, Cross sections for the proton-induced production of krypton isotopes from Rb, Sr, Y, and Zr for energies up to 1600 MeV. Nucl. Instrum. Methods Phys. Res. Sect. B 145, 293–319 (1998)
E.Z. Buthelezi, F. Nortier, I.W. Schroeder, Excitation functions for the production of Sr-82 by proton bombardment of Rb-nat at energies up to 100 MeV. Appl. Radiat. Isot. 64, 915–924 (2006)
F. Tárkányi, S.M. Qaim, G. Stöcklin, Excitation-functions of high-energy \(^{{3}}\text{ He }\) and alpha-particle induced nuclear-reactions on natural krypton with special reference to the production of \(^{{82}}\text{ Sr }\). Appl. Radiat. Isot. 41, 91–95 (1990)
H. Takayoshi, N. Hiroshi, Y. Yasukazu, T. Hirokatsu, H. Hiromi, K. Yoshiyuki, Excitation functions of proton induced nuclear reactions on 85Rb. Int. J. Appl. Radiat. Isot. 31, 141–151 (1980)
F.T. Tárkányi, A.V. Ignatyuk, A. Hermanne, R. Capote, B.V. Carlson, J.W. Engle, M.A. Kellett, T. Kibédi, G.N. Kim, F.G. Kondev, M. Hussain, O. Lebeda, A. Luca, Y. Nagai, H. Naik, A.L. Nichols, F.M. Nortier, S.V. Suryanarayana, S. Takács, M. Verpelli, Recommended nuclear data for medical radioisotope production: diagnostic positron emitters. J. Radioanal. Nucl. Chem. 319, 533–666 (2019)
C. Deptula, V.A. Khalkin, S.H. Kim, O. Knotek, V.A. Konov, P. Mikecz, L.M. Poponenkova, E. Rurarz, N.G. Zaitseva, Excitation functions and yields for medically generator Sr82-Rb82, Xe123-I123 and Bi201-Pb201-Tl201 obtained with 100 MeV protons. Nukleonika 35, 3–47 (1990)
V. Zagryadskii, S. Latushkin, V. Novikov, A. Ogloblin, V. Unezhev, D. Chuvilin, A. Shatrov, D. Yartsev, Experimental determination of Kr-80, Kr-82, Kr-83(alpha, xn)Sr-82 cross sections for reaction threshold to 60 MeV alpha-particles. Atom Energy + 110, 99–103 (2011)
Acknowledgements
This work was done in the frame of MTA-FWO (Vlaanderen) research projects. The authors acknowledge the support of research projects and of their respective institutions in providing the materials and the facilities for this work. This work was also partly supported (F. Ditroi) by IAEA RER Project 1020 and by IAEA CRP F22069.
Funding
Open Access funding provided by ELKH Institute for Nuclear Research
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Aurora Tumino
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tárkányi, F., Hermanne, A., Ditrói, F. et al. Activation cross section data of deuteron induced nuclear reactions on rubidium up to 50 MeV. Eur. Phys. J. A 57, 21 (2021). https://doi.org/10.1140/epja/s10050-020-00327-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epja/s10050-020-00327-1