Chiral phase transition in the linear sigma model within Hartree factorization under $(1-q)$ expansion and free particle approximation in the Tsallis nonextensive statistics

Abstract

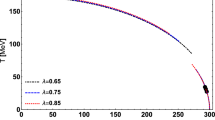
We studied chiral phase transition in the linear sigma model within the Tsallis nonextensive statistics under some approximations. The statistics has two parameters: the temperature T and the entropic parameter q. The normalized q-expectation value and the physical temperature $T_{\mathrm {ph}}$ were employed in this study. The normalized q-expectation value was expanded as a series of the value $(1-q)$, where the absolute value $|1-q|$ is the measure of the deviation from the BG statistics. We applied the Hartree factorization and the free particle approximation, and obtained the equations for the condensate, the sigma mass, and the pion mass. The physical temperature dependences of these quantities were obtained numerically. We found following facts. The condensate at q is smaller than that at $q'$ for $q>q'$. The sigma mass at q is lighter than that at $q'$ for $q>q'$ at low physical temperature, and the sigma mass at q is heavier than that at $q'$ for $q>q'$ at high physical temperature. The pion mass at q is heavier than that at $q'$ for $q>q'$. The difference between the pion masses at different values of q is small for $T_{\mathrm {ph}}\le 200$ MeV. In other words, the condensate and the sigma mass are affected by the Tsallis nonextensive statistics with $|1-q| = 0.1$, and the pion mass is also affected by the statistics of $|1-q|=0.1$ except for $T_{\mathrm {ph}}\le 200$ MeV.

Appendices

Hartree factorization

In this appendix, we summarize the Hartree factorization [48, 49] for this paper to be self-contained. The basic idea is to represent the operators in quadratic expression.

1.1 Single Field

We begin with a single field $\varphi$ with the constraint $\langle \varphi \rangle =0$. The operator $\varphi ^{2n}$ is approximated by the following form.

$$\begin{aligned} \varphi ^{2n} \sim A (\langle \varphi ^2 \rangle )^{n-1} \varphi ^2 + B (\langle \varphi ^2 \rangle )^{n-1} \langle \varphi \rangle \varphi + C (\langle \varphi ^2 \rangle )^{n} . \end{aligned}$$

(36)

The second term vanishes because of the constraint $\langle \varphi \rangle =0$. We focus on the coefficients A and C.

The coefficient A is obtained by counting the combination of $\varphi$. The number of pairs constructed from $\varphi ^{2n}$ is given by ${}_{2n} C_2$. It is possible to do this procedure recursively, we find the combination of $(n-1)$ pairs

$$\begin{aligned} {}_{2n}C_2 \times {}_{2n-2}C_2 \times \cdots \times {}_{4}C_2 = \frac{(2n)(2n-1)\cdots 3 }{2^{n-1}} = \frac{(2n)!}{2^n} . \end{aligned}$$

(37)

This is over-counting, and we must divide the value by the number of the orders of $(n-1)$ pairs. Therefore, we get

$$\begin{aligned} A = \frac{(2n)!}{2^n (n-1)! } . \end{aligned}$$

(38)

Next, we approximate $\langle \varphi ^{2n} \rangle$ by $E \langle \varphi ^2 \rangle ^n$. The coefficient E is obtained in the same manner:

$$\begin{aligned} E = \frac{(2n)!}{2^n n! } . \end{aligned}$$

(39)

We obtain the coefficient C by taking the expectation value of Eq. (36). This gives

$$\begin{aligned} \langle \varphi ^{2n} \rangle \sim E \langle \varphi ^2 \rangle ^n = (A+C) \langle \varphi ^2 \rangle ^n . \end{aligned}$$

(40)

The coefficient C is

$$\begin{aligned} C = - \frac{(2n)! (n-1)}{2^n n!} . \end{aligned}$$

(41)

The Hartree factorization of $\varphi ^{2n}$ is given by

$$\begin{aligned} \varphi ^{2n}&\sim \frac{(2n)!}{2^n (n-1)!} (\langle \varphi ^2 \rangle )^{n-1} \varphi ^2 - \frac{(2n)! (n-1)}{2^n n!} (\langle \varphi ^2 \rangle )^{n} . \end{aligned}$$

(42)

For example, the Hartree factorization of $\varphi ^4$ is given by

$$\begin{aligned} \varphi ^{4} \sim 6 \langle \varphi ^2 \rangle \varphi ^2 - 3 (\langle \varphi ^2 \rangle )^{2} . \end{aligned}$$

(43)

In the same way, we obtain the Hartree factorization of $\varphi ^{2n+1}$:

$$\begin{aligned} \varphi ^{2n+1} \sim \frac{(2n+1)!}{2^n n!} (\langle \varphi ^2 \rangle )^n \varphi . \end{aligned}$$

(44)

This gives the Hartree factorization of $\varphi ^3$:

$$\begin{aligned} \varphi ^{3} \sim 3 \langle \varphi ^2 \rangle \varphi . \end{aligned}$$

(45)

1.2 Two Fields

Next, we treat two fields, $\varphi$ and $\psi$, with $\langle \varphi \rangle =0$, $\langle \psi \rangle =0$, and $\langle \varphi \psi \rangle =0$. The Hartree factorization of $\varphi ^{2m} \psi ^{2n}$ and $\varphi ^{2m} \psi ^{2n+1}$ are derived in the similar way.

The Hartree factorization of $\varphi ^{2m} \psi ^{2n}$ is given by the following form.

$$\begin{aligned} \varphi ^{2m} \psi ^{2n} \sim&\varphi ^{2} {\mathrm { terms}} + \psi ^{2} {\mathrm { terms}} + \varphi \psi {\mathrm { terms}} \nonumber \\&+ \langle \varphi ^2 \rangle ^{m} \langle \psi ^2 \rangle ^{n} {\mathrm { terms}} . \end{aligned}$$

(46)

The coefficients of $\varphi ^2$, $\psi ^2$, and $\varphi \psi$ are constructed from $\langle \varphi ^2 \rangle$, $\langle \psi ^2 \rangle$, and $\langle \varphi \psi \rangle$. For example, the first term of Eq. (46) may contain several terms such as $\langle \varphi ^2 \rangle ^{m-2} \langle \psi ^2 \rangle ^{n-1} \langle \varphi \psi \rangle ^2 \varphi ^{2}$. The term $\langle \varphi ^2 \rangle ^{m-2} \langle \psi ^2 \rangle ^{n-1} \langle \varphi \psi \rangle ^2 \varphi ^{2}$ vanishes because of the assumption $\langle \varphi \psi \rangle =0$. The remaining form of the first term is $\langle \varphi ^2 \rangle ^{m-1} \langle \psi ^2 \rangle ^{n}\varphi ^{2}$. Therefore, the Hartree factorization under the present assumptions is given by

$$\begin{aligned} \varphi ^{2m} \psi ^{2n}&\sim A (\langle \varphi ^2 \rangle )^{m-1} (\langle \psi ^{2} \rangle )^{n} \varphi ^{2} \nonumber \\&\quad + B (\langle \varphi ^2 \rangle )^{m} (\langle \psi ^{2} \rangle )^{n-1} \psi ^{2} + C (\langle \varphi ^2 \rangle )^{m} (\langle \psi ^2 \rangle )^{n} . \end{aligned}$$

(47)

The coefficient A in Eq. (47) is obtained in the similar way. The coefficient A is given by

$$\begin{aligned} A = \frac{(2m)!}{2^m (m-1)!} \times \frac{(2n)!}{2^n n!} . \end{aligned}$$

(48)

The coefficient B in Eq. (47) is given by

$$\begin{aligned} B = \frac{(2m)!}{2^m m!} \times \frac{(2n)!}{2^n (n-1)!} . \end{aligned}$$

(49)

The term $\langle \varphi ^{2m} \psi ^{2n} \rangle$ is approximated as $E (\langle \varphi ^{2} \rangle )^m (\langle \psi ^{2} \rangle )^n$. The coefficient E is given by

$$\begin{aligned} E = \frac{(2m)!}{2^m m!} \times \frac{(2n)!}{2^n n!} . \end{aligned}$$

(50)

We obtain the coefficient C by taking the average of Eq. (47). We get the equation

$$\begin{aligned} E = A+B+C. \end{aligned}$$

(51)

The final representation of the Hartree factorization of $\varphi ^{2m} \psi ^{2n}$ with $\langle \varphi \rangle =\langle \psi \rangle =\langle \varphi \psi \rangle =0$ is

$$\begin{aligned} \varphi ^{2m} \psi ^{2n}&\sim \left( \frac{(2m)! }{2^m (m-1)!} \frac{(2n)!}{2^n n!} \right) (\langle \varphi ^2 \rangle )^{m-1} (\langle \psi ^{2} \rangle )^{n} \varphi ^{2} \nonumber \\&\quad + \left( \frac{(2m)!}{2^m m!} \frac{(2n)!}{2^n (n-1)!} \right) (\langle \varphi ^2 \rangle )^{m} (\langle \psi ^{2} \rangle )^{n-1} \psi ^{2} \nonumber \\&\quad - (m+n-1) \left( \frac{(2m)!}{2^m m!} \frac{(2n)!}{2^n n!} \right) (\langle \varphi ^2 \rangle )^{m} (\langle \psi ^2 \rangle )^{n} . \end{aligned}$$

(52)

The Hartree factorization of $\varphi ^2 \psi ^2$ is given with Eq. (52) with $m=n=1$. The factorization is

$$\begin{aligned} \varphi ^2 \psi ^2 \sim \varphi ^2 \langle \psi ^2 \rangle + \langle \varphi ^2 \rangle \psi ^2 - \langle \varphi ^2 \rangle \langle \psi ^2 \rangle . \end{aligned}$$

(53)

We obtain the Hartree factorization of $\varphi ^{2m} \psi ^{2n+1}$, as in the case of $\varphi ^{2m} \psi ^{2n}$. The Hartree factorization of $\varphi ^{2m} \psi ^{2n+1}$ with the assumptions $\langle \varphi \rangle =\langle \psi \rangle =\langle \varphi \psi \rangle =0$ is given by

$$\begin{aligned} \varphi ^{2m} \psi ^{2n+1} \sim \frac{(2m)!}{2^m m!} \frac{(2n+1)!}{2^n n!} (\langle \varphi ^2 \rangle )^m (\langle \psi ^2 \rangle )^n \psi . \end{aligned}$$

(54)

This result gives the factorization of $\varphi ^2 \psi$:

$$\begin{aligned} \varphi ^2 \psi \sim \langle \varphi ^2 \rangle \psi . \end{aligned}$$

(55)

The above discussion will be extended to multi-fields.

Limits of Tsallis distribution

In this appendix, we discuss two limits of Tsallis distribution: the temperature approaches zero and the entropic parameter q approaches one.

We treat the following type of Tsallis distribution,

$$\begin{aligned} f(E_i; T_{\mathrm {ph}}, q) = \frac{1}{Z} \Big [ 1- (1-q) \beta _{\mathrm {ph}}(E_i -\overline{E}) \Big ]_{+}^{\frac{1}{1-q}} , \end{aligned}$$

(56)

where Z is the normalization constant, $\overline{E}$ is the average of the energy, and $\beta _{\mathrm {ph}}$ is $1/T_{\mathrm {ph}}$. The notation $[x]_{+}$ indicates x for $x \ge 0$ and 0 for $x < 0$.

We use the notation $E_i$ which is the energy level labeled with the index i, and $E_i$ satisfies the following relation:

$$\begin{aligned} E_0< E_1< \cdots< E_p < \cdots . \end{aligned}$$

(57)

We can employ the escort average:

$$\begin{aligned} \overline{E}= \frac{\sum _i E_i ( f(E_i; T_{\mathrm {ph}}, q) )^q}{\sum _i ( f(E_i; T_{\mathrm {ph}}, q) )^q} . \end{aligned}$$

(58)

We can employ the conventional average instead of the escort average:

$$\begin{aligned} \overline{E}= \frac{\sum _i E_i f(E_i; T_{\mathrm {ph}}, q) }{\sum _i f(E_i; T_{\mathrm {ph}}, q) } . \end{aligned}$$

(59)

Firstly, we treat the quantity, ${\lim \limits _{\beta _{\mathrm {ph}}{\rightarrow } \infty } \lim \limits _{q{\rightarrow }1} f(E_i{;} T_{\mathrm {ph}}, q)}$. We assume that the average energy $\overline{E}$ does not show the singularity as q approaches one. That is, $\overline{E}$ converges to a value. Under the assumption, we have

$$\begin{aligned} \lim _{q \rightarrow 1} f(E_i; T_{\mathrm {ph}}, q)&= \frac{1}{Z_{q=1}} \exp (-\beta _{\mathrm {ph}}(E_i - \overline{E}_{q=1}) ) , \end{aligned}$$

(60)

where $Z_{q=1}$ is the value of Z at $q=1$ and $\overline{E}_{q=1}$ is the value of $\overline{E}$ at $q=1$. This is the Boltzmann-Gibbs distribution, and therefore the distribution has the following property:

$$\begin{aligned} \lim _{T_{\mathrm {ph}}\rightarrow +0} \lim _{q \rightarrow 1} f(E_i; T_{\mathrm {ph}}, q) = \left\{ \begin{array}{ll} 1 &{} \qquad (E_i = E_0) \\ 0 &{} \qquad (E_i > E_0) \end{array} \right. . \end{aligned}$$

(61)

Secondly, we treat the quantity, ${ \lim \limits _{q{\rightarrow } 1}\lim \limits _{\beta _{\mathrm {ph}}{\rightarrow } \infty } f(E_i{;} T_{\mathrm {ph}}{,} q)}$. The quantity, ${ \lim _{\beta _{\mathrm {ph}}\rightarrow \infty } f(E_i; T_{\mathrm {ph}}, q)}$, is discussed for $q<1$ and $q>1$.

For $q<1$, we assume a certain expectation value $\overline{E}$. The state that satisfies $1- (1-q) \beta _{\mathrm {ph}}(E_i -\overline{E}) \ge 0$ affects the expectation value. This equation is rewritten as

$$\begin{aligned} E_i - \overline{E}\le \frac{1}{(1-q) \beta _{\mathrm {ph}}} . \end{aligned}$$

(62)

Therefore, in the limit that $\beta _{\mathrm {ph}}$ approaches infinity, we have the condition:

$$\begin{aligned} E_i \le \overline{E}. \end{aligned}$$

(63)

The notation $E_h$ denotes the highest energy level that satisfies the above condition. The value $E_h$ satisfies $E_h \le \overline{E}$. The average $\overline{E}$ is not larger than $E_h$, therefore the expectation value $\overline{E}$ is equal to $E_h$: $\overline{E}= E_h$. However, the average $\overline{E}$ is less than $E_h$ when the energy level $E_i$ that satisfies $E_i < E_h$ exists. This contradiction comes from the assumption that there is the energy level $E_i$ that satisfies $E_i < E_h$. This indicates that $E_h$ is the lowest energy level: $E_h =E_0$. This fact implies that $\overline{E}$ is equal to $E_0$ in the limit, $\beta _{\mathrm {ph}}\rightarrow \infty$, for $q<1$. The distribution in the limit is

$$\begin{aligned} \lim _{T_{\mathrm {ph}}\rightarrow +0} f(E_i; T_{\mathrm {ph}}, q<1) = \left\{ \begin{array}{ll} 1 &{} \quad (E_i = E_0) \\ 0 &{} \quad (E_i > E_0) \end{array}\right. . \end{aligned}$$

(64)

For $q>1$, the following condition should be satisfied: $1 + (q-1) \beta _{\mathrm {ph}}(E_i - \overline{E}) \ge 0.$ This condition is rewritten as

$$\begin{aligned} E_i - \overline{E}\ge - \frac{1}{(q-1) \beta _{\mathrm {ph}}} . \end{aligned}$$

(65)

In the limit, $\beta _{\mathrm {ph}}\rightarrow \infty$, the condition is

$$\begin{aligned} E_i \ge \overline{E}. \end{aligned}$$

(66)

It is not easy to solve the self-consistent equation, Eq. (58) or Eq. (59). Therefore, we assume that $\overline{E}$ is a certain value $\overline{E}^{(0)}$. The state that satisfies $E_i > \overline{E}^{(0)}$ does not affect the expectation value in the limit, $\beta _{\mathrm {ph}}\rightarrow \infty$, because $f(E_i, T_{\mathrm {ph}}, q)$ is proportional to $1/(1+(q-1)\beta _{\mathrm {ph}}(E_i - \overline{E}^{(0)}))^{1/(q-1)}$. The state that satisfies $E_i < \overline{E}^{(0)}$ does not satisfies the condition. Therefore, the value $\overline{E}^{(0)}$ is equal to $E_{l^{(0)}}$ which is the lowest energy level that satisfies the condition.

We recalculate the right-hand side of Eq. (58) or Eq. (59). The value $\overline{E}$ in the right-hand side is set to $\overline{E}^{(0)}$, and the value $\overline{E}$ in the left-hand side is obtained. The notation $\overline{E}^{(1)}$ denotes $\overline{E}$ in the left-hand side, hereafter. The state i with $E_i>\overline{E}^{(0)}$ does not contribute to the expectation value, and therefore $\overline{E}^{(1)} \le \overline{E}^{(0)}=E_{l^{(0)}}$. It seems that the state i with $E_i < \overline{E}^{(0)}$ does not affect the expectation value. However, the condition should be replaced with $E_i \ge \overline{E}^{(1)}$ when $\overline{E}^{(1)}$ is less than $\overline{E}^{(0)}$, and the state with $i<l^{(0)}$ probably affects the expectation value. With the same reason for $\overline{E}^{(0)}$, $\overline{E}^{(1)}$ is equal to $E_{l^{(1)}}$, where $E_{l^{(1)}}$ is the lowest energy level of $E_{i}$ that satisfies the replaced condition.

Above discussion can be repeated with the average value $\overline{E}^{(1)}$. Therefore, we expect the following sequence:

$$\begin{aligned} \overline{E}^{(0)}> \overline{E}^{(1)}> \overline{E}^{(2)} > \cdots \ge E_0 . \end{aligned}$$

(67)

As a result, we have $\overline{E}= E_0$ in the limit, $\beta _{\mathrm {ph}}\rightarrow \infty$, for $q>1$. Strictly speaking, above sequence might not be satisfied because the case of $\overline{E}^{(j+1)} = \overline{E}^{(j)}$ might occur. Except for such improbable cases, we expect the following relation because $\overline{E}= E_0$ satisfies the self-consistent equation in the limit, $\beta _{\mathrm {ph}}\rightarrow \infty$:

$$\begin{aligned} \lim _{T_{\mathrm {ph}}\rightarrow +0} f(E_i; T_{\mathrm {ph}}, q>1) = \left\{ \begin{array}{ll} 1 &{} \quad (E_i = E_0) \\ 0 &{} \quad (E_i > E_0) \end{array}\right. . \end{aligned}$$

(68)

These results, Eqs. (64) and (68), indicate that

$$\begin{aligned} \lim _{T_{\mathrm {ph}}\rightarrow +0} f(E_i; T_{\mathrm {ph}}, q) = \left\{ \begin{array}{ll} 1 &{} \quad (E_i = E_0) \\ 0 &{} \quad (E_i > E_0) \end{array}\right. . \end{aligned}$$

(69)

Therefore, we have

$$\begin{aligned} \lim _{q \rightarrow 1} \lim _{T_{\mathrm {ph}}\rightarrow +0} f(E_i; T_{\mathrm {ph}}, q) = \left\{ \begin{array}{ll} 1 &{} \quad (E_i = E_0) \\ 0 &{} \quad (E_i > E_0) \end{array}\right. . \end{aligned}$$

(70)

The right-hand side of Eq. (70) is equivalent to the right-hand side of Eq. (61).