Abstract
In this paper we present a review of progress in addressing the challenge to understand and describe the vast complexity and multi-level organisation associated with biological systems. We begin with a review of past and current approaches, key lessons, and unresolved challenges, which require a new conceptual framework to address them. After summarizing the core of the problem, which is linked to computational complexity, we review recent developments within the theoretical framework of scale relativity, which offers new insights into the emergence of structure and function (at multiple scales), providing a new integrative approach to biological systems. The theoretical framework describes the critical role of thermodynamics and quantum vacuum fluctuations in the emergence of charge-induced macroscopic quantum fields (effectively a new quantum field theory) at multiple scales, which underpin a macroscopic quantum description of biological systems as a complex exemplar of condensed matter. The theory is validated through a new biomimetic experimental approach, which leads to the emergence of plant and individual cell-like structures with the intrinsic capacity to divide, differentiate and form multicellular structures. We discuss how this theoretical framework could be applied to extend our understanding of cardiac systems biology and physiology, and challenges such as cancer and neurodegenerative disease. We also consider the potential of these new insights to support a new approach to the development of emerging quantum technologies.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The purpose of this review is to provide an update on progress made globally over the past decade in integrative systems biology, physiology and medicine, and in our theoretical and experimental research programme dedicated to the development of a scale-relative biology. It builds upon a large corpus of previous research papers, reviews and books in which we introduced and discussed advances of this fast-growing research field and presented the rationale and motivation for exploring the scale-relativity theory framework in biology. As a background, we refer the reader in particular to our foundational review papers and books introducing scale-relativity theory in integrative systems biology [1, 2], introducing the principle of biological relativity and providing an overview of its significance in evolution and physiology [3, 4] and the comprehensive theoretical and mathematical foundations of scale-relativity theory in physics and its applications to other sciences including biology [5, 6].
In Sect. 2 we review recent advances in systems biology and systems medicine, and how they impact physiology, biotechnology and synthetic biology. Section 3 considers the limitations of current theoretical and computational frameworks and methods to facilitate integration across the vast complexity and range of scales associated with biological systems, introducing the principle of biological relativity. In Sect. 4 we explain why the theoretical framework of scale relativity offers a possible solution to the challenge of computational complexity and multi-scale modelling in biological systems, thus complementing other proposed components of a future integrated theory of biology. Section 5 presents a detailed account of the physical principles that govern the emergence of biological structures, supported by recent experimental results, which represent examples of the emergence of macroscopic quantum systems in the context of scale-relativity theory. In Sect. 6 we review the impact of these results on our understanding of the physics of cell division, whilst Sect. 7 considers their generic potential implications in biological systems. In Sect. 8 we briefly highlight new insights into the emergence of life. Finally, we describe in Sect. 9 how we plan to apply the scale-relative biology framework to cardiac systems biology and physiology and provide in Sect. 10 our conclusions and perspectives for the development of future work.
2 Systems and synthetic biology are revisiting physiology and biotechnology
The past two decades have witnessed a dynamic resurgence of systems approaches in biology, under the umbrella of “systems and synthetic biology”. This is reflected in the number of attempts to define this burgeoning field from a variety of conceptual, historical or technical perspectives. Through a systematic review of founding papers up to 2010 [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39], we concluded that this body of work essentially represented a revisit of earlier, incompletely successful attempts at developing formal theories for modelling biological complexity in morphogenesis and metabolic networks taking into account their variability and non-linear dynamics [40,41,42,43,44,45,46,47,48,49]. During the past decade, several interesting trans-disciplinary efforts have been developed to overcome the difficulties encountered initially, such as those reviewed in a special issue on new approaches to a theory of organisms [50], advances in mathematical biology and physiology [51,52,53,54] or a recent discussion on the new physics needed to probe the origin of life [55, 56]. The recent advances in genomics and bioinformatics have leveraged high-throughput experimental and computational platforms for the collection of comprehensive data on the genome, transcriptome, proteome, metabolome and microbiome. The analysis of these data has benefitted from concepts and methods developed in systems theory, engineering sciences, and the various mathematical and computational tools available for modelling of structure-function relationships and dynamics.
A focus on functional properties occurring at multiple levels in biological systems represents a rejuvenation of physiology and biotechnology through mathematics, computer science and engineering, challenging the dominant paradigm of molecular biology based on analytical reductionism. During the last ten years, systems approaches have thus started to pervade all areas of animal, human, plant and microbial biology as reflected in a very extensive and fast-growing literature and numerous reviews, as summarised in recent reference texbooks [57, 58].
From both a conceptual and practical point of view, we consider systems biology as an integrative research strategy, designed to tackle the complexity of biological systems and their behaviour at all levels of organisation (from molecules, cells and organs to organisms and ecosystems) in normal and perturbed conditions. It deliberately combines analytical reductive and integrative systemic approaches [59,60,61,62]. Taking advantage of this conceptual duality in a pragmatic manner, it aims at developing a quantitative and integrated understanding of biological structures and functions as system properties differing from those of the individual interacting components.
Systems biology approaches operate through iterations between theory and practice, integrating large datasets collected with various targeted and global measurement technologies. This enables formulation of predictive mathematical and computational models as simplified representations of functional and regulatory networks. They have to be as complex as necessary to account for specific details, whilst being computationally tractable as well as providing a reasonable and useful answer to the question addressed.
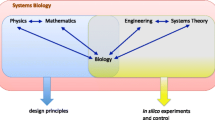
Biological hypotheses derived from such models are tested computationally and experimentally through perturbation experiments, to help refine the models iteratively. As indicated in Fig. 1, systems biology approaches, whether they are data or model-driven, must be combined into question-driven inquiries, to take into account causation occurring between organisational levels [1, 3, 15, 63,64,65,66,67,68].
In this context, evolution, development, physiology and disease are viewed as dynamic processes that vary structurally and functionally on widely different scales in space and time between biological states that are constrained by the functional interrelationships between pathway and network components, as well as the influences of the physical environment [54, 69]. Indeed, it is now widely accepted that “nothing in biology makes sense except in the light of evolution” [70, 71], a notion that has important consequences from an operational point of view for defining life and the historical conditions of its emergence [72,73,74]. Grounded on these conceptual and methodological advances, systems biology forms the basis for a more profound understanding of biological systems properties, and an extension of genetic engineering into synthetic biology: designing and building biological systems with novel properties from a set of pre-defined modular components [75,76,77,78,79,80,81], which has developed as an active biotechnology engineering field on its own over the past decade [82, 83]. It must be stressed, however, that while some of the synthetic constructs thus developed are inspired by identified biological properties, many reflect on engineering principles that most likely have never been implemented in real life forms, simply because the extensive biological variability that developed through evolution represents only a relatively small subset of the virtually infinite possible combinations of life building blocks and environmental influences into actual functionally organised biological systems.
A successful development of systems and synthetic biology approaches, and their application to human biology and medicine in a predictive, preventive, personalised and participatory manner led to the emergence of “systems medicine” during the past ten years. Its effective implementation requires improved interaction between scientific and engineering disciplines, and improved sharing of data, tools and models [34, 84,85,86,87,88,89,90,91,92,93]. Within this context, the literature has grown very rapidly, as witnessed by hundreds of review articles and a number of successful use cases combining high-throughput functional genomics platforms to process biological samples and analyse the data produced with bioinformatics, computational and mathematical modelling and simulation tools, including advanced machine learning methods [94,95,96,97,98,99,100,101]. As summarised in a comprehensive reference texbook [102], case studies include neurological, cancer, respiratory, allergic and infectious diseases supporting pharmaceutical research and development to tackle patient needs.
A prominent example of the impact of systems biology in advancing our understanding of the underlying mechanisms of disease development is reported in chronic obstructive pulmonary disease, one of the leading cause of morbidity worldwide. Studies across multiple molecular, cellular, tissular and organ levels indicate a significant impact on clinical practice, patient and healthcare management [103,104,105,106,107]. The experience gained in such projects highlights the need for a profound revision of the training of life scientists and medical doctors to accomodate the cross-disciplinary nature of systems medicine [108,109,110].
This work also pointed to the need to better define and understand healthy states, which serve as reference for preventive measures before disease onset. A wide range of wearable health devices connected through the “Internet of Things” [111, 112] for real time measurement of parameters related to physiology (e.g. blood pressure, body weight), lifestyle practices and environmental exposures (e.g. nutrition, exercise, sleep and stress), has provided the opportunity to overcome the limitation of conventional clinical assays and advanced functional genomics measurements, which are generally limited to snapshots or at best limited time series. Initial work using either category alone has demonstrated the ability to detect early deviations from normal individual states before appearance of clinical signs of disease onset [113, 114]. These pioneering examples laid the foundation for the development of a “science of wellness”, leveraging connected devices and advanced intelligence methods for data analysis and representation to support disease and health maps [115,116,117,118,119,120,121] raising novel challenges for disease definition and deployment of integrated care for both individuals and entire populations [122,123,124,125,126]. Thus, understanding biological systems and treating diseases can now be envisioned through the identification and manipulation of global perturbed networks rather than unique failing components.
3 A grand challenge of systems biology: multi-scale integration
In recent years the field has thus made a number of significant advances, including extracting functional and regulatory order through integration of multiple functional genomics data, literature mining and systemic modelling, supported by high-throughput technologies, high-resolution imaging, and mathematical and computational modelling formalisms, which are the focus of intense community efforts for data integration and standardisation. The objective is to make sense of the wealth of big datasets generated [34, 84, 127,128,129,130,131]. For example, progress has been made in the development of a theory of robustness and fragility, and assessment of the role of modularity and coupling of networks and pathways in biological systems [15, 65, 132,133,134,135,136].
Spatial and temporal scales in the Human Physiome Project [144]. According to the principle of biological relativity, all arrows should be considered as bidirectional
Importantly, a variety of experimental schemes have highlighted the role of stochastic fluctuations or “biological noise” at the molecular, modular or cellular levels in driving the behaviour, development and evolution of biological systems [59, 137,138,139,140,141,142].
At another level, realistic integrated models of functioning heart, lung and muscle have been developed in the frame of the Physiome Project and are being extended in the Virtual Human Physiological Project [84, 143,144,145,146,147,148,149,150,151,152,153,154].
Systems biology approaches start to impact on the drug discovery process in the biotechnology and pharmaceutical industry. However, in each of its implementations, the systems biology research strategy relies on ad hoc combinations of measurement technologies and formalisms for mathematical modelling.
Although multiple and wide-ranging structural organisation levels and time frames are recognised as essential features of living systems, the use of various, often incompatible mathematical and computer formalism makes data integration and model comparison or coupling difficult if not impossible [1, 11, 16, 19, 24, 51, 155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175]. For example, deterministic and stochastic, continuous and discrete modelling are being used to study e.g. morphogenesis with agent-based methods and organ structure with finite element lattices, cellular pathways with Boolean and logic networks, molecular reactions with partial and ordinary differential equations (Fig. 2).
The increasing complexity of models make fine, coarse and detailed numerical simulations computationally intractable, despite the exponential growth of computing power.
On-going attempts to overcome these limitations aim mostly at the development of an integrative computational framework, few of them tackling it at a more conceptual level, taking into account concepts from systems engineering, ecology, complexity and critical transitions that in their extended forms are the basis of a theory of organisms that takes into account the fact that multiple levels of organisation are entangled in biological systems as the result of their history [28, 90, 176,177,178,179]. For example, allometric scale laws that relate mass and energy metabolism according to quarter-power laws have been uncovered since the 1930s, and recently shown to extend across 27 orders of magnitude of size from molecules to entire organisms. This suggests elements for a unifying theory of biological structure and organisation, based on power laws across multiple scales, but without relating them to fundamental principles from which they can be derived [180,181,182,183,184]. Although such power laws appear also pervasive in a large array of human-related activities including the development of cities, economies, and companies [184], their universality in biological systems when assessed under carefully controlled conditions has not been confirmed [185,186,187].
4 A solution to the challenge of computational complexity and multi-scale modelling
Multi-scale integration thus represents a frontier challenge that needs to be addressed if systems biology is to develop to its full potential. Our assessment is that most mathematical and physical theories are unsuitable, as they do not properly address the space and time scales characteristic of biological systems and are unable to make experimentally testable predictions relevant to the most fundamental biological questions such as the origin of biological structures and of life itself. A key exception to this is the theory of scale relativity, which represents a theory of self-organisation across all scales in nature.
Within the present review we provide an update on theoretical and experimental developments, within the framework of scale relativity, which are valid not just for biological systems, but condensed matter in general. This represents an important step, establishing the principle that biological systems are not privileged, but can be regarded as complex exemplars of condensed matter.
The fundamental challenge in modelling biological systems relates to computational complexity. Due to intrinsic disorder (chaos) in a biological system, modelling at even the smallest scales (e.g., the folding of an intrinsically disordered protein [188]) can prove intractable. It therefore follows that it is impossible to model a complex biological system at all scales simultaneously. A solution to this challenge requires a systematic process of renormalisation at each scale, to reduce computation complexity. The theory of scale relativity offers such an approach and we see the beginnings of a coherent theoretical framework, which allow one to take into account effects occurring within and across multiple scales and organisational levels. Without such an approach, the predictive power of systems biology and its application to address fundamental and medical questions will remain limited.
For a comprehensive background on the theory of scale relativity, we refer the reader to a number of papers and books [2, 5, 6, 189,190,191,192,193,194]. Meanwhile, in what follows, we review the most recent updates on theory and experiment relevant to biological systems, which build on these foundations.
5 The physical principles that govern the emergence of biological structures
From a biological perspective, the seeds of a new approach begin with a proposal by Prigogine et al. [195,196,197,198] that “many body” complex systems can be regarded as irreducibly probabilistic, in a manner analogous with quantum mechanics (QM). This principle, developed through a more recent programme of work [1, 199,200,201], considers a description of biological systems within the context of the theoretical foundations of QM and the debate about irreversible laws linked to determinism and probabilistic descriptions in physics.
When considering the foundations of standard QM, at the very smallest scales we see a fundamental irreversibility (symmetry breaking) under the reflection \({|\mathrm{d}t|}\rightarrow -{|\mathrm{d}t|}\), which is at the origin of the complex number \({\mathbb {C}}\) representation of quantum mechanics [200]. This complex representation is reflected in two real \({\mathbb {R}}\), irreversible processes, which together form a complex reversible system (a complex path integral), which leads to the wave function.
Within this context, we consider the emergence of the cell as a biological system, which begins with external forces impacting on molecular assembly. In the first instance, thermal fluctuations lead to decoherence and classical physics. At another level, quantum vacuum and thermal fluctuations (collectively “environmental fluctuations”) act as a sea of harmonic oscillators.
A combination of “environmental fluctuations” and levels of ionisation (which dictate charge density \(\rho \)), have a fundamental impact on the trajectory and dynamics of particles as they interact to form larger structures. As \( \rho \) increases, repulsive forces (Coulomb interactions) between adjacent charged particles create a barrier to bonding, allowing for greater freedom to interact with environmental fluctuations.
The diffusive system of environmental fluctuations can be written in the form of the Fokker–Planck equation,
Alternatively, via a series of calculations, described in [200], the system of fluctuations can take the form of a Euler equation (Eq. (2)), in which D represents a standard diffusion coefficient, with the force expressed in terms of the probability density P,
The ‘diffusion force’ derives from an external potential,
which introduces a square root of probability, normally associated with quantum systems, in the description of a classical diffusion process.
At the molecular scale, as levels of charge density in the system increase, charges loosely cluster, with \(\mathring{A}\)-scale holes within clusters creating an attractive potential well [202]. At this scale, a small cluster of charges can be seen as a quantum fluid,
which is expected to be the solution of the Schrödinger equation
where \(\phi \) represents an external potential or potentials, including \(\phi _{\mathrm{diff}}\) (Eq. (3)).
Introducing \(\rho \) and phase, defined as a dimensioned action A of the wave function \(\psi _n= \sqrt{\rho _n} \times e^{{i A_n}/\hbar }\) along with the velocity field of the quantum fluid (n), given by \(V_n=(\hbar /m) \nabla { A_n/\hbar }\), we can rewrite the Schrödinger equation in equivalent form as Euler (Eq. (6)) and continuity equations (Eq. (7)), which reflect the real and imaginary part of the Schrödinger equation,
where \(Q_n\) represents a localised quantum potential,
which is implicit in the Schrödinger equation (Eq. (5)), but now explicit in the Euler equation (Eq. (6)).
As reported in [200], when \(\rho \rightarrow 0\), BaCO\(_3\)-SiO\(_2\) molecular assembly, unhindered by repulsive charges, results in the growth of a crystal lattice illustrated in Fig. 3a. By contrast, as \(\rho \) increases, charged molecules become more dynamic. Figure 3b represents successive solutions, during evolution of a time-dependent Schrödinger equation in a 2D harmonic oscillator potential, which leads to a model of bifurcation in a molecular system. The jump from a one-body to a two-body, branched structure occurs as the energy level increases from the fundamental level (\(n=0\)) to the first excited level (\(n=1\)). An iterative bifurcation process leads to a branched molecular assembly, high levels of disorder and a fractal charge density distribution.
As \(\rho \) increases, beyond a critical percolation threshold, the interaction of quantum potentials \(Q_n\) associated with individual charges, leads to the emergence of a charge-induced fractal network of interconnected channels (Fig. 4), with local potential wells acting as the roots of the network [200].
The system reflects a transition from a collection of charges \(\psi _n = \sqrt{\rho _n} \times e^{{i A_n}/\hbar }\) (where \(A_n\) is a microscopic action), into macroscopic fractal fluctuations, which define a macroscopic wave function \(\psi _N\),
where \(A_N\) is a macroscopic action, \(Q_N\) (Eq. (10)) is \(\psi _{D}\)’s associated macroscopic quantum potential (MQP) and \(\hbar \) is substituted with a macroscopic parameter \({{\widetilde{D}}}\), which characterises the amplitude of fractal fluctuations across the MQP and is therefore specific to the system.Footnote 1 We have
Taking \(\psi _{N}\) and its associated macroscopic quantum potential (MQP), we can now write a macroscopic Schrödinger-like equation (Eq. (11)), and its equivalent Euler and continuity equations (Eqs. (12) and (13)), in which \(Q_N\) (Eq. (10)) becomes explicit [200]. We have
The charge-induced fractal field guides the trajectory of macroscopic fluctuations. At a quantum critical percolation threshold, destructive interference effects cancel out of most frequencies, leaving a coherent resonant frequency [202]. Examples of phenomena in intrinsically disordered condensed matter dictated by this effect include coherent random lasing (CRL) and high temperature superconductivity (HTSC) [202, 204,205,206]. In the case of HTSC, the symmetry breaking linked with a quantum critical fractal network of charges triggers a classical to quantum “Lifschitz transition” and a corresponding “Feshbach resonance” associated with macroscopic quantum coherence [203].
Reproduced from [200]. A disordered distribution of individual charges (left). The interaction of quantum potentials associated with each charge, collectively create a geometric network of hills and valleys (right)
When we consider either standard or macroscopic forms of the Schrödinger equation (Eqs. (5) and (11)), the external potential (\(\phi \)), associated with thermal fluctuations, competes with quantum potentials (\(Q_n, Q_N\)) implicit in the Schrödinger equations.
An important insight into the transition is revealed when comparing the diffusion system (Eq. (2)) with its quantum analogue (Eq. (14)),
Comparison between the two systems highlights a striking level of equivalence, except that in the quantum case, the diffusion constant is now complex (\({{\widetilde{D}}}\)) and the quantum force, which derives from an internal quantum potential, generated by its fractal geodesics,
is the exact opposite of the external diffusive potential (Eq. (3)).
When the diffusive potential (Eq. (3)) exceeds the internal quantum potential (Eq. (15)), it leads to a process of decoherence described by “quantum Brownian motion” [207, 208]. During collapse of the wave function, the emergence of ‘pointer states’ is linked to the collapse of the fractal velocity field, to its more stable roots [200]. These roots form the preferred set of states of an open system most robust against environmental interaction, which accounts for the transition from a probabilistic to a deterministic classical description.
This competing system of processes is fundamental to the emergence of a cell, its division and formation of a range of different biological structures. To illustrate how this translates into practice at macroscopic scales, we first consider examples of structures grown from BaCO\(_3\)-SiO\(_2\) solutions, where the primary source of charge is represented by protons released through dissolution of atmospheric CO\(_2\) [200]. As a case study, a fern-like (fractal leaf) structure (Fig. 5a), reflects partial decoherence of a macroscopic wave function. Despite its fractal dimension (\(D_F\)), it still exhibits a component of long-range order, its \(D_F\) being determined by the strength of the residual field (\(Q_N\)), relative to external diffusive forces. As \(\rho \) increases, we see an increase in \(D_F\) relating to packing of dendritic nm-scale fibrils from which the structure was constructed, leading to a more classic leaf-like form (Fig. 5b). For further examples of different emergent proton-driven plant-like structures see [200].
A further increase in \(\rho \) through the incorporation of gibberellic acid (GA) as a charged biomolecule into the BaCO\(_3\)-SiO\(_2\) system reported in [201], resulted in the emergence of a spherical non-differentiated stem cell-like structure of \(\approx 15\, \upmu \)m diameter (Fig. 5c). The structure is composed of densely packed (\(\approx 5\) nm diameter) dendrites, grown symmetrically from a centre to fill the space via an iterative process of bifurcation. The structure closely resembles a real cell (without a cell wall) with BaCl\(_2\)-Na\(_2\)SiO\(_3/\)GA composite dendrites replicating the dendritic structures formed by microtubules and actin filaments, which dominate the cytoplasm where most cellular activities, including cell division occur [201].
The result is interesting from a number of different perspectives: (i) We see the emergence of the synthetic cell (Fig. 5c) as an experimental exemplar of closure of constraints, typically associated with a biological system [210]; (ii) Fig. 8b showing a division process, reflects the synthetic cell as an autopoietic system [211]; (iii) A charge-induced fractal network (a macroscopic path integral) represents an essential ingredient for the emergence of a coherent macroscopic quantum-like system that underpins autopoiesis, which could not have emerged from a classically ordered structure such as a liposome; (iv) With scale relativity, we have a clearly described physical theory and mathematical framework available to account for the experimental exemplars of closure of constraints and autopoiesis. Both theory and experiment represent a step change beyond earlier theoretical biology studies on autopoiesis [209,210,211], and others that emphasise the possible role of protein or lipid soups with autocatalytic properties in the formation of protocellular assemblies [212,213,214,215].
At a critical point in the decline of \(\rho \), \(Q_N\) becomes insufficient to support the emergence of a long-range fractal architecture (such as Fig. 5a), but is sufficient to disrupt the formation of a crystal lattice, leading to a disordered, tumour-like structure. Finally, as noted in Fig. 3a, where \(\rho \rightarrow 0\), full macroscopic quantum decoherence of the field is reflected in the formation of a crystalline lattice.
The smallest scale at which we expect a macroscopic quantum potential (MQP) to emerge begins with molecular assembly into a range of intrinsically disordered proteins followed by larger and more complex nm-scale structures, which form the building blocks for larger, sub-cellular structures [200, 201, 216]. At this scale it is thought that short-range electromagnetic field fluctuations associated with the quantum vacuum play a key role in assembly, by coupling synergistically with the charge-induced complex velocity field, to create a two-component MQP and its associated structure [200].
Evidence to support the hypothesis of macroscopic quantum coherence in intrinsically disordered structures at this scale includes CRL in nano-fibres [217] and experimental confirmation of macroscopic quantum coherence in a protein complex [218].
As shown in Fig. 5c, as these nm-scale structures grow, cells that play a significant structural role have the potential to reach a typical (average) scale of 10–40 \(\upmu \)m, except in special cases such as the extension of the axon and dendrites from the body of nerve cells,
Beyond this scale, van der Waals forces are exceeded by gravitational forces, which represent a physical constraint on cell diameter [200]. Biological systems circumvent this limitation on scale through either an increase in cell length (which has limited benefits, except in special cases such as the extension of the axon and dendrites from the body of nerve cells), the formation of large multinucleated structures (e.g., during the life cycle of some organisms such as Physarum polycephalum), or more effectively through cell division to create larger scale structures, which we consider in Sect. 6.
Before discussing the process of cell division we consider the impact of increasing \(\rho \) beyond the level which leads to a spherical cell-like structures (Fig. 5c) through the inclusion of cytokinin (CK) as a charged biomolecule. In the first instance we begin to see extended spiral structures, as illustrated in Fig. 6a. As reported in [201], this scale of spiral structure appears in both single-celled spiral diatoms such as Chaetoceros debilis and multicellular organisms such as Arapidopsis thaliana, where spiral structures occur in tracheary elements.
To account for this type of spiral structure we first consider Fig. 6b, which represents an early model for the emergence of a spin-like internal angular momentum in fractal spiral curves [5]. The figure illustrates how “spin” naturally emerges within a 4D spacetime, in which all four dimensions, including the invariant proper time s, are fractal.
a Growth of continuous spiral, as a result of a travelling, rotating wave package when \(D_F=2\). Each stage of assembly adds to previous growth, creating an aggregated time series. As time progresses, a consumption led decline in charge density means \(D_F \rightarrow \, <2\), which leads to decline in energy, an increase in wavelength and a vanishing spiral at the end of the growth process. b Schematic representation of a fractal curve in spacetime from [5]. The evolution of its coordinates is described by four fractal functions of the normalised curvilinear coordinate s intrinsic to the fractal curve. c Very high levels of charge density lead to more ordered packing and a linear arrangement of nano-fibrils, until a decline in charge density leads to a more spherical, cell-like structure at the end of the growth process. d Numerical simulation of a typical spinorial geodesic in a fractal space, from [219]
When considering spin in a quantum system, the angular momentum \(L_z=m r^2{\dot{\varphi }}\) of a point mass following a classical spiral path should vanish as \(r\rightarrow 0\). However, as explained in [201], while \({\dot{\varphi }}\) diverge and r tends to zero, the product \(r^2{\dot{\varphi }}\) remains finite when \(D_F = 2\), while it is vanishing for \(D_F < 2\) and divergent for \(D_F > 2\).
Following this interpretation, fractal geodesics of \(D_F=2\) account for the extended spiral structure in Fig. 6a. Meanwhile, a growth led decline in \(\rho \) over time leads to an associated decline in \(D_F\) (\(D_F\rightarrow \,\, <2\)) and energy in the system, which accounts for the larger diameter, vanishing spiral at the end of the extended spiral in Fig. 6a.
By contrast, a further, significant increase in \(\rho \) through an increase in CK concentration [201], led to disappearance of spin and the emergence of a linear fibril assembly, such as that illustrated in Fig. 6c. The linear assembly relates to an increase in charge packing density beyond a critical point of disorder at \(D_F=2\), which leads to increased order and a decline in quantum coherence. In other words, the chaos-induced symmetry breaking vanishes, with symmetry being recovered at the scale at which nano-fibrils aggregate. This is reflected in more ordered packing of nano-fibrils in the main stem, a phenomenon observed in the packing of cellulose nano-fibrils in certain layers of plant cell walls [200, 201, 220]. However, as \(\rho \) declines during the growth process, it reaches a point where the symmetry breaks once again and a spherical, cell-like structure (in this instance) emerges as secondary structure.
Within standard, non-relativistic QM, intrinsic spin is generally described by the Pauli equation [5, 6, 219]. In order to account for what we have observed in terms of the Pauli equation, we briefly review its geometric origins. As described earlier, the origin of a complex wavefunction and the Schrödinger equation is underpinned by breaking of the symmetry \(d_+/dt, d_-/dt\), which we now write in terms of the invariant proper time (s). Breaking the symmetry \(ds \leftrightarrow -ds\), leads to a two valuedness, reflected in two total derivatives \(d_+/ds, d_-/ds\). Meanwhile, the inclusion of spin comes from a discrete symmetry breaking on the spacetime differential element \(dx^{\mu } \leftrightarrow -dx^{\mu }\). This emerges from the fact that in general, \(v[x^\mu (s,dx^\mu ),s] \ne v[x^\mu (s,-dx^\mu ),s]\), where the velocity field v is a function of the fractal coordinates, which in turn depend on the four resolutions \(dx^\mu \), with \(\mu = 0,1,2,3\).
This second two valuedness, accounted for through algebra doubling from complex numbers \({\mathbb {C}}\) to quaternions \({\mathbb {H}}\), corresponds to a second doubling of the total derivatives to give \(d_{++}/ds\), \(d_{+-}/ds\), \(d_{-+}/ds\) and \(d_{--}/ds\), and a doubling of the partial derivative \(\partial /\partial x^{\mu } \rightarrow (\partial _+/\partial x^{\mu }, \partial _-/\partial x^{\mu })\). This leads to a doublet (\(\psi ^1,\psi ^2\)) of complex wave functions (a Pauli spinor), which naturally emerges within the framework of manifolds carrying a quaternionic structure [221].
On first consideration, one might expect that the Pauli equation should logically proceed from the symmetry breaking \(dt \leftrightarrow -dt\) (for a non-relativistic motion) and \(dx^{\mu } \leftrightarrow -dx^{\mu }\) (for the appearence of spinors). However, as shown by Célérier and Nottale [219], it is not possible to take this approach directly writing a non-relativistic equation for spin-1/2 particles. It can only be derived as a non-relativistic approximation of the Dirac equation. This requires a further (third) doubling linked to breaking of the symmetry \(x^{\mu }\leftrightarrow -x^{\mu }\), due to the breaking of parity P and time-reversal T symmetries specific to the relativistic case. This third doubling means the four total derivatives double once again to become \({\tilde{d}}_{++}/ds\), \({\tilde{d}}_{+-}/ds\), \({\tilde{d}}_{-+}/ds\) and \({\tilde{d}}_{--}/ds\).
For each of these cases, one finds the total derivative
and its tilde counterpart. These transformations are accounted for through the introduction of a bi-quaternionic velocity field, which leads to the Dirac spinor and the derivation of the Dirac equation. The Pauli equation is then derived at the non-relativistic limit of the Dirac equation [201, 219].
Figure 6d represents a model of a spiral fractal path underpinned by a Pauli spinor, which confirms the earlier fractal model of spin in Fig. 6b as an emergent property of 4D fractal spacetime. The spiral in Fig. 6d represents just one of an infinite number of possible realisations of an electron as a point particle. This contrasts with the macroscopic spiral (Fig. 6a), which reflects the physical integration of a consecutive series of slices of a 2D fractal space, analogous with Fig. 6b. The structure that emerges from integration of this set of fractal geodesics dictates that time must now also be fractal, creating a composite four-dimensional spacetime construct, which underpins a macroscopic quaternionic wavefunction (a Pauli spinor). The result illustrates the fundamental relativistic and quantum nature of spin (even in a non-relativistic scenario), which is attributed to the non-differentiability of the quantum spacetime geometry and not only of the quantum space [6].
A further difference between Fig. 6a and a set of electron trajectories is that only the field (defined by a MQP), is coherent rather than a fully coherent fluid, vortex-like structure in the electron case. Figure 6a represents an emergent matter wave (rather than a point particle), which rotates in a fractal 4D spacetime as a continuous wavefront, at non-relativistic speeds.
To accommodate intrinsic spin in macroscopic systems, we treat the Pauli equation in the same way as the Schrödinger equation in its more generic form (Eq. (11)), where \(\hbar = 2m{{\widetilde{D}}}\) in standard QM. The result (Eq. (17)) is a new, more generic version of the Pauli equation:
in which the charge q could potentially include mean charge on a biomolecule or macroscopic quantum object such as a protein complex or a cell.
a A monoculture of spherical structures with evidence of a division process. b The process of cell division. In order to grow beyond a critical point, a symmetric one-body structure, composed of a fractal fluid of molecular trajectories becomes unstable and is forced to divide. Here frozen in time, we see an unstable intermediate step in the dynamic transition from a one-body to a two-body structure. c A branched multicellular structure
6 The physics of cell division
A theoretical approach to cell division, previously described in [2, 6, 200, 201], is captured in Fig. 7a and b. Figure 7a reveals stationary solutions of a time-dependent Schrödinger equation in a 3D harmonic oscillator potential, whilst Fig. 7b, reveals successive figures, giving the isovalues of the density of probability for 16 time steps. The first and last steps (\(1, n=0\) and \(16, n=1\)) are solutions of the stationary (time-independent) Schrödinger equation, whilst intermediate steps are exact solutions of the time-dependent Schrödinger equation reflecting transient structures. The model has a number of features in common with the bifurcation process in Fig. 3b, the key difference being that in the case of bifurcation, the previous structures remain and add to themselves instead of disappearing as in cell division. The only other difference lies in the quantum of action, with Fig. 3b being based on \(\hbar \) rather than a macroscopic constant in (Fig. 7b), although the bifurcation process (Fig. 3b) is also valid for a macroscopic quantum system at both sub-cellular and multicellular scales.
Evidence to support the proposed theory of cell division has been reported in [201]. Figure 8a reveals a collection of cell-like structures comparable to Fig. 5c, with some captured in a process of division. The process of “cell division” was confirmed by observation of a range of intermediate steps in the process [201]. As an example, Fig. 8b captures the transition from a one-body to a two-body structure. Like Figs. 7a and 8b it reflects a point-like probability density. However, the two-body system is also connected by a bundle of nm-scale dendrites, which evolve in time as a fractal fluid of geodesics, within a sea of dynamic, environmental fluctuations. Within this figure we can clearly see a division process, supported by a single, interconnected system of coherent fluctuations, in which, at each point in the initial one-body system, trajectories exist that connect the two-body structures.
The hypothesis of cell division as a macroscopic quantum process in which the energy associated with higher levels of quantisation is linked to increasing charge density [201] is supported by results where an increase in \(\rho \) leads to an increase in cell duplication, as well as bifurcation of the cellular structure, as shown in Fig. 8c. This type of branched multicellular structure bears a striking resemblance to early stem cell division in Arabidopsis thaliana reported in [201].
The results indicate that the cytosol, as an integral part of a living cell, provides the fractal architecture to support a charge-induced macroscopic quantum system, which supports the theory of the emergence of a cell and its subsequent division as a macroscopic quantum processes. The capacity to divide represents a critical step in addressing both the conservation of genetic information and gravitational constraints on the scale of a cell through the creation of multicellular structures. Without it the replication of genetic material and the emergence/evolution of the vast range of structures and functions within more complex multicellular organisms could not exist.
Bifurcation processes, driven by environmental fluctuations are fundamental to the emergence of the fractal architecture required to form a macroscopic quantum system (order out of chaos). Depending on conditions, the process of bifurcation repeats itself over a broad range of scales, to create a diverse range of structures, from proteins to cell organelles and cell walls, which constitute a living cell. The cell as the ‘quantum of life’, then has the potential to repeat the process, building new networks and structures through spontaneous duplication and bifurcation to create multicellular structures.
The fractal dimension of a multicellular structure (which equates with cell packing density), and the average (fractional) charge on each cell, collectively dictate charge density and its spatial distribution. As we have shown [200, 201], depending on the specific set of internal conditions and their interaction with the external environment, we can expect to see the emergence of a diverse range of multicellular systems.
This paradigmatic representation of a cell and its division implies that a lipid bilayer or membrane is not a fundamental requirement for the physical process of cell division. However, it is of course essential for storage and containment as the putative cell begins to develop beyond the stage we are presently considering.
7 Process control in a biological system
Having summarised key elements in the emergence of a macroscopic quantum system we consider how this translates more generally into biological systems.
The organisation, development and functioning of complex biological systems are the result of a dynamic interplay of multiple processes operating at the level of the organism, its organs, cells and molecules, all levels being in constant interaction with environmental influences, and between themselves, with no privileged level of causation according to the principle of biological relativity [3]. An important process is the transcription of the genetic code of the genome DNA into several types of RNA, the transcriptome, including messenger RNAs, which are then translated into a wide range of functional proteins, the proteome. There is growing evidence that this process is heavily regulated through changes in molecular and cellular networks of interactions, contributing to multiple types of inheritance [69, 222]. In this context, it has been proposed [59] that living systems have the ability to organise themselves as the result of a conjunction occurring through the variable part of a mostly stable physical organisation, and the stable part of a network of small fluctuations, thus operating in a “biological spacetime” involving a variable number of biological dimensions, a conjecture that is consonant with the principles underlying scale and biological relativity [3, 6] as well as the theory of organisms [50].
The proteome represents a critical source of charged macromolecules and catalysts, whose enzymatic activities, in association with ions (e.g., H\(^+\), K\(^+\), Na\(^+\), Ca\(^{2+}\), Cl\(^-\) and HCO\(^-\)), lead to the production of specific charged molecules, such as hormones and metabolites (the metabolome) to control cellular dynamics (fluxome and electrome [223]) and fate.
A biological system emerges in a quantised way, in dynamic interaction with its environment, constructed through a complex set of multi-scale assembly processes, with each macroscopic wave function being generated from the square root of charge density (\(\psi \propto \sqrt{\rho }\)). At each scale, individual units of charge are associated with a collection of wave functions at a lower scale.
The smallest units of charge range from individual ions, nucleic acids, amino acids and hormones, which play a key role in the emergence of structures such as proteins and nm-scale sub-cellular components.
Once a mesoscale quantum system such as a protein has been created, environmental fluctuations and charge density once again play a key role in the assembly of larger scale MQPs and the subsequent emergence of larger, sub-cellular structures (e.g., mitochondria and membraneless organelles [224]). In this larger scale of assembly, charge density is now defined as an average at the scale of the specific structural unit. As an example, the very large build up of protons (\(H^+\)) in the mitochondrial inter-membrane space means a large electrostatic potential develops between the 1000–2000 mitochondria per cell and their surrounding cytoplasm.
Reproduced from [2]. Solutions of increasing organisational complexity of the scale-Schrödinger equation for a harmonic oscillator scale potential (left), which give the probability for a structure to occur at a given relative scale. These solutions can be interpreted as describing systems characterised by an increasing number of embedded structural levels (right)
Looking at the bigger picture, the net result is a dynamic electromagnetic landscape supported by an assembly of “charged units”, which collectively dictate the form and function of a diverse range of cell types.
Following emergence of “the cell,” individual cells act as macroscopic units of charge in a multicellular network, which has the potential to create an interconnected, multi-scale system of MQPs. These increasing scales of organisation, illustrated simplistically in Fig. 9, reflect a series of quantised transitions from “a fundamental state” (\(n=0\)) to excited levels (\(n=1, 2, 3\ldots \)). Jumps in organisational complexity, linked with increases in the energy of the system at each scale (associated with increases in the charge density), lead to a nested set of macroscopic wave functions and macroscopic equations of state, such as a Schrödinger equation.
Solutions of these equations yield new, larger scales of organisation, which have the potential to take on many different forms. Figure 10 illustrates just one example of a flower, but it could include a range of structures such as seeds, leaves and fruits to whole organisms.
A flower-like structure, reproduced from Nottale and Auffray [2]. The flower represents a solution of a Schrödinger equation describing a growth process from a centre, with “petals”, “sepals” and “stamen” traced along angles of maximal probability density
a A range of structures of D. discoideum at different stages in its life cycle. b A rotating structure during the “streaming phase” of D. discoideum, composed of up to 100,000 individual cells. c End of the accretion stage. d A profile analogous to the end of the accretion stage obtained as a solution of a Schrödinger equation in a central 1/r potential and self-attraction
A living exemplar of this type of process is represented by Dictyostelium discoideum [225]. Under stress, the organism transitions from a community of up to 100,000 single-celled amoeba, into a range of multicellular structures, which reflect different steps in its development cycle, some of which are illustrated in Fig. 11a. The cell assembly process, stimulated by charged biomolecules in the form of cyclic adenosine monophosphate (cAMP), represents a more complex version of multicellular aggregation, described in Fig. 8c.
Considering the example of D. discoideum in more detail, Fig. 11b reveals a multicellular, 2D rotating structure during the “streaming phase”, which represents the first step in the process of cellular assembly. Control is conventionally ascribed to “chemotaxis”. However, the foundations of scale relativity offer a new more detailed insight into the emergence of this rotating, vortex-like structure, which is underpinned by a spinorial (quaternionic) macroscopic wave function, emerging from a fractal network of charges. The charge density variable at this stage is dictated by the molecular distribution of cAMP plus the charge associated with each individual cell.
aD. discoideum at the beginning of its 3D growth phase. b A model of (a) as a solution of a two-dimensional Schrödinger equation in a central potential. c Fruiting body of D. discoideum selected from Fig. 11a. (d). A BaCO\(_3\)-SiO\(_2\)/CK based structure creating the equivalent of the fruiting body, in Fig. 12c, but at the scale of a single cell
Once cells aggregate into a single entity, one can consider charge density in terms of cell packing density, the mean charge on each cell and possibly charge associated with glycoproteins, which allow for cell-cell adhesion.
At the end of the streaming phase, the next step in cellular assembly, takes the form of an annular structure (Fig. 11c), which is very well described by the solution of a two-dimensional Schrödinger equation in a central potential (Laguerre polynomials) similar to atomic orbitals (Fig. 11d). The square of the modulus of the wave function is here directly interpreted as density, which provides the height of the ring along the third dimension z.
Figure 12a shows a next stage in growth beyond the annulus (Fig. 11c), with growth reflecting a natural transfer of the nature and effect of the density \(\rho =|\psi |^2\). Figure 12b represents a model of this stage obtained as a solution of a Schrödinger equation in a central 1/r potential with self-attraction. The model used is a solution of a differential equation (Eq. (18)), with the density given by \(\rho = \int z[r] \mathrm{d}r\), which is also obtained in astrophysical conditions by identifying “dark matter” with a quantum potential created by self-gravitation of the gaseous content of a galaxy. It naturally yields a cusp in the central region, as observed. We have
As illustrated in Fig. 11a, the organism has the capacity to change structure through a series of stages, before the final phase of a fruiting body. By way of confirmation that the process of emergence observed in BaCO\(_3\)-SiO\(_2\)-based structures shows a similar set of principles, Fig. 12d shows an example of a BaCO\(_3\)-SiO\(_2\)/CK structure (grown under the same conditions as Fig. 6c), which shows a striking resemblance to that of the D. discoideum fruiting body in Fig. 12c. The essential difference between the two structures is reflected in their scales. Figure 12d (\(\approx 100\,\,\upmu \)m in height) is built from \(\approx 10 \) nm-scale fibres as the quantised unit of charge, whilst Fig. 12c represents a multicellular structure (\(\approx 20{\,}000\,\,\upmu \)m in height) built from \(\approx 10 \,\, \upmu \)m-scale cells as the quantised unit of charge. This difference in scales give some insight into the universal applicability of the charge-induced quantised fields and associated forces that govern a specific structure, irrespective of scale.
The system we have described represents a powerful toolbox, which has been selected for and refined during the evolutionary process to control charge density and its spatial distribution at the scale and location where the action (growth) takes place, thus defining the physical environment that dictates the emergence of a specific structure.
Through this process we see the emergence of a multi-scale, hierarchical field theory, with quantisation of the field at each scale, forming building blocks for the next level. Due to high levels of interaction and interdependency between scales, a change of charge density at one level will fundamentally effect structure and function at other scales.
This principle fits well with the principle of “biological relativity” established by Noble [30, 61, 67, 69], which expresses concretely the fact that “there is no necessarily privileged level in a biological system” which would determine events occurring at the other levels, only there are interactions between multiple levels. The fundamentally relative character of scales and biological levels makes it possible to consider these two notions as equivalent. The intracellular, cellular and tissular levels can be defined only one with respect to the others, e.g. what is interior at the cell level become exterior for the nucleus, and what is exterior becomes interior at the tissue level, requiring specific characterisation of the various boundaries between levels, as they play a fundamental role in the process of biological individuation [54, 226, 227].
Biology is currently dominated by the central dogma of molecular biology, resulting in confusions between molecular and cellular interpretations of heredity [228]. Using the common framework of scale relativity and its intrinsic integrative character, we propose to integrate the diverse elements of biological theories to provide a basis for a unified theory of living systems in the context of their evolution and development.
Our initial focus will be on exploring the extent to which cellular characteristics can be derived from more fundamental principles that constrain their occurrence in the scale-relativity framework, so—- that they could be amenable to experimental manipulations. By providing fundamental explanations for complex processes and self-organisation in natural systems, scale relativity offers the opportunity to revisit basic biological questions, and at the same time opens avenues to develop novel modes of intervention to modulate the behaviour of living systems.
8 The origins of life
The results reported in [201] offer a number of important new insights into the emergence of life. Given an appropriate set of initial conditions, a putative cell in the form of a dendritic fractal cytoplasm could have emerged as a crude “cell-like” macroscopic quantum object, with the intrinsic capacity to divide. If a metaphorical protein soup in a primeval swamp was able to support an on-going supply of ions, amino acids and proteins, it could have signalled the spontaneous emergence and evolution of both single and multicellular structures.
Whilst such a simple self-replicating system cannot in itself be described as a living system, it appears entirely plausible that given a sufficiently large number of iterations, an extended evolutionary process could lead to the emergence of a system that could be defined as living.
Under such conditions, DNA as we know it would not have been an essential ingredient in the early stages of such a process, but could have started its evolutionary process in parallel with other structural developmental processes. However, whilst DNA may not have been an essential requirement of early, putative life forms, it would have been essential for later development, contributing to the formation of proteins and metabolites required to support macroscopic quantum processes. In this framework, the genome operates as an “organ of the cell” memorizing information on past sucessful evolutionary processes as discussed in [69].
9 Application to cardiac systems biology
In cardiac physiology, models of cardiac activity have been developed for over a half century, starting with the application of the Hodgkin–Huxley theory to cardiac Purkinje fibres [229, 230]. The models have then been enriched to include many ion channel proteins, and mechanisms for calcium signalling [231, 232]. The different types of cardiac cells have been modelled in animals and human and are now applied successfully in drug development and testing [60, 233]. Insights have been derived as much from the failures as from the successes of iterative interactions between thought experiments based on conceptual models, quantitative simulations user computer models, and experimentation [13]. Many other models have now been developed, refined, analysed systematically, and made available publicly on the CellML website [234,235,236,237,238]. These cellular models, combined into multi-scale tissue and organ models, have been the basis for the construction of the virtual heart, the first virtual organ ever to be built through the exemplar Human Physiome Project [13, 144, 147, 239]. These models are revealing cross talk and interdependence between cardiac structure and function, ion channel function and cell or tissue behaviour, or electrophysiology and mechanics, all the way from proteins to the entire organ [240,241,242,243].
Indeed, cardiac physiology represents the most advanced field with regard to multi-scale analysis, as detailed models are available for a variety of biological processes. These include models of metabolic and signalling pathways; models of ion channels and their interactions with drugs, using chemical equations and Markov models; detailed single-cell electrophysiological models of the Hodgkin–Huxley type incorporating many membrane channel types and process compartmentalisation; tissue models including ordered variations in gene expression and activity across, e.g. the ventricular wall or the sinus node-atrial boundary; and detailed anatomical models derived from imaging data [158, 236, 244, 245].
We propose to start applying the scale-relativity tools to the simplest Nobel 1963 model based on the Hodgkin–Huxley equations, and then to proceed with its generalisations. The advantage of these simple models is that they are known to support computer simulations that reproduce experimental data, increasingly with predictive power. Moreover, they can be treated analytically even for problems involving conduction of waves of excitation through multiple cells arranged into a fibre [246]. For example, in the continuous model approximation, an effective diffusive current describes the electrical current in such an extended fibre. The equation of propagation of the membrane potential takes the form of a diffusion-like equation: \(C_m\partial V/\partial t= \sigma \partial ^2V/\partial x ^2-g_r \left(V-V_r \right)\). This type of equation is at the heart of the scale-relative description. It can be extended by adding to the model a backward equation taking into account irreversibility on small time scales, which leads to representing the velocity vector by a dual system of equations. In turn, it may be transformed into a Schrödinger-type equation, and its solutions could be analysed, compared to experimental data, and predictions of the extended models tested in isolated animal cardiac cells in culture using the battery of usual molecular, cellular and physiological techniques in normal and perturbed conditions [247].
10 Conclusions and future work
One of the key objectives of the theory of scale relativity is to develop a new, first principles, geometric approach to understanding the foundations of quantum theory that may ultimately lead to a unified theory of quantum mechanics and general relativity. Although a completely unified approach remains an outstanding challenge, development of the theoretical framework that underpins this work has led to progress in addressing a number of important fundamental questions relating to standard QM, in addition to a new (analogous) theoretical framework of macroscopic quantum systems that can lead to a better understanding of biological systems.
Relevant examples of progress in standard QM include derivation of the Schrödinger, Pauli and Dirac equations from first principles. Meanwhile at another level, the principle of relativity of scales, which is added to the current principle of relativity involving position, orientation and motion, states that there is no absolute scale in nature and that only scale ratios have physical meaning. Within this theory, a new law (corresponding to a Lorentz group of scale transformations), marked by a relative transition between Galilean scale relativity and Lorentzian scale relativity is valid at very small scales toward the Planck scale [248]. The transition is identified with the Compton scale of elementary particles, where their various physical quantities become explicitly dependent on scale. Within special (Lorentzian) scale relativity theory, the Planck length-scale plays for scale laws a role similar to that of the velocity of light for the laws of motion [248]. It is invariant under scale transformations, unreachable and unpassable, whatever the scale which has been taken as reference. The validity of this new approach is illustrated in its application to solving the “proton radius puzzle” [248]. The results offer convincing support for the hypothesis that the proton scale is not absolute, but depends on the reference scale used to measure it.
For clarity we stress that whilst many elements of Galilean scale-relativity theory are directly relevant to biological systems, the principle of special scale relativity (as with special relativity) is not directly applicable at scales typical of biological systems. In the same way that we only see the full relevance of special relativity and the application of the Dirac equation at velocities approximating the speed of light, we only see the full implications of the special scale-relativity theory at or beyond the Compton scale of elementary particles. However, this statement does not reflect the full picture as there is still an important connection at a fundamental level. For example, the connection between biological systems and special relativity emerges when considering the description of macroscopic spin emerging from fractal networks [201]. In order to describe spin in a non-relativistic scenario, derivation of the motion relativistic case of the Dirac equation is first required to derive the non-relativistic Pauli equation.
Whilst the full implications of special relativity or special scale-relativistic scenarios are not directly relevant in condensed matter or biological systems, we are required to consider the fractal geometries underlying the different systems, which are critical in defining emergent properties such as spin and scalable structures in both Galilean and Lorentzian relativistic scenarios.
Within the context of scalable structures, one of the key elements of the principle of scale relativity relates to how emergent structures at different specific scales are each formed from the product of a fractal distribution of charges at a lower scale, driven by environmental fluctuations in competition with internal forces dictated by charge density and its spatial distribution (see Eqs. (2)–(3) and (14)–(15) and related discussion). In other words, a basic set of principles that underpin any specific scale are repeated at multiple scales.
These basic principles do not detract from the very complex set of synchronised processes operating within a living cell that still require more careful analysis. At one level, this work sheds new light on the role of multi-scale fractal structures and their ubiquity in biological systems, with the emergence of larger scale ordered structures being governed by competition between the external diffusive force, and internal macroscopic quantum forces. At another level genetic diversification has led to an almost infinite set of potential conditions, principally defined by charge density (ion and charged biomolecule concentration) and its distribution, which leads to a vast range of possible structures.
The results so far provide convincing evidence that biological processes, structures and systems are in no way privileged. The difficulties associated with understanding living systems is tied up in the vast set of complex, interacting systems, which goes some way to accounting for the lack of progress in the deconstruction of processes into their individual component mechanisms. However, as a first step in understanding this complexity, we have shown that it is possible to recover differentiability and reversibility at the scale of macroscopic wave functions which define structures and processes at different scales.
This important theoretical development is supported by a growing body of evidence to support the theory that macroscopic quantum processes play a key role in living systems, and this may well prove to become a defining criterion of what constitutes a living system.
We note that these macroscopic quantum systems differ from standard QM in that only bosons remain coherent, leading to a new class of quantum systems [200, 202, 203], which is exemplified by complexed proteins [218], high temperature superconducting materials [202,203,204,205,206] and coherent random lasing [202, 217].
Whilst this limits the quantum properties of a macroscopic system, many phenomena associated with standard quantum theory are recovered. These include quantisation, non-dissipation, self-organisation, confinement, structuration conditioned by the environment and macroscopic quantum decoherence, evolutionary time described by the time-dependent Schrödinger equation, which describes models of bifurcation and duplication and, finally, intrinsic spin through disorder-induced spiral structures, when charge density and its spatial distribution meet certain criteria. However, as highlighted in [201], not all properties associated with standard quantum mechanics are recovered in the macroscopic theory. The application of the scale relativity/fractal spacetime theory to standard QM is based on the description of spacetime, toward small scales, as a pure, fully non-differentiable continuum. Within this framework, “particles” (accounted for by a wave function) reflect the various manifestations of the geodesics of this non-differentiable continuum in which scale divergence is without any lower limit, so that there is no hidden parameter in this case. The various properties of elementary “particles” (mass, charge, spin, etc.) emerge as manifestations of the geometric properties of this fluid of geodesics. There is no “trajectory”, but there are only purely geometric paths. Quantum phenomena such as entanglement, indistinguishability of identical particles, or spin–statistics relations are simple and natural consequences of such a purely geometric description.
Within the context of macroscopic quantum-type systems, based on a macroscopic constant larger than \(\hbar \), the situation is different and therefore also the interpretation. These systems are characterised by their fractality on a given range of scales, with an upper limit (the Einstein–de Broglie scale) as in standard quantum mechanics, but now there also is a lower limit. In this case there are particles in the commonly used sense, which follow trajectories, even though their possible realisations are infinite in number, fractal and locally irreversible, which leads to quantum-type equations.
The two situations therefore share a description in terms of wave function solutions of a Schrödinger or Pauli equation (although not with the same constant). They therefore share most of the consequences of this behaviour, except those derived from complete non-differentiability (entanglement, indistinguishability, etc.).
The disorder-induced fields which underpin these systems have their equivalence in the gauge fields of the electromagnetic, weak and strong interaction forces. However, this new quantum field theory of macroscopic quantum systems has yet to be described in a comprehensive manner as the proposal of a macroscopic Schrödinger or Pauli equation represents only a first approximation. As in standard QM, these equations do not help our understanding of the detailed mechanisms associated with quantum decoherence. Dealing with this issue requires a significant new step in our understanding of the foundations of quantum mechanics, which requires a detailed mathematical description, to be reported in a future paper.
Whilst the scale-relativity framework described so far represents at best a first approximation of reality, progress to date [1, 199,200,201] has highlighted an important set of general principles, which can play the role of signposts, to facilitate new research that can accelerate our understanding of biological systems.
We have so far seen a limited number of examples of possible emergent structures using CO\(_2\), as a source of charge density [200]. We have also demonstrated the potential to mimic biological systems using charged biomolecules (GA and CK) to more precisely control the emergence of cell-like structures, cell division and the growth of simple, multicellular structures [201]. However, the growth of larger and more complex structures was constrained by a fixed concentration of key ingredients which declined over time. This can be addressed in future work with the design of a system with a feedback loop, which provides a continuous supply of material and a constant set of conditions (over time), to support the growth of large-scale, multicellular structures. To get maximum information on the sequence of events during growth, emergent structures need to be monitored in real time through live cell imaging techniques using time-lapse microscopy.
It is anticipated that a successful system design could lead to a new, “cellular” approach to the development of larger and more complex multicellular structures and new materials. This concept starts to become attractive from a technological perspective if we consider the theory that a range of macroscopic quantum phenomena show a remarkably similar underlying set of physical principles [200,201,202,203]. A key objective of future work will be to develop a generic, first principles approach to the development of room temperature macroscopic quantum systems, which can support technologies such as HTSC, CRL and quantum computing.
As part of such an approach, as more detailed information on living systems emerges where we can identify specific combinations of biomolecules, ions and local conditions with the emergence of different morphologies and functionalities, we aim to test our understanding of their influence by replicating the conditions in simpler, more controlled inorganic growth experiments.
This approach is expected to offer further insights into the role of the genome, proteome, transcriptome, metabolome, fluxome and electrome in guiding physical processes and their impact on the emergence of structure and function at different scales within biological systems. As we improve our understanding of the mechanisms associated with biological processes, it should also lead to an improved understanding of the mechanisms and associated diseases that undermine these processes. It is anticipated that this knowledge may be useful in supporting new ab initio approaches to drug design and disease mitigation.
While the theories of motion relativity are well established in physics, the theory of scale relativity is still a matter of active research and discussion. Its multiple successful predictions [199,200,201,202, 249,250,251,252] are resolving or redefining fundamental problems considered as intractable in the classical framework. It thus proposes a significant change of paradigm that has yet to be accepted by most physicists. The choice of the scale-relativity theory to extend the physical and mathematical framework of systems biology is therefore very challenging. However, the obvious general occurrence of scales and organisation levels in biological systems supports the proposal that such a fundamental theory of scales in nature could be particularly well adapted to provide the basis for developing an integrated theory for biology.
The trans-disciplinary nature of the proposed approach calls for sustained efforts in training and education to facilitate interactions at the interface across the multiple disciplines involved, with a particular emphasis on biology, computer and engineering sciences, mathematics and physics [199, 253].
The existence of scales and levels of organisation in biology raises many questions concerning the ways in which causation occurs across scales and levels. The principle of biological relativity [3] is based on distinguishing between the causation by initial and boundary conditions and the causation by the molecular dynamics represented by the differentials in the equations used to model biological processes. The former include the constraints by higher levels of organisation, represented by the large downward facing arrows in Fig. 1. Taken together the upward and downward forms of causation are sometimes referred to as circular causality. This might give the impression that there is a temporal sequence here, with one form (usually the upward form) being first. That this is not the case is the outcome of a recent study of this issue [54] which shows that the two forms are best represented mathematically as simultaneous. The article also gives many physiological examples of high-level activity causing changes at the molecular level of organisation in biology. The details of causation across scales and levels are therefore beginning to be worked out.
We expect that the successful demonstration in biological systems of the predictive power of an extended framework that uses the mathematical toolbox of scale relativity for multi-scale integration will have enormous consequences in all areas of biology and medicine where similar hurdles need to be overcome. By validating the conceptual extensions of the systems biology framework, it will also provide a solid foundation for the development of a genuine integrated theory of life based on first principles. Much work remains to validate experimentally the conceptual and methodological extensions of the systems biology framework provided by scale relativity, and to integrate them successfully with the principles underlying the theories of evolution, development and functioning of organisms into an integrated theory of life.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: This is a review article, it has no associated data].
Change history
17 June 2020
The original version of this article was revised due to a retrospective Open Access order.
References
C. Auffray, L. Nottale, Scale relativity theory and integrative systems biology: 1. Founding principles and scale laws. Prog. Biophys. Mol. Biol. 97, 79–114 (2008)
L. Nottale, C. Auffray, Scale relativity theory and integrative systems biology: 2. Macroscopic quantum-type mechanics. Prog. Biophys. Mol. Biol. 97, 115–157 (2008)
D. Noble, A theory of biological relativity: no privileged level of causation. Interface Focus 2, 55–64 (2012)
D. Noble, Dance to the Tune of Life—Biological Relativity (Cambridge University Press, Cambridge, 2017)
L. Nottale, Fractal Space-Time and Microphysics. Towards a Theory of Scale Relativity (World Scientific, Singapore, 1993)
L. Nottale, Scale relativity and fractal space-time, in A new approach to Unifying Relativity and Quantum Mechanics (Imperial College Press, London 2011)
T. Ideker, T. Galitski et al., A new approach to decoding life: systems biology. Annu. Rev. Genom. Hum. Genet. 2, 343–372 (2001)
H. Kitano, Foundations of Systems Biology (MIT Press, Cambridge, 2001)
O. Wolkenhauer, Systems biology: the reincarnation of systems theory applied in biology? Brief. Bioinform. 2(3), 258–270 (2001)
E.H. Davidson, J.P. Rast et al., A genomic regulatory network for development. Science 295(5560), 1669–1678 (2002)
A. Goldbeter, Computational approaches to cellular rhythms. Nature 420(6912), 238–245 (2002)
H. Kitano, Systems biology: a brief overview. Science 295(5560), 1662–1664 (2002)
D. Noble, Modeling the heart-from genes to cells to the whole organ. Science 295(5560), 1678–1682 (2002)
C. Auffray, S. Imbeaud et al., From functional genomics to systems biology: concepts and practices. C. R. Biol. 326(10–11), 879–892 (2003)
A.L. Barabási, Z.N. Oltvai, Network biology: understanding the cell’s functional organization. Nat. Rev. Genet. 5(2), 101–113 (2004)
J.K. Nicholson, E. Holmes et al., The challenges of modeling mammalian biocomplexity. Nat. Biotechnol. 22(10), 1268–1274 (2004)
H.V. Westerhoff, B.O. Palsson, The evolution of molecular biology into systems biology. Nat. Biotechnol. 22(10), 1249–1252 (2004)
L. Alberghina, H.V. Westerhoff, Systems Biology: Definitions and Perspectives (Springer, Heidelberg, 2005)
P.V. Coveney, P.W. Fowler, Modelling biological complexity: a physical scientist’s perspective. J. R. Soc. Interface 2(4), 267–280 (2005)
E. Klipp, R. Herwig, A. Kowald, C. Wierling, H. Lehrach, Systems Biology in Practice: Concepts, Implementation and Application (Wiley-VCH, Weinheim, 2005)
M.A. O’Malley, J. Dupré, Fundamental issues in systems biology. Bioessays 27(12), 1270–1276 (2005)
U. Alon, An Introduction to Systems Biology: Design Principles of Biological Circuits (Chapman and Hall, Boca Raton, 2006)
E.H. Davidson, The Regulatory Genome: Gene Regulatory Networks in Development and Evolution (Academic Press, New York, 2006)
F.J. Doyle 3rd, J. Stelling, Systems interface biology. J. R. Soc. Interface 3(10), 603–616 (2006)
B.O. Palsson, Systems Biology: Properties of Reconstructed Networks (Cambridge University Press, Cambridge, 2006)
Z. Szallasi, J. Stelling, V. Periwal, System Modelling in Cellular Biology (MIT Press, Cambridge, 2006)
F.J. Bruggeman, H.V. Westerhoff, The nature of systems biology. Trends Microbiol. 15(1), 45–50 (2007)
O. Wolkenhauer, Defining systems biology: an engineering perspective. IET Syst. Biol. 1(4), 204–206 (2007)
W. Kolch, Defining systems biology: through the eyes of a biochemist. IET Syst. Biol. 2(1), 5–7 (2008)
D. Noble, Claude Bernard, the first systems biologist, and the future of physiology. Exp. Physiol. 93(1), 16–26 (2008)
M.A. Yildirim, M. Vidal, Systems engineering to systems biology. Mol. Syst. Biol. 4, 185 (2008)
A. Zewail, Physical Biology—From Atoms to Medicine (Imperial College Press, London, 2008)
C. Auffray, D. Noble, Origins of systems biology in William Harvey’s masterpiece on the movement of the heart and the blood in animals. Int. J. Mol. Sci. 10, 1658–1669 (2009)
C. Auffray, Z. Chen et al., Systems medicine: the future of medical genomics and healthcare. Genome Med. 1(1), 2 (2009)
M. Vidal, A unifying view of 21st century systems biology. FEBS Lett. 583(24), 3891–3894 (2009)
H.V. Westerhoff, C. Winder et al., Systems biology: the elements and principles of life. FEBS Lett. 583(24), 3882–3890 (2009)
H.Y. Chuang, M. Hofree et al., A decade of systems biology. Annu. Rev. Cell. Dev. Biol. 26, 721–744 (2010)
M. Cloutier, P. Wellstead, The control systems structures of energy metabolism. J. R. Soc. Interface 7(45), 651–665 (2010)
D. Noble, Biophysics and systems biology. Philos. Trans. A Math. Phys. Eng. Sci. 368(1914), 1125–1139 (2010)
L. von Bertalanffy, General System Theory: Foundations, Development, Applications (Penguin, Harmondsworth, 1945), p. 311
N. Wiener, Cybernetics or Control and Communication in the Animal and the Machine (MIT Press, Cambridge, 1948), p. 232
A. Turing, The chemical basis of morphogenesis. Philos. Trans. R. Soc. Lond. Ser. B 237, 37–72 (1952)
C.H. Waddington, The Strategies of the Genes: A Discussion of Some Aspects of Theoretical Biology (Allen and Unwin, London, 1957), p. 262
R. Rosen, A relational theory of biological systems. Bull. Math. Biophys. 20, 245–341 (1958)
P. Glansdorff, I. Prigogine, Structure, Stabilitè et Fluctuations (Masson, Paris, 1971), p. 288
A.C. Guyton, T.G. Coleman, H.J. Granger, Circulation: overall regulation. Annu. Rev. Physiol. 34, 13–44 (1972)
M.A. Savageau, Biochemical Systems Theory (Addison-Wesley, Reading, 1976), p. 379
H.R. Simon, The Sciences of the Artificial (MIT Press, Cambridge, 1981), p. 247
S.A. Kauffman, The Origins of Order: Self-Organization and Selection in Evolution (Oxford University Press, New York, 1993), p. 734
A.M. Soto, G. Longo, D. Noble, M. Montévil, P.A. Miquel, M. Mossio, From the century of the genome to the century of the organism: new theoretical approaches. Prog. Biophys. Mol. Biol. 122, 1–3 (2016)
D. Gavaghan, A. Garny, P.K. Maini, P. Kohl, Mathematical models in physiology. Philos. Trans. A Math. Phys. Eng. Sci. 364, 1099–1106 (2006)
J.M. Osborne, A. Walter, S.K. Kershaw, G.R. Mirams, A.G. Fletcher, P. Pathmanathan, D. Gavaghan, O.E. Jensen, P.K. Maini, H.M. Byrne, A hybrid approach to multi-scale modelling in cancer. Philos. Trans. A Math. Phys. Eng. Sci. 368, 5013–5028 (2010)
P.K. Maini, T.E. Woolley, R.E. Baker, E.A. Gaffney, S.S. Lee, Turing’s model for biological pattern formation and the robustness problem. Interface Focus 2, 487–496 (2012)
R. Noble, K. Tasaki, P.J. Noble, D. Noble, Biological relativity requires circular causality but not symmetry of causation: so, where, what and when are the boundaries? Front. Physiol. 10, 827 (2019)
S.A. Kauffman, A World Beyond Physics: The Emergence and Evolution of Life (Oxford University Press, Oxford, 2019)
S.M. Walker, The new physics needed to probe the origins of life. Nature 569, 36–38 (2019)
A. Prokop, B. Csukas (eds.), Systems Biology—Integrative Biology and Simulation Tools (Springer, Dordrecht, 2013) (eBook). https://doi.org/10.1007/978-94-007-6803-1
F. Capra, P.L. Luisi, The Systems View of Life—A Unifying Vision (Cambridge University Press, Cambridge, 2014)
C. Auffray, S. Imbeaud et al., Self-organized living systems: conjunction of a stable organization with chaotic fluctuations in biological space-time. Philos. Trans. A Math. Phys. Eng. Sci. 361(1807), 1125–1139 (2003)
D. Noble, Computational models of the heart and their use in assessing the actions of drugs. J. Pharmacol. Sci. 107(2), 107–117 (2008)
D. Noble, Genes and causation. Philos. Trans. A Math. Phys. Eng. Sci. 366(1878), 3001–3015 (2008)
O. Wolkenhauer, S. Green, The search for organizing principles as a cure against reductionism in systems medicine. FEBS J. 280, 5938–5948 (2013)
S. Brenner, Complexity in Biological Information Processing, vol. 239 (Wiley, New York, 2001), pp. 150–158
D. Bray, Molecular networks: the top-down view. Science 301(5641), 1864–1865 (2003)
T. Ideker, D. Lauffenburger, Building with a scaffold: emerging strategies for high- to low-level cellular modeling. Trends Biotechnol. 21(6), 255–262 (2003)
I. Wilson, Top-down versus bottom-up-rediscovering physiology via systems biology? Mol. Syst. Biol. 3, 113 (2007)
D. Noble, Prologue: mind over molecule: activating biological demons. Ann. N. Y. Acad. Sci. 1123, xi–xix (2008)
A.L. Barabási, N. Gulbahce, J. Loscalzo, Network medicine: a network-based approach to human disease. Nat. Rev. Genet. 12, 56–68 (2011)
D. Noble, Evolution viewed from physics, physiology and medicine. Interface Focus 7, 20160159 (2017)
J. Huxley, Evolution in Action (Harper and Brothers, New York, 1952), p. 152
T. Dobzhansky, Nothing in biology makes sense except in the light of evolution. Am. Biol. Teach. 35, 125–129 (1973)
S.J. Gould, The Structure of Evolutionary Theory (Harvard University Press, Cambridge, 2002)
K. Ruiz-Mirazo, J. Juli Peretó, A. Moreno, A universal definition of life: autonomy and open-ended evolution. Orig. Life Evolut. Biosph. 34(3), 323–346 (2004)
M. Montévil, Measurement in biology is methodized by theory. Biol. Philos. 34, 35 (2019)
A.P. Arkin, Synthetic cell biology. Curr. Opin. Biotechnol. 12(6), 638–644 (2001)
R. Brent, A partnership between biology and engineering. Nat. Biotechnol. 22(10), 1211–1214 (2004)
S.A. Benner, A.M. Sismour, Synthetic biology. Nat. Rev. Genet. 6(7), 533–543 (2005)
D. Endy, Foundations for engineering biology. Nature 438(7067), 449–453 (2005)
P.M. Boyle, P.A. Silver, Harnessing nature’s toolbox: regulatory elements for synthetic biology. J. R. Soc. Interface 6(Suppl 4), S535–546 (2009)
G.T. Reeves, S.E. Fraser, Biological systems from an engineer’s point of view. PLoS Biol. 7(1), e21 (2009)
C. Kiel, E. Yus et al., Engineering signal transduction pathways. Cell 140(1), 33–47 (2010)
P.S. Freemont, R.I. Kitney, Synthetic Biology—A Primer (Imperial College Press, London, 2012)
D.G. Gibson, C.A. Hutchison, H.O. Smith, J.C. Venter (eds.), Synthetic Biology—Tools for Engineering Biological Systems. (Cold Spring Harbor Laboratory Press, Cold Spring Harbor, New York, 2017)
P. Kohl, D. Noble, Systems biology and the virtual physiological human. Mol. Syst. Biol. 5, 292 (2009)
M. OreÍic, J. Lötjönen, H. Soininen, Systems medicine and the integration of bioinformatic tools for the diagnosis of Alzheimer’s disease. Genome Med. 1, 83 (2009)
G. Siest, M.A. Nezhad, D. Bagrel, S. El Shamieh, D. Lambert, N.C. Ndiaye, P. Shahabi, S. Visvikis-Siest, Functional genomics towards personalized healthcare and systems medicine. Pers. Med. 8, 227–242 (2011)
L. Hood, M. Flores, A personal view on systems medicine and the emergence of proactive P4 medicine: predictive, preventive, personalized and participatory. New Biotechnol. 29, 613–624 (2012)
L. Hood, R. Balling, C. Auffray, Revolutionizing medicine in the 21st century through systems approaches. Biotechnol. J. 7, 992–1001 (2012)
L. Hood, C. Auffray, Participatory medicine: a driving force for revolutionizing healthcare. Genome Med. 5, 110 (2013)
O. Wolkenhauer, C. Auffray, R. Jaster, G. Steinhoff, O. Dammann, The road from systems biology to systems medicine. Pediatr. Res. 73, 502–507 (2013)
M. Gustafsson, C.E. Nestor, H. Zhang, A.L. Barabási, S. Baranzini, S. Brunak, K.F. Chung, H.J. Federoff, A.C. Gavin, R.R. Meehan, P. Picotti, M.À. Pujana, N. Rajewsky, K.G. Smith, P.J. Sterk, P. Villoslada, M. Benson, Modules, networks and systems medicine for understanding disease and aiding diagnosis. Genome Med. 6, 82 (2014)
C. Zhang, Q. Hua, Applications of genome-scale metabolic models in biotechnology and systems medicine. Front Physiol. 6, 413 (2016)
M. Benson, Clinical implications of omics and systems medicine: focus on predictive and individualized treatment. J. Intern. Med. 279, 229–240 (2016)
F. Iris, Psychiatric systems medicine: closer at hand than anticipated but not with the expected portrait. Pharmacopsychiatry 45, S12–21 (2012)
P.D. Caie, K. Schuur, A. Oniscu, P. Mullen, P.A. Reynolds, D.J. Harrison, Human tissue in systems medicine. FEBS J. 280, 5949–5956 (2013)
M.L. Würstle, E. Zink, J.H. Prehn, M. Rehm, From computational modelling of the intrinsic apoptosis pathway to a systems-based analysis of chemotherapy resistance: achievements, perspectives and challenges in systems medicine. Cell Death Dis. 5, e1258 (2014)
J.P. Boissel, C. Auffray, D. Noble, L. Hood, F.H. Boissel, Bridging systems medicine and patient needs. CPT Pharmacomet. Syst. Pharmacol. 4, e00026 (2015)
T. Tillmann, A.R. Gibson, G. Scott, O. Harrison, A. Dominiczak, P. Hanlon, Systems Medicine 2.0: potential benefits of combining electronic health care records with systems science models. J. Med. Internet Res. 17, e64 (2015)
T. Haase, D. Börnigen, C. Müller, T. Zeller, Systems medicine as an emerging tool for cardiovascular genetics. Front. Cardiovasc. Med. 3, 27 (2016)
J. Menche, E. Guney, A. Sharma, P.J. Branigan, M.J. Loza, F. Baribaud, R. Dobrin, A.L. Barabási, Integrating personalized gene expression profiles into predictive disease-associated gene pools. NPJ Syst. Biol. Appl. 3, 10 (2017)
D.M. Camacho, K.M. Collins, R.K. Powers, J.C. Costello, J.J. Collins, Next-generation machine learning for biological networks. Cell 173, 1581–1592 (2018)
U. Schmitz, O. Wolkenhauer, Systems Medicine (Springer, Dordrecht, 2016). https://doi.org/10.1007/978-1-4939-3283-2. (eBook)
A. Agustí, P. Sobradillo, B. Celli, Addressing the complexity of chronic obstructive pulmonary disease: from phenotypes and biomarkers to scale-free networks, systems biology, and P4 medicine. Am. J. Respir. Crit. Care Med. 183, 1129–1137 (2011)
D. Gomez-Cabrero, J. Menche, I. Cano, I. Abugessaisa, M. Huertas-Migueláñez, A. Tenyi, I. Marin de Mas, N.A. Kiani, F. Marabita, F. Falciani, K. Burrowes, D. Maier, P. Wagner, V. Selivanov, M. Cascante, J. Roca, A.L. Barabási, J. Tegnér, Systems medicine: from molecular features and models to the clinic in COPD. J. Transl. Med. 12, S4 (2014)
I. Marín de Mas, E. Fanchon, B. Papp, S. Kalko, J. Roca, M. Cascante, Molecular mechanisms underlying COPD-muscle dysfunction unveiled through a systems medicine approach. Bioinformatics 33, 95–103 (2017)
I.M.L. Augustin, M.A. Spruit, S. Houben-Wilke, F.M.E. Franssen, L.E.G.W. Vanfleteren, S. Gaffron, D.J.A. Janssen, E.F.M. Wouters, The respiratory physiome: clustering based on a comprehensive lung function assessment in patients with COPD. PLoS One 13, e0201593 (2018)
G. Noell, R. Faner, A. Agustí, From systems biology to P4 medicine: applications in respiratory medicine. Eur. Respir. Rev. 27, 170110 (2018)
A. Cesario, C. Auffray, P. Russo, L. Hood, P4 medicine needs P4 education. Curr. Pharm. Des. 20, 6071–6072 (2014)
D. Rozman, J. Acimovic, B. Schmeck, Training in systems approaches for the next generation of life scientists and medical doctors. Methods Mol. Biol. 1386, 73–86 (2016)
D. Gomez-Cabrero, F. Marabita, S. Tarazona, I. Cano, J. Roca, A. Conesa, P. Sabatier, J. Tegnér, Guidelines for developing successful short advanced courses in systems medicine and systems biology. Cell Syst. 5, 168–175 (2017)
D. Dias, Paulo Silva Cunha, J., Wearable health devices-vital sign monitoring, systems and technologies. Sensors (Basel) 18, E2414 (2018)
F. Qureshi, S. Krishnan, Wearable hardware design for the internet of medical things (IoMT). Sensors (Basel) 18, E3812 (2018)
L. Smarr, Quantifying your body: a how-to guide from a systems biology perspective. Biotechnol. J. 7, 980–991 (2012)
R. Chen, G.I. Mias, J. Li-Pook-Than, L. Jiang, H.Y. Lam, R. Chen, E. Miriami, K.J. Karczewski, M. Hariharan, F.E. Dewey, Y. Cheng, M.J. Clark, H. Im, L. Habegger, S. Balasubramanian, M. O’Huallachain, J.T. Dudley, S. Hillenmeyer, R. Haraksingh, D. Sharon, G. Euskirchen, P. Lacroute, K. Bettinger, A.P. Boyle, M. Kasowski, F. Grubert, S. Seki, M. Garcia, M. Whirl-Carrillo, M. Gallardo, M.A. Blasco, P.L. Greenberg, P. Snyder, T.E. Klein, R.B. Altman, A.J. Butte, E.A. Ashley, M. Gerstein, K.C. Nadeau, H. Tang, M. Snyder, Personal omics profiling reveals dynamic molecular and medical phenotypes. Cell 148, 1293–1307 (2012)
L. Hood, N.D. Price, Demystifying disease, democratizing health care. Sci. Transl. Med. 6, 225ed5 (2014)
H. Kitano, Artificial Intelligence to win the Nobel Prize and beyond: creating the engine for scientific discovery. AI Mag. 37, 39–49 (2016)
M. Saqi, J. Pellet, I. Roznovat, A. Mazein, S. Ballereau, B. De Meulder, C. Auffray, Systems medicine: the future of medical genomics, healthcare, and wellness. Methods Mol. Biol. 1386, 43–60 (2016)
N.D. Price, A.T. Magis, J.C. Earls, G. Glusman, R. Levy, C. Lausted, D.T. McDonald, U. Kusebauch, C.L. Moss, Y. Zhou, S. Qin, R.L. Moritz, K. Brogaard, G.S. Omenn, J.C. Lovejoy, L. Hood, A wellness study of 108 individuals using personal, dense, dynamic data clouds. Nat. Biotechnol. 35, 747–756 (2017)
H. Fröhlich, R. Balling, N. Beerenwinkel, O. Kohlbacher, S. Kumar, T. Lengauer, M.H. Maathuis, Y. Moreau, S.A. Murphy, T.M. Przytycka, M. Rebhan, H. Röst, A. Schuppert, M. Schwab, R. Spang, D. Stekhoven, J. Sun, A. Weber, D. Ziemek, B. Zupan, From hype to reality: data science enabling personalized medicine. BMC Med. 16, 150 (2018)
A. Mazein, M. Ostaszewski, I. Kuperstein, S. Watterson, N. Le Novère, D. Lefaudeux, B. De Meulder, J. Pellet, I. Balaur, M. Saqi, M.M. Nogueira, F. He, A. Parton, N. Lemonnier, P. Gawron, S. Gebel, P. Hainaut, M. Ollert, U. Dogrusoz, E. Barillot, A. Zinovyev, R. Schneider, R. Balling, C. Auffray, Systems medicine disease maps: community-driven comprehensive representation of disease mechanisms. NPJ Syst. Biol. Appl. 4, 21 (2018)
E.J. Topol, High-performance medicine: the convergence of human and artificial intelligence. Nat. Med. 25, 44–56 (2019)
H. Vogt, E. Ulvestad, T.E. Eriksen, L. Getz, Getting personal: can systems medicine integrate scientific and humanistic conceptions of the patient? J. Eval. Clin. Pract. 20, 942–952 (2014)
R. Berlin, R. Gruen, J. Best, Systems medicine-complexity within, simplicity without. J. Healthc. Inform. Res. 1, 119–137 (2017)
S. Schleidgen, S. Fernau, H. Fleischer, C. Schickhardt, A.K. Oßa, E.C. Winkler, Applying systems biology to biomedical research and health care: a précising definition of systems medicine. BMC Health Serv. Res. 17, 761 (2017)
R. Apweiler, T. Beissbarth, M.R. Berthold, N. Blüthgen, Y. Burmeister, O. Dammann, A. Deutsch, F. Feuerhake, A. Franke, J. Hasenauer, S. Hoffmann, T. Höfer, P.L. Jansen, L. Kaderali, U. Klingmüller, I. Koch, O. Kohlbacher, L. Kuepfer, F. Lammert, D. Maier, N. Pfeifer, N. Radde, M. Rehm, I. Roeder, J. Saez-Rodriguez, U. Sax, B. Schmeck, A. Schuppert, B. Seilheimer, F.J. Theis, J. Vera, O. Wolkenhauer, Whither systems medicine? Exp. Mol. Med. 50, e453 (2018)
R. Berlin, R. Gruen, J. Best, Systems medicine disease: disease classification and scalability beyond networks and boundary conditions. Front. Bioeng. Biotechnol. 6, 112 (2018)
C.E. Wheelock, V.M. Goss, D. Balgoma, B. Nicholas, J. Brandsma, P.J. Skipp, S. Snowden, D. Burg, A. D’Amico, I. Horvath, A. Chaiboonchoe, H. Ahmed, S. Ballereau, C. Rossios, K.F. Chung, P. Montuschi, S.J. Fowler, I.M. Adcock, A.D. Postle, S.E. Dahlén, A. Rowe, P.J. Sterk, C. Auffray, R. Djukanovic, U-BIOPRED Study Group, Application of’ omics technologies to biomarker discovery in inflammatory lung diseases. Eur. Respir. J. 42, 802–825 (2013)
C. Auffray, R. Balling, I. Barroso, L. Bencze, M. Benson, J. Bergeron, E. Bernal-Delgado, N. Blomberg, C. Bock, A. Conesa, S. Del Signore, C. Delogne, P. Devilee, A. Di Meglio, M. Eijkemans, P. Flicek, N. Graf, V. Grimm, H.J. Guchelaar, Y.K. Guo, I.G. Gut, A. Hanbury, S. Hanif, R.D. Hilgers, Á. Honrado, D.R. Hose, J. Houwing-Duistermaat, T. Hubbard, S.H. Janacek, H. Karanikas, T. Kievits, M. Kohler, A. Kremer, J. Lanfear, T. Lengauer, E. Maes, T. Meert, W. Müller, D. Nickel, P. Oledzki, B. Pedersen, M. Petkovic, K. Pliakos, M. Rattray, J.R. I Màs, R. Schneider, T. Sengstag, X. Serra-Picamal, W. Spek, L.A. Vaas, O. van Batenburg, M. Vandelaer, P. Varnai, P. Villoslada, J.A. Vizcaíno, J.P. Wubbe, G. Zanetti, Making sense of big data in health research: towards an EU action plan. Genome Med. 8, 71 (2016)
Y. Liang, A. Kelemen, Computational dynamic approaches for temporal omics data with applications to systems medicine. BioData Min. 10, 20 (2017)
B. De Meulder, D. Lefaudeux, A.T. Bansal, A. Mazein, A. Chaiboonchoe, H. Ahmed, I. Balaur, M. Saqi, J. Pellet, S. Ballereau, N. Lemonnier, K. Sun, I. Pandis, X. Yang, M. Batuwitage, K. Kretsos, J. van Eyll, A. Bedding, T. Davison, P. Dodson, C. Larminie, A. Postle, J. Corfield, R. Djukanovic, K.F. Chung, I.M. Adcock, Y.K. Guo, P.J. Sterk, A. Manta, A. Rowe, F. Baribaud, C. Auffray, U-BIOPRED Study Group and the eTRIKS Consortium, A computational framework for complex disease stratification from multiple large-scale datasets. BMC Syst. Biol. 12, 60 (2018)
C.X. Li, C.E. Wheelock, C.M. Sköld, Å.M. Wheelock, Integration of multi-omics datasets enables molecular classification of COPD. Eur. Respir. J. 51, 1701930 (2018)
B.N. Kholodenko, Cell-signalling dynamics in time and space. Nat. Rev. Mol. Cell. Biol. 7(3), 165–176 (2006)
H. Kitano, Towards a theory of biological robustness. Mol. Syst. Biol. 3, 137 (2007)
L. Alberghina, T. Hofer et al., Molecular networks and system-level properties. J. Biotechnol. 144(3), 224–233 (2009)
S.I. Berger, R. Iyengar, Network analyses in systems pharmacology. Bioinformatics 25(19), 2466–2472 (2009)
O. Wolkenhauer, C. Auffray, O. Brass, J. Clairambault, A. Deutsch, D. Drasdo, F. Gervasio, L. Preziosi, P. Maini, A. Marciniak-Czochra, C. Kossow, L. Kuepfer, K. Rateitschak, I. Ramis-Conde, B. Ribba, A. Schuppert, R. Smallwood, G. Stamatakos, F. Winter, H. Byrne, Enabling multiscale modeling in systems medicine. Genome Med. 6, 21 (2014)
J.M. Raser, E.K. O’Shea, Noise in gene expression: origins, consequences, and control. Science 309(5743), 2010–2013 (2005)
G. Balázsi, A. van Oudenaarden, J.J. Collins, Cellular decision making and biological noise: from microbes to mammals. Cell 144, 910–25 (2011)
M. Richard, G. Yvert, How does evolution tune biological noise? Front. Genet. 5, 374 (2014)
D. Jia, M.K. Jolly, P. Kulkarni, H. Levine, Phenotypic plasticity and cell fate decisions in cancer: insights from dynamical systems theory. Cancers (Basel) 9, E70 (2017)
C.S. Simon, A.K. Hadjantonakis, C. Schröter, Making lineage decisions with biological noise: lessons from the early mouse embryo. Wiley Interdiscip. Rev. Dev. Biol. 7, e319 (2018)
R. Noble, D. Noble, Harnessing stochasticity: how do organisms make choices? Chaos 28, 106309 (2018)
D. Noble, From genes to whole organs: connecting biochemistry to physiology. Novartis Found. Symp. 239, 111–123 (2001). (discussion 123-118, 150-119)
P. Hunter, P. Robbins et al., The IUPS human physiome project. Pflugers Arch. 445(1), 1–9 (2002)
D. Noble, Systems biology and the heart. Biosystems 83(2–3), 75–80 (2006)
S.R. Thomas, P. Baconnier et al., SAPHIR: a physiome core model of body fluid homeostasis and blood pressure regulation. Philos. Trans. A Math. Phys. Eng. Sci. 366(1878), 3175–3197 (2008)
J. Bassingthwaighte, P. Hunter et al., The cardiac physiome: perspectives for the future. Exp. Physiol. 94(5), 597–605 (2009)
D. Noble, Systems biology, the Physiome Project and oriental medicine. J. Physiol. Sci. 59(3), 249–251 (2009)
Thomas S. Randall, Kidney modeling and systems physiology. Wiley Interdiscip. Rev. Syst. Biol. Med. 1, 172–190 (2009)
M.H. Tawhai, E.A. Hoffman, C.L. Lin, The lung physiome: merging imaging-based measures with predictive computational models. Wiley Interdiscip. Rev. Syst. Biol. Med. 1, 61–72 (2009)
D. Noble, A. Garny, P.J. Noble, How the Hodgkin–Huxley equations inspired the cardiac physiome project. J. Physiol. 590, 2613–2628 (2012)
R.D. Britten, G.R. Christie, C. Little, A.K. Miller, C. Bradley, A. Wu, T. Yu, P. Hunter, P. Nielsen, FieldML, a proposed open standard for the physiome project for mathematical model representation. Med. Biol. Eng. Comput. 51, 1191–207 (2013)
P.J. Hunter, N.P. Smith, The cardiac physiome project. J. Physiol. 594, 6815–6816 (2016)
M. Viceconti, P. Hunter, The virtual physiological human: ten years after. Annu. Rev. Biomed. Eng. 18, 103–23 (2016)
D. Noble, Modelling the heart: insights, failures and progress. Bioessays 24(12), 1155–1163 (2002)
A. Hastings, M.A. Palmer, Mathematics and biology. A bright future for biologists and mathematicians? Science 299(5615), 2003–2004 (2003)
J.E. Cohen, Mathematics is biology’s next microscope, only better; biology is mathematics’ next physics, only better. PLoS Biol. 2(12), e439 (2004)
E.J. Crampin, M. Halstead et al., Computational physiology and the physiome project. Exp. Physiol. 89(1), 1–26 (2004)
R. Chaturvedi, C. Huang et al., On multiscale approaches to three-dimensional modelling of morphogenesis. J. R. Soc. Interface 2(3), 237–253 (2005)
G.S. Ayton, G.A. Voth, Multiscale simulation of transmembrane proteins. J. Struct. Biol. 157(3), 570–578 (2007)
I.M. van Leeuwen, C.M. Edwards et al., Towards a multiscale model of colorectal cancer. World J. Gastroenterol. 13(9), 1399–1407 (2007)
S. Bornholdt, Boolean network models of cellular regulation: prospects and limitations. J. R. Soc. Interface 5(Suppl 1), S85–94 (2008)
K.S. Burrowes, A.J. Swan et al., Towards a virtual lung: multi-scale, multi-physics modelling of the pulmonary system. Philos. Trans. A Math. Phys. Eng. Sci. 366(1879), 3247–3263 (2008)
E. Flenner, F. Marga et al., Relating biophysical properties across scales. Curr. Top. Dev. Biol. 81, 461–483 (2008)
B. Novak, J.J. Tyson, Design principles of biochemical oscillators. Nat. Rev. Mol. Cell Biol. 9(12), 981–991 (2008)
J. Southern, J. Pitt-Francis et al., Multi-scale computational modelling in biology and physiology. Prog. Biophys. Mol. Biol. 96(1–3), 60–89 (2008)
S. Cerutti, D. Hoyer et al., Multiscale, multiorgan and multivariate complexity analyses of cardiovascular regulation. Philos. Trans. A Math. Phys. Eng. Sci. 367(1892), 1337–1358 (2009)
L. Endler, N. Rodriguez et al., Designing and encoding models for synthetic biology. J. R. Soc. Interface 6(Suppl 4), S405–417 (2009)
A.J. Engler, P.O. Humbert et al., Multiscale modeling of form and function. Science 324(5924), 208–212 (2009)
M. Meier-Schellersheim, I.D. Fraser et al., Multiscale modeling for biologists. Wiley Interdiscip. Rev. Syst. Biol. Med. 1(1), 4–14 (2009)
W.W. Chen, M. Niepel et al., Classic and contemporary approaches to modelling biochemical reactions. Genes Dev. 24(17), 1861–1875 (2010)
F. Lévi, A. Okyar et al., Circadian timing in cancer treatments. Annu. Rev. Pharmacol. Toxicol. 50, 377–421 (2010)
B. de Bono, P. Hunter, Integrating knowledge representation and quantitative modelling in physiology. Biotechnol. J. 7, 958–972 (2012)
D.P. Nickerson, D. Ladd, J.R. Hussan, S. Safaei, V. Suresh, P.J. Hunter, C.P. Bradley, Using CellML with OpenCMISS to simulate multi-scale physiology. Front. Bioeng. Biotechnol. J. 2, 79 (2015)
D. Waltemath, O. Wolkenhauer, How modeling standards, software, and initiatives support reproducibility in systems biology and systems medicine. IEEE Trans. Biomed. Eng. 63, 1999–2006 (2016)
O. Wolkenhauer, M. Mesarovic, Feedback dynamics and cell function: why systems biology is called systems biology. Mol. Biosyst. 1(1), 14–16 (2005)
C. Trefois, P.M. Antony, J. Goncalves, A. Skupin, R. Balling, Critical transitions in chronic disease: transferring concepts from ecology to systems medicine. Curr. Opin. Biotechnol. 34, 48–55 (2015)
G. Longo, M. Montévil, From physics to biology by extending criticality and symmetry breakings. Prog. Biophys. Mol. Biol. 106, 340–347 (2011)
A.M. Soto, G. Longo, P.A. Miquel, M. Montévil, M. Mossio, N. Perret, A. Pocheville, C. Sonnenschein, Towards a theory of organisms: three founding principle in search of a useful integration. Prog. Biophys. Mol. Biol. 122, 77–82 (2016)
J.H. Brown, G.B. West, Scaling in Biology (Oxford University Press, Oxford, 2000)
G.B. West, W.H. Woodruff et al., Allometric scaling of metabolic rate from molecules and mitochondria to cells and mammals. Proc. Natl. Acad. Sci. USA 99(Suppl 1), 2473–2478 (2002)
G.B. West, J.H. Brown, The origin of allometric scaling laws in biology from genomes to ecosystems: towards a quantitative unifying theory of biological structure and organization. J. Exp. Biol. 208(Pt 9), 1575–1592 (2005)
G.B. West, A. Bergman, Toward a systems biology framework for understanding aging and health span. J. Gerontol. A Biol. Sci. Med. Sci. 64, 205–208 (2009)
G.B. West, Scale (Penguin Press, New York, 2017)
C.R. White, R.S. Seymour, Allometric scaling of mammalian metabolism. J. Exp. Biol. 208, 1611–1619 (2005)
D.S. Glazier, The 3/4-power law is not universal: evolution of isometric, ontogenetic metabolic scaling in pelagic animals. BioScience 56, 325–332 (2006)
M. Montévil, G. Longo, Perspectives On Organisms: Biological Time, Symmetries And Singularities (Springer, Berlin, 2014)
A.V. Melkikh, D.K.F. Meijer, On a generalized Levinthal’s paradox: the role of long and short range interactions in complex bio-molecular reactions, including protein and DNA folding. Prog. Biophys. Mol. Biol. 132, 57–79 (2018)
L. Nottale, Fractals and the quantum theory of space-time. Int. J. Mod. Phys. A A4, 5047–5117 (1989)
L. Nottale, The theory of scale relativity. Int. J. Mod. Phys. A 7, 4899 (1992)
L. Nottale, Scale relativity, fractal space-time and quantum mechanics. Chaos Solitons Fractals 4, 361 (1994)
L. Nottale, Scale relativity and quantization of extra-solar planetary systems. Astron. Astrophys. Lett. 315, L9 (1996)
L. Nottale, La relativité dans tous ses états (Hachette, Paris, 1998)
L. Nottale, Generalized quantum potentials. J. Phys. A Math. Theor. 42, 275306 (2009). arXiv:0812.0941
I. Prigogine, C. George, F. Henin, Dynamical and statistical descriptions of n-body systems. Physica 45, 418–434 (1969)
I. Prigogine, C. George, F. Henin, L. Rosenfeld, A unified formulation of dynamics and thermodynamics. Chem. Scr. 4, 5–32 (1973)
I. Prigogine, T. Petrosky, H. Hasegawa, S. Tasaki, Integrability and chaos in classical and quantum mechanics. Chaos Solitons Fractals 1, 3–24 (1991)
I. Prigogine, The End of Certainty: Time, Chaos, and the New Laws of Nature (The Free Press, New York, 1997)
L. Nottale, Scale relativity and fractal space-time: theory and applications. in Proceedings of First International Conference on the Evolution and Development of the Universe (8–9 October 2008, ENS, Paris, 2008)
P. Turner, L. Nottale, The physical principles underpinning self-organization in plants. Prog. Biophys. Mol. Biol. 123, 48–73 (2017)
P. Turner, L. Nottale, J. Zhao, E. Pesquet, New insights into the physical processes that underpin cell division and the emergence of different cellular and multicellular structures. Prog. Biophys. Mol. Biol. 150, 13–42 (2020)
P. Turner, L. Nottale, The origins of macroscopic quantum coherence in high temperature super conductivity. Phys. C 515, 15–30 (2015)
P. Turner, L. Nottale, A new ab initio approach to the development of high temperature superconducting materials. J. Supercond. Nov. Magn. 29, 3113–3118 (2016). https://doi.org/10.1007/s10948-016-3756-z
M. Fratini, N. Poccia, A. Ricci, G. Campi, M. Burghammer, G. Aeppli, A. Bianconi, Scale-free structural organization of oxygen interstitials in La2CuO4+y. Nature 466, 841–844 (2010)
N. Poccia, A. Ricci, A. Bianconi, Fractal structure favouring superconductivity at high temperatures in a stack of membranes near a strain quantum critical point. J. Supercond. Nov. Magn. 24, 1195–1200 (2011)
N. Poccia, A. Ricci, G. Campi, M. Fratini, A. Puri, D. Di Gioacchino, A. Marchelli, M. Reynolds, M. Burghammer, N.L. Saini, G. Aeppli, A. Bianconi, Optimum inhomogeneity of local lattice distortions in \(La_2CuO_{4+y}\). Proc. Natl. Acad. Sci. USA 109(39), 15685–15690 (2012)
W.H. Zurek, Decoherence, einselection, and the quantum origins of the classical. Rev. Mod. Phys. 75, 715 (2003)
M. Schlosshauer, The quantum-to-classical transition and decoherence. arXiv:1404.2635v1 [quant-ph] (2014)
M. Montévil, M. Mossio, The inert vs. the living state of matter: extended criticality, time geometry, anti-entropy–an overview. Front. Physiol 3, 39 (2012)
M. Montévil, M. Mossio, Biological organization as closure of constraints. J. Theor. Biol. 7, 179–191 (2015)
F.G. Varela, H.R. Maturana, R. Uribe, Autopoiesis: the organization of living systems, its characterization and a model. Curr. Mod. Biol. 5, 187–196 (1974)
S.A. Kauffman, Autocatalytic sets of proteins. J. Theor. Biol. 119, 1–24 (1986)
D. Segré, D. Lancet, Composing life. EMBO Rep. 1, 217–222 (2000)
D. Lancet, R. Zidovetzki, O. Markovitch, Systems protobiology: origin of life in lipid catalytic networks. J. R. Soc. Interface 15, 20180159 (2018)
A. Kahana, D. Lancet, Protobiotic systems chemistry analyzed by molecular dynamics. Life 9, E38 (2019)
G. Vattay, S. Kauffman, Quantum biology on the edge of quantum chaos. arXiv:1202.6433v1 (2012)
F. Quochi, F. Cordella, A. Mura, G. Bongiovanni, F. Balzer, H.-G. Rubahn, One-dimensional random lasing in a single organic nanofiber. J. Phys. Chem. B 109, 21690–21693 (2005)
B. Zhang, W. Song, P. Pang, Y. Zhao, G. Vattay, S. Lindsay, Observation of giant conductance fluctuations in a protein. Nano Futures 1(3), 035002 (2017)
M.N. Célérier, L. Nottale, The Pauli equation in scale relativity. J. Phys. A 39, 12565 (2006). arXiv:quant-ph/0609107v1
P. Turner, M. Kowalczyk, A. Reynolds, New Insights into the Micro-fibril Architecture of the Wood Cell Wall (COST Action E54 Book. COST Office, Brussels, 2011)
S.L. Adler, Quaternionic Quantum Mechanics and Quantum Fields (Oxford University Press, New York, 1995)
L. David, Y. Ben-Harosh, E. Stolovicki, L.S. Moore, M. Nguyen, R. Tamse, J. Dean, E. Mancera, L.M. Steinmetz, E. Braun, Multiple genomic changes associated with reorganization of gene regulation and adaptation in yeast. Mol. Biol. Evol. 30, 1514–1526 (2013)
A. De Loof, The cell’s self-generated “electrome”: the biophysical essence of the immaterial dimension of Life? Commun. Integr. Biol. 9(5), e1197446 (2016). https://doi.org/10.1080/19420889.2016.1197446
M. Crabtree, T. Nott, These Organelles have no membranes. The Scientist. (December 2018). https://www.the-scientist.com/features/these-organelles-have-nomembranes-65090
E. Eveno, C. Auffray, L. Nottale, Application de la relativité d’échelle chez l’amibe Dictyostelium discoideum. Premières Rencontres d’Avignon (2007–2009) autour de la Relativité d’Echelle, Actes Avignon, sous la direction de L. Nottale et Ph. Martin (2012)
J.J. Kupiec, The Origins of the Individuals (World Scientific, Singapore, 2009)
P.A. Miquel, S.Y. Su-Young Hwang, From physical to biological individuation. Prog. Biophys. Mol. Biol. 122, 51–57 (2016)
D. Noble, Central dogma or central debate? Physiology 33, 246–249 (2018)
D. Noble, Cardiac action and pacemaker potentials based on the Hodgkin–Huxley equations. Nature 188, 495–497 (1960)
D. Noble, A modification of the Hodgkin–Huxley equations applicable to Purkinje fibre action and pace-maker potentials. J. Physiol. 160, 317–352 (1962)
D. DiFrancesco, D. Noble, A model of cardiac electrical activity incorporating ionic pumps and concentration changes. Philos. Trans. R. Soc Lond. B Biol. Sci. 307(1133), 353–398 (1985)
D.W. Hilgemann, D. Noble, Excitation-contraction coupling and extracellular calcium transients in rabbit atrium: reconstruction of basic cellular mechanisms. Proc. R. Soc. Lond. B Biol. Sci. 230(1259), 163–205 (1987)
K.H. ten Tusscher, D. Noble et al., A model for human ventricular tissue. Am. J. Physiol. Heart Circ. Physiol. 286(4), H1573–1589 (2004)
C.H. Luo, Y. Rudy, A dynamic model of the cardiac ventricular action potential. II. Afterdepolarizations, triggered activity, and potentiation. Circ. Res. 74(6), 1097–1113 (1994)
C.M. Lloyd, M.D. Halstead et al., CellML: its future, present and past. Prog. Biophys. Mol. Biol. 85(2–3), 433–450 (2004)
A. Garny, D. Noble et al., Dimensionality in cardiac modelling. Prog. Biophys. Mol. Biol. 87(1), 47–66 (2005)
P.K. Shreenivasaiah, S.H. Rho et al., An overview of cardiac systems biology. J. Mol. Cell. Cardiol. 44(3), 460–469 (2008)
A. Garny, D. Noble et al., Cellular Open Resource (COR): current status and future directions. Philos. Trans. A Math. Phys. Eng. Sci. 367(1895), 1885–1905 (2009)
R.L. Winslow, A. Varghese et al., Generation and propagation of ectopic beats induced by spatially localized Na-K pump inhibition in atrial network models. Proc. Biol. Sci. 254(1339), 55–61 (1993)
M. Allessie, J. Ausma et al., Electrical, contractile and structural remodeling during atrial fibrillation. Cardiovasc. Res. 54(2), 230–246 (2002)
D.M. Hodgson, L.V. Zingman et al., Cellular remodeling in heart failure disrupts K(ATP) channel-dependent stress tolerance. EMBO J. 22(8), 1732–1742 (2003)
P. Kohl, C. Bollensdorff et al., Effects of mechanosensitive ion channels on ventricular electrophysiology: experimental and theoretical models. Exp. Physiol. 91(2), 307–321 (2006)
P. Kohl, D. Noble, Life and mechanosensitivity. Prog. Biophys. Mol. Biol. 97(2–3), 159–162 (2008)
K. Tai, P. Fowler, Y. Mokrab, P. Stansfeld, M.S. Sansom, Molecular modeling and simulation studies of ion channel structures, dynamics and mechanisms. Methods Cell. Biol. 90, 233–265 (2008)
S.A. Niederer, M. Fink et al., A meta-analysis of cardiac electrophysiology computational models. Exp. Physiol. 94(5), 486–495 (2009)
R. Hinch, An analytical study of the physiology and pathology of the propagation of cardiac action potentials. Prog. Biophys. Mol. Biol. 78(1), 45–81 (2002)
G. Iribe, C.W. Ward et al., Axial stretch of rat single ventricular cardiomyocytes causes an acute and transient increase in Ca2+ spark rate. Circ. Res. 104(6), 787–795 (2009)
L. Nottale (2019). Scale relativity of the proton radius: solving the puzzle. arXiv:1904.05772 (2019)
L. Nottale, Quantum-like gravity waves and vortices in a classical fluid (2009). arXiv:0901.1270
L. Nottale, Scale relativity and fractal space-time: applications to quantum physics, cosmology and chaotic systems. Chaos Solitons Fractals 7, 877 (1996)
D. da Rocha, L. Nottale, Gravitational structure formation in scale relativity. Chaos Solitons Fractals 16, 565 (2003)
L. Nottale, Scale-relativistic cosmology. Chaos Solitons Fractals 16, 539 (2003)
B. Tadmor, B. Tidor, Interdisciplinary research and education at the biology-engineering-computer science interface: a perspective. Drug Discov. Today 10(17), 1183–1189 (2005)
Acknowledgements
Our work has been supported in part by the CNRS, Oxford University and Edinburgh Napier University. We thank our colleagues from the Systemoscope Consortium and the Physiome Project for useful discussions and insights. We also thank the anonymous reviewers for constructive comments, which helped to improve the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by T. Duguet
The original version of this article was revised due to a retrospective Open Access order.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Auffray, C., Noble, D., Nottale, L. et al. Progress in integrative systems biology, physiology and medicine: towards a scale-relative biology. Eur. Phys. J. A 56, 88 (2020). https://doi.org/10.1140/epja/s10050-020-00090-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epja/s10050-020-00090-3