Abstract
We review the physics opportunities of the Future Circular Collider, covering its e+e-, pp, ep and heavy ion programmes. We describe the measurement capabilities of each FCC component, addressing the study of electroweak, Higgs and strong interactions, the top quark and flavour, as well as phenomena beyond the Standard Model. We highlight the synergy and complementarity of the different colliders, which will contribute to a uniquely coherent and ambitious research programme, providing an unmatchable combination of precision and sensitivity to new physics.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Preface
The 2013 Update of the European Strategy for Particle Physics (ESPPU) [1] stated, inter alia, that “...Europe needs to be in a position to propose an ambitious post-LHC accelerator project at CERN by the time of the next Strategy update” and that “CERN should undertake design studies for accelerator projects in a global context, with emphasis on proton–proton and electron-positron high-energy frontier machines. These design studies should be coupled to a vigorous accelerator R&D programme, including high-field magnets and high-gradient accelerating structures, in collaboration with national institutes, laboratories and universities worldwide”.
In response to this recommendation, the Future Circular Collider (FCC) study was launched [2] as a world-wide international collaboration under the auspices of the European Committee for Future Accelerators (ECFA). The FCC study was mandated to deliver a Conceptual Design Report (CDR) in time for the following update of the European Strategy for Particle Physics.
European studies of post-LHC circular energy-frontier accelerators at CERN had actually started a few years earlier, in 2010–2013, for both hadron [3,4,5] and lepton colliders [6,7,8], at the time called HE-LHC/VHE-LHC and LEP3/DLEP/TLEP, respectively. In response to the 2013 ESPPU, in early 2014 these efforts were combined and expanded into the FCC study.
After 10 years of physics at the Large Hadron Collider, the particle physics landscape has greatly evolved. The proposed lepton collider FCC-ee is a high-precision instrument to study the Z, W, Higgs and top particles, and offers great direct and indirect sensitivity to new physics. Most of the FCC-ee infrastructure could be reused for a subsequent hadron collider FCC-hh. The latter would provide proton–proton collisions at a centre-of-mass energy of 100 TeV and directly produce new particles with masses of up to several tens of TeV. It will also measure the Higgs self-coupling with unprecedented precision. Heavy-ion collisions and ep collisions would contribute to the breadth of the overall FCC programme.
Five years of intense work and a steadily growing international collaboration have resulted in the present Conceptual Design Report, consisting of four volumes covering the physics opportunities, technical challenges, cost and schedule of several different circular colliders, some of which could be part of an integrated programme extending until the end of the twenty-first century.
Geneva, December 2018


2 Executive summary
In 10 years of physics at the LHC, the particle physics landscape has greatly evolved. Today, an integrated Future Circular Collider programme consisting of a luminosity-frontier highest-energy lepton collider followed by an energy-frontier hadron collider promises the most far-reaching particle physics programme that foreseeable technology can deliver.
The legacy of the first phase of the LHC physics programme can be briefly summarised as follows: (a) the discovery of the Higgs boson, and the start of a new phase of detailed studies of its properties, aimed at revealing the deep origin of electroweak (EW) symmetry breaking; (b) the indication that signals of new physics around the TeV scale are, at best, elusive; and (c) the rapid advance of theoretical calculations, whose constant progress and reliability inspire confidence in the key role of ever improving precision measurements, from the Higgs to the flavour sectors. Last but not least, the LHC success has been made possible by the extraordinary achievements of the accelerator and of the detectors, whose performance is exceeding all expectations.
The future circular collider, FCC, hosted in a 100 km tunnel, builds on this legacy, and on the experience of previous circular colliders (LEP, HERA and the Tevatron). The \(\mathrm{e}^+\mathrm{e}^-\) collider (FCC-ee) would operate at multiple centre of mass energies \(\sqrt{s}\), producing \(5\times 10^{12}\,\hbox {Z}^0\) bosons (\(\sqrt{s}\sim \,91\,\hbox {GeV}\)), \(10^{8}\) WW pairs (\(\sqrt{s}\sim \,160\,\hbox {GeV}\)), over \(10^{6}\) Higgses (\(\sqrt{s}\sim \,240\,\hbox {GeV}\)), and over \(10^{6}\) tŧ pairs (\(\sqrt{s}\sim \,350\)–\(365\,\hbox {GeV}\)). The 100 TeV pp collider (FCC-hh) is designed to collect a total luminosity of \(20\,\hbox {ab}^{-1}\), corresponding to the production of e.g. more than \(10^{10}\) Higgs bosons produced. FCC-hh can also be operated with heavy ions (e.g. PbPb at \(\sqrt{s_\mathrm{NN}}=39\,\hbox {TeV}\)). Optionally, the FCC-eh, with 50 TeV proton beams colliding with 60 GeV electrons from an energy-recovery linac, would generate \(\sim 2\,\hbox {ab}^{-1}\) of \(3.5\,\hbox {TeV}\) ep collisions.
The integrated FCC programme sets highly ambitious performance goals for its accelerators and experiments. For example, it will:
-
(a)
Uniquely map the properties of the Higgs and EW gauge bosons, pinning down their interactions with an accuracy order(s) of magnitude better than today, and acquiring sensitivity to, e.g., the processes that, during the time span from \(10^{-12}\) and \(10^{-10}\,\hbox {s}\) after the Big Bang, led to the creation of today’s Higgs vacuum field.
-
(b)
Improve by close to an order of magnitude the discovery reach for new particles at the highest masses and by several orders of magnitude the sensitivity to rare or elusive phenomena at low mass. In particular, the search for dark matter (DM) at FCC could reveal, or conclusively exclude, DM candidates belonging to large classes of models, such as thermal WIMPs (weakly interacting massive particles).
-
(c)
Probe energy scales beyond the direct kinematic reach, via an extensive campaign of precision measurements sensitive to tiny deviations from the Standard Model (SM) behaviour. The precision will benefit from event statistics (for each collider, typically several orders of magnitude larger than anything attainable before the FCC), improved theoretical calculations, synergies within the programme (e.g. precise \(\alpha _s\) and parton distribution functions (PDF) provided to FCC-hh by FCC-ee and FCC-eh, respectively) and suitable detector performance.
A more complete overview of the FCC physics potential is presented in CDR volumes 1–3. This document highlights some of the most significant findings of those studies that, in addition to setting targets for the FCC achievements, have driven the choice of the collider parameters (energy, luminosity) and their operation plans, and contributed to the definition of the critical detector features and parameters.
3 Higgs studies
The achievements and prospects of the LHC Higgs programme are opening a new era, in which the Higgs boson is moving from being the object of a search, to become an exploration tool. The FCC positions itself as the most powerful heir of the future LHC Higgs’ legacy. On one side it will extend the range of measurable Higgs properties (e.g. its elusive \(\mathrm{H}\rightarrow \mathrm{gg}, \mathrm{c}\bar{\mathrm{c}}\) decays, its total width, and its self-coupling), allowing more incisive and model-independent determinations of its couplings. On the other, the combination of superior precision and energy reach provides a framework in which indirect and direct probes of new physics complement each other, and cooperate to characterise the nature of possible discoveries.
The FCC-ee will measure Higgs production inclusively, from its presence as a recoil to the Z in \(10^6\) \(\mathrm{e}^+\mathrm{e}^- \rightarrow {\mathrm{ZH}}\) events. This allows the absolute measurement of the Higgs coupling to the Z, which is the starting point for the model-independent determination of its total width, and thus of its other couplings through branching ratio measurements. The leading Higgs couplings to SM particles (denoted \(g_{\mathrm{HXX}}\) for particle X) will be measured by FCC-ee with a sub-percent precision, as shown in Table S.1. The FCC-ee will also provide a first measurement of the Higgs self-coupling to 32%. As a result of the model dependence being removed by FCC-ee, a fully complementary programme will be possible at FCC-hh and FCC-eh, to complete the picture of Higgs boson properties. This will include the measurement to the percent level of rare Higgs decays such as \(\hbox {H}\rightarrow \upgamma \upgamma \), \(\upmu \upmu \), \(\hbox {Z}\upgamma \), the detection of invisible ones (\(\hbox {H}\rightarrow 4\upnu \)), the measurement of the \(g_{\mathrm{Htt}}\) coupling with percent precision and the measurement of the Higgs self-coupling to 5–7%, as shown for FCC-hh in Table S.2.
The Higgs couplings to all gauge bosons and to the charged fermions of the second and third generation, except the strange quark, will be known with a precision ranging from a few per mil to \(\sim 1\%\). In addition, the prospect of measuring, or at least strongly constraining, the couplings to the three lightest quarks and also to the electron by a special FCC-ee run at \(\sqrt{\mathrm{s}}= \mathrm{m}_\mathrm{H}\) is being evaluated. The synergies among all components of the FCC Higgs programme are underscored by a global fit of Higgs parameters, shown in Fig. S.1, and discussed in full detail in CDR volume 1. Finally, it is worth noting that the tagged \(\mathrm{H} \rightarrow {\mathrm{gg}}\) channel at FCC-ee will offer an unprecedented sample of pure high energy gluons.
One-\(\sigma \) precision reach at the FCC on the effective single Higgs couplings, Higgs self-coupling, and anomalous triple gauge couplings in the EFT framework. Absolute precision in the EW measurements is assumed. The different bars illustrate the improvements that would be possible by combining each FCC stage with the previous knowledge at that time (precisions at each FCC stage considered individually, reported in Tables S.1 and S.2 in the \(\kappa \) framework, are quite different)
By way of synergy and complementarity, the integral FCC programme appears to be the most powerful future facility for a thorough examination of the Higgs boson and EWSB.
4 Electroweak precision measurements
As proven by the discoveries that led to the consolidation of the SM, EW precision observables (EWPO) can play a key role in establishing the existence of new physics and guiding its theoretical interpretation. It is anticipated that this will continue to be the case well after the HL-LHC, and expect the FCC to lead the progress in precision measurements, as improved precision equates to discovery potential.
The broad set of EWPO’s accessible to FCC-ee, thanks to immense statistics at the various beam energies and to the exquisite centre-of-mass energy calibration, will give it access to various possible sources and manifestations of new physics. Direct effects could occur because of the existence of a new interaction such as a \(\hbox {Z}^\prime \) or \(\hbox {W}^\prime \), which could mix or interfere with the known ones; from the mixing of light neutrinos with their heavier right handed counterparts, which would effectively reduce their coupling to the W and Z in a flavour dependent way. New weakly coupled particles can affect the W, Z or photon propagators via loops, producing flavour independent corrections to the relation between the Z mass and the W mass or the relation between the Z mass and the effective weak mixing angle; or the loop corrections can occur as vertex corrections, leading to flavour dependent effects as is the case in the SM for e.g. the \(\hbox {Z}\rightarrow \mathrm{b}\bar{\mathrm{b}}\) couplings. The measurements above the tŧ production threshold, directly involving the top quark, as well as precision measurements of production and decays of \(10^{11}\uptau \)’s and \(2\times 10^{12}\) b’s, will further enrich this programme. Table S.3 shows a summary of the target precision for EWPO’s at FCC-ee. The FCC-hh achieves indirect sensitivity to new physics by exploiting its large energy, benefiting from the ability to achieve precision of a previously unexpected level in pp collisions, as proven by the LHC. EW observables, such as high-mass lepton or gauge-boson pairs, have a reach in the multi-TeV mass range, as shown in Fig. S.2. Their measurement can expose deviations that, in spite of the lesser precision w.r.t. FCC-ee, match its sensitivity reach at high mass. For example, the new physics scale \(\Lambda \), defined by the dim-6 operator \(\hat{W}=1/\Lambda ^2 \, (D_\rho W^a_{\mu \nu })^2\), will be constrained by the measurement of high-mass \(\ell \nu \) pairs to \(\Lambda > 80~\hbox {TeV}\). High-energy scattering of gauge bosons, furthermore, is a complementary probe of EW interactions at short distances. The FCC-eh, with precision and energy in between FCC-ee and FCC-hh, integrates their potential well. For example, its ability to separate individual light quark flavours in the proton, gives it the best sensitivity to their EW couplings. Furthermore, its high energy and clean environment enable precision measurements of the weak coupling evolution at very large \(Q^2\). More details can be found in volume 1 of the FCC CDR. The FCC EW measurements are a crucial element of, and a perfect complement to, the FCC Higgs physics programme.
Left: integrated lepton transverse (dilepton) mass distribution in \({\mathrm{pp}}\rightarrow \hbox {W}^*\rightarrow \ell \upnu \) (\({\mathrm{pp}}\rightarrow \hbox {Z}^*/\upgamma ^*\rightarrow \ell ^+\ell ^-\)). One lepton family is included, with \(\vert \eta _\ell \vert <2.5\). Right: integrated invariant mass spectrum for the production of gauge boson pairs in the central kinematic range \(\vert y \vert <1.5\). No branching ratios included
Manifestations of models with a singlet-induced strong first order EWPT. Left: discovery potential at HL-LHC and FCC-hh, for the resonant di-Higgs production, as a function of the singlet-like scalar mass \(m_2\). \(4\uptau \) and \(\hbox {b}\bar{\hbox {b}}\upgamma \upgamma \) final states are combined. Right: correlation between changes in the HZZ coupling (vertical axis) and the HHH coupling scaled to its SM value (horizontal axis), in a scan of the models’ parameter space. All points give rise to a first order phase transition
5 The electroweak phase transition
Explaining the origin of the cosmic matter-antimatter asymmetry is a challenge at the forefront of particle physics. One of the most compelling explanations connects this asymmetry to the generation of elementary particle masses through electroweak symmetry-breaking (EWSB). This scenario relies on two ingredients: a sufficiently violent transition to the broken-symmetry phase, and the existence of adequate sources of CP-violation. As it turns out, these conditions are not satisfied in the SM, but they can be met in a variety of BSM scenarios. CP violation relevant to the matter-antimatter asymmetry can arise from new interactions over a broad range of mass scales, possibly well above 100 TeV. Exhaustively testing these scenarios may, therefore, go beyond the scope of the FCC. On the other hand, for the phase transition to be sufficiently strong, there must be new particles with masses typically below one TeV, whose interactions with the Higgs boson modify the Higgs potential energy in the early universe. Should they exist, these particles and interactions would manifest themselves at FCC, creating a key scientific opportunity and priority for the FCC, as shown by various studies completed to date.
The FCC should conclusively probe new states required by a strong 1st order EW phase transition.
As an example, we show the results of the study of the extension of the SM scalar sector with a single real singlet scalar. The set of model parameters leading to a strongly first order phase transition is analyzed from the perspective of a direct search, via the decays of the new singlet scalar to a pair of Higgs bosons, and of precision measurements of Higgs properties. The former case results in the plot on the left of Fig. S.3: FCC-hh with \(30\,\hbox {ab}^{-1}\) has sensitivity greater than 5 standard deviations to all relevant model parameters. For these models, the deviations in the Higgs self-coupling and in the Higgs coupling to the Z boson are then shown in the scatter plot on the right of Fig. S.3. With the exception of a small parameter range, most of these models lead to deviations within the sensitivity reach of FCC, allowing the cross-correlation of the direct discovery via di-Higgs decays to the Higgs property measurements. This will help the interpretation of a possible discovery, and assess its relevance for the nature of the EW phase transition.
6 Dark matter
No experiment, at colliders or otherwise, can probe the full range of dark matter (DM) masses allowed by astrophysical observations. However there is a very broad class of models for which theory motivates the GeV–10’s TeV mass scale, and which therefore could be in the range of the FCC. These are the models of weakly interacting massive particles (WIMPs), present during the early universe in thermal equilibrium with the SM particles. These conditions, broadly satisfied by many models of new physics, establish a correlation between the WIMP masses and the strength of their interactions, resulting in mass upper limits. While the absolute upper limit imposed by unitarity is around 110 TeV, most well motivated models of WIMP DM do not saturate this bound, but rather have upper limits on the DM mass in the TeV range. As an example, DM WIMP candidates transforming as a doublet or triplet under the SU(2) group of weak interactions, like the higgsinos and winos of supersymmetric theories, have masses constrained below \(\sim 1\) and \(\sim 3~\hbox {TeV}\), respectively. The full energy and statistics of FCC-hh are necessary to access these large masses. With these masses, neutral and charged components of the multiplets are almost degenerate due to SU(2) symmetry, with calculable mass splittings induced by electromagnetic effects, in the range of few hundred MeV. The peculiar signatures of these states are disappearing tracks, left by the decay of the charged partner to the DM candidate and a soft, unmeasured charged pion. Dedicated analysis, including detailed modeling of various tracker configurations and realistic pile-up scenarios, are documented in CDR volume 3. The results are shown in Fig. S.4.
The FCC covers the full mass range for the discovery of these WIMP Dark Matter candidates.
Expected discovery significance for higgsino and wino DM candidates at FCC-hh, with 500 pile-up collisions. The black and red bands show the significance using different layouts for the pixel tracker, as discussed in volume 3. The bands’ width represents the difference between two models for the soft QCD processes
7 Direct searches for new physics
At the upper end of the mass range, the reach for the direct observation of new particles will be driven by the FCC-hh. The extension with respect to the LHC will scale like the energy increase, namely by a factor of 5 to 7, depending on the process. The CDR detector parameters have been selected to guarantee the necessary performance up to the highest particle momenta and jet energies required by discovery of new particles with masses up to several tens of TeV. Examples of discovery reach for the production of several types of new particles, as obtained in dedicated detector simulation studies, are shown in Fig. S.5. They include \(\hbox {Z}^\prime \) gauge bosons carrying new weak forces and decaying to various SM particles, excited quarks \(\hbox {Q}^*\), and massive gravitons \(\hbox {G}_{\mathrm{RS}}\) present in theories with extra dimensions. Other standard scenarios for new physics, such as supersymmetry or composite Higgs models, will likewise see the high-mass discovery reach greatly increased. The top scalar partners will be discovered up to masses of close to 10 TeV, gluinos up to 20 TeV, and vector resonances in composite Higgs models up to masses close to 40 TeV. The direct discovery potential of FCC is not confined to the highest masses. In addition to the dark matter examples given before, volume 1 of the FCC CDR documents the broad, and in most cases unique, reach for less-than-weakly coupled particles, ranging from heavy sterile neutrinos (see Fig. S.5, right) down to the see-saw limit in a part of parameter space favorable for generating the baryon asymmetry of the Universe, to axions and dark photons.
The FCC has a broad, and in most cases unique, reach for less-than-weakly coupled particles. The Z running of FCC-ee is particularly fertile for such discoveries.
8 QCD matter at high density and temperature
Collisions of heavy ions at the energies and luminosities allowed by the FCC-hh will open new avenues in the study of collective properties of quark and gluons.
The thermodynamic behaviour of Quantum Chromodynamics (QCD) presents features that are unique amongst all other interactions. Collisions of heavy ions at the energies and luminosities allowed by the FCC-hh will open new avenues in the study of collective properties of quark and gluons, as extensively shown in the CDR volume 1. Heavy ions accelerated to FCC energies give access to an uncharted parton kinematic region at x down to \(10^{-6}\), which can be explored also exploiting the complementarity of proton–nucleus and electron–nucleus collisions at the FCC-hh/eh. The quark gluon plasma (QGP) could reach a temperature as high as 1 GeV, at which charm quarks start to contribute as active thermal degrees of freedom in the equation of state of the QGP. In the studies of the QGP with hard probes the FCC has a unique edge, thanks to cross section increases with respect to LHC by factors ranging from \(\sim 20\) for Z+jet production, to \(\sim 80\) for top production. Just one example is presented here: FCC will provide large rates of highly-boosted top quarks and the \(\mathrm{q}\overline{\mathrm{q}}\) jets from \(\hbox {t}\rightarrow \hbox {W}\rightarrow \mathrm{q}\overline{\mathrm{q}}\) are exposed to energy loss in the QGP with a time delay (see Fig. S.6-left), providing access to time-dependent density measurements for the first time. The effect of this time-delayed quenching can be measured using the reduction of the reconstructed W mass, as shown in Fig. S.6-right, where the modifications under different energy loss scenarios are considered as examples.
Left: FCC-hh mass reach for different s-channel resonances. Right: summary of heavy sterile neutrino discovery prospects at all FCC facilities. Solid lines are shown for direct searches at FCC-ee (black, in Z decays), FCC-hh (blue in W decays) and FCC-eh (in production from the incoming electron). The dashed line denotes the impact on precision measurements at the FCC-ee, it extends up to more than 60 TeV
9 Parton structure
The FCC-eh resolves the parton structure of the proton in an unprecedented range of x and \(\hbox {Q}^2\) to very high accuracy, providing a per mille accurate measurement of the strong coupling constant.
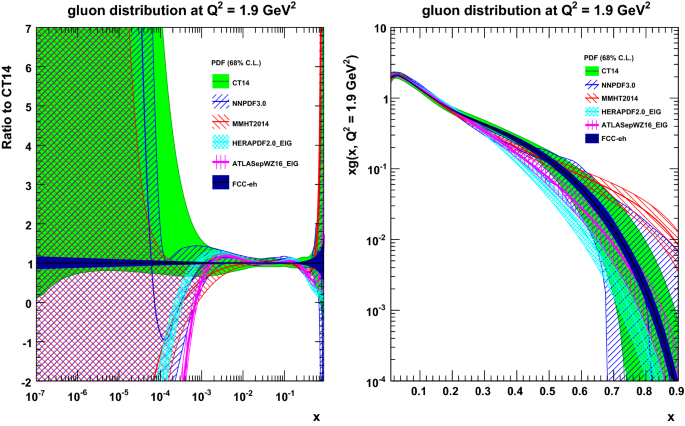
Deep inelastic scattering measurements at FCC-eh will allow the determination of the PDF luminosities with the precision shown in Fig. S.7. These results provide an essential input for the FCC-hh programme of precision measurements and improve the sensitivity of the search for new phenomena, particularly at high mass. The FCC-eh measurements will extend the exploration of parton dynamics into previously unexplored domains: the access to very low Bjorken-x is expected to expose the long-predicted BFKL dynamic behaviour and the gluon saturation phenomena required to unitarise the high-energy cross sections. The determination of the gluon luminosity at very small x will also link directly to ultra-high energy (UHE) neutrino astroparticle physics, enabling more reliable estimates of the relevant background rates.
Left: total delay time for the QGP energy-loss parameter \(\hat{q} = 4~\hbox {GeV}^2/\hbox {fm}\) as a function of the top transverse momentum (black dots) and its standard deviation (error bars). The average contribution of each component is shown as a coloured stack band. The dashed line corresponds to a \(\hat{q} = 1~\hbox {GeV}^2/\hbox {fm}\). Right: reconstructed W boson mass, as a function of the top \(p_T\). The upper axis refers to the average total time delay of the corresponding top \(p_T\) bin
Relative PDF uncertainties on parton-parton luminosities, resulting from the FCC-eh PDF set, as a function of the mass of the heavy object produced, \(M_X\), at \(\sqrt{s} = 100\) TeV. Shown are the gluon-gluon (top left), quark–antiquark (top right), quark-gluon (bottom left) and quark–quark (bottom right) luminosities
10 Flavor physics
The FCC flavour programme receives important contributions from all 3 machines, FCC-ee, hh, and eh.
The Z run of the FCC-ee will fully record, with no trigger, \(10^{12}\) \(\hbox {Z}\rightarrow \mathrm{b}\bar{\mathrm{b}}\) and \(\hbox {Z}\rightarrow \mathrm{c}\bar{\mathrm{c}}\) events. This will give high statistics of all b- and c-flavoured hadrons, making FCC-ee the natural continuation of the B-factories, Table S.4.
Of topical interest will be the study of possible lepton flavour and lepton number violation. FCC-ee, with detection efficiencies internally mapped with extreme precision, will offer 200000 \(\hbox {B}_{0}\rightarrow \mathrm{K}^{*}(892)\hbox {e}^+\hbox {e}^-\), 1000 \(\hbox {K}^{*}(892) \uptau ^+ \uptau ^-\) and 1000 (100) \(\hbox {B}_{s}\) (resp. \(\hbox {B}_0\)) events, one order of magnitude more than the LHCb upgrade. The determination of the CKM parameters will be correspondingly improved. First observation of CP violation in B mixing will be within reach; a global analysis of BSM contributions in box mixing processes, assuming Minimal Flavour Violation, will provide another, independent, test of BSM physics up to an energy scale of 20 TeV.
Tau physics in Z decays was shown to be extremely precise already at LEP; with \(1.7\times 10^{11}\) pairs, FCC-ee will achieve precision of \(10^{-5}\) or better for the leptonic branching ratios and the charged lepton-to-neutrino weak couplings – this allowing a measurement of \(G_F\) and tests of charged-weak-current universality at the \(10^{-5}\) precision level. Finally, lepton number violating processes, such \(\hbox {Z}\rightarrow \uptau \upmu /e\), \(\uptau \rightarrow 3 \upmu \), \(\hbox {e}\upgamma \) or \(\upmu \upgamma \), can be detected at the \(10^{-9}\)–\(10^{-10}\) level, offering sensitivity to several types of neutrino-mass generation models.
11 Introduction
In 10 years of physics at the LHC, the picture of the particle physics landscape has greatly evolved. The legacy of this first phase of the LHC physics programme can be briefly summarised as follows: (a) the discovery of the Higgs boson, and the start of a new phase of detailed studies of its properties, aimed at revealing the deep origin of electroweak (EW) symmetry breaking; (b) the indication that signals of new physics around the TeV scale are, at best, elusive; (c) the rapid advance of theoretical calculations, whose constant progress and reliability inspire confidence in the key role of ever improving precision measurements, from the Higgs to the flavour sectors. Last but not least, the LHC success has been made possible by the extraordinary achievements of the accelerator and of the detectors, whose performance is exceeding all expectations.
The future circular collider, FCC, hosted in a 100 km tunnel, builds on this legacy, and on the experience of previous circular colliders (LEP, HERA and the Tevatron). The \(\mathrm{e}^+\mathrm{e}^-\) collider (FCC-ee) would operate at multiple centre of mass energies \(\sqrt{s}\), producing \(10^{13}~\hbox {Z}^0\) bosons (\(\sqrt{s}\sim \,91\,\hbox {GeV}\)), \(10^{8}\) WW pairs (\(\sqrt{s}\sim \,160\,\hbox {GeV}\)), over \(10^{6}\) Higgses (\(\sqrt{s}\sim \,240\,\hbox {GeV}\)), and over \(10^{6}\) tŧ pairs (\(\sqrt{s}\sim \,350\)–\(365\,\hbox {GeV}\)). The 100 TeV pp collider (FCC-hh) is designed to collect a total luminosity of \(20\,\hbox {ab}^{-1}\), corresponding e.g. to more than \(10^{10}\) Higgs bosons produced. FCC-hh would also enable heavy-ion collisions, and its 50 TeV proton beams, with 60 GeV electrons from an energy-recovery linac, would generate \(\sim 2\,\hbox {ab}^{-1}\) of \(3.5\,\hbox {TeV}\) ep collisions at the FCC-eh.
The FCC sets highly ambitious performance goals for its accelerators and experiments, and promises the most far reaching particle physics programme that foreseeable technology can deliver. For example, in direct relation to the points above, the FCC will:
-
(a)
Uniquely map the properties of the Higgs and EW gauge bosons, pinning down their interactions with an accuracy order(s) of magnitude better than today, and acquiring sensitivity to, e.g., the processes that, during the time span from \(10^{-12}\) and \(10^{-10}\,\hbox {s}\) after the Big Bang, led to the creation of today’s Higgs vacuum field.
-
(b)
Improve by close to an order of magnitude the discovery reach for new particles at the highest masses and similarly increase the sensitivity to rare or elusive phenomena at low mass. In particular, the search for dark matter (DM) at FCC could reveal, or conclusively exclude, DM candidates belonging to large classes of models, such as thermal WIMPs (weakly interacting massive particles).
-
(c)
Probe energy scales beyond the direct kinematic reach, via an extensive campaign of precision measurements sensitive to tiny deviations from the Standard Model (SM) behaviour. The precision will benefit from event statistics (for each collider, typically several orders of magnitude larger than anything attainable before the FCC), improved theoretical calculations, synergies within the programme (e.g. precise \(\alpha _s\) and parton distribution functions provided to FCC-hh by FCC-ee and FCC-eh, respectively) and suitable detector performance.
This volume of the Conceptual Design Report is dedicated to an overview of the FCC physics potential. It focuses on the most significant targets of the potential FCC research programme but, for the sake of space, not covering a large body of science that will nevertheless be accessible (and which is documented in various other reports, listed in the Appendix). The studies presented here, in addition to setting plausible targets for the FCC achievements, have helped in making the choice of the colliders’ parameters (energy, luminosity) and their operation plans. Furthermore, these studies contributed to the definition of the critical detector features and parameters, as described in Volumes 2 and 3 of the CDR. While at first discussing the targets of each collider separately, the second part of this volume puts their synergy and complementarity in perspective, underscoring the added benefit to science brought by the unity and coherence of the whole programme.
In addition to summarising the outcome of the work done during this CDR phase of the FCC physics studies, for the benefit of the whole particle physics community, this document is intended to stimulate an expert discussion of the FCC physics potential, in the context of the forthcoming review of the European Strategy for Particle Physics. While occasionally technical, the average level is intended to benefit a general audience of colleagues in neighboring areas of physics, such as cosmology and astroparticle or cosmic ray physics. With this in mind, this introductory chapter now continues with a broader overview of the questions and challenges that may be left open by the end of the HL-LHC, illustrating the virtues that make the FCC the ideal instrument to address them. The chapter concludes with a description of the structure of this volume.
11.1 Physics scenarios after the LHC and the open questions
Quantum physics gives two alternatives to probe nature at smaller scales: high-energy particle collisions, which induce short-range interactions or produce heavy particles; and high-precision measurements, which can be sensitive to the ephemeral influence of heavy particles enabled by the uncertainty principle. The SM emerged out of these two approaches, with a variety of experiments worldwide during the past 40 years pushing both the energy and the precision frontiers. The discovery of the Higgs boson at the LHC is a perfect example: precise measurements of Z boson decays at previous lepton machines such as CERN’s Large Electron Positron (LEP) collider, pointed indirectly but unequivocally to the Higgs’ existence. But it was the LHCs mighty pp collisions that provided the high energy necessary to produce it directly. With the Higgs exploration fully under-way at the LHC, and the machine set to operate for the next 20 years, the time is ripe to consider what tool should come next to continue the journey. The Future Circular Collider (FCC) facility is emerging as an ideal option. The FCC-ee will improve the precision of Higgs and other SM measurements by orders of magnitude. The FCC-hh will have a direct discovery potential over five times greater than the LHC, and the FCC-eh, in addition to contributing to Higgs studies and searches, will measure the proton’s substructure with unique precision.
To be able to chart the physics landscape of future colliders, first, the questions that may or may not remain at the end of the LHC programme in the mid-2030s have to be envisaged. At the centre of this, and perhaps the biggest guaranteed physics goal of the FCC programme, is the understanding of the Higgs boson. While there is no doubt that the Higgs was the last undiscovered piece of the SM, it is not the closing chapter of the millennia-old reductionist tale. The Higgs is the first of its kind – an elementary scalar particle – and it therefore raises deep theoretical questions that beckon a new era of exploration.
Consider the Higgs boson mass: in the SM the mass of the Higgs boson, and the EW scale itself, cannot be predicted. Instead, these are phenomenological parameters that demand explanation. To examine the nature of this question, consider an analogy with the more familiar example of superconductors. The Ginzburg–Landau theory (GL) [9] is a phenomenological model that describes the macroscopic behaviour of type-1 superconductors. This model contains a scalar field \(\phi \), with free energy given by
where the ellipsis denote additional terms not relevant to this discussion. This equation describes a scalar field of charge \(Q=2\) with a mass and a quartic interaction. These parameters are temperature dependent. At high temperature the mass-squared is positive and the scalar field has a vanishing expectation value throughout the superconductor. However, below the critical temperature \(T_c\) the mass-squared is negative, leading to a non-vanishing expectation value of \(\phi \) throughout the superconductor. This expectation value essentially generates a mass for the photon within the superconductor, leading to the basic phenomenology of superconductivity.
The GL theory is a phenomenological model and offers no explanation as to the fundamental origin of the parameters of the model, including the mass. It also does not explain the fundamental origin of the scalar field itself. Ultimately, these questions were answered by Bardeen, Cooper, and Schrieffer, in the celebrated BCS theory of superconductivity [10]. The scalar field is a composite of electrons, and its mass relates to the fundamental microscopic parameters describing the material.
The situation is analogous for the Higgs boson of the SM. In fact, the analogy with the GL model is striking, with the exception that the model is relativistically invariant and the gauge forces non-Abelian. Unlike with superconductivity, currently neither the fundamental origin of the SM scalar field nor the origin of the mass and self-interaction parameters in the Higgs scalar potential are known. Now that the Higgs boson has been discovered, the next stage of exploration for any future high energy physics programme is to determine these microscopic origins.
In addition to the pressing need to understand the microscopic physics that can explain the origin of the EW scale \(\Lambda _{SM}\), it is also known that there is a more fundamental microscopic scale at small distances; the Planck scale \(M_P\), at which quantum gravitational effects become important. Thus, unlike in the GL model, an enormous hierarchy between the scale of the phenomenological model (the EW scale) and the next (known) microscopic scale in nature is observed. This puzzle is known as the ‘Hierarchy Problem’ and it galvanises the need to understand the origin of the Higgs potential.
This puzzle can be resolved if there is an additional new microscopic scale near \(\Lambda _{SM}\), involving new particles and interactions, and if this new physics offers an explanation for the hierarchy \(\Lambda _{SM} \ll M_P\). Such a scenario would solve the hierarchy problem. Comparing precise measurements of the Higgs boson properties with precision SM predictions, indirectly searches for evidence of these theories. The SM provides an uncompromising script for the Higgs interactions and any deviation from it would demand its extension. Furthermore, one may also search for the presence of the relevant new particles directly at high energies. In Sect. 9 both approaches are brought together to show how the FCC can address the fundamental question of the origin of the Higgs boson mass and corner a high energy resolution of the hierarchy problem.
Even setting to one side grandiose theoretical ideas such as quantum gravity, there are other physical reasons why the Higgs may provide a window to undiscovered sectors. As it carries no spin and is electrically neutral, the Higgs may have so-called ‘relevant’ interactions with new neutral scalar particles and hidden sectors of particle physics. These interactions, even if they only take place at very high energies, remain relevant at low energies – contrary to interactions between new neutral scalars and the other SM particles. Motivated by this, examples of how the Higgs boson may be probed at FCC facilities to search for interactions with new hidden sectors beyond the SM are shown in Sect. 15.
The possibility of new hidden sectors already has strong experimental support: although the SM is very well understood, this does not account for a large portion of all the matter in the universe. Today there is overwhelming evidence from astrophysical observations that a large fraction of the observed matter density in the universe is invisible. This so-called Dark Matter (DM) makes up 26% of the total energy density in the universe and more than 80% of the total matter [11]. Despite numerous observations of the astrophysical properties of DM, not much is known about its fundamental nature. This makes the discovery and identification of DM one of the most pressing questions in science.
The current main constraints on a particle DM candidate \(\chi \) are that it: (a) should gravitate like ordinary matter, (b) should not carry colour or electromagnetic charge, (c) is massive and non-relativistic at the time the CMB forms, (d) is long lived enough to be present in the universe today (\(\tau \gg \tau _{\mathrm{universe}}\)), and (e) does not have too strong self-interactions (\(\sigma /M_{\mathrm{DM}} \lesssim 100~{\mathrm{GeV}}^{-3}\)). While no SM particles satisfy these criteria, they do not pose very strong constraints on the properties of new particles to play the role of DM. In particular the allowed range of masses spans almost 80 orders of magnitude. Particles with mass below \(10^{-22}~\text {eV}\) would have a wave length so large that they wipe out structures on the kPc (kilo-Parsec) scale and larger [12], disagreeing with observations, while on the other end of the scale micro-lensing and MACHO (Massive Astrophysical Compact Halo Objects) searches put an upper bound of \(2\times 10^{-9}\) solar masses or \(10^{48}~\text {GeV}\) on the mass of the dominant DM component [13,14,15]. Section 12 details how FCC facilities can attack this pressing question, providing comprehensive exploration of the class of ‘thermal freeze-out’ DM, which picks out a particular broad mass range as a well-motivated experimental target, as well as unique probes of weakly coupled dark sectors.
Returning to the matter which is observable in the Universe, the SM alone cannot explain the origin of the matter-antimatter asymmetry that created enough matter for us to exist, otherwise known as baryogenesis. Since the asymmetry was created in the early universe when temperatures and energies were high, higher energies must be explored to uncover the new particles responsible for it and the LHC can only start this search. In particular, a well-motivated class of scenarios, known as EW baryogenesis theories, can explain the matter-antimatter asymmetry by modifying how the transition from high temperature EW-symmetric phase to the low-temperature symmetry-broken phase occurred. Since this phase transition occurred at temperatures near the weak scale, the new states required to modify the transition cannot have mass too far above the weak scale, singling out the FCC facility as the leading experimental facility to explore the nature of this foundational epoch of the early Universe. The role the FCC can play in exploring the dynamics of the EW phase transition is discussed in Sect. 11.
Another outstanding question lies in the origin of the neutrino masses, which the SM alone cannot account for. As with dark matter, there are numerous theories for neutrino masses, such as those involving ‘sterile’ neutrinos, which are within reach of lepton and hadron colliders, as discussed in Sect. 13.
These and other outstanding questions might also imply the existence of further spatial dimensions, or larger symmetries that unify leptons and quarks or the known forces. The LHC’s findings notwithstanding, the FCC will be needed to explore these fundamental mysteries more deeply and possibly reveal new paradigm shifts. The rest of this introduction gives a brief overview of the roles to be played by the various accelerators.
11.2 The role of FCC-ee
The capabilities of circular \(\mathrm{e}^+\mathrm{e}^-\) colliders are well illustrated by LEP, which occupied the LHC tunnel from 1989 to 2000. Its point-like collisions between electrons and positrons and precisely known beam energy allowed the four LEP experiments to test the SM to new levels of precision, particularly regarding the properties of the W and Z bosons. Putting such a machine in a 100 km tunnel and taking advantage of advances in accelerator technology such as superconducting radio-frequency cavities would offer even greater levels of precision on a greater number of processes. For example, it would be possible to adapt the collision energy during about 15 years of operation, to examine physics at the Z pole, at the WW production threshold, at the peak of ZH production, and above the \(\mathrm{t}\overline{\mathrm{t}}\) threshold. Controlling the beam energy at the 100 keV level would allow exquisite measurements of the Z and W boson masses, whilst collecting samples of up to \(10^{13}\) Z and \(10^8\) W bosons, not to mention several million Higgs bosons and top quark pairs. The experimental precision would surpass any previous experiment and challenge cutting edge theory calculations.
FCC-ee would quite literally provide a quantum leap in our understanding of the Higgs. Like the W and Z gauge bosons, the Higgs receives quantum EW corrections typically measuring a few per cent in magnitude due to fluctuations of massive particles such as the top quark. This aspect of the gauge bosons was successfully explored at LEP, but now it is the turn of the Higgs – the keystone in the EW sector of the SM. The millions of Higgs bosons produced by FCC-ee, with its clinically precise environment, would push the accuracy of the measurements to the per mille level, accessing the quantum underpinnings of the Higgs and probing deep into this hitherto unexplored frontier. In the process \(\mathrm{e}^+\mathrm{e}^- \rightarrow \hbox {HZ}\), the mass recoiling against the Z has a sharp peak that allows a unique and absolute determination of the Higgs decay-width and production cross section. This will provide an absolute normalisation for all Higgs measurements performed at the FCC, enabling exotic Higgs decays to be measured in a model independent manner.
The high statistics promised by the FCC-ee programme goes far beyond precision Higgs measurements. Other signals of new physics could arise from the observation of flavour changing neutral currents or lepton-flavour-violating decays, by the precise measurements of the Z and H invisible decay widths, or by direct observation of particles with extremely weak couplings, such as right-handed neutrinos and other exotic particles. The precision of the FCC-ee programme on EW measurements would allow new physics effects to be probed at scales as high as 100 TeV, anticipating what the FCC-hh must focus on.
11.3 The role of FCC-hh
The FCC-hh would operate at seven times the LHC energy, and collect about 10 times more data. The discovery reach for high-mass particles – such as \(\hbox {Z}^\prime \) or \(\hbox {W}^\prime \) gauge bosons corresponding to new fundamental forces, or gluinos and squarks in supersymmetric theories – will increase by a factor five or more, depending on the final statistics. The production rate of particles already within the LHC reach, such as top quarks or Higgs bosons, will increase by even larger factors. During the planned 25 years of data taking, a total of more than \(10^{10}\) Higgs bosons will be created, several thousand times more than collected by the LHC through Run 2 and 200 times more than will be available by the end of its operation. These additional statistics will enable the FCC-hh experiments to improve the separation of Higgs signals from the huge backgrounds that afflict most LHC studies, overcoming some of the dominant systematics that limit the precision attainable at the LHC. While the ultimate precision of most Higgs properties can only be achieved with FCC-ee, several demand complementary information from FCC-hh. For example, the direct measurement of the coupling between the Higgs and the top quark requires that they be produced together, requiring an energy beyond the reach of the FCC-ee. At 100 TeV, almost \(10^9\) out of the \(10^{12}\) top quarks produced will radiate a Higgs boson, allowing the top-Higgs interaction to be measured at the 1% level – several times better than at the HL-LHC and probing deep into the quantum structure of this interaction. Similar precision can be reached for Higgs decays that are too rare to be studied in detail at FCC-ee, such as those to muon pairs or to a Z and a photon. All of these measurements will be complementary to those obtained with FCC-ee and will use them as reference inputs to precisely correlate the strength of the signals obtained through various production and decay modes.
One respect in which a 100 TeV proton–proton collider would really come to the fore is in revealing how the Higgs behaves in private. As the Higgs scalar potential defines the potential energy contained in a fluctuation of the Higgs field, these self-interactions are neatly defined as the derivatives of the scalar EW potential. Since the Higgs boson is an excitation about the minimum of this potential, its first derivative is zero. Its second derivative is simply the Higgs mass squared, which is already known to few per mille accuracy. But the third and fourth derivatives are unknown and, unless access to Higgs self-interactions is gained, they could remain so. The rate of Higgs pair production events, which in some part occur through Higgs self-interactions, would grow by a factor of 40 at FCC-hh, with respect to 14 TeV, and enable this unique property of the Higgs to be measured with an accuracy reaching 5%. Among many other uses, such a measurement would comprehensively explore classes of models that rely on modifying the Higgs potential to drive a strong first order phase transition at the time of EW symmetry breaking, a necessary condition to induce baryogenesis.
FCC-hh would also allow an exhaustive exploration of new TeV-scale phenomena. Indirect evidence for new physics can emerge from the scattering of W bosons at high energy – where the Higgs boson plays a key role in controlling the rate growth – from the production of Higgs bosons at very large transverse momentum, or by testing the far ‘off-shell’ nature of the Z boson via the measurement of lepton pairs with invariant masses in the multi-TeV region. The plethora of new particles predicted by most models of symmetry-breaking alternatives to the SM can be searched for directly, thanks to the immense mass reach of 100 TeV collisions. The search for DM, for example, will cover the possible space of parameters of many theories relying on weakly interacting massive particles, guaranteeing a discovery or ruling them out. Several theories that address the hierarchy problem will also be conclusively tested. For supersymmetry, the mass reach of FCC-hh pushes beyond the regions motivated by the hierarchy problem alone. For composite Higgs theories, the precision Higgs coupling measurements and searches for new heavy resonances will fully cover the motivated territory. A 100 TeV proton collider will even confront exotic scenarios such as the twin Higgs, which are extremely difficult to test. These theories predict very rare or exotic Higgs decays, possibly visible at FCC-hh thanks to its enormous Higgs production rates.
11.4 The role of FCC-eh
Smashing protons into electrons at very high energy opens up a whole different type of physics, which until now has only been explored in detail at the HERA collider. FCC-eh would collide a 60 GeV electron beam from a linear accelerator external and tangential to the main FCC tunnel, with a 50 TeV proton beam. It would collect factors of thousands more luminosity than HERA while exhibiting the novel concept of synchronous, symbiotic operation alongside the pp collider. The facility would serve as the most powerful, high-resolution microscope onto the substructure of matter ever built. High-energy ep collisions would provide precise information on the quark and gluon structure of the proton, and how they interact.
This unprecedented facility would complement and enhance the study of the Higgs, and broaden the new physics searches also performed at FCC-hh and FCC-ee. Unexpected discoveries such as quark substructure might also arise. Uniquely, in ep collisions new particles can be created in the annihilation of the electron and a (anti)quark, or may be radiated in the exchange of a photon or other vector bosons. FCC-eh could also provide access to Higgs self-interactions and extended Higgs sectors, including scenarios involving DM. If neutrino oscillations arise from the existence of heavy sterile neutrinos, direct searches at the FCC-eh would have great discovery prospects in kinematic regions complementary to FCC-hh and FCC-ee, giving the FCC complex a striking potential to shine light on the origin of neutrino masses.
11.5 The study of hadronic matter at high density and high temperature
The thermodynamic behaviour of Quantum Chromodynamics (QCD) presents features which are unique among all other interactions. Their manifestations play a key role in fundamental aspects of the study of the universe, from cosmology to astrophysics, and high-energy collisions in the laboratory provide a unique opportunity to unveil their properties. Through collisions of heavy ions (N) at ultrarelativistic energies, the collective properties of the elementary quark and gluon fields of QCD can be investigated, providing a unique test bed for the study of strongly-interacting matter and of the conditions of the early universe at about \(10~\upmu \) s after the Big Bang. The increase in the centre-of-mass energy and integrated luminosity at the FCC-hh with respect to the LHC opens up unique opportunities for physics studies of the Quark-Gluon Plasma (QGP), as discussed in Sect. 16. Among these: charm quarks may start to contribute as active thermal degrees of freedom in the equation of state of the QGP, whose temperature would approach 1 GeV; boosted \(\hbox {t} \rightarrow \hbox {W} \rightarrow \hbox {q}\overline{\hbox {q}}\) decay chains can be used to measure the temporal evolution of the QGP density for the first time; the higher centre-of-mass energy of FCC enables the exploration of a previously-uncharted kinematic region at small Bjorken-x, where parton saturation is expected to appear, also exploiting the complementarity of the pN and eN collision programmes at the FCC-hh/eh.
11.6 Unknown unknowns
That no new particles beyond the Higgs have yet been found, or any significant deviations from theory was yet detected at the LHC, does not mean that the open questions introduced above have somehow evaporated. Rather, it shows any expectations for early discoveries beyond the SM at the LHC – often based on theoretical, and in some cases aesthetic, arguments – were misguided. In times like this, when theoretical guidance is called into question, experimental answers must be pursued as vigorously as possible. The combination of accelerators that are being considered for the FCC project offers, by their synergies and complementarities, an extraordinary tool for investigating these questions.
There are numerous instances in which the answer nature has offered was not a reply to the question first posed. For example, Michelson and Morley’s experiment, designed to study the ether’s properties, ended up disproving its existence and led to Einstein’s theory of relativity. The KamiokaNDE experiment, originally built to observe proton decays, discovered neutrino masses instead. The LHC itself could have well disproven the SM (and may still do so, with its future more precise measurements and continued searches!), by discovering that the Higgs boson is not an elementary but a composite particle.
The possibility of unknown unknowns does not diminish the importance of an experiment’s scientific goals. On the contrary it demonstrates that the physics goals for future colliders can play the crucial role of getting a new facility off the ground, even if a completely unanticipated discovery results.
11.7 The goals and structure of this volume
In recent years the prospect of an FCC facility has stimulated a large activity worldwide, leading to many workshops, the corresponding reports and a vast literature of individual publications (a collection of the key events and documents that emerged directly from the FCC study group is presented in the Appendix). It is impossible here to do justice to all the results that have been obtained, and which underscore the immense potential of the FCC to drive the progress of high-energy physics in the decades to come. This volume is therefore limited to highlight a selection of the most outstanding and unique results that the FCC can deliver, also providing the framework to define the challenging detector requirements that are discussed in more detail in the other volumes of the FCC CDR.
This document is divided in four parts. In the first part, following this introduction, a short summary of the parameters and target performance of the FCC accelerators is presented. The second part presents the key measurements and the expected results that experiments at each of the three FCC accelerators can achieve in the main areas of the programme: EW physics, Higgs properties, QCD, top quark and flavour. The third part discusses the synergy and complementarity of the three machines, showing, through some concrete examples, how the overall FCC physics programme benefits from all of its components, leading to a unique and superior measurement and discovery potential. Here topics directly related to the main open questions of the field are covered: global fits of EW and Higgs properties; the search for possible natural solutions to the hierarchy problem; the structure of the Higgs potential and the nature of the EW phase transition; the search for massive sterile neutrinos; the possible origin of violation of lepton flavour universality; and additional searches for BSM phenomena. The high energies achieved by the FCC-hh also enable a rich and original programme of heavy ion collisions, whose most significant goals will be presented in the latter part of the document. Finally an Appendix lists the major physics meetings and reports organised and produced in the context of the FCC CDR study phase.
The FCC offers further opportunities beyond what has been considered so far, for example the full exploitation of the injector complex, which has been briefly discussed in Ref. [16]. Furthermore, like at the LHC, one expects the FCC-hh general-purpose detectors to be complemented by dedicated experiments, optimally addressing the study of flavour or forward physics. The detailed exploration of these additional components of the programme has not yet started.
A systematic comparison of the FCC potential against that of other future projects is not made. In many cases the measurement targets of other projects will be updated soon in view of the forthcoming European Strategy. The comparison against the HL-LHC, or the use of HL-LHC projections in combination with FCC ones, is likewise limited to a few examples, since updated HL-LHC projections have been emerging from the Workshop on the “Physics of HL-LHC, and prospects for HE-LHC” in parallel with the completion of this volume of the FCC CDR, making it impossible to properly acknowledge here all relevant results. The Workshop reports [17,18,19,20,21] include also an overview of the current physics studies for HE-LHC. Only part of these results are contained in this volume, distributed among the various chapters (for a more coherent overview see, however, Chapter 1 of Volume 4 of the FCC CDR).
As anticipated above, the picture of the FCC physics potential that will emerge from this document represents just a partial snapshot of the huge landscape of knowledge that the FCC will generate. This picture of prospects will evolve with time, as more information is collected by the LHC and other experiments worldwide and, as the key questions of the field become more focused, more priorities might emerge. The studies to sharpen the FCC physics case even further will therefore continue well beyond this CDR.
12 The future circular colliders
This section summarises the main features of the accelerators that are of relevance to the physics programme, which were used in the projections of the physics potential. These include the reference performance of the various options and configurations, operational issues and relevant machine/detector interface issues. All the details are given in the relevant chapters of the other volumes of this CDR.
12.1 FCC-ee
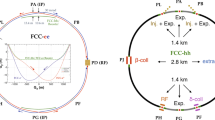
The FCC-ee is designed to deliver \(\hbox {e}^+\hbox {e}^-\) collisions to study with the highest possible statistics the Z, W, and Higgs bosons, the top quark, and, in Z decays, the b and c quarks and the tau lepton. The high performance is obtained by combining the experience gained on LEP at high energies with the high luminosity features developed on the b-factories. It is designed to fit in the footprint of the hadron collider, so as to ensure the feasibility of the ultimate goal of the FCC project. Figure 2.1 shows the layout of the FCC-ee together with FCC-hh.
The layouts of FCC-hh (left), FCC-ee (right), and a zoom in on the trajectories across interaction point G (right middle). The FCC-ee rings are placed 1 m outside the FCC-hh footprint in the arc. The \(\mathrm{e}^+\) and \(\mathrm{e}^-\) rings are separated by 30 cm horizontally in the arc. The main booster follows the footprint of the FCC-hh. The interaction points are shifted by 10.6 m towards the outside of FCC-hh. The beams coming toward the IP are straighter than the outgoing ones in order to reduce the synchrotron radiation at the IP
The main design principles of FCC-ee are as follows.
-
It is a double ring collider with electrons and positrons circulating in separate vacuum chambers. This allows a large and variable number of bunches to be stored. The beam intensity can thus be increased in inverse proportion to the synchrotron radiation (SR) per particle per turn, to keep the total power constant to a set value of 100 MW for both beams, for all energies.
-
A common low emittance lattice for all energies, except for a small rearrangement in the RF section for the \(\mathrm{t}\overline{\mathrm{t}}\) mode. The optics are optimised at each energy by changing the strengths of the magnets.
-
The length of the free area around the IP (\(L^*\)) and the strength of the detector solenoid are kept constant at 2.2 m and 2 T, respectively, for all energies.
-
A top-up injection scheme maintains the stored beam current and the luminosity at the highest level throughout the experimental run. This is achieved with a booster synchrotron situated in the collider tunnel itself.
As a requirement, the luminosity figures are very high (Fig. 2.2), ranging from \(2\times 10^{36}\hbox {cm}^{-2}\hbox {s}^{-1}\) per IP at the Z pole, and decreasing with the fourth power of the energy to \(1.5\times 10^{34}\hbox {cm}^{-2}\hbox {s}^{-1}\) per IP at the top energies. The run plan spanning 15 years including commissioning is shown in Table 2.1. The number of Z bosons planned to be produced by FCC-ee (up to \(5\times 10^{12}\)), for example, is more than five orders of magnitude larger than the number of Z bosons collected at LEP (\(2 \times 10^7\)), and three orders of magnitude larger than that envisioned with a linear collider (a few \(10^9\)).
Transverse radiative polarisation will build up to sufficient levels at the Z and WW threshold to ensure a semi-continuous calibration of the beam energies by resonant depolarisation during luminosity data taking (\(\sim 5\) times per hour on dedicated non-colliding bunches). The overall centre-of-mass calibration will be performed with a precision of \(\sim 100~\hbox {keV}\) at these energies. This will allow measurements of the W and Z masses and widths with a precision of a few hundred keV.
Longitudinal polarisation has not been included in the baseline plan; it was shown that, although a high level of beam polarisation brings interesting sensitivity for some observables, the information it could bring can generally be retrieved from the angular distribution or the polarisation of the final state particles. It was therefore decided to concentrate, at least at the level of the design study, on the transverse polarisation for centre-of-mass determination at ppm level, a unique feature of circular colliders.
A couple more running options have been considered for running the FCC-ee, but are not part of the baseline.
The first one is the possibility to search for the \(\mathrm{e}^+\mathrm{e}^- \rightarrow \mathrm{H}\) production at a centre-of-mass energy equal to the Higgs boson mass [22]. This possibility requires running with a centre-of-mass energy spread reduced by a factor 10-40 to be commensurate with the Higgs boson total width. This has been studied in [23] and in the FCC-ee CDR in Section 2.10.1 s-channel Higgs Production. This measurement must be performed after the ZH energy point has been completed, so that the Higgs boson mass is already known to better than 10 MeV. In the Standard Model this process is suppressed by the square of the electron mass (Yukawa coupling), and the cross-section is very low compared with the backgrounds. Nevertheless a precision of the order of the Standard Model cross-section might be achieved, which would be sensitive to a small admixture of a non-standard process.
The second possibility is to increase the total integrated luminosity by designing the ring with four interaction points and detectors, as was done in LEP. This is particularly interesting for the study of the Higgs boson at centre-of-mass of 240 and above 350 GeV. As will be discussed in the Higgs section this would provide FCC-ee with an overall improvement on most Higgs and top observables, which are statistically limited. Most interestingly, this would enrich the discovery potential of the project with an increased sensitivity of possibly up to \(5\sigma \) to the Higgs self-coupling from its energy-dependent effect on the ZH cross-section [24].
The FCC-ee experimental environment and detectors have been discussed in Chapter 7 of the FCC-ee CDR Volume, Experiment environment and detector designs. A few important features are summarised below.
The Machine-Detector Interface governs the geometry of the detector that is close to the beam line. The central detector magnetic field is limited to 2 Tesla by the fact that the beams cross at a 30 mrad angle, to avoid that the residual transverse fields generate emittance blow up and loss of luminosity.
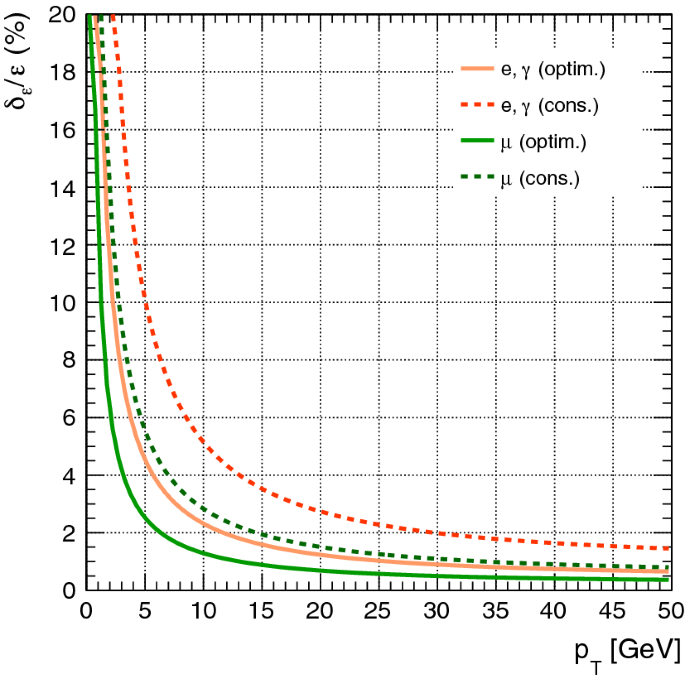
The strong focusing of the beams ( \(\beta _y \simeq 1~\hbox {mm}\)) requires a short distance between the focusing quadrupoles \(L^*=2.2~\hbox {m}\). This forces the luminosity detectors to stand even closer; a luminosity measurement with a relative experimental precision of \(10^{-4}\) will require a mechanical tolerance of \(1~\upmu \hbox {m}\) on the radial dimension of the luminosity calorimeter. Several observables rely on an excellent luminosity measurement (the Z line shape, the W pair threshold and the Higgs and top production cross-sections and mass determination).
A small beam pipe (1.5 cm inner radius) and the possibility to bring a vertex detector to a small distance from the interaction point are results of the strong beam focusing. This, combined with a state-of-the art vertex detector, would lead to an excellent impact parameter resolution of \(\sigma _{d_0} = a \oplus b / p\sin ^{3/2}\theta \), with \(a = 3~\upmu \hbox {m}\) and \(b=15~\upmu \hbox {m GeV}\). Together with the small size of the interaction region, \( \sigma _x = 6.4~\upmu \hbox {m}\, \sigma _y = 0.028~\upmu \hbox {m}\, \sigma _z = 420~\upmu \hbox {m}\), this will provide outstanding efficiency for the physics of, and with, heavy flavours at the Z, the Higgs and the top.
12.2 FCC-hh and HE-LHC
The FCC-hh collider design, performance and operating conditions are discussed in detail in Volume 3, Chapter 2, and summarized in Table 2.2. The key parameters are the total centre-of-mass energy, 100 TeV, and the peak initial (nominal) luminosity of \({5 (25)} \times 10^{34}~\hbox {cm}^{-2}\,\hbox {s}^{-1}\), with 25 ns bunch spacing. At nominal luminosity, the pile-up reaches 850 interactions per bunch crossing. The feasibility and performance of alternative bunch spacings of 12.5 and 5 ns are under study (see Volume 2, Section 2.2.5). With two high-luminosity interaction points, and taking into account the luminosity evolution during a fill and the turn-around time, the optimum integrated luminosity per day is estimated to be 2.3 (8.2) \(\hbox {fb}^{-1}\). The total integrated luminosity at the end of the programme will obviously depend on its duration. Assuming a 25 year life cycle, with 10+15 years at initial/nominal parameters, allows a goal of \(5+15=20~\hbox {ab}^{-1}\) to be set . This has been shown to be adequate for the foreseeable scenarios [26]. A luminosity range up to 30 \(\hbox {ab}^{-1}\)is considered for most of the physics studies. This allows the ultimate physics potential to be assessed, considering that the two experiments will probably combine their final results for the most sensitive measurements.
The current design allows for two further interaction points (IPs), where the pp luminosity can reach \({2} \times 10^{34}~\hbox {cm}^{-2}\,\hbox {s}^{-1}\), with a free distance between IP and the focusing triplets of 25 m. Apart from the case of heavy ion collisions, no discussion of possible FCC-hh experiments using these lower-luminosity IPs will be presented.
For the HE-LHC the assumptions are for a collision energy \(\sqrt{S}=27~\hbox {TeV}\) and a total integrated luminosity of 15 \(\hbox {ab}^{-1}\), to be collected during 20 years of operation.
12.3 FCC-hh: operations with heavy ions
It has been shown that the FCC-hh could operate very efficiently as a nucleus-nucleus or proton–nucleus collider, analogously to the LHC. Previous studies [27, 28] have revealed that it enters a new, highly-efficient operating regime, in which a large fraction of the injected intensity can be converted to useful integrated luminosity. Table 2.3 summarises the key parameters for PbPb and pPb operation. Two beam parameter cases were considered, baseline and ultimate, which differ in the \(\beta \)-function at the interaction point, the optical function \(\beta ^*\) at the interaction point, and the assumed bunch spacing, defining the maximum number of circulating bunches. The luminosity is shown for one experiment but the case of two experiments was also studied: this decreases the integrated luminosity per experiment by 40%, but increases the total by 20%. The performance projections assume the LHC to be the final injector synchrotron before the FCC [29]. A performance efficiency factor was taken into account to include set-up time, early beam aborts and other deviations from the idealised running on top of the theoretical calculations. Further details on the performance of the heavy-ion operation in FCC-hh can be found in Section 2.6 of the FCC-hh CDR Volume.
12.4 FCC-eh
The FCC-eh is designed to run concurrently with the FCC-hh. The electron-hadron interaction has a negligible effect on the multi TeV energy hadron beams, protons or ions. The electron beam is provided by an energy recovery linac (ERL) of \(E_e=60\,\hbox {GeV}\) energy which emerges from a 3-turn racetrack arrangement of two linacs, located opposite to each other. This ERL has been designed and studied in quite some detail with the LHeC design. For FCC-eh, for geological reasons, the ERL would be positioned at the inside of the FCC tunnel and tangential to the hadron beam at point L. There will be one detector only, but forming two data taking collaborations may be considered, for example, to achieve cross check opportunities for this precision measurement and exploratory programme.
The choice of \(E_e=60\,\hbox {GeV}\) is currently dictated by limiting cost. Desirably one would increase it, to reduce the beam energy uncertainty and access extended kinematics, but that would increase the cost and effort in a non-linear way. This could happen, nevertheless, if one expected, for example, leptoquarks with a mass of \(4\,\hbox {TeV}\) which the FCC-eh would miss with a \(60\,\hbox {GeV}\) beam. Currently, the energy chosen, taken from the LHeC design, is ample and adequate for a huge, novel programme in deep inelastic physics as has been sketched above.
In concurrent operation, the FCC-eh would operate for 25 years, with the FCC-hh. This provides an integrated luminosity of \(\mathcal {O}(2)\,\hbox {ab}^{-1}\), at a nominal peak luminosity above \(10^{34}\,\hbox {cm}^{-2}\,\hbox {s}^{-1}\), at which the whole result of HERA’s 15 year programme could be reproduced in about a day or two, with kinematic boundaries extended by a factor of 100. The pile-up at FCC-eh is estimated to be just 1. The forward detector has to cope with multi-TeV electron and hadron final state energies, while the backward detector (in the direction of the e beam) would only see energies up to \(E_e=60\,\hbox {GeV}\). The size of the detector corresponds to about that of CMS at the LHC.
Special runs are possible at much lower yet still sizeable luminosity, such as with reduced beam energies. There is also the important programme of electron-ion scattering which extended the kinematic range of the previous lepton–nucleus experiments by 4 orders of magnitude. This is bound to revolutionise the understanding of parton dynamics and substructure of nuclei and it will shed light on the understanding of the formation and development of the Quark-Gluon Plasma.
13 The measurement potential
14 EW measurements
14.1 Introduction
The Standard Model (SM) allowed the prediction of the properties and approximate mass values of the W and Z, of the top and of the Higgs boson, well before the actual observations of these particles. A long history of experiments and theoretical maturation has been essential in motivating and designing the facilities built for their observation. The inputs to these predictions have come from precise measurements and theoretical calculations in the flavour and, more conclusively, in the electroweak (EW) sector of the SM. It is expected that flavour and EW precision observables (EWPO) will continue to drive the progress in this field and to play a key role in establishing the existence of new physics and guiding its theoretical interpretation. Improved precision equates to discovery potential.
Some aspects of flavour physics at FCC, in the context of BSM searches, are reviewed in Sects. 7 and 14. Here the focus is on the EW physics programme of FCC.
The broad set of EWPO’s accessible to FCC-ee, and its immense statistics at the various beam energies in its running plan, will give it access to various possible sources and manifestations of new physics. Direct effects could occur because of the existence of a new interaction such as a \(\hbox {Z}^\prime \) or \(\hbox {W}^\prime \), which could mix or interfere with the known ones; from the mixing of light neutrinos with their heavier right handed counterparts, which would effectively reduce their coupling to the W and Z in a flavour dependent way. New weakly coupled particles can affect the W, Z or photon propagators via loops, producing flavour independent corrections to the relation between the Z mass and the W mass or the relation between the Z mass and the effective weak mixing angle; or the loop corrections can occur as vertex corrections, leading to flavour dependent effects as is the case in the SM for e.g. the \(\hbox {Z}\rightarrow \hbox {b}\bar{\hbox {b}}\) couplings. The measurements above the tŧ production threshold, directly involving the top quark, will further enrich this programme.
The FCC-hh achieves indirect sensitivity to new physics by exploiting its large energy, benefiting, as proven by the LHC, from the ability to achieve precision of a previously unexpected level in pp collisions. EW observables, such as high-mass lepton or gauge-boson pairs, can expose deviations that, in spite of the lesser precision w.r.t. FCC-ee, match its sensitivity reach at high mass. High-energy scattering of gauge bosons, furthermore, is a complementary probe of EW interactions at short distances.
The FCC-eh, with precision and energy in between FCC-ee and FCC-hh, integrates their potential well. For example, its ability to separate individual quark flavours in the proton, gives it unique sensitivity to their EW couplings. Furthermore, its high energy and clean environment enable precision measurements of the weak coupling evolution at very large \(Q^2\).
As shown later in Sect. 8, the FCC EW measurements are a crucial element of, and a perfect complement to, the FCC Higgs physics programme.
14.2 FCC-ee
14.2.1 Overview
Precision Electroweak measurements at FCC-ee will constitute an important part of the physics programme, with a sensitivity to new physics that is very broad and largely complementary to that offered by measurements of the Higgs boson properties. Building in part on LEP experience, with the benefit of huge statistics and of the improved prospects for beam energy calibration, a very significant jump in precision can be achieved. This is shown in Table 3.1, which summarises the main quantities and experimental errors compared to the present ones.
Furthermore, ancillary measurements of the presently precision-limiting input parameters for precision EW calculations can be performed at FCC-ee thanks to the high statistics. This is the case of the top quark mass from the scan of the tŧ production threshold, of the direct measurement of the QED running coupling constant at the Z mass from the \(Z\hbox {-}\upgamma \) interference, and of the strong coupling constant by measurements of the hadronic to leptonic branching fractions of the Z, the W and the \(\uptau \) lepton.
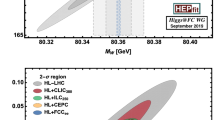
The importance of these ancillary measurements is illustrated by the present situation of the SM fit to the precision measurements available to date [30]. The SM predictions and their uncertainty for the W mass and the effective weak mixing angle [31], based on the input parameters \((m_\mathrm{Z}\), \(\alpha _{\mathrm{QED}}(m_\mathrm{Z})\), \(G_F\), \(\alpha _\mathrm{S}(m_\mathrm{Z})\), \(m_\mathrm{H}\), \(m_{\mathrm{top}})\) and on the present estimates of theoretical uncertainties, stand as follows.
These predictions are consistent with the world average of their direct measurements:
but one can note that the uncertainty stemming from parametric and theoretical uncertainties is of similar order of magnitude as the present experimental errors, and would be limiting if the experimental precision on these quantities were to be improved by one or two orders of magnitude.
14.2.2 Electroweak programme at the Z\(^0\) peak
Measurements at the Z resonance are described in the LEP/SLD physics report [32]. FCC-ee will be able to deliver about \(2\times 10^5\) times the integrated luminosity that was produced by LEP at the Z pole, i.e., typically \(10^{11}\) \(\mathrm{Z} \rightarrow \upmu ^+\upmu ^-\) or \(\uptau ^+\uptau ^-\) decays and \(3\times 10^{12}\) hadronic Z decays. Measurements with a statistical uncertainty up to 300 times smaller than at LEP (from a few per mille to \(10^{-5}\)) are therefore at hand. Two elements are new with respect to LEP operations: (i) the centre-of-mass energy calibration will be much improved, with beam energy measurements by resonant depolarisation performed on a continuous basis and for both beams [33]; (ii) further improvements in efficiencies for heavy flavour observables will result from the improved impact parameter resolution. The data taking at the Z is organised to optimise the EW output of the programme.
Data taken at the Z pole will be distributed at three energies corresponding to near half integer spin tunes \(\nu _{\mathrm{spin}} = {\hbox {E}_{\mathrm{beam}} }/0.44065686(1)\) to allow for precision measurements of the \(\mathrm{e}^+\) and \(\mathrm{e}^-\) beam energies by resonant depolarisation. The energies are chosen to optimise the sensitivity to \(\alpha _{\mathrm{QED}}(\hbox {m}_\mathrm{Z})\), which as shown by [34] can be extracted from the \(\hbox {Z-}\upgamma \) interference in the leptonic forward–backward asymmetry. In the vicinity of the Z pole, \(\hbox {A}_{\mathrm{FB}}^{\mu \mu }\) exhibits a strong \(\sqrt{s}\) dependence
caused by the off-peak interference between the Z and the photon exchange in the process \({\mathrm{e}^+\mathrm{e}^-} \rightarrow \upmu ^+\upmu ^-\). As displayed in Fig. 3.1, the statistical uncertainty of this measurement of \(\alpha _{\mathrm{QED}}(m_\mathrm{Z})\) is optimised just below (\(\sqrt{s} = 87.9~\hbox {GeV}\)) and just above (\(\sqrt{s} = 94.3~\hbox {GeV}\)) the Z pole. The half integer spin tune energy points \(\sqrt{s} = 87.7~\hbox {GeV}\) (\(\nu _{spin} = 99.5\)) and \(\sqrt{s} = 93.9~\hbox {GeV}\) (\(\nu _{spin} = 106.5\)) are close enough in practice. Together with the peak point at \(\sqrt{s} = 91.2~\hbox {GeV}\) (\(\nu _{spin} = 103.5\)) they constitute the proposed Z-pole run plan; about half the data will be taken at the peak point. This scan will at the same time provide measurements of the Z mass and width with very adequate precision.
It is shown in Ref. [34] that the experimental precision on \(\alpha _{\mathrm{QED}}\) can be improved by a factor 4 with \(40~{\mathrm{ab}}^{-1}\) at each of these two off-peak points, leaving an integrated luminosity of \(80~{\mathrm{ab}}^{-1}\) at the Z pole itself. Because most systematic uncertainties are common to both points and almost perfectly cancel in the slope determination, the experimental uncertainty is statistics dominated as long as the centre-of-mass energy spread (90 MeV at the Z pole) can be determined to a relative accuracy better than 1%, which is achievable at the FCC-ee every few minutes [35]. More studies are needed to understand if the \( \alpha _{\mathrm{QED}}(m_\mathrm{Z}^2)\) determination can profit from the centre-of-mass energy dependence of other asymmetries or from the angular distribution in the \(\hbox {Z}\rightarrow \hbox {e}^+ \hbox {e}^-\) final state. It should be emphasized that this direct determination of \(\alpha _{\mathrm{QED}}(m_\mathrm{Z}^2)\) is insensitive to sources of systematic uncertainties that affect the classical method from the dispersion integral over low energy \({\mathrm{e}^+\mathrm{e}^-}\) data. Compared with the projected improvement by a factor 2–3 of this calculation with future data at SuperKEKb or tau-charm factories, the FCC-ee offers the opportunity of a competitive, statistically-limited, and robust measurement with the same detectors as and in the energy range needed for EW precision measurements.
Top row, left: the Z line shape with the Z and \(\upgamma \) exchange contribution and the \(\hbox {Z}-\upgamma \) interference. Top row, right: the muon pair forward–backward asymmetry has a strong slope around the Z-pole resulting from the \(Z\hbox {-}\upgamma \) interference. Bottom row: relative statistical accuracy of the \(\alpha _{\mathrm{QED}}\) determination from the muon forward–backward asymmetry at the FCC-ee, as a function of the centre-of-mass energy. The integrated luminosity is assumed to be \(80~{\mathrm{ab}}^{-1}\) around the Z pole. The dashed blue line shows the current uncertainty
At the same time forward–backward and polarisation asymmetries at the Z pole are a powerful experimental tool to measure \(\sin ^2\theta _\mathrm{W}^{\mathrm{eff}}\), which regulates the difference between the right-handed and left-handed fermion couplings to the Z. With unpolarised incoming beams, the amount of Z polarisation at production is
by definition of the effective weak mixing angle \(\sin ^2\theta _\mathrm{W}^{\mathrm{eff}}\). The resulting forward–backward asymmetry for a pair of fermion–antifermion f at the Z pole amounts to \(A^{\mathrm{ff}}_{\mathrm{FB}}=\frac{3}{4} \mathcal{A}_\mathrm{e} \mathcal{A}_\mathrm{f}\). As a by-product of the continuous measurements of the beam polarisation for the beam energy calibration, the experimental control of the longitudinal polarisation of each of the beams can be made with the polarimeter (FCC-ee CDR, section 2.7) with great accuracy.
Among the other asymmetries to be measured at the FCC-ee, the \(\uptau \) polarisation asymmetry in the \(\uptau \rightarrow \uppi \upnu _{\uptau }\) decay mode provides a similarly accurate determination of \(\sin ^2\theta _\mathrm{W}^{\mathrm{eff}}\), with a considerably reduced \(\sqrt{s}\) dependence. In addition, the scattering angle dependence of the \(\uptau \) polarisation asymmetry provides an individual determination of both \(A_\mathrm{e}\) and \(A_{\uptau }\), which allows, in combination with the \(A_{\mathrm{FB}}^{\mu \mu }\) and the three leptonic partial width measurements, the vector and axial couplings of each lepton species to be determined. Similarly, heavy-quark forward–backward asymmetries (for b quarks, c quarks and, possibly s quarks) together with the corresponding Z decay partial widths and the precise knowledge of \(A_\mathrm{e}\) from the \(\uptau \) polarisation, provide individual measurements of heavy-quark vector and axial couplings.
Within the same scan of the Z, cross-sections for hadronic and leptonic final states will be measured with a precision limited by the luminosity measurement. The design of the luminometer aims for a point-to-point relative precision of \(10^{-5}\) and absolute normalisation with a precision of \(10^{-4}\) (limited by the projected hadronic vacuum polarization systematics in the theoretical calculation of the Bhabha cross section), see FCC-ee CDR Section 7. Several results are expected from the scan: the Z mass \(\mathrm {m}_\mathrm{Z}\) and width \(\Gamma _\mathrm{Z}\) will be extracted with a statistical precisions of 5 and 8 keV respectively, and a systematic uncertainty given by the centre-of-mass uncertainties of 100 keV; the ratio of hadronic to leptonic partial widths \(\mathrm {R}_{\ell }^{\mathrm{Z}}\), from which \(\alpha _{\mathrm{s}} (\hbox {m}_\mathrm{Z})\) will be derived with a precision better than 0.00016 – one order of magnitude better than today; the peak cross-section \(\sigma _{\mathrm{had}}^0\) will determine the number of light neutrino species \(\hbox {N}_\nu \) with a precision of 0.001 of a neutrino species.
An absolute (relative) uncertainty of 0.001 (\(5\times 10^{-5}\)) on the ratio of the Z hadronic-to-leptonic partial widths (\(\mathrm {R}_{\ell }^{\mathrm{Z}}\)) is thus well within the reach of the FCC-ee. A smaller relative uncertainty is expected for the ratios of the Z leptonic widths of different flavours, allowing a stringent test of neutral current lepton universality at the \(\times 10^{-5}\) level. A similar precision is expected for the test of universality of the charged current from the semi-leptonic decays and life-time measurement of \(10^{11}\,\uptau \) decays.
14.2.3 The number of light neutrino species
The measurement of the Z decay width into invisible states is of great interest as it constitutes a direct test of the unitarity of the neutrino mixing matrix – or of the existence of right-handed quasi-sterile neutrinos, as pointed out in Ref. [36]. At LEP, it was mostly measured at the Z pole from the peak hadronic and leptonic cross-sections to be \(N_{{\upnu }} = 2.984 \pm 0.008\), when expressed in number of active neutrinos. The measurement of the peak hadronic cross-section at the Z pole is dominated by systematic uncertainties, originating on one hand from the theoretical prediction of the low-angle Bhabha-scattering cross section (used for the integrated luminosity determination), and from the experimental determination of the absolute integrated luminosity, on the other. At the FCC-ee, a realistic target for this systematics-limited uncertainty is bounded from below to 0.001, based on ongoing progress with the theoretical calculations and detector technology.
At higher centre-of-mass energies, the use of radiative return to the Z [37], \({\mathrm{e}^+\mathrm{e}^-} \rightarrow \,\hbox {Z}\upgamma \), is likely to offer a more accurate measurement of the number of neutrinos. Indeed, this process provides a clean photon-tagged sample of on-shell Z bosons, with which the Z properties can be measured. From the WW threshold scan alone, the cross section of about 5 pb [38,39,40,41] ensures that fifty million \(\hbox {Z}\upgamma \) events are produced with a \(\mathrm{Z} \rightarrow \upnu \overline{{\upnu }}\) decay and a high-energy photon in the detector acceptance. The \(25\times 10^6\) \(\hbox {Z}\upgamma \) events with leptonic Z decays in turn provide a direct measurement of the ratio \(\Gamma _\mathrm{Z}^{\mathrm{inv}}/\Gamma _\mathrm{Z}^{\mathrm{lept}}\), in which uncertainties associated with absolute luminosity and photon detection efficiency cancel. The 150 million \(\hbox {Z}\upgamma \) events with either hadronic or leptonic Z decays will also provide a cross check of the systematic uncertainties and backgrounds related to the QED predictions for the energy and angular distributions of the high energy photon. The invisible Z width will thus be measured with a dominant statistical error corresponding to 0.001 neutrino families. Data at higher energies contribute to further reduce this uncertainty by about 20%. A somewhat lower centre-of-mass energy, for example \(\sqrt{s} = 125~\hbox {GeV}\) – with both a larger luminosity and a larger \(\hbox {Z}\upgamma \) cross section and potentially useful for Higgs boson studies (Sect. 4.2.2) – would be even more appropriate for this important measurement, allowing a statistical precision of around 0.0004 neutrino families.
14.2.4 The \(\mathrm{W^+ W^-}\) and \(\mathrm{t}\bar{\mathrm{t}}\) thresholds
The safest and most sensitive way to determine the W boson and top quark masses and widths is to measure the sharp increase of the \({\mathrm{e}^+\mathrm{e}^-} \rightarrow \mathrm{W^+ W^-}\) and \({\mathrm{e}^+\mathrm{e}^-} \rightarrow \mathrm{t}\bar{\mathrm{t}}\) cross sections at the production thresholds, at centre-of-mass energies around twice the W and top masses (Fig. 3.2). In both cases, the mass can be best determined at a quasi-fixed point where the cross section dependence on the width vanishes: \(\sqrt{s} \simeq 162.5~\hbox {GeV}\) for \(m_\mathrm{W}\) and \(342.5~\hbox {GeV}\) for \(m_{\mathrm{top}}\). The cross section sensitivity to the width is maximum at \(\sqrt{s} \simeq 157.5~\hbox {GeV}\) for \(\Gamma _\mathrm{W}\), and \(344~\hbox {GeV}\) for \(\Gamma _{\mathrm{top}}\).
Production cross section of W boson (left) and top-quark pairs (right) in the vicinity of the production thresholds, with different values of the masses and widths. In the left panel, the pink and green bands include variations of the W mass and width by \(\pm \, 1\) GeV. In the right panel, the grey and green bands include variations of the top-quark mass and width by \(\pm \, 0.2\) and \(\pm \, 0.15\) GeV. The dots with error bars indicate the result of a 10-point energy scan in steps of 1 GeV, with 0.02 \({\mathrm{ab}}^{-1}\) per point
With \(12~{\mathrm{ab}}^{-1}\) equally shared between 157.5 and \(162.5~\hbox {GeV}\), a simultaneous fit of the W mass and width to the \(\mathrm{e}^+\mathrm{e}^- \rightarrow \mathrm{W}^+\mathrm{W}^-\) cross-section measurements yields a precision of 0.5 MeV on \(m_\mathrm{W}\) and 1.2 MeV on \(\Gamma _\mathrm{W}\). Lest the measurements be limited by systematic uncertainties, the following conditions need to be met. The centre-of-mass energies must be measured with a precision of 0.5 MeV. The point-to-point variation of the detector acceptance (including that of the luminometer) and the WW cross section prediction must be controlled within a few \(10^{-4}\). Finally, the background must be known at the few per-mil level. These conditions are less stringent than the requirements at the Z pole – where the centre-of-mass energies must be measured to 0.1 MeV or better and the point-to-point variations of the luminometer acceptance must be controlled to \(5\times 10^{-5}\), etc. In addition, the backgrounds can be controlled by an additional energy point below the W-pair production threshold.
An experimental precision of 0.5 \((1.2)~\hbox {MeV}\) for the W mass (width) is well within reach at the FCC-ee, with \(12~{\mathrm{ab}}^{-1}\) accumulated at the W pair production threshold.
The situation is slightly different for the top quark. A multipoint scan in a \(4~\hbox {GeV}\) window will be needed for the top mass determination, for several reasons. First, \(m_{\mathrm{top}}\) might not be known to better than \(\pm \, 0.5~\hbox {GeV}\) from the theoretical interpretation of the hadron collider measurements. More importantly, such a window is needed to accurately map out the full shape of the threshold, including the 1S resonance (Fig. 3.2, right panel). In addition, the \(\mathrm{t}\bar{\mathrm{t}}\) cross section depends on the top Yukawa coupling, arising from the Higgs boson exchange at the \(\mathrm{t}\bar{\mathrm{t}}\) vertex (Sect. 4.2.2). This dependence can be fitted away with supplementary data at centre-of-mass energies slightly above the \(\mathrm{t}\bar{\mathrm{t}}\) threshold. The non-\(\mathrm{t}\bar{\mathrm{t}}\) background, on the other hand, needs to be evaluated from data at centre-of mass energies slightly below the \(\mathrm{t}\bar{\mathrm{t}}\) threshold.
With a luminosity of \(25~{\mathrm{fb}}^{-1}\) recorded at eight different centre-of-mass energies (340, 341, 341.5, 342, 343, 343.5, 344, and \(345~\hbox {GeV}\)), the top-quark mass and width can be determined with statistical precisions of \(\pm \, 17~\hbox {MeV}\) and \(\pm \, 45~\hbox {MeV}\), respectively. The uncertainty on the mass improves to less than \(10~\hbox {MeV}\) if the width is fixed to its SM value. Each of the centre-of-mass energies can be measured with a precision smaller than \(10~\hbox {MeV}\) from the final state reconstruction [42] of \({\mathrm{e}^+\mathrm{e}^- \rightarrow W^+W^-}\), \({\mathrm{ZZ}}\), and \(\hbox {Z}\upgamma \) events and from the knowledge of the W and Z masses, which causes a \(3~\hbox {MeV}\) uncertainty on the top-quark mass. Today, the uncertainty on the theoretical value due to missing higher orders QCD corrections in the \(\mathrm{e}^+\mathrm{e}^- \rightarrow \mathrm{t} \bar{\mathrm{t}}\) process is at the \(40~\hbox {MeV}\) level for the top quark mass and width.
To conclude on the top, an uncertainty of 17 (45) MeV is achievable for the top-quark mass (width) measurement at the FCC-ee, with \(0.2~{\mathrm{ab}}^{-1}\) accumulated around the \(\mathrm{t}\bar{\mathrm{t}}\) threshold. The corresponding parametric uncertainties on the SM predictions of \(\sin ^2\theta _\mathrm{W}^{\mathrm{eff}}\) and \(m_\mathrm{W}\) are accordingly reduced to \(6\times 10^{-7}\) and 0.11 MeV, respectively.
14.2.5 Summary and demands on theoretical calculations
Table 3.1 summarises some of the most significant FCC-ee experimental accuracies and compares them to those of the present measurements.
Some important comments are in order:
-
FCC-ee will provide a set of ground breaking measurements of a large number of new-physics sensitive observables, with improvement with respect to the present status by a factor of 20-50 or even more; moreover it will improve input parameters, \(\mathrm {m}_\mathrm{Z}\) of course, but also \(\mathrm {m}_{\mathrm{top}}\), \(\alpha _{\mathrm{s}} (\hbox {m}_\mathrm{Z})\) and, for the first time a direct and precise measurement of \(\alpha _{\mathrm{QED}} (\hbox {m}_\mathrm{Z})\). Consequently, parametric uncertainties in the electroweak predictions will be reduced considerably. Once, and only when, all the above measurements are performed, the total parametric uncertainty on the W mass and on \(\sin ^2\theta _\mathrm{W}^{\mathrm{eff}}\) predictions (0.6 MeV and \(10^{-5}\), respectively), dominated by the in-situ precision on \(\alpha _{\mathrm{QED}}(m_\mathrm{Z}^2)\), will match the uncertainty on their direct determination (0.5 MeV and \(5\times 10^{-6}\), respectively). The FCC-ee is the only future \({\mathrm{e}^+\mathrm{e}^-}\) collider project able to accomplish this tour-de-force, a prerequisite for an optimal sensitivity to new physics.
-
Table 3.1 is only a first sample of the main observables accessible. Work on the future projections of experimental and theory requirements are, and will need to be, the subject of further dedicated studies within the FCC-ee design study groups. Important contributions are expected from b, c and \(\uptau \) physics at the Z pole, such as forward–backward and polarisation asymmetries. Also the tau lepton branching fraction and lifetime measurements, especially if a more precise tau mass becomes available, will provide another dimension of precision measurements.
-
While statistical precisions follow straightforwardly from the integrated luminosities, the systematic uncertainties do not. It is quite clear that for the Z and W mass and width the centre-of-mass energy uncertainty will dominate, and that for the total cross-sections (thus the determination of the number of neutrinos) the luminosity measurement error will dominate. These have been the subject of considerable work already. However there is no obvious limit in the experimental precision reachable for such observables as \(\mathrm {R}_{\ell }^{\mathrm{Z}}\) or \(\mathrm {R}_\mathrm{b} \) or the top quark pair cross-section measurements.
-
While the possible experimental systematic error levels for \( \mathrm {R}_{\ell }^{\mathrm{Z}}\), \(\mathrm {R}_\mathrm{b}\), \(\mathrm {A}_{\mathrm{FB}}^\mathrm{b},0\), \(\mathrm {A}_{\mathrm{FB}}^{\mathrm{pol},\tau }\) have been indicated, these should be considered as indicative, and are likely to change, hopefully improve, with closer investigation. Heavy flavour quantities will readily benefit from the improved impact parameter resolution available at FCC-ee due to the smaller beam pipe and considerable improvements in silicon trackers. Also since LEP and SLD the knowledge of both \(\uptau \) and b physics has benefited considerably from the b-factories and will benefit further with SuperKEKB.
Table 3.1 clearly sets the requirements for theoretical work: the aim should be to either provide the tools to compare experiment and theory at a level of precision better than the experimental errors, or to identify which additional calculation or experimental input would be required to achieve it. Another precious line of research to be done jointly by theoreticians and experimenters will be to try to find observables or ratios of observables for which theoretical uncertainties are reduced.
The work that experiment requires from the theoretical community can be separated into a few classes.
-
QED (mostly) and QCD corrections to cross-sections and angular distributions that are needed to convert experimentally measured cross-sections back to ‘pseudo-observables’: couplings, masses, partial widths, asymmetries, etc. that are close to the experimental measurement (i.e. the relation between measurements and these ‘pseudo-observables’ does not alter the possible ‘new physics’ content). Appropriate event generators are essential for the implementation of these effects in the experimental procedures.
-
Calculation of the pseudo-observables with the precision required in the framework of the SM with the required precision so as to take full advantage of the experimental precision.
-
Identify the limiting issues and the questions related to the definition of parameters, in particular the treatment of quark masses and more generally QCD objects.
-
An investigation of the sensitivity of the proposed experimental observables (or new ones) to the effect of new physics in a number of important scenarios. This is essential work to be done early, before the project is fully designed, since it potentially affects the detector design and the running plan.
The overall challenge is laid out in great detail in an extended Report [46], which emerged from the Workshop Precision EW and QCD calculations for the FCC studies: methods and tools [47], held at CERN in January 2018. A preliminary evaluation of needs [46], leads to the conclusion that at least the full three-loop calculations are needed for Z pole and for the propagator EW corrections, and probably two-loop calculations for the EW corrections to the WW cross-section. Matching the experimental precisions across-the-board has been estimated to require a dedicated effort of 500 person-years. This has been listed as strategic, high-priority, item in Appendix A of the FCC-ee CDR. The CERN workshop was the start of a process that will be both exciting and challenging. Its conclusions are reproduced here: “We anticipate that at the beginning of the FCC-ee campaign of precision measurements, the theory will be precise enough not to limit their physics interpretation. This statement is however conditional to sufficiently strong support by the physics community and the funding agencies, including strong training programmes”.
14.3 FCC-hh
The large samples of electroweak (EW) gauge bosons produced by FCC-hh could offer many different opportunities for important measurements. In particular, the huge kinematic reach of 100 TeV collisions enables probes of EW dynamics, both within and beyond the SM, that are largely complementary to those accessible via the FCC-ee precision measurements.Footnote 1 This section documents some of the most relevant production properties of EW gauge bosons, focusing on the large-\(Q^2\) reach and preparing the ground for the discussion of unique new measurements that will be presented in Sect. 8.
14.3.1 Drell–Yan processes
The Drell–Yan (DY) process, namely the production of lepton pairs from quark–antiquark annihilations into vector gauge bosons, is the primary EW observable in hadronic collisions. The total production rates of \(\hbox {W}^\pm \) and \(\hbox {Z}^0\) bosons at 100 TeV are about 1.3 and \(0.4~\upmu \hbox {b}\), respectively. This corresponds to samples of \(\mathcal{O}(10^{10-11})\) leptonic decays per \(\hbox {ab}^{-1}\). The inclusive production rates are known today up to next-to-next-to-leading order (NNLO) in QCD, leading to a theoretical uncertainty on the rates of \(\mathcal{O}(1\%)\).
This will certainly be improved over the next few years, as the \(\hbox {N}^3\hbox {LO}\) is already within reach. The uncertainties due to the parton distribution functions (PDFs), shown in Table 3.2, are larger, and depend strongly on the required rapidity range, which defines the small-x range being probed. This implies that DY measurements will contribute to improve knowledge of the PDFs (a systematic study has not been carried out as yet). FCC-eh will of course pin these down with the greatest precision, as shown in Sect. 5.3. In particular, Fig. 5.14 shows a projected precision for the qq̄ luminosity at the 5 per mille level. This could lead to the process \(\hbox {Z}\rightarrow \ell ^+\ell ^-\) becoming a luminometer with a (sub-)percent precision.
In Table 3.2 the rates for HE-LHC are also shown: they are a factor of 2 larger than at 14 TeV, and their PDF uncertainty, based on today’s PDF fits, is smaller than at 100 TeV, due to the larger values of x that are being probed.
The extended kinematic reach for DY final states is shown in Fig. 3.3, where the integrated spectra of the W boson transverse mass (\(M^2_T=2p_{T,\ell }p_{T,\nu }(1-\cos \theta _{\ell \nu })\)) and of the \(\upgamma /\hbox {Z}\) dilepton mass are plotted. Notice the accidental similarity of those spectra: while leptonic rates for W’s are typically \(\mathcal{O}(10)\) larger than for Z’s, a given value of \(M_T\) corresponds to events with a larger dilepton invariant mass, thus reducing the respective rate. Further applications of these high-mass DY measurements at 100 TeV, to probe BSM effects induced by the existence of new weakly interacting particles or of higher-dimension operators, are presented later in Sect. 8.
14.3.2 Gauge boson pair production
Pair production is the most direct and sensitive probe of triple gauge-boson interactions (TGCs). Early measurements at LEP2 have confirmed the gauge nature of the couplings and set strong constraints on deviations. By violating gauge invariance and its delicate cancellations among amplitudes, anomalous TGCs typically give rise to deviations from the SM that grow quadratically with the gauge bosons energy. As in the case of far-off-shell DY production (discussed in Sect. 8.3), high-mass gauge boson pairs can therefore provide powerful BSM constraints [49]. The total SM production rates are shown in Table 3.3, up to the NNLO QCD order [50]. More details on the various aspects of the inclusive production are given in Ref. [25], where a thorough discussion of diphoton production, at large \(M_{\gamma \gamma }\) and at large \(p_T^{\gamma \gamma }\) for \(M_{\gamma \gamma } \sim m_H\), can also be found.
Next the integrated invariant mass distributions of gauge boson pairs are shown in Fig. 3.4. A central rapidity cut is imposed to suppress the t-channel contributions to WW and WZ production, which reduce the role of the TGC vertex. Notice that the rate for WW at large mass is larger than for dileptons, suggesting that diboson measurements may have a comparable reach in \(Q^2\). Of course the full exploitation of these final states benefits from the possibility of using gauge boson hadronic decays, challenging the detector performance in terms of jet tagging through the substructure analysis (see Sect. 15.3.1 for examples in the case of high-mass \(\hbox {Z}^{\prime }\rightarrow \hbox {VV}\) decays). The exploration of these high-mass diboson processes to constrain higher-dimension operators has just started. A first study of the WZ (fully leptonic) final states was presented in Ref. [49]. The longitudinal component of the amplitude, \(\mathcal{A}(\hbox {u}_\mathrm{L}\overline{\hbox {d}}_\mathrm{L} \rightarrow \hbox {W}_\mathrm{L}^+\hbox {Z}_\mathrm{L})\) (and its charge conjugate) may receive contributions from dimension-6 operators, growing with energy and parameterised [49] as \(\delta \mathcal{A}=a^{(3)}/(2\sqrt{2}) E^2 \sin \theta \), where \(E,\;\theta \) are the W energy and scattering angle in the CM frame. The \(\sin \theta \) behaviour allows the isolation of this contribution from the production of transverse gauge bosons, further justifying the focus on central production, where \(\sin \theta \) is maximum. A systematic uncertainty for the extraction of the signal of \(\sim 1\%\) allows constraints to be set at the level of \(a^{(3)} \lesssim 1/(20~\mathrm {TeV})^2\). These studies are complementary to analyses that could be done with the \(\hbox {q}'\overline{\hbox {q}} \rightarrow \hbox {WH}\) process, which, by gauge invariance, would be modified by the \(a^{(3)}\) correction in the same way as WZ. For a further discussion of these studies see Sect. 8.
14.3.3 Gauge boson(s) production via vector boson scattering and fusion
Vector boson fusion (VBF) and vector boson scattering (VBS) processes provide crucial signatures to probe the mechanism of EW symmetry breaking. The rates at FCC-hh, subject to various sets of cuts aimed at reducing the QCD backgrounds, are given in Table 3.4. They account for off-shell and non-resonant contributions. The details of the generation (scales, PDF, etc) are given in Ref. [25], where several additional kinematic distributions are collected. The sets of cuts considered here are as follows:
As shown in Table 3.4, the available statistics range between tens of thousands and hundred million events, depending on the final state. The use of hadronic decays could increase these rates even more. Examples of analyses to constrain EFT operators, and their impact on BSM models, are discussed in Sect. 8.
The discussion of longitudinal vector boson scattering, of relevance to the study of Higgs couplings, is presented in Sect. 4.3.1.
14.4 FCC-eh
Electroweak precision measurements in deep-inelastic electron-proton scattering, have a long tradition, with a number of groundbreaking results [51,52,53]. At HERA, precision measurements had been limited by both the \({\mathrm{ep}}\) centre-of-mass energy of \(\sqrt{s}=920\,~\text {GeV} \) and the luminosities of about \(0.5\,{\mathrm{fb}}^{-1}\) recorded by the H1 or ZEUS experiments [54,55,56,57]. In contrast, the FCC-eh with its considerably increased centre-of-mass energy of \(3.5\,~\text {TeV} \) and a targeted integrated luminosity of up to \(3\,{\mathrm{ab}}^{-1}\) will allow unique precision EW measurements in deep-inelastic scattering and perform tests of new physics beyond the EW scale and up to the TeV masses.
In the following, prospects for the determination of EW parameters from inclusive NC and CC DIS data at FCC-eh are studied. Additional direct measurements will provide further constraints, such as measurements of Higgs boson (see Sect. 4.5) and top-quark production cross sections (Sect. 6.4). The uncertainty values of EW parameters are estimated by performing fits of theoretical predictions to simulated inclusive NC and CC DIS data (see Sect. 5.3.1 for details). In order to account for correlations with uncertainties of the PDFs, which are expected to be determined from the same data, the fits include also the determination of parameters of the PDF parameterisations. The methodology closely follows the prescription outlined in Sect. 5.3.1 and Ref. [57]. EW effects are included in the calculations through 1-loop weak corrections [58,59,60,61,62], and all calculations are performed in the on-shell renormalisation scheme, which utilises the fine structure constant \(\alpha \) and the weak boson masses, \(m_Z\) and \(m_W\), as main input parameters.Footnote 2
Single differential cross sections for unpolarised \(\mathrm{e}^+\mathrm{p}\) and \(\mathrm{e}^-\mathrm{p}\) NC and CC DIS for FCC-eh in comparison to HERA measurements and LHeC expectations. The lepton beam polarisations of ± 80% will considerably change the expected NC cross section in regions where \(\upgamma \) Z and pure Z exchange becomes important, whereas the CC cross section scales linearly with the lepton beam polarisation
The neutral current (NC) and charged current (CC) DIS cross sections for unpolarised inclusive DIS are displayed in Fig. 3.5. While CC DIS is mediated exclusively by the W boson, the weak boson contribution to NC DIS becomes significant at higher scales, \(Q^2 \gtrsim 100\,\mathrm {GeV}^2 \), through \(\upgamma \) Z interference and pure Z exchange [65].
The expected uncertainties for the light-quark weak neutral couplings (\(g_{Au}\), \(g_{Ad}\), \(g_{Vu}\), \(g_{Vd}\)) from FCC-eh inclusive DIS data compared with the Standard Model expectations and the currently most precise measurements [32, 56, 57, 66]. At the displayed scale, the contours of the present measurements are truncated to a large extent. For comparison, also the prospects for the LHeC are displayed. A global fit to the light-quark EW couplings, including the FCC-ee projections, is shown in Fig. 8.8 and in Table 8.2
The determination of the vector- and axial-vector weak neutral current couplings, ideally performed separately for any of the individual quark or lepton flavour, represents a major precision test of the EW theory. Their precision measurements can provide constraints on various BSM models. The sensitivity to the light-quark vector and axial-vector couplings to the \(\mathrm{Z}\) boson (\(g_{Au}\), \(g_{Ad}\), \(g_{Vu}\), \(g_{Vd}\)) is investigated by performing a \(g_{Au}+g_{Ad}+g_{Vu}+g_{Vd}+\hbox {PDF}\) fit to the simulated NC and CC DIS data at the FCC-eh. The two-dimensional uncertainty contours (\(\Delta \chi ^2=2.3\)) are displayed in Fig. 3.6 for each single quark flavour and compared to recent measurements [32, 56, 57, 66]. While the current determinations from \(\mathrm{e}^+\mathrm{e}^-\), \(\hbox {ep}\) or \(\hbox {p}\bar{\hbox {p}}/\hbox {pp}\) data have all similar uncertainties, the FCC-eh will provide a measurement with unprecedented precision. Uncertainties smaller than about 1 % are expected. Due to the \(\upgamma \) Z interference term, DIS data provide also access to the sign of the coupling parameters, and thus FCC-eh does not exhibit any ambiguity as it is the case for the \(\mathrm{Z}\)-pole measurements.
Also electron coupling parameters are accessible at the FCC-eh and a determination of heavy-quark couplings can be explored if additional flavour-dependent final states are observed, e.g. in charm-production or \(\mathrm{b}\)-quark production. Even if these parameters will only be measured with uncertainties similar to those of the high-precision measurements at the \(\mathrm{Z}\) pole, FCC-eh will allow a unique measurement of the scale-dependence of the weak neutral current couplings in a single experiment. For instance, a considerable precision for \(Q^2\) dependent measurements of the light-quark weak neutral-current couplings can be expected in the range of \(\sqrt{Q^2}\) from a few 10 \(~\text {GeV}\) up to about 1.5 \(~\text {TeV}\) with uncertainties down to a few permille. At low scales such measurements are limited by the dominating contribution of the pure photon exchange, and at high scales by the kinematic limit and the integrated luminosity.
More explicitly, the effective weak neutral current couplings can be expressed in terms of the \(\rho \) and \(\kappa \) parameters:
\(\rho \) and \(\kappa \) receive \(Q^2\) dependent higher-order radiative corrections [67]. The determination of the vector and axial-vector couplings can be translated into a determination of the effective weak mixing angle, \(\sin ^2\theta _w^{\mathrm{eff}}=\kappa _{f}{\mathrm{sin}}^2\theta _W\). For \(\sin ^2\theta _w^{\mathrm{eff}}\), an ultimate precision of down to \(1.0\cdot 10^{-3}\) can be achieved when using FCC-eh inclusive DIS data. More meaningful flavour specific measurements and measurements in conjunction with the \(\rho \) parameters, yield more conservative estimates. By exploiting the \(Q^2\) dependence of the inclusive DIS data, a unique scale-dependent measurement of the effective weak mixing angle is feasible over two orders of magnitude in \(\sqrt{Q^2}\). Using cross section ratios, such as the polarisation asymmetry, charge asymmetry, or the CC/NC cross section ratio, further improvements can be achieved since systematic uncertainties are expected to cancel, at least partially [68, 69]. On the theory side, a cancellation of the \(\rho \) parameter in ratios of cross sections, as it is the case for Z-pole measurements or in polarised Møller scattering, does not take place since the contributions from pure photon exchange and \(\upgamma \) Z-interference, which do not carry the same \(\rho \) dependence, are not negligible.
Direct measurements of CC cross sections at the W-pole are exclusively performed at hadron colliders. This restricts the current availability of precise measurements of charged current coupling parameters. In DIS at FCC-eh, CC cross sections can be measured with high precision. From the theoretical point of view, this is possible because CC scattering is mediated exclusively by W bosons, i.e. no interference with other exchange bosons is diluting the contribution of CC couplings. From the experimental side, precision measurements can be performed since the event kinematics can be fully reconstructed by recording the hadronic final state. While at HERA the uncertainties of charged current cross sections have been limited by the measurement of the hadronic final state, limited integrated luminosities, challenging trigger requirements and the moderate kinematic reach, FCC-eh will greatly improve on all of these aspects.
The uncertainty of the \(\mathrm{W}\)-boson mass determination is obtained from a \(m_W+\hbox {PDF-fit}\) of the CC and NC cross sections (the \(\mathrm{Z}\)-boson mass \(m_Z\) is an external input in this study). The expected uncertainties of \(m_W\) are
where the dominant sensitivity to \(m_W\) arises from the normalisation of the CC cross section and the W-boson propagator term \(\tfrac{m_W^2}{m_W^2+Q^2}\). While the expected precision of \(m_W\), \(\Delta m_W=10\,~\text {MeV} \) would not improve a future 0.6 MeV determination from FCC-ee (see Table 3.1), it would exceed the precision of the current world average [70] (\(\Delta m_W=\pm 12\,~\text {MeV} \)), being about a factor of two more precise than the most precise result of a single experiment [71, 72] to date. Current determinations of \(m_W\) from hadron-collider experiments have a considerable PDF uncertainty of about \(\gtrsim 7\,~\text {MeV} \) [70], but measurements at the FCC-eh will provide further support for such precision measurements in hadron-hadron collisions by its ability to perform combined fits of EW parameters and PDFs.
In addition, the measurement of CC DIS cross sections allows a precise and unique test of the scale dependence of charged current coupling parameters. For instance, FCC-eh will allow a test of the \(Q^2\) dependence of the CC form factor \(\rho _{CC}\) [59, 61]. The absolute value of \(\rho _{CC}\) can be measured at FCC-eh with a precision of down to 1.5 per mille, and its scale dependence will be measurable up to \(\sqrt{Q^2}\simeq 1.5\,~\text {TeV} \) with an uncertainty of about 2.2 per mille. At low scales, the FCC-eh measurement of CC DIS cross sections will be limited by trigger constraints and at high scales by the available integrated luminosity.
The measurement of charm production cross sections in CC DIS will be possible for the first time with high precision.
In summary, the inclusive NC and CC DIS cross sections measured at FCC-eh provide an opportunity to perform high-precision determinations, in the space-like region, of fundamental EW parameters and test EW processes at the level of quantum corrections with high precision. The high precision for light-quark NC couplings and the possibility to determine scale dependencies (e.g. of the EW mixing angle) highlight the complementarity of the ep EW physics programme to that with ee.
15 Higgs measurements
15.1 Introduction
Since the discovery of the Higgs boson, many studies of its properties and couplings have been carried out at the LHC, confirming the SM expectations at the 10–20% level. Significant improvements will take place in the next years and through the HL-LHC phase, reaching, in several cases, a precision of few percent [73], where a 5% deviation from the SM could expose BSM scales in the range of 1 TeV. The extraordinary achievements and prospects of the LHC programme are opening a new era, in which the Higgs boson is moving from being the object of a search, to become an exploration tool. The FCC positions itself as the most powerful heir of the future LHC Higgs’ legacy. On one side it will extend the range of measurable Higgs properties (e.g. its elusive \(\hbox {H}\rightarrow \hbox {gg}, \hbox {c}\bar{\hbox {c}}\) decays, its total width, and its self-coupling), allowing more incisive and model-independent determinations of its couplings. On the other, the combination of superior precision and energy reach provides a framework in which indirect and direct probes of new physics complement each other, and cooperate to characterise the nature of possible discoveries.
Higgs boson physics, based on \(\sim 10^6\) Higgs decays, is at the heart of the experimental programme of the FCC-ee. FCC-ee will measure Higgs production inclusively from its presence as a recoil to the Z in the reaction \(\hbox {e}^+\hbox {e}^- \rightarrow \hbox {Z H}\). This allows the absolute measurement of the Higgs coupling to the Z, which is the starting point for the model-independent determination of its total width, and thus of its other couplings through branching ratio measurements. The leading Higgs couplings to SM particles (denoted \(g_{\mathrm{HXX}}\) for particle X) will be measured by FCC-ee with a sub-percent precision.
The model dependence being removed by FCC-ee, a fully complementary programme will be possible at FCC-hh and FCC-eh, to complete the picture of Higgs boson properties. This will include, for example, the measurement to the percent level of rare Higgs decays such as \(\hbox {H}\rightarrow \upgamma \upgamma \), \(\upmu \upmu \), \(\hbox {Z}\upgamma \), the detection of invisible ones (\(\hbox {H}\rightarrow 4\upnu \)), and the measurement of the \(g_{\mathrm{Htt}}\) coupling with percent precision.
Indirect (at FCC-ee) and direct (at FCC-hh and FCC-eh) measurements will measure the Higgs self-coupling, probing the nature of the Higgs potential, as will be discussed later in Sects. 10 and 11.
The synergies among all components of the FCC Higgs programme will be underscored in Sect. 8, where global fits of Higgs and EW parameters will be performed. By way of synergy and complementarity, the FCC appears to be the most powerful future facility for a thorough examination of the Higgs boson and EWSB.
15.2 FCC-ee
15.2.1 Model-independent coupling determination from the Higgs branching fractions
The goal of the FCC-ee programme is to achieve a model-independent percent or sub-percent accuracy determination of the Higgs width and Higgs couplings. This precision is needed to access the 10 TeV energy scale, and maybe to exceed it, by an analysis of a possible pattern of deviations among all couplings. Similarly, higher-order corrections to Higgs couplings in the SM are at the level of a few %. The quantum structure of the Higgs sector can therefore be tested only if the precise measurement of its properties is pushed to a few per mille level, or better.
An experimental sample of at least one million Higgs bosons has to be analysed to potentially reach this statistical precision. Production at \({\mathrm{e}^+\mathrm{e}^-}\) colliders proceeds mainly via the Higgsstrahlung process \({\mathrm{e}^+\mathrm{e}^-} \rightarrow {\mathrm{HZ}}\) and WW fusion \({\mathrm{e}^+\mathrm{e}^-} \rightarrow (\hbox {WW} \rightarrow \hbox {H})\upnu \overline{{\upnu }}\). The cross sections are displayed in Fig. 4.1 as a function of the centre-of-mass energy. The total cross section presents a maximum at \(\sqrt{s}=260~\hbox {GeV}\), but the event rate per unit of time is largest at \(240~\hbox {GeV}\), as a consequence of the specific circular-collider luminosity profile. As the cross section amounts to \(200~\hbox {fb}\) at \(\sqrt{s}=240~\hbox {GeV}\), the production of one million events requires an integrated luminosity of at least \(5~{\mathrm{ab}}^{-1}\). This sample, dominated by HZ events, is usefully complemented by about 180,000 HZ events and 45,000 WW-fusion events, to be collected with \(1.5~{\mathrm{ab}}^{-1}\) at \(\sqrt{s}=365~\hbox {GeV}\).
The Higgs boson production cross section as a function of the centre-of-mass energy in unpolarised \({\mathrm{e}^+\mathrm{e}^-}\) collisions. The blue and green curves stand for the Higgsstrahlung and WW fusion processes, respectively, and the red curve displays the total production cross section. The vertical dotted lines indicate the centre-of-mass energies of choice at the FCC-ee for the measurement of the Higgs boson properties
Left: A schematic view, transverse to the detector axis, of an \({\mathrm{e}^+\mathrm{e}^-} \rightarrow ~\hbox {HZ}\) event with \(\hbox {Z} \rightarrow ~\upmu ^+\upmu ^-\) and with the Higgs boson decaying hadronically. The two muons from the Z decay are indicated. Right: distribution of the mass recoiling against the muon pair, determined from the total energy-momentum conservation, with an integrated luminosity of \(5~{\mathrm{ab}}^{-1}\) and the CLD detector design. The peak around \(125~\hbox {GeV}\) (in red) consists of HZ events. The rest of the distribution (in blue and pink) originate from ZZ and WW production
At \(\sqrt{s} = 240~\hbox {GeV}\), the determination of Higgs boson couplings follows the strategy described in Refs. [8, 74], with an improved analysis that exploits the superior performance of the CLD detector design (see the FCC-ee CDR, Sect. 7). The total Higgs production cross section is determined by counting \({\mathrm{e}^+\mathrm{e}^-} \rightarrow {\mathrm{HZ}}\) events tagged with a leptonic Z decay, \(\mathrm{Z}\rightarrow \ell ^+\ell ^-\), independently of the Higgs boson decay. An example of such an event is displayed in Fig. 4.2 (left). The mass \(m_{\mathrm{Recoil}}\) of the system recoiling against the lepton pair is calculated with precision from the lepton momenta and the total energy-momentum conservation: \(m_{\mathrm{Recoil}}^2 = s +m_\mathrm{Z}^2 - 2\sqrt{s}(E_{\ell ^+}+E_{\ell ^-})\), so that HZ events have \(m_{\mathrm{Recoil}}\) equal to the Higgs boson mass and can be easily counted from the accumulation around \(m_\mathrm{H}\). Their number allows the HZ cross section, \(\sigma _{\mathrm{HZ}}\), to be precisely determined in a model-independent fashion. This precision cross-section measurement alone is a powerful probe of the SM predictions for the Higgs boson at the loop level. Under the assumption that the coupling structure is identical in form to the SM, this cross section is proportional to the square of the Higgs boson coupling to the Z, \(g_{\mathrm{HZZ}}\).
Building upon this powerful measurement, the Higgs boson width can then be inferred by counting the number of HZ events in which the Higgs boson decays into a pair of Z bosons. Under the same coupling assumption, this number is proportional to the ratio \(\sigma _{\mathrm{HZ}} \times \Gamma (\mathrm{H} \rightarrow {\mathrm{ZZ}}) / \Gamma _\mathrm{H}\), hence to \(g_{\mathrm{HZZ}}^4/\Gamma _\mathrm{H}\). The measurement of \(g_{\mathrm{HZZ}}\) described above thus allows \(\Gamma _\mathrm{H}\) to be extracted. The numbers of events with exclusive decays of the Higgs boson into \(\mathrm{b}\bar{\mathrm{b}}\), \(\mathrm{c} \bar{\mathrm{c}}, \hbox {gg}, \uptau ^+\uptau ^-\), \(\upmu ^+\upmu ^-\), \(\mathrm{W}^+\mathrm{W}^-\), \(\upgamma \upgamma \), \(\hbox {Z}\upgamma \), and invisible Higgs boson decays (tagged with the presence of just one Z boson and missing mass in the event) measure \(\sigma _{\mathrm{HZ}} \times \Gamma (\mathrm{H} \rightarrow {\mathrm{XX}}) / \Gamma _\mathrm{H}\) with precisions indicated in Table 4.1.
With \(\sigma _{\mathrm{HZ}}\) and \(\Gamma _\mathrm{H}\) known, the numbers of events are proportional to the square of the \(g_{\mathrm{HXX}}\) coupling involved. In practice, the width and the couplings are determined with a global fit, which closely follows the logic of Ref. [75]. The results of this fit are summarised in Table 4.2 and are compared to the same fit applied to HL-LHC projections [73] and to those of other \({\mathrm{e}^+\mathrm{e}^-}\) colliders [76,77,78] exploring the 240-to-380 GeV centre-of-mass energy range. Table 4.2 also shows that the extractions of \(\Gamma _\mathrm{H}\) and of \(g_{\mathrm{HWW}}\) from the global fit are significantly improved by the addition of the WW-fusion process at \(\sqrt{s} = 365~\hbox {GeV}\), as a result of the correlation between the HZ and \(\upnu \overline{{\upnu }}\) H processes.
In addition to the unique electroweak precision measurement programme presented earlier, the FCC-ee provides the best model-independent precisions for all couplings accessible from Higgs boson decays among the \({\mathrm{e}^+\mathrm{e}^-}\) collider projects at the EW scale. With larger luminosities delivered to several detectors at several centre-of-mass energies (240, 350, and 365 GeV), the FCC-ee improves on the model-dependent HL-LHC precision by an order of magnitude for all non-rare decays, and is therefore able to test the Higgs boson at the one-loop level of the SM, without the need of a costly \({\mathrm{e}^+\mathrm{e}^-}\) centre-of-mass energy upgrade. The FCC-ee also determines the Higgs boson width with a precision of 1.3%, which in turn allows the HL-LHC measurements to be interpreted in a model-independent way as well. Other \({\mathrm{e}^+\mathrm{e}^-}\) colliders at the EW scale are limited by the precision with which the HZ or the WW fusion cross sections can be measured, i.e., by the luminosity delivered either at 240–250 GeV, or at 365–380 GeV, or both.
15.2.2 The top Yukawa coupling and the Higgs self-coupling
Several Higgs boson couplings are not directly accessible from its decays, either because the masses involved, and therefore the decay branching ratios, are too small to allow for an observation within \(10^6\) events – as is the case for the couplings to the particles of the first SM family: electron, up quark, down quark – or because the masses involved are too large for the decay to be kinematically open – as is the case for the top-quark Yukawa coupling and for the Higgs boson self coupling. Traditionally, bounds on the top Yukawa and Higgs cubic couplings are extracted from the (inclusive and/or differential) measurement of the \(\mathrm{t}\bar{\mathrm{t}} \mathrm{H}\) and \({\mathrm{HH}}\) production cross sections, which require significantly higher centre-of-mass energy, either in \({\mathrm{e}^+\mathrm{e}^-}\) or in proton–proton collisions. The \(\mathrm{t}\bar{\mathrm{t}} \mathrm{H}\) production has already been detected at the LHC with a significance larger than \(5\sigma \) by both the ATLAS [79] and CMS [80] collaborations, corresponding to a combined precision of the order of 20% on the cross section and which constitutes the first observation of the top-quark Yukawa coupling. The role FCC-ee can play in measuring the Higgs self-coupling is discussed in detail in Sect. 10.
The precise determination of the top Yukawa coupling to \(\pm \, 5\%\) is often used as another argument for \({\mathrm{e}^+\mathrm{e}^-}\) collisions at a centre-of-mass energy of 500 GeV or above. This coupling will, however, be determined with a similar or better precision already by the HL-LHC (\(\pm \, 3.4\%\), model dependent), and constrained to \(\pm \, 3.1\%\) through a combined model-independent fit with FCC-ee data (Table 4.2). The FCC-ee also has access to this coupling on its own, through its effect at quantum level on the \(\mathrm{t}\bar{\mathrm{t}}\) cross section just above production threshold, \(\sqrt{s} = 350~\hbox {GeV}\). Here too, the FCC-ee measurements at lower energies are important to fix the value of the strong coupling constant \(\alpha _\mathrm{S}\) (Sect. 3.2). This precise measurement allows the QCD effects to be disentangled from those of the top Yukawa coupling at the \(\mathrm{t}\bar{\mathrm{t}}\) vertex. A precision of \(\pm \, 10\%\) is achievable at the FCC-ee on the top Yukawa coupling. A very high energy machine, such as the FCC-hh, has the potential to reach a precision better than \(\pm \, 1\%\) with the measurement of the ratio of the ttH to the ttZ cross sections, when combined with the top EW couplings precisely measured at the FCC-ee (Sect. 6.2).
15.2.3 The electron Yukawa coupling
The measurement of the electron Yukawa coupling is challenging due to the small size of the electron mass. If, for a variety of reasons, the FCC schedule called for a prolongation of the FCC-ee operation, a few additional years spent at centre-of-mass energy in the immediate vicinity of the Higgs boson pole mass, \(\sqrt{s} \simeq 125.09~\hbox {GeV}\), would be an interesting option. At this energy, the resonant production of the Higgs boson in the s channel, \({\mathrm{e}^+\mathrm{e}^- \rightarrow H}\), has a tree-level cross section of 1.64 fb, reduced to 0.6 fb when initial-state radiation is included, and to 0.3 fb if the centre-of-mass energy spread were equal to the Higgs boson width of 4.2 MeV [81].
A much larger spread, typically of the order of 100 MeV, is expected when the machine parameters are tuned to deliver the maximum luminosity, rendering the resonant Higgs production virtually invisible. The energy spread can be reduced with monochromatisation schemes [82], at the expense of a similar luminosity reduction. It is estimated that \(2 (7)~{\mathrm{ab}}^{-1}\) can be delivered in one year of running at \(\sqrt{s} \simeq 125.09~\hbox {GeV}\) with a centre-of-mass energy spread of 6 (10) MeV. From a preliminary cut-and-count study in ten different Higgs decay channels, the resonant Higgs boson production is expected to yield a significance of \(0.4\sigma \) within a year in both scenarios, allowing an upper limit to be set on the electron Yukawa coupling to 2.5 times the SM value. The SM sensitivity can be reached in five years [83].
The FCC-ee therefore offers a unique opportunity to set stringent upper bounds on the electron Yukawa coupling. These bounds are of prime importance when it comes to interpreting electron electric dipole measurements in setting constraints on new physics. The bounds on top CP violating couplings given in Ref. [84], for example, are invalidated if the electron Yukawa coupling is neither fixed to its SM value nor constrained independently.
15.2.4 CP studies
By probing the coupling of the Higgs boson to weak gauge bosons the LHC established that the spin-parity quantum numbers of the Higgs boson are consistent with \(J^{PC}=0^{++}\) [85, 86]. The data leave room, however, for significant CP violation in the interactions of the Higgs boson. New physics at the TeV scale could result in a small pseudoscalar contribution that is more significant in the coupling to fermions than in those to gauge bosons. The large H \( \rightarrow \uptau ^+\uptau ^-\) sample provided by the FCC-ee offers a unique handle to deepen the understanding of the CP properties of the Higgs boson by measuring the CP phase \(\Delta \) of the \(\hbox {H}\uptau \uptau \) coupling, which determines the mixing angle between the scalar and pseudoscalar contribution in the \(H \rightarrow \uptau ^+\uptau ^-\) decay. In the subsequent decays \(\uptau ^\pm \rightarrow \uprho ^\pm \upnu _{{\uptau }} \rightarrow \uppi ^\pm \uppi ^0\upnu _{{\uptau }}\), the relative orientation of the two charged pions contains information on the CP phase \(\Delta \). About 1000 HZ events in which the Higgs boson decays into a \(\uptau \) pair and both \(\uptau \)’s decay into a \(\uprho \), are expected in \(5~{\mathrm{ab}}^{-1}\) at \(\sqrt{s} = 240~\hbox {GeV}\). With this sample, the FCC-ee can measure \(\Delta \) with a precision of about 10 degrees, under the assumption that the \(\uptau \) decays can be fully reconstructed.
15.3 FCC-hh
Two elements characterise Higgs production at the FCC-hh: the large statistics (see Table 4.3), and the large kinematic range, which, for several production channels, probes \(p_T\) in the multi-TeV region (see Fig. 4.3).
These factors lead to an extended and diverse sensitivity to possible deviations of the Higgs properties from their SM predictions: the large rates enable precise measurements of branching ratios for rare decay channels such as \(\upgamma \upgamma \) or \(\upmu \upmu \), and push the sensitivity to otherwise forbidden channels such as \(\uptau \upmu \). The large kinematic range can be used to define cuts improving the signal-to-background ratios and the modelling or experimental systematics, but it can also amplify the presence of modified Higgs couplings, described by higher-dimension operators, whose impact grows with \(Q^2\). Overall, the Higgs physics programme of FCC-hh is a fundamental complement to what can be measured at FCC-ee, and the two Higgs programmes greatly enrich each other. This section contains some examples of these facts, and documents the current status of the precision projections for Higgs measurements. A more extensive discussion of Higgs production properties at 100 TeV and of possible measurements is given in Ref. [87].
Figure 4.3 shows the Higgs rates above a given \(p_T\) threshold, for various production channels. It should be noted that these rates remain above the level of one million up to \(p_T\sim 1~\hbox {TeV}\), and there is statistics for final states like \(\hbox {H}\rightarrow \hbox {b}\bar{\hbox {b}}\) or \(\hbox {H}\rightarrow \uptau \uptau \) extending up to several TeV. Furthermore, for \(p_T(\mathrm {H})\gtrsim 1~\hbox {TeV}\), the leading production channel becomes tŧH, followed by vector boson fusion when \(p_T(\mathrm {H})\gtrsim 2~\hbox {TeV}\). The analysis strategies to separate various production and decay modes in these regimes will therefore be different to what is used at the LHC. Higgs measurements at 100 TeV will offer many new options and precision opportunities with respect to the LHC, as it happened with the top quark moving from the statistics-hungry Tevatron to the rich LHC.
For example, Ref. [87] shows that \(S/\hbox {B}\) improves for several final states at large \(p_T\). In the case of the important \(\upgamma \upgamma \) final state, Section 3.2.1 of that document showed that \(S/\hbox {B}\) increases from \(\sim 3\%\) at low \(p_T\) (a value similar to what observed at the LHC), to \(\gtrsim 1\) at \(p_T\gtrsim 300~\hbox {GeV}\). In this range of few hundred GeV, some experimental systematics will also improve, from the determination of the energies (relevant e.g. for the mass resolution of \(\hbox {H}\rightarrow \upgamma \upgamma \) or bb̄) to the mitigation of pile-up effects.
The analyses carried out so far for FCC-hh are still rather crude when compared to the LHC standards, but help to define useful targets for the ultimate attainable precision and the overall detector performance. The details of the present detector simulations for Higgs physics at FCC-hh are contained in Ref. [88].
The target uncertainties considered include statistics (taking into account analysis cuts, expected efficiencies, and the possible irreducible backgrounds) and systematics (limited here to the identification efficiencies for the relevant final states, and an overall 1% to account for luminosity and modelling uncertainties). While these estimates do not reflect the full complexity of the experimental analyses in the huge pile-up environment of FCC-hh, the systematics assumptions that were used are rather conservative. Significant improvements in the precision of reconstruction efficiencies would arise, for example, by applying tag-and-probe methods to large-statistics control samples. Modelling uncertainties will likewise improve through better calculations, and broad campaigns of validation against data. By choosing here to work with Higgs bosons produced at large \(p_T\), the challenges met by triggers and reconstruction in the high pile-up environment are eased. The projections given here are therefore considered to be reasonable targets for the ultimate precision, and useful benchmarks to define the goals of the detector performance.
The consideration of the reconstruction efficiency of leptons and photons is relevant in this context since, to obtain the highest precision by removing global uncertainties such as luminosity and production modelling, ratios of different decay channels can be exploited. The reconstruction efficiencies are shown in Fig. 4.4 as a function of \(p_T\). The uncertainties on the electron and photon efficiencies are assumed to be fully correlated, but totally uncorrelated from the muon one. The curves in Fig. 4.4 reflect what is achievable today at the LHC, and it is reasonable to expect that smaller uncertainties will be available at the FCC-hh, due to the higher statistics that will allow statistically more powerful data-driven fine tuning. For example, imposing the identity of the Z boson rate in the ee and \(\upmu \upmu \) decay channels will strongly correlate the e and \(\upmu \) efficiencies.
The absolute uncertainty expected in the measurement of the production and decay rates for several final states (considering just the \(\hbox {gg}\rightarrow \hbox {H}\) production channel) is shown in Fig. 4.5, as a function of the minimum \(p_T\) of the event samples. The curves labeled by “stat+syst” include the optimal reconstruction efficiency uncertainties shown in Fig. 4.4. The curves labeled by “stat+syst+lumi” include a further 1%, to account for the overall uncertainty related to luminosity and production systematics. The luminosity itself could be known even better than that by using a standard candle process such as Z production, where both the partonic cross section and the PDF luminosity will be pinned down by future theoretical calculations, and by the FCC-eh, respectively. As shown in Fig. 5.14, the gg luminosity in the mass range between \(m_H\) and several TeV will be measured by FCC-eh at the few per mille level.
Several comments on these figures are in order. First of all, it should be noted that the inclusion of the systematic uncertainty leads to a minimum in the overall uncertainty for \(p_T\) values in the range of few hundred GeV. The very large FCC-hh statistics make it possible to fully benefit from this region, where experimental systematics are getting smaller. The second remark is that the measurements of the Higgs \(p_T\) spectrum can be performed with a precision better than 10%, using very clean final states such as \(\upgamma \upgamma \) and \(4\ell \), up to \(p_T\) values well in excess of 1 TeV, allowing the possible existence of higher-dimension operators affecting Higgs dynamics to be probed up to scales of several TeV.
Independently of future progress, the systematics related to production modelling and to luminosity cancel entirely by taking the ratio of different decay modes, provided selection cuts corresponding to identical fiducial kinematic domains for the Higgs boson are used. This can be done for the final states considered in Fig. 4.5. Ratios of production rates for these channels provide absolute determinations of ratios of branching ratios, with uncertainties dominated by the statistics, and by the uncorrelated systematics such as reconstruction efficiencies for the different final state particles. These ratios are shown in Fig. 4.6. The curves with the systematics labeled as “cons” use the conservative reconstruction uncertainties plotted in Fig. 4.4.
These results are summarised in Table 4.4, separately showing the statistical and systematic uncertainties obtained in our studies. As remarked above, there is in principle room for further progress, by fully exploiting data-driven techniques to reduce the experimental systematics. At the least, one can expect that these potential improvements will compensate for the current neglect of other experimental complexity, such as pile-up. The most robust measurements will involve the ratios of branching ratios. Taking as a given the value of the HZZ coupling (and therefore \(B(\hbox {H}\rightarrow 4\ell )\)), which will be measured to the few per-mille level by FCC-ee, from the FCC-hh ratios it could be possible to extract the absolute couplings of the Higgs to \(\upgamma \upgamma \) (0.4%), \(\upmu \upmu \) (0.7%), and \(\hbox {Z}\upgamma \) (0.9%).
The ratio with the tŧZ process is considered for the tŧH process, as proposed in Ref. [89]. This allows the removal of the luminosity uncertainty, and reducing the theoretical systematics on the production modelling below 1%. An updated study of this process, including the FCC-hh detector simulation, is presented in Ref. [88]. Assuming FCC-ee will deliver the expected precise knowledge of \(B(\hbox {H}\rightarrow \hbox {b}\bar{\hbox {b}})\), and the confirmation of the SM predictions for the Ztŧ vertex, the tŧH/tŧZ ratio should therefore allow a determination of the top Yukawa coupling to 1%.
The limit quoted in Table 4.4 on the decay rate of the Higgs boson to new invisible particles is obtained from a study of large missing-\(E_T\) signatures. The analysis, discussed in detail in Ref. [88], relies on the data-driven determination of the leading SM backgrounds from W/Z+jets. The integrated luminosity evolution of the sensitivity to invisible H decays is shown in Fig. 4.7. The SM decay \(\hbox {H}\rightarrow 4\upnu \), with branching ratio of about \(1.1\times 10^{-3}\), will be seen after \(\sim 1~\hbox {ab}^{-1}\), and the full FCC-hh statistics will push the sensitivity to \(2\times 10^{-4}\). The implications of this measurement for the search of dark matter or dark sectors coupling to the Higgs boson are discussed in Sect. 12 of this volume.
Last but not least, Table 4.4 reports a 7% expected precision in the extraction of the Higgs self-coupling \(\lambda \). This result is discussed in more detail, with other probes of the Higgs self-interaction, in Sect. 10.
15.3.1 Longitudinal vector boson scattering
The scattering of the longitudinal components of vector bosons is particularly sensitive to the relation between gauge couplings and the VVH coupling. A thorough analysis of same-sign \(\hbox {W}_\mathrm{L} \hbox { W}_\mathrm{L}\) scattering, in the context of the FCC-hh detector performance studies, is documented in Ref. [88]. The extraction of the \(\hbox {W}^\pm _\mathrm{L} \hbox { W}^\pm _\mathrm{L}\) signal requires the removal of large QCD backgrounds (\(\hbox {W}^\pm \hbox {W}^\pm +\hbox {jets}\), \(\hbox {WZ}+\hbox {jets}\)) and the separation of large EW background of transverse-boson scattering. The former is suppressed by requiring a large dilepton invariant mass and the presence of two jets at large forward and backward rapidities. The longitudinal component is then extracted from the scattering of transverse states by exploiting the different azimuthal correlations between the two leptons. The precision obtained for the measurement of the \(\hbox {W}_\mathrm{L} \hbox { W}_\mathrm{L}\) cross section as a function of integrated luminosity, is shown in Fig. 4.9 (left). The three curves correspond to different assumptions about the rapidity acceptance of the detector and drive the choice of the detector design, setting a lepton (jet) acceptance out to \(\vert \eta \vert =4(6)\). The small change in precision when increasing the jet cut from \(p_T>30\) to \(p_T>50\,\hbox {GeV}\) indicates a strong resilience of the results against the presence of large pile-up. The quoted precision, reaching the value of 3% at 30 \(\hbox {ab}^{-1}\), accounts for the systematic uncertainties of luminosity (1%), lepton efficiency (0.5%), PDF (1%) and the shape of the distributions used in the fit (10%). The right plot in Fig. 4.9 shows the impact of rescaling the WWH coupling by a factor \(\kappa _W\). The effect is largest at the highest dilepton invariant masses, as expected. The measurement precision, represented by the small vertical bars, indicates a sensitivity to \(\delta \kappa _W\) at the percent level, as shown also in Table 4.5.
15.4 HE-LHC
The Higgs production rates at 27 TeV are collected in Table 4.3. The rate increase relative to HL-LHC is dominated by the factor of 5 expected increase in the total integrated luminosity. For most of the production processes, the cross section increase is limited to a factor between 3 and 5. Figures 4.8 and 4.10 present the results of a preliminary study similar to that presented for FCC-hh, namely using boosted Higgs final states to improve the S/B and to define common fiducial regions used in the measurement of ratios of branching ratios. The detector simulation is based on the Delphes, with parameters drawn from the projected performance of the HL-LHC detectors. Given the reduced kinematic reach of 27 TeV, compared to 100 TeV, the \(p_T\) range is extended down to 50 GeV. For the rate-limited final states \(\hbox {H}\rightarrow \upmu \upmu \) and \(\hbox {H}\rightarrow \ell \ell \upgamma \), the uncertainty in this \(p_T\) range is statistics dominated. The study of these channels will therefore require an optimisation of the selection cuts, to include lower \(p_T\) Higgses. In the low-\(p_T\) domain, the Higgs precision studies at 27 TeV will resemble more those carried out at HL-LHC. A fair comparison between HL-LHC and HE-LHC would therefore require much more detailed studies, accounting for the larger pile-up, and based on a concrete detector design.
Same as Fig. 4.5, for the HE-LHC
Left: precision in the determination of the scattering of same-sign longitudinal W bosons, as function of luminosity, for various kinematic cuts. Right: sensitivity of the longitudinal boson scattering cross section w.r.t. deviations of the WWH coupling from its SM value (\(\kappa _W=1\)), for various selection cuts on the final-state dilepton invariant mass. The vertical bars represent the precision of the measurement, for 30 \(\hbox {ab}^{-1}\)
The results of the studies for the Higgs self-coupling at HE-LHC are discussed in Sect. 10.
15.5 FCC-eh
The main Higgs production mechanisms at FCC-eh are charged-current (CC) and neutral-current DIS, namely \(\hbox {ep}\rightarrow \upnu \,\hbox {HX}\) via WW fusion (\(\sigma = 1\,\hbox {pb}\)), and \(\hbox {ep}\rightarrow \hbox {eH}\,\hbox {X}\) via ZZ fusion (\(\sigma = 0.15\,\hbox {pb}\)). The WW fusion process dominates the rate, providing excellent direct sensitivity to the HWW coupling. The total Higgs event rate at FCC-eh is about \(2.3 \cdot 10^6\) events for \(2\,\hbox {ab}^{-1}\), broken down by decay channel in Table 4.6. These rates enable precise determinations of the Higgs couplings to bosons and fermions in decay channels with branching fraction at the per mille level.
The high energy of the FCC-eh configuration thus allows for very precise measurements of the main SM Higgs couplings. It will also lead to accurate measurements of the ttH coupling, of the Higgs-to-invisible decay, the self-coupling of the Higgs boson and to sensitive searches for exotic Higgs phenomena. Related initial studies are briefly summarised below.
As mentioned in Sect. 4.3, the FCC-eh measurements will also critically improve the systematics of Higgs measurements at FCC-hh, through the very precise PDF and \(\alpha _s\) determinations. This is particularly true of the gg parton luminosity, which drives the \(\hbox {gg}\rightarrow \hbox {H}\) production channel: at 100 TeV this is sensitive to Bjorken x values in the range of \(10^{-3}\), where even small deviations from the DGLAP evolution paradigm, due e.g. to gluon saturation, could influence the ultimate percent precision goal.
15.5.1 SM Higgs decays
The study of SM Higgs decays, summarised in [90], has been performed in two steps. First, detailed simulations and analyses were made of the dominant \(\mathrm{H} \rightarrow \mathrm{b}\bar{\mathrm{b}}\) [91,92,93,94] and of the challenging \(\mathrm{\mathrm H} \rightarrow \mathrm{c}\bar{\mathrm{c}}\) [94, 95] channels. Signals and backgrounds were generated by Madgraph5/Madevent, with the fragmentation and hadronisation in PYTHIA followed by a Delphi-based simulation of the baseline ep detector. Both cut-based and boosted decision tree (BDT) analyses were performed in independent evaluations.
Second, an analysis of NC and CC events was established for the seven most frequent decay channels listed in Table 4.6. Acceptances and backgrounds were estimated with Madgraph, and efficiencies for the leptonic and hadronic decay channels of W, Z and \(\uptau \) were taken from prospective studies of Higgs coupling measurements at the LHC [96]. This provided a systematic scale factor f, which comprised the signal-to-background ratio, the product of acceptance, A, and reconstruction efficiency \(\epsilon \), as \(f^2 = (1 + B/S)/(A \epsilon )\). The error on the signal strength \(\mu _i\) for each of the Higgs decay channels i is determined as \(\delta \mu _i / \mu _i = f_i / \sqrt{N_i}\). Here, \(N_i\) are the event numbers listed in Table 4.6. This second estimate could be successfully benchmarked with the detailed simulations for charm and beauty decays described above.
Same as Fig. 4.6, for the HE-LHC
The results of the signal strength determinations are illustrated in Fig. 4.11, for the FCC-eh and, for comparison for the two lower energy ep collider configurations, the LHeC, in which the electron ERL is coupled with the HL-LHC, and its high energy version, the HE-LHC. The electron beam energy has been kept constant at \(60\,\hbox {GeV}\) while the proton energy of the LHC-based colliders is 7 or \(14\,\hbox {TeV}\), respectively. One finds that the FCC-eh prospects for the experimental uncertainties on the signal strength vary between below \(0.5\%\) for the most abundant channel and up to \(5\%\) for the \(\upgamma \upgamma \) decay. The FCC-eh results presented in Fig. 4.11 are input to a joint pp-ep-ee FCC Higgs coupling analysis as is presented elsewhere in this paper. They can also be used for an independent and complete coupling strength analysis in ep alone.
15.5.2 Determination of Higgs couplings
The amplitude of the subprocess, \(\hbox {VV}\rightarrow \hbox {H}\rightarrow \hbox {XX}\) (\(\hbox {X}=\hbox {b}, \hbox {W}, \hbox {g}, \uptau , \hbox {c}, \hbox {Z}, \upgamma \)) involves a coupling to the vector boson V, scaling as \(\kappa _V\), and the coupling to the decay particle X, proportional to \(\kappa _X\), modulated by a \(\kappa \) dependent factor due to the total decay width. This leads to the following scaling of the signal strength
which is the ratio of the experimental to the theoretical cross sections, expected to be 1 in the SM. Measurements of this quantity at the LHC are currently accurate to \(\mathcal {O}\)(20) % and will reach the \(\mathcal {O}\)(5) % level at the HL-LHC. With the joint CC and NC measurements of the various decays, considering the seven most abundant ones illustrated in Fig. 4.11, one constrains with the above equation the seven \(\kappa _X\) parameters. The joint measurement of NC and CC Higgs decays provides 9 constraints on \(\kappa _W\) and 9 on \(\kappa _Z\) together with 2 each for the five other decay channels considered. Since the dominating channel of \(\hbox {H}\rightarrow \hbox {b}\bar{\hbox {b}}\) is precisely determined, there follows a strikingly precise determination of the \(\kappa \) values, to about or below one percent, as is shown in Fig. 4.12. A feature worth noting is the“transfer” of precision in signal strength from the \(\mu _b\) in the CC channel to \(\kappa _W\). This overall level of precision may as well be used to constrain EFT parameters, a task beyond the standalone FCC-eh analysis presented here.
An interesting consistency check of the EW theory is provided by the relation of the ratio of the CC and NC Higgs production cross sections, \(\kappa _W^2/\kappa _Z^2\), which in the SM should be equal to \(\cos ^4\theta _W\). This is estimated to determine the weak mixing angle, \(\sin ^2\theta _W\) to about \(2\,\%\). In addition, direct measurements will be obtained for the charm-to-bottom decay ratios, testing to percent accuracy the relative coupling of the Higgs boson to the 3rd and 2nd generations.
15.5.3 Top and invisible Higgs couplings
A fundamental quantity to be accessed, linking the two heaviest SM elementary particles, is the ttH coupling, and its associated CP phase \(\zeta _t\), expected to vanish in the SM. An update of the LHCeC analysis documented in Ref. [97] shows that FCC-eh could achieve a precision of 1.9% in the determination of \(\zeta _t\).
The Higgs-to-invisible decay may provide a key to BSM physics. In the SM it has a \(0.1\%\) branching ratio from \(H \rightarrow 4 \nu \). Verification of that process is an important means to establish the nearly full set of SM Higgs decays in ep and exclude, or detect, new physics. To suppress the neutrino missing-energy background, invisible decays of the Higgs bosons were considered in NC scattering. The main backgrounds are W and Z DIS production. Complementing a parton level study of this process for the LHeC [98], a complete Madgraph-PYTHIA-Delphes analysis was performed, including other relevant backgrounds such as single top and W photoproduction. The resulting uncertainty on the invisible Higgs branching ratio is estimated to be 1.2%.
15.5.4 Exotic Higgs phenomena
Extended gauge theories predict the existence of further Higgs bosons, such as a fiveplet, singly charged Higgs \(H_5^{\pm }\) boson [99], which can be searched for at FCC-eh. The Higgs boson may decay to non-SM particles and open a window to new physics. A prime example in the FCC-eh study [100, 101] is the possible Higgs decay into two scalars followed by their decays into two b quarks. Both case studies, for an extended H sector and for exotic decays, are briefly illustrated.
The charged Higgs bosons are produced via the ZW fusion process \(\hbox {pe}\rightarrow \hbox {j}\,\hbox {e}\, \hbox {H}_5^{\pm }\), and decay as \(\hbox {H}_5 \rightarrow \hbox {Z}\,\hbox {W}\rightarrow \ell ^+\ell ^-\,\hbox {jj}\). With the FCC-eh detector-level simulation, a multi-variate analysis is performed to yield limits on \(\sigma (\hbox {p}\, \hbox {e}^- \rightarrow \hbox {j } \hbox {e}^- H_5^{\pm }) \times \hbox {BR}(\hbox {H}_5^{\pm } \rightarrow \hbox {Z}\, \hbox {W}^\pm )\) and on the model parameter \(\sin \theta _H\) (not shown here). The limits, obtained in Ref. [102] for \(2.5\,\hbox {ab}^{-1}\) and for charged Higgs masses between 200 and \(1000\,\hbox {GeV}\), are shown in Fig. 4.13.
Limits on \(\sigma (\hbox {p}\, \hbox {e}^- \rightarrow \hbox {j } \hbox {e}^- \hbox {H}_5^{\pm }) \times {\mathrm{BR}}(\hbox {H}_5^{\pm } \rightarrow \hbox {Z}\, \hbox {W}^\pm )\) as functions of \(M_{H_5}\) at the FCC-eh with unpolarised electron beams and a luminosity of \(2.5~\hbox {ab}^{-1}\). For each band, the bottom (top) of the shaded region denotes the significance curve with 0% (10%) systematic uncertainty on the background
An exotic Higgs decay mode into two new light scalars in a 4b final state is considered in a BDT study [101] following the method investigated for the LHeC [100]. Such a decay is well motivated in the Next to Minimal Supersymmetric Standard Model (NMSSM) and extended Higgs sector models, complementing pp studies where the complex 4b final state would be difficult measure. The study was performed for scalar masses of 20 and \(60\,\hbox {GeV}\). Backgrounds from top and multijets and from W, Z or H and jets were shown to be well under control. For a \(20\,\hbox {GeV}\) mass scalar, sensitivity was observed down to a branching fraction of 1% for 1 \(\hbox {ab}^{-1}\) of luminosity.
16 QCD measurements
16.1 FCC-ee
High-luminosity \(\mathrm{e}^{+}\mathrm{e}^{-}\) collisions at the FCC-ee provide an extremely clean environment, with a fully-controlled QED initial-state with known kinematics, to uniquely probe quark and gluon dynamics with very large statistical samples. At variance with pp collisions, QCD phenomena appear only in the final state and are amenable to perturbative calculations over most of the accessible phase space, free from complications due to initial-state parton distribution functions, multiparton interactions, beam-remnants, etc. FCC-ee thereby provides the best conditions possible to carry out very precise extractions of the strong coupling, as well as to study parton radiation and fragmentation, with cleanly-tagged light quarks, gluons, and heavy quarks. The main QCD physics goals of FCC-ee, summarised in Refs. [43, 103], are:
-
1.
Permille extraction of the QCD coupling \(\alpha _s\).
-
2.
High-precision analyses of perturbative parton radiation including high-order leading (\(\hbox {N}^n\hbox {LO}\)) corrections and logarithmic (\(\hbox {N}^n\hbox {LL}\)) resummations for jet substructure, quark/gluon/heavy-quark discrimination, and q,g,c,b parton-to-hadron fragmentation functions studies.
-
3.
High-precision non-perturbative QCD studies including colour reconnection, parton hadronisation, final-state multiparticle correlations, and very rare hadron production and decays.
Compared to QCD studies at LEP, FCC-ee offers vastly increased statistical samples (\(10^{12}\) and \(10^7\) partons from Z and W decays, respectively) and provides access to the previously unreachable Higgs boson and top-quark hadronic final states (\(10^5\) jets). The expected experimental samples at the Z pole will be \(10^5\) larger than at LEP and therefore the statistical uncertainties will be reduced by a factor of 300. In the W case, one goes from about 11 000 jets per experiment at LEP2, to tens of millions at FCC-ee, enabling truly high-statistics \(\hbox {e}^{+}\hbox {e}^{-}\rightarrow \hbox {W}^+\hbox {W}^-\) measurements for the first time. The latter will be a highly fruitful testing ground, e.g. for colour reconnection studies (likewise for \(\hbox {e}^{+}\hbox {e}^{-} \rightarrow \hbox {t}\bar{\hbox {t}}\) events) [104], and for precise extractions of \(\alpha _\mathrm{s}\) from W decays [45], competitive with those at the Z pole. A small selection of representative QCD measurements accessible at the FCC-ee [43, 103] is presented below.
16.1.1 High-precision \(\alpha _\mathrm{s}\) determination
The combination of various high-precision hadronic observables at the FCC-ee, with state-of-the-art pQCD calculations at NNLO accuracy or beyond, will lead to an \(\alpha _\mathrm{s}\) determination with per mille uncertainty, at least five times better than today [43, 105]. First, the huge statistics of hadronic \(\uptau \), W, and Z decays, studied with \(\hbox {N}^3\hbox {LO}\) perturbative calculations, will provide \(\alpha _\mathrm{s}\) extractions with very small uncertainties: \(<1\%\) from \(\uptau \), and \(\sim 0.2\%\) from W and Z bosons. Figure 5.1 shows the expected \(\alpha _\mathrm{s}\) extractions from the NNLO analysis of the ratio of W hadronic and leptonic decays \(\hbox {R}_{\mathrm{W}} = \Gamma _{\mathrm{had}}/\Gamma _\ell \) (left) [45], and from three hadronic observables (\(\Gamma _\mathrm{Z}\), \( \sigma _0^{\mathrm{had}} = 12 \pi /m_\mathrm{Z} \cdot \Gamma _\mathrm{e}\Gamma _{\mathrm{had}}/\Gamma _\mathrm{Z}^2\), and \(R^0_\ell = \Gamma _{\mathrm{had}}/\Gamma _\ell \)) at the Z pole (right) [30]. In addition, the availability of millions of jets (billions at the Z pole) measured over a wide \(\sqrt{s}\approx \) 90–350 GeV range, with light-quark/gluon/heavy-quark discrimination and reduced hadronisation uncertainties (whose impact decreases roughly as \(1/\sqrt{s}\)), will provide \(\alpha _\mathrm{s}\) extractions with \(<1\%\) precision from various independent observables: hard and soft fragmentation functions, jet rates, and event shapes. Last but not least, photon-photon collisions, \(\gamma \,\gamma \rightarrow \) hadrons, will allow for an accurate extraction of the QCD photon structure function (\(F_2^\gamma \)) and thereby of \(\alpha _\mathrm{s}\).
Left: expected \(\alpha _\mathrm{s}\) extraction from the hadronic/leptonic W decay ratio (\(\hbox {R}_{\mathrm{W}}\)) at the FCC-ee (the diagonal blue line assumes CKM matrix unitarity) [45]. Right: precision on \(\alpha _\mathrm{s}\) derived from the electroweak fit today (blue band) [30] and expected at the FCC-ee (yellow band, without theoretical uncertainties and with the current theoretical uncertainties divided by a factor of four)
16.1.2 High-precision parton radiation studies
16.1.3 Jet rates and event shapes
Jet rates at the one-in-a-million level in \(\mathrm{e}^{+}\mathrm{e}^{-}\) at the Z pole will be available at the FCC-ee, including: 4-jet events up to \(k_T\sim 30~\hbox {GeV}\) (corresponding to \(|\ln (y)|\sim 2\), for jet resolution parameter \(y = k_T^2/s\)), 5-jet events at \(k_T \sim 20~\hbox {GeV}\) (\(|\ln (y)|\sim 3\)), 6-jet events at \(k_T \sim 12~\hbox {GeV}\) (\(|\ln (y)|\sim 4\)), and 7-jet events at \(k_T\sim 7.5~\hbox {GeV}\) (\(|\ln (y)|\sim 5\)). Such results will be compared to theoretical calculations with accuracy beyond the NNLO+NNLL provided currently by the eerad3 [106], Mercutio2 [107], and ColorFULNNLO [108] (NNLO), and ares [109] (NNLL) codes, thereby leading to \(\alpha _\mathrm{s}\) extractions with uncertainties well below the few-percent level of today. In general, with the FCC-ee luminosities that are envisioned, jet measurements will extend along the six axes of higher accuracy, finer binning, higher jet resolution scales, larger numbers of resolved final-state objects, more differential distributions, and possibility to place stringent additional cuts to isolate specific interesting regions of the n-jet phase spaces not strongly constrained by LEP measurements [110].
Event shapes (part of the more generic “angularities” variables) are uniquely studied in \(\mathrm{e}^{+}\mathrm{e}^{-}\) and since they are theoretically described in fixed-order pQCD up to NNLO accuracy [106, 111, 112], they have been used, in particular, for high precision extractions of \(\alpha _\mathrm{s}\). However, like other QCD observables that depend on widely separated energy scales, they are affected by (i) logarithmic enhancements, resummed today up to \(\hbox {N}^3\hbox {LL}\) using pQCD [113, 114] and SCET [115] techniques, and (ii) hadronisation corrections, often estimated with MC generators [116,117,118,119]. The FCC-ee operating at different c.m. energies will enormously help to control resummation and hadronisation effects in event-shape distributions reducing, in particular, non-perturbative uncertainties from a \(9\%\) effect at \(\sqrt{s} = 91.2~\hbox {GeV}\) to a \(2\%\) at 400 GeV [103, 115].
16.1.4 Jet substructure and parton flavour studies
Separation between quarks and gluons, and between light (u, d, s) and heavy (c, b) quarks, is of prime importance in precision SM measurements and BSM searches. Parton flavour discrimination is based on the comparison of jet substructure properties to MC predictions. At \(\mathrm{e}^{+}\mathrm{e}^{-}\) colliders so far, gluon jets only appear at relative order \(\alpha _s\) – the cleanest gluon studies at LEP focused on \(\mathrm{Z}\rightarrow \mathrm{b}\bar{\mathrm{b}} \mathrm{g}\) events at the price of smaller statistics – and hence their radiation pattern is less well constrained than that of quarks. At FCC-ee, both the \(10^5\) larger statistics at the Z pole and the unique \(\mathrm{H}\rightarrow {\mathrm{gg}}\) sample of order \(10^4\) events yield unprecedented opportunities for enhanced parton-flavour studies. Heavy-quark fragmentation will also be open to detailed studies with large statistical samples in top, Z, W, and H decays to b (and c) quarks, and in gluon fragmentation with \(\mathrm{g}\rightarrow \mathrm{b}\bar{\mathrm{b}}\) (and \(\mathrm{g}\rightarrow \mathrm{c}\bar{\mathrm{c}}\)) splittings.
Hadron-level distributions of the LHA variable for the \(\mathrm{e}^+ \mathrm{e}^- \rightarrow \mathrm{u} \bar{\mathrm{u}}\) (“quark jet”) sample (left) and the \(\mathrm{e}^+ \mathrm{e}^- \rightarrow {\mathrm{gg}}\) (“gluon jet”) sample (right) predicted by seven parton-shower generators at \(Q = 200~~\text {GeV} \) and jet radius \(R= 0.6\) [120]
The quark/gluon radiation patterns currently predicted by Pythia 8.215 [121], Herwig 2.7.1 [122, 123], Sherpa 2.2.1 [124], Vincia 2.001 [125], \(\textsc {Deductor 1.0.2}+ \textsc {Pythia}\) [126], Ariadne 5.0.\(\beta \) [127], and \(\textsc {Dire 1.0.0}+\textsc {Sherpa}\) [128] event generators have been investigated in Ref. [120] in terms of generalised angularities \(\lambda ^{\kappa }_{\beta } = \sum _{i \in \text {jet}} z_i^\kappa \theta _i^\beta \) [129], where different \((\kappa , \beta )\) pairs map onto variables of common use in the literature: hadron multiplicity (0,0), \(p_T^D\) (2,0), “Les Houches Angularity” (1,0.5) [130], jet width (1,1), and jet mass (1,2). Figure 5.2 shows the hadron-level distributions of the IRC-safe LHA variable in the quark (left) and gluon (right) samples for \(\mathrm{e}^{+}\mathrm{e}^{-}\) collisions at FCC-ee energies. Little variation among generators is seen for quarks, which is not surprising since most of these programs have been tuned to match LEP data (though LEP never measured the LHA itself). Larger variations are seen for the gluon sample among the generators; this is expected since there is no data to directly constrain \(\mathrm{e}^+ \mathrm{e}^- \rightarrow {\mathrm{gg}}\). The differences already appear at the parton level prior to hadronisation. These results show how \(\mathrm{Z}\rightarrow \mathrm{q}\bar{\mathrm{q}}\) and \(\mathrm{H}\rightarrow {\mathrm{gg}}\) jet substructure measurements at the FCC-ee will bring crucial information for the development of MC event generators at the interface between perturbative showering and nonperturbative hadronisation, helping to significantly improve quark-gluon taggers, an important tool in collider physics.
16.1.5 High-precision non-perturbative QCD
Controlling the uncertainties linked to colour reconnection, hadronisation, final-state spin correlations, etc. – optimally studied in the clean environment provided by \(\mathrm{e}^{+}\mathrm{e}^{-}\) collisions – is basic for many high-precision SM studies. Among the goals of FCC-ee is to produce a legacy of truly precise measurements to constrain many aspects of nonperturbative (NP) dynamics to the 1% level or better, leaving an important legacy for MC generators for the FCC-eh and FCC-hh physics programme, much as those from LEP proved crucial for the parton shower models used today at the LHC.
Searches for Colour Reconnection (CR) effects are best studied in the process \(\mathrm{e}^{+}\mathrm{e}^{-} \rightarrow \mathrm{W}^+ \mathrm{W}^- \rightarrow \mathrm{q}_1 \bar{q}_2 \mathrm{q}_3 \bar{q}_4\), where CR could lead to the formation of alternative “flipped” singlets \(\mathrm{q}_1 \bar{q}_4\) and \(\mathrm{q}_3\bar{q}_2\), and correspondingly more complicated string topologies [131]. The combination of results from all four LEP collaborations excluded the no-CR null hypothesis at 99.5% CL [132], but statistics was too small to allow for any quantitative studies. At FCC-ee, with the W mass determined to better than 1 MeV by a threshold scan, the semileptonic WW measurements (unaffected by CR) can be used to probe the impact of CR in the hadronic WW events. Table 5.1 lists the shift in the reconstructed W mass predicted by different Pythia 8 CR models. Effects are reasonably small near the threshold, increase with energy and eventually decrease as the W’s decay further apart. Most models tend to shift the W mass upwards, when away from the threshold region. The “gluon move” (GM) variants [133] illustrate that different aspects of a CR model may go in opposite directions and partly cancel and the new QCD-based CS model [134] is an example where mass shifts are expected to be tiny. Alternative CR constraints have been proposed at the FCC-ee through the study of event shape observables sensitive to string overlap, such as sphericity for different hadron flavours, as described in “rope hadronisation” approaches [135].
\(\Xi ^-\) spectra measured by the ALEPH experiment at LEP I (left) and by the CMS experiment at the LHC compared to the predictions from modern event generators [136]
The process of parton hadronisation is modelled phenomenologically in MC event generators with moderate success. The production of baryons (in particular containing strange quarks) remains poorly understood and is hard to measure in the complicated hadron-hadron environment. Also, the standard assumption of universality – that models developed from \(\mathrm{e}^{+}\mathrm{e}^{-}\) data can be applied directly to hadron-hadron collisions – has been challenged at the LHC where strong final-state effects, more commonly associated with heavy-ion physics and quark-gluon-plasma formation, such as the ridge effect [137] or the increase of strangeness production in high-multiplicity pp events [138], are not explained by the standard MCs, with or without colour reconnection. The large statistical samples available at the FCC-ee will allow parton hadronisation in the QCD vacuum to be controlled with subpercent uncertainties, and thereby better understanding any collective final-state effects in hadron collisions. Starting with multiply-strange baryons whose total production rates could only be determined with 5%–20% accuracy at LEP [139, 140]; and going further to excited [140, 141], exotic, and/or multiply heavy hadrons, with implications for more advanced fragmentation models (Fig. 5.3 shows the spectra of hyperons where MC generator programs fail today describe the LEP [142] and LHC data). For \(\Lambda \)–\(\Lambda \) correlation distributions, the FCC-ee samples of about \(4\cdot 10^8\) hadronic Z decays will have statistical uncertainties matching the best LEP systematic uncertainties, corresponding to total errors reduced by a factor of about 10.
16.2 FCC-hh
All phenomena in pp collisions are driven by QCD dynamics. Even EW interactions are subject to QCD effects, whether through the densities of the initial state partons (parton distribution functions, PDFs), or through higher-order corrections that can significantly alter the production of EW objects. QCD is therefore the primary tool to predict and interpret physics at FCC-hh. The theoretical precision has greatly improved recently, thanks to new powerful techniques and to extensive validation efforts made possible by the LHC data. More and more processes are known to NNLO, with theoretical systematics down to the few per-cent level. PDF uncertainties are likewise being reduced, thanks to the LHC data and to ever-improving theoretical frameworks. It is thus impossible to firmly predict what the landscape will be for the precision of QCD calculations in hadronic collisions at the end of the HL-LHC. More progress will also be made during the FCC era, with a great reduction of the systematics for fundamental quantities such as \(\alpha _S\) and PDFs from FCC-ee and FCC-eh, respectively. All in all, it seems therefore that 1% is an ambitious but justified target for the ultimate precision that one can expect at least in the most prominent QCD production processes of interest to FCC-hh, like jet production. This precision can be put towards a better sensitivity to BSM phenomena. Precision in hadronic collisions has already turned from being a goal, to becoming a tool, and this will be even more so at FCC-hh.
This section on QCD focuses on jet observables, stressing aspects that are unique to the 100 TeV environment, to show how far the sensitivity to large mass scales can be pushed. As in previous examples from the EW and Higgs Sections, it is shown here that the extensive kinematic reach of 100 TeV and the large statics, together with an improved theoretical control, can promote hadronic observables in pp collisions to precision probes.
A large collection of additional QCD processes (multijets, vector bosons plus jets, jet substructure), and relative kinematic distributions, are shown in Ref. [25].
Figure 5.4 shows the inclusive production rate for central jets (\(\vert \eta \vert <2.5\)), and the corresponding statistical uncertainties as a function of integrated luminosity. The statistics at 30 \(\hbox {ab}^{-1}\) allows \(p_T\) values in the range of 25-30 TeV to be reached, with uncertainties smaller than 10% up to \(p_T\sim 22~\hbox {TeV}\). Combining with a target 1% systematics, the potential overall precision of the measurements is shown in Fig. 5.5.
For the theoretical predictions, 1% is an ambitious but achievable goal, thanks to progress in the perturbative calculations and in the knowledge of the PDFs. For measurements sensitive to the shape of the distribution (e.g. the running of \(\alpha _S\) or the search of shape anomalies due to higher-dimension operators), the absolute luminosity determination does not contribute to the systematics. The jet energy resolution will only lead to a predictable smearing of the \(p_T\) spectrum. Furthermore, the energy resolution itself will be very small, limited in the multi-TeV region by the 2.6% constant term, as reported in Volume 3, Section 7.5.2. The stochastic contribution, even in presence of 1000 pile-up events, scales in the region \(\vert \eta \vert <1.3\) like \(104\%/\sqrt{p_T/\mathrm {GeV}}\), and drops below the % level for \(p_T\gtrsim 10~\hbox {TeV}\). The leading experimental systematics will most likely be associated with the determination of the absolute jet-energy scale (JES). A great deal of experience is being accumulated at the LHC on the JES calibration [143, 144], combining, among others, test-beam data, hardware monitoring via sources, and data-driven balancing techniques. The latter rely on events such as \(\hbox {Z}[\rightarrow \mathrm {e}^+\mathrm {e}^-]+\hbox {jet}\), \(\upgamma +\hbox {jet}\) or multijets. The precise measurement of EM energy deposit of photons and electrons allows the calibration of the jet energy, up to energy levels where there is sufficient statistics. At larger energies, leading jets are calibrated against recoil systems composed of two or more softer jets. In their final calibration of approximately 20 \(\hbox {fb}^{-1}\) of 8 TeV data from run 1, CMS [144] achieved a JES uncertainty for central jets of about 0.3% in the 200–300 GeV range. ATLAS [143], using 3.2 \(\hbox {fb}^{-1}\) of 13 TeV data, determined a more conservative uncertainty of less than 1% for central jets with \(p_T\) in the range 100–500 GeV. A naive rescaling of the statistics based on the rates for \(\hbox {Z}/\upgamma +\hbox {jet}\) and multijet processes at the FCC-hh, suggests that the CMS and ATLAS calibrations can extend the \(p_T\) range at 100 TeV and 30 \(\hbox {ab}^{-1}\) by factors of \(\sim 20\) and \(\sim 15\), respectively, taking it into the multi-TeV range. The impact of the JES uncertainty on the jet rates, as a function of the \(p_T\) threshold and for various uncertainty assumptions (0.2%, 0.5% and 1%), is shown in Fig. 5.6. The most optimistic JES determination, to 0.2%, is certainly ambitious, but not too far from the 0.3% quoted by CMS. This precision would allow the uncertainty in the jet cross section spectrum to be maintained at the 1–2% level for \(p_T\) up to \(\sim 10~\hbox {TeV}\).
Left plot: combined statistical and \(1\%\) systematic uncertainties, at 30 \(\hbox {ab}^{-1}\), vs \(p_T\) threshold; these are compared to the rate change induced by the presence of 4 or 8 TeV gluinos in the running of \(\alpha _S\). Right plot: the gluino mass that can be probed with a \(3\sigma \) deviation from the SM jet rate (solid line), and the \(p_T\) scale at which the corresponding deviation is detected
An overall systematics in the percent range could then provide a very powerful tool to explore deviations from the SM. An example is given in Fig. 5.5, which shows the rate variation induced by the running of \(\alpha _S(Q)\) modified by the presence of a colour-octet of (Majorana) fermions (e.g. supersymmetric gluinos). They lead to a slow-down of the \(\alpha _S\) running, and an increase in rate. The \(3\sigma \) sensitivity, as a function of integrated luminosity, is shown in the right plot of Fig. 5.5, assuming the combination of statistical uncertainty (\(\delta _{stat}=1/\sqrt{N}\)) and of a systematics \(\delta _{sys}\) of 1 or 2%. The \(3\sigma \) are defined in a simple way, verifying the existence of a minimum-\(p_T\) threshold, \(p_{T,min}\), such that \((N_{\tilde{g}} - N_{SM})/N_{SM}>3\sigma (p_T)\), where \(N_{SM}\) is the number of events with \(p_T>p_{T,min}\) expected in the SM, \(N_{\tilde{g}}\) is the larger rate due to the gluino modification in \(\alpha _S\) running, and \(\sigma (p_T)=\sqrt{\delta _{stat}^2+\delta _{sys}^2}\). More sensitive algorithms can of course be used, taking full benefit of the shape modification of the distribution. In the example, the sensitivity extends up to gluino masses of 7.5 (5) TeV, for 1% (2%) systematics. The \(p_T\) scales at which the 3\(\sigma \) deviation is achieved are given by the dashed lines. The presence of additional coloured particles (like generations of scalar quarks) would further enhance the signature. While the precision in the absolute measurement of \(\alpha _S(M_Z)\) obtained by FCC-ee and FCC-eh cannot be matched by FCC-hh, the energy lever-arm available at 100 TeV provides a unique probe of the presence of new strongly interacting states in the TeV region, independent of the specific model of new physics and of the possible (more or less visible) decay modes of the new particles.
A similar study of the jet \(p_T\) spectrum at HE-LHC is shown in Figs. 5.7 and 5.8. It can be seen that, at 27 TeV, luminosities in the range of several \(\hbox {ab}^{-1}\) are necessary to access the multi-TeV region with sufficient statistics, where experimental systematics related to the jet energy scales can be of \(\mathcal {O}(\%)\), thus gaining sensitivity to a possible anomalous running of \(\alpha _S\).
Same as Fig. 5.4, but for HE-LHC
Same as Fig. 5.5, but for HE-LHC, with 15 \(\hbox {ab}^{-1}\) of luminosity
Dijet production at large invariant mass provides a signature for higher-dimension operators, e.g. four-quark interactions induced by a possible underlying composite nature of quarks. High-mass dijets are also a dominant background in the search for resonances. The rates, as a function of the dijet mass M(jj), are shown in Fig. 5.9, considering two regions in \(\Delta \eta (jj)\): \(\vert \Delta \eta \vert <5\) and \(\vert \Delta \eta \vert <2\). The first region is dominated by small-angle scattering and, while rates are much larger, the average \(p_T\) is smaller, and less sensitive to new physics at large \(Q^2\). The latter region is more central, and closer to the domain where BSM effects could show up. Here the statistics extends well over \(M(jj)=50~\hbox {TeV}\). The composition of the initial states for central dijet production, as a function of M(jj), are shown in the right plot of Fig. 5.9. The qg channel dominates in the range \(2<M(jj)/\mathrm {GeV}< 20\), while above 20 TeV the “elastic” qq scattering dominates, thanks to the larger valence quark contributions. The composition in the case of inclusive jet production is similar, at scales \(p_T^{jet}\sim M(jj)/2\). As discussed in the next section, the uncertainty in the partonic luminosity for these channels will be brought well below the percent level by the PDF measurements at FCC-eh. Further implications of these results, in the search for high-mass resonances in hadronic final states, are presented in Sect. 15.
16.3 FCC-eh
Deep inelastic electron-proton scattering (DIS) determines the momentum densities of partons (quarks and gluons) as functions of x and \(Q^2\), which are the fraction of the proton momentum carried by the parton, and the square of the electron 4-momentum transferred to the proton respectively. The ensuing parton distribution functions (PDFs) are a probe of the hadron internal dynamics and are the key ingredient for the prediction and interpretation of the results of pp collider experiments.
With the high centre of mass energy of FCC-eh, the range in x covered by scattering processes with \(Q^2 \ge 1\,\hbox {GeV}^2\) extends from \(8 \times 10^{-8}\) to 1. This reach at extremely low values of x will expose the behaviour of QCD in a new regime, characterised by high gluon densities and non-linear dynamics. These deviations from the standard DGLAP behaviour can have an impact on \(\hbox {gg}\rightarrow \hbox {Higgs}\) production, where one of the two initial-state gluons will always have x smaller than \(\sqrt{x_1x_2} = M_H/2E_p \simeq 0.001\). The small x range is also relevant to the interactions of cosmic ultra high energy neutrinos. Furthermore, with the projected integrated luminosity of \(2-3\,\hbox {ab}^{-1}\), the FCC-eh measurements can reach the \(x \sim 1\) region, where cross sections drop quickly as \(\propto (1-x)^3\) when \(x \rightarrow 1\).
The FCC-eh provides a huge extension of phase space and enables many other measurements on QCD properties to be made and new dynamics in ep possibly to be discovered. This section focuses on PDFs and small x physics, thus neglecting various other important subjects such as jets, in DIS and photoproduction, or 3D proton structure, searches for instantons or the study of the transition from hadron to parton degrees of freedom, as \(Q^2\) crosses the \(\mathcal{O}(\hbox {GeV}^2)\) threshold. A more complete picture of the programme of QCD physics possible at FCC-eh can be found in the LHeC report, Ref. [69].
16.3.1 Parton distributions
High energy, high luminosity DIS is the best means to determine the proton PDFs, an essential element of the FCC-hh and FCC-eh programme. They key targets and expected outcomes of the FCC-eh PDF programme are highlighted here:
-
The FCC-eh will resolve the partonic content of the proton in all of its individual components, and in an unprecedented range of \(Q^2\) and x. The valence and sea quarks, and the gluon distribution, will be measured to high accuracy, free of earlier limiting systematics such as nuclear corrections and higher twist effects.
-
The FCC-eh will deliver the PDF inputs necessary to enhance the FCC-hh programme of precision measurements and BSM searches at high mass. The improvement in the PDF knowledge will have to match, or better, the precision achieved with the next generation of multi-loop calculations.
-
The PDF measurements will also yield a one or two per mille precision on \(\alpha _s(M_Z^2)\). As discussed in Ref. [145], this level of precision will greatly improve the theoretical predictions (e.g. of the scale of grand unification) and will be necessary to clarify the existing tensions between various \(\alpha _s\) determinations, in view of the anticipated increased precision from Lattice QCD, and from FCC-ee.
-
Novel insight will be obtained on QCD dynamics, where HERA’s limited energy and statistics have left several important issues open: factorisation at high x, BFKL dynamics at small x, role of heavy-quark thresholds in the extraction of charm and bottom quark PDFs, etc.
The FCC-eh will provide a coherent set of NC and CC data, from which PDFs can be extracted using theoretically robust \(\hbox {N}^k\hbox {LO}\) calculations (with \(k \ge 3\)), in presence of negligible hadronisation corrections, and at the large values of \(Q^2\) that brings them closer to the kinematics of FCC-hh. The use of FCC-eh PDFs in the search for new physics at FCC-hh will remove ambiguities in the interpretation of possible anomalies, where new physics effects could otherwise be attributed to PDF effects, or vice versa.
16.3.2 The PDF analysis
As input observables, the present simulation of PDF measurements only uses the inclusive NC and CC cross sections, analysed in the xFitter [146,147,148] framework, with settings based on the HERAPDF2.0 QCD fit analysis [55]. Future studies will add the input provided by many other measurements, such as \(F_L\), jet cross sections, and heavy quark production. Studies of the latter, in particular, will greatly benefit from the small beam spot size and new generation silicon detectors with large acceptance. As an example, accurate charm tagging of Ws fusion in CC scattering, using both \(\mathrm{e}^+\) and \(\mathrm{e}^-\) beams, will allow separate measurements of the strange and anti-strange quark densities.
The simulation of pseudodata relies on the detector described in [69] and its development and extension towards the FCC-eh, described in the FCC-hh Volume of the FCC CDR. The numerical simulation procedure was gauged with full H1 Monte Carlo results. The uncertainty assumptions correspond to H1’s achievements with improvements, where justified, by at most a factor of two. Five data sets (A–E) were generated, under the conditions summarised in Table 5.2, mostly for \(\mathrm{e}^-\mathrm{p}\) but also for \(\mathrm{e}^+\mathrm{p}\) and for \({\mathrm{ePb}}\) scattering.Footnote 3 These sets were used in the initial prospect studies for PDFs and electroweak physics.
The NLO analysis follows the HERA PDF fit procedure [55], with a minimum \(Q^2\) cut of \(3.5\,\hbox {GeV}^2\) and a starting scale \(Q^2_0=1.9~\hbox {GeV}^2\), chosen to be below the charm mass threshold. The fits are extended to lowest x for illustration, even though at such low x values non-linear effects are expected to appear, eventually altering the evolution laws. The parameterised default PDFs are the valence distributions \(\hbox {u}_v\) and \(\hbox {d}_v\), the gluon distribution g, and the \(\bar{\mathrm{U}}\) and \(\bar{\mathrm{D}}\) distributions, where \(\bar{\mathrm{U}} =\bar{\mathrm{u}}\), \(\bar{\mathrm{D}} = \bar{\mathrm{d}} +\bar{\mathrm{s}}\). The following standard functional form is used to parameterise the PDFs
where the normalisation parameters (\(A_{uv}, A_{dv}, A_g\)) are constrained by quark counting and momentum sum rules. No correlation assumption is made on the up and down valence and sea quark distributions. It was checked that the final results of PDF uncertainties are robust against changes in the parameterisations. The experimental uncertainties on the PDFs are determined using the \(\Delta \chi ^2=1\) criterion based on the simulated NC and CC cross sections and their correlated and uncorrelated expected errors.
16.3.3 Quark distributions
Knowledge of the valence quark distributions, at both large and small x, is extremely limited, as illustrated in Fig. 5.10, which compares the results from a variety of modern PDF sets (CT14 [149], MMHT2014 [150], NNPDF3.0 [48], HERAPDF2.0 [55] and ATLASepWZ16 [151]). At high x, this has to do with the limited luminosity, challenging systematics rising \(\propto 1/(1-x)\) and nuclear correction uncertainties and, at low x, with the small size of the valence quark distributions as compared to the sea quarks and, not least, the limited x range of previous DIS experiments.
The impressive improvement that can be expected from an FCC-eh is illustrated in the same figure. The up valence quark distribution is better known than the down valence, since for lepton-proton scattering it enters with a four-fold weight in \(F_2\) due to the quark electric charge ratio squared. At FCC-eh the weak probes alter the relative weight of up and down distributions and as a consequence a substantial improvement is then achieved for \(\mathrm{d}_\mathrm{v}\) as well. The huge improvements at large x are a consequence of the high precision measurements of the NC and CC inclusive cross sections, which at high x tend to \(4 \mathrm{u}_\mathrm{v}+\mathrm{d}_\mathrm{v}\) and \(\mathrm{u}_\mathrm{v}~(\mathrm{d}_\mathrm{v})\) for electron (positron) scattering, respectively. The vast improvements compared to HERA constraints come from the much higher luminosity and extension in kinematic reach. They also profit from improved energy calibration at FCC-eh with respect to HERA. Such precise determination of the valence quark distributions at large x has strong implications for BSM searches. Precision measurements at high x in \({\mathrm{ep}}\) may be confronted with accurate predictions and measurements in \({\mathrm{pp}}\) Drell Yan scattering and possibly confirm or question the principle of factorisation. In addition, they can also resolve the mystery of the \({\mathrm{d/u}}\) ratio at large x, where currently there are conflicting theoretical pictures, and where current data, plagued by higher twists and nuclear corrections, have remained inconclusive.
Figure 5.11 shows the distributions of \(\overline{\mathrm{U}}\) and \(\overline{\mathrm{D}}\). Note the very high precision determination for the FCC-eh PDF, despite the relaxation of any assumptions, present in other determinations, which would force \(\bar{\mathrm{u}} \rightarrow \bar{\mathrm{d}}\) as \(x \rightarrow 0\).
16.3.4 Gluon distribution
The result for the gluon distribution from the FCC-eh inclusive NC and CC data is presented in Fig. 5.12, and compared to several other modern PDF sets. On the left, the distribution is presented as a ratio to CT14, and is displayed on a log-x scale to highlight the small x region. On the right, the \(x\mathrm{g}\) distribution is shown on a linear-x scale, accentuating the region of large x. The determination of \(x\mathrm{g}\) is predicted to be radically improved with the FCC-eh NC and CC precision data, which extend down to lowest x values close to \(10^{-7}\) and large x close to \(x=1\).
Below \(x \simeq 10^{-3}\), the HERA data have almost vanishing constraining power due to kinematic range limitations, and so the gluon is simply not determined at low x. With the FCC-eh, a precision of a few percent at small x becomes possible down to nearly \(x \simeq 10^{-6}\). This improvement primarily comes from the extension of range and precision in the measurement of \(\partial F_2/\partial \log Q^2\), which at small x is a measure of \(x\mathrm{g}\). The precision determination of the quark distributions, discussed previously, also strongly constrains \(x\mathrm{g}\) as quark and gluon distributions have to fulfil the momentum sum rule.
While the analysis performed here has used standard DGLAP evolution, the precise measurement of \(F_\mathrm{L}\) at the FCC-eh (not yet considered here), in addition to \(F_2\), can discover whether \(x\mathrm{g}\) saturates, and whether the DGLAP equations need to be replaced by non-linear parton evolution equations, as is also discussed in [145].
At large \(x \ge 0.3\) the gluon distribution becomes very small and huge variations appear in its current determination from different PDF groups, differing by orders of magnitude. This is related to uncertainties on jet measurements, theoretical uncertainties, and the fact that HERA did not have sufficient luminosity to cover the high x region where, moreover, the sensitivity to \(x\mathrm{g}\) diminishes, since the valence quark evolution is insensitive to it. For FCC-eh, the sensitivity at large x comes as part of the overall package: large luminosity allowing access to x values close to 1; fully constrained quark distributions; as well as strong constraints at small x which feed through to large x via the momentum sum rule. The high precision illustrated will be crucial for BSM searches at high scales as it provides the necessary precise and independent input for distinguishing possible new physics and QCD expectation. It is also important for testing QCD factorisation and scale choices, as well as electroweak effects.
It is also worth noting that additional information on the gluon will be provided at the FCC-eh in measurements of \(F_L\), \(F_2^{c,b}\) and jet cross sections, which have not been included in the current initial prospect study.
16.3.5 Parton luminosities
The FCC-eh PDF precision, in a huge kinematic range, will be a crucial base for searches at the FCC-hh extending to high masses, \(M_X=sx_1x_2\), for precision Higgs or electroweak physics, and for correctly interpreting the measurements at small x, where DGLAP evolution may be superseded by non-linear evolution laws.
Figure 5.13 shows the results for four relevant combinations of parton luminosities (as defined in [152]) for the production of a massive object with mass \(M_X\). The results are displayed as fractional uncertainties on the parton luminosities, for the FCC-eh PDFs described in this section and, to set a scale, compared to the PDF4LHC15 [153] set of parton distributions. One observes a roughly ten-fold improvement in the uncertainties. Figure 5.14 zooms into the FCC-eh results of Fig. 5.13, showing a precision systematically well below the percent level, except at the largest masses. Considering that the FCC-hh direct discovery reach at the highest masses will extend up to 40–50 TeV (see Sect. 15.3.1), the FCC-eh precision perfectly matches the discovery needs.
Relative PDF uncertainties on parton-parton luminosities from the PDF4LHC15 and FCC-eh PDF sets, as a function of the mass of the produced heavy object, \(M_X\), at \(\sqrt{s} = 100~\hbox {TeV}\). Shown are the gluon-gluon (top left), quark–antiquark (top right), quark-gluon (bottom left) and quark–quark (bottom right) luminosities
Relative PDF uncertainties on parton-parton luminosities from the FCC-eh PDF set, as a function of the mass of the heavy object produced, \(M_X\), at \(\sqrt{s} = 100~\hbox {TeV}\). Shown are the gluon-gluon (top left), quark–antiquark (top right), quark-gluon (bottom left) and quark–quark (bottom right) luminosities
16.3.6 Small x physics
16.3.7 Resummation at small x
As centre of mass energy in a scattering process becomes very large, the corresponding values of the Bjorken x variable for the partons participating in the collision become very small. From the theoretical point of view there are number of interesting phenomena that can occur in that regime. In the standard description of the hard processes, the presence of a large scale in the hard process allows for the use of the collinear framework in which the hadronic cross section becomes factorised into hard scattering partonic cross sections and the parton distribution functions which are evolved using the DGLAP evolution equations. The latter ones resum powers of large logarithms of the hard scale, i.e powers of \(\alpha _s \ln Q^2\). However, when Bjorken x is small there is a possibility that other logarithms, namely \(\alpha _s \ln 1/x\) become large and need to be resummed appropriately. The resummation of such logarithms in the QCD is performed via Balitskii–Fadin–Kuraev–Lipatov (BFKL) evolution [154, 155]. This equation is an appropriate evolution in perturbative QCD in the Regge limit, that is when the centre of mass energy s is much larger than any other scales in the scattering problem. The BFKL evolution is known up to NLO in QCD. Unfortunately, it has been known for a long time that higher order corrections are very large and need to be resummed. Appropriate resummation schemes have been constructed, [156, 157] and they take into account momentum sum rules and matching to the DGLAP evolution. Recently, global fits have been performed that include the resummation of low x terms within the DGLAP framework [158] and results show marked improvement in the description of the HERA data, particularly at low x and low \(Q^2\). The effects in this kinematic regime are still subtle, but they will have a very large impact at future \({\mathrm{ep}}\) colliders. In Fig. 5.15 predictions for \(F_2\) and \(F_L\) are shown for the FCC-eh using the resummed NNPDF3.1sx fits. It is clear from the plots that the resummed prescription results in the steeper rise of the \(F_2\) structure function below \(x=10^{-4}\) and gives much larger value for the longitudinal structure function \(F_L\).
Structure function \(F_2\) (left) and longitudinal structure function \(F_L\) (right) as a function of x for fixed \(Q^2=5\,\hbox {GeV}^2\) computed in the NNLO+NLLx scheme within NNPDF3.1sx calculation (blue bands). Shown also for comparison is the NNLO prediction (red bands). Figures taken from [55]
16.3.8 Elastic diffraction of vector mesons
The growth of the gluon density at small x is expected to ultimately lead also to parton saturation. Gluon splitting begins competing with gluon recombination, slowing down the growth of the gluon density and of the cross sections with increasing energy or decreasing Bjorken x. Parton saturation and the parton rescattering processes are the perturbative QCD mechanisms that ensure that unitarity bounds on the growth of cross sections are preserved. To test how close the scattering amplitudes are to the unitarity limit is a non-trivial problem. One of the best and cleanest ways to probe the scattering amplitude as a function of impact parameter of the collision is through the process of exclusive vector meson production in \({\mathrm{ep}}\) DIS. In such a process the proton undergoes an elastic collision, thus remaining intact and the final state is characterised by the presence of a large rapidity gap and an additional vector meson. This process can be measured in photoproduction as well as in the regime where the photon virtuality is non-zero, as a function of the \(\upgamma \) p energy W and the momentum transfer t. In Fig. 5.16 the differential cross section in t is shown for the elastic photoproduction of \(\hbox {J}/\Psi \) vector mesons for two values of the \(\upgamma \) p energy, \(W=1\) and \(W=2.5 \; {\mathrm{TeV}}\). In each case three predictions are shown, two from models that include saturation and one without the saturation [159]. The models with saturation predict a distinct feature in the t distribution, namely the dip. The model without the saturation shows exponential dependence on t. Such behaviour is to be expected on general grounds, since the t distribution of the cross section can be related to the Fourier transform of the scattering amplitude in impact parameter space. In the case of the unsaturated model the density profile in impact parameter space is Gaussian and therefore it would give the exponential distribution in the t momentum transfer. On the other hand, if the scattering amplitude is modified by the saturation effects, and is close to the unitarity limit, the deviations from the Gaussian profile are to be expected and therefore the Fourier transform will lead to the emergence of dips. Another characteristic feature of saturation is the dependence of the position of the dips on the energy, the higher the energy the lower are the positions of the dips in t. The exact location of the dips depends on the details of the model, as demonstrated in Fig. 5.16, but the general tendency is present in both models. Thus, studying the position and the energy dependence of the dips in elastic vector meson production can provide a powerful means to test the saturation and provides detailed information about the internal spatial structure of the proton.
Left: diffractive kinematic plane for FCC-eh as compared to HERA and LHeC. Right: relative uncertainty on the gluon diffractive distribution after the fits including the simulated diffractive data at FCC-eh (magenta) and LHeC (blue) as compared to the error bands from the extraction using only HERA data (black)
16.3.9 Inclusive diffraction and diffractive parton densities
The FCC-eh will provide an extended kinematic range in which one can study diffractive parton densities (dPDFs). At the HERA collider it was observed that about 10–15% of events are diffractive, i.e. events which were characterised by the large rapidity gap, absence of any activity in the detector. Unlike the standard inelastic hard scattering processes, the description of such processes is theoretically challenging. The emergence of the rapidity gap is attributed to the exchange of a colourless object with the quantum numbers of the vacuum, the Pomeron. For the cases when the hard scale is present in the diffractive process, i.e. for large values of \(Q^2\), factorisation has been proved [160]. In this approach the diffractive cross section can be factorised into the part which is perturbatively calculable, the partonic cross section, and the dPDFs. The latter can be interpreted (at least in the lowest orders of perturbation theory) as the conditional probabilities of finding a parton in the proton, under the condition that the proton remains intact after the scattering. The kinematic plane in \((x,Q^2)\) that could be probed at FCC-eh is shown in Fig. 5.17, on the left panel. Here, \(\beta \) is the momentum fraction of the parton with respect to the Pomeron and \(\xi \) is the momentum fraction of the Pomeron with respect to the hadron, so that \(x=\xi \beta \). It can be seen that the FCC-eh would allow x values that are smaller by a factor of 200 than those at HERA, to be probed. Shown in the right panel of Fig. 5.17 are the error bands on the extracted dPDFs, from the fits to the simulated diffractive data. The data were simulated assuming an integrated luminosity of \(2\,\hbox {fb}^{-1}\) and a \(5\%\) Gaussian error due to systematics. This shows a significant reduction of the error bands on the extracted dPDFs by a factor \(10-15\) as compared to HERA. This will allow the precision study of the inclusive diffraction at FCC-eh.
17 Top quark measurements
17.1 Introduction
The top quark, with its large mass, is special among all quarks. It is the known particle that most strongly influences the Higgs boson and its potential, leading to prominent puzzles about the origin of EW symmetry breaking. Its mass, measured today by ATLAS [161] and CMS [162] at about \(172.5\pm 0.5~\hbox {GeV}\), leads to a value of its Yukawa coupling \(y_{\mathrm{top}}=\sqrt{2}m_{\mathrm{top}}/v\) equal to 1 to better than 1%. Is this accidental, or is it a consequence of some yet unknown underlying dynamics? The top mass is also very close, within 1%, to the critical value [163] that separates the domain of stability of the Higgs potential up to the Planck scale \(M_P\) from the domain where the potential becomes unstable well before \(M_P\). The study of the top quark goes therefore hand in hand with that of the Higgs, and forms one of the key priorities of any future collider.
The direct measurement of top quark properties has so far been confined to hadron colliders. Lepton colliders, through EW precisions tests at the Z pole or flavour observables such as \(\mathrm{B}^0\bar{\mathrm{B}}^0\) mixing, provided important information, essential to establish the overall consistency of the SM, but could not so far match the Tevatron and LHC in determining top quark properties such as its mass and couplings. The FCC will redefine this landscape. Operations of FCC-ee at and above the \(\mathrm{e}^+\mathrm{e}^- \rightarrow t\bar{t}\) threshold will dominate the precision in the measurement of the top mass \(\mathrm{m}_{\mathrm{top}}\) and of its EW neutral couplings, to fulfil the needs of enhanced EW precision from the running at the Z peak. While losing to FCC-ee the hadron-colliders’ dominance in measurements such as \(\mathrm{m}_{\mathrm{top}}\), the FCC-hh will continue leading the search for rare or exotic decay modes, and will use the immense kinematic reach to expose, directly or indirectly, new phenomena at high-mass scales. This sensitivity will be complemented by FCC-eh studies, where the top coupling to the W boson and possible FCNC interactions leading to \(\hbox {eq}\rightarrow \hbox {et}\) (\(\hbox {q}=\hbox {u,c}\)) transitions can be studied in a uniquely clean environment.
By testing the top quark properties precisely and from all directions over an extended range of distance scales, the FCC will provide the most powerful tool to reveal the secrets held by the top, as briefly summarised in this chapter.
17.2 FCC-ee
The production rate for top quark pairs at the FCC-ee around threshold at \(\sqrt{s}=350\,\hbox {GeV}\) is of order 0.5 pb. Collecting 1.5 \(\hbox {ab}^{-1}\) around the \(\mathrm{t}\bar{\mathrm{t}}\) threshold leads to a very clean sample of \(10^6~\mathrm{t}\bar{\mathrm{t}}\) events. This expected luminosity will be collected with a carefully optimised run plan that comprises about 0.2 \(\hbox {ab}^{-1}\) around the pair production threshold for the precision measurement of the top mass and width, and of the top Yukawa coupling, which affects the line-shape. The rest of the data will be collected at \(\sqrt{s}=365\,\hbox {GeV}\) for the optimal measurement of the top EW coupling to the Z and the photon, which can be measured below the percent level without the need of polarised beams. In addition, this clean sample can be used to search for exotic production or decay of top quarks via flavour changing neutral currents (FCNC). The anomalous single top production via the tZq and \(t\upgamma \hbox {q}\) vertices can be studied also with the 5 \(\hbox {ab}^{-1}\) collected at \(\sqrt{s}=240\,\hbox {GeV}\).
17.2.1 Precision measurements at the threshold
The precise measurement of the top quark mass is a major goal of the FCC-ee physics programme. At an \(\mathrm{e}^+\mathrm{e}^-\) collider the possibility of performing an energy scan around the top pair production threshold provides the highest accuracy. The \(\mathrm{t}\bar{\mathrm{t}}\) production cross-section shape at around twice the top mass depends strongly on \(\mathrm{m}_{\mathrm{top}}\), but also on the width of the top quark \(\Gamma _{top}\) (Fig. 6.1), the strong coupling constant and the Yukawa coupling \(\mathrm{y}_{\mathrm{top}}\). The theoretical uncertainties around the top threshold region have been reviewed in Ref. [164], and they drive the optimum choice of the scan points in the centre of mass energy. The extraction of the top mass value can be performed as a one parameter fit fixing the value of the other inputs to their SM expectations, or as a simultaneous fit to measure the mass, width, or the Yukawa coupling at the same time, as shown in Fig. 6.2. The resulting statistical uncertainty on \(\mathrm{m}_{\mathrm{top}}\) (\(\Gamma _{\mathrm{top}}\)) is 17 MeV (45 MeV). The corresponding systematic error due to the knowledge of the centre of mass energy (to be known with a precision smaller than 10 MeV) is 3 MeV. The precise measurement of \(\alpha _{s}\) to \(2\times 10^{-4}\) by measurements at lower energies contributes with 5 MeV to the top mass uncertainty. The current status of the theory uncertainty from the NNNLO calculations is of the order of 40 MeV for the mass and the width. The top Yukawa coupling could be extracted indirectly with a 10% uncertainty.
17.2.2 Precision measurement of the top electroweak couplings
In many extensions to the standard model couplings of top quark pairs to \(\hbox {Z}/\upgamma ^{*}\) can be enhanced. These are directly probed at FCC-ee as they represent the main production mechanism for \(\mathrm{t}\bar{\mathrm{t}}\) production at \(\mathrm{e}^+\mathrm{e}^-\) colliders. It is essential to be able to disentangle the tŧZ and \(\hbox {t}\bar{\hbox {t}}\upgamma \) processes to provide separation among different new physics models. In the case of linear \(\mathrm{e}^+\mathrm{e}^-\) colliders this is one of the motivations to implement longitudinal polarisation of the beams. However, it has been shown [165] that FCC-ee’s very large statistics can fully compensate for the lack of polarisation. The information needed to disentangle the contribution from the Z boson and photon can be extracted from the polarisation of the final-state particles in the process \(\mathrm{e}^+\mathrm{e}^-\rightarrow \mathrm{t}\bar{\mathrm{t}}\), as any anomalous coupling would alter the top polarisation as well. In that case, this anomalous polarisation would be transferred in a maximum way to the top-quark decay products via the weak decay \(\hbox {t}\rightarrow \hbox {Wb}\), leading to an observable modification of the final kinematics. The best variables to study are the angular and energy distributions of the leptons from the W decays. A likelihood fit of the double-differential cross section of the lepton angle \(\cos {\theta }\) and the reduced lepton energy \(x=\frac{2 E_\ell }{m_{top}} \sqrt{\frac{1-\beta }{1+\beta }}\) measured in top semi-leptonic decays at \(\sqrt{s}=365\,\hbox {GeV}\) with one million \(\mathrm{t}\bar{\mathrm{t}}\) events allows a precision of 0.5% (1.5%) to be obtained for the vector (axial) coupling of the top to the Z and 0.1% for the vector coupling to the photon. The fit includes conservative assumptions on the detector performance, such as lepton identification and angular/momentum resolution and b quark jet identification. The precision of these measurements would allow testing and characterisation of possible new physics models that could affect the EW couplings of the top quark, see for example Fig. 6.3. These data are also sensitive to the top-quark CP-violating form factors [165].
FCC-ee measurement uncertainties in the left and right coupling of the top to the Z (left) and to the photon (right) displayed as an ellipse. In the left plot the SM value at (0,0) is compared to predicted deviations from various composite Higgs model for \(f\le 1.6\,\hbox {TeV}\). The 4DCHMM [166] benchmark point A is represented with a cyan marker
17.2.3 Search for FCNC in top production or decay
The flavour-changing neutral currents (FCNC) interactions of top quarks are highly suppressed in the SM, leading to branching ratios of the order of \(10^{-13}\)–\(10^{-14}\). However, several extensions of the SM are able to relax the GIM suppression of the top quark FCNC transitions due to additional loop diagrams mediated by new particles. Significant enhancements for the FCNC top quark rare decays can take place, for example, in some supersymmetric two-Higgs-doublet models. Evidence of an FCNC signal will therefore indicate the existence of new physics. CMS and ATLAS obtained the best experimental upper limits on FCNC couplings from single top quark production and from top quark decays, and their sensitivity will greatly increase at the HL-LHC. The FCC-ee can perform a search for FCNC in top decay using the \(2\,\hbox {ab}^{-1}\) collected above the top pair production threshold. It can also profit from studying the anomalous single top production process with the \(5\,\hbox {ab}^{-1}\) at \(\sqrt{s}=240\,\hbox {GeV}\). The sensitivity of the FCC-ee to the quark FCNC couplings \(\hbox {tq}\upgamma \) and tqZ (\(\hbox {q}=\hbox {u,c}\)) has been studied in the \(\mathrm{e}^-\mathrm{e}^+ \rightarrow \hbox {Z}/\upgamma \rightarrow \hbox {t}\bar{\hbox {q}}\) (ŧq) channel, with a leptonic decay of the W boson. These preliminary analyses show that the FCC-ee can reach a sensitivity for \(\hbox {BR}(\hbox {t}\rightarrow \hbox {q}\upgamma )\) and \(\hbox {BR}(\hbox {t}\rightarrow \hbox {qZ})\) of about \(10^{-5}\), which is slightly below the sensitivity of HL-LHC, see Fig. 6.4. More optimised studies are expected in the future. It is therefore expected that FCC-ee could confirm and help characterise a top FCNC decay signature (e.g. distinguish \(\hbox {q}=\hbox {u}\) from \(\hbox {q}=\hbox {c}\)), should this be detected at the HL-LHC.
Summary of 95% C.L. limits in the search for FCNC in top production or decays for various future collider options, compared to current LHC limits. The study of the top FCNC decays reach at \(\mathrm{e}^+\mathrm{e}^-\) linear colliders was recently presented in Ref. [167]
17.3 FCC-hh
The production rate of top quark pairs at FCC-hh is \(\sim 35~\hbox {nb}\) (Table 6.1), over 30 times larger than at the LHC. This leads to \(\sim 10^{12}\) top quarks produced during FCC-hh operation, to be used to explore the top properties via both its production and decay features. As discussed in the case of EW and Higgs production, the extended kinematic reach of top quarks leads to sensitivity to EFT operators [168] describing possible deviations from the EW and QCD top couplings, complementary to what can be probed through the precise measurements at FCC-ee. The large statistics allow also to extend the search for flavour-changing neutral currents (FCNC) and other decays suppressed or forbidden in the SM. Furthermore, each \(\mathrm{t}\bar{\mathrm{t}}\) event triggered by either quark, allows the study of the decays of the W boson and of the b hadrons arising from the decay of the second quark in a rather unbiased and inclusive way. This can be exploited for flavour physics studies [169], studies of rare W decays [170], and possibly precision tests of lepton flavour universality (\(\hbox {W}\rightarrow \uptau ~ \hbox {vs W}\rightarrow \upmu \)).
The full measurement potential of this sample of over \(10^{12}\) top quarks is still far from having been thoroughly explored, and just a few examples are presented here.
The kinematic reach for top quarks is shown in Fig. 6.5. The \(p_T\) spectrum of individual top quarks, or of gluon-initiated jets splitting into a pair of top quarks whose directions are contained within a \(\Delta R<0.4\) cone, reaches 15 TeV. The invariant mass distribution for top quark pairs produced at large angle (\(\vert \eta _{t}-\eta _{\bar{t}}\vert < 2\)) extends up to 25 TeV, providing an irreducible background to searches for high-mass resonances decaying to top quarks. Studies of top tagging via jet-substructure techniques in such high mass regions are documented in Chapter 9.3 of Ref. [25], and in the context of resonant searches, in Sect. 15 of this volume. High-mass top pairs can also be used to probe possible anomalous couplings of the top to the gluon [171], via interactions such as:
A cross section analysis suggests that using \(m_{t\bar{t}}\gtrsim 10\) TeV at the FCC offers the best balance between the sensitivity of the high energy behaviour and the statistics in this regime [171]. This leads to an improvement of the chromodipole moment constraints by an order of magnitude, as compared with a similar analysis for the high energy LHC run, see Fig. 6.6.
(Left) Sensitivity of the \(\sqrt{s}=14\) TeV LHC, and the \(\sqrt{s}=100\) TeV FCC to the chromomagnetic and chromoelectric dipole moments \(d_V\) and \(d_A\) from high-mass tŧ production. Three different definitions for the boosted regime at the FCC are shown. (Right) A comparison of constraints on \(d_V\) and \(d_A\) from past, present, and future hadron colliders. For more details, see Ref. [171]
17.3.1 Single top production
Production of single tops at large \(p_T\), while suppressed w.r.t. top pairs, provides a further mean to test the top EW couplings at short distances. Total production rates for the different single-top channels are given in Table 6.2. Figure 6.7 shows the integrated rates for the production of high-\(p_T\) single tops, in the three production channels: t-channel (\({\mathrm{qb}}\rightarrow \mathrm{t}+\hbox {jet}\)), s-channel (\(\mathrm{q}\bar{\mathrm{q}}^{\,\prime }\rightarrow \mathrm{t}+\mathrm{b}\)) and \({\mathrm{gb}}\rightarrow {\mathrm{tW}}\) (here the t and \(\bar{\mathrm{t}}\) rates are equal). It can be seen from the plot that while the \({\mathrm{tj}}\) final state is always dominant, in the \(p_T\) range up to \(\sim 6\) \(~\text {TeV}\) \(\sigma (\bar{\mathrm{t}}\mathrm{j}) \sim \sigma ({\bar{\mathrm{t}}\mathrm{W}}^+)\), and beyond this range \(\sigma (\bar{\mathrm{t}}\mathrm{j}) \sim \sigma (\bar{\mathrm{t}}\mathrm{b})\), implying that some minimal discrimination power to separate the W and the b from the light jets would allow the separation of the less frequent production modes, using the \(\bar{\mathrm{t}}\) channel. Comparing with the t rates from \(\mathrm{t}\bar{\mathrm{t}}\) production, Fig. 6.5, notice however, that a reduction factor of \(\mathcal {O}\)(10) is required to suppress the t and \(\mathrm{t}\bar{\mathrm{t}}\) jet backgrounds to the level of single top final states. Detailed studies of possible applications are not yet available.
17.3.2 Associated production
The associated production of top quarks and gauge bosons (tŧV, with \(\hbox {V}=\hbox {Z,W},\upgamma \)) offers additional handles to study top properties (ttH production is discussed in Sect. 4.3). The SM rates for various processes are shown in Table 6.3, at NLO in QCD. Scale uncertainties are in the range of 10%, and PDF ones at the few % level. A large collection of kinematic distributions is shown in Ref. [25].
The production of \(\hbox {t}\bar{\hbox {t}}\hbox {Z}\) and \(\hbox {t}\bar{\hbox {t}}\upgamma \) allows direct measurement of the top EW couplings, and testing of the possible presence of anomalous interactions [174, 175]. For the Z, these can be parameterised as:
and the FCC-hh constraints are shown in Table 6.4. While the precision on the SM couplings \(C_{1,V/A}\) is inferior to that obtained from FCC-ee (see Sect. 6.2.2 and Ref. [165]), the precision of the anomalous couplings \(C_{2,V/A}\) is comparable or better to that of FCC-ee, also thanks to the absence of the \(\hbox {Z}/\upgamma ^*\) mixing which is present in \(\mathrm{e}^+\mathrm{e}^-\rightarrow t\bar{t}\).
The qq̄ initial state contribution to tŧ production generates a central/forward charge asymmetry, due to the preferential (reduced) emission of the top (anti)quark in the direction of the initial state (anti)quark:
This asymmetry can be sensitive to the presence of BSM contributions, as shown by the large attention [176] dedicated to an early anomaly reported by the Tevatron experiments. In pp collisions at 100 TeV, \(A_c\) is greatly diluted by the dominance of the gg initial state, and its expected value, \(A_c=0.12\%\), will make it very hard to measure. The asymmetry is enhanced by a factor of 10, however, for the tŧW process, which is dominated by a \(\hbox {q}\bar{\hbox {q}}^{\prime }\) initial state. This is shown in Table 6.5, where the SM asymmetries expected for the \(\hbox {t}\bar{\hbox {t}}\upgamma \) and tŧZ channels are also reported. The statistical uncertainty in the determination of \(A_c\) from tŧW was estimated in Ref. [177] to be \(\delta A_c/A_c \sim 3\%\), using fully leptonic final states.
17.3.3 Rare top decays
The large tŧ production rate at FCC-hh opens the door to multiple searches of rare or forbidden top decays. The factor of 30 increase in rate w.r.t. HL-LHC, and the tenfold increase in integrated luminosity, in principle, allow improvement of the HL-LHC reach by a factor of 10 or more. Some examples of concrete studies carried out so far are briefly summarised here.
17.3.4 \(\hbox {t}\rightarrow \hbox {Hq}\)
The large statistics allows searching for the FCNC \(\hbox {t}\rightarrow \hbox {Hq}\) (\(\hbox {q}=\hbox {u,c}\)) decay using the very clean \(\hbox {H}\rightarrow \upgamma \upgamma \) decay. A study presented in Ref. [179] reconstructs the SM top decay in fully hadronic and in semileptonic final states, requiring the invariant mass of the decay products to lie in the range [150,200] GeV. The candidate FCNC decay is required to have \(m_{q\gamma \gamma }\) in the range [160,190] GeV, with the \(\upgamma \upgamma \) pair mass within 2 GeV of the Higgs mass. All final state objects are subject to standard kinematic cuts on minimum \(p_T\) and \(\vert \eta \vert <2.5\) (see Ref. [179] for the details). b-tagging and fake-tags efficiencies reflect conservative assumptions relative to the CDR FCC-hh detector performance. A further charm-tagging requirement is set on the light-quark jet, to select the q=c channel. The dominant background comes from the tŧH process, with a S/B ratio in excess of 10, and much smaller contributions, of \(\mathcal {O}\)(1%), from \(\upgamma \upgamma \,\hbox {jjW}\) and \(\upgamma \upgamma \,\hbox {t}\bar{\hbox {t}}\). For 10 \(\hbox {ab}^{-1}\), 95% CL limits are set, combining both hadronic and semileptonic decays, with no (5%) systematics on background rates. For the tagged-charm analysis the limits are \(\hbox {BR}(\hbox {t}\rightarrow \hbox {Hc})<4.9\times 10^{-6}\; (1.6\times 10^{-5})\). Without charm tagging, these improve to \(\hbox {BR}(\hbox {t}\rightarrow \hbox {Hq})<2.5\times 10^{-6}\; (2.8\times 10^{-5})\).
17.3.5 \(\hbox {t}\rightarrow \upgamma \,\hbox {q}\)
The analysis of the \(\hbox {t}\rightarrow \upgamma \,\hbox {q}\) was carried out in the context of the FCC-hh detector performance studies, using the Delphes detector parameterisation, and is documented in more detail in the comprehensive volume of the FCC-hh CDR. A brief summary is given here.
The search focuses on the boosted-top regime, and reconstructs two recoiling fat jets with \(p_T>400~\hbox {GeV}\): one b-tagged, the other one formed by the photon and the light jet. The following backgrounds are included, and assigned an overall \(\pm \, 30\%\) systematic uncertainty: SM tŧ decays, \(\hbox {t}\bar{\hbox {t}}\upgamma \), \(\hbox {V}+\hbox {jets}\), single top and single top plus a photon. A BDT algorithm is applied to characterise the substructure of the two fat jets, to reduce the backgrounds. The resulting limits, for 30 \(\hbox {ab}^{-1}\)and at 95% CL, are: \(\hbox {BR}(\hbox {t}\rightarrow \upgamma \,\hbox {c})<2.4\times 10^{-7}\) and \(\hbox {BR}(\hbox {t}\rightarrow \upgamma \,\hbox {u})<1.8\times 10^{-7}\). No explicit study was performed of the \(\hbox {t}\rightarrow \hbox {Zq}\) decays. The current HL-LHC projections are in the range of few \(10^{-5}\). Considering the increase in statistics by a factor of 300 (cross section times luminosity), and assuming an improvement proportional to the square root of statistics, suggests a limit at the FCC-hh in the range of \(10^{-6}\).
17.4 FCC-eh
SM top quark production at the FCC-eh is dominated by the charged-current (CC) DIS process, \(\hbox {ep}\rightarrow \hbox {t}+\hbox {X}\). An example graph is shown in Fig. 6.8 (left). At the nominal FCC-eh centre-of-mass energy of 3.5 TeV, the total cross section is 15.3 pb [180]. The other important top quark production mode is tŧ photoproduction, with a total cross section of 1.14 pb [181]. An example graph is shown in Fig. 6.8 (right). The statistics of over \(10^7\) events per \(\hbox {ab}^{-1}\), the EW origin of the production processes, and the limited backgrounds, allow FCC-eh to achieve high-precision measurements of the top quark properties, complementary to FCC-ee and FCC-hh. Selected highlights are summarised here.
17.4.1 Wtq couplings
The flagship measurement is the direct measurement of the CKM matrix element \(|V_{tb}|\), independent of assumptions such as the unitarity of the CKM matrix. An early analysis of single top production [182] showed that even only 0.1 \(\hbox {ab}^{-1}\) at the LHeC allow measurement of \(V_{tb}\) with a 1% precision (the best LHC measurement so far, by CMS [183], reports a 4.1% uncertainty). The FCC-eh will clearly improve on this.
The same analysis can also be used to search for anomalous left- and right-handed Wtb vector and tensor couplings, analysing the following effective Lagrangian:
where \(f_1^L \equiv 1 + \Delta f_1^L\). In the SM \(f_1^L=1\), and \(f_1^R= f_2^L=f_2^R=0\). Using hadronic top quark decays only, the expected accuracies in a measurement of these couplings as a function of the integrated luminosity are presented in Fig. 6.9 (left).Footnote 4 The couplings can be measured with accuracies of \(1\%\) for the SM \(f_1^L\) coupling (therefore allowing the determination of \(|V_{tb}|\) with a \(1\%\) accuracy as discussed above), of \(4\%\) for \(f_2^L\), of \(9\%\) for \(f_2^R\), and of \(14\%\) for \(f_1^R\), assuming an integrated luminosity of \(1\ {\mathrm{ab}}^{-1}\).
Similarly, the CKM matrix elements \(|V_{tx}|\) (\(x=d,s\)) can be extracted using a parameterisation of deviations from their SM values with very high precision in W boson and bottom (light) quark associated production channels, where the W boson and b-jet (light jet) final states can be produced via s-channel single top quark decay or t-channel top quark exchange [184]. The following processes were considered:
-
Signal 1: \(\hbox {p } \hbox { e}^- \rightarrow \nu _\mathrm{e} \bar{\hbox {t}}+\hbox {X} \rightarrow \nu _\mathrm{e} \hbox {W}^- \bar{\hbox {b}}+\hbox {X} \rightarrow \nu _\mathrm{e} \ell ^-\nu _\ell \bar{\hbox {b}}+\hbox {X}\)
-
Signal 2: \(\hbox {p } \hbox { e}^- \rightarrow \nu _\mathrm{e} \hbox {W}^- \hbox {b}+\hbox {X} \rightarrow \nu _\mathrm{e} \ell ^-\nu _\ell \hbox {b}+\hbox {X}\)
-
Signal 3: \(\hbox {p } \hbox { e}^- \rightarrow \nu _\mathrm{e} \bar{\hbox {t}}+\hbox {X} \rightarrow \nu _\mathrm{e} \hbox {W}^- \hbox {j}+\hbox {X} \rightarrow \nu _\mathrm{e} \ell ^-\nu _\ell \hbox {j}+\hbox {X}\)
An analysis including a detailed detector simulation, using the Delphes package [182], leads to the accuracies on \(|V_{ts}|\) at the \(2\sigma \) confidence level (C.L.) shown as a function of the integrated luminosity in Fig. 6.9 (right). With \(2\, {\mathrm{ab}}^{-1}\) of integrated luminosity and an electron polarisation of \(80\%\), the \(2\sigma \) limits improve on existing limits from the LHC [185] (interpreted by [186]) by almost an order of magnitude. The study of Signal 3 alone allows achieving an accuracy of the order of the actual SM value of \(|V_{ts}^{\mathrm{SM}}|=0.04108^{+0.0030}_{-0.0057}\) as derived from an indirect global CKM matrix fit [187], providing the first direct high precision measurement of this top coupling. In these studies, upper limits at the \(2\sigma \) level down to \(|V_{ts}|<0.037\), and \(|V_{td}|<0.037\) can be achieved.
17.4.2 FCNC top quark couplings
Single top quark DIS production can also be used [188] to search for the FCNC couplings \(\hbox {tq}\upgamma \) and tqZ (q = u,c), as given in
where \(g_e\) (\(g_W\)) is the electromagnetic (weak) coupling constant, \(c_W=\cos \theta _W\), \(\lambda ^{L,R}_q\) and \(\kappa ^{L,R}_q\) are the strengths of the anomalous top FCNC couplings (vanishing in the SM), and \(P_L\) (\(P_R\)) denotes the left (right) handed projection operators. The selection of the final states requires at least one electron and three jets (hadronic top quark decay) with high transverse momentum and within the pseudorapidity acceptance range of the detector. The distributions of the invariant mass of two jets (reconstructing the W boson mass) and an additional jet tagged as b-jet (reconstructing the top quark mass) are used to further reduce the background, mainly given by W+jets production. Signal and background interference effects are included. A detector simulation with Delphes [182] is applied.
The expected limits on the branching ratios \(\hbox {BR}(\hbox {t}\rightarrow \hbox {q}\upgamma )\) and \(\hbox {BR}(\hbox {t}\rightarrow \hbox {qZ})\) as a function of the integrated luminosity are presented in Fig. 6.10 (left). The 95% CL limits of \(\hbox {BR}(\hbox {t}\rightarrow \hbox {q}\upgamma )<8.5 \cdot 10^{-7}\) and \(\hbox {BR}(\hbox {t}\rightarrow \hbox {qZ})<6.0 \cdot 10^{-6}\) are expected for 2 \(\hbox {ab}^{-1}\). This is precise enough to actually study concrete new phenomena models, such as SUSY, little Higgs, and technicolor, that have the potential to produce FCNC top quark couplings. As can be seen in Fig. 6.4, the limits on \(\hbox {BR}(\hbox {t}\rightarrow \hbox {q}\upgamma )\) \((\hbox {BR}(\hbox {t}\rightarrow \hbox {qZ}))\) will improve on existing LHC limits by 2 (1) orders of magnitude. The sensitivity on FCNC \(\hbox {tq}\upgamma \) couplings even exceeds expected sensitivities from the HL-LHC and from the ILC with \(500\,{\mathrm{fb}}^{-1}\) at \(\sqrt{s}=250\,\mathrm {GeV}\) [189], and from the FCC-ee.
Another example for a sensitive search for anomalous top quark couplings is the one for FCNC tHq couplings as defined in
This can be studied in CC DIS production, where singly produced top anti-quarks could decay via such couplings into a light anti-quark and a Higgs boson decaying into a bottom quark–antiquark pair, \(\hbox {ep}\rightarrow \upnu _e\bar{\hbox {t}}\rightarrow \upnu _e\hbox {H}\bar{\hbox {q}}\rightarrow \upnu _e\hbox {b}\bar{\hbox {b}} \bar{\hbox {q}}\) [190]. Another signal involves the FCNC tHq coupling in the production vertex, i.e. a light quark from the proton interacting with a W boson radiated from the initial electron, producing a b quark and a Higgs boson decaying into a bottom quark–antiquark pair, \(\hbox {ep}\rightarrow \upnu _e\hbox {Hb}\rightarrow \upnu _e\hbox {b}\bar{\hbox {b}}\hbox {b}\) [190]. This channel is superior in sensitivity to the previous one due to the clean experimental environment when requiring three identified b-jets. The largest backgrounds are given by \(\hbox {Z}\rightarrow \hbox {b}\bar{\hbox {b}}\), SM \(\hbox {H}\rightarrow \hbox {b}\bar{\hbox {b}}\), and single top quark production with hadronic top quark decays. A \(5\%\) systematic uncertainty for the background yields is added. Furthermore, the analysis assumes parameterised resolutions for electrons, photons, muons, jets and unclustered energy using typical parameters taken from the ATLAS experiment. Furthermore, a b-tag rate of 60%, a c-jet fake rate of 10%, and a light-jet fake rate of 1% are assumed. The selection is optimised for the different signal contributions separately. Figure 6.10 (right), shows the expected upper limit on the branching ratio \(\hbox {BR}(\hbox {t}\rightarrow \hbox {Hu})\) for various CL’s, as a function of the integrated luminosity for the \(\hbox {ep} \rightarrow \upnu _e\hbox {Hb}\rightarrow \upnu _e\hbox {b}\bar{\hbox {b}}\hbox {b}\) signal process. For an integrated luminosity of 1 \(\hbox {ab}^{-1}\), an upper limit of \(\hbox {BR}(\hbox {t}\rightarrow \hbox {Hu})< 2.2 \cdot 10^{-4}\) is expected. This improves on current limits from the LHC, as can be seen in Fig. 6.4. This shows the competitiveness of the FCC-eh results, and documents the complementarity of the reach from the three FCC colliders.
17.4.3 Other top quark property measurements and searches for new physics
Other results not presented here involve, for example, the study of the CP-nature in \(\mathrm{t}\bar{\mathrm{t}}\mathrm{H}\) production [97], searches for anomalous \(\mathrm{t}\bar{\mathrm{t}}\upgamma \) and \(\mathrm{t}\bar{\mathrm{t}}\mathrm{Z}\) chromoelectric and chromomagnetic dipole moments in \(\mathrm{t}\bar{\mathrm{t}}\) production [191], the study of top quark spin and polarisation [192], and the investigation of the top quark structure function inside the proton [69, 193].
18 Flavour physics measurements
18.1 FCC-ee
The \(\mathcal{O}(5 \times 10^{12}\)) Z decays to be delivered by the FCC-ee can be exploited to further enrich the knowledge of flavour physics of quarks and leptons, beyond what will emerge by the start of the FCC-ee program from the upgraded LHCb experiment [194] and the Belle II experiment [195]. Table 7.1 shows the anticipated production yields of heavy-flavoured particles at the two \(\mathrm{e}^+\mathrm{e}^-\) facilities, where the closer experimental environments allow for a more direct comparison.
The large statistics, the clean experimental environment (as for the Belle II experiment), the production of all species of heavy flavours, and large boosts (as in the LHCb experiment), give the FCC-ee a potential edge, presented here through several examples. These correspond to very challenging experimental measurements and are meant to highlight the physics potential: the measurement of the rare decay \(\bar{\mathrm{B}}^0 \rightarrow \mathrm{K}^{*0}(892)\uptau ^+\uptau ^-\), which completes and enhances the understanding of EW penguin mediated decays and can serve as a highly efficient model-discriminator should the present flavour anomalies remain; \(\uptau \) physics, including the search for charged lepton flavour violation (LFV) in Z and \(\uptau \) decays as well as lepton flavour universality violation (LFUV) in \(\uptau \) decays; and, finally, the assessment of model-independent BSM constraints induced by heavy-flavoured neutral meson oscillation measurements.
18.1.1 Flavour anomalies and electroweak penguins in \(b \rightarrow s\) quark transitions
Processes involving the quark transition \(b \rightarrow s \ell ^+ \ell ^-\) are receiving increasing phenomenological [196,197,198,199] and experimental [200,201,202] interest. The reported departures from SM predictions are questioning LFU and suggest a presence of BSM effects, for example in the form of new vector bosons or leptoquark mediated transitions. Should these deviations be confirmed, it is of utmost importance to complete our understanding with observables involving the \(\uptau \) lepton. The decays \(\hbox {B}_s\rightarrow \uptau ^+ \uptau ^-\) and \(\bar{\hbox {B}}^0 \rightarrow \hbox {K}^{*0}(892)\uptau ^+\uptau ^-\) are therefore obvious candidates to study. The excellent knowledge of the decay vertices, thanks to the multibody hadronic \(\uptau \) decays, allows the decay kinematics to be fully solved in spite of the final-state neutrino. The decay \(\bar{\hbox {B}}^0 \rightarrow \hbox {K}^{*0}(892)\uptau ^+\uptau ^-\) has been studied using Monte Carlo events propagated through a fast simulation featuring a parametric FCC-ee detector, with tracking and vertexing performance inspired from the ILD detector design [203].
Figure 7.1 shows the reconstructed invariant mass distribution of simulated SM signal and background events corresponding to \(5 \times 10^{12}\) Z-bosons. More than a thousand reconstructed events can be expected at the FCC-ee, opening the way to measurements of the angular properties of the decay [204]. Table 7.2 compares the (anticipated) reconstructed yields for these decay modes, at the Belle II, LHCb upgrade and FCC-ee experiments. For completeness, the projected precisions [20] for the determinations of \(\mathcal{B}(\hbox {B}_\mathrm{s} (\hbox {B}^0) \rightarrow \upmu ^+\upmu ^-)\) at HL-LHC are 12.9% (29%) with ATLAS, and 7% (16%) with CMS.
Invariant mass reconstruction of \(\bar{\hbox {B}}^0 \rightarrow \hbox {K}^{*0}(892)\uptau ^+\uptau ^-\) candidates (green line), where \(\uptau \rightarrow 3\uppi \upnu _{\tau }\) and \(\hbox {K}^*\rightarrow \hbox {K}^+\uppi ^-\), allowing the decay vertices to be reconstructed. The two dominant backgrounds are included: \(\bar{\hbox {B}}_\mathrm{s} \rightarrow \hbox {D}_\mathrm{s}^+\hbox {D}_\mathrm{s}^- \hbox {K}^{*0}(892)\) (red) and \(\bar{\hbox {B}}^0 \rightarrow \hbox {D}_\mathrm{s}^+ \bar{\hbox {K}}^{*0}(892)\uptau ^-{\upnu }_{\tau }\) (pink)
Similar decays, such as \(\Lambda _b^0\rightarrow \Lambda ^{*}(1520)\uptau ^+\uptau ^- \), benefit from the same topological reconstruction advantages. Likewise, in view of completing the LFUV tests, the study of the decay \(\hbox {B}^0 \rightarrow \hbox {K}^*(892) \hbox {e}^+\hbox {e}^-\) can be performed with unrivalled statistics.
18.1.2 Lepton flavour violation in Z-boson decays and tests of lepton flavour universality
The observation of LFV in Z-boson decays, \(\hbox {Z}\rightarrow \hbox {e}\upmu \), \(\upmu \uptau \) or \(\hbox {e}\uptau \) would provide indisputable evidence for physics beyond the SM, e.g. the existence of new particles such as sterile neutral fermions. This scenario is particularly attractive since it could address all the outstanding experimental or observational arguments for BSM physics: neutrino masses and mixing, a potential dark matter candidate, and the origin of baryonic asymmetry in the universe through leptogenesis [205, 206]. The search for LFV Z decays is also complementary to the direct searches for heavy neutral fermions.
A phenomenological study [207] has been undertaken to study the potential of FCC-ee to probe the existence of sterile neutral fermions in light of the improved determination of neutrino oscillation parameters, the new bounds on low-energy LFV observables as well as cosmological bounds. This work also addressed the complementarity of these searches with the current and expected precision of similar searches at lower energy experiments. The best sensitivity to observe or constrain LFV in the \(\hbox {e}\upmu \) sector is then obtained by the experiments based on the muon-electron conversion in nuclei [208]. In contrast, the study of the decays \(\hbox {Z}\rightarrow \hbox {e}\uptau \) and \(\hbox {Z}\rightarrow \upmu \uptau \) would provide unique insight in connection to the third generation. This goes beyond the models of sterile neutral fermions and can also probe e.g. the leptoquark mediators advocated as a possible resolution of the flavour anomalies.
The current limits [209,210,211,212] on LFV Z decays sit in the ballpark of \(\mathcal {O}(10^{-6}-10^{-5})\). The FCC-ee would improve them by several orders of magnitude and could probe BSM predictions down to \(\mathcal{O}(10^{-9})\) branching fractions [213].
Branching fraction of \(\uptau \rightarrow \hbox {e} \overline{{\upnu }} \upnu \) versus \(\uptau \) lifetime. The current world averages of the direct measurements are indicated with the blue ellipse. Suggested FCC-ee precisions are provided with the yellow ellipse. The SM functional dependence of the two quantities, depending on the \(\uptau \) mass, is displayed by the red band
The very large samples of \(\uptau \) decays at FCC-ee will also allow for significantly improved tests of Lepton Flavour Universality (LFU). The present status of such tests and their theoretical implications are summarised in Ref. [214]. There is a close connection between the present LFU anomalies in B physics, and LFU tests in \(\uptau \) decays, where an improved precision would allow to probe several existing explanations of these phenomena, see e.g. Refs. [215, 216]. In \(\uptau \) decays, firstly, the ratio of the weak charged current couplings between muons and electrons, \(g_\mu /g_{\mathrm{e}}\), can be extracted from the ratio of the partial widths of the two leptonic decay modes, \(\uptau \rightarrow \upmu \upnu \upnu \) and \(\uptau \rightarrow \hbox {e}\upnu \upnu \). The LEP data [217,218,219,220,221] support LFU to a precision of 0.14% [222]. Secondly, the ratio of the weak couplings between \(\uptau \) and electron (muon) can be extracted from the ratio of the partial widths of \(\uptau \rightarrow \hbox {e}\upnu \upnu \) (\(\uptau \rightarrow \upmu \upnu \upnu \)) and \(\upmu \rightarrow \hbox {e}\upnu \upnu \). Current measurements support this universality to a precision of 0.15% [222], with an uncertainty dominated by the measurement of the \(\uptau \) leptonic branching fractions and lifetime [223]. These will be reduced at FCC-ee, thanks to a factor of 100 improvement in the statistical precision and to the expected vertexing performance of its detectors. Figure 7.2 shows the current world average situation for the \(\uptau \rightarrow \hbox {e}\) universality test. An overall improvement in precision of a factor of ten in the \(\uptau \) branching fraction and lifetime measurements is also suggested. To improve on the situation beyond this would require also a better measurement of the \(\uptau \) mass, from a next generation of \(\uptau \)-factory experiments at the production threshold.
18.1.3 Charged lepton flavour violation in \(\tau \) lepton decays
Very stringent tests of charged lepton flavour violation (CLFV) have been performed in muon decay experiments where branching fraction limits below \(10^{-12}\) on both of the decay modes \(\upmu ^-\rightarrow \mathrm {e}^-\upgamma \) and \(\upmu ^-\rightarrow \hbox {e}^-\hbox {e}^+\hbox {e}^-\) have been established. All models predicting CLFV in the muon sector imply a violation also in the tau sector, whose strength is often enhanced by several orders of magnitude, usually by some power in the tau-to-muon mass ratio. Studying CLFV processes in tau decays offers several advantages compared to muon decays. Since the tau lepton is heavy, more CLFV processes can be studied. In addition to the modes \(\uptau \rightarrow \upmu /\hbox {e}+\upgamma \) and \(\uptau \rightarrow \upmu /\hbox {e}+\ell ^+ \ell ^-\), CLFV can be also studied in several semileptonic modes. The expected \(3\times 10^{11}\uptau \) produced at FCC-ee exceed the Belle II (\(50~\hbox {ab}^{-1}\)) statistics by about a factor of three, raising the possibility that FCC-ee may provide competitive sensitivities.
The focus here is on \(\uptau \rightarrow 3\upmu \) and \(\uptau \rightarrow \upmu \upgamma \) as golden modes for evaluating the sensitivity to CLFV. With the excellent FCC-ee invariant mass resolution, the search for \(\uptau \rightarrow 3\upmu \) is expected to be essentially background free, and to achieve a signal efficiency higher than Belle II, thanks to the boosted topology. The sensitivity could then reach branching fractions of \(\mathcal {O}(10^{-10})\), a level which is very interesting as it would probe deep into current models connected to LFU anomalies in B physics [216, 224].
On the other hand, the \(\uptau \rightarrow \upmu \upgamma \) search is limited by backgrounds, namely \(\hbox {e}^+\hbox {e}^-\rightarrow \uptau ^+\uptau ^-\upgamma \), with one \(\uptau \rightarrow \upmu \upnu \upnu \) decay, and the invariant mass of the \(\upmu \upgamma \) pair in the signal region. An experimental study [213] of the signal and this dominant background, including realistic detector resolutions and efficiencies, indicates that a sensitivity down to a branching fractions of \(2\times 10^{-9}\) should be within FCC-ee reach.
18.1.4 Search for BSM physics in \(\Delta F = 2\) quark transitions
The B-factories’ results have established the global profile of CP violation in the quark flavour sector below the electroweak scale [225]. This has been reinforced by the latest results from the LHCb experiment, in particular related to the CKM angle \(\gamma \) [226], although the current direct experimental precision does not yet match the indirect constraints from CKM unitarity [187]. The SM is able to accommodate the data both from the B-meson and from kaon systems within the present experimental and theoretical uncertainties. However, this remarkable agreement of data with the CKM picture leaves room for BSM contributions to CP-violating transitions. In particular, a valuable approach to corner these contributions consists in a model-independent bottom-up quantification of the room left for new flavour structures and additional CP-violating phases. A useful analysis framework is minimal flavour violation [227] (MVF), where new quark flavour structures remain aligned and proportional to the SM Yukawa couplings. In these BSM scenarios, charged-current decays are dominated by the (tree-level) SM, and the CKM matrix remains unitary, while deviations can take place, for example, in \(\Delta F=2\) transitions leading to neutral meson mixing. To probe deviations from the SM, and to possibly challenge MFV scenarios, increased precision on \(|V_{ub}|\) and \(\gamma \) is required [187]. Additional parameters accounting for BSM contributions to neutral B meson mixing are subsequently cornered using oscillation observables, namely the mixing-induced CP-violating phases \(\sin 2\beta \) and \(\phi _s\), the oscillation frequencies of \(\hbox {B}_d\) and \(\hbox {B}_s\) mesons \(\Delta m_d\) and \(\Delta m_d\) and the flavour specific semileptonic asymmetries sensitive to CP-violation in the mixing. The latter is a very small effect in the SM and is unobserved to date. The present limits can be pushed by FCC-ee towards the SM predictions. Table 7.3 shows the precision of the relevant ensemble of measurements expected at the FCC-ee together with a comparison with the projected Belle II and the HL-LHC experiments (including the LHCb upgrade) sensitivities. Similar precisions are obtained for FCC-ee and HL-LHC experiments projections. Having measurements performed in two different experimental conditions will be important.
The possible BSM contributions to mixing observables can be parameterised in a model-independent way via two additional parameters [228], describing the size and the phase of the extra terms in the mixing amplitudes. Measurements at the FCC-ee will be sensitive to BSM contributions to the amplitudes of \(\hbox {B}^0\) and \(\hbox {B}^0_s\) mixing larger than 5% of the SM ones. These potential deviations can be related to the energy scale \(\Lambda \) associated with the new effective local operators at play. In MFV scenarios, where the new flavour structures are aligned with the SM Yukawa couplings, energy scales up to 20 TeV can be probed by the joint measurement of the properties of the \(\hbox {B}^0\) and \(\hbox {B}^0_s\) meson mixings and the tree-level CKM parameters. Releasing the constraint of MFV, scales up to several hundred TeV can be probed.
18.1.5 Additional flavour physics opportunities
The aforementioned illustrations of measurements or searches for rare decays are experimentally very challenging. The study of their sensitivity reach has shown that the statistics available at a high-luminosity Z-factory, complemented by state-of-the-art detector performance, can potentially allow their measurement at unequalled precision. They can serve as benchmarks to open the way to other flavour physics observables in both quark and lepton sectors and are for the most part related to the understanding of flavour in presence of BSM Physics. Their experimental sensitivity will be studied in the next stage of the FCC-ee design study. Here a few additional possibilities, for which an FCC-ee experiment will definitely be able to push the experimental envelope, are listed. The FCNC-mediated leptonic decays \(\hbox {B}_{d,s}\rightarrow \hbox {ee}\), \(\upmu \upmu \), \(\uptau \uptau \), as well as the EW penguin dominated \(\hbox {b}\rightarrow \hbox {s}\upnu \upnu \), provide SM candles and are sensitive to several realisations of BSM Physics. The observation of \(\hbox {B}_{s}\rightarrow \uptau \uptau \) is invaluable to complement our understanding of present LFUV anomalies and likely uniquely reachable at FCC-ee. The charged-current mediated leptonic decays \(\hbox {B}_{u,c}\rightarrow \upmu \upnu \) or \(\uptau \upnu \), provide another test of LFU in charged current. They offer, on the other hand, a possibility to determine the CKM elements \(|V_{ub} |\) \(|V_{cb} |\) with minimum theoretical uncertainties [229]. The cleanliness of the \(\mathrm{e}^+\mathrm{e}^-\) experimental environment will be beneficial to the study of the decay modes involving \(\hbox {B}_s\), \(\hbox {B}_c\) or b-baryons with neutral final state particles, as well as the many-body fully hadronic b-hadron decays. The harvest of CP-eigenstates in several b-hadron decays will allow comprehensive measurements of the CP-violating weak phases. Rare exclusive Z decays [230] might probe both new physics and perturbative QCD factorisation.
18.2 FCC-hh
While flavour is and will remain a key pillar of high-energy physics, it is early to evaluate in detail the role that FCC-hh can have in furthering our knowledge. The high-\(Q^2\) aspects of flavour physics are an integral part of the physics programme of the multipurpose detectors, and are covered in other sections of this volume (see e.g. Sect. 6.3 for flavour aspects of the top quark, and Sect. 14 for the search of possible new heavy particles arising from the current flavour anomalies). The low-\(Q^2\) aspects related, for example, to charm and bottom decays, could benefit instead from dedicated detectors, like LHCb. In this area, it is more difficult to predict today what the key open questions will be after the completion of the LHCb and Belle2 programmes. The energy and luminosity of FCC-hh will not be the most important elements in extending the reach of LHCb, while progress will most likely arise from future developments in detector and data acquisition technologies and from improved theoretical control of non-perturbative systematics. It is planned to start addressing these issues in the next phase of the FCC-hh studies, relying also on the forthcoming experience of the LHCb upgrade programme and on the future physics results. This section is therefore limited to documenting basic information, such as cross sections and distributions of bottom quarks, outlining the landscape of what to expect in terms of rates and kinematics. More details can be found in Section 11 of Ref. [25].
The total bb̄ production cross section at 100 TeV is about 3mb, an increase by a factor of \(\sim 5\) relative to the LHC, corresponding to several percent of the inelastic pp cross section. This implies that dozens of bb̄ pairs will be produced in a single bunch crossing at the expected levels of pile-up. The 3 mb has a large uncertainty, since the dominant fraction of the total rate comes from gluons at very small x values, where the knowledge of PDFs is rather poor today (see Ref. [25] for a detailed discussion). The upper plot of Fig. 7.3 shows that, for a detector like LHCb, covering the rapidity region \(2.5<y<5\), about 50% of the b events produced at 100 TeV would originate from gluons with momentum \(x<10^{-5}\).
The uncertainties are reduced if one considers central production or large \(p_T\), which strongly bound the relevant x range. Table 7.4 shows the rates for central production, \(|y|<2.5\), and various transverse momentum cuts for charm, bottom and top quarks. The ratios with respect to the production at the LHC (13 TeV) are also given. As expected, large \(p_T\) production in particular gets a large boost from 13 to 100 TeV, being larger by a factor of about 30-40 than at the LHC for a \(p_T\) cut of 100 GeV. If the \(p_T\) cut is pushed to 1 TeV, central heavy quark production at the 100 TeV is about a factor of one thousand larger than at the LHC.
Figure 7.4 shows the rapidity distributions for b quarks produced above some thresholds of \(p_T\) and, for b quarks produced in the region \(2.5<\vert y \vert < 5\), the integrated spectrum in longitudinal momentum \(p_z\), comparing results at 14 and 100 TeV. As shown in the previous table, note that, while the total production rate grows only by a factor of \(\sim 5\) from 14 to 100 TeV, the rate increase can be much larger once kinematic cuts are imposed on the final state. For example, at 100 TeV b quarks are produced in the forward region \(2.5<\vert y \vert < 5\) with \(p_z>1~\hbox {TeV}\) at the rate of \(10\,\upmu \hbox {b}\), 100 times more than at the LHC. To what extent this opens opportunities for new interesting measurements to be exploited by the future generation of detectors, remains to be studied.
19 Interpretation and sensitivity to new physics
20 Global EFT fits to EW and Higgs observables
20.1 Introduction
The Large Hadron Collider (LHC) has probed the SM at energies higher than ever before, reaching regions never explored so far. With the discovery of a scalar particle consistent with the Higgs boson, the SM can in principle be consistent up to the Planck scale. Nonetheless, in many UV completions predicting a light Higgs, e.g. supersymmetric or composite Higgs models, one requires other new particles with masses around the EW scale. So far, though, the LHC has not seen any robust hints of new physics, which indicates that any new particles must be either too weakly coupled to the SM or too heavy to be produced. The masses of these new degrees of freedom will always be the product, \(m_*=g_* \cdot f\), of the coupling \(g_*\) of the new physics sector times the dynamic scale, f, characterising this new sector. For weakly coupled new physics, one expects to see the new resonances before observing the effects of the new interactions. When \(g_*\) increases, the masses increase and the new interactions might become the first indirect manifestation of new physics. Both effects of the new particles or the new interactions can be seen indirectly, for example, by modifying the differential cross sections of particular processes with respect to the SM prediction. Such modifications can occur mostly at the threshold or in the tail of distributions. In the former case, extremely precise measurements in a clean environment like the ones performed at FCC-ee will offer the best sensitivity. In the latter case, new physics corrections can grow with the energy probed and scale as \((E/m_*)^n\), with \(n> 0\), in which case FCC-hh will benefit from high centre of mass energy to achieve similar sensitivity, in spite of lesser precision. Charged and neutral Drell–Yan processes, EW diboson production and Higgs–Strahlung production are explicit examples that receive energy-growing corrections from new physics with \(n=2\). Even with a limited precision of 10%, when probed at the modest energy of 1 TeV, these observables have the same discovery power as a 0.1% precision measurement performed at 100 GeV. FCC-eh will be particularly relevant to improve the knowledge of the PDFs, arguably one of the biggest sources of uncertainties for any FCC-hh analysis. In addition, FCC-eh is also helpful in determining the gauge boson couplings to individual quark flavours, complementing the results from FCC-ee.
As new physics is being constrained to lie further and further above the EW scale, the description of its effects at future colliders seems to fall in a low-energy regime. Effective field theories (EFTs) therefore look like prime exploration tools [231,232,233,234,235]. Given that the parity of an operator dimension is that of \((\Delta B-\Delta L)/2\) [236], all operators conserving baryon and lepton numbers are of even dimension:
where \(\Lambda \) is a mass scale and \(C_i^{(d)}\) are the dimensionless coefficients of the \(\mathcal {O}^{(d)}_i\) operators of canonical dimension d. The SM effective field theory (SMEFT) allows for a systematic exploration of the theory space in the direct vicinity of the SM, encoding established symmetry principles. As a standard quantum field theory, it relies on a Lagrangian, and its predictions admit a perturbative expansion. Notice that the basis of operators can be built under the assumption that EW symmetry is linearly realised, thus that the Higgs boson is part of an EW doublet, or can be more general with a Higgs that would be an EW singlet. The remainder of this section, focuses mainly on the former case.
The interplay between EW and Higgs measurements is particularly relevant, since several higher-dimensional operators affecting Higgs processes can also be tested in EW measurements. Therefore in order to keep the extraction of the Higgs couplings under control, it is essential to reduce the uncertainties on these operators as much as possible.
This chapter considers a fit to the observables discussed in Sects. 4, 5 and 10, relying on the experimental sensitivities reported there for the different FCC stages/colliders. These measurements will also be combined with those expected at the end of the HL-LHC, as reported in the document from the HL/HE-LHC Physics Workshop, Ref. [18].
Contours of 68% confidence level in the \((m_{\mathrm{top}}, m_\mathrm{W})\) plane obtained from fits of the SM to the EW precision measurements offered by the FCC-ee, under the assumption that all relevant theory uncertainties can be reduced to match the experimental uncertainties: the red ellipse is obtained from the FCC-ee measurements at the Z pole, while the blue ellipses arise from the FCC-ee direct measurements of the W and top masses. The two dotted lines around the SM prediction illustrate the uncertainty from the Z mass measurement if it were not improved at the FCC-ee. The green ellipse corresponds to the current W and top mass uncertainties from the Tevatron and the LHC. The potential future improvements from the LHC are illustrated by the black dashed ellipse
20.2 Electroweak fit at FCC-ee and FCC-eh
Once the W boson and the top-quark masses are measured with precisions of a few tenths and a few tens of MeV, respectively, and with the measurement of the Higgs boson mass at the LHC (to be further improved at the FCC-ee), the SM predictions of a number of observables sensitive to EW radiative corrections become absolute, with no remaining additional parameters. Any deviation in the relation between \(m_\mathrm{W}\), \(m_\mathrm{H}\) and \(m_{\mathrm{top}}\) will be a demonstration of the existence of new particle(s). The FCC-ee offers the opportunity to measure such quantities with precisions between one and two orders of magnitude better than the present status. The theoretical prediction of these quantities with a matching precision is an incredible challenge, but the genuine ability of these tests of the completeness of the SM to discover new weakly-interacting particles beyond those already known is a fundamental motivation to take it up and bring it to a satisfactory conclusion.
The result of the fit of the SM to all the EW precision observables measured at the FCC-ee is displayed in Fig. 8.1 as 68% C.L. contours in the \((m_{\mathrm{top}},m_\mathrm{W})\) plane. It is obtained under the assumption that all relevant theory uncertainties can be reduced to match the experimental uncertainties. This fit is compared to the direct \(m_\mathrm{W}\) and \(m_{\mathrm{top}}\) measurements at the \(\mathrm{W}^+\mathrm{W}^-\) and the \(\mathrm{t}\bar{\mathrm{t}}\) thresholds. A comparison with the precisions obtained with the current data at lepton and hadron colliders, as well as with LHC projections, is also shown. FCC-ee will also provide significant improvement on other EW observables (see Volume 2 of the FCC CDR for details).
From the fit to the different EW precision observables it is also possible to extract the sensitivity to new physics via its modification of the different EW couplings to fermions. At the Z-pole, FCC-ee measurements of the rates and asymmetries of the different fermion decays of the Z provide a clean and model-independent handle to most fermion couplings. Separating the Z couplings to the light quarks is, however, quite challenging, especially for down and strange quarks. This issue can be overcome by the FCC-eh’s remarkable sensitivity in the measurement of the neutral current interactions of the light quarks. Finally, the Z interactions with the top quark, not directly accessible at the Z pole, can be measured at the percent level at the FCC-ee running slightly above threshold. In this way, combining the FCC-ee and FCC-eh measurements, deviations from the SM predictions for the couplings of the individual quarks and leptons of the three generations can be tested with a precision from 0.01% for the leptons to a few percent for the heavy quarks, without having to rely on any flavour universality assumption. The results obtained from an EFT fit to all relevant EW measurements from FCC-ee/eh are shown in Fig. 8.2.Footnote 5
20.3 Electroweak observables at FCC-hh
Drell–Yan (DY) production is an example where energy helps accuracy [239] and where FCC-hh will be at its best. Charged DY, \(\mathrm {pp} \rightarrow \ell \upnu \), and neutral DY, \(\mathrm {pp} \rightarrow \ell ^+ \ell ^-\), can receive at high mass large corrections from the W and Y oblique parameters defined by [240]:
The parameters of these operators, which capture the universal modifications of the EW gauge boson propagators, are already constrained at the per mille level from LEP-2 precision measurements and from the W mass measurements at Tevatron and LHC (as well as other precision measurements at the Z pole at LEP/SLD). FCC-hh will nonetheless benefit from the large production rate at very high masses, as shown in Fig. 3.3. This will improve the current constraints by two orders of magnitude, as shown in Table 8.1. In terms of a new physics scale \(\Lambda \) defined by \(g_*^2/\Lambda ^2=(W,Y)/4m_W^2\), these values correspond to \(\Lambda \gtrsim g_*\times 80~\hbox {TeV}\). These constraints on W and Y are stronger than those achievable at FCC-ee and could only be matched by measurements at a mutli-TeV-scale future lepton collider. This underscores the important role that hadronic data can have in probing high scales via precise EW measurements at high \(Q^2\).
One further use of the lever arm in \(Q^2\) is the determination of the running of EW couplings, by measuring the transverse (invariant) mass spectrum of (di)leptons produced by far off-shell W (Z) bosons [241]. This is a crucial piece of information to reduce the parametric uncertainties in global fits, as well as a useful tool to indirectly probe the existence of new heavy EW charged particles.
Corrections to the lepton transverse mass distribution in \(\hbox {pp}\rightarrow \hbox {W}^*\rightarrow \ell \upnu \) due to the running of the SU(2) coupling \(\alpha _2\), at 100 and 27 TeV. The potential impact of a new Majorana fermion \(\tilde{\mathrm{w}}\), SU(2) triplet, is shown, for \(m_{\tilde{\mathrm{w}}} = 200~\hbox {GeV}\) and 1 TeV
The running is sensitive to the existence of any weakly-coupled particle, and could in principle flag elusive states that are not found by direct searches. The effect of the running of the SU(2) coupling (\(\alpha _2\)) is most directly probed by the production of off-shell Ws at large mass. Figure 8.3 shows the relative difference between no-running and running, in the SM and in presence of an SU(2) triplet of Majorana fermions (e.g. a supersymmetric wino) of mass 200 GeV or 1 TeV [241]. The uncertainties shown in the figure include the statistical uncertainty combined with a constant 1% systematics, representing a possible estimate of the future precision with which DY processes can be predicted. The luminosity does not contribute to the systematics, since the evidence of running comes from the shape of the distribution, not its absolute value. Scale uncertainties are already at this level, and will improve. PDF uncertainties will be reduced to the percent level by HL-LHC, and well below that at FCC-eh, as shown in Fig. 5.14. Here the renormalisation scale for \(\alpha _2\) is taken at the average value of \(M_{\ell \nu }\) for a sample of events with transverse mass larger than the given minimum threshold. The value of \(M_T(\ell \nu )\) that gives the best sensitivity to the running is in the range of 4-5 TeV. Notice that at these mass values EW Sudakov effects are not negligible: as shown in ref. [25], NLO EW corrections reduce the QCD rate for W DY with \(M_T>5~\hbox {TeV}\) by 50% (of which 15% is due to the \(\alpha _2\) running shown in Fig. 3.3). It is anticipated nevertheless, that high-order EW corrections will be known already by the end of HL-LHC, leaving a residual uncertainty consistent with the 1% assumption made above.
It is noted here that one achieves a \(\sim 2\sigma \) sensitivity to the presence of a 1 TeV wino. This is not meant to provide firm evidence for a discovery, but shows the impact that such a measurement could have in helping characterise a possible direct discovery of new EW states. For comparison, the result of the same analysis at HE-LHC is shown. A more systematic study of the sensitivity to various combinations of new weakly interacting particles and global fit of the running couplings using both charged and neutral DY FCC-hh data, are presented in Ref. [241].
20.4 Higgs couplings fit
While the Higgs boson discovery has been a milestone in the history of high-energy physics, a lot remains to be understood about it. Its existence as a fundamental scalar field raised new challenging questions from phenomenological puzzles to deep quantum field theory conundrums. The principles dictating the structure of the Higgs sector remain unclear in contrast with the gauge sector of the SM that is the realm of local symmetries. The dedicated experimental exploration of the Higgs sector is called for to unravel its profile, to better understand the role it played/will play in the history of the universe and to push the frontier of knowledge of Nature at the smallest scales. This exploration is multiform and will benefit from the different options offered by the whole FCC programme: (1) a precise measurement of the on-shell Higgs couplings to all the SM particles at the sub-percent level, (2) an access to extreme regions of phase space probing, in particular, the Higgs couplings away from its mass-shell, (3) a study of rare production and decay channels to reveal small couplings to either light SM particles or to new particles of a dark sector. Section 4 details the numbers of Higgs bosons produced at FCC-ee/eh/hh in the various channels. It should be kept in mind that, for the expected total luminosities, about \(10^6\), \(2\cdot 10^6\) and \(10^{10}\) Higgs bosons will be produced in total FCC-ee/eh/hh respectively (see Fig. 4.1; Tables 4.6, 4.3).
The LHC and HL-LHC will provide insights on the Higgs boson couplings to the SM gauge bosons and to the heaviest SM fermions (\(\hbox {t, b}, \uptau , \upmu \)), with a precision that at best will reach the few percent level, and typically under a number of model-dependent assumptions, in particular on the Higgs boson decays that the LHC cannot access directly. Interactions between the Higgs boson and new particles at a higher energy scale \(\Lambda \) could modify the Higgs boson couplings to SM particles, either at tree level or via quantum corrections. Coupling deviations with respect to the SM predictions are in general smaller than 10% for \(\Lambda =1~\hbox {TeV}\), with a dependence that is inversely proportional to \(\Lambda ^2\). A per-mille level accuracy on a given coupling measurement would allow access to the 10 TeV energy scale, and maybe to exceed it through an analysis of the deviation patterns among all couplings. Similarly, quantum corrections to Higgs couplings are at the level of a few % in the SM. Capturing the quantum corrections that modify the Higgs properties requires that measurements be pushed to a precision of a few per mil or better.
The Higgs coupling measurements have been widely studied in the corresponding design studies through global fits in the so-called \(\kappa \) framework [242, 243]. While very helpful in illustrating the precision reach of Higgs measurements, this \(\kappa \) framework can miss interactions of Lorentz structure different from that of the SM, or correlations deriving from gauge invariance, notably between Higgs couplings to different gauge bosons. The on-shell measurements of the Higgs production and decays can also be nicely complemented by studying the behaviour of 2-to-2 scattering processes at higher energy or by measuring the tail of the distributions of the Higgs kinematics. Hence the interest of FCC-hh in the detailed exploration of the Higgs sector.
20.4.1 On-shell Higgs couplings at FCC
Many EFT studies have been performed, for Higgs measurements at LHC [244,245,246,247,248,249,250], EW precision observables at LEP [251,252,253,254], diboson measurements at both LEP [255] and LHC [256, 257], and the combination of measurements in several sectors [258]. Among the studies performed in the context of future Higgs factories [259,260,261,262,263,264,265], many estimated constraints on individual dimension-six operators. A challenge related to the consistent use of the EFT framework is indeed the simultaneous inclusion of all operators up to a given dimension which is required for this approach to retain its power and generality. As a result, various observables have to be combined to efficiently constrain all directions of the multidimensional space of effective-operator coefficients. The first few measurements included bring the most significant improvements by lifting large approximate degeneracies. Besides Higgsstrahlung production and decay rates in different channels, angular distributions contain additional valuable information [261, 266]. Higgs production through weak-boson fusion provides complementary information of increasing relevance at higher centre-of-mass energies. This is actually the dominant Higgs production mode at FCC-eh. Relying on the absolute normalisation of the Higgs couplings at FCC-ee, the FCC-eh measurements will help to further improve the precision of the Higgs couplings to weak bosons (see Fig. 8.4).
FCC-hh will provide complementary information on the Higgs couplings that cannot be directly accessed at FCC-ee alone. First, the enormous sample of Higgs bosons produced will retain some sensitivity to small couplings, like the muon Yukawa coupling or even the strange quark Yukawa coupling, and will therefore unambiguously establish (or disprove) the Higgs to the second generation of quarks and leptons. Second, the higher energy will definitively open up new channels, like \(\hbox {t}\bar{\hbox {t}}\hbox {H}\) and \(\hbox {gg} \rightarrow \hbox {HH}\), and will offer a direct access to new couplings like the top Yukawa couplings and the Higgs cubic self-interaction, two interactions of paramount importance to the cosmological evolution of the Universe. While FCC-ee has no direct access to the Higgs cubic self-coupling, \(g_{HHH}\), an indirect bound can be obtained from a global fit of the single Higgs observables including the quantum corrections from \(g_{HHH}\) [265], see Sect. 10.4. Similarly, the top Yukawa coupling can in principle be assessed at FCC-ee via its quantum corrections to \(\hbox {t}\bar{\hbox {t}}\) production close to the threshold, see the discussion in Sect. 4.2.2. Direct determinations of the top Yukawa and Higgs self-coupling have also been considered at ep colliders, where in particular the cleanliness of the final state configuration in the charged current and neutral current VBF double Higgs production with a pile-up of 1 allows the \(\hbox {H}\rightarrow \hbox {bb}\) decays to be considered. Preliminary studies [97, 267] estimated that these two couplings could be constrained at the FCC-eh at the 1% and 10% level, respectively, with an integrated luminosity of 1 and \(10\,\hbox {ab}{}^{-1}\) at 1.8 TeV and 5 TeV (see also Sect. 10.6). At FCC-hh, the top Yukawa coupling can also be measured accurately by studying the cross section ratio \(\sigma (\hbox {t}\bar{\hbox {t}}\hbox {H})/\sigma (\hbox {t}\bar{\hbox {t}}\hbox {Z})\) [89]. Indeed, to the extent that the \(\hbox {q}\bar{\hbox {q}}\) initiated processes remain subdominant, as it is indeed the case at FCC-hh, the two channels share identical production dynamics and the correlated scale and parametric uncertainties will cancel out in the ratio of the cross sections. Furthermore the proximity of the Z and Higgs mass ensures that the PDF uncertainties also drop out, leading to a very clean theoretical prediction of the ratio of cross sections. Confronted with experimental measurement, one can then infer the value of the top Yukawa with an accuracy of order 1% after \(20\,\hbox {ab}{}^{-1}\) of luminosity is collected. FCC-hh offers an alternative way to asses the top Yukawa coupling by studying the rare production of a Higgs boson with a single top quark [268, 269], that increases by more than 2 orders of magnitude when the centre-of-mass energy goes from 14 TeV to 100 TeV [172]. This remarkable growth, together with the unique sensitivity of this process to the sign of the top Yukawa coupling, makes this reaction a golden channel for a precise measurement of this coupling by focussing on the semileptonic decays of the top quark and the \(\hbox {H}\rightarrow \hbox {bb}\) and \(\hbox {H}\rightarrow \upgamma \upgamma \) decay channels.
As the sensitivities to operator coefficients can vary with \(\sqrt{s}\), high-energy FCC-ee runs above the Higgs threshold will constrain different directions of the parameter space and therefore resolve degeneracies. Beam polarisation, more easily implemented at linear colliders, could be similarly helpful. Finally, the Higgs and anomalous triple gauge couplings (aTGCs) are related in a gauge-invariant EFT, and a subset of operators relevant for Higgs physics can be efficiently bounded through diboson production \(\hbox {e}^+\hbox {e}^-/\hbox {pp} \rightarrow \hbox {WW}\) either at threshold [248, 255] or at high-energy [49].
Assuming that the EW and CP-violating observables are perfectly constrained to be SM-like and that BSM physics is flavour universal, it was shown that there are 11 independent combinations of operators that contribute to Higgs (including its self-coupling) and aTGC measurements [244, 245, 247, 255]. Since FCC-ee/eh/hh have the sensitivity to pin down the Higgs couplings to the second family of quarks and leptons, the top, charm, bottom, tau, and muon Yukawa couplings can be treated separately, leaving a total of 13 degrees of freedom to consider. While all non-redundant basis are equivalent, the Higgs basis [235] is particularly convenient to extract the sensitivity to the Higgs couplings and separate them from the EW sector. The fit can also be performed in the Warsaw or any other basis and the results translated as expected sensitivity on Higgs and aTGC (pseudo)observables, as is done here.
Figure 8.4 gives the one-sigma precision reach on the 9 effective single Higgs couplings and 3 aTGC, combining measurements performed at the different stages of the FCC project in an EFT fit assuming absolute precision in EW measurements. The various modified Yukawa interactions are denoted by \(g_{Hff}\), while the effective Higgs couplings, \(g_{HXX}^{\mathrm{eff}}\), are defined as \((g_{HXX}^{\mathrm{eff}})^2\equiv \Gamma _{H\rightarrow X}/\Gamma ^{\mathrm{SM}}_{H\rightarrow X}\). For the aTGC parameters the standard notation is used, \(\delta g_{1Z}\), \(\delta \kappa _\gamma \) and \(\lambda _Z\). These projections are compared to the reach of the Higgs measurements at the HL-LHC, combined with the diboson production measurements at LEP-2.
One-sigma precision reach at the FCC on the effective single Higgs couplings and aTGC. An absolute precision in the EW measurements is assumed. The different bars illustrate the improvements that would be possible by combining each FCC stage/collider with the previous knowledge at that time (the precisions, not reported here, at each FCC stage/collider considered individually would obviously be quite different). Note that, without a run above the \(\hbox {t}\bar{\hbox {t}}\hbox {H}\) threshold, circular \(\hbox {e}^+\hbox {e}^-\) colliders alone do not directly constrain the \(g_{Hgg}\) and \(g_{Htt}\) couplings individually. The combination with LHC measurements however resolves this flat direction
The estimated reach of Higgs measurements at the HL-LHC derives from the projections by the ATLAS and CMS collaborations presented in Ref. [18]. The constraints from the diboson measurements at LEP-2 are obtained from Ref. [255]. (See Ref. [17] for recent studies of projections at the HL-LHC.Footnote 6) Compared with LHC and LEP, FCC-ee/eh will improve the measurements of several EFT parameters by roughly one order of magnitude. A combination with the LHC measurements provides a marginal improvement for most of the parameters. For \(g_{H\gamma \gamma }^{\mathrm{eff}}\), \(g_{HZ\gamma }^{\mathrm{eff}}\) and \(g_{H\mu \mu }\), the improvements are more significant, as the small rates and clean signals make the LHC reaches comparable to that of lepton colliders. Other couplings, e.g., \(g_{HVV}^{\mathrm{eff}}\) and \(g_{Hbb}\), are also indirectly improved in the combination. It should be noted that the measurements of the \(\hbox {H}\rightarrow \hbox {gg}\) branching fraction only constrain a linear combination of \(g_{Hgg}^{\mathrm{eff}}\) and \(g_{Htt}\). These two couplings are thus only constrained independently by lepton colliders when \(\mathrm{t}\bar{\mathrm{t}}\mathrm{H}\) production is measured. Therefore, combination with LHC measurements is required for the FCC-ee to constrain these couplings independently.
FCC-hh will make significant changes to this picture in three ways. Firstly, the high statistics sample is instrumental in revealing the small couplings involved in the rare Higgs decays (\(g_{H\mu \mu }, g_{H\gamma \gamma }^{\mathrm{eff}}\) and \(g_{HZ\gamma }^{\mathrm{eff}}\)). The last bar in Fig. 8.4 gives the combined FCC-ee/eh/hh precision reach on the 12 single Higgs/aTGC couplings. Note that the high precision on the rare decays benefits from the FCC-hh measurement of the ratio of branching ratios, e.g. \(\hbox {BR}(\hbox {H}\rightarrow \upgamma \upgamma )/\hbox {BR}(\hbox {H}\rightarrow 2\hbox {e}2\upmu )\), where uncertainties associated to the production cancel out. These ratio measurements are then combined with the FCC-ee/eh determination of the \(g_{HVV}^{\mathrm{eff}}\) coupling, thus allowing the value of \(g_{H\gamma \gamma }^{\mathrm{eff}}\) coupling to be inferred. Secondly, the high energy opens up the \(\hbox {t}\bar{\hbox {t}}\hbox {H}\) channel, which offers a direct probe of the top Yukawa coupling. Finally, high energy also gives access to the Higgs cubic self-interaction via \(\hbox {gg}\rightarrow \hbox {HH}\).
It is noted that a precise knowledge of the top Yukawa coupling and local contributions to the Higgs interactions with gluons are important in the direct determination of the Higgs cubic coupling at the FCC-hh. Indeed, the two diagrams contributing to diHiggs production in the SM involve the top Yukawa coupling, and several diagrams involving \(\hbox {HHt}\bar{\hbox {t}}\), \(\mathrm {Hgg}\) and \(\mathrm {HHgg}\) interactions also contribute in the EFT approach, see Fig. 10.1 in Sect. 10. The \(\mathrm {HHgg}\) and \(\mathrm {Hgg}\) couplings are controlled by the same operator, while the same interactions that modify the top Yukawa also generate (independently) the \(\hbox {HHt}\bar{\hbox {t}}\) contact terms. All these extra contributions can therefore be constrained using single Higgs processes. In the diHiggs study presented in Sect. 10 a projected sensitivity for \(g_{HHH}\) of \(6.5\%\) is reported. This is obtained, however, assuming that any interaction entering in \(\hbox {gg}\rightarrow \hbox {HH}\rightarrow \hbox {b}\bar{\hbox {b}}\upgamma \upgamma \) other than the cubic coupling takes the SM value. To show the impact of the uncertainties of the other interactions from the fit performed above, for illustration purposes, the inclusive diHiggs production rate from the cut-based study presented in Ref. [270] is considered. The Higgs trilinear coupling only enters in a subset of the full list of diagrams contributing to \(\hbox {gg}\rightarrow \hbox {HH}\), and the above uncertainty in \(g_{HHH}\) can then be translated into a precision for the diHiggs signal strength of \(\sim 3.3\%\). Taking into account the uncertainties on the EFT parameters from the FCC fit, which set constraints at the percent level or below on \(g_{Htt}\) and \(g_{Hgg}^{\mathrm{eff}}\), the sensitivity to the diHiggs coupling would degrade to nearly \(10\%\), being notably affected by the uncertainty on \(g_{Htt}\). The use of this inclusive rate is, however, not a very good approximation to the detailed study of Sect. 10, where a 2 dimensional likelihood fit on the diphoton and diHiggs invariant masses is used to extract the Higgs trilinear coupling after the corresponding selection cuts. While, as shown in the results of the full analysis performed in [270], the diHiggs invariant mass distribution is certainly affected in a different way by \(g_{HHH}\) and the other interactions, even after taking into account differential \(m_{\mathrm{HH}}\) information some dependence on \(g_{Htt}\) still remains. Taking this into account, and in absence of a full EFT study following the guidelines of the analysis in Sect. 10, it is believed that a slightly more conservative value for \(g_{HHH}\) uncertainty at the level of \(8\%\) would provide a more model-independent estimate of the sensitivity to the Higgs trilinear coupling in the \(\hbox {HH}\rightarrow \hbox {b}\bar{\hbox {b}}\upgamma \upgamma \) channel. This uncertainty can be further improved by combining the information of other decays channels in \(\hbox {gg}\rightarrow \hbox {HH}\), see Sect. 10.5.2. Finally, while current detailed studies of Higgs pair production at FCC-hh are only available for \(\hbox {gg}\rightarrow \hbox {HH}\), making use of other Higgs pair production mechanisms, e.g. via vector boson fusion, and combining with the measurements at FCC-eh, could also help to improve the model-independent determination of \(g_{HHH}\).
The results presented so far have been reported in terms of a fit using the SMEFT formalism. As mentioned above, many design studies have explored the sensitivity to deviations of the Higgs couplings using the \(\kappa \)-framework [242, 243]. While this does not rely a priori on the assumption of a mass gap between the weak scale and the scale of new physics, it is not the most general parameterisation of new physics in the Higgs sector either. This phenomenological approach defines \(\kappa _i\) scaling factors such that the Higgs production cross sections or decay widths associated with the SM particle i scale as \(\kappa _i^2\) with respect to the SM predictions. The results from the fit to the FCC Higgs data in the \(\kappa \) formalism are shown in Fig. 8.5, in a format that resembles that of Fig. 8.4. Although the results in the \(\kappa \) framework are not theoretically robust compared to those from the EFT, they help to emphasise some of the complementarities between the different FCC colliders, showing, for instance, the added value of the FCC-eh measurements in constraining the Higgs couplings to vector bosons (see the improvement in \(\kappa _W\)). Note that, especially for the couplings to electroweak vector bosons, the results of the \(\kappa \) fit are not directly comparable to those of the SMEFT fit. In particular, the latter incorporates all the correlations associated with gauge invariance or custodial symmetry, which are absent in the general form of the \(\kappa \) framework. On the other hand, because of the absence of such correlations, the \(\kappa \)-fit result could also give, within its limitations, information that goes beyond some of the assumptions implicit in the SMEFT results presented above.
One-sigma precision reach at the FCC on the different coupling scaling factors for each SM particle, within the \(\kappa \)-framework. For the HL-LHC fit the Higgs width is assumed to be SM-like and also \(\kappa _c=1\) is set. All the other fits are performed lifting these restrictions, thus allowing for possible extra contributions to the Higgs width. The precision on \(\Gamma _H\) is also shown in these cases
20.4.2 Higgs differential measurements at FCC-hh
At the LHC, the Higgs is predominantly produced at the threshold in processes with a characteristic scale of the order of the Higgs mass itself. From the LHC experimental measurements one infers the values of the Higgs couplings around the weak scale, while the couplings at higher scale, those that matter for the unitarisation of the scattering amplitudes, can only be surmised from a hypothesised renormalisation group evolution. The abundant Higgs production rates at FCC-hh change the situation and allow the exploration of rarer regions of phase space, see Fig. 4.3 in Sect. 4. This situation first opens new opportunities to reduce both theoretical and experimental systematic uncertainties. As an example, for \(p_T(\mathrm{H})>300\,\hbox {GeV}\), the signal over background ratio for \(\hbox {H}\rightarrow \upgamma \upgamma \) at FCC-hh becomes of order 1, about 100 times larger than in absence of a \(p_T\) cut, offering a cleaner measurement. Contrary to the \(\upgamma \upgamma \) decay, the signal-over-background ratio in the dimuon channel deteriorates at larger \(p_T(\mathrm{H})\), but it still allows for a precision in the rate measurement better than 2% for \(p_T(\mathrm{H})\) up to 200 GeV. This could allow for a 1% determination of the muon Yukawa coupling. In addition to reducing the uncertainties, the differential distributions can also help to remove strong correlations that plague fits of inclusive measurements. As an example, Fig. 8.6 shows how the boosted Higgs production and the off-shell Higgs production at FCC-hh can help resolving individually the top Yukawa coupling from a contact interaction between Higgs and gluons.
95% (solid) and 68% (dashed) exclusion contours in the (top Yukawa, Higgs-gluon contact interaction) plane obtained from FCC-hh projections. Red corresponds to off-shell, gray to boosted and orange to double Higgs production, while the purple band indicates the 68% region from \(\hbox {t}\bar{\hbox {t}}\hbox {H}\). From Ref. [271]
Another remarkable example of useful information extracted from kinematic distributions is the study of Higgsstrahlung, \(\hbox {pp} \rightarrow \hbox {Z} (\ell ^+ \ell ^-)\hbox {H}(\bar{\hbox {b}}\hbox {b})\), or equivalently \(\hbox {pp} \rightarrow \hbox {WW}\), at large invariant mass [49, 272, 273]. These processes receive contributions, which grow with the energy, from four different directions in the EFT parameter space. These directions are also tested by low energy measurements, e.g. Z-pole measurements or aTGC. The large energy range probed by FCC-hh would improve current bounds from LHC or LEP by an order of magnitude or more.Footnote 7 For instance, an extrapolation of the analysis presented in [273] to the FCC-hh shows that –assuming perfect Z-pole measurements– \(|\delta g_1^Z|\) would be found to be smaller than \(2\cdot 10^{-4}\) at \(95\%\) C.L. after \(30\,\hbox {ab}{}^{-1}\). This result utilises sub-jet techniques to exploit the \(\hbox {H}\rightarrow \hbox {b}\bar{\hbox {b}}\) decay, and assumes a 1% experimental uncertainty.
The access to rare corners of Higgs production phase space also offers new indirect sensitivity to BSM effects at large \(Q^2\). For instance, it was shown in [275] that the tail of the \(p_T(\mathrm{H})\) spectrum can reveal degenerate light stop scenarios that would otherwise leave no deviation in the inclusive rate measurements. See also [276, 277] for similar searches for fermionic top partners in composite and little Higgs models.
20.5 Global fits
An incomparable advantage of an EFT analysis is that it allows for a global picture combining measurements of different types of observables at various scales. In the previous sections the fits to EW and Higgs plus diboson measurements were discussed separately. Whilst they are at the leading order, the fit to the W mass and precision observables measured at the Z-pole can be performed without making any assumption about the Higgs interactions, the same is not true in the opposite direction, since modifications of the couplings of the SM fermions to the weak bosons enter directly in the electroweak Higgs production processes. In Sect. 8.4 it was assumed that the knowledge of the EW observables was absolutely accurate. In this section a simultaneous fit of EW, diboson and Higgs data is performed, and the impact of such an assumption in a global fit by taking into consideration the finite precision for all these observables is quantified. Also included in the global fit is the differential information in measurements of \(\hbox {pp}\rightarrow \hbox {WZ}\) and \(\hbox {pp}\rightarrow \hbox {ZH}\) at FCC-hh from the studies in [49, 273].
Figure 8.7 shows the precision of the Higgs couplings and aTGCs resulting from a fit combining the measurements at FCC-ee/eh/hh and including now the finite precision of the EW measurements obtained at the FCC-ee/eh. The one sigma uncertainties from the global fit nearly match those presented in Sect. 8.4. One of the most notable exceptions is the top Yukawa coupling. The extraction of the \(\hbox {t}\bar{\hbox {t}}\hbox {H}\) coupling from the FCC-hh measurement of the ratio \(\sigma (\hbox {t}\bar{\hbox {t}}\hbox {H})/\sigma (\hbox {t}\bar{\hbox {t}}\hbox {Z})\) depends on the knowledge, in particular, of the EW coupling of the top quark to the Z boson. The current best handle on this coupling at the LHC is via \(\hbox {pp}\rightarrow \hbox {t}\bar{\hbox {t}}\hbox {Z}\) production. HL-LHC measurements will however not be able to measure the EW top couplings better than 10–20%. FCC-hh would further reduce the uncertainty on this type of measurement, achieving an overall precision at the level of 5% for \(g_{V,A}^t\), which would still limit the precision on the determination on \(g_{Htt}\) at FCC. While the precise FCC-ee measurement of the \(\hbox {Zt}\bar{\hbox {t}}\) couplings at the percent level deviates from the assumption of perfect EW measurements in Fig. 8.7, it is needed to bring the uncertainty of \(g_{Htt}\) down to the percent level via the \(\sigma (\hbox {t}\bar{\hbox {t}}\hbox {H})/\sigma (\hbox {t}\bar{\hbox {t}}\hbox {Z})\) measurement. As explained in Sect. 8.4, a precise knowledge of the top Yukawa coupling is also very important from the point of view of a direct measurement of the Higgs cubic coupling at FCC-hh. This also establishes an indirect correlation between the FCC-hh measurement of the Higgs trilinear and the \(\hbox {t}\bar{\hbox {t}}\hbox {Z}\) measurement at FCC-ee, and further illustrates the importance of the latter. While the small deterioration in the precision of \(g_{Htt}\) in the global fit to \(\sim 2\%\), due to the finite precision of the measurement of the \(\hbox {Zt}\bar{\hbox {t}}\) couplings, would have some impact in the determination of \(g_{HHH}\) via \(\hbox {gg}\rightarrow \hbox {HH}\rightarrow \hbox {b}\bar{\hbox {b}}\upgamma \upgamma \), a precision of \({\delta g_{HHH}}/{g_{HHH}}\sim 9-10\%\) is still expected to be possible at FCC-hh. As discussed in Sect. 8.4.1 and more in detail in Sect. 10, a combination of all the possible measurements at the different FCC components could allow that value to be improved. It is therefore concluded that a model-independent determination of \(g_{HHH}\) at the level of \(5-10\%\) is expected to be within the FCC reach.
One-sigma precision reach of the combination of FCC-ee/eh/hh on the 12 effective single Higgs couplings and aTGC from the global fit to EW and Higgs observables, compared with the results presented in Sect. 8.4 assuming perfect EW measurements
Within the SMEFT framework the fact that electroweak symmetry is implemented linearly and the Higgs is part of an EW doublet, also connects both EW and Higgs processes. For instance, dimension 6 interactions modifying the \(\hbox {Zq}\bar{\hbox {q}}\) couplings will, in general, also generate \(\hbox {HZq}\bar{\hbox {q}}\) contact interactions. These introduce corrections to Higgstrahlung production at pp colliders that grow with the energy, as described in the previous section. As shown in Fig. 8.2, the \(\hbox {Zq}\bar{\hbox {q}}\) couplings are typically less constrained by the FCC-ee/eh EW precision measurements than the leptonic counterparts. The access to very large energies at the FCC-hh could therefore complement the precision studies performed at lower energies. Figure 8.8 shows homologous results to those from Fig. 8.2 but from the global fit including also Higgs measurements and projections for high-\(p_T\) measurements in diboson processes. As expected, while the leptonic couplings remain unaffected by adding the new measurements, comparing the results of the global fit to those in Sect. 8.2 an improvement in the new physics reach in EW interaction for the first family of quarks is observed. The stronger limits in the couplings for d quarks then also translates via the constraints from other EW observables into tighter bounds for the strange quark values.
To conclude, the results presented in this chapter are summarised in Table 8.2. There the reach of the different couplings that would be possible by the end of the LHC era are compared with the measurements that would be possible at the FCC, after combining the physics programmes of all its components: the FCC-ee, FCC-eh and FCC-hh. The improvement of one order of magnitude – in some cases even more – in almost all of the parameters arises after exploiting the strengths of each type of collider (unparalleled precision in low-energy measurements at the FCC-ee, access to very energies and the high-luminosity at the FCC-hh and the FCC-eh, with a good combination of high-energies and a clean environment) and the complementarity between the measurements possible at each of them.
21 The origin of the Higgs mass
21.1 Introduction
As discussed in Sect. 1.1, the origin of the Higgs boson mass and the associated hierarchy problem remain a core question in fundamental physics. There are essentially two different possibilities for the microscopic nature of the Higgs. The Higgs field could be a composite, in analogy with the Bardeen–Cooper–Schrieffer (BCS) theory of superconductivity, or it could be a fundamental field, and both possibilities have a plethora of experimental signatures. This section highlights how the FCC project could reveal these experimental signatures and shed further light on the origin of the Higgs potential.
21.2 Supersymmetry
Supersymmetry is a possible extension of the observed spacetime symmetry of nature, transforming fermions into bosons and vice versa. If supersymmetry were a property of nature, it must be broken at some scale above the TeV scale, given we do not observe degenerate super-multiplets. But one of its properties, relevant to the discussion of the Higgs boson, would persist: the natural co-existence in supersymmetric models of very large hierarchies of scales, thus directly addressing the hierarchy problem. Furthermore, in supersymmetric theories the Higgs mass is no longer a free parameter, like in the SM, but it is a function of the more fundamental supersymmetry breaking parameters. In other words, the Higgs mass becomes calculable. Thus, if supersymmetry was observed in nature, there would be an explanation for the microscopic origin of the Higgs boson mass and, as a result, of the EW scale. Decades of searches have pushed the masses of supersymmetric particles to higher and higher values, reducing their effectiveness in explaining the hierarchy between the EW and Planck scales. Nonetheless, supersymmetry still maintains a forefront role in addressing the puzzles posed by the Higgs.
With regard to the Higgs mass, the most important supersymmetric partner particles are those that interact with the Higgs boson most strongly. In practice, these are the top squarks (stops), EW gauginos, and Higgsinos. Thus if supersymmetry plays some role in resolving the hierarchy problem these particles should show up near to the weak scale. One can search for the presence of these particles indirectly, using high precision measurements at low energies. In particular, the leading indirect effect of stops is that they modify some of the properties of the Higgs boson. The most notable modifications are to the interactions between the Higgs boson and gluons and also between the Higgs boson and the photon. None of these interactions exist at the classical level (the photon and the gluon being massless particles, they do not directly interact with the Higgs boson), but they are generated by quantum corrections. This is why they are particularly sensitive to new strongly coupled degrees of freedom like stops. At FCC-ee high precision measurements of these interactions can thus reveal the presence of these particles. Furthermore, supersymmetry requires a minimal interaction strength between the stop and the Higgs boson, thus the main free parameter is only the mass of the particles. In the left panel of Fig. 9.1 the combined projected indirect constraints on stops from LHC Higgs measurements are shown alongside projected constraints at FCC-ee and FCC-hh. Since the precision of Higgs coupling measurements is greatest at FCC-ee the latter constraints are dominated by the FCC-ee measurements. Dedicated studies at FCC-hh, using e.g. H+jet production at high invariant mass, could further reveal the structure of the indirect corrections to the Higgs interactions.
Left: Projected \(2 \sigma \) indirect reach solely from Higgs coupling constraints on stops from FCC-ee and FCC-hh [278]. Right: Projected direct FCC-hh \(2 \sigma \) and \(5 \sigma \) discovery reach for supersymmetric Higgsinos, Winos, sleptons, stops, squarks, and gluinos (see Ref. [279] for details). HL-LHC projections are only shown for coloured sparticles and projections for Higgsinos and Winos are currently under investigation
At high energies it is also possible to produce the supersymmetric partner particles directly. The experimental signatures typically involve final states featuring jets and missing energy, however a plethora of dedicated searches are required to cover the full suite of possible experimental signatures. In the right hand panel of Fig. 9.1 the direct discovery reach at FCC-hh is shown for a variety of supersymmetric particles. Details of the phenomenological studies are presented in the extensive review of BSM searches at FCC-hh, Ref. [279]. Further dedicated analyses have been carried out in the framework of the FCC-hh detector performance studies. The study of the reach for Higgsino and Wino, in the context of DM searches, is presented in Sect. 12. The search for stops is reviewed in the next section. The direct reach shown in Fig. 9.1 extends far beyond the indirect precision Higgs coupling reach, in some cases to well above 10 TeV. As a result, the combined FCC projects could comprehensively and unambiguously determine whether supersymmetry is realised in proximity to the weak scale and thus whether supersymmetry resolves the hierarchy problem.
It is typically assumed in supersymmetric models that an additional discrete global symmetry, R-parity, is respected. Such a symmetry is useful for stabilising dark matter candidates and/or forbidding observable proton decay. However, it is possible that R-parity is violated in a manner that is consistent with such constraints. In models with R-parity violation it is possible to have single, rather than pair, production of sparticles. This can be probed by multi-lepton and multijet signatures at the FCC-hh. At the FCC-eh, furthermore, one can constrain anomalous Yukawa interactions involving electrons and the first generation quarks. For instance, an e-d-\(\tilde{\mathrm{t}}\) Yukawa interaction can be probed at the level of \(\lambda _{131} \lesssim 0.01\).
21.2.1 Direct stop search at FCC-hh
A dedicated study of stop production at FCC-hh, which corroborates earlier phenomenological estimates of the reach [280], exposes some of the detector challenges met when using hadronic decays of highly energetic top quarks, helping to define the detector design criteria. Here the main findings of the detailed analysis of Ref. [281] are presented.
Stops are pair produced via qq̄ or gg initial states, and the leading decay \(\tilde{\hbox {t}}\rightarrow \hbox {t}\tilde{\chi }^0\) is considered. The final state of interest has two high-energy b-tagged jets and large  , caused by the neutralinos \(\tilde{\chi }^0\). Hadronically decaying multi-TeV top quarks fall within the calorimeter granularity of \((\Delta \eta ,\Delta \phi )=(0.1,0.1)\), and track-based algorithms are used to explore their internal structure, adapting and optimising standard jet substructure techniques used at the LHC. The leading backgrounds include tŧ production (the neutrino source of
, caused by the neutralinos \(\tilde{\chi }^0\). Hadronically decaying multi-TeV top quarks fall within the calorimeter granularity of \((\Delta \eta ,\Delta \phi )=(0.1,0.1)\), and track-based algorithms are used to explore their internal structure, adapting and optimising standard jet substructure techniques used at the LHC. The leading backgrounds include tŧ production (the neutrino source of  is suppressed by vetoing the presence of charged leptons), \(\hbox {t}\bar{\hbox {t}}\hbox {Z}(\rightarrow \upnu \upnu )\), and poorly measured jet final states. A large separation \(\Delta \phi \) between the jets and the
is suppressed by vetoing the presence of charged leptons), \(\hbox {t}\bar{\hbox {t}}\hbox {Z}(\rightarrow \upnu \upnu )\), and poorly measured jet final states. A large separation \(\Delta \phi \) between the jets and the  direction is used to reduce the latter two backgrounds. Additional backgrounds like \(\hbox {V}+\hbox {jets}\), \(\hbox {t}\bar{\hbox {t}}\hbox {W}\) or \(\hbox {tt}\bar{\hbox {t}}\bar{\hbox {t}}\) are determined to be small. The overall background contribution is estimated by transferring the rates obtained in control samples to the signal region, assigning 10% (nominal, based on the LHC experience) or 20% (conservative) overall uncertainties. The final results are shown in Fig. 9.2, proving a sensitivity (\(5\sigma \) discovery reach) reach up to 10 (8) TeV in mass, for neutralino masses up to 4 (3) TeV.
direction is used to reduce the latter two backgrounds. Additional backgrounds like \(\hbox {V}+\hbox {jets}\), \(\hbox {t}\bar{\hbox {t}}\hbox {W}\) or \(\hbox {tt}\bar{\hbox {t}}\bar{\hbox {t}}\) are determined to be small. The overall background contribution is estimated by transferring the rates obtained in control samples to the signal region, assigning 10% (nominal, based on the LHC experience) or 20% (conservative) overall uncertainties. The final results are shown in Fig. 9.2, proving a sensitivity (\(5\sigma \) discovery reach) reach up to 10 (8) TeV in mass, for neutralino masses up to 4 (3) TeV.
21.3 Composite Higgs
Another class of models that can provide a microscopic origin for the Higgs mass and naturally accommodate the large hierarchy between the EW scale and the Planck scale are known as ‘Composite Higgs’ models. These models bear some resemblance to the story of the Ginzburg–Landau (GL) and BCS models of superconductivity, wherein the bosonic scalar field observed at low energies (long distances) is, at the microscopic level, actually a composite of fermionic degrees of freedom. A stronger similarity holds with the pions in QCD. In QCD at high energies the fundamental degrees of freedom are the quarks and gluons studied at high energy colliders. However, below the scale at which the QCD interactions become strong, the quarks and gluons become confined into composite states. The lightest of these states are the pions, which are made of a quark–antiquark pair.
In composite Higgs models the setup is qualitatively the same. At high energies one would have new gauge interactions and new fermions. As one goes to lower energies the gauge interaction becomes strong and the quarks and gluons of this new gauge group would confine. The full Higgs boson doublet, including the Goldstone bosons which are eventually eaten by the W and Z bosons, could then be a composite of the fundamental quark degrees of freedom. Furthermore, composite Higgs models have a microscopic origin for the mass of the Higgs boson. Just as the QCD pion masses may be calculated from the more fundamental QCD gauge coupling and quark mass parameters, in a composite Higgs model the Higgs mass could equally well be calculated, as a prediction, from the fundamental microscopic theory.
In QCD the strong coupling scale naturally arises a long way from the Planck scale because the QCD gauge coupling evolves logarithmically as a function of the energy scale at which it is probed. Thus, the QCD gauge coupling changes only by an \(\mathcal {O}(1)\) amount when the energy scale is changed exponentially. In this way it can be seen that there is no puzzle why the QCD strong coupling scale is many orders of magnitude from the Planck scale. In just the same way, in a composite Higgs model the strong coupling scale of the new gauge group can naturally be many orders of magnitude below the Planck scale, as it, too, would only evolve logarithmically as a function of energy.
Just as with QCD, to access the fundamental degrees of freedom hiding within the Higgs boson would require going to high energies, eventually above the energy scale at which the new gauge interactions became strong. However, even if only energies below the strong coupling scale can be accessed, it is possible to look for evidence of the new strongly-coupled interactions at high energies. Again, the analogy with QCD pions is useful. As with supersymmetry, the main avenues are indirect and direct exploration. Information on the high energy structure of the microscopic QCD theory behind the pions was extracted early on by observing the decays of pions into photon pairs, which revealed the structure of electromagnetic charges of the underlying QCD degrees of freedom. Similarly, by measuring the production and decay of the Higgs boson and searching for deviations from the SM predictions, evidence of new underlying dynamics at high energies can be revealed. Typically these deviations are parameterised through the dimensionless ratio \(\xi = v^2/f^2\), where v is the EW scale and f is the ‘compositeness scale’ of the new strong interactions [232]. The deviations in the SM Higgs interaction strengths from Higgs compositeness enter proportionally in this parameter, meaning that the precision Higgs coupling measurements indirectly probe the scale of the new strongly coupled interactions. Estimates for the indirect reach are shown in the right panel of Fig. 9.3.
Left: Projected \(2 \sigma \) indirect reach from Higgs coupling constraints on fermionic top partners from FCC-ee and FCC-hh [278]. Right: In increasingly lighter shades, current LHC and projected future HL-LHC and FCC-hh direct discovery reach for heavy composite vector resonances decaying to dileptons or gauge boson pairs. Indirect Higgs coupling constraints on the compositeness scale f, through the parameter \(\xi = v^2/f^2\) are also shown, where the \(\xi =0.004\) line corresponds to FCC-ee reach (see Refs. [279, 282] for details)
In QCD the pions did not come alone. In particular, a related set of heavier ‘vector’ (spin-1) mesons with gauge charges related to the pions, such as the \(\uprho \)-meson, showed up at higher energies. Such vector mesons are characteristic of strongly coupled gauge theories of this class and so, if the Higgs boson is a composite of a strongly coupled gauge group, new heavy \(\uprho \) -meson vector resonances with EW gauge charges should show up at colliders at masses not too far above the Higgs mass scale. Direct searches for these resonances are possible as they can be produced in EW processes, or in quark–antiquark annihilations. They will decay back into SM particles such as leptons and quarks, and will hence show up as a resonant peak in these final states. Estimates for the direct reach at FCC-hh are shown in the right panel of Fig. 9.3.
Finally, as in supersymmetric theories, in composite Higgs models new coloured top partners also typically arise, with mass not far above the Higgs mass. Their origin is related to the different global symmetry structures that can arise at the scale of the new strong interactions. Unlike in supersymmetry, however, these top partners are fermions, with spin-1 / 2. As they are coloured they can be produced directly at hadron colliders, leading to a broad range of experimental signatures. Since they are coloured and interact with the Higgs boson they will also typically modify the strength of interaction between the Higgs boson and gluons. Thus it is possible to search for their presence indirectly by measuring this interaction. The left panel of Fig. 9.3 shows the mass scale of top partners that can be probed through this indirect constraint at FCC-ee and FCC-hh.
Composite Higgs models are motivated from a number of directions. Composite scalar fields have already shown up in nature, from the Cooper-pairs in superconductors to pions in QCD, thus it is very plausible that the Higgs boson could have similar origins. Furthermore, these models can explain the hierarchy between the EW and Planck scales, and describe the microscopic origin of the Higgs mass. The FCC project, through a combination of indirect and direct searches for Higgs compositeness, would comprehensively determine if the Higgs is made up of smaller microscopic constituents.
21.4 Neutral naturalness
The coloured ‘top partners’ are a common feature of both supersymmetric and composite Higgs models. Essentially this is because both scenarios require a new symmetry to be present at energies just above the EW scale: a space-time symmetry for supersymmetry, and a continuous global symmetry in composite Higgs models. Since the SM alone cannot exhibit these symmetries, new fields are required to allow for full representations of the new symmetry to be present at high energies. The SM fields are then packaged in multiplets along with the new fields, thus the new fields typically share similar gauge charges as the SM fields they pair up with. This is, for example, the reason that the partners of the top quark are charged under QCD in supersymmetric and composite Higgs models.
The above argument is not a theorem. It has been demonstrated that there exist approaches to the hierarchy problem where the new symmetries can be realised in such a way that the fields that play the role of top partners are not coloured. These are known as ‘Neutral Naturalness’ models. The first examples of this were the ‘Twin Higgs’ models [283, 284], featuring completely gauge neutral fermionic top partners, and ‘Folded Supersymmetry’ models [285], featuring bosonic top partners that are not coloured, but do carry EW charges. As the top partners do not couple to gluons in these models, their production is very suppressed at hadron colliders. As a result, the experimental search strategies are necessarily very different than for the coloured top partners of supersymmetric or composite Higgs models.
Twin Higgs models are similar in nature to composite Higgs models, thus the universal modification of Higgs couplings is still present, although the interaction with the top partners no longer modifies the Higgs interactions with gluons. In this model the top partners are charged under a new ‘Twin’ QCD gauge group and, much as the Higgs inherits an interaction with the gluons from its interaction with the top quark, the SM Higgs boson inherits an interaction with the Twin QCD gluons. As they are lighter than the Higgs boson, it may decay to Twin gluons, which hadronise into confined states of Twin ‘glueballs’ and subsequently decay back into SM states through the interaction with the Higgs boson. Furthermore, in some cases there is an entire Twin copy of the SM, with many new light states which the Higgs boson can decay to. Thus the characteristic collider signatures for this class of models include exotic Higgs boson decays which may also be displaced, depending on the interaction strength. In Folded SUSY the situation is qualitatively similar, as there is also a new QCD-like gauge group, known as ‘Folded QCD’.
Higgs boson branching ratio into hidden sector glueballs as a function of top partner mass in a variety of Neutral Naturalness models. This decay is denoted as invisible since, although the final state is not itself invisible, it is well hidden under the background. FCC-ee sensitivity to these exotic decays through a global fit to the total Higgs signal strength is also shown
One may search for the exotic decays directly through searches for soft displaced objects. It is also possible to search for the top partners directly. However a robust model-independent prediction of this model is that, due to its exotic new decay channels, the Higgs boson obtains a new contribution to its width that is effectively invisible, in the sense that these decays do not show up in standard search channels. This branching ratio is plotted in Fig. 9.4, alongside the experimental reach at FCC-ee, demonstrating that the most relevant regions of parameter space in these models, with light top partners, are experimentally accessible at FCC.
22 The nature of the Higgs potential
22.1 Introduction
In the SM, expanding the Higgs field potential about small fluctuations in the Higgs field the potential takes the form
Each of these parameters determines the shape of the Higgs potential and may be determined as
The first parameter, whose theoretical origins raise deep questions regarding physics above the electroweak scale, as described in Sect. 9, is the Higgs boson mass. This parameter has already been measured to an accuracy of better of \(\sim 2 \times 10^{-3}\). The mass determines the local curvature of the potential, however to experimentally measure the global shape of the scalar potential one must measure the third derivative and beyond.
The third derivative of the potential determines the Higgs self-interaction and in the SM its value is fixed. In terms of Feynman diagrams, this is the strength with which the Higgs boson scatters off itself. As the self-interaction provides the first information about the shape of the Higgs potential, its measurement is of fundamental importance. For instance, the dynamic process by which electroweak symmetry was spontaneously broken in the early universe is dictated by the shape of the Higgs potential, as discussed in Sect. 11. In contrast to the precision of the mass measurement, at the HL-LHC one can only expect a measurement of this parameter at a relative accuracy of \(\sim \mathcal {O}(50 \%)\) at 68% CL.
Thus, with HL-LHC measurements alone, this fundamental aspect of the physics behind the Higgs boson, and the structure of the SM itself, would remain essentially unexplored. This qualitative aspect is clear, however, it is pertinent to ask if the Higgs self-coupling could be measured, what target accuracy of measurement would be desired?
A primary goal for future Higgs measurements is to unambiguously measure a non-zero value of the self-interaction and eventually establish its existence with a significance of greater than \(5 \sigma \). As a rough guide to the desired measurement precision, expanding around the SM value and assuming a Gaussian likelihood function, a relative accuracy of better than \(\mathcal {O}(50\%)\) is required to establish a non-zero value of the self-coupling at the \(95\%\) confidence level, and \(\mathcal {O}(20\%)\) for \(5\sigma \) discovery. Any measurement of this sensitivity would firmly establish that the Higgs boson interacts with itself.
The next experimental goal should be to probe the quantum structure of the Higgs potential. Although there is no single target that one can propose for this purpose, electroweak loop corrections are typically in the realm of \(\mathcal {O}(\text {few} \%)\), thus to begin probing the quantum structure of the Higgs potential the experimental measurements need to be sensitive to typical quantum corrections of this magnitude. These simple physical considerations establish clear qualitative targets for future Higgs physics.
22.2 Origins of a modified Higgs self-coupling
Before considering experimental probes in more detail, what is meant by the Higgs self-coupling must be unambiguously defined. If, in the measurements, the assumption is made that the only final state particles contributing to a given experimental observable are the SM particles then, by assumption, any new particles beyond the SM must have mass greater than the energy scale of the observed final state. In this case it is possible, in full generality, capture the leading effects of any new particles beyond the SM by working with the SM effective action including all of the dimension-6 operators. Thus a Lagrangian of the following form must be considered:
where the dimension-6 operators contain a mass scale in the denominator, which is related, through couplings, to the mass scale of any new particles. To perform a general analysis one should include all of the dimension-6 operators in the predictions for experimental observables and then combine measurements to try and disentangle the role of various operators.
Focussing now on the Higgs scalar potential, it is given in its gauge invariant form, where the Higgs doublet is denoted as \(\mathcal {H}\) and the dimension-6 correction which parameterises the effects of physics beyond the SM is included, as
Moving to work in terms of the physical fluctuations about the Higgs vacuum one has \( \mathcal {H} = (0,\frac{H+v}{\sqrt{2}})\), where the vacuum expectation value of the Higgs field has been measured to be \(v=246\) GeV. Also the Higgs boson mass has been measured to be \(M_H = 125\) GeV. In terms of the measured parameters the self-coupling is
Thus it can be seen that the dimension-6 operator shown in Eq. 10.4 modifies the Higgs self-coupling from the value predicted within the SM. As potential deviations from the SM prediction are of interest, the fractional deviation is denoted as
This means that any measurement sensitive to the Higgs self-coupling will probe the coefficient of this operator and any discussion of measuring deviations in the Higgs self-coupling may be framed in terms of the magnitude of this operator.
22.3 Higgs self-coupling probes at FCC
At the FCC two approaches to measure the Higgs self-coupling, known as ‘direct’ and ‘indirect’, can be followed. In the former the Higgs self-coupling enters at tree-level and in the latter it enters via processes at the loop level. In general, to unambiguously probe the coefficient of any dimension-6 operator one should perform a global fit of all available observations, including the effects of all operators in all physical observables. In the case that the heavy particles contribute dominantly to some subset of dimension-6 operators, it is well-motivated to include only those operators in the analysis, even though the result now becomes model-dependent, owing to the assumption made that other operator coefficients are small.
In the case of Higgs pair production at FCC-hh, for example via the gluon-fusion process \(\hbox {gg}\rightarrow \hbox {HH}\), the Higgs self-coupling enters at tree level. The ‘direct’ constraint on \(\delta \kappa _\lambda \) from a global analysis [270] would require the inclusion of other dimension-6 operators that may contribute, for example those involving gluons or top quarks that give rise to the diagrams in the second row of Fig. 10.1. But assuming that the deviations induced by these additional operators are already constrained to be small, as justified by the high precision achievable at the FCC in the measurement of ggh and ggt couplings, one may directly extract a constraint on \(\delta \kappa _\lambda \) from the study of Higgs-pair production.
For the case of indirect constraints the situation is somewhat different. For a given single-Higgs production process one has the tree-level process but also higher loop processes in which the Higgs self-coupling may enter, as discussed in Sect. 4.2. The first discussion of such effects was in [286], however, it was more recently emphasised for current and future experiments in [287]. Using these effects one may search for the influence of a modified Higgs self-coupling on experimental observables involving a single Higgs boson. Such probes are known as ‘indirect’. For indirect probes, if additional dimension-6 operators contribute to this process at tree-level then, for a comparable magnitude of coefficient, they would lead to deviations that are a loop factor greater than from the self-coupling effects. Thus to assume that the self-coupling modification is the leading source of deviations in an observable would necessarily imply the assumption that the other operators that contribute at tree-level have coefficients that are smaller than the self-coupling by more than a loop factor. This assumption is too strong to cover a wide range of scenarios for new physics beyond the SM that might modify the self-coupling, thus for an indirect probe it is only realistic to perform a global analysis, allowing all dimension-6 operators to enter the scattering process whilst considering all available measurements to over constrain the system of unknown coefficients.
22.4 FCC-ee: indirect probe
With the large luminosity delivered at 240 and 365 GeV, the FCC-ee has privileged sensitivity to the Higgs self-coupling by measuring its centre-of-mass-energy-dependent effects at the quantum level on single Higgs observables [287], such as the HZ and the \(\upnu \upnu ~\hbox {H}\) production cross sections, representative diagrams of which are displayed in Fig. 10.2.
From Ref. [288], sample Feynman diagrams illustrating the effects of the Higgs trilinear self-coupling on single Higgs process at next-to-leading order
In Fig. 10.3 the results of a global analysis for FCC-ee are shown. This figure is taken from [288], to which the reader is referred for details. Notably, through a global analysis which allows for the presence of all dimension-6 operators with arbitrary coefficients, at FCC-ee a robust and model-independent measurement of the Higgs self-coupling can be made with a precision of \(44\%\), to be compared with the HL-LHC projection, in which the precision is around \(50\%\). This would establish, at better than \(95\%\) confidence level, a non-zero value for the Higgs self-coupling and would probe a scale of \(\Lambda \sim 1\) TeV in Eq. 10.4. In this analysis the FCC-ee precision electroweak measurements at lower energies (Sect. 3.2) are equally important to fix extra parameters that would otherwise enter the global Higgs fit and open flat directions that cannot be resolved.
22.5 FCC-hh: direct probes
At FCC-hh, the Higgs self-coupling can be probed directly via Higgs-pair production. The cross sections for several production channels are given [289] in Table 10.1, where the quoted systematics reflect today’s state of the art, and are therefore bound to be significantly improved by the time of FCC-hh operations.
The most studied channel, in view of its large rate, is gluon fusion (see Fig. 10.1). In the SM there is a large destructive interference between the diagram with the top-quark loop and that with the self-coupling. While this interference suppresses the SM rate, it makes the rate more sensitive to possible deviations from the SM couplings, the sensitivity being enhanced after NLO corrections are included, as shown in the case of \(\hbox {gg}\rightarrow \hbox {HH}\) in Ref. [290], where the first NLO calculation of \(\sigma (\hbox {gg}\rightarrow \hbox {HH})\) inclusive of top-mass effects was performed. For values of \(\kappa _\lambda \) close to 1, \(1/\sigma _{\mathrm{HH}} d\sigma _{\mathrm{HH}}/d\kappa _\lambda \sim -1\), and a measurement of \(\kappa _\lambda \) at the few percent level requires therefore, the measurement and theoretical interpretation of the Higgs-pair rate at a similar level of precision. Table 10.1 shows that the current theoretical systematics on the signal is at the 5% level (for a complete discussion see [291]), which is already competitive with the statistical and experimental systematics, to be presented shortly. It is reasonable to predict a further reduction to the percent level.
The following summarises the results obtained as part of the FCC-hh detector performance studies, which are presented in more detail in the accompanying FCC-hh CDR Volumes.
22.5.1 \(\hbox {gg}\rightarrow \hbox {HH}\rightarrow \hbox {b}\bar{\hbox {b}}\upgamma \upgamma \)
The most promising decay channel, optimising the compromise between statistics and backgrounds, is \(\hbox {HH}\rightarrow \hbox {b}\bar{\hbox {b}}\upgamma \upgamma \), with a 0.25% branching ratio. The main backgrounds are tŧH, \(\upgamma \upgamma +\hbox {jets}\), \(\upgamma +\hbox {jets}\) (with one jet mis-identified as a photon) and \(\hbox {H}(\rightarrow \upgamma \upgamma )+\hbox {jets}\) production. The Monte Carlo events for signal and background were processed through the Delphes [292] simulation of the FCC-hh detector. The photon identification efficiency is assumed to be \(\epsilon _{\gamma }=95\%\) for \(|\eta | < 2.5\) and \(\epsilon _{\gamma }=90\%\) for \(2.5< |\eta | < 4.0\) for all photon \(p_T\). The light jet to photon mis-identification probability (fake-rate) is parameterised by the function \(\epsilon _{j \rightarrow \gamma }= 0.002 \exp (-p_T/\;30\;\mathrm {GeV})\). The b-tagging efficiency \(\epsilon _{b}\) and the light (charm) mistag rates \(\epsilon _{l(c) \rightarrow b}\) are assumed to be \(\epsilon _{b}=85\%\) and \(\epsilon _{l(c) \rightarrow b}=1\) (5)%. The reference \(\upgamma \upgamma \) mass resolution is \(\delta m_{\gamma \gamma }=1.3~\hbox {GeV}\).
Events are required to contain at least two isolated photons and two b-tagged jets, with \(p_T(\upgamma ,\hbox {b})>30~\hbox {GeV}\) and \(|\eta (\upgamma ,\mathrm{b})|<3.0\). Jets are clustered using particle-flow candidates with the anti-\(k_T\) algorithm with radius parameter R=0.4. The leading \(\upgamma \) and b-jet have \(p_T > 60~\hbox {GeV}\), and the di-photon and di-jet pairs \(p_T > 125~\hbox {GeV}\). Furthermore, the invariant mass of the b-jet pair satisfies \(100<m_{\mathrm{bb}} < 130\) GeV. A veto on leptons with \(p_T(\ell ) > 25\) GeV and \(|\eta (\ell )| < 3.0\), and the cut \(\Delta R_{\mathrm{bb}} < 2.0\), suppress the tŧH background.
The signal extraction is performed via a 2-dimensional likelihood fit over the photon-pair and the Higgs-pair invariant masses. The negative log-likelihood (NLL) distribution for the parameter \(\kappa _{\lambda }\) with respect to the best-fit value obtained for varying systematics, background normalisation and detector assumptions is shown in Figs. 10.4 and 10.5. The \(1\sigma \) and \(2\sigma \) lines correspond to the 68% and 95% confidence levels (CL) respectively.
Expected precision on the Higgs self-coupling modifier \(\kappa _{\lambda }\) with no systematic uncertainties (only statistical), 1% signal uncertainty, 1% signal uncertainty together with 1% uncertainty on the Higgs backgrounds (left) and assuming respectively \(\times 1\), \(\times 2\), \(\times 0.5\) background yields (right).)
Figure 10.4 (left) shows the sensitivity obtained with different assumptions about the uncertainties. With only the statistical uncertainty (blue curve), it is found that \(\delta \kappa _{\lambda }=5.5\%\). When a 1% systematic uncertainty on the signal normalisation is included (red curve) the expected precision decreases to \(\delta \kappa _{\lambda }=6\%\). An additional uncertainty of 1% on the single Higgs backgrounds normalisation (green curve) is shown under the assumption that the QCD background can be extrapolated from a control sample defined by \(|m_{\gamma \gamma }- m_\mathrm{H}| > 10~\hbox {GeV}\), with high statistics into the signal region. For the single Higgs background defining such a control sample is more challenging and therefore an uncertainty of 1% on the normalisation is assumed, motivated by expected precision on this process at the FCC-hh [89]. In this scenario the expected precision is \(\delta \kappa _{\lambda }= 6.5\%\). Figure 10.4 (right) shows how the precision is affected by varying the overall background yields by factors of 2 and 0.5 and find an impact on the overall \(\kappa _{\lambda }\) precision of \(\approx \pm \, 1\%\).
Figure 10.5 shows the dependence of sensitivity on the detector performance assumptions. The left plot assumes a \(\upgamma \upgamma \) mass resolution \(\delta m_{\gamma \gamma }=2.9~\hbox {GeV}\). The central plot modifies the photon reconstruction efficiency, and the right one modifies the jet-to-photon fake rate. Each of these scenarios degrades the precision on the self-coupling by 1-2%. These scenarios roughly match the expected performance of the ATLAS and CMS detectors at HL-LHC [293, 294], and should therefore be considered as conservative.
Expected precision on the Higgs self-coupling modifier \(\kappa _{\lambda }\) obtained by varying the photon reconstruction performance. Left: Comparison of two scenarios with nominal (\(\Delta m_{{\upgamma \upgamma }}=1.3~\hbox {GeV}\)) and degraded (\(\Delta m_{{\upgamma \upgamma }}=2.9~\hbox {GeV}\)) energy resolution. Centre: Comparison of two scenarios with nominal (\(\epsilon _{{\upgamma }}=95\%\)) and degraded (\(\epsilon _{{\upgamma }}=85\%\)) photon reconstruction efficiency. Right: Comparison of three scenarios with nominal, degraded (\(\times 5\)) and improved (\(\times 0.2\)) photon mistag rate
22.5.2 Other final states in \(\hbox {gg}\rightarrow \hbox {HH}\)
Decay modes other than \(\hbox {HH}\rightarrow \hbox {b}\bar{\hbox {b}}\upgamma \upgamma \) have also been considered in the detector performance studies. These include \(\hbox {b}\bar{\hbox {b}}\hbox {ZZ}^{*}[\rightarrow 4\ell ]\) (\(\ell =\hbox {e},\upmu \)), \(\hbox {b}\bar{\hbox {b}}\hbox {WW}^{*}[\rightarrow 2\hbox {j}\ell \upnu ]\), and \(4\hbox {b}+\hbox {jet}\). A summary of the target precision in the measurement of \(\kappa _\lambda \) is given in Table 10.2, where the results were obtained with the baseline detector performance parameters, and a 1% systematics on the rates of the signals and of the leading backgrounds.
Additional studies, of a more phenomenological nature, have appeared in the literature. Typically these adopt simplified detector simulations, based however, on benchmark performance parameters consistent with the FCC-hh baseline assumptions.
Reference [295] performs a kinematic analysis of various HH distributions in the \(\hbox {b}\bar{\hbox {b}}\upgamma \upgamma \) final state, considering quantities such as the invariant mass \(m_{\mathrm{HH}}\), the Higgs \(p_T\) and various angular correlations. The \(m_{\mathrm{HH}}\) spectrum is strongly sensitive to the Higgs self-coupling. At threshold, \(m_{\mathrm{HH}}=2m_\mathrm{H}\), the SM amplitude exactly vanishes, due to the interference between box and self-coupling diagrams. For \(\kappa _\lambda \sim 2\) a strong dip develops instead for \(m_{\mathrm{HH}}=2m_\mathrm{t}\). At large \(m_{\mathrm{HH}}\), the self-coupling contribution dies off due to the \(1/m^2_{\mathrm{HH}}\) s-channel propagator. These effects are clearly visible in the left plot of Fig. 10.6. The \(\kappa _\lambda \) sensitivity obtained from the detector study based on the Delphes [292] parameterisation of the HL-LHC ATLAS and CMS detector performances is shown on the right plot. The projected 1\(\sigma \) sensitivity at 100 TeV (30 \(\hbox {ab}^{-1}\)) is 5%, consistent with the results of the FCC-hh detector performance study. Reference [295] also quotes a 15% sensitivity for the HE-LHC.
Studies of the Higgs self-coupling sensitivity at HE-LHC have also been carried out by the ATLAS and CMS experiments in the context of the HL/HE-LHC Workshop [18]. The results are summarised in the right plot of Fig. 10.6, showing a 10–20% sensitivity at 68% CL. Independent results have appeared in Ref. [296].
For FCC-hh, reference [297] proposed using a boosted HH final state, recoiling against a jet, to maintain the HH invariant mass as close to threshold as possible, enhancing the sensitivity to the Higgs self-coupling, while enabling the use of boosted-object substructure techniques to reconstruct the \(\hbox {H}\rightarrow \hbox {b}\bar{\hbox {b}}\) decay. In the case of the \(\hbox {b}\bar{\hbox {b}}\uptau \uptau \) final state, a \(\pm \,8\%\) precision on \(\kappa _\lambda \) is obtained at 68% CL.
To summarise, within the stated assumptions on the expected performance of the FCC-hh detector, a precision target on the Higgs self-coupling of \(\delta \kappa _{\lambda }=5\%\) in the \(\hbox {gg}\rightarrow \hbox {HH}\) channel appears achievable, by exploiting several techniques and decay modes, and assuming the future theoretical progress in modelling signals and backgrounds.
22.5.3 Other probes of multi-linear Higgs interactions
Given the rates shown in Table 10.1, the next process of interest for the production of Higgs pairs is vector boson fusion, the relevant diagrams being shown in Fig. 10.7. A study of this process at 100 TeV, to explore the sensitivity to higher-dimension operators, was presented in Ref. [298]. Here the emphasis was on the high-\(m_{\mathrm{HH}}\) domain, where the behaviour of the longitudinal-longitudinal component of the amplitude is characterised by the destructive interference between the first two diagrams:
where \(c_{2V}\) and \(c_V\) represent, respectively, the coefficients of the VVHH and VVH couplings, normalised to their SM values. \(\delta _c = c_{2V}^2-c_V\) vanishes in the SM and in extensions where the Higgs belongs to an SU(2) doublet, and the growth of the amplitude with energy is suppressed. The study of the high-\(m_{\mathrm{HH}}\) behaviour is therefore a powerful probe of \(\delta _c\) and of the gauge structure of the Higgs sector. Ref. [298] chose the HH\(\rightarrow \)4b final state, applying boosted-jet tagging techniques – justified by the high \(p_T\) of the Higgs bosons in the relevant kinematic region – to minimise the dominant backgrounds (\(4\hbox {b}, 2\hbox {b}2\hbox {j}, \hbox {t}\bar{\hbox {t}}2\hbox {j}, \hbox {Hjj}\)). An example of the impact of \(\delta _c\ne 0\) is shown in Fig. 10.8, where the di-Higgs mass spectrum in the SM and in a \(c_V=1\), \(c_{2V}=0.8\) scenario are compared to the expected backgrounds (in the parton-level simulation). After the detector simulation of fully showered event, Ref. [298] carried out a detailed study of the shape of the mass distribution, resulting in the probability density distribution for \(\delta c_{2V}\) shown in the right plot of Fig. 10.8. Several robustness tests have been performed, including assigning large uncertainties on the background rates. The signal itself is already known with a precision at level of few percent (see Table 10.1), which will improve with time (see e.g. Fig. 5.14 for the expected PDF uncertainty from FCC-eh on the dominant qq initial-state channel, well below the percent level in the few-TeV region considered here). Since \(c_V\) will be measured with a few per-mille precision at FCC-ee (independently of whether it agrees or not with the SM), and given that at the cubic Higgs self-coupling contribution is suppressed at the multi-TeV mass values considered in this analysis, the constraints on \(\delta _c\) at FCC-hh will translate directly into a constraint on \(c_{2V}\) of better than \(\pm \, 1\%\).
Direct constraints on the quartic Higgs coupling via triple Higgs production (Fig. 10.9) were studied in Refs. [299,300,301]. The study of Ref. [299] considered \(\hbox {pp}\rightarrow \hbox {HHH}\rightarrow \hbox {b}\bar{\hbox {b}}\hbox {b}\bar{\hbox {b}}\upgamma \upgamma \). The cross section of \(\sim 5\hbox {fb}\), and \(\hbox {BR}=0.23\%\), lead to about 400 events with 30 \(\hbox {ab}^{-1}\), before analysis cuts. The large backgrounds make it difficult to confirm production at the SM rate, but allow constraints on possible deviations from the SM to be set, as shown in Fig. 10.10. Here \(c_3=\delta \kappa _\lambda \) and \(d_4\) is the fractional deviation of the quartic coupling from its SM value. The presence of \(c_3\) is due to the fact that the cubic coupling enters in several of the diagrams for the HHH production (see Fig. 10.9). The relation \(d_4=6c_3\), shown in the figure, corresponds to scenarios in which the SM is corrected by the sole presence of a \(|\mathrm{H}|^6\) operator, as in Eq. 10.4. Fuks et al. [301] studied the final state \(\hbox {HHH}\rightarrow \hbox {b}\bar{\hbox {b}}\hbox {b}\bar{\hbox {b}}\uptau \uptau \), achieving a \(2\sigma \) sensitivity to the SM quartic coupling.
22.6 Double Higgs production at FCC-eh
The final states arising from double-Higgs production are particularly clean at the FCC-eh, due to the simple structure of the final state \(\hbox {ep}\rightarrow \hbox {e}(\upnu )\hbox {HX}\), and to the low pile-up environment. The simple nature of the elementary process, \(\hbox {VV}\rightarrow \hbox {HH}\), gives direct access to the HHWW coupling and to the measurement of the Higgs self-coupling. A first study of this process in DIS was documented in Ref. [267], including sensitivity to anomalous couplings. The application to FCC-eh of this cut-based analysis for the \(\hbox {HH}\rightarrow 4\hbox {b}\) final state, leads to a precision on the measurement of the Higgs self-coupling of about 20%. The addition of all major decays, and replacing the cut-based with a BDT analysis, promises to deliver a 10% precision, with 3 \(\hbox {ab}^{-1}\) of data.
22.7 Summary
FCC provides several independent probes of the higher-order terms in the Higgs potential and interactions. FCC-ee will give an indirect measurement of the cubic Higgs self-coupling to 44% precision. The direct measurement of \(\hbox {gg}\rightarrow \hbox {HH}\) production at FCC-hh can improve this to the 5% level (10–20% at HE-LHC), combining several decay modes and different analysis strategies. The study of HH production in vector boson fusion at FCC-eh will give a complementary measurement, at the 10% level. Considering HH pairs at high mass in vector boson fusion at FCC-hh, will, in turn, determine the VVHH coupling to better than 1%, constraining the scale of new higher-dimension operators up to values in the range of 5-10 TeV.
Altogether, the FCC provides the most sensitive probe of Higgs self-interactions among the currently proposed future facilities.
23 Studies of the EW phase transition
23.1 Introduction
Explaining the origin of the cosmic matter-antimatter asymmetry is a challenge at the forefront of particle physics. One of the most compelling explanations connects this asymmetry to the generation of elementary particle masses through electroweak symmetry-breaking (EWSB). This scenario relies on two ingredients: a sufficiently violent transition to the broken-symmetry phase, and the existence of adequate sources of CP-violation. As it turns out, these conditions are not satisfied in the SM, but they can be met in a variety of BSM scenarios. CP violation relevant to the matter-antimatter asymmetry can arise from new interactions over a broad range of mass scales, possibly well above 100 TeV. Exhaustively testing these scenarios may therefore go beyond the scope of the FCC. For the phase transition to be sufficiently strong, on the other hand, there must be new particles with masses typically below one TeV, whose interactions with the Higgs boson modify the Higgs potential energy in the early universe. Should they exist, these particles and interactions would manifest themselves at FCC, creating a key scientific opportunity and priority for the FCC. This section therefore focuses on the problem of establishing the nature of the EW phase transition and reviews the role played by the FCC.
23.2 The electroweak phase transition
To understand the possible connection between EWSB and the matter-antimatter asymmetry, consider the potential energy carried by the Higgs field \(\varphi \) in the hot, early Universe. This energy is given by the temperature-dependent Higgs potential, \(V_{\mathrm{EFF}}(\varphi , T)\). In the regime where \(T>> M_W\), this potential takes the simple form
In the SM one has \(e=0\), while D, \(T_0\), E and \({\bar{\lambda }}\) are all non-vanishing functions of the zero temperature parameters of the theory (e.g., gauge, Yukawa, and Higgs self-couplings). At any temperature, the minimum of energy is obtained when \(\varphi \) equals its vacuum expectation value v(T), with \(v(0) = 246~\hbox {GeV}\). The Higgs boson field is just the difference \(H=\varphi -v(0)\).
At sufficiently high temperatures, the minimum energy lies at the origin, i.e., \(v(T) = 0\). As the universe cools, however, the minimum eventually moves away from the origin, corresponding to the onset of EWSB . Determining the nature of this EWSB transition is a fundamental challenge for particle physics. If this transition was sufficiently violent – a so-called, first order EW phase transition (EWPT) – the conditions would have been ripe for generating the cosmic matter-antimatter asymmetry. Such a first order EWPT would have been analogous to the more familiar phase transition when steam condenses into liquid, a phase of matter with less symmetry. The parameters of the \(T=0\) Higgs potential, together with the Higgs interactions with the other SM particles, determine behaviour of \(V_{\mathrm{EFF}}(\varphi ,T)\). Thus, by experimentally measuring Higgs boson properties, one can directly infer the thermal history of EWSB and thereby determine whether or not the matter-antimatter asymmetry could have been created in conjunction with the generation of elementary particle masses.
With the SM form of the \(T=0\) Higgs potential and Higgs couplings to other SM particles, lattice studies imply that for a 125 GeV Higgs boson, the EWSB transition is of a cross over type [302,303,304,305], which fails to provide the violent strong first order conditions needed for creation of the matter-antimatter asymmetry [306]. On the other hand, BSM scenarios that contain new bosonic degrees of freedom that interact with the Higgs boson could change the picture dramatically(see e.g., [307, 308]). A strong first order transition may arise through BSM-induced changes in the zero-temperature vacuum structure of the scalar potential and/or finite-temperature quantum corrections that modify the parameters in Eq. 11.1 In addition, the presence of “BSM Higgses” may allow for a richer thermal history than in the SM universe, including the presence of new symmetry-breaking phases that preceded the presence of the “Higgs phase” [309,310,311].
23.3 Collider probes
Searches for BSM scalars at the LHC have begun to explore this possibility, largely precluding a strong first order transition if the new scalars have strong interactions [312, 313]. On the other hand, the presence of scalars that carry only EW quantum numbers (EW multiplets) or no SM quantum numbers at all (singlets), are more challenging to observe at the LHC, even by the conclusion of the HL phase. Direct production cross sections can be as small as a few fb in regions of parameter space consistent with a strong first order EWPT. Studies completed to date, however, indicate that the FCC-hh with \(30~\hbox {ab}^{-1}\) should provide a definitive probe of these new states. Indirect effects entering through modifications of the Higgs self-coupling or the rate for \(\hbox {h}\rightarrow \upgamma \upgamma \) may be observable at the HL-LHC or even the HE-LHC, but can be as small as a few percent, pointing to the precision achievable only with the FCC-hh.
The simplest illustration of these possibilities is the extension of the SM scalar sector with a single real singlet scalar [314,315,316,317,318,319,320,321,322,323,324,325,326], the “xSM” [327] (for analogous studies with a complex singlet, see [328, 329]). Singlet scalars occur copiously in extensions of the SM, but examination of the additional degrees of freedom and interactions is not essential for identifying the EWPT dynamics. The xSM contains two Higgs-like scalars, \(\hbox {h}_{1}\) and \(\hbox {h}_{2}\) that are admixtures of the neutral component of the SM Higgs doublet and the singlet. The associated interactions in the scalar potential can readily lead to a strong first order EWPT when the SM-like state \(\hbox {h}_1\) has a mass of 125 GeV, as opposed to the pure SM case. The associated collider signatures include modifications of the Higgs self-coupling, which may be as small as a few percent; a shift in the associated production (\(\hbox {Zh}_1\)) cross section; and direct production of scalar pairs, which provides direct access to combinations of couplings appearing in the scalar potential.
In pp collisions, a pair of SM-like scalars \(\hbox {h}_1\) can be produced through an on-shell \(\hbox {h}_2\). Each \(\hbox {h}_1\) then decays to the conventional Higgs boson decay products, yielding various combinations. The possibilities for discovery through the “resonant di-Higgs production” process are illustrated in Fig. 11.1, where the results are obtained by combining the \(4\uptau \) and \(\hbox {b}\bar{\hbox {b}}\upgamma \upgamma \) final states [314]. Each coloured band gives the projected significance \(N_\sigma \) of observation as a function of the \(\hbox {h}_2\) mass, with the \(N_\sigma \) range obtained by varying over all other model parameters consistent with a strong first order EWPT, constraints from EW precision observables, and present LHC Higgs signal strength determinations. The maximum \(\hbox {h}_2\) mass consistent with a strong first order EWPT is just below 900 GeV. As one can see, the HL-LHC discovery potential is limited to a relatively modest portion of the light \(\hbox {h}_2\) parameter space, whereas the FCC-hh with \(30~\hbox {ab}^{-1}\) would enable discovery over the entire first order EWPT-viable parameter space in this model.
Non-resonant production of other combinations of scalars can also be observable at the FCC-hh and provide complementary information about the couplings in the scalar potential. For example, pairs of singlet-like scalars \(\hbox {h}_2\) can be produced through an off-shell \(\hbox {h}_1\). The singlet-like scalars can then either decay visibly to Standard Model final states [325], or, in the presence of additional symmetries, can escape the detector invisibly [322]. The FCC-hh sensitivity to these processes is illustrated in Fig. 11.2. On the left, the coloured points correspond to the phenomenologically allowed EWPT parameter space for a particular choice of the \(\hbox {h}_2\) mass and mixing angle, and the darker (lighter) shaded regions indicate the \(5\sigma \) (\(2\sigma \)) reach in the \(\hbox {pp}\rightarrow \hbox {h}_2 \hbox { h}_2\rightarrow \,2\hbox {j}\,3\ell \,3\upnu \) channel at the FCC-hh with \(30~\hbox {ab}^{-1}\). The right hand side of Fig. 11.2 shows the FCC-hh sensitivity to \(\hbox {pp}\rightarrow \hbox {h}_2 \hbox { h}_2\,\hbox {jj}\), where \(\hbox {h}_2\) escapes the detector invisibly. The lighter shaded regions feature a strong first-order EWPT. In both the visible and invisible cases, the FCC-hh can conclusively probe the EWPT-compatible parameter space shown and provide valuable information about the scalar potential.
Discovery potential for the singlet-induced strong first order EWPT using resonant di-Higgs production combining \(4\uptau \) and \(\hbox {b}\bar{\hbox {b}}\upgamma \upgamma \) final states [314]. Vertical axis gives significance as a function of the singlet-like scalar mass \(m_2\) for the HL-LHC (blue band) and the FCC-hh with \(3~\hbox {ab}^{-1}\) and \(30~\hbox {ab}^{-1}\) (purple and red bands, respectively)
Singlet-like scalar pair production as a signature of the EWPT in the xSM. Left: FCC-hh sensitivity to \(\hbox {pp}\rightarrow \hbox {h}_2 \hbox { h}_2\rightarrow \,2\hbox {j}\,3\ell \,3\upnu \) for a given \(\hbox {h}_2\) mass and mixing angle. Here, \(\lambda _{221}\) and \(b_3\) are the \(\hbox {h}_2 \hbox { h}_2 \hbox { h}_1\) and singlet cubic couplings, respectively. Darker (lighter) shaded regions indicate \(5\sigma \) (\(2\sigma \)) sensitivity assuming \(30~\hbox {ab}^{-1}\) integrated luminosity. Coloured points feature a strong first-order EWPT. Also shown for comparison are the sensitivity projections for \(\hbox {h}_1\) self-coupling measurements (dashed contours) and precision measurements of the ZH production cross-section (solid red contours). From Ref. [325]. Right: FCC-hh sensitivity to \(\hbox {pp}\rightarrow \hbox {h}_2 \hbox { h}_2\,\hbox {jj}\) in the xSM with a \(\mathbb {Z}_2\) symmetry. \(\hbox {h}_2\) escapes the detector as missing energy. \(m_S\) is the singlet mass and \(\lambda _{HS}\) is the Higgs portal coupling. Lighter shaded regions indicate points compatible with a strong first-order EWPT, and the labelled contours indicate the expected FCC-hh sensitivity given \(30~\hbox {ab}^{-1}\) integrated luminosity. From Ref. [322]
The FCC will also provide the opportunity to observe additional signatures of a strong first order EWPT. In the xSM, the mixing between the doublet and singlet states will imply reductions in the Higgs signal strengths compared to those for a pure SM Higgs boson. This possibility is illustrated in Fig. 11.3 which shows the correlation between cosine of the mixing angle and the \(\hbox {h}_2\) mass. The points in the brown region correspond to parameter choices leading to a strong first order EWPT and that are consistent with constraints from EW precision tests. All points to the left of the red line correspond to deviations from SM Higgs signal strengths that would be observable at the FCC-ee and as well as discovery of the resonant di-Higgs signal at the FCC-hh.
First order EWPT-viable parameter choices for the singlet extended Standard Model. Allowed region (brown) is bounded by constraints from EW precision tests. Horizontal and vertical axes give cosine of the doublet-singlet mixing angle and singlet-like scalar mass, respectively. Vertical lines give prospective sensitivities of the HL-LHC and the FCC-ee (“Circ \(\mathrm{e}^+\mathrm{e}^-\)”). Adapted from Ref [314]
Equally important signatures include deviations of the Higgs triple self-coupling and its coupling to a pair of \(\hbox {Z}^0\) bosons. First, a large \(\mathcal {O}\)(1) deviation in the triple Higgs coupling may arise, and it can be measured well by both FCC-hh in the study of double Higgs production and also indirectly at FCC-ee with an NLO global fit of single Higgs data. Second, a large deviation in the Higgs coupling with Z-bosons may also characterise regions of the parameter space featuring a first order phase transition. These possibilities are illustrated in Fig. 11.4. The top panel shows the correlation between the Higgs triple self-coupling scaled to its SM value (horizontal axis: \(\lambda _3/\lambda _{3,{\mathrm{SM}}}\), also labelled as \(\kappa _\lambda \) in Sect. 10) and the HZZ coupling (vertical axis), with the prospective FCC sensitivities indicated in red [324]. The bottom panel gives the correlation between the self-coupling scaled to its SM value (horizontal axis: \(g_{111}/g_{111}^{\mathrm{SM}}=\kappa _\lambda \)) and the critical temperature (vertical axis) for singlet-like scalar masses too light to admit resonant di-Higgs production [330]. Interestingly, the self-coupling measurement could provide a probe of this important thermodynamic property of the transition that would be otherwise difficult to test experimentally.
Parameter space scan for a singlet model extension of the Standard Model. The points indicate a first order phase transition. These points lead to signals observable at future colliders. Upper panel: correlation between changes in the HZZ coupling (vertical axis) and the HHH coupling scaled to its SM value (horizontal axis). Lower panel: correlation between critical temperature \(T_c\) (vertical axis) and the HHH coupling scaled to its SM value (horizontal axis). SM prediction for the latter is indicated as \(g_{111}/g_{111}^{\mathrm{SM}}=1\). Adapted from Refs. [324, 330]
EW phase diagram for the real triplet extension of the SM scalar sector. Horizontal axis gives the triplet mass and vertical axis indicates the triplet-Higgs coupling. Light blue and green regions correspond to cross-over and first order transitions. Dark green (“DR breaks down”) and grey regions indicate parameter choices for which the present non-perturbative computations are not applicable. Dashed lines indicate relative shift in the Higgs diphoton decay rate. From Ref. [331]
Despite the simplicity of the xSM, its first order EWPT dynamics clearly illustrate the rich array of FCC discovery opportunities. It is also possible that an extended Higgs sector involving electroweakly-charged scalars also catalyse a strong first order EWPT and lead to an equally rich set of signatures. Perhaps, the most widely studied such scenario is the Two Higgs Doublet Model (2HDM). In this case, it has been shown that the strong phase transition would be correlated with the presence of the \(\hbox {A}^0\rightarrow \hbox {Z H}^0\) decay and that a nearly definitive probe of this possibility could be achieved with the LHC [332, 333]. Alternatively, the existence of a scalar EW triplet with vanishing hypercharge could lead to EWSB through either a single transition to the Higgs phase or through a succession of transitions [309]. Recent results that exploit non-perturbative methods have shown how a precise measurement of the Higgs di-photon decay rate could probe the nature of the transition in this scenario [331]. Figure 11.5 illustrates this possibility. The horizontal and vertical axes give the triplet mass and coupling to Higgs boson, respectively. The light blue and green regions correspond to a cross-over transition and first order phase transition, respectively. The dashed lines indicate the relative reduction in the Higgs diphoton decay rate relative to SM Higgs expectations. When combined with knowledge of the triplet mass, a precise measurement of the diphoton decay rate would indicate whether the transition is first order or crossover. For a \(5\sigma \) observation, a measurement of \(\Gamma (\hbox {H}\rightarrow \upgamma \upgamma )\) at the anticipated FCC precision would be needed. In addition to such a measurement at the FCC, the very small (radiative) mass splitting between the charged and neutral components of the triplet \(\Delta m_{\Sigma } = 166~\hbox {MeV}\) could allow one to directly probe the scalar EW triplet scenario through disappearing track searches. In addition, the FCC-eh would have unique capabilities to reconstruct the very soft visible decay products of the charged state [334], yielding yet another important probe of this scenario.
23.4 Summary
These studies illustrate the prospective power of the FCC to determine the thermal history of EW symmetry breaking and the complementarity between the FCC-hh and FCC-ee colliders. While the LHC will provide initial insights into this important question, it will require the FCC to provide the most comprehensive and, likely, definitive probe. If the FCC discovers new particle interactions indicative of a first order EWPT, then it would be known that the conditions needed for generating the matter-antimatter asymmetry of the Universe were present during the era of EWSB. Complementary probes (at low- and high-energies) of possible new CP-violating interactions would then show if the asymmetry was, indeed, created in conjunction with the generation of elementary particle masses. If not, then it would be concluded that the origin of matter arose during some other period of cosmic history.
One should keep in mind that the thermal history of EWSB remains an area of intensive theoretical research. It entails a mixture of model-building, phenomenological explorations and refinement of theoretical methods. An extensive review of these directions, including detailed background regarding the aforementioned examples, will appear in a forthcoming white paper that will accompany this document [335].
24 Searches for dark matter and dark sectors
24.1 Introduction
In Sect. 1.1 the status of the dark matter (DM) puzzle was discussed, including the possible range of masses the DM particles could take. No experiment, at colliders or otherwise, can probe the full range of masses allowed by astrophysical observations. However there is a very broad class of models for which theory motivates masses up to the 10’s \(~\text {TeV}\) range, and which therefore could be in the range of the FCC.
If at any point in the history of the early universe the DM is in thermal equilibrium with the SM particles, then its relic density today can be estimated by studying how it decouples from the SM, a process known as freeze-out. For particles which are held in equilibrium by pair creation and annihilation processes, \((\chi \chi \leftrightarrow {\mathrm{SM}})\) one finds the simple relation that [336]
where \(\langle \sigma v \rangle \) is the velocity averaged annihilation cross section of the DM candidate \(\chi \) into SM particles, \(\Omega _{\mathrm{DM}}h^2 \approx 0.12\) is the observed relic abundance of DM [11], \(M_{\mathrm{pl}}\) is the Planck scale and order one factors have been neglected.
For a particle annihilating through processes which do not involve any larger mass scales, the annihilation cross section scales as \(\langle \sigma v \rangle \sim g_{\mathrm{eff}}^4/M_{\mathrm{DM}}^2\), where \(g_{\mathrm{eff}}\) is the effective coupling strength which parameterises the process. It follows that
This approximate relation implies that a DM candidate with a mass at or below the TeV scale and which couples to the SM with a strength similar to the weak interactions naturally has a relic density in agreement with observations. Furthermore, as the DM mass is reduced, ever weaker couplings are required. On one hand this is the main reason why it is hoped to find evidence for DM at the LHC, but on the other hand it already shows that a higher energy collider will be necessary to efficiently probe the WIMP paradigm for DM.
Equation 12.2 shows that as the mass of DM increases, in order to maintain the observed relic abundance, the annihilation cross section also has to increase. This becomes inconsistent with unitarity of the annihilation amplitudes at \(M_{\mathrm{DM}} \lesssim 110~\text {TeV}\), the so called unitarity bound on the mass of DM [337, 338]. Most well motivated models of WIMP DM do not saturate this bound, but rather have upper limits on the DM mass in the TeV range.
Complementarity of different search strategies for Wino DM, with reach adapted from [339]. The top line ‘LZ’ shows projected direct detection reach, which is far from the mass range motivated by the relic abundance. Below that are the indirect detection constraints, which are subject to astrophysical uncertainties. For instance, in the galactic centre (GC) constraint the lighter and darker shading show limits for different assumptions for DM halo profiles, demonstrating that the desired mass range is not covered in general. Collider constraints include searches for prompt and non-prompt signatures and demonstrate that only at 100 TeV can the disappearing tracks search cover the motivated mass range
For DM masses at the lower end of the WIMP spectrum, one typically expects that annihilation proceeds through a mediator with \(M_{\mathrm{med}} > 2 M_{\mathrm{DM}}\). Then the annihilation cross section is suppressed by \((M_{\mathrm{DM}}^4/M_{\mathrm{med}}^4)\). Assuming that no mediator particle exists with a mass below the Higgs mass, then this puts a lower bound near to a \(~\text {GeV}\) on the mass of the WIMP DM candidate, while an even wider range of DM masses becomes accessible if the mediator is lighter but very weakly coupled to the SM.
24.2 Discovering WIMPs: an example
The WIMP paradigm, originally interpreted as concerning neutral DM particles charged under the EW gauge group, has been subjected to extensive experimental searches for decades. However, an exhaustive exploration of this compelling paradigm will require a collider reach covering the entire relevant mass range. To illustrate the role of FCC-hh in this regard a long-known WIMP DM candidate, the so-called ‘Wino’, will be considered. The Wino will serve as a concrete example of a WIMP to demonstrate the rich interplay between collider and non-collider probes of WIMP DM. It should be noted that there are numerous WIMP candidates, each with its own unique set of signatures.
The Wino is a neutral Majorana fermion transforming in the adjoint representation of \(\text {SU}(2)_W\), which happens to arise automatically in supersymmetric models, as the partner of the EW gauge bosons. However, it is also compelling as a stand-alone DM candidate, irrespective of supersymmetry.
The Wino is elusive, as no tree-level direct detection processes are possible where the Wino scatters on a nucleus in an underground detector. This scattering only occurs at one-loop, leading to suppressed rates. Indirect detection signatures arise from Wino DM annihilation in the centre of our galaxy and in surrounding dwarf galaxies. The final-state annihilation products give rise to photons, which can be observed with gamma-ray telescopes.
Due to the relatively large annihilation cross section, the mass range that generates the observed abundance of dark matter falls above the reach of the LHC, and thus higher energy colliders are necessary.
A compilation of future constraints on Wino DM is presented in Fig. 12.1. While some astrophysical probes can reach the upper limit of \(\sim 3~\hbox {TeV}\), they are subject to large astrophysical uncertainties, and only the FCC-hh can directly access the entire preferred mass range, providing the only robust discovery opportunity for this well-motivated DM candidate. In this high-mass range, the charged and neutral Wino are degenerate, up to a small and calculable mass splitting induced by electromagnetic effects. This selects \(\chi ^\pm \rightarrow \uppi ^\pm \chi ^0\) as the only allowed decay, with a very soft charged pion, prone to escape detection, and a long lifetime, due to the limited decay phase space. The signature is therefore a heavy charged track, seemingly disappearing in the detector [340]. Thus combining the high CM energy of FCC-hh with dedicated search strategies allows this classic WIMP paradigm to be conclusively explored.
The collider reach shown in Fig. 12.1 was the result of an early study, however, in the next section it is shown that, even with pile-up included, the reach for FCC-hh extends beyond the estimate shown in Fig. 12.1.
24.2.1 The search for disappearing tracks at FCC-hh and FCC-eh
Long-lifetime particles arise in a multitude of BSM models, not necessarily related to DM, and their exhaustive coverage may require dedicated detectors [340]. The case of heavy DM Winos, on the other hand, can be addressed by the baseline FCC-hh detector. A thorough analysis of the disappearing track signal has been performed in the context of the FCC-hh detector performance study, as discussed in Refs. [341, 342]. The findings are summarised here, but reference should be made to that technical note for all details.
Expected discovery significance at \(30~\hbox {ab}{}^{-1}\) with 500 pile-up collisions. The black (red) band shows the significance using the default and alternative tracker layouts described in the text and in Refs. [341, 342]. The band width represents the difference between the two models of the soft QCD processes
The analysis considers both cases of a Wino and of a Higgsino, namely an \(\hbox {SU}(2)_W\) doublet, whose upper mass limit as thermal DM candidate reaches \(\sim 1~\hbox {TeV}\). The charged/neutral mass splittings are 160 and 355 MeV for Wino and Higgsino, respectively. This leads to lifetimes of 0.2 and 0.023 ns (60 and 7 mm) for a 3 TeV Wino and a 1 TeV Higgsino. The disappearing-track signature relies on the detection of a short track, defined by a set of hits in the innermost tracking layers. The generation of the signals used concrete supersymmetric models, processed through a dedicated simulation of the FCC-hh tracker, in presence of up to 500 pile-up events as benchmarks. Various models for the final-state structure of these pile-up events have been considered, assuming both the expected mixture of inelastic and diffractive final states, and a purely inelastic final state, leading in this case to an overestimate of the final-state multiplicities and of the tracker occupancy, and thus a conservative estimate of the rate of fake disappearing tracks. Additional physics backgrounds, such as W+jets and tŧ, are included, considering the possibility of interactions of the W-decay leptons with the detector material, which could strongly deflect them and lead to an apparent disappearing-track signature. To enhance the signal over backgrounds, events are selected to have a disappearing track with \(p_T>100\,\hbox {GeV}\), a jet with large \(p_T\), and large \(E\!\!\!\!/_T\), with optimal thresholds chosen for each particle (wino or higgsino) and tracker configuration. The final sensitivities are shown in Fig. 12.2, in the case of PU = 500. The default (alternative) tracker configuration has a 5th layer at the radius of 270 (150) mm from the beam. The disappearing track signature is reconstructed from hits in the first 5 layers for both tracker configurations. The alternative configuration is clearly more powerful, and allows a 4–6\(\sigma \) sensitivity to be reached for the most difficult 1 TeV Higgsino case (the range reflects the choice of model for the final-state description of pile-up events). The \(5\sigma \) sensitivity for Winos extends up to over 4 TeV. The introduction of 50ps hit-timing information from the pixel layers increases these sensitivities by several \(\sigma \hbox {s}\) [341, 342]. This study underscores the potential of FCC-hh to discover thermal DM WIMPS in the relevant mass range, and provides an important input to the specification of the tracking detector layout.
Projected regions in the Higgsino parameter space where more than the indicated number of one (top) or two (bottom) LLPs are observed at the FCC-eh with a 60 GeV electron beam. Light shading indicates the uncertainty in the predicted number of events due to different hadronisation and LLP reconstruction assumptions. The green region represents the \(2\sigma \) sensitivity estimate in the presence of \(\uptau \) backgrounds. The black curves are projected bounds from disappearing track searches, for the HL-LHC (optimistic and pessimistic). Figure and analysis details are found in [334]
Wino and higgsino DM can be produced via vector-boson-fusion at FCC-eh. In this clean detector environment the soft decays and disappearing tracks can be fully reconstructed, requiring a different strategy than at a hadron collider. In Fig. 12.3 shows the parameter space which can be covered from non-prompt long-lived particle searches at FCC-eh. Thanks to the very low level of pile-up expected in ep collisions, the background is low, compensating for the lower production rate and making the FCC-eh facility an excellent place to study long-lived particles such as Higgsinos. These searches cover masses up to \(\sim 400~\hbox {GeV}\) and mass splittings from the splitting of the minimal Higgsino model up to larger values.
Note that although indirect detection constraints are strong for Winos and Higgsinos with low masses, they may still form some subcomponent of dark matter and thus the full mass range accessible to colliders is of scientific interest, even for masses below the value which reproduces the entire observed abundance.
24.3 Simplified models: an example
Since the initial proposal, a vast theoretical zoo of WIMP DM candidates has been proposed, and the original interpretation has been broadened to include additional ‘mediator’ particles, beyond the EW gauge bosons, which facilitate the annihilation of DM particles into SM particles. To capture the broad collider features of many specific DM models so-called ‘Simplified Models’ have been developed. These models contain only the DM particle and a single mediator and take a variety of forms.
One commonly considered example that considered here contains neutral fermionic DM and a vector mediator, with interactions of the form
For such a model one can produce the DM particles, in association with a jet, through the vector mediator \(\overline{\mathrm{q}} \mathrm{q} \rightarrow g \mathrm{Z}' \rightarrow g \overline{\chi } \chi \). This gives rise to a characteristic ‘missing energy’ signature, since the gluon, observed as a jet, recoils against the invisible DM particles. One may also search for this class of models by searching for the new mediator itself, through resonant decays back into quarks \(\overline{\mathrm{q}} \mathrm{q} \rightarrow \mathrm{Z}' \rightarrow \overline{\mathrm{q}} \mathrm{q}\). The relative strength of discovery opportunity between these two channels depends on the choices of coupling strengths in the models. Since the \(\hbox {Z}^\prime \) mediator exchange also dominates the annihilation of the DM particles into SM particles one may, for a given choice of couplings, calculate the predicted DM abundance and compare the preferred parameter ranges for a successful DM candidate with the collider searches.
Left: Expected sensitivity of monojet (green) and dijet resonance (blue) searches at the 100 TeV collider (dashed lines) compared to the expected sensitivity of the LHC at 14 TeV (dotted lines) and the parameter values that reproduce the observed relic abundance (red, solid). The grey regions are excluded by perturbative unitarity (cf. [343]). Right: Expected sensitivity at a 100 TeV collider (dashed) and LHC14 (dotted) for thermal WIMPs in the \(g_\mathrm{q}\hbox {-}g_{\mathrm{DM}}\) parameter plane, when setting \(m_{\mathrm{med}}\) to the largest value compatible with the observed relic abundance (as indicated by the black dashed lines). The DM mass, \(m_{\mathrm{DM}}\), is fixed as 0.45 \(m_{\mathrm{med}}\). Figures and analysis details may be found in [279]
Note that this model has only four free parameters: the DM mass \(m_{\mathrm{DM}}\), the mediator mass \(m_{\mathrm{med}}\), the mediator coupling to quarks \(g_\mathrm{q}\), and the mediator coupling to DM \(g_{\mathrm{DM}}\). For illustration, in the left panel of Fig. 12.4, \(g_\mathrm{q}\) and \(g_{\mathrm{DM}}\) are set to specific values and the two mass parameters are varied. Monojet and mediator resonance searches are shown in green and blue respectively. The preferred parameter space which generates the observed relic abundance is shown in red. One can see from this figure that with FCC-hh the entire preferred mass range can be covered.
To illustrate this reach in a different parameter plane in the right panel of Fig. 12.4, \(g_\mathrm{q}\) and \(g_{\mathrm{DM}}\) are now varied independently and the choice \(m_{\mathrm{DM}} = 0.45 m_{\mathrm{med}}\) is made. Finally, \(m_{\mathrm{med}}\) is set to the values which reproduces the observed relic abundance. One can see that for these choices, over the full range of coupling values the FCC-hh searches can access the parameter ranges which generate the observed relic abundance.
In summary, it can be seen that with the FCC-hh one can discover the heavy mediator states responsible for connecting the DM to the visible sector and, for this simplified model, cover essentially all of the parameter space of relevance.
24.4 Exploring the dark sector
There are additional classes of DM models which do not involve EW-charged particles, but which are still relevant for DM searches at hadron colliders. These are mainly theoretical models where the DM may be in thermal equilibrium with the SM at some point, due to interactions between the dark sector and the SM, but the relic abundance is not determined by the usual freeze out mechanism. Popular examples include models of asymmetric DM (ADM), where the relic abundance is determined by an asymmetry in DM versus anti-DM in the early universe [344, 345], possibly related to the baryon asymmetry of the universe, and models where the DM annihilates to an additional (lighter) state in the dark sector first, which later decay to SM particles:
Necessary ingredients include an interaction to bring the dark sector into thermal equilibrium with the SM at early times, and a way to transfer entropy from the dark sector back to the visible sector after the relic abundance is set. For the ADM scenario this means that the symmetric abundance has to annihilate efficiently, either to SM particles as in the WIMP scenario (but with a cross section somewhat larger than in the WIMP case), or alternatively into lighter, unstable particles of the dark sector.
The entropy transfer must happen before the onset of big bang nucleosynthesis (BBN) at temperatures around \(10~\text {MeV}\). This puts an upper bound on the lifetime of the unstable dark sector particle of \(\tau _a \ll 1~\hbox {s}\). From the collider perspective this means that the new dark sector particles can either decay promptly, with a displaced vertex, or could be collider stable, and all three regimes need to be probed to conclusively explore these non-WIMP scenarios. This motivates the search for further unstable dark sector states which may be light and very weakly coupled to SM states. Although they may themselves not form the dark matter, such dark sector states are strongly motivated.
One popular class of dark sector particles are ‘Axion-like particles’ (ALPs). The reason such particles are commonly studied is that their interactions enjoy an approximate symmetry which enables them to be naturally light. This approximate symmetry also significantly constrains the possible form of the interactions between the ALP and SM particles, which are typically very weak. Thus not only are these particles worthy of study because they may be naturally light, but they may also couple weakly to the SM.
Due to gauge invariance, if the ALP couples to the \(\text {U}(1)_Y\) or \(\text {SU}(2)_W\) gauge fields it will inherit a coupling to both \(\upgamma \upgamma \) and \(\upgamma \hbox {Z}\). At FCC-ee and FCC-hh an enormous number of Z bosons will be produced, far exceeding the statistics obtained at LEP or the LHC. Thus at FCC one can access parameter space that has not yet been explored by searching for the process \(\mathrm{Z}\rightarrow \hbox {a}\upgamma \), \(\mathrm{a}\rightarrow \upgamma \upgamma \).
Figure 12.5 shows the estimated reach for ALPs coupled to \(\text {U}(1)_Y\) or \(\text {SU}(2)_W\) topological terms at the FCC as compared to the HL-LHC. This reach should also be compared with the previous reach at LEP and with beam dump and astrophysical constraints at lower masses. Significant effort has been expended in the pursuit of new light and very weakly coupled force carriers at the so-called intensity frontier. Intensity frontier reach is limited by the CM energy available within a given process, hence the intensity frontier exploration of the dark sector has thus far been limited to beam dump energies. It is clear from Fig. 12.5 that FCC-ee and FCC-hh open unexplored territory in the intensity frontier, probing the dark sector at interaction strengths that are typically considered the realm of the intensity frontier, as can be seen from the comparison with beam dump limits, but extending the reach by two orders of magnitude in mass reach and to even weaker couplings than can be accessed with beam dump experiments.
Parameter regions which can be probed in the decay \(\hbox {Z}\rightarrow \upgamma \) a with \(\hbox {a}\rightarrow \upgamma \upgamma \) by the HL-LHC, FCC-ee, and FCC-hh. Figure adapted directly from [346]
24.5 Summary
Humankind is in the dark regarding the majority of matter in the universe and, while theoretical motivations may help pave the path to understanding DM, physicists are compelled to broaden the experimental hunt to any motivated masses or interaction strengths.
The FCC-hh would essentially provide a comprehensive search for WIMP DM, covering some of the most challenging scenarios such as Wino DM. Accessing DM models, or more general dark sectors, that are even more weakly interacting will require high intensity and high precision. The FCC-ee facility would provide both, enabling the discovery of dark sector states that are too massive to be probed with conventional low energy colliders or beam dumps.
25 Searches for massive neutrinos
25.1 Introduction
If in the SM one considers only the renormalisable operators and does not introduce additional fermions, there is no operator that can generate neutrino masses. This is contrary to decades of experimental measurements, which indicate non-vanishing mass differences between neutrino flavours (see Ref. [64] for a recent review). Thus the SM must be extended in order to accommodate neutrino masses.
One possibility is to mimic the structure of the other SM fermions and introduce right-handed neutrinos, usually denoted by N. In this case one may generate a Dirac mass from a renormalisable coupling with the left-handed neutrinos, as for all other SM fermion masses. This interaction would take the form
When the Higgs boson obtains a vacuum expectation value \(\langle H \rangle = v\), the SM neutrinos obtain a Dirac mass
If Dirac neutrino masses arise in this way one would expect them to follow similar coupling patterns and mass ranges as the other SM fermions, which span the range \(511 \text { keV} \le m_f \le 174 \text { GeV}\). In fact, this is far from being the case, and measurements of neutrino mass measurements, combined with cosmological observations, indicate that neutrino masses are extremely small, \(m_{{\upnu }} \lesssim \text { eV}\). This suggests that, while the tiny neutrino masses may be simply due to a tiny Yukawa coupling, they may also have a very different origin.
Rather than extending the particle content of the SM, one may consider the SM as an effective theory. In this case one should also consider non-renormalisable interactions, suppressed by the effective scale at which the theory is ‘UV-completed’ into a different microscopic theory. In this case, the interactions are ordered by their relevance in scattering experiments. The most relevant interactions are the renormalisable interactions of the SM with mass dimension four. The next most important interactions arise at mass dimension 5, and so on. It turns out that the only dimension-5 operator in the SM is the so-called Weinberg operator [347]
This operator is particularly special as, when the Higgs boson obtains a vacuum expectation value, the SM neutrinos obtain a Majorana mass
In this way the microscopic origin of neutrino masses would be fundamentally different from the other SM fermions, providing a qualitative explanation to the significant difference in mass scales between the charged fermions and the neutrinos. Quantitatively, the Majorana neutrino masses are of the form
There is a large number of possible microscopic ‘UV-completions’ that give rise to this Weinberg operator, and to the same low-energy effects.
25.2 Searches at FCC
To determine the fundamental origin of neutrino masses will require experimental answers to two questions:
-
are neutrino masses of Dirac type, with their origin in an interaction of the form Eq. (13.1), or are they of Majorana type, with their origin in an interaction of the form Eq. (13.3)? These two interactions have a different symmetry structure, the former preserving a global symmetry, known as lepton-number \(\text {U}(1)_L\), and the latter explicitly breaking this symmetry. These differences lead to experimentally observable effects at low energies, with the classic example being the neutrinoless double \(\beta \)-decay, which is searched for in laboratory experiments.
-
If neutrino masses are Majorana, then what is the microscopic origin of the interaction Eq. (13.3)? If the microscopic theory contains \(\lambda \sim \mathcal {O}(1)\) couplings, then to obtain the desired Majorana neutrino masses the typical mass scales in the microscopic theory must be very large indeed, \(M\sim 10^{14}\,\hbox {GeV}\), and there is little hope of probing these states at colliders. However, if the microscopic theory gives rise to small couplings \(\lambda \ll \mathcal {O}(1)\), then it may be that \(M\ll 10^{14}\,\hbox {GeV}\), and the new microscopic states may be within reach at colliders.
The first experimental question lies outside of the scope of future colliders, however the latter question falls within the purview of high energy experiments and thus there is focus on it.
Sensitivities of the different signatures to the active-sterile mixing and masses of sterile neutrinos at the FCC-ee. For details on the signatures see Ref. [348]
Summary of heavy sterile neutrino search prospects at all FCC facilities. Solid lines are shown for direct searches and the dashed line denotes an indirect constraint. These limits are taken from Ref. [348] where further details of the signatures and searches are provided
The simplest scenario that gives rise to Eq. (13.3) is known as the see-saw model [349,350,351,352]. In this model one adds an additional right-handed neutrino to the SM, as in Eq. (13.1), but the right-handed neutrino has also a Majorana mass, which arises at a high mass scale where \(\text {U}(1)_L\) breaking effects are important. Thus the full set of interactions is
By directly diagonalising the mass matrix, or by integrating out N, one finds that the Majorana neutrino mass of Eq. (13.4) is generated. Furthermore, the mixing angle between left and right handed neutrinos is \(\Theta \sim \lambda v/2 M\). The mass may thus be correlated with the mixing angle as
For right-handed neutrinos near the weak scale, the mixing angle is thus very small, leading to very challenging detection prospects. Going beyond this simplest model, however, there are scenarios, known as ‘Symmetry Protected’ models (see e.g. [206, 353,354,355,356,357]), in which the mixing angle may be significantly enhanced while still generating small neutrino masses. In these models one extends the field content further, to include neutral Dirac neutrinos, such that the action is of the form
These interactions respect a conserved \(\text {U}(1)_L\) symmetry and the left-handed SM neutrino may now have a large mixing with the new sterile neutrinos, even though the model still predicts an exactly massless neutrino. Additional terms that break the \(\text {U}(1)_L\) symmetry can then generate the very light neutrino mass. In this way the mixing angle becomes uncorrelated with the prediction for the light neutrino masses. The former can be large, while the latter is controlled by small \(\text {U}(1)_L\)-breaking terms. This setup significantly enhances detection prospects, since now for sterile neutrino masses in the mass range accessible to colliders one may have large mixing angles that enable the additional pseudo-Dirac sterile neutrinos to be produced and detected.
In this class of models, there are a variety of different search strategies to pursue. The search prospects at FCC-ee are summarised in Fig. 13.1. Typically the heavy neutrino may be produced via electroweak processes, and then decay to final states involving leptons. Sensitivity to heavy neutrinos is significantly enhanced below the Z boson mass threshold, since in this case an on-shell Z-boson may decay to a SM neutrino and a heavy neutrino, giving spectacular signatures that can include displaced leptons. In the clean detector environment of the FCC-ee these signatures would be clearly visible. Above the Z-boson mass direct sensitivity is also achieved through W and Higgs boson decays. Mixing between sterile and SM neutrinos also leads to modifications of low energy electroweak processes involving neutrinos, such as, for example, muon decays. This leads to strong indirect constraints due to the impact on the complete electroweak precision measurement fit to the SM. These indirect constraints are also shown in Fig. 13.1.
The direct production of larger sterile neutrino masses requires higher energies. At FCC-eh the dominant production mechanism is via t-channel exchange of a W-boson, where the electron is converted to a sterile neutrino. The clean environment then enables significant direct discovery prospects, exceeding the indirect precision electroweak constraints, up to masses of \(\sim \,\hbox {TeV}\). The full suite of FCC sterile neutrino search prospects is summarised in Fig. 13.2.
25.3 Summary
Neutrino mass physics at the FCC takes a special rôle in the global picture of neutrino physics; the origin of neutrino masses can only be tested at colliders when its mass is in the range around the electroweak scale. In particular the FCC-ee can test the type-I seesaw predicted heavy neutrinos when the latter have masses around a few tens of GeV. In the ‘Symmetry protected’ models, this type-I seesaw prediction for the mixing can be interpreted as a lower limit, which makes an actual test of the seesaw mechanism in this mass range possible. It is remarkable that this is a range of mass and mixing in which the generation of the Universe’s baryon asymmetry via leptogenesis is possible [358]. The parameter space of these models that is tested by the FCC-ee is complementary with respect to tests via beam dump experiments such as SHiP. There is also complementarity with respect to low energy measurements of rare processes, such as \(\upmu \rightarrow \hbox {e}\upgamma \), which will continue to create important synergies.
Tests of heavy neutrinos with masses of several 100 GeV at the FCC-eh are the most promising search strategy that can also provide the heavy neutrino mass. The indirect test of heavy neutrinos via precision measurements of the electroweak observables allows tests of heavy neutrinos up to \(\sim 100~\hbox {TeV}\), albeit it is insensitive to their mass scale. There is no other experiment being discussed at present with such a reach with respect to the heavy neutrino mass scale that does not rely on it violating the lepton number or flavour.
From a more general BSM point of view, the heavy neutrinos provide an interesting connection to Dark Matter, Baryogenesis via Leptogenesis, and feebly interaction dark sectors, also referred to as ‘Neutrino Portal’. In most models of this kind, the search prospects at the FCC improve with respect to the case of the ‘Symmetry protected’ models, for instance due to the presence of additional production processes. Heavy neutrino models are also naturally connected to the Higgs sector and can provide additional production and decay processes, that would yield a rich field of study for the FCC.
26 High energy probes of flavour anomalies
26.1 Introduction
Precision flavour physics provides some of the most sensitive indirect probes of new high-mass phenomena, via measurements that can receive contributions from higher-dimension operators. Possible deviations from the SM expectations can then be tested at the FCC-hh, whose 100 TeV centre of mass energy could be sufficiently large to directly produce and study the particles and interactions responsible for such anomalies.
As an example, this chapter describes studies of the anomalies that have recently appeared in neutral current B meson decays [200, 359]. Other anomalies have also emerged in the charged current B meson decays, though we focus on the neutral current case since the scale of new physics underlying those anomalies could potentially be much higher. These may yet be due to a statistical fluctuation or to subtle systematics, but today they illustrate well how new physics could lie around the corner. They are therefore used as a case study to investigate the overlap in sensitivity between FCC-hh and flavour observables, to demonstrate the complementarity between the two approaches.
Consider the flavour-changing neutral current (FCNC) transition, \(\hbox {b}\rightarrow \hbox {s}\upmu ^+\upmu ^-\), which is loop-induced in the SM. Below the weak boson mass scale the process is parameterised by four-fermion operators,
where \(X, Y = \{ L, R \}\). A loop factor suppresses the SM value of the operator’s coefficient. This makes it especially sensitive to any additional contribution. In particular, new physics may mediate this interaction at tree level, as shown in Fig. 14.1. The two possibilities are classified as either a \(\hbox {Z}^{\prime }\), or as a leptoquark, where the \(\hbox {Z}^{\prime }\) is a vector boson that acts like a heavier, flavour-violating version of the Z, and the leptoquark can be either scalar or vector and is defined as mediating a coupling between a lepton and a quark. Of course, more possibilities exist at loop level. But since the scale of new physics would be lower (for an effect of the same size) the focus is on the sensitivity to tree-level mediators.
Through these effective operators the \(\hbox {Z}^{\prime }\) and leptoquark mediators are indirectly probed in the decays \(\hbox {B}\rightarrow \hbox {K}^{(*)}\upmu ^+\upmu ^-\). Their rates and distributions are sensitive to the chiralities of the fields in the operators. For simplicity, \(\mathcal {O}_{LL}\), which also happens to best fit the current anomalies [360,361,362,363,364,365,366], is chosen. These deviations in angular observables and the \(R_{\mathrm{K}^{(*)}}\) ratios indicate a violation of lepton flavour universality. In this normalisation, the operator coefficient in the Lagrangian can be written as
The anomalies favour a non-zero value (relative to the SM) of \(\bar{c}_{LL} \simeq -\,1.33\) [366]. As discussed previously, this is taken to be a representative scenario for motivating the study without attaching any particular significance to the anomalies themselves. In the absence of any deviation, this value would be the typical sensitivity at the edge of being excluded by current experiments.
The size of the coefficient depends quadratically on the couplings and inversely on the mass squared of the mediator. For a given size, there is a degeneracy between the two: the stronger the coupling, the heavier the mass scale. However, theoretical considerations impose upper limits on the couplings. For example, with \(|\bar{c}_{LL}| \simeq 1.33\), perturbative unitarity sets a bound of \(\Lambda \lesssim \mathcal {O}(100)\) TeV and partial wave unitarity requires the scale of new physics to be less than 80 TeV [367]. There are also model-dependent experimental limits. It will be seen that these can restrict the scale of UV completions even more, potentially well within the reach of the FCC-hh [368, 369]. The coefficient, and others generated by additional model-dependent flavour structure, may also give rise to indirect effects in the tails of di-lepton distributions at high \(p_T\) that can be constrained at the LHC [369, 370].
26.2 Naive \(\hbox {Z}^\prime \) and leptoquark models
In the following, consider “naive” simplified models containing mainly the essential couplings required to generate the \(\mathcal {O}_{LL}\) operator. For the \(\hbox {Z}^{\prime }\), these are couplings to left-handed muon-muon and bottom-strange pairs; for leptoquarks, they will couple to left-handed bottom-muon and strange-muon pairs. Other couplings will most likely, and sometimes necessarily, be present. For leptoquarks, any additional couplings will be neglected in order to estimate the sensitivity in a conservative scenario. In the \(\hbox {Z}^{\prime }\) case, two simplified flavour models are chosen, as described below. Any additional couplings will typically make the mediators more easily discoverable, so sensitivity to these naive models implies sensitivity to more realistic models.
The couplings for the naive \(\hbox {Z}^{\prime }\) Lagrangian may be written as
Below the \(\hbox {Z}^{\prime }\) mass \(M_{\mathrm{Z}'}\), this contributes to the \(O_{LL}\) operator with a coefficient
\(\alpha _{\mathrm{EM}}\) is the electromagnetic fine structure constant, \(v \simeq 246\,\hbox {GeV}\) the electroweak scale, and \(V_{ij}\) the CKM matrix. The sensitivity to this naive model, with no additional couplings, was estimated in Ref. [368]. This is strictly more conservative than necessary, as it is impossible to avoid generating other couplings when going from the gauge to mass eigenstate. In Ref. [369], the “mixed-up” model (MUM) and “mixed-down” model (MDM) were defined by fixing the naive gauge-eigenstate couplings through rotations in either the up or down sectors respectively. The projected sensitivity to these simplified models is presented in the next section.
For the scalar leptoquark \(S_3\), with quantum numbers \((\bar{3}, 3, 1/3)\) under \(SU(3)_C \times SU(2)_L \times U(1)_Y\), a Yukawa term generates the operator coefficient
where \(y_{b\mu ,s\mu }\) is the Yukawa coupling and \(M_{\mathrm{LQ}}\) the leptoquark mass. Vector leptoquarks can similarly contribute to the \(\mathcal {O}_{LL}\) operator, though their couplings to gluons are more model-dependent than the scalar case. For \(\mathcal {O}(1)\) couplings their limits will typically be stronger than for scalar leptoquarks. The focus is therefore on the scalar case.
26.3 Projected sensitivity at FCC-hh
To project the leptoquark sensitivity at FCC-hh, current searches at the LHC are extrapolated using the method of Ref. [282]. It assumes the limit is determined by the number of background events. The same limit then applies for the corresponding mass with the same number of backgrounds at higher energy and luminosity. For more details of the analysis and results, refer to Ref. [368].
Projected 95% CL exclusion limit at FCC-hh for leptoquark pair production on the left and single production on the right. The solid and dashed lines are for 1 and 10 \(\hbox {ab}^{-1}\). The dotted lines are the signal cross-section computed at NLO on the left, and, on the right, LO for couplings \(y=1, 2, 12\) in red, black, and green, respectively
For leptoquark pair production, the 95% CL limits on the production cross section times branching ratio in the \(\upmu \upmu \,\hbox {jj}\) final state, as obtained by CMS at 8 TeV with \(19.6\,\hbox {fb}^{-1}\) of integrated luminosity, are extrapolated. The results are shown on the left plot of Fig. 14.2. The solid red line is for FCC-hh with \(1\,\hbox {ab}^{-1}\), and the dashed red line is for \(10\,\hbox {ab}^{-1}\). The dotted red line represents the pair production cross section, calculated at NLO using the code of Ref. [371] (see also Ref. [372]). It can be seen that FCC-hh can exclude leptoquarks with masses up to 10 and 12 TeV, thus improving by an order of magnitude the current limit of \(\sim 1~\hbox {TeV}\) at the LHC.
Single production of leptoquarks can extend the mass reach for large couplings, though in this case the sensitivity is more model-dependent. The direct search for a single leptoquark at CMS, with 8 TeV and \(19.6~\hbox {fb}^{-1}\), is extrapolated. The 95% CL limits plotted on the right in Fig. 14.2 are again denoted by solid and dashed red lines for 1 and \(10\,\hbox {ab}^{-1}\) of luminosity. Also plotted is the leading-order single production cross section for couplings \(y=1, 2,\) and 12 in dotted red, black, and green, respectively. This shows that for \(\mathcal {O}(1)\) couplings the projected sensitivity on the leptoquark mass extends to 15 TeV and higher, even reaching 21 TeV for \(y \sim 4\uppi \).
Turning to the \(\hbox {Z}^\prime \) projections: these are estimated using MC event generation with fast detector simulation, as described in Ref. [369]. The resulting 95% CL sensitivity is displayed in Fig. 14.3 for the MUM scenario on the left and the MDM on the right. The \(\hbox {Z}^\prime \) couplings are fixed to their anomaly-compatible values while varying \(g_{{\upmu \upmu }}\) and \(M_{\mathrm{Z}'}\), with strong constraints coming from the \(\hbox {B}_s\) mixing [373] (red region). The neutrino trident constraints in green are negligible. The blue dashed line is for a more recent, stronger \(\hbox {B}_s\) mixing constraint [374] (however, see Ref. [375]). The grey region shows the reach of the FCC-hh, and the dashed grey contours are the width of the \(\hbox {Z}^\prime \) relative to its mass. It can be seen that the FCC-hh can probe a sizeable region of the large width parameter space for the MUM, and covers the entire parameter space for the MDM. For comparison, the reach of the HE-LHC and of HL-LHC are represented by blue and red regions, respectively. The HL-LHC in particular, will not be sensitive at all to the MUM and can only probe a portion of the narrow width regime of the MDM parameter space.
95% CL sensitivity to MUM (left) and MDM (right) \(\hbox {Z}^\prime \) models in the anomaly-compatible parameter space varying \(g_{\mu \mu }\) and \(M_{\mathrm{Z}'}\). The grey shaded regions are the reach of the FCC-hh. The dashed grey contours give the \(\hbox {Z}^\prime \) width as a fraction of its mass. The red and green regions are excluded by \(\hbox {B}_s\) mixing and neutrino trident measurements, respectively. The blue dashed line is for the \(\hbox {B}_s\) mixing constraint of Ref. [374]. For comparison, the light blue and red regions show the reach of the HE-LHC and HL-LHC, respectively
26.4 Summary
The FCC-hh will be the ideal machine to directly probe new physics at higher energies. Indirect measurements from precision flavour physics can give important hints and limits on where (not) to expect such new physics. This complementarity between the global flavour programme and the FCC project is well illustrated here, where the sensitivity of FCC-hh to \(\hbox {Z}^{\prime }\) and leptoquarks that may be responsible for current anomalies in B meson decays were studied. The coverage of FCC-hh can reach masses above 10 TeV, an order of magnitude greater than current LHC bounds, allowing for the direct exploration of new physics scales that can otherwise only be accessed indirectly with low energy observables.
27 Searches for other BSM phenomena
27.1 Introduction
The history of particle physics has shown that, while open theoretical puzzles have in many cases successfully guided experimental progress, it is always possible that the complete microscopic story has not yet conceived. Thus exotic and unanticipated discoveries are always possible. Likewise, the exploration should be continued of scenarios in which basic underlying assumptions of the SM (and of most BSM models), like the elementary nature of quarks and leptons, are violated, as well as SM extensions that are not necessarily singled out by specific theoretical puzzles (e.g. generic extensions of the SM gauge group).
The FCC project is sensitive to many such possibilities beyond those discussed in the preceding sections. In this section the landscape of exotic BSM signatures that could be discovered by the FCC will be sketched, focusing first on low-mass signals, and turning then to the upper end of the mass reach. This summary is by no means complete, many more studies are discussed in the literature, and are documented for example in the 2016 FCC-hh BSM report [279].
27.2 Low-mass signatures
Collider events are characterised by the signals left in particle detectors, which depend e.g. on the types of particle and associated four-momenta at production, their multiplicity, their kinematic distributions, and the position of their origin. Exotic signatures can be discriminated from SM processes by virtue of some distinctive feature, such as high multiplicities, vertices macroscopically displaced from the initial interaction point, and so on. Some of these features can be particularly elusive, and their detection greatly benefits from the clean environment of \(\mathrm{e}^+\mathrm{e}^-\) collisions, as discussed in this section.
27.2.1 Exotic Higgs decays
Since there are numerous theoretical questions surrounding the nature of the Higgs boson, looking for exotic signatures associated with it is well motivated. For example, being the only neutral scalar boson in the SM, it could readily interact with new hidden sector particles and even decay into them if energetically possible. This property is known as the ‘Higgs portal’, which refers to the fact that of all the SM particles, only the Higgs may have a renormalisable, gauge invariant, interaction with other gauge-neutral scalar particles beyond the SM. If these particles are denoted as \(\phi \), then this interaction takes the form
Once produced, these states may then decay back into SM particles or other stable neutral particles in the hidden sector. From a collider perspective, this means that the Higgs boson could have rare exotic decays beyond those dictated by the SM alone. If there are N particles in the final state of an exotic Higgs decay then the typical energy of the final state particles will be \(E\sim M_H/N\). Thus already for \(N=4\) the final state particles will be soft and may hide under other SM backgrounds, or simply evade the trigger requirements. In some cases this can make the search for exotic Higgs decays particularly challenging. A selection of exotic Higgs decay topologies are shown in Fig. 15.1.
Despite the fact that more Higgs bosons will be produced at the HL-LHC than at the FCC-ee, in cases where event triggering at a hadron collider becomes challenging the clean detector environment of FCC-ee would deliver a discovery potential which is many orders of magnitude greater than at the LHC. A study of exotic Higgs decays at FCC-ee is presented in [376] and the results are summarised in Fig. 15.2. It is notable that in channels with missing energy the sensitivity to exotic Higgs boson decays is significantly greater at FCC-ee than HL-LHC, providing an unparalleled microscope with which to determine the nature of the Higgs boson and discover evidence of new hidden sector particles.
The 95% C.L. upper limit on selected Higgs exotic decay branching fractions at HL-LHC and \(\hbox {FCC-}ee\). This figure is taken from [376]
A notable feature of the Higgs portal interaction in Eq. 15.1 is that this interaction respects a \(\mathcal {Z}_2\) symmetry, \(\phi \rightarrow -\, \phi \). Such a symmetry can make \(\phi \) stable or, if it is explicitly broken by some small amount, \(\phi \) may be long-lived. This alone motivates searching for exotic decays of the Higgs boson to particles that decay on a macroscopic time scale. Such scenarios arise frequently in theories beyond the SM, such as models of neutral naturalness discussed in Sect. 9.4. Projections for sensitivity to such exotic Higgs decays are shown in Fig. 15.3 for a variety of collider scenarios, including the HL-LHC, FCC-hh, LHeC and FCC-eh. At hadron colliders two different triggering strategies are considered. One involves VBF-tagging and displaced vertices and the other only a single lepton and displaced vertices.
Projected exclusion limits on exotic Higgs decay branching fractions to LLPs X as a function of lifetime \(c \tau \) for the LHeC, FCC-eh (60) and FCC-eh (240). The excluded branching ratio scales linearly with luminosity under the assumption of no background. The LLP mass in the plot is 20 GeV. For comparison, an estimate for the sensitivity of proton colliders without background is shown (blue), as well as a very optimistic estimate which assumes extremely short-lived LLP reconstruction (orange), from [377]. This plot is taken from [334]
It is notable that at FCC-hh one can access exotic Higgs decays down to branching ratios smaller than \(10^{-6}\), demonstrating extreme sensitivity to very exotic Higgs decays. Furthermore, due to the cleaner detection environment, the FCC-eh projections can push to shorter lifetimes than are accessible at FCC-hh.
27.2.2 Exotic Z decays
Since it is also neutral under the unbroken gauge symmetries of the SM, similar considerations apply to the Z-boson. As it is lighter than the Higgs, exotic Z-boson decays lead to even softer final states which may hide under SM backgrounds at the LHC. Thus, once again, the clean detector environment of FCC-ee comes to the fore in the search for light hidden sector states coupled to the Z-boson.
The 95% C.L. sensitivity reach for various exotic Z decay branching ratios at the future Z-factory, where the Tera Z benchmark corresponds to the FCC-ee Z-pole run. This figure is taken from [378], where further details on the various decay topologies considered, including any model-dependence, are presented
In Fig. 15.4 the experimental sensitivity to various exotic Z-boson decays is shown at FCC-ee (Tera Z) as compared to the HL-LHC. As with exotic Higgs decays, in various cases the discovery reach is extended by many orders of magnitude thanks to the large statistics and low backgrounds.
As an example, for Z-boson decays to missing energy and a pair of photons the branching ratio sensitivity approaches \(\text {BR}\sim 10^{-10}\). For weak-scale particles this corresponds to an extremely weak coupling, once again demonstrating that the FCC project extends the intensity frontier of fundamental physics to the electroweak scale.
27.3 High-energy signatures
The former examples concern exotic signatures at low energies, where a clean detector environment and low trigger thresholds are crucial to the exploration of light and weakly-coupled hidden sectors. If one is agnostic as to the theoretical puzzles surrounding the SM then, by their nature, unexpected discoveries may lie at any mass scale. Through the production and decay of SM states, such as the Higgs or Z boson, the FCC-ee collider delivers extreme sensitivity to weakly coupled light states. The LHC has shown that it has sensitivity in low-mass/low-coupling regions previously inaccessible to hadron colliders; for example, by setting constraints on DM mediators in the 100 GeV mass region, increasing the trigger acceptance by exploiting final states where the new particles recoil against high-\(p_T\) jets or photons [379, 380]. These new search opportunities have only been explored, in the FCC studies so far, in the context of the measurement of the H\(\rightarrow \)invisible decays (see Sect. 4.3). More studies will certainly follow, and meanwhile the focus here is on the projections for more standard searches of high-mass resonances in pp [381] and ep collisions.
27.3.1 s-Channel resonances in pp
The search for heavy resonances in pp collisions can be organised in terms of the production process. Typically one considers annihilation of coloured partons in the gg, qg, qq or qq̄ channels, or VBF. The nature of the resonance, and the ultimate discovery reach, will depend on the production process, due to the different partonic luminosities. By and large, one expects that for all these channels the FCC-hh will extend the HL-LHC mass reach by factors of 5 or more, depending on the mass, and reflecting the increase of beam energy. This is shown in Fig. 15.5, where different lines show how, on a purely statistical basis and making basic assumptions on the scaling of backgrounds, a projected discovery or exclusion reach for the HL-LHC will evolve at the FCC-hh (or at the HE-LHC). While these results are qualitatively indicative, detailed studies of specific benchmark models have been carried out by the detector performance working group, to establish the discovery potential more firmly and to guide the choice of detector specifications. The measurement of objects with a mass of several tens of TeV will, in fact, pose new challenges relative to the LHC. For example, in this multi-TeV domain, hadronic decays of final-state top quarks or W/Z gauge bosons appear as collimated jets, and require enhanced calorimeter granularity to apply substructure discriminators tagging the object and reducing the potentially overwhelming QCD dijet backgrounds. The details of the studies, including the assumptions about detector performance, can be found in Ref. [383].
Left (right): the discovery/exclusion mass reach for resonance searches at FCC-hh (HE-LHC), as a function of the equivalent target for the HL-LHC [382]
The sensitivity to new \(\hbox {Z}^\prime \) gauge bosons decaying to leptons is shown in Fig. 15.6, for a set of extra-U(1) models considered in the literature [384, 385]. The right plot of this figure shows the luminosity required for a \(5\sigma \) discovery of a sequential-SM (SSM) \(\hbox {Z}^\prime \) (namely a gauge boson with couplings to the SM particles identical to those of the Z), as a function of its mass. The sensitivity to new massive vector resonances appearing in the context of composite Higgs models (see Sect. 9), and decaying to lepton pairs, was shown in Fig. 9.3. The direct search reach obtained there is consistent with the general results shown here, and extends to several 10’s TeV for \(\mathcal {O}(1)\) couplings.
Left (centre): Cross section times branching ratio 95% CL limits versus mass, for the \(\hbox {ee}+\upmu \upmu (\uptau \uptau )\) final states, compared to the expectations of several \(\hbox {Z}^\prime \) models. Right: luminosity required for the \(5\sigma \) discovery of a SSM \(\hbox {Z}^\prime \) in the dilepton channel, versus the hypothetical resonance mass
To explore the sensitivity to hadronic final states, three scenarios have been considered: a \(\hbox {Z}^\prime \) in \(\hbox {q}\bar{\hbox {q}} \rightarrow \hbox {Z}^\prime \rightarrow \hbox {t}\bar{\hbox {t}}\), a Randall–Sundrum graviton [386] in \(\hbox {gg/q}\bar{\hbox {q}} \rightarrow \hbox {G}_{\mathrm{RS}}\rightarrow \hbox {W}^+\hbox {W}^-\rightarrow \) jets, and an excited quark resonance [387, 388] in \(\hbox {qg}\rightarrow \hbox {Q}^*\rightarrow \hbox {dijet}\). The \(5\sigma \) discovery range reaches 18 TeV (24) for \(\hbox {Z}_{\mathrm{SSM}}'\rightarrow \hbox {t}\bar{\hbox {t}}\) (\(\hbox {Z}_{\mathrm{TC2}}'\)), 22 TeV for \(\hbox {G}_{\mathrm{RS}}\rightarrow \hbox {WW}\) and 40 TeV for the excited quark. The corresponding exclusion limits are shown in Fig. 15.7.
Sensitivity to various resonance models using fully hadronic final states. For left to right: excited quarks \(\hbox {Q}^*\) in the dijet channel; \(\hbox {Z}^\prime \) in the \(\hbox {t}\bar{\hbox {t}}\) hadronic channel (SSM and top-assisted technicolour [389], TC2, models); \(\hbox {G}_{\mathrm{RS}}\) in the WW fully hadronic channel. From Ref. [383]
27.3.2 FCC-hh: pair production
Looking beyond such resonances, heavy particles with SM gauge charges feature in many scenarios beyond the SM. Typically, the production cross section may be calculated for a given particle mass and gauge representation. As a hadron collider, the FCC-hh discovery reach for new coloured particles is extensive. As a simple example for illustration, the pair production cross section for colour octet particles of various spins at the LHC versus FCC-hh is shown in Fig. 15.8. At a given mass value the cross section at 100 TeV is orders of magnitude greater than at 14 TeV. Not only does this demonstrate a significant increase in the discovery potential at FCC-hh, but also implies that if a new particle were discovered in the HL-LHC runs, it would be possible to study this particle in significantly greater qualitative detail at FCC-hh.
27.3.3 FCC-eh: leptoquarks
Going to more exotic possibilities, leptoquark particles can arise in a number of BSM scenarios. In Sect. 14 leptoquarks models connected to current flavour anomalies were discussed. However, other leptoquark scenarios could also potentially exist at high energies. If a leptoquark interacts with the first generation then the FCC-eh provides a unique possibility to search for it, through e-p collisions. Figure 15.9 shows the reach for an example model in which \(\lambda _{\mathrm{LQ}}\) is the Yukawa coupling between a scalar leptoquark coupled to an electron and a down-quark. \(M_{\mathrm{LQ}}\) is the leptoquark mass. Even for relatively small Yukawa couplings, masses in the multi-TeV regime can be probed.
27.4 Summary
The preceding examples provide a small snapshot into the discovery capacity of the FCC programme for exotic BSM signatures. This discovery reach goes far beyond more familiar frameworks such as supersymmetry and extends from new resonances beyond the SM at high energies, down to extremely weakly coupled states at low masses below the weak scale. The landscape of new physics signals pursued at the LHC has evolved significantly since the beginning of operation. So, too, will the suite of discoverable new physics signatures possible at FCC, as theoretical and experimental ideas mature.
28 Physics with heavy ions
29 Physics with heavy ions
29.1 Introduction
The operation of the FCC-hh with heavy-ion beams is part of the accelerator design, as discussed in Sect. 2.4. For a centre-of-mass energy \(\sqrt{s}= 100~\hbox {TeV}\) for pp collisions, the relation \(\sqrt{s_{\mathrm{NN}}}= \sqrt{s} \sqrt{Z_1 Z_2 / A_1 A_2}\) gives the energy per nucleon–nucleon collision of \(\sqrt{s_{\mathrm{NN}}} = 39.4~\hbox {TeV}\) for PbPb (\(Z=82\), \(A=208\)) and 62.8 TeV for pPb collisions. The present estimate of the integrated luminosity per month of running is larger by factors 10–30 than the current projection for the future LHC runs [390]. The possibility of using nuclei smaller than Pb, like e.g. \(^{40}\hbox {Ar}\), \(^{84}\hbox {Kr}\) or \(^{129}\hbox {Xe}\), to achieve larger instantaneous luminosity is also under consideration.
The thermodynamic behaviour of QCD presents features which are unique among all other interactions. Their manifestations play a key role in fundamental aspects of the study of the universe, from cosmology to astrophysics, and high-energy collisions in the laboratory provide a unique opportunity to unveil their properties. The collective properties of the elementary quark and gluon fields of QCD can be investigated through collisions of heavy ions at ultrarelativistic energies, providing a unique test bed for the study of strongly-interacting matter and, in general, of the many-body properties of a non-Abelian quantum field theory (QFT). The increase in the centre-of-mass energy and integrated luminosity with respect to the LHC opens up novel opportunities for physics studies of the Quark-Gluon Plasma (QGP), as described in [28]. The main scientific motivation to carry out measurements with heavy ions at the FCC can be summarised as follows.
FCC provides novel access to QCD thermodynamics and QCD equilibration processes. Substantially increasing the centre-of-mass energy leads to the creation of initially denser and hotter strongly-interacting systems that expand for a longer duration and over a larger volume, thereby developing stronger collective phenomena. Extrapolations of LHC measurements indicate that both the initial energy density and the volume of the system increase by a factor of about two from \(\sqrt{s_{\mathrm{NN}}} = 5.5~\hbox {TeV}\) to 39 TeV, up to values of about \(40~\hbox {GeV/fm}^3\) (at \(\tau =1~\hbox {fm}/c\)) and \(11{,}000~\hbox {fm}^3\), respectively. The FCC collision energies reach a range of temperatures (\(T\sim 1~\hbox {GeV}\)) where charm quarks start to contribute as active thermal degrees of freedom in the QGP equation of state, thus playing a novel role in QCD equilibration processes. In addition, the large increase in the particle multiplicity and in integrated luminosity will allow for the systematic study of flow-like features in the pp and p–A collision systems and it will facilitate the characterisation of important signatures of collectivity on the level of single events rather than event samples only. This opens new opportunities for understanding the equilibration processes that lead to hydrodynamisation and thermalisation in QCD and, in general, in non-Abelian QFTs. These opportunities are discussed in Sect. 16.2.
FCC allows an unprecedented characterisation of dense QCD matter through hard-scattering processes. High-energy partons produced in heavy-ion collisions are known to undergo strong medium-induced modifications, often referred to as jet quenching. Jet quenching measurements provide quantitative information on the transport properties of hot and dense QCD matter. As detailed in Sect. 16.3, the FCC will provide a much larger abundance of hard-scattering processes than the LHC, as well as novel probes such as the top quark and, potentially, the Higgs boson [391,392,393,394]. A remarkable example is provided by high-momentum (thus, highly boosted) \(t \rightarrow \hbox {W} \rightarrow \hbox {q}\overline{\hbox {q}}\) decay chains, which are promising probes of the QGP time evolution and of the role of colour coherence [391]. The secondary production of charm quarks in scatterings between quark and gluon constituents of the hot QCD medium is expected to be as large as 80% of the initial production in partonic hard scatterings and it represents a novel observable sensitive to the medium temperature evolution [395, 396]. This secondary production of \(\hbox {c}\overline{\hbox {c}}\) pairs could lead, via the recombination mechanism, to an enhancement of the \(\hbox {J}/\uppsi \) yield in Pb–Pb compared to pp collisions, rather than the suppression that is observed at LHC energies. In addition, a first observation of \(\Upsilon \) formation from \(\hbox {b}\overline{\hbox {b}}\) recombination is expected.
FCC explores saturated parton densities in a previously-uncharted, ultra-dense kinematic domain. Partons densities at small x are expected to reach saturation of phase space in the initial-state of high energy heavy-ion collisions. This is a qualitatively-novel kinematic regime where the parton evolution is governed by non-linear evolution equations, and where a large fraction of parton scatterings take place at perturbative scales. As discussed in Sect. 16.4, the higher centre-of-mass energy of FCC allows one to explore a wide previously-uncharted kinematic range in the \((x,\,Q^2)\) plane, where saturation is expected to set in. Complementary proton–nucleus and electron–nucleus collision programmes at the FCC-hh/eh are both needed to fully explore this opportunity and also to determine the largely unconstrained nuclear partons densities. Proton–nucleus collisions have the advantage of a larger coverage at small x, e.g. down to \(x\sim 10^{-6}\) at a rapidity of \(|y|\approx 5\). On the other hand, electron–nucleus collisions provide a fully constrained kinematics (precise determination of x and \(Q^2\)).
29.2 QGP studies: bulk properties and soft observables
A central goal of a heavy-ion programme at a hadron collider is to explore how collective properties emerge from the fundamental fields of QCD and their non-Abelian interactions. So-called “soft observables”, that is particles at low transverse momentum, are important in this context since they are the experimentally accessible decay products of the medium that is formed during the collision, and since they provide the most direct signals of collective behaviour. The QGP phase in PbPb collisions at \(\sqrt{s_{\scriptscriptstyle {\mathrm{NN}}}} =39~\hbox {TeV}\) is expected to have larger volume, lifetime, energy density and temperature than PbPb collisions at LHC energy. Also, the enlarged spatio-temporal extension of the system created is expected to be accompanied by larger collective effects and the larger multiplicity per event increases the statistical precision with which statements about collectivity can be made.
29.2.1 Global characteristics of Pb–Pb collisions
Extrapolating measurements of charged particle multiplicity, transverse energy and femtoscopic correlations at lower energies, one can obtain estimates for the growth of global event characteristics from LHC to FCC. In particular, up to the top LHC energy, the growth of charged hadron event multiplicity per unit rapidity in PbPb collisions is consistent with a slowly-rising power-law: \(\mathrm{d}N_{\mathrm{ch}}/\mathrm{d}\eta \,(\eta =0) \propto (\sqrt{s_{\scriptscriptstyle {\mathrm{NN}}}})^{0.3}\). As shown in Table 16.1, this amounts to an increase of a factor \(\sim 1.8\) from LHC to FCC.
Left: space-time profile at freeze-out from hydrodynamical calculations for central PbPb collisions at \(\sqrt{s_{\scriptscriptstyle {\mathrm{NN}}}} =5.5~\hbox {TeV}\) and \(39~\hbox {TeV}\). Right: time evolution of the QGP temperature as estimated on the basis of the Bjorken relation and the Stefan–Boltzmann equation (see text for details)
Figure 16.1 (left) shows results for the freeze-out hypersurfaces of central PbPb collisions at different collision energies. This figure quantifies the expectation that the denser system created at higher collision energy has to expand to a larger volume and for a longer time before reaching the freeze-out temperature at which decoupling to hadrons sets in. The arrows overlaid with the freeze-out hypersurface in Fig. 16.1 (left) indicate the transverse flow of the fluid element at decoupling. This provides quantitative support for the qualitative expectation that in a larger and more long-lived system, collective effects can grow stronger. In general, the global event characteristics listed in Table 16.1 determine the spatio-temporal extent of the “cauldron” in which QCD matter evolved, and they constrain the thermodynamic conditions that apply after thermalisation. The transverse energy per unit rapidity \(\mathrm{d}E_\mathrm{T}/\mathrm{d}\eta \) (see Table 16.1) measured is of particular importance since it constrains the initial energy density. The energy density is expected to increase by a factor of two from LHC to FCC, reaching a value of \(35-40~\hbox {GeV/fm}^3\) at the time of \(1~\hbox {fm}/c\) [28]. The time-dependence of the QGP plasma temperature for Pb–Pb collisions at the LHC and at the FCC is plotted in Fig. 16.1 (right). The figure shows that while the increase at a given time is a modest 30% when going from LHC to FCC, the thermalisation time of the system is expected to be significantly smaller. One may reach initial temperatures as large as \(T_0\approx 800-1000~\hbox {MeV}\) at the time \(\mathcal {O}(0.02\, {\mathrm{fm}}/c)\) after which both nuclei traverse each other at FCC energies.
29.2.2 Collective phenomena from heavy-ion to pp collisions
One of the most important characteristics of flow-like phenomena in heavy-ion collisions is the study of the azimuthal dependence of particle production. For a single inclusive hadron spectrum, this can be done, for instance, by measuring the azimuthal harmonics \(v_n\) in a Fourier decomposition in the azimuthal angle \(\varphi \) with respect to the nucleus–nucleus reaction plane orientation. At FCC energies, the two-fold larger multiplicity in central PbPb collisions may open up the possibility to carry out flow measurements on an event-by-event basis and to become sensitive to dependencies of transport coefficients that are very difficult to address at the LHC. For example, the different azimuthal coefficients \(v_n\) are sensitive to the various possibilities for the temperature dependence of shear viscosity to entropy density ratio, \(\eta /s(T)\), and this sensitivity becomes stronger with increasing multiplicity and for higher harmonics. This is illustrated in the CERN Yellow Report [28] using the theoretical framework described in Ref. [397].
In recent years, surprisingly, small and dense systems probed in high multiplicity p–A and pp collisions were found to display flow-like phenomena. In particular, pAu, dAu and \(^3\hbox {HeAu}\) collisions at RHIC, as well as pPb and high-multiplicity pp collisions at the LHC have been shown to feature similar ridge-like structures, \(v_2\) anisotropy and, in some of the systems, including high-multiplicity pp collisions, even \(v_3\) anisotropy as seen in collisions between large nuclei [137, 398,399,400,401,402,403]. These findings raise fundamental questions about whether the flow-like patterns in small and dense systems are only similar in appearance to what one observes in heavy-ion collisions, or whether the idea of a minimal scale for the onset of collective phenomena needs to be revisited. As illustrated in the CERN Yellow Report [28], the high-multiplicity tail of event-distributions in proton–proton collisions at \(\sqrt{s} = 100~\text {TeV}\) will become accessible at the FCC-hh up to multiplicities of at least 100 charged particles per unit of pseudorapidity. This makes it feasible to apply statistically-demanding analysis techniques for the identification of flow-like phenomena, such as higher-order cumulant analyses, across system size, including the smallest pp collision system.
29.3 QGP studies: hard probes
29.3.1 Jet quenching
The modification of jet properties in heavy-ion collisions with respect to the proton–proton case, commonly referred to as jet quenching, results from the interaction of jet constituents with the QGP that they traverse. Over the last few years, as several jet properties were measured in heavy-ion collisions, the theoretical understanding of jet–QGP interactions has evolved from the early descriptions of single parton energy loss towards an overall understanding of how full jets are modified by the QGP. The increase in centre-of-mass energy, the abundance of probes, especially those involving electroweak bosons together with jets, and the qualitatively new processes available (e.g. boosted systems, see below) make of the FCC-hh the best-suited future machine for a deeper understanding of this physics.
29.3.2 Hard processes at FCC-hh energies
The large increase in energy and luminosity from the LHC to the FCC provides new tools to study the matter created in the collisions of heavy ions. In Fig. 16.2 (left), cross sections for different processes and different energies are computed with MCFM [404] at the highest available order. The increases amount to a factor \(\sim 6\) for beauty production, \(\sim 10\) for Z production, \(\sim 20\) for \(\hbox {Z}+\hbox {jet}\) and \(\sim 80\) for top production. The large yields in Z+jets (several tens of millions) will enable the study of the jet quenching process with excellent calibration of the jet energy. In principle, the measurement of the energy lost by the jet in Z+jet would provide a good experimental measurement of the distribution of the parton energy losses in hot QCD matter.
Left:\(\sqrt{s}\)-dependence of the cross sections for hard processes of interest for a heavy-ion programme, calculated with MCFM [404] at the highest available order. Right: Expected top-quark \(p_{\mathrm{T}} \) distribution in PbPb in the fully-leptonic decay modes at \(\sqrt{s_{\scriptscriptstyle {\mathrm{NN}}}} =39~\hbox {TeV}\) after acceptance and efficiency cuts with the statistical uncertainties for the baseline scenario \(L_{\mathrm{int}}=33~\hbox {nb}^{-1}\) (adapted from [392])
The motivations for measurements of top quarks in heavy-ion collisions at FCC are multifold. For example, in p–Pb collisions the cross sections efficiently probe the nuclear gluon PDFs in a wide range in momentum fraction x at high scale \(Q\sim m_\mathrm{t}\) [392] (see Sect. 16.4.1). In Pb–Pb collisions, the top-quark observables are sensitive to the energy-loss of heavy quarks [405] and by selecting boosted (very high-\(p_\mathrm{T}\)) top quarks one could also probe the QGP medium at later times as the decays of boosted top quarks become Lorentz time dilated (see next section). For example, the estimated measurable yields (using per-month luminosities from Sect. 2.3) with realistic analysis cuts and conservative 50% efficiency for b-jet tagging are 3.1 (baseline \(L_{\mathrm{int}}\)) – 10.3 (ultimate) \(\times 10^5\) in Pb–Pb collisions for \(\hbox {t}\overline{\hbox {t}}\rightarrow \hbox {b}\overline{\hbox {b}}\,\ell \ell \,\upnu \upnu \).
As mentioned above, the \(p_\mathrm{T}\) reach of top quarks in Pb–Pb collisions is of special importance for QGP studies. Figure 16.2 (right) shows the estimated \(p_\mathrm{T}\) spectrum of the yields (per year) in Pb–Pb collisions for top-quark pair production. The figure indicates that one could measure top quarks up to approximately \(p_\mathrm{T} \approx 1.8~{\mathrm{TeV}}/c\), even considering only one run in the baseline luminosity scenario. At mid-rapidity, \(p_\mathrm{T}\) as large as this would correspond approximately to a factor of 10 time dilation in the top decay (see next section).
Another potential novel probe of the QGP medium at FCC energies is the Higgs boson. The Higgs boson has a lifetime of \(\tau \approx 50~\hbox {fm}/c\), which is much larger than the time extent of the QGP phase. It has been argued that the Higgs boson interacts strongly with the quarks and gluons of the QGP and the interactions induce its decay in the gluon–gluon or quark–antiquark channels, thus depleting the branching ratio to the most common “observation” channels \(\upgamma \upgamma \) or \(\hbox {ZZ}^\star \) [394]. More recent detailed theoretical calculations, including virtual corrections, predict however no visible suppression of the scalar boson [406]. The cross section for Higgs boson production in Pb–Pb collisions is expected to increase by a factor larger than 20 when going from \(\sqrt{s_{\scriptscriptstyle {\mathrm{NN}}}} =5.5~\text {TeV}\) to \(\sqrt{s_{\scriptscriptstyle {\mathrm{NN}}}} =39~\text {TeV}\) [393]. The statistical significance of the Higgs boson observation in the \(\upgamma \upgamma \) decay channel in one Pb–Pb run at FCC-hh was estimated to be 5.5 (9.5) \(\sigma \) in the baseline (ultimate) luminosity scenarios [393].
29.3.3 Boosted tops and the space-time picture of the QGP
The FCC will provide large rates of highly-boosted heavy particles, such as tops, Z and W bosons. It is expected that when these particles decay the density profile of the QGP has already evolved. It has been argued that the hadronically-decaying W bosons in events with a \(\hbox {t}\bar{\hbox {t}}\) pair can provide unique insights into the time structure of the QGP [391]. This is because the time decays of the top and the W bosons are followed by a time-delay in the interaction of the decay products of the W boson with the surrounding medium due to a colour coherence effect. The sum of the three times, that reaches values of several \(\hbox {fm}/c\) for boosted tops, would be the time at which the interaction with the QGP begins, providing a unique way to directly measure the time structure of the QGP evolution. In addition, due to colour coherence effects, energy loss would be initially absent for the colour-singlet \(\hbox {q}\overline{\hbox {q}}\) decay products of a highly-boosted W boson: the two quarks would start to be quenched only when their distance becomes larger than the colour correlation length of the medium, which depends on the transport coefficient \(\hat{q}\) (the average transverse momentum squared that particles exchange with the medium per unit mean-free path) [407].
The effect on the reconstructed masses of the top and W is studied, for \(\hbox {t}\bar{\hbox {t}}\) events decaying semileptonically, with different energy loss scenarios as a proof of concept of the potential of these observables to access completely novel quantities in heavy-ion collisions. As shown in Fig. 16.3 (left), times in the range \(0.3-3~\hbox {fm}/c\) are obtained when adding the time delay from Lorentz boosts of the decaying top quark and W boson and the time in which a singlet antenna remains in a colour coherent state.
Left: Total delay time for \(\hat{q} = 4~\hbox {GeV}^2/\hbox {fm}\) as a function of the top transverse momentum (black dots) and its standard deviation (error bars). The average contribution of each component is shown as a coloured stack band. The dashed line corresponds to a \(\hat{q} = 1~\hbox {GeV}^2/\hbox {fm}\). Right: Reconstructed W boson mass at FCC energies \(\sqrt{s_{\scriptscriptstyle {\mathrm{NN}}}} = 30~\hbox {TeV}\), as a function of the top \(p_{\mathrm{T}} \). The upper axis refers to the average total time delay of the corresponding top \(p_{\mathrm{T}} \) bin
The reconstructed W jet mass as a function of top transverse momentum at \(\sqrt{s_{\scriptscriptstyle {\mathrm{NN}}}} = 39~\hbox {TeV}\) is shown in Fig. 16.3 (right). For details of the simulation and reconstruction procedure see [391]. The shaded region corresponds to the statistical uncertainty obtained with a bootstrap analysis considering central Pb–Pb collisions for \(L_{\mathrm{int}} = 30~\hbox {nb}^{-1}\) for the Pb–Pb energy loss scenarios and \(L_{\mathrm{int}} = 2~\hbox {fb}^{-1}\) for the pp reference. Energy loss was simulated considering that all particles, except the W boson decay products, lose \(15\%\) of their initial momentum. Average time delays \(\tau _m = 1; 2.5; 5\) and \(10~\hbox {fm}/c\) were considered as effective QGP time evolution profiles. Figure 16.3 (right) shows a clear separation between the totally quenched case and those in which the time-delay effectively reduces the interaction with the QGP and hence the quenching, especially for the highest boosts considered that will be accessible at the FCC. This large sensitivity will only be possible at the FCC and partially at the HE-LHC, while only marginally with the present LHC programme [391].
29.3.4 Heavy flavour and quarkonia
Heavy quarks (charm and bottom) are among the hard probes that have provided important insights on the formation and the characteristics of the QGP [408]. On one hand, quarkonium states are sensitive to the formation and to the temperature of a deconfined plasma via the mechanism of colour-charge screening, which is thought to be to some extent balanced by the recombination of heavy quarks and antiquarks from the plasma. On the other hand, the production of hadrons with open heavy flavour is sensitive to the QGP-induced modification of the momentum and direction of heavy quarks, thus providing insight on the interaction mechanisms of heavy quarks with the constituents of the QGP and on its transport properties.
Here the focus is on a few selected aspects that could represent novel or particularly remarkable observations at FCC energy, namely: (i) large production of thermal charm from interactions of light quarks and gluons within the QGP; (ii) observation of an enhancement of charmonium production with respect to the binary scaling of the yields in pp collisions, as consequence of (re)generation; (iii) observation of a colour screening and (re)generation for the most tightly-bound quarkonium state, the \(\Upsilon \)(1S).
29.3.5 Thermal charm production
Interactions between gluons or light quarks of the QGP can lead to the production of \(\hbox {c}\overline{\hbox {c}}\) pairs if the energy in the centre of mass of the interaction is of the order of twice the charm quark mass \(\sqrt{\hat{s}}\sim 2\,m_c\sim 3~\hbox {GeV}\). In Sect. 16.2.1 it was estimated that an initial temperature \(T_0\) larger than 800 MeV could be reached at FCC. In Ref. [396] a detailed hydrodynamical calculation gives \(T_0=580~\hbox {MeV}\) at initial time \(\tau _0=0.6~\hbox {fm}/c\) for LHC (\(\sqrt{s_{\scriptscriptstyle {\mathrm{NN}}}} =5.5~\text {TeV}\)) and \(T_0=840~\hbox {MeV}\) at \(\tau _0=0.3~\hbox {fm}/c\) for FCC. With these QGP temperatures a sizeable fraction of the gluons and light quarks have energies larger than the charm quark mass and \(\hbox {c}\overline{\hbox {c}}\) pairs can be produced in their interactions. This production is concentrated in the initial \(\sim 1~\hbox {fm}/c\) of the QGP evolution.
Figure 16.4 shows the predictions [395, 396] for the time-dependence of the \(\hbox {c}\overline{\hbox {c}}\) rapidity density at mid-rapidity in central Pb–Pb collisions at FCC. The value at the initial time \(\tau _0\) corresponds to the initial hard-scattering cross section. Both calculations show a rapid increase after \(\tau _0\) with a final value that is up to 80% larger than the initial production. The increase obtained for top LHC energy is of about 15%. The thermal charm production would result in an enhancement of charmed hadron production at very low \(p_\mathrm{T}\), with respect to the expectation from binary scaling of the production in pp collisions, after correction for the nuclear initial-state effects (PDF modification), that should be measured using proton–nucleus collisions. This enhancement provides a handle on the temperature of the QGP.
The abundance of charm quarks also has an effect on the QGP equation of the state: the inclusion of the charm quark in the lattice QCD calculations results in a sizeable increase of \(P/T^4 \propto n_{\mathrm{d.o.f.}}\) for \(T>400~\hbox {MeV}\), as discussed in the CERN Yellow Report [28].
29.3.6 Quarkonium suppression and (re)generation
The measurements of the nuclear modification factor of \(\hbox {J}/\uppsi \) at the LHC [409,410,411] are described by models that include dissociation caused by colour-charge screening and a contribution of recombination (usually denoted (re)generation) from deconfined c and \(\overline{\hbox {c}}\) quarks in the QGP [412,413,414]. The (re)generation contribution is expected to be proportional to the rapidity density of \(\hbox {c}\overline{\hbox {c}}\) pairs in the QGP. Therefore, it is predicted to be much larger at FCC than LHC energies, as a consequence of the larger hard-scattering production cross section of \(\hbox {c}\overline{\hbox {c}}\) pairs and the possible sizeable thermal production, discussed in the previous section. This could lead to the observation of an enhancement of \(\hbox {J}/\uppsi \) production with respect to binary scaling of the yield in pp collisions, i.e. \(R_{\mathrm{AA}}>1\), which would be a striking evidence of \(\hbox {c}\overline{\hbox {c}}\) recombination from a deconfined QGP. Figure 16.5 (left) shows the predicted \(\hbox {J}/\uppsi \) \(R_{\mathrm{AA}} \) at FCC energy, as obtained with the Statistical Hadronization Model [415]. The model predicts \(R_{\mathrm{AA}} (p_{\mathrm{T}}>0)>1\) in central collisions and an increase of about 40% with respect to top LHC energy.
The measurement of \(\Upsilon \) production would be particularly interesting at the high energies and temperatures reached at the FCC. The LHC data are consistent with a scenario in which the excited states 2S and 3S are partially or totally suppressed by colour screening, while the 1S, which is the most tightly bound state, has no or little direct melting. Its suppression by about 50% can be attributed to the lack of feed-down from the (melted) higher states (see e.g. Ref. [408] for a recent review). At FCC energies, on one hand, the temperature could be large enough to determine a full melting even of the tightly-bound 1S state, on the other hand the large abundance of \(\hbox {b}\overline{\hbox {b}}\) pairs in the QGP could induce substantial \(\Upsilon \) (re)generation. The possibly large effect of (re)generation of bottomonia from b and \(\overline{\hbox {b}}\) quarks is illustrated by the prediction of the Statistical Hadronisation Model [414, 416] for the \(R_{\mathrm{AA}} \) of \(\Upsilon \)(1S) as a function of centrality, shown in the right panel of Fig. 16.5. The predictions are calculated for values of \(d\sigma _{b\overline{b}}/dy\) in nucleon–nucleon collisions ranging from 73 to \(163~\upmu \hbox {b}\), as obtained at NLO [417], which result in 15–40 \(\hbox {b}\overline{\hbox {b}}\) pairs in central Pb–Pb collisions. The resulting \(\Upsilon \)(1S) \(R_{\mathrm{AA}} \) in central Pb–Pb collisions is predicted to range between 0.3 and 1.2. The role of the two effects – degree of survival of initial bottomonia and contribution of (re)generation – could be separated by means of precise measurements of the \(\hbox {b}\overline{\hbox {b}}\) cross section and of the B meson and \(\Upsilon R_{\mathrm{AA}} \) and elliptic flow \(v_2\) (the regenerated \(\Upsilon \) states could exhibit a \(v_2\) such that \(0<v_2^{\Upsilon }<v_2^{B}\)).
29.4 Nuclear PDF measurements and search for saturation
29.4.1 Studies in hadronic pA and AA collisions
29.4.2 Small-x PDFs, factorisation, saturation
Parton saturation [418, 419] is based on the idea that standard linear parton branching leads, at small values of momentum fraction x, to parton densities so high that non-linear dynamics (like gluon recombination) becomes important and parton densities are tamed to grow from power-like to logarithmically. Non-linear effects are expected to become important when the density of gluons per unit transverse area exceeds a certain limit, the saturation density. This regime of QCD is interesting in its own right, to study non-linear dynamics of gluon fields in a controlled environment, but it is also important as an initial state for collisions of nuclei in which a Quark-Gluon Plasma is formed.
In the framework of QCD collinear factorisation, Parton Distribution Functions of nucleons inside nuclei (nuclear PDFs) can be obtained in standard global fit analysis with the usual linear evolution equations. The differences with respect to free nucleon PDFs are parameterised in a nuclear modification factor \(R_i^\mathrm{A}(x,Q^2)\) with \(i=g,\,q_{\mathrm{valence}},\,q_{\mathrm{sea}}\) (see e.g. Ref. [420]). The description of present data with this approach is excellent and no sign of tension has been found yet. However, collinear factorisation is expected to break down when the gluon phase-space becomes saturated. In these conditions, the small-x partons in the nuclear wave function would act coherently, not independently as assumed with factorisation. The Colour Glass Condensate (CGC) is the non-perturbative, but weak coupling description of such a system, which relies on resummation of powers of parton density (see e.g. Ref. [421]). The onset of saturation is usually discussed in terms of the saturation momentum \(Q_\mathrm{S}^2\), defined as the scale at which the transverse area of the nucleus is completely saturated and gluons start to overlap. It can be shown that \(Q^2_\mathrm{S} \sim {A}^{1/3} \big (\sqrt{s_{\scriptscriptstyle {\mathrm{NN}}}} \big )^\lambda e^{\lambda y}\), with \(\lambda \approx 0.3\) [28]. Saturation affects the processes in the region \(Q^2\,\lesssim \, Q^2_\mathrm{S}\) therefore, the regime of high gluon density is best accessed at a high-\(\sqrt{s_{\scriptscriptstyle {\mathrm{NN}}}} \) hadron collider with measurements at low \(p_{\mathrm{T}} \) and forward rapidity, which probe small x and small \(Q^2\). At present, no conclusive evidence has been provided for the existence of parton saturation, although a number of observations are consistent with its expectations [28]. In order to firmly establish the existence of this new high-energy regime of QCD and clarify the validity of the different approaches to factorisation and evolution, new kinematic regions must be explored using higher collision energies in order to have a large lever arm in \(Q^2\) in a region that, while perturbative, lies inside the saturation domain. The FCC offers the energies and the possibility of combining proton and nuclear beams, as are required for a detailed understanding of the mechanism underlying saturation, see Fig. 16.6.
Regions of the \(x-Q^2\) plane covered with nuclear DIS and Drell–Yan data and with p–A and e–A collisions at RHIC, LHC, HE-LHC and FCC (left) and exclusive quarkonium photoproduction in \(\upgamma \)–A collisions (right). For p–A at the LHC and the FCC, thin lines correspond to different rapidities in the laboratory frame \(y_{\mathrm{lab}} = 0,1, 2, 3, 4, 5, 6\) from right to left, with the left edge defined by \(y_{\mathrm{lab}} = 6.6\). Values of \(Q^2_\mathrm{S}(x)\) for Pb are shown for illustration
There is a strong complementarity between the physics programmes at hadron colliders and at the proposed electron–hadron colliders (Electron-Ion Collider in the USA [422], Large Hadron Electron Collider LHeC [69] and FCC-eh). With a kinematic reach in the TeV scale in the c.m.s. (Fig. 16.6, left), the latter two projects are well-positioned to reach conclusive evidence for the existence of a new non-linear regime of QCD. They are clearly complementary to the FCC-hh, providing a precise knowledge of the partonic structure of nucleons and nuclei and of small-x dynamics.
29.4.3 Searching for saturation with forward-rapidity photons and di-jets in pA collisions
A full discussion of the observable sensitive to saturation at FCC-hh can be found in the CERN Yellow Report [28]. Here the focus is on two observables, both of which require measurements at a forward rapidity of \(y\approx 4\) or larger: single-inclusive spectra of photons and hadrons and azimuthal correlations of dijets.
Single-inclusive measurements of charged hadrons, and photons and jets are the simplest observables that probe the gluon density. The two latter are somewhat safer from a theoretical point of view, as they are to a large extent free from hadronisation effects. Photons are sensitive to the small-x gluons via the dominant quark–gluon Compton scattering, as well as hadrons through underlying gluon–gluon scattering that fragments into hadrons at moderate \(p_{\mathrm{T}} \) values. As shown in Fig. 16.6 (left), measurements at mid-rapidity and \(p_{\mathrm{T}} < 10 ~\text {GeV}/c \) at the FCC potentially cover the saturation region with \(Q\approx p_{\mathrm{T}} \) and x in the range \(10^{-5}\)–\(10^{-4}\), which is at much lower x and therefore larger gluon density than measurements at the LHC. Forward measurements, e.g. at \(y \approx 4\), would be even more interesting, as they cover \(x \approx 10^{-6}\). Figure 16.7 (left) shows the ratios of \(p_{\mathrm{T}} \)-differential cross sections of direct photons at rapidity 4 and 6 with respect to rapidity 2, calculated in the CGC framework [423, 424]: saturation is expected to lead to a strong suppression for \(p_{\mathrm{T}} <10~\text {GeV}/c\) (the high-\(p_{\mathrm{T}} \) suppression at \(\eta =6\) is an artifact of the calculation).
Forward dijets offer more potential to experimentally constrain the x region probed, in particular at low \(p_{\mathrm{T}}\). CGC models predict a characteristic suppression of the recoil jet, because (mini-)jets can be produced by scattering a parton off the colour field in the nucleus where the recoil momentum is carried by multiple gluons, unlike in a standard (semi-)hard 2-to-2 scattering where all the recoil momentum is carried by a single jet [423, 425]. First measurements of di-hadron correlations at forward rapidity at RHIC show hints of the predicted suppression of recoil yield. However, the measurements are close to the kinematic limit and other mechanisms have been proposed to explain the suppression. The FCC has a large potential for recoil measurements of hadrons, photons and jets, probing a broad range in x and \(Q^2\), while staying far away from the kinematic limit. Figure 16.7 shows the expected broadening of the \(\Delta \varphi \) distribution in pPb with respect to pp collisions (middle) for dijets at forward rapidity [426, 427], as well as the expected nuclear modification factor for dijets as a function of the transverse momentum of the leading jet \(p_{\mathrm{T,jet}}\), in the recoil region (right). A clear suppression is visible in the recoil region persisting to much larger \(p_{\mathrm{T,jet}}> 100~~\text {GeV}/c \) than at the LHC, where the suppression is small at \(p_{\mathrm{T,jet}}\approx 50~~\text {GeV}/c \). These calculations clearly show saturation effects up to high \(p_{\mathrm{T}}\), much larger than \(Q_\mathrm{S}\), as long as the dijet transverse momentum imbalance does not exceed a few times \(Q_\mathrm{S}\).
Left: ratio of direct photons at forward rapidities \(\eta =2, 4, 6\) obtained in the CGC formalism in pPb collisions [423, 424]. Middle: Forward dijet \(\Delta \varphi \) correlation in pPb compared to pp collisions at FCC [426]. Right: nuclear modification factor of back-to-back dijets at LHC and FCC energies
29.4.4 Constraining nuclear parton densities at large \(Q^2\)
Several final states allow the constraint of nPDFs at large \(Q^2\) at the FCC-hh [28]: W and Z bosons, dijets, top quarks. The focus here is on the latter case, because it is a unique opportunity offered by the FCC-hh’s increase of energy over the LHC, and it offers the possibility to access the nuclear PDF at the unprecedented large scale \(Q=m_{\mathrm{top}}\) [392, 393] in an experimentally and theoretically well-controlled fashion. To estimate the impact that the FCC would have on nuclear gluon densities, the computed top-pair cross sections in pp, pPb and PbPb with analysis cuts (see [28]) have been binned in the rapidity, \(y_\ell \), of the decay leptons of \(\hbox {t}\rightarrow \hbox {W}\rightarrow \ell \). Figure 16.8 (left) shows PbPb pseudodata for the expected nuclear modification factors of the decay leptons. The effects that these, and the pPb, pseudodata would have in the EPS09 [428] global fit of nuclear PDFs are quantified via the Hessian reweighting technique [429] and shown in the middle and right panels of the figure. The nPDF uncertainties are reduced by more than 50% over a large range of x.
Left: FCC pseudodata for the nuclear modification factor for top production in PbPb collisions. Middle and right: Original EPS09 gluon nuclear modification at \(Q=m_{\mathrm{top}}\) and estimated improvement obtained by reweighting using the PbPb (middle panel) and pPb (right panel). The figures are adapted from Ref. [392]
29.4.5 Exclusive photoproduction of heavy quarkonia
Charged particles accelerated at high energies generate electromagnetic fields that can be considered as quasireal \(\upgamma \) beams of very low virtuality \(Q^{2} < 1/R^{2}\) [430,431,432], where R is the radius of the charge, i.e., \(Q^2\approx 0.08~\hbox {GeV}^2\) for protons (\(R\approx 0.7~\hbox {fm}\)), and \(Q^2<4\cdot 10^{-3}~\hbox {GeV}^2\) for nuclei (\(R_\mathrm{A}\approx 1.2\,A^{1/3}~\hbox {fm}\)). Given that the photon flux scales with the square of the emitting charge (\(Z^2\)), the emission of quasireal photons from the Pb-ion is strongly enhanced compared to that from proton beams (although the latter feature large photon energies). The maximum centre-of-mass energies of photon-induced interactions in “ultraperipheral” collisions (UPCs) of proton [433] and lead (Pb) beams [434] – occurring at impact parameters larger than the sum of their radii – at the FCC are \(W_{\gamma \mathrm{p}}^{\mathrm{max}} =10~\hbox {TeV}\) and \(W_{\gamma A}^{\mathrm{max}} =7~\hbox {TeV}\).
Exclusive photoproduction of vector mesons in UPCs of protons or ions is depicted in Fig. 16.9 (left). Since the gluon couples directly to the c or b quarks and the cross section is proportional to the gluon density squared in such processes, they provide a very clean probe of the gluon density in the “target” hadron, with the large mass of quarkonia providing a hard scale for pQCD calculations. Their measured cross sections rise steeply with photon-hadron centre-of-mass energy \(W_{\gamma \mathrm{p}}\), following a power-law dependence \(W_{\gamma \mathrm{p}}^{\delta }\) with \(\delta =0.7\)–1.2 [435, 436], reflecting the steep rise in the gluon density in the hadrons at increasingly lower values of parton fractional momentum x (Fig. 16.9, right). At the FCC, \(\hbox {J}/\uppsi \) and \(\Upsilon \) photoproduction will reach photon-hadron c.m. energies as large as \(W_{\gamma \,p}\approx 10~\hbox {TeV}\), and thereby probe the gluon density in the proton and nucleus in an unexplored region down to \(x\approx M_{J/\psi ,\Upsilon }^2/W_{\gamma \mathrm{p}}^2\approx 10^{-7}\), at least two orders of magnitude below the range probed at the LHC (Fig. 16.6, right). The evolution of the cross section with energy is very sensitive to the underlying small-x dynamics as shown by the bands in Fig. 16.9 (right) showing different theoretical predictions based on LO and NLO pQCD calculations [437], colour dipole formalism [438], and gluon saturation approaches (CGC) [159].
Left: Diagram representing exclusive quarkonia photoproduction in UPCs. Right: Dependence of the exclusive \(\hbox {J}/\uppsi \) photoproduction cross section on the photon-hadron c.m. energy in the regions covered by HERA, LHC and future FCC studies [159]
29.4.6 Electron–nucleus collisions
The FCC-eh offers huge possibilities for studies of electron–nucleus collisions. With a centre-of-mass energy of 2.2 TeV per nucleon and an instantaneous luminosity of \(5.4 \times 10^{33}~\hbox {cm}^{-2}\hbox {s}^{-1}\) in ePb, see Sect. 2.4, it will enlarge the kinematic region in x and \(Q^2\) presently studied in DIS by four orders of magnitude towards smaller x and larger \(Q^2\). This is illustrated in Fig. 16.6 (left) where the region explored in ePb at the FCC-eh is shown [439] together with those accessible with the same colliding system at the LHeC and with pPb collisions at LHC and FCC-hh. The enlargement factor will be of roughly one order of magnitude With respect to the LHeC, see [440].
Such huge enhancement of the kinematic region to be explored implies completely new possibilities for the characterisation of the partonic structure of nuclei, at the level of both standard collinear parton densities and their transverse profile. These points will be developed in the following subsections. It will also provide large opportunities to discover and characterise a possible new non-linear regime of QCD driven by density, see Sect. 5.3.2. All these aspects, and others not mentioned here due to space limitations, will have a large impact on the understanding of heavy-ion collisions at high energies [441].
29.4.7 Determination of nuclear parton densities
Nuclear parton densities (nPDFs) are basically unknown at present for \(x<10^{-2}\), see e.g. [440, 442]. This is due to the restricted kinematic region explored by present experiments, see Fig. 16.6 (left), and the fact that from the \(\sim 1000\) points used in present extractions of nPDFs, only \(\sim 50\) are for a Pb nucleus, the others corresponding to 13 other nuclei. If neutrino DIS data are included, \(\sim 800\) data points on Pb are added but in a restricted region in \(x-Q^2\). These facts make a fit to a single nucleus impossible. On the other hand, eA collisions at the FCC-eh will allow the extraction of all PDFs for a single nucleus, by making use of both neutral and charge currents and of heavy flavour measurements [445]. Therefore, these studies will produce not only large improvements in the precision of nPDFs but also a brand new view of the partonic structure of a nucleus.
The possibilities at the EIC and the HL-LHC are discussed in [440] and here the results of the ultimate determination of the parton densities in a Pb nucleus at the FCC-eh are shown. The analysis [439] was done in the xFitter framework, and considers 150 (484) ePb data points for the FCC-eh (LHeC) (see Sect. 5.3.1) with standard HERAPDF2.0 parameterisation, tolerance and cuts. The results, illustrated in Fig. 16.10, show that a complete analysis for the Pb nucleus is possible and that the uncertainties will be largely diminished compared to the present situation. With the lack of knowledge about nPDFs producing large uncertainties in the interpretation and, above all, in the precise characterisation of the properties of the medium produced in high-energy heavy-ion collisions it is expected that this result will have large implications on nucleus-nucleus collisions.
Uncertainty in the determination of the ratio of the gluon distribution in a Pb nucleus over that in a proton, at the FCC-eh, the LHeC and its combination. Also show is the result of a recent analysis [442]. Note that while at the FCC-eh a tolerance criterium \(\Delta \chi ^2=1\) can be used, it being a single experiment, present analyses use a much larger value (\(\sim 50\)) in order to accommodate data from different experiments and types of collisions. Note also that in present analysis the glue is basically unknown both for \(x<0.01\) and for \(x>0.2\), with the shape of the uncertainty band dictated by the functional form of the initial conditions
Reduced cross sections for inclusive diffraction in ePb in different kinematic regions that could be measured at the FCC-eh (see Sect. 5.3.2), \(\xi \) being the fraction of the nucleon momentum taken by the diffractive system and \(\beta \) the fraction of momentum of the diffractive system taken by the parton struck. Red and green points correspond to two different models for the nuclear effects on DPDFs [443]
29.4.8 Diffraction
The FCC-eh will extend previous analyses of the diffractive parton densities, DPDFs – the conditional probabilities of finding partons in a hadron or nucleus, with the hadron or nucleus remaining intact - to a much larger kinematic region in ep. On the other hand, DPDFs in nuclei have never been measured and they could be in a large kinematic region at the FCC-eh as illustrated in Fig. 16.11, see Sect. 5.3.2.
On the other hand, there are also large possibilities to measure exclusive production of vector mesons (\(\hbox {J}/\uppsi \) in this case), both for coherent diffraction \(\hbox {ePb}\rightarrow \hbox {ePb}+\hbox {J}/\uppsi \) where the nucleus remain intact and for incoherent diffraction \(\hbox {ePb}\rightarrow \hbox {ePb}^*+\hbox {J}/\uppsi \) where the nucleus dissociates. The former dominates at small momentum transfer while the latter does at large momentum transfer. This is illustrated in Fig. 16.12. While these measurements required detailed studies on forward instrumentation, they are known to be very sensitive to the transverse distribution of partons in the nucleus, its smooth or lumpy distribution and the possible existence of non-linear effects [446].
29.5 Contributions to other sectors of high-energy physics
29.5.1 \(\upgamma \upgamma \) collisions
Photon-photon collisions in UPCs of proton [433] and Pb beams [434] have been experimentally observed at the LHC [448,449,450,451]. Although the \(\upgamma \) spectrum is harder for smaller charges –which favours proton over nuclear beams in the production of heavy diphoton systems– each photon flux scales with the squared charge of the hadron, \(Z^2\), and thus \(\upgamma \upgamma \) luminosities are extremely enhanced for ion beams (\(Z^4=5\cdot 10^{7}\) in the case of PbPb). The figure of merit for UPC processes is the effective \(\upgamma \upgamma \) luminosity, \(\mathrm {d}\mathcal {L}_{\mathrm{eff}}/\mathrm {d}W_{{\upgamma \upgamma }} \equiv \mathcal {L}_{AB}\,\mathrm {d}\mathcal {L}_{\gamma \,\gamma }/\mathrm {d}W_{{\upgamma \upgamma }}\), where \(\mathcal{L}_{\mathrm{AB}}\) is the collider luminosity for the \(A\,B\) system and \(\mathrm {d}\mathcal {L}_{{\upgamma \upgamma }}/\mathrm {d}W_{{\upgamma \upgamma }}\) is the photon–photon luminosity as a function of the \(\upgamma \upgamma \) centre-of-mass energy \(W_{{\upgamma \upgamma }}\), obtained integrating the two photon fluxes over all rapidities y. Figure 16.13 (left) shows a comparison of the \(\mathrm {d}\mathcal {L}_{\mathrm{eff}}/\mathrm {d}W_{{\upgamma \upgamma }}\) reachable as a function of \(W_{{\upgamma \upgamma }}\) for five different colliding systems at LHC and FCC energies. Two-photon centre-of-mass energies at the FCC will for the first time reach the range beyond 1 TeV. Clearly, Pb–Pb at \(\sqrt{s_{\scriptscriptstyle {\mathrm{NN}}}} =39~\hbox {TeV}\) provides the largest two-photon luminosities of all colliding systems. The vertical lines in Fig. 16.13 (left) show the thresholds for photon-fusion production of Higgs, \(\hbox {W}^+\hbox {W}^-\), ZZ, and tŧ, which are sensitive to different tests of the electroweak sector of the Standard Model (SM) [447], such as anomalous quartic-gauge couplings and top-electroweak moments. In particular, the Higgs boson cross sections are \(\sigma (\upgamma \upgamma \rightarrow \hbox {H}) = 1.75~\hbox {nb}\) and 1.5 pb in PbPb and pPb collisions at \(\sqrt{s_{\scriptscriptstyle {\mathrm{NN}}}} = 39\) and 63 TeV which, for the nominal luminosities per month, imply \(\sim 200\) and 45 Higgs bosons produced (corresponding to 110 and 25 bosons in the bb̄ decay mode, respectively). Figure 16.13 (right) shows the expected dijet invariant mass distribution after cuts, with \(\sim 21\) signal counts over \(\sim 28\) for the sum of backgrounds in a window \(m_{\mathrm{b}\overline{\mathrm {b}}} = 117-133~\hbox {GeV}\) around the Higgs peak [447]. Reaching \(5\sigma \) statistical significance requires to combine two runs (or two different experiments).
Left: Effective luminosities as a function of \(\upgamma \upgamma \) c.m. energy (\(W_{\gamma \,\gamma }\)) for five colliding systems at FCC and LHC energies and their nominal luminosities. Right: Expected dijet invariant mass distribution for \(\upgamma \upgamma \) production of H(bb̄) (hatched Gaussian) and qq̄ continuum (dashed line) in PbPb (\(\sqrt{s_{\scriptscriptstyle {\mathrm{NN}}}} = 39~\hbox {TeV}\)) UPCs, after event selection and reconstruction [447]
The very rare elastic scattering of two photons in vacuum \(\upgamma \upgamma \rightarrow \upgamma \upgamma \) was recently observed for the first time in UPCs at the LHC [452, 453]. The increase in \(\upgamma \upgamma \rightarrow \upgamma \upgamma \) yields from LHC to FCC is of \(\mathcal {O}(200)\) thanks to factors of \(\times 30\) larger cross sections times luminosities, and \(\times 2\) in the experimental acceptance [454, 455]. At the FCC, due to the higher diphoton masses reached, this process may be sensitive to physics beyond the SM through new heavy charged particles contributing to the virtual loop such as, e.g., from SUSY particles [456]. Light-by-light (LbyL) scattering has also been proposed as a tool to search for monopoles [457], axions [458, 459], unparticles [460], low-scale gravity effects [461], and non-commutative interactions [462].
29.5.2 Fixed-target collisions using the FCC proton and Pb beams
The fixed-target mode offers specific advantages compared to the collider mode such as accessing the high Feynman \(x_F\) domain, achieving high luminosities yet in parasitic way, varying the atomic mass of the target almost at will, and polarising the target [28, 463]. The c.m.s. energy in the fixed-target mode is about 200–300 GeV for Pb and proton beams, respectively. The region of central c.m.s. rapidities is highly boosted at an angle with respect to the beam axis of about one degree in the laboratory frame such that the entire backward hemisphere, \(y_{\mathrm{c.m.s.}}<0\), becomes easily accessible with standard experimental techniques at \(2<\eta _{\mathrm{lab}} <6\). A fixed-target setup would allow one to significantly extend a large number of measurements carried out at RHIC towards very backward rapidities with much larger luminosities. As it was discussed in [463], RHIC luminosities in pp collisions at 200 GeV are limited and do not allow the study of vector boson production close to threshold which probes the large x content in the proton and nucleus, 0.7 and above. These studies become possible with fixed-target collisions at FCC. With a longitudinally polarised target, vector boson production gives access to (anti)quark helicity distributions in the proton at very large x. With deuterium and helium targets, measurements can also be carried out on the neutron. Using a transversely polarised target allows one to access transverse-momentum dependent distributions (TMDs) which are connected to the orbital angular momentum carried by the partons at larger scales than with any other facilities. Given the similarities with a setup like AFTER@LHC, the reader is also guided to Refs. [464] for more in-depth discussions on the physics reach of the fixed-target mode above the 100 GeV domain.
Notes
The possibility of improving the direct determination of SM parameters (e.g. \(m_W\) or \(\sin ^2\theta _W\)) will not be addressed here, since it is unlikely that FCC-hh can match the precision achievable at FCC-ee. A significant reduction in the PDF systematics entering the uncertainty of both \(m_W\) or \(\sin ^2\theta _W\) at the LHC will certainly be greatly reduced by the end of HL-LHC, and even more by FCC-eh. But a reliable assessment of the experimental systematics would require a simulation of the FCC-hh experimental conditions well beyond today’s level of realism.
Note that the assumed luminosities far exceed the values required for the PDFs, as the statistical uncertainties are negligible, except for corners of phase space at the highest \(Q^2\) and x. In forthcoming studies one has to separate and evaluate the luminosity needs for Higgs, BSM, PDF, top and electroweak studies more carefully. Obviously the highest luminosity demand will come from precision Higgs physics and rare, BSM processes.
This plot was produced under the assumption of the LHeC [69] with a proton beam energy of 7 TeV, and therefore represents very conservative results.
The EFT fits to EW and Higgs observables presented in this chapter have been performed using the HEPfit package [237, 238]. The calculations are done using a modification of the basis presented in [233], where the operators denoted as \(\mathcal{O}_{\varphi WB}=\varphi ^\dagger \sigma _a \varphi W_{\mu \nu }^a B^{\mu \nu }\) and \(\mathcal{O}_{\varphi D}=|\varphi ^\dagger D_\mu \varphi |^2\) are redefined away in favor of 2 interactions that do not enter in EW precision observables, namely \(iD_\mu \varphi ^\dagger D_\nu \varphi B^{\mu \nu }\) and \(iD_\mu \varphi ^\dagger \sigma _a D_\nu \varphi W^{a~\!\mu \nu }\). The output of the fits is translated in terms of the induced modifications of corresponding effective couplings of the SM particles, e.g. the \(\mathrm {Zf\bar{f}}\) couplings \(g_{L,R}^f\), as shown in the figure.
In this regard, we note that, while the precision of such projections can clearly exceed the LEP-2 bounds, the sensitivity to aTGC in these studies results mainly from new physics effects that are quadratic in the anomalous couplings. We do not include these results in our fits.
Studies of anomalous neutral TGC at the FCC-hh have also been considered in the literature [274]. Within the EFT approach used, however, these are only generated at dimension 8 and go beyond the scope of the dimension 6 study presented here.
References
CERN Council, European Strategy Session of Council, 30 May 2013, CERN-Council-S/106 (2013)
Future Circular Collider Study Kickoff Meeting, University of Geneva, 12–15 February 2014 (2014). http://indico.cern.ch/e/fcc-kickoff
E. Todesco, F. Zimmermann (eds.), in Proc. EuCARD-AccNet-EuroLumi Workshop: The High-Energy Large Hadron Collider—HE-LHC10, Malta, 14–16 October 2010, CERN-2011-003 (2010). arXiv:1111.7188 [physics.acc-ph]
J.A. Osborne, C.S. Waaijer, Pre-Feasability Assessment for an 80 km Tunnel Project at CERN, Contribution to the Update of the European Strategy for Particle Physics, No. 165, 27 July 2012. http://indico.cern.ch/event/175067/call-for-abstracts/165/file/1.pdf
Joint Snowmass-EuCARD/AccNet-HiLumi meeting ‘Frontier Capabilities for Hadron Colliders 2013’ a.k.a. EuCARD VHE-LHC Day, CERN, 21–22 February 2013 (2013). http://indico.cern.ch/event/223094
A. Blondel, F. Zimmermann, A High Luminosity e\(^+\)e\(^-\) Collider in the LHC Tunnel to Study the Higgs Boson (2011). arXiv:1112.2518
EuCARD LEP3 workshop, 18 June 2012; 2nd EuCARD LEP3 workshop 23 October 2012; 3rd EuCARD TLEP3 workshop, 10 January 2013; 4th EuCARD TLEP workshop, 4–5 April 2013 (2012 and 2013)
The TLEP Design Study Working Group, First Look at the Physics Case of TLEP. JHEP 01, 164 (2014). https://doi.org/10.1007/JHEP01(2014)164, arXiv:1308.6176 [hep-ex]
V.L. Ginzburg, L.D. Landau, On the theory of superconductivity. Zh. Eksp. Teor. Fiz. 20, 1064–1082 (1950)
J. Bardeen, L.N. Cooper, J.R. Schrieffer, Theory of superconductivity. Phys. Rev. 108, 1175–1204 (1957). https://doi.org/10.1103/PhysRev.108.1175
Planck Collaboration, P.A.R. Ade et al., Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 594, A13 (2016). https://doi.org/10.1051/0004-6361/201525830, arXiv:1502.01589 [astro-ph.CO]
W. Hu, R. Barkana, A. Gruzinov, Cold and fuzzy dark matter. Phys. Rev. Lett. 85, 1158–1161 (2000). https://doi.org/10.1103/PhysRevLett.85.1158. arXiv:astro-ph/0003365 [astro-ph]
K. Griest, A.M. Cieplak, M.J. Lehner, Experimental limits on primordial black hole dark matter from the first 2 yr of Kepler data. Astrophys. J. 786(2), 158 (2014). https://doi.org/10.1088/0004-637X/786/2/158. arXiv:1307.5798 [astro-ph.CO]
MACHO, EROS Collaboration, C. Alcock et al., EROS and MACHO combined limits on planetary mass dark matter in the galactic halo. Astrophys. J. 499, L9 (1998). arXiv:astro-ph/9803082 [astro-ph]. Preprint UNSW-AST-AFS1-98, https://doi.org/10.1086/311355
J. Yoo, J. Chaname, A. Gould, The end of the MACHO era: limits on halo dark matter from stellar halo wide binaries. Astrophys. J. 601, 311–318 (2004). https://doi.org/10.1086/380562. arXiv:astro-ph/0307437 [astro-ph]
B. Goddard et al., Physics Opportunities with the FCC-hh Injectors, CERN Yellow Report No. 3, pp. 693–705 (2017). https://doi.org/10.23731/CYRM-2017-003.693, arXiv:1706.07667 [physics.acc-ph]
HL-LHC, HE-LHC Working Group Collaboration, P. Azzi et al., Standard Model Physics at the HL-LHC and HE-LHC. arXiv:1902.04070 [hep-ph]. Preprint CERN-LPCC-2018-03
Physics of the HL-LHC Working Group Collaboration, M. Cepeda et al., Higgs Physics at the HL-LHC and HE-LHC. arXiv:1902.00134 [hep-ph]. Preprint CERN-LPCC-2018-04
X. Cid Vidal et al., Beyond the Standard Model Physics at the HL-LHC and HE-LHC. arXiv:1812.07831 [hep-ph]. Preprint CERN-LPCC-2018-05
A. Cerri et al., Opportunities in flavour physics at the HL-LHC and HE-LHC. arXiv:1812.07638 [hep-ph]. Preprint CERN-LPCC-2018-06
Z. Citron et al., Future physics opportunities for high-density QCD at the LHC with heavy-ion and proton beams, in HL/HE-LHC Workshop: Workshop on the Physics of HL-LHC, and Perspectives at HE-LHC, Geneva, June 18–20, 2018 (2018). arXiv:1812.06772 [hep-ph]
D. d’Enterria, D. Wojcik, R. Aleksan, Search for resonant s-channel Higgs production at FCC-ee, in 7th, 8th, 10th FCC-ee Physics Workshops, Geneva, June 2014; LPNHE-Paris, Oct. 2014; CERN, Feb. 2016 (2014). https://indico.cern.ch/event/313708/
M.A. Valdivia Garcia, F. Zimmermann, Optimized monochromatization for direct Higgs production in future circular e\(^{+}\)e\(^{-}\) colliders, in 8th Int. Particle Accelerator Conf. (IPAC’17), Copenhagen, Denmark, 14–19 May, 2017, pp. 2950–2953 (2017)
A. Blondel, P. Janot, Future strategies for the discovery and the precise measurement of the Higgs self coupling. arXiv:1809.10041 [hep-ph]
M.L. Mangano et al., Physics at a 100 TeV pp Collider: Standard Model Processes, CERN Yellow Report No. 3, pp. 1–254 (2017). arXiv:1607.01831 [hep-ph]. Preprint CERN-TH-2016-112, FERMILAB-FN-1021-T. https://doi.org/10.23731/CYRM-2017-003.1
I. Hinchliffe, A. Kotwal, M.L. Mangano, C. Quigg, L.-T. Wang, Luminosity goals for a 100-TeV pp collider. Int. J. Mod. Phys. A 30(23), 1544002 (2015). https://doi.org/10.1142/S0217751X15440029. arXiv:1504.06108 [hep-ph]. Preprint CERN-PH-TH-2015-089, FERMILAB-CONF-15-125-E-T, LBNL-176221
M. Schaumann, Potential performance for Pb–Pb, p–Pb and p–p collisions in a future circular collider. Phys. Rev. ST Accel. Beams 18(9), 091002 (2015). https://doi.org/10.1103/PhysRevSTAB.18.091002. arXiv:1503.09107 [physics.acc-ph]
A. Dainese et al., Heavy ions at the Future Circular Collider, CERN Yellow Report No. 3, pp. 635–692 (2017). arXiv:1605.01389 [hep-ph]. Preprint CERN-TH-2016-107. https://doi.org/10.23731/CYRM-2017-003.635
J. Jowett et al., The 2016 proton–nucleus run of the LHC, Proceedings of IPAC2017, Copenhagen, TUPVA014 (2017). https://doi.org/10.18429/JACoW-IPAC2017-TUPVA014
J. Haller, A. Hoecker, R. Kogler, K. Mönig, T. Peiffer, J. Stelzer, Update of the global electroweak fit and constraints on two-Higgs-doublet models. arXiv:1803.01853 [hep-ph]
Gfitter Group Collaboration, M. Baak, J. Cúth, J. Haller, R. Hoecker, A.and Kogler, K. Mönig, M. Schott, J. Stelzer, The global electroweak fit at NNLO and prospects for the HC and ILC, Eur. Phys. J. C 74, 3046 (2014). arXiv:1407.3792 [hep-ph]. Preprint DESY-14-124. https://doi.org/10.1140/epjc/s10052-014-3046-5
The LEP Electroweak Working Group, the SLD Electroweak Group, the SLD Heavy Flavour Group, and the ALEPH, DELPHI, L3, OPAL and SLD Collaborations, Precision electroweak measurements on the Z resonance. Phys. Rep. 427, 257–454 (2006). arXiv:hep-ex/0509008 [hep-ex]. Preprint SLAC-R-774. https://doi.org/10.1016/j.physrep.2005.12.006
M. Koratzinos, A. Blondel, E. Gianfelice-Wendt, F. Zimmermann, FCC-ee: energy calibration, in Proceedings of 6th International Particle Accelerator Conference (IPAC 2015): Richmond, May 3–8, 2015, p. TUPTY063 (2015). arXiv:1506.00933 [physics.acc-ph] https://inspirehep.net/record/1374263/files/arXiv:1506.00933.pdf
P. Janot, Direct measurement of \(\alpha _{QED}(m_{Z}^{2})\) at the FCC-ee. JHEP 02, 053 (2016). arXiv:1512.05544 [hep-ph]. https://doi.org/10.1007/JHEP02(2016)053. https://doi.org/10.1007/JHEP11(2017)164 [Erratum: JHEP11, 164 (2017)]
P. Janot, Presentation given at the first FCC-ee beam polarization and energy calibration workshop, proceedings in preparation. https://indico.cern.ch/event/669194/contributions/2764992/attachments/1547206/2429244/EnergySpread.pdf (2017)
C. Jarlskog, Neutrino counting at the Z-peak and right-handed neutrinos. Phys. Lett. B 241, 579–583 (1990). https://doi.org/10.1016/0370-2693(90)91873-A
G. Barbiellini, X. Berdugo, G. Bonvicini, P. Colas, L. Mirabito et al., Neutrino Counting Preprint CERN-TH-5528-89. http://cds.cern.ch/search?sysno=000112318CER
OPAL Collaboration, G. Abbiendi et al., Photonic events with missing energy in \(e^+ e^-\) collisions at \(\sqrt{s} = 189\) GeV. Eur. Phys. J. C 18, 253–272 (2000). arXiv:hep-ex/0005002 [hep-ex]. Preprint CERN-EP-2000-050. https://doi.org/10.1007/s100520000522
ALEPH Collaboration, A. Heister et al., Single photon and multiphoton production in \(e^{+}e^{-}\) collisions at \(\sqrt{s}\) up to 209-GeV. Eur. Phys. J. C 28, 1–13 (2003). Preprint CERN-EP-2002-033. http://link.springer.com/article/10.1140%2Fepjc%2Fs2002-01129-7
L3 Collaboration, P. Achard et al., Single photon and multiphoton events with missing energy in \(e^{+} e^{-}\) collisions at LEP. Phys. Lett. B 587, 16–32 (2004). arXiv:hep-ex/0402002 [hep-ex]. Preprint CERN-EP-2003-068. https://doi.org/10.1016/j.physletb.2004.01.010
DELPHI Collaboration, J. Abdallah et al., Photon events with missing energy in \(e^+ e^-\) collisions at \(\sqrt{s} = 130\) to \(209\) GeV. Eur. Phys. J. C 38, 395–411 (2005). arXiv:hep-ex/0406019 [hep-ex]. Preprint CERN-EP-2003-093. https://doi.org/10.1140/epjc/s2004-02051-8
M. Béguin, Poster presented at the 2018 FCC collaboration meeting in Amsterdam (2018). https://indico.cern.ch/event/656491/contributions/2960955/attachments/1628478/2594424/poster_Beguin_FCCweek2018.pdf
D. d’Enterria, P.Z. Skands (eds.), in Proceedings of High-Precision \(\alpha _s\) Measurements from LHC to FCC-ee (CERN, Geneva, 2015). arXiv:1512.05194 [hep-ph]. http://lss.fnal.gov/archive/2015/conf/fermilab-conf-15-610-t.pdf
SLD Collaboration, K. Abe et al., Measurement of the branching ratio of the Z0 into heavy quarks. Phys. Rev. D 71, 112004 (2005). arXiv:hep-ex/0503005 [hep-ex]. Preprint SLAC-PUB-9941. https://doi.org/10.1103/PhysRevD.71.112004
D. d’Enterria, M. Srebre, \(\alpha _s\) and \(\rm V_{cs}\) determination, and CKM unitarity test, from W decays at NNLO. Phys. Lett. B 763, 465–471 (2016). arXiv:1603.06501 [hep-ph]. https://doi.org/10.1016/j.physletb.2016.10.012
A. Blondel et al., Standard model theory for the FCC-ee: the Tera-Z, in Mini Workshop on Precision EW and QCD Calculations for the FCC Studies: Methods and Techniques. CERN, Geneva, January 12–13, 2018 (2018). arXiv:1809.01830 [hep-ph]
Mini workshop: Precision EW and QCD calculations for the FCC studies: methods and techniques. https://indico.cern.ch/event/669224/
NNPDF Collaboration, R.D. Ball et al., Parton distributions for the LHC Run II. JHEP 04, 040 (2015). arXiv:1410.8849 [hep-ph]. Preprint EDINBURGH-2014-15, IFUM-1034-FT, CERN-PH-TH-2013-253, OUTP-14-11P, CAVENDISH-HEP-14-11. https://doi.org/10.1007/JHEP04(2015)040
R. Franceschini, G. Panico, A. Pomarol, F. Riva, A. Wulzer, Electroweak precision tests in high-energy diboson processes. JHEP 02, 111 (2018). https://doi.org/10.1007/JHEP02(2018)111. arXiv:1712.01310 [hep-ph]. Preprint CERN-TH-2017-252, RM3-TH-17-1
D. de Florian, M. Grazzini, C. Hanga, S. Kallweit, J.M. Lindert, P. Maierhöfer, J. Mazzitelli, D. Rathlev, Differential Higgs boson pair production at next-to-next-to-leading order in QCD. JHEP 09, 151 (2016). https://doi.org/10.1007/JHEP09(2016)151. arXiv:1606.09519 [hep-ph]. Preprint DESY-16-107, FR-PHENO-2016-007, ICAS-08-16, MITP-16-061, ZU-TH-20-16
C.Y. Prescott et al., Parity nonconservation in inelastic electron scattering. Phys. Lett. B 77, 347 (1978). https://doi.org/10.1016/0370-2693(78)90722-0. Preprint SLAC-PUB-2148
C.Y. Prescott et al., Further measurements of parity nonconservation in inelastic electron scattering. Phys. Lett. B 84, 524 (1979). https://doi.org/10.1016/0370-2693(79)91253-X. Preprint SLAC-PUB-2319
H1 Collaboration, T. Ahmed et al., First measurement of the charged current cross-section at HERA. Phys. Lett. B 324, 241 (1994). Preprint DESY-94-012. https://doi.org/10.1016/0370-2693(94)90414-6
H1 Collaboration, A. Aktas et al., A determination of electroweak parameters at HERA. Phys. Lett. B 632, 35 (2006). arXiv:hep-ex/0507080 [hep-ex]. Preprint DESY-05-093. https://doi.org/10.1016/j.physletb.2005.10.035
H1 and ZEUS Collaborations, H. Abramowicz et al., Combination of measurements of inclusive deep inelastic \({e^{\pm }p}\) scattering cross sections and QCD analysis of HERA data. Eur. Phys. J. C 75(12), 580 (2015). arXiv:1506.06042 [hep-ex]. Preprint DESY-15-039. https://doi.org/10.1140/epjc/s10052-015-3710-4
ZEUS Collaboration, H. Abramowicz et al., Combined QCD and electroweak analysis of HERA data. Phys. Rev. D 93(9), 092002 (2016). arXiv:1603.09628 [hep-ex]. Preprint DESY-16-039. https://doi.org/10.1103/PhysRevD.93.092002
H1 Collaboration, V. Andreev et al., Determination of electroweak parameters in polarised deep-inelastic scattering at HERA. arXiv:1806.01176 [hep-ex]. Preprint DESY-18-080
M. Böhm, H. Spiesberger, Radiative corrections to neutral current deep inelastic lepton nucleon scattering at HERA energies. Nucl. Phys. B 294, 1081 (1987). https://doi.org/10.1016/0550-3213(87)90624-9. Preprint Print-87-0119 (WURZBURG)
M. Böhm, H. Spiesberger, Radiative corrections to charged current deep inelastic electron-proton scattering at HERA. Nucl. Phys. B 304, 749 (1988). https://doi.org/10.1016/0550-3213(88)90652-9. Preprint PRINT-88-0076 (WURZBURG)
DYu. Bardin, C. Burdik, P.C. Khristova, T. Riemann, Electroweak radiative corrections to deep inelastic scattering at HERA, neutral current scattering. Z. Phys. C 42, 679 (1989). https://doi.org/10.1007/BF01557676. Preprint PHE-88-15
DYu. Bardin, K.C. Burdik, P.K. Khristova, T. Riemann, Electroweak radiative corrections to deep inelastic scattering at HERA, charged current scattering. Z. Phys. C 44, 149 (1989). https://doi.org/10.1007/BF01548593. Preprint JINR-E2-89-145
W. Hollik, D.Yu. Bardin, J. Blümlein, B.A. Kniehl, T. Riemann, H. Spiesberger, Electroweak parameters at HERA: Theoretical aspects, in Workshop on Physics at HERA, Hamburg, October 29–30, 1991, p. 923 (1992)
A. Sirlin, Radiative corrections in the \(\text{ SU }(2)_{\rm L} \times \text{ U }(1)\) theory: a simple renormalization framework. Phys. Rev. D 22, 971 (1980). https://doi.org/10.1103/PhysRevD.22.971. Preprint PRINT-80-0267 (IAS,PRINCETON)
Particle Data Group Collaboration, C. Patrignani et al., Review of particle physics. Chin. Phys. C 40(10), 100001 (2016). https://doi.org/10.1088/1674-1137/40/10/100001
M. Klein, T. Riemann, Electroweak interactions probing the nucleon structure. Z. Phys. C 24, 151 (1984). https://doi.org/10.1007/BF01571719. Preprint PHE 83-08
D0 Collaboration, V.M. Abazov et al., Measurement of \(\sin ^2\theta _{\rm eff}^{\ell }\) and \(Z\)-light quark couplings using the forward–backward charge asymmetry in \(p\bar{p} \rightarrow Z/\gamma ^{*} \rightarrow e^{+}e^{-}\) events with \({\cal{L}}=5.0\) fb\(^{-1}\) at \(\sqrt{s}=1.96\) TeV. Phys. Rev. D 84, 012007 (2011). arXiv:1104.4590 [hep-ex]. Preprint FERMILAB-PUB-11-190-E. https://doi.org/10.1103/PhysRevD.84.012007
H. Spiesberger, Precision electroweak tests at HERA. Adv. Ser. Direct. High Energy Phys. 14, 626 (1995). https://doi.org/10.1142/9789814503662_0016. Preprint BI-TP-93-03
J. Blümlein, M. Klein, T. Riemann, Testing the electroweak Standard Model at HERA, in Physics at future accelerators, Proceedings, 10th Warsaw symposium on elementary particle physics, Kazimierz, May 24–30, 1987, p. 39 (1987)
LHeC Study Group Collaboration, J.L. Abelleira Fernandez et al., A large hadron electron collider at CERN: report on the physics and design concepts for machine and detector. J. Phys. G 39, 075001 (2012). arXiv:1206.2913 [physics.acc-ph]. Preprint SLAC-R-999, CERN-OPEN-2012-015, LHEC-NOTE-2012-001-GEN. https://doi.org/10.1088/0954-3899/39/7/075001
Particle Data Group Collaboration, M. Tanabashi et al., Review of particle physics. Phys. Rev. D 98(3), 030001 (2018). https://doi.org/10.1103/PhysRevD.98.030001
CDF Collaboration, T.A. Aaltonen et al., Precise measurement of the W-boson mass with the collider detector at Fermilab. Phys. Rev. D 89(7), 072003 (2014). arXiv:1311.0894 [hep-ex]. Preprint FERMILAB-PUB-13-515-E. https://doi.org/10.1103/PhysRevD.89.072003
ATLAS Collaboration, M. Aaboud et al., Measurement of the \(W\)-boson mass in \(pp\) collisions at \(\sqrt{s}=7\) TeV with the ATLAS detector. Eur. Phys. J. C 78(2), 110 (2018). arXiv:1701.07240 [hep-ex]. Preprint CERN-EP-2016-305. https://doi.org/10.1140/epjc/s10052-017-5475-4
A. Hoecker, private communication (2018). https://indico.cern.ch/event/716380/contributions/2944841/attachments/1660046/2660284/epfaculty-hoecker-1jun2018.pdf
P. Azzi, C. Bernet, C. Botta, P. Janot, M. Klute, P. Lenzi, L. Malgeri, M. Zanetti, Prospective studies for LEP3 with the CMS detector. arXiv:1208.1662 [hep-ex]. Preprint CMS-NOTE-2012-003
M.E. Peskin, Comparison of LHC and ILC capabilities for Higgs boson coupling measurements. arXiv:1207.2516 [hep-ph]. Preprint SLAC-PUB-15178
T. Barklow, K. Fujii, S. Jung, R. Karl, J. List, T. Ogawa, M.E. Peskin, J. Tian, Improved formalism for precision Higgs coupling fits. Phys. Rev. D 97(5), 053003 (2018). https://doi.org/10.1103/PhysRevD.97.053003. arXiv:1708.08912 [hep-ph].Preprint DESY-17-120, KEK-PREPRINT-2017-22, SLAC-PUB-17129, DESY-17-120—KEK-PREPRINT-2017-22—SLAC-PUB-17129
H. Abramowicz et al., Higgs physics at the CLIC electron-positron linear collider. Eur. Phys. J. C 77(7), 475 (2017). https://doi.org/10.1140/epjc/s10052-017-4968-5. arXiv:1608.07538 [hep-ex]. Preprint CLICDP-PUB-2016-001
M. Ruan, private communication (2017). http://ias.ust.hk/program/shared_doc/2017/201701hep/HEP_20170124_Manqi_Ruan.pdf
ATLAS Collaboration, M. Aaboud et al., Observation of Higgs boson production in association with a top quark pair at the LHC with the ATLAS detector. arXiv:1806.00425 [hep-ex]. Preprint CERN-EP-2018-138, CERN-EP-2018-138
CMS Collaboration, A.M. Sirunyan et al., Observation of \(\rm t\overline{t}\)H production. Phys. Rev. Lett. 120(23), 231801 (2018). arXiv:1804.02610 [hep-ex]. Preprint CMS-HIG-17-035, CERN-EP-2018-064, CMS-HIG-17-035, CERN-EP-2018-064. https://doi.org/10.1103/PhysRevLett.120.231801, https://doi.org/10.1130/PhysRevLett.120.231801
S. Jadach, R.A. Kycia, Lineshape of the Higgs boson in future lepton colliders. Phys. Lett. B 755, 58–63 (2016). https://doi.org/10.1016/j.physletb.2016.01.065. arXiv:1509.02406 [hep-ph]
M.A. Valdivia Garcia, A. Faus-Golfe, F. Zimmermann, Towards a monochromatization scheme for direct Higgs production at FCC-ee. Preprint CERN-ACC-2016-0077. https://cds.cern.ch/record/2159683
D. d’Enterria, Higgs physics at the future circular Collider. PoS ICHEP 2016, 434 (2017). https://doi.org/10.22323/1.282.0434. arXiv:1701.02663 [hep-ex]
J. Brod, U. Haisch, J. Zupan, Constraints on CP-violating Higgs couplings to the third generation. JHEP 11, 180 (2013). https://doi.org/10.1007/JHEP11(2013)180. arXiv:1310.1385 [hep-ph]. Preprint NSF-KITP-13-229
ATLAS Collaboration, G. Aad et al., Study of the spin and parity of the Higgs boson in diboson decays with the ATLAS detector. Eur. Phys. J. C 75(10), 476 (2015). arXiv:1506.05669 [hep-ex]. Preprint CERN-PH-EP-2015-114. https://doi.org/10.1140/epjc/s10052-015-3685-1. https://doi.org/10.1140/epjc/s10052-016-3934-y [Erratum: Eur. Phys. J. C 76(3), 152 (2016)]
CMS Collaboration, V. Khachatryan et al., Constraints on the spin-parity and anomalous HVV couplings of the Higgs boson in proton collisions at 7 and 8 TeV. Phys. Rev. D 92(1), 012004 (2015). arXiv:1411.3441 [hep-ex]. Preprint CMS-HIG-14-018, CERN-PH-EP-2014-265. https://doi.org/10.1103/PhysRevD.92.012004
R. Contino et al., Physics at a 100 TeV pp collider: Higgs and EW symmetry breaking studies, CERN Yellow Report No. 3, pp. 255–440 (2017). arXiv:1606.09408 [hep-ph]. Preprint CERN-TH-2016-113. https://doi.org/10.23731/CYRM-2017-003.255
M. Selvaggi, Higgs measurements at FCC-hh, CERN-ACC-2018-0045. CERN, Geneva (2018). Preprint CERN-ACC-2018-0045. https://cds.cern.ch/record/2642471, Placeholder draft
M.L. Mangano, T. Plehn, P. Reimitz, T. Schell, H.-S. Shao, Measuring the top Yukawa coupling at 100 TeV. J. Phys. G 43(3), 035001 (2016). https://doi.org/10.1088/0954-3899/43/3/035001. arXiv:1507.08169 [hep-ph]
U. Klein, FCC-eh as a Higgs Facility (2018). https://indico.cern.ch/event/656491/contributions/2947252/
T. Han, B. Mellado, Higgs boson searches and the H b anti-b coupling at the LHeC. Phys. Rev. D 82, 016009 (2010). https://doi.org/10.1103/PhysRevD.82.016009. arXiv:0909.2460 [hep-ph]
M. Tanaka, Study of the Higgs Measurements at the LHeC, Bachelor Thesis. Tokyo Institute of Technology (2014) (in Japanese)
E. Kay, Higgs Studies at a High Luminosity LHeC, Master Thesis. Liverpool University (2014)
U. Klein, Higgs heavy flavour studies using jet probabilities (2015). https://indico.cern.ch/event/356714/contributions/844946/
D. Hampson, I. Harris, Finding Higgs to Charm decays in ep, Master and Bachelor Theses. Liverpool University (2016–2017)
C. Englert, R. Kogler, H. Schulz, M. Spannowsky, Higgs coupling measurements at the LHC. Eur. Phys. J. C 76(7), 393 (2016). https://doi.org/10.1140/epjc/s10052-016-4227-1. arXiv:1511.05170 [hep-ph]. Preprint IPPP-15-66, DCPT-15-132
B. Coleppa, M. Kumar, S. Kumar, B. Mellado, Measuring CP nature of top-Higgs couplings at the future Large Hadron electron collider. Phys. Lett. B 770, 335–341 (2017). https://doi.org/10.1016/j.physletb.2017.05.006. arXiv:1702.03426 [hep-ph]
Y.-L. Tang, C. Zhang, S.-H. Zhu, Invisible Higgs decay at the LHeC. Phys. Rev. D 94(1), 011702 (2016). https://doi.org/10.1103/PhysRevD.94.011702. arXiv:1508.01095 [hep-ph]
H. Georgi, M. Machacek, Doubly charged Higgs bosons. Nucl. Phys. B 262, 463–477 (1985). https://doi.org/10.1016/0550-3213(85)90325-6. Preprint HUTP-85/A051
S. Liu, Y.-L. Tang, C. Zhang, S.-H. Zhu, Exotic Higgs decay \(h\rightarrow \phi \phi \rightarrow 4b\) at the LHeC. Eur. Phys. J. C 77(7), 457 (2017). https://doi.org/10.1140/epjc/s10052-017-5012-5. arXiv:1608.08458 [hep-ph]
U. Klein, M. O’Keefe, Study of the Higgs to 4b decay in ep scattering, Master Thesis. Liverpool University (2017)
G. Azuelos, H. Sun, K. Wang, Search for singly charged Higgs bosons in vector-boson scattering at ep colliders. Phys. Rev. D 97(11), 116005 (2018). https://doi.org/10.1103/PhysRevD.97.116005. arXiv:1712.07505 [hep-ph]. Preprint DESY-17-150
D. d’Enterria, P.Z. Skands (eds.), in Proceedings, Parton Radiation and Fragmentation from LHC to FCC-ee (2017). arXiv:1702.01329 [hep-ph]
J.R. Christiansen, T. Sjöstrand, Color reconnection at future \(\text{ e }^{+}\) \(\text{ e }^{-}\) colliders. Eur. Phys. J. C 75(9), 441 (2015). https://doi.org/10.1140/epjc/s10052-015-3674-4. arXiv:1506.09085 [hep-ph]. Preprint LU-TP-15-25, MCNET-15-15
D. d’Enterria, \(\alpha _s\) status and perspectives (2018), in 26th International Workshop on Deep Inelastic Scattering and Related Subjects (DIS 2018) Port Island, Kobe, Japan, April 16–20, 2018 (2018). arXiv:1806.06156 [hep-ex]
A. Gehrmann-De Ridder, T. Gehrmann, E.W.N. Glover, G. Heinrich, EERAD3: event shapes and jet rates in electron–positron annihilation at order \(\alpha _s^3\). Comput. Phys. Commun. 185, 3331 (2014). arXiv:1402.4140 [hep-ph]. Preprint ZU-TH-05-14, IPPP-14-15, MPP-2014-23. https://doi.org/10.1016/j.cpc.2014.07.024. http://eerad3.hepforge.org. http://eerad3.hepforge.org
S. Weinzierl, Jet algorithms in electron–positron annihilation: Perturbative higher order predictions. Eur. Phys. J. C 71, 1565 (2011). arXiv:1011.6247 [hep-ph]. https://doi.org/10.1140/epjc/s10052-011-1717-z. https://doi.org/10.1140/epjc/s10052-011-1565-x [Erratum: Eur. Phys. J. C 71, 1717 (2011)]
V. Del Duca, C. Duhr, A. Kardos, G. Somogyi, Z. Trocsanyi, Three-jet production in electron-positron collisions at next-to-next-to-leading order accuracy. Phys. Rev. Lett. 117(15), 152004 (2016). https://doi.org/10.1103/PhysRevLett.117.152004. arXiv:1603.08927 [hep-ph]
A. Banfi, H. McAslan, P.F. Monni, G. Zanderighi, A general method for the resummation of event-shape distributions in \(e^{+} e\) annihilation. JHEP 05, 102 (2015). https://doi.org/10.1007/JHEP05(2015)102. arXiv:1412.2126 [hep-ph]. Preprint OUTP-14-18P
OPAL Collaboration, N. Fischer, S. Gieseke, S. Kluth, S. Platzer, P. Skands, Measurement of observables sensitive to coherence effects in hadronic Z decays with the OPAL detector at LEP. Eur. Phys. J. C 75(12), 571 (2015). arXiv:1505.01636 [hep-ex]. Preprint COEPP-MN-15-2. https://doi.org/10.1140/epjc/s10052-015-3766-1
A. Gehrmann-De Ridder, T. Gehrmann, E.W.N. Glover, G. Heinrich, NNLO corrections to event shapes in e+ e\(-\) annihilation. JHEP 12, 094 (2007). https://doi.org/10.1088/1126-6708/2007/12/094. arXiv:0711.4711 [hep-ph]. Preprint ZU-TH-27-07, IPPP-07-90, EDINBURGH-2007-47
V. Del Duca, C. Duhr, A. Kardos, G. Somogyi, Z. Ször, Z. Trócsányi, Z. Tulipánt, Jet production in the CoLoRFulNNLO method: event shapes in electron–positron collisions. Phys. Rev. D 94(7), 074019 (2016). https://doi.org/10.1103/PhysRevD.94.074019. arXiv:1606.03453 [hep-ph]. Preprint CERN-TH-2016-138, CP3-16-29, NSF-KITP-16-084
R. Abbate, M. Fickinger, A.H. Hoang, V. Mateu, I.W. Stewart, Thrust at \(\text{ N }^3\)LL with power corrections and a precision global fit for alphas (mZ). Phys. Rev. D 83, 074021 (2011). https://doi.org/10.1103/PhysRevD.83.074021. arXiv:1006.3080 [hep-ph]. Preprint MIT-CTP-4101, MPP-2010-7
A.H. Hoang, D.W. Kolodrubetz, V. Mateu, I.W. Stewart, \(C\)-parameter distribution at N\(^3\)LL’ including power corrections. Phys. Rev. D 91(9), 094017 (2015). https://doi.org/10.1103/PhysRevD.91.094017. arXiv:1411.6633 [hep-ph]. Preprint UWTHPH-2014-07, MIT-CTP-4596, LPN14-123
G. Bell, A. Hornig, C. Lee, J. Talbert, \(e^+ e^-\) angularity distributions at NNLL\(^\prime \) accuracy. arXiv:1808.07867 [hep-ph]. Preprint SI-HEP-2018-19, LA-UR-18-24071, DESY-18-083
Z. Nagy, D.E. Soper, Effects of subleading color in a parton shower. JHEP 07, 119 (2015). https://doi.org/10.1007/JHEP07(2015)119. arXiv:1501.00778 [hep-ph]. Preprint DESY-14-250
H.T. Li, P. Skands, A framework for second-order parton showers. Phys. Lett. B 771, 59–66 (2017). https://doi.org/10.1016/j.physletb.2017.05.011. arXiv:1611.00013 [hep-ph]. Preprint COEPP-MN-16-25, COEPP-MN-16-26
S. Hoche, F. Krauss, S. Prestel, Implementing NLO DGLAP evolution in parton showers. JHEP 10, 093 (2017). https://doi.org/10.1007/JHEP10(2017)093. arXiv:1705.00982 [hep-ph]. Preprint SLAC-PUB-16965, FERMILAB-PUB-17-134-T, IPPP-17-34, DCPT-17-68, MCNET-17-06
S. Hoeche, D. Reichelt, F. Siegert, Momentum conservation and unitarity in parton showers and NLL resummation. arXiv:1711.03497 [hep-ph]. Preprint SLAC-PUB-17173, MCNET-17-20
P. Gras, S. Höche, D. Kar, A. Larkoski, L. Lönnblad, S. Plätzer, A. Siódmok, P. Skands, G. Soyez, J. Thaler, Systematics of quark/gluon tagging. JHEP 07, 091 (2017). https://doi.org/10.1007/JHEP07(2017)091. arXiv:1704.03878 [hep-ph]. Preprint MIT-CTP-4885, COEPP-MN-17-2, MCNET-17-04
T. Sjostrand, S. Ask, J.R. Christiansen, R. Corke, N. Desai, P. Ilten, S. Mrenna, S. Prestel, C.O. Rasmussen, P.Z. Skands, An introduction to PYTHIA 8.2. Comput. Phys. Commun. 191, 159–177 (2015). https://doi.org/10.1016/j.cpc.2015.01.024. arXiv:1410.3012 [hep-ph]. Preprint LU-TP-14-36, MCNET-14-22, CERN-PH-TH-2014-190, FERMILAB-PUB-14-316-CD, DESY-14-178, SLAC-PUB-16122
M. Bahr et al., Herwig++ Physics and Manual. Eur. Phys. J. C 58, 639–707 (2008). https://doi.org/10.1140/epjc/s10052-008-0798-9. arXiv:0803.0883 [hep-ph]. Preprint CERN-PH-TH-2008-038, CAVENDISH-HEP-08-03, KA-TP-05-2008, DCPT-08-22, IPPP-08-11, CP3-08-05
J. Bellm et al., Herwig++ 2.7 Release Note. arXiv:1310.6877 [hep-ph]. Preprint IPPP-13-88, MCNET-13-15, DCPT-13-176, DESY-13-186, KA-TP-31-2013, ZU-TH-23-13
T. Gleisberg, S. Hoeche, F. Krauss, M. Schonherr, S. Schumann, F. Siegert, J. Winter, Event generation with SHERPA 1.1. JHEP 02, 007 (2009). https://doi.org/10.1088/1126-6708/2009/02/007. arXiv:0811.4622 [hep-ph]. Preprint FERMILAB-PUB-08-477-T, SLAC-PUB-13420, ZU-TH-17-08, DCPT-08-138, IPPP-08-69, EDINBURGH-2008-30, MCNET-08-14
N. Fischer, S. Prestel, M. Ritzmann, P. Skands, Vincia for Hadron Colliders. Eur. Phys. J. C 76(11), 589 (2016). https://doi.org/10.1140/epjc/s10052-016-4429-6. arXiv:1605.06142 [hep-ph], Preprint COEPP-MN-16-11, MCNET-16-13, SLAC-PUB-16529, NIKHEF-2016-020
Z. Nagy, D.E. Soper, A parton shower based on factorization of the quantum density matrix. JHEP 06, 097 (2014). https://doi.org/10.1007/JHEP06(2014)097. arXiv:1401.6364 [hep-ph], Preprint DESY-13-241
C. Flensburg, G. Gustafson, L. Lonnblad, Inclusive and exclusive observables from dipoles in high energy collisions. JHEP 08, 103 (2011). https://doi.org/10.1007/JHEP08(2011)103. arXiv:1103.4321 [hep-ph], Preprint LU-TP-11-13, CERN-PH-TH-2011-058, MCNET-11-08
S. Höche, S. Prestel, The midpoint between dipole and parton showers. Eur. Phys. J. C 75(9), 461 (2015). https://doi.org/10.1140/epjc/s10052-015-3684-2. arXiv:1506.05057 [hep-ph], Preprint SLAC-PUB-16304, MCNET-15-13
A.J. Larkoski, J. Thaler, W.J. Waalewijn, Gaining (mutual) information about quark/gluon discrimination. JHEP 11, 129 (2014). https://doi.org/10.1007/JHEP11(2014)129. arXiv:1408.3122 [hep-ph], Preprint MIT–CTP-4572, NIKHEF-2014-026
J.R. Andersen et al., Les Houches 2015: physics at TeV Colliders Standard Model Working Group Report in 9th Les Houches Workshop on Physics at TeV Colliders (PhysTeV 2015) Les Houches, France, June 1–19, 2015 (2016). arXiv:1605.04692 [hep-ph], http://lss.fnal.gov/archive/2016/conf/fermilab-conf-16-175-ppd-t.pdf
T. Sjostrand, V.A. Khoze, On color rearrangement in hadronic W+ W\(-\) events. Z. Phys. C 62, 281–310 (1994). https://doi.org/10.1007/BF01560244. arXiv:hep-ph/9310242 [hep-ph], Preprint CERN-TH-7011-93, DTP-93-74
The LEP Electroweak Working Group and the ALEPH, DELPHI, L3, OPAL Collaborations, Electroweak measurements in electron–positron collisions at W-boson-pair energies at LEP. Phys. Rep. 532, 119–244 (2013). arXiv:1302.3415 [hep-ex], Preprint CERN-PH-EP-2013-022, https://doi.org/10.1016/j.physrep.2013.07.004
S. Argyropoulos, T. Sjöstrand, Effects of color reconnection on \(t\bar{t}\) final states at the LHC. JHEP 11, 043 (2014). https://doi.org/10.1007/JHEP11(2014)043. arXiv:1407.6653 [hep-ph], Preprint LU-TP-14-23, DESY-14-134, MCNET-14-15
J.R. Christiansen, P.Z. Skands, String formation beyond leading colour. JHEP 08, 003 (2015). https://doi.org/10.1007/JHEP08(2015)003. arXiv:1505.01681 [hep-ph], Preprint COEPP-MN-15-1, LU-TP-15-16, MCNET-15-09
C. Bierlich, G. Gustafson, L. Lönnblad, A shoving model for collectivity in hadronic collisions. arXiv:1612.05132 [hep-ph], Preprint MCNET-16-48, LU-TP-16-64
A. Karneyeu, L. Mijovic, S. Prestel, P.Z. Skands, MCPLOTS: a particle physics resource based on volunteer computing. Eur. Phys. J. C 74, 2714 (2014). https://doi.org/10.1140/epjc/s10052-014-2714-9. arXiv:1306.3436 [hep-ph], Preprint CERN-PH-TH-2013-105, DESY-13-104, LU-TP-13-23, NSF-KITP-13-116
CMS Collaboration, V. Khachatryan et al., Observation of long-range near-side angular correlations in proton–proton collisions at the LHC. JHEP 09, 091 (2010). arXiv:1009.4122 [hep-ex], Preprint CMS-QCD-10-002, CERN-PH-EP-2010-031, https://doi.org/10.1007/JHEP09(2010)091
ALICE Collaboration, J. Adam et al., Enhanced production of multi-strange hadrons in high-multiplicity proton–proton collisions. Nat. Phys. 13, 535–539 (2017). arXiv:1606.07424 [nucl-ex], Preprint CERN-EP-2016-153, https://doi.org/10.1038/nphys4111
DELPHI Collaboration, P. Abreu et al., Strange baryon production in Z hadronic decays. Z. Phys. C 67, 543–554 (1995). Preprint CERN-PPE-95-039, CERN-PPE-95-39, https://doi.org/10.1007/BF01553980
OPAL Collaboration, G. Alexander et al., Strange baryon production in hadronic Z0 decays. Z. Phys. C 73, 569–586 (1997). Preprint CERN-PPE-96-099, CERN-PPE-96-99, https://doi.org/10.1007/s002880050349
OPAL Collaboration, R. Akers et al., Inclusive strange vector and tensor meson production in hadronic Z0 decays. Z. Phys. C 68, 1–12 (1995). Preprint CERN-PPE-95-027, CERN-PPE-95-27, https://doi.org/10.1007/BF01579799
OPAL Collaboration, G. Abbiendi et al., A study of parton fragmentation in hadronic Z0 decays using Lambda anti-Lambda correlations. Eur. Phys. J. C 13, 185–195 (2000). arXiv:hep-ex/9808031 [hep-ex], Preprint CERN-EP-98-114, https://doi.org/10.1007/s100520000207, https://doi.org/10.1007/s100520050685
ATLAS Collaboration, M. Aaboud et al., Jet energy scale measurements and their systematic uncertainties in proton–proton collisions at \(\sqrt{s} = 13\) TeV with the ATLAS detector. Phys. Rev. D 96(7), 072002 (2017). arXiv:1703.09665 [hep-ex], Preprint CERN-EP-2017-038, https://doi.org/10.1103/PhysRevD.96.072002
CMS Collaboration, V. Khachatryan et al., Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV. JINST 12(02), P02014 (2017). arXiv:1607.03663 [hep-ex], Preprint CMS-JME-13-004, CERN-PH-EP-2015-305, https://doi.org/10.1088/1748-0221/12/02/P02014
M. Klein, Future deep inelastic scattering with the LHeC. arXiv:1802.04317 [hep-ph], http://inspirehep.net/record/1654806/files/1802.04317.pdf
S. Alekhin et al., HERAFitter. Eur. Phys. J. C 75(7), 304 (2015). https://doi.org/10.1140/epjc/s10052-015-3480-z. arXiv:1410.4412 [hep-ph], Preprint DESY-14-188, DESY-REPORT-14-188, FERMILAB-PUB-14-603-CMS
ZEUS, H1 Collaboration, F.D. Aaron et al., Combined measurement and QCD analysis of the inclusive e+\(-\) p scattering cross sections at HERA. JHEP 01, 109 (2010). arXiv:0911.0884 [hep-ex], Preprint DESY-09-158, https://doi.org/10.1007/JHEP01(2010)109
H1 Collaboration, F.D. Aaron et al., A precision measurement of the inclusive \(ep\) scattering cross section at HERA. Eur. Phys. J. C 64, 561 (2009). arXiv:0904.3513 [hep-ex], Preprint DESY-09-005, DESY09-005, https://doi.org/10.1140/epjc/s10052-009-1169-x
S. Dulat, T.-J. Hou, J. Gao, M. Guzzi, J. Huston, P. Nadolsky, J. Pumplin, C. Schmidt, D. Stump, C.P. Yuan, New parton distribution functions from a global analysis of quantum chromodynamics. Phys. Rev. D 93(3), 033006 (2016). https://doi.org/10.1103/PhysRevD.93.033006. arXiv:1506.07443 [hep-ph]
L.A. Harland-Lang, A.D. Martin, P. Motylinski, R.S. Thorne, Parton distributions in the LHC era: MMHT 2014 PDFs. Eur. Phys. J. C 75(5), 204 (2015). https://doi.org/10.1140/epjc/s10052-015-3397-6. arXiv:1412.3989 [hep-ph], Preprint LCTS-2014-47, IPPP-14-97, DCPT-14-194
ATLAS Collaboration, M. Aaboud et al., Precision measurement and interpretation of inclusive \(W^+\) , \(W^-\) and \(Z/\gamma ^*\) production cross sections with the ATLAS detector. Eur. Phys. J. C 77(6), 367 (2017). arXiv:1612.03016 [hep-ex], Preprint CERN-EP-2016-272, https://doi.org/10.1140/epjc/s10052-017-4911-9
R.D. Ball, L. Del Debbio, S. Forte, A. Guffanti, J.I. Latorre, J. Rojo, M. Ubiali, A first unbiased global NLO determination of parton distributions and their uncertainties. Nucl. Phys. B 838, 136–206 (2010). https://doi.org/10.1016/j.nuclphysb.2010.05.008. arXiv:1002.4407 [hep-ph], Preprint EDINBURGH-2010-05, IFUM-952-FT, FR-PHENO-2010-014, CP3-10-08
J. Butterworth et al., PDF4LHC recommendations for LHC Run II. J. Phys. G 43, 023001 (2016). https://doi.org/10.1088/0954-3899/43/2/023001. arXiv:1510.03865 [hep-ph], Preprint OUTP-15-17P, SMU-HEP-15-12, TIF-UNIMI-2015-14, LCTS-2015-27, CERN-PH-TH-2015-249
I.I. Balitsky, L.N. Lipatov, The Pomeranchuk singularity in quantum chromodynamics. Sov. J. Nucl. Phys. 28, 822–829 (1978). [Yad. Fiz. 28, 1597 (1978)]
E.A. Kuraev, L.N. Lipatov, V.S. Fadin, The Pomeranchuk singularity in nonabelian gauge theories. Sov. Phys. JETP 45, 199–204 (1977). [Zh. Eksp. Teor. Fiz. 72, 377 (1977)]
M. Ciafaloni, D. Colferai, G.P. Salam, A.M. Stasto, Renormalization group improved small x Green’s function. Phys. Rev. D 68, 114003 (2003). https://doi.org/10.1103/PhysRevD.68.114003. arXiv:hep-ph/0307188 [hep-ph], Preprint DESY-03-060, DFF-404-05-03, LPTHE-03-20
G. Altarelli, R.D. Ball, S. Forte, Resummation of singlet parton evolution at small x. Nucl. Phys. B 575, 313–329 (2000). https://doi.org/10.1016/S0550-3213(00)00032-8. arXiv:hep-ph/9911273 [hep-ph], Preprint CERN-TH-99-317, RM3-TH-99-11, EDINBURGH-99-18
R.D. Ball, V. Bertone, M. Bonvini, S. Marzani, J. Rojo, L. Rottoli, Parton distributions with small-x resummation: evidence for BFKL dynamics in HERA data. Eur. Phys. J. C 78(4), 321 (2018). https://doi.org/10.1140/epjc/s10052-018-5774-4. arXiv:1710.05935 [hep-ph], Preprint EDINBURGH-2017-15, NIKHEF-2017-027, OUTP-17-12P
N. Armesto, A.H. Rezaeian, Exclusive vector meson production at high energies and gluon saturation. Phys. Rev. D 90(5), 054003 (2014). https://doi.org/10.1103/PhysRevD.90.054003. arXiv:1402.4831 [hep-ph]
J.C. Collins, Proof of factorization for diffractive hard scattering. Phys. Rev. D 57, 3051–3056 (1998). arXiv:hep-ph/9709499 [hep-ph], Preprint PSU-TH-189, https://doi.org/10.1103/PhysRevD.61.019902, https://doi.org/10.1103/PhysRevD.57.3051, [Erratum: Phys. Rev. D 61, 019902 (2000)]
ATLAS Collaboration, M. Aaboud et al., Measurement of the top quark mass in the \(t\bar{t}\rightarrow \) lepton+jets channel from \(\sqrt{s}=8\) TeV ATLAS data and combination with previous results. arXiv:1810.01772 [hep-ex], Preprint CERN Preprint ID: CERN-EP-2018-238
CMS Collaboration, V. Khachatryan et al., Measurement of the top quark mass using proton–proton data at \({\sqrt{s}} = 7\) and 8 TeV. Phys. Rev. D 93(7), 072004 (2016). arXiv:1509.04044 [hep-ex], Preprint CMS-TOP-14-022, CERN-PH-EP-2015-234, https://doi.org/10.1103/PhysRevD.93.072004
G. Degrassi, S. Di Vita, J. Elias-Miro, J.R. Espinosa, G.F. Giudice, G. Isidori, A. Strumia, Higgs mass and vacuum stability in the Standard Model at NNLO. JHEP 08, 098 (2012). https://doi.org/10.1007/JHEP08(2012)098. arXiv:1205.6497 [hep-ph], Preprint CERN-PH-TH-2012-134, RM3-TH-12-9
F. Simon, Impact of theory uncertainties on the precision of the top quark mass in a threshold scan at future e+e\(-\) colliders. PoS ICHEP 2016, 872 (2017). https://doi.org/10.22323/1.282.0872. arXiv:1611.03399 [hep-ex], Preprint MPP-2016-325
P. Janot, Top-quark electroweak couplings at the FCC-ee. JHEP 04, 182 (2015). https://doi.org/10.1007/JHEP04(2015)182. arXiv:1503.01325 [hep-ph]
S. De Curtis, M. Redi, A. Tesi, The 4D composite Higgs. JHEP 04, 042 (2012). https://doi.org/10.1007/JHEP04(2012)042. arXiv:1110.1613 [hep-ph]
CLICdp Collaboration, H. Abramowicz et al., Top-quark physics at the CLIC electron–positron linear collider. arXiv:1807.02441 [hep-ex], Preprint CLICdp-Pub-2018-003, CLICDP-PUB-2018-003
D. Barducci et al., Interpreting top-quark LHC measurements in the standard-model effective field theory. arXiv:1802.07237 [hep-ph], Preprint CERN-LPCC-2018-01
O. Gedalia, G. Isidori, F. Maltoni, G. Perez, M. Selvaggi, Y. Soreq, Top B physics at the LHC. Phys. Rev. Lett. 110(23), 232002 (2013). https://doi.org/10.1103/PhysRevLett.110.232002. arXiv:1212.4611 [hep-ph], Preprint CERN-PH-TH-2012-352, CP3-12-56
M. Mangano, T. Melia, Rare exclusive hadronic W decays in a \(t\bar{t}\) environment. Eur. Phys. J. C 75(6), 258 (2015). https://doi.org/10.1140/epjc/s10052-015-3482-x. arXiv:1410.7475 [hep-ph]
J.A. Aguilar-Saavedra, B. Fuks, M.L. Mangano, Pinning down top dipole moments with ultra-boosted tops. Phys. Rev. D 91, 094021 (2015). https://doi.org/10.1103/PhysRevD.91.094021. arXiv:1412.6654 [hep-ph], Preprint CERN-PH-TH-2014-259
P. Torrielli, Rare Standard Model processes for present and future hadronic colliders. arXiv:1407.1623 [hep-ph], Preprint ZU-TH-22-14
F. Maltoni, D. Pagani, I. Tsinikos, Associated production of a top-quark pair with vector bosons at NLO in QCD: impact on \(t \bar{t} H\) searches at the LHC. arXiv:1507.05640 [hep-ph], Preprint CP3-15-20
R. Röntsch, M. Schulze, Probing top-Z dipole moments at the LHC and ILC. JHEP 08, 044 (2015). https://doi.org/10.1007/JHEP08(2015)044. arXiv:1501.05939 [hep-ph], Preprint CERN-PH-TH-2015-004, FERMILAB-PUB-15-010-T
M. Schulze, Y. Soreq, Pinning down electroweak dipole operators of the top quark. Eur. Phys. J. C 76(8), 466 (2016). https://doi.org/10.1140/epjc/s10052-016-4263-x. arXiv:1603.08911 [hep-ph], Preprint CERN-TH-2016-070, MIT-CTP-4790
J.A. Aguilar-Saavedra, D. Amidei, A. Juste, M. Perez-Victoria, Asymmetries in top quark pair production at hadron colliders. Rev. Mod. Phys. 87, 421–455 (2015). https://doi.org/10.1103/RevModPhys.87.421. arXiv:1406.1798 [hep-ph], Preprint CERN-PH-TH-2014-101
F. Maltoni, M.L. Mangano, I. Tsinikos, M. Zaro, Top-quark charge asymmetry and polarization in \(t\overline{t}W\) production at the LHC. Phys. Lett. B 736, 252–260 (2014). https://doi.org/10.1016/j.physletb.2014.07.033. arXiv:1406.3262 [hep-ph], Preprint CP3-14-23, CERN-PH-TH-2014-102, LPN14-075
J.A. Aguilar-Saavedra, E. Álvarez, A. Juste, F. Rubbo, Shedding light on the \(t \bar{t}\) asymmetry: the photon handle. JHEP 04, 188 (2014). https://doi.org/10.1007/JHEP04(2014)188. arXiv:1402.3598 [hep-ph]
A. Papaefstathiou, G. Tetlalmatzi-Xolocotzi, Rare top quark decays at a 100 TeV proton-proton collider: \(t \rightarrow bWZ\) and \(t\rightarrow hc\). Eur. Phys. J. C 78(3), 214 (2018). https://doi.org/10.1140/epjc/s10052-018-5701-8. arXiv:1712.06332 [hep-ph], Preprint NIKHEF-2017-069, MCNET-17-24
S. Dutta, A. Goyal, M. Kumar, B. Mellado, Measuring anomalous \(Wtb\) couplings at \(e^-p\) collider. Eur. Phys. J. C 75(12), 577 (2015). https://doi.org/10.1140/epjc/s10052-015-3776-z. arXiv:1307.1688 [hep-ph]
H. Denizli, A. Senol, A. Yilmaz, I. Turk Cakir, H. Karadeniz, O. Cakir, Top quark FCNC couplings at future circular hadron electron colliders. Phys. Rev. D 96(1), 015024 (2017). https://doi.org/10.1103/PhysRevD.96.015024. arXiv:1701.06932 [hep-ph]
S. Ovyn, X. Rouby, V. Lemaitre, DELPHES, a framework for fast simulation of a generic collider experiment. arXiv:0903.2225 [hep-ph], Preprint CP3-09-01
CMS Collaboration, V. Khachatryan et al., Measurement of the t-channel single-top-quark production cross section and of the \(\mid V_{tb} \mid \) CKM matrix element in pp collisions at \(\sqrt{s}\)= 8 TeV. JHEP 06, 090 (2014). arXiv:1403.7366 [hep-ex], Preprint CMS-TOP-12-038, CERN-PH-EP-2014-032, https://doi.org/10.1007/JHEP06(2014)090
H. Sun, Measuring the CKM matrix element \(V_{td}\) and \(V_{ts}\) at the electron proton colliders, in Proceedings of the 26th International Workshop on Deep Inelastic Scattering and Related Subjects (DIS 2018) 16–20 April 2018, Kobe (2018)
CMS Collaboration, V. Khachatryan et al., Measurement of the ratio \(\cal{B}(t \rightarrow Wb)/\cal{B}(t \rightarrow Wq)\) in pp collisions at \(\sqrt{s}\) = 8 TeV. Phys. Lett. B 736, 33–57 (2014). arXiv:1404.2292 [hep-ex], Preprint CMS-TOP-12-035, CERN-PH-EP-2014-052, https://doi.org/10.1016/j.physletb.2014.06.076
J.A. Aguilar-Saavedra, Top flavor-changing neutral interactions: theoretical expectations and experimental detection. Acta Phys. Polon. B 35, 2695–2710 (2004). arXiv:hep-ph/0409342 [hep-ph]
J. Charles et al., Current status of the Standard Model CKM fit and constraints on \(\Delta F=2\) new physics. Phys. Rev. D 91(7), 073007 (2015). https://doi.org/10.1103/PhysRevD.91.073007. arXiv:1501.05013 [hep-ph], Preprint LPT-ORSAY-15-04
O. Cakir, A. Yilmaz, I. Turk Cakir, A. Senol, H. Denizli, Probing top quark FCNC \(tq\gamma \) and \(tqZ\) couplings at future electron–proton colliders. arXiv:1809.01923 [hep-ph]
Top Quark Working Group Collaboration, K. Agashe et al., Working Group Report: Top Quark in Proceedings, 2013 Community Summer Study on the Future of U.S. Particle Physics: Snowmass on the Mississippi (CSS2013): Minneapolis, July 29–August 6, 2013 (2013). arXiv:1311.2028 [hep-ph], http://www.slac.stanford.edu/econf/C1307292/docs/Top-21.pdf
H. Sun, X. Wang, Exploring the anomalous top-Higgs FCNC couplings at the electron proton colliders. Eur. Phys. J. C 78(4), 281 (2018). https://doi.org/10.1140/epjc/s10052-018-5761-9. arXiv:1602.04670 [hep-ph]
A.O. Bouzas, F. Larios, Probing tt\(\gamma \) and ttZ couplings at the LHeC. Phys. Rev. D 88(9), 094007 (2013). https://doi.org/10.1103/PhysRevD.88.094007. arXiv:1308.5634 [hep-ph]
S. Atag, B. Sahin, Effect of top quark spin on the Wtb couplings in e+ p collisions. Phys. Rev. D 73, 074001 (2006). https://doi.org/10.1103/PhysRevD.73.074001
G.R. Boroun, Geometrical scaling behavior of the top structure functions ratio at the LHeC. Phys. Lett. B 744, 142–145 (2015). https://doi.org/10.1016/j.physletb.2015.03.051. arXiv:1503.01590 [hep-ph]
LHCb Collaboration, I. Bediaga et al., Physics case for an LHCb Upgrade II—opportunities in flavour physics, and beyond, in the HL-LHC era. arXiv:1808.08865, Preprint LHCB-PUB-2018-009, CERN-LHCC-2018-027
Belle II Collaboration, E. Kou et al., The Belle II Physics Book. arXiv:1808.10567 [hep-ex], Preprint KEK Preprint 2018-27, BELLE2-PUB-PH-2018-001, FERMILAB-PUB-18-398-T, JLAB-THY-18-2780, INT-PUB-18-047, UWThPh 2018-26
W. Altmannshofer, D.M. Straub, New physics in \(B \rightarrow K^*\mu \mu \)? Eur. Phys. J C 73, 2646 (2013). https://doi.org/10.1140/epjc/s10052-013-2646-9. arXiv:1308.1501 [hep-ph], Preprint FERMILAB-PUB-13-310-T, MITP-13-047
A. Buras, F. De Fazio, J. Girrbach, M.V. Carlucci, The anatomy of quark flavour observables in 331 models in the flavour precision era. JHEP 02, 023 (2013). arXiv:1211.1237 [hep-ph], Preprint FLAVOUR(267104)-ERC-25, BARI-TH-12-658, https://doi.org/10.1007/JHEP02(2013)023
R. Gauld, F. Goertz, U. Haisch, An explicit Z’-boson explanation of the \(B \rightarrow K^* \mu ^+ \mu ^-\) anomaly. JHEP 01, 069 (2014). https://doi.org/10.1007/JHEP01(2014)069. arXiv:1310.1082 [hep-ph]
S. Descotes-Genon, L. Hofer, J. Matias, J. Virto, Global analysis of \(b\rightarrow s\ell \ell \) anomalies. JHEP 06, 092 (2016). https://doi.org/10.1007/JHEP06(2016)092. arXiv:1510.04239 [hep-ph], Preprint LPT-ORSAY-15-68, QFET-2015-29, SI-HEP-2015-19
LHCb Collaboration, R. Aaij et al., Test of lepton universality using \(B^{+}\rightarrow K^{+}\ell ^{+}\ell ^{-}\) decays. Phys. Rev. Lett. 113, 151601 (2014). arXiv:1406.6482 [hep-ex], Preprint CERN-PH-EP-2014-140, LHCB-PAPER-2014-024, https://doi.org/10.1103/PhysRevLett.113.151601
LHCb Collaboration, R. Aaij et al., Angular analysis of the \(B^{0} \rightarrow K^{*0} \mu ^{+} \mu ^{-}\) decay using 3 fb\(^{-1}\) of integrated luminosity. JHEP 02, 104 (2016). arXiv:1512.04442 [hep-ex], Preprint CERN-PH-EP-2015-314, LHCB-PAPER-2015-051, https://doi.org/10.1007/JHEP02(2016)104
Belle Collaboration, A. Abdesselam et al., Angular analysis of \(B^0 \rightarrow K^\ast (892)^0 \ell ^+ \ell ^-\) in LHC Ski 2016 (2016). arXiv:1604.04042 [hep-ex], https://inspirehep.net/record/1446979/files/arXiv:1604.04042.pdf
F. Gaede, S. Aplin, R. Glattauer, C. Rosemann, G. Voutsinas, Track reconstruction at the ILC: the ILD tracking software. J. Phys. Conf. Ser. 513(2), 022011 (2014). http://stacks.iop.org/1742-6596/513/i=2/a=022011
J.F. Kamenik, S. Monteil, A. Semkiv, L.V. Silva, Lepton polarization asymmetries in rare semi-tauonic \( b \rightarrow s \) exclusive decays at FCC-\(ee\). Eur. Phys. J. C 77(10), 701 (2017). https://doi.org/10.1140/epjc/s10052-017-5272-0. arXiv:1705.11106 [hep-ph]
T. Asaka, S. Blanchet, M. Shaposhnikov, The nuMSM, dark matter and neutrino masses. Phys. Lett. B 631, 151–156 (2005). https://doi.org/10.1016/j.physletb.2005.09.070. arXiv:hep-ph/0503065 [hep-ph]
R.N. Mohapatra, J.W.F. Valle, Neutrino mass and Baryon number nonconservation in superstring models. Phys. Rev. D 34, 1642 (1986). https://doi.org/10.1103/PhysRevD.34.1642. Preprint MdDP-PP-86-127
A. Abada, V. De Romeri, S. Monteil, J. Orloff, A.M. Teixeira, Indirect searches for sterile neutrinos at a high-luminosity Z-factory. JHEP 04, 051 (2015). https://doi.org/10.1007/JHEP04(2015)051. arXiv:1412.6322 [hep-ph], Preprint LPT-Orsay-14-78, PCCF-RI-14-07
COMET Collaboration, Y. Kuno, A search for muon-to-electron conversion at J-PARC: the COMET experiment. PTEP 2013, 022C01 (2013). Preprint 2013PTEP.2013b2C01K, https://doi.org/10.1093/ptep/pts089
L3 Collaboration, O. Adriani et al., Search for LFV in \(Z\) decays. Phys. Lett. B 316, 427–434 (1993). Preprint CERN-PPE-93-151, https://doi.org/10.1016/0370-2693(93)90348-L
OPAL Collaboration, R. Akers et al., A search for LFV \(Z^0\) decays. Z. Phys. C 67, 555–564 (1995). Preprint CERN-PPE-95-043, CERN-PPE-95-43, https://doi.org/10.1007/BF01553981
DELPHI Collaboration, P. Abreu et al., Search for LF number violating \(Z^0\) decays. Z. Phys. C 73, 243–251 (1997). Preprint CERN-PPE-96-129, https://doi.org/10.1007/s002880050313
ATLAS Collaboration, G. Aad et al., Search for the LFV decay \(Z \rightarrow e\mu \) in pp collisions at \(\sqrt{s}\)= 7 TeV with the ATLAS detector. Phys. Rev. D 90(7), 072010 (2014). arXiv:1408.5774 [hep-ex], Preprint CERN-PH-EP-2014-195, https://doi.org/10.1103/PhysRevD.90.072010
M. Dam, Tau-lepton physics at the FCC-ee circular e\(^+\)e\(^-\) collider. Sci. Post Phys. Proc., 41 (2019). arXiv:1811.09408 [hep-ex], https://doi.org/10.21468/SciPostPhysProc.1.041
A. Pich, Precision tau physics. Prog. Part. Nucl. Phys. 75, 41–85 (2014). https://doi.org/10.1016/j.ppnp.2013.11.002
A. Greljo, G. Isidori, D. Marzocca, On the breaking of lepton flavor universality in B decays. JHEP 07, 142 (2015). https://doi.org/10.1007/JHEP07(2015)142. arXiv:1506.01705 [hep-ph], Preprint ZU-TH-16-15
F. Feruglio, P. Paradisi, A. Pattori, Revisiting lepton flavor universality in B decays. Phys. Rev. Lett. 118(1), 011801 (2017). https://doi.org/10.1103/PhysRevLett.118.011801. arXiv:1606.00524 [hep-ph]
ALEPH Collaboration, S. Schael et al., Branching ratios and spectral functions of \(\tau \) decays: final ALEPH measurements and physics implications. Phys. Rep. 421(5), 191–284 (2005)
DELPHI Collaboration, P. Abreu et al., Measurements of the leptonic branching fractions of the tau. Eur. Phys. J. C 10(2), 201–218 (1999)
L3 Collaboration, M. Acciarri et al., Measurement of the tau branching fractions into leptons. Phys. Lett. B 507(1), 47–60 (2001)
G. Abbiendi et al., A measurement of the \(\tau ^- \rightarrow \text{ e }^-\bar{\nu }_{{\rm e}} \nu _\tau \) branching ratio. Phys. Lett. B 447(1), 134–146 (1999)
OPAL Collaboration, G. Abbiendi et al., A measurement of the \(\tau ^- \rightarrow \mu ^-\bar{\nu }_\mu \nu _\tau \) branching ratio. Phys. Lett. B 551(1), 35–48 (2003)
A. Lusiani, HFLAV branching fractions fit and measurements of Vus with lepton data. Sci. Post Phys. Proc. 1 (2019). https://doi.org/10.21468/SciPostPhysProc.1.001
Belle Collaboration, K. Belous et al., Measurement of the \(\tau \)-lepton Lifetime at Belle. Phys. Rev. Lett. 112, 031801 (2014)
M. Bordone, C. Cornella, J. Fuentes-Martin, G. Isidori, Low-energy signatures of the \(\text{ PS }^3\) model: from \(B\)-physics anomalies to LFV. JHEP 10, 148 (2018). https://doi.org/10.1007/JHEP10(2018)148. arXiv:1805.09328 [hep-ph], Preprint ZU-TH-18/18, ZU-TH-18-18
Belle, BaBar Collaboration, A.J. Bevan et al., The physics of the B factories. Eur. Phys. J. C 74, 3026 (2014). arXiv:1406.6311 [hep-ex], Preprint SLAC-PUB-15968, KEK-PREPRINT-2014-3, FERMILAB-PUB-14-262-T, https://doi.org/10.1140/epjc/s10052-014-3026-9
LHCb Collaboration, M.W. Kenzie, M.P. Whitehead, Update of the LHCb combination of the CKM angle \(\gamma \) (2018). LHCb-CONF-2018-002, CERN-LHCb-CONF-2018-002
G. D’Ambrosio, G.F. Giudice, G. Isidori, A. Strumia, Minimal flavor violation: an effective field theory approach. Nucl. Phys. B 645, 155–187 (2002). https://doi.org/10.1016/S0550-3213(02)00836-2. arXiv:hep-ph/0207036 [hep-ph], Preprint CERN-TH-2002-147, IFUP-TH-2002-17
A. Lenz, U. Nierste, J. Charles, S. Descotes-Genon, A. Jantsch, C. Kaufhold, H. Lacker, S. Monteil, V. Niess, S. T’Jampens, Anatomy of new physics in \(B - \bar{B}\) mixing. Phys. Rev. D 83, 036004 (2011). https://doi.org/10.1103/PhysRevD.83.036004. arXiv:1008.1593 [hep-ph], Preprint HU-EP-10-43-TTP10-33, DO-TH-10-05, SFB-CPP-10-68, LPT-ORSAY-10-59, CPT-P040-2010
A.G. Akeroyd, C.H. Chen, S. Recksiegel, Measuring \(B^\pm \rightarrow \tau ^\pm \nu \) and \(B^\pm _c \rightarrow \tau ^\pm \nu \) at the \(Z\) peak. Phys. Rev. D 77, 115018 (2008). https://doi.org/10.1103/PhysRevD.77.115018. arXiv:0803.3517 [hep-ph], Preprint TUM-HEP-683-08
Y. Grossman, M. König, M. Neubert, Exclusive radiative decays of W and Z bosons in QCD factorization. JHEP 04, 101 (2015). https://doi.org/10.1007/JHEP04(2015)101. arXiv:1501.06569 [hep-ph], Preprint MITP-15-002
W. Buchmuller, D. Wyler, Effective Lagrangian analysis of new interactions and flavor conservation. Nucl. Phys. B 268, 621–653 (1986). https://doi.org/10.1016/0550-3213(86)90262-2. Preprint CERN-TH-4254/85
G.F. Giudice, C. Grojean, A. Pomarol, R. Rattazzi, The strongly-interacting light Higgs. JHEP 06, 045 (2007). https://doi.org/10.1088/1126-6708/2007/06/045. arXiv:hep-ph/0703164 [hep-ph], Preprint CERN-PH-TH-2007-47
B. Grzadkowski, M. Iskrzynski, M. Misiak, J. Rosiek, Dimension-six terms in the standard model Lagrangian. JHEP 10, 085 (2010). https://doi.org/10.1007/JHEP10(2010)085. arXiv:1008.4884 [hep-ph], Preprint IFT-9-2010, TTP10-35
R. Contino, M. Ghezzi, C. Grojean, M. Muhlleitner, M. Spira, Effective Lagrangian for a light Higgs-like scalar. JHEP 07, 035 (2013). https://doi.org/10.1007/JHEP07(2013)035. arXiv:1303.3876 [hep-ph], Preprint CERN-PH-TH-2013-047, KA-TP-06-2013, PSI-PR-13-04
LHC Higgs Cross Section Working Group Collaboration, D. de Florian et al., Handbook of LHC Higgs Cross Sections: 4. Deciphering the Nature of the Higgs Sector. arXiv:1610.07922 [hep-ph], Preprint FERMILAB-FN-1025-T, CERN-2017-002-M, https://doi.org/10.23731/CYRM-2017-002
A. Kobach, Baryon number, Lepton number, and operator dimension in the standard model. Phys. Lett. B 758, 455–457 (2016). https://doi.org/10.1016/j.physletb.2016.05.050. arXiv:1604.05726 [hep-ph], Preprint PHYS.LETT.-B758-(2016)-455-457
HEPfit Collaboration, HEPfit: a code for the combination of indirect and direct constraints on high energy physics models (in preparation)
HEPfit Collaboration. http://hepfit.roma1.infn.it
M. Farina, G. Panico, D. Pappadopulo, J.T. Ruderman, R. Torre, A. Wulzer, Energy helps accuracy: electroweak precision tests at hadron colliders. Phys. Lett. B 772, 210–215 (2017). https://doi.org/10.1016/j.physletb.2017.06.043. arXiv:1609.08157 [hep-ph], Preprint CERN-TH-2016-205
R. Barbieri, A. Pomarol, R. Rattazzi, A. Strumia, Electroweak symmetry breaking after LEP-1 and LEP-2. Nucl. Phys. B 703, 127–146 (2004). https://doi.org/10.1016/j.nuclphysb.2004.10.014. arXiv:hep-ph/0405040 [hep-ph], Preprint CERN-PH-TH-2004-075, IFUP-TH-2004-13, UAB-FT-565
D.S.M. Alves, J. Galloway, J.T. Ruderman, J.R. Walsh, Running electroweak couplings as a probe of new physics. JHEP 02, 007 (2015). https://doi.org/10.1007/JHEP02(2015)007. arXiv:1410.6810 [hep-ph]
LHC Higgs Cross Section Working Group Collaboration, A. David, A. Denner, M. Duehrssen, M. Grazzini, C. Grojean, G. Passarino, M. Schumacher, M. Spira, G. Weiglein, M. Zanetti, LHC HXSWG interim recommendations to explore the coupling structure of a Higgs-like particle. arXiv:1209.0040 [hep-ph], Preprint CERN-PH-TH-2012-284, LHCHXSWG-2012-001
LHC Higgs Cross Section Working Group Collaboration, J.R. Andersen et al., Handbook of LHC Higgs Cross Sections: 3. Higgs Properties. arXiv:1307.1347 [hep-ph], Preprint CERN-2013-004, FERMILAB-CONF-13-667-T, https://doi.org/10.5170/CERN-2013-004
J. Elias-Miro, J.R. Espinosa, E. Masso, A. Pomarol, Higgs windows to new physics through d=6 operators: constraints and one-loop anomalous dimensions. JHEP 11, 066 (2013). https://doi.org/10.1007/JHEP11(2013)066. arXiv:1308.1879 [hep-ph]
A. Pomarol, F. Riva, Towards the ultimate SM fit to close in on Higgs physics. JHEP 01, 51 (2014). https://doi.org/10.1007/JHEP01(2014)151. arXiv:1308.2803 [hep-ph]
J. Ellis, V. Sanz, T. You, Complete Higgs sector constraints on dimension-6 operators. JHEP 07, 036 (2014). https://doi.org/10.1007/JHEP07(2014)036. arXiv:1404.3667 [hep-ph], Preprint KCL-PH-TH-2014-15, LCTS-2014-14, CERN-PH-TH-2014-061
A. Falkowski, Effective field theory approach to LHC Higgs data. Pramana 87(3), 39 (2016). https://doi.org/10.1007/s12043-016-1251-5. arXiv:1505.00046 [hep-ph], Preprint LPT-ORSAY-15-33
A. Butter, O.J.P. Eboli, J. Gonzalez-Fraile, M.C. Gonzalez-Garcia, T. Plehn, M. Rauch, The Gauge-Higgs legacy of the LHC Run I. JHEP 07, 152 (2016). https://doi.org/10.1007/JHEP07(2016)152. arXiv:1604.03105 [hep-ph], Preprint YITP-SB-16-10
J. de Blas, M. Ciuchini, E. Franco, S. Mishima, M. Pierini, L. Reina, L. Silvestrini, The Global Electroweak and Higgs Fits in the LHC era, in 5th Large Hadron Collider Physics Conference (LHCP 2017) Shanghai, May 15–20, 2017 (2017). arXiv:1710.05402 [hep-ph]
J. de Blas, O. Eberhardt, C. Krause, Current and future constraints on Higgs couplings in the nonlinear effective theory. JHEP 07, 048 (2018). https://doi.org/10.1007/JHEP07(2018)048. arXiv:1803.00939 [hep-ph], Preprint IFIC-17-48, FTUV-18-0305, FERMILAB-PUB-18-058-T
Z. Han, W. Skiba, Effective theory analysis of precision electroweak data. Phys. Rev. D 71, 075009 (2005). https://doi.org/10.1103/PhysRevD.71.075009. arXiv:hep-ph/0412166 [hep-ph]
M. Ciuchini, E. Franco, S. Mishima, L. Silvestrini, Electroweak precision observables, new physics and the nature of a 126 GeV Higgs boson. JHEP 08, 106 (2013). https://doi.org/10.1007/JHEP08(2013)106. arXiv:1306.4644 [hep-ph]
A. Falkowski, F. Riva, Model-independent precision constraints on dimension-6 operators. JHEP 02, 039 (2015). https://doi.org/10.1007/JHEP02(2015)039. arXiv:1411.0669 [hep-ph], Preprint LPT-ORSAY-14-77
A. Efrati, A. Falkowski, Y. Soreq, Electroweak constraints on flavorful effective theories. JHEP 07, 018 (2015). https://doi.org/10.1007/JHEP07(2015)018. arXiv:1503.07872 [hep-ph], Preprint LPT-ORSAY-15-23
A. Falkowski, M. Gonzalez-Alonso, A. Greljo, D. Marzocca, Global constraints on anomalous triple gauge couplings in effective field theory approach. Phys. Rev. Lett. 116(1), 011801 (2016). https://doi.org/10.1103/PhysRevLett.116.011801. arXiv:1508.00581 [hep-ph]
A. Falkowski, M. Gonzalez-Alonso, A. Greljo, D. Marzocca, M. Son, Anomalous triple gauge couplings in the effective field theory approach at the LHC. JHEP 02, 115 (2017). https://doi.org/10.1007/JHEP02(2017)115. arXiv:1609.06312 [hep-ph], Preprint ZU-TH-34-16
Z. Zhang, Time to go beyond triple-gauge-boson-coupling interpretation of \(W\) pair production. Phys. Rev. Lett. 118(1), 011803 (2017). https://doi.org/10.1103/PhysRevLett.118.011803. arXiv:1610.01618 [hep-ph], Preprint MCTP-16-24, DESY-16-189
J. Ellis, V. Sanz, T. You, The effective standard model after LHC Run I. JHEP 03, 157 (2015). https://doi.org/10.1007/JHEP03(2015)157. arXiv:1410.7703 [hep-ph], Preprint KCL-PH-TH-2014-41, LCTS-2014-41, CERN-PH-TH-2014-201
N. Craig, M. Farina, M. McCullough, M. Perelstein, Precision Higgsstrahlung as a probe of new physics. JHEP 03, 146 (2015). https://doi.org/10.1007/JHEP03(2015)146. arXiv:1411.0676 [hep-ph]
B. Henning, X. Lu, H. Murayama, What do precision Higgs measurements buy us?. arXiv:1404.1058 [hep-ph], Preprint UCB-PTH-14-06, IPMU14-0082
N. Craig, J. Gu, Z. Liu, K. Wang, Beyond Higgs couplings: probing the Higgs with angular observables at future \(\text{ e }^{+}\) \(\text{ e }^{-}\) colliders. JHEP 03, 050 (2016). https://doi.org/10.1007/JHEP03(2016)050. arXiv:1512.06877 [hep-ph], Preprint FERMILAB-PUB-15-569-T
J. Ellis, T. You, Sensitivities of prospective future e+e\(-\) colliders to decoupled new physics. JHEP 03, 089 (2016). https://doi.org/10.1007/JHEP03(2016)089. arXiv:1510.04561 [hep-ph], Preprint KCL-PH-TH-2015-47, LCTS-2015-35, CERN-PH-TH-2015-244, DAMTP-2015-62, CAVENDISH-HEP-15-09
J. de Blas, M. Ciuchini, E. Franco, S. Mishima, M. Pierini, L. Reina, L. Silvestrini, Electroweak precision observables and Higgs-boson signal strengths in the Standard Model and beyond: present and future. JHEP 12, 135 (2016). https://doi.org/10.1007/JHEP12(2016)135. arXiv:1608.01509 [hep-ph], Preprint KEK-TH-1919
J. Ellis, P. Roloff, V. Sanz, T. You, Dimension-6 operator analysis of the CLIC sensitivity to new physics. JHEP 05, 096 (2017). https://doi.org/10.1007/JHEP05(2017)096. arXiv:1701.04804 [hep-ph], Preprint KCL-PH-TH-2017-04, CERN-TH-2017-009, CAVENDISH-HEP-17-01, CERN-PH-TH-2017-009, DAMTP-2017-01
G. Durieux, C. Grojean, J. Gu, K. Wang, The leptonic future of the Higgs. JHEP 09, 014 (2017). https://doi.org/10.1007/JHEP09(2017)014. arXiv:1704.02333 [hep-ph], Preprint DESY-17-018
M. Beneke, D. Boito, Y.-M. Wang, Anomalous Higgs couplings in angular asymmetries of \(H \rightarrow Z\ell ^{+} \ell ^{-}\) and \(\text{ e }^{+}\) \(\text{ e }^{-} \rightarrow HZ\). JHEP 11, 028 (2014). https://doi.org/10.1007/JHEP11(2014)028. arXiv:1406.1361 [hep-ph], Preprint TUM-HEP-849-14, TTK-14-11, SFB-CPP-14-28, TUM-HEP-949-14
M. Kumar, X. Ruan, R. Islam, A.S. Cornell, M. Klein, U. Klein, B. Mellado, Probing anomalous couplings using di-Higgs production in electron-proton collisions. Phys. Lett. B 764, 247–253 (2017). https://doi.org/10.1016/j.physletb.2016.11.039. arXiv:1509.04016 [hep-ph], Preprint WITS-MITP-019
M. Farina, C. Grojean, F. Maltoni, E. Salvioni, A. Thamm, Lifting degeneracies in Higgs couplings using single top production in association with a Higgs boson. JHEP 05, 022 (2013). https://doi.org/10.1007/JHEP05(2013)022. arXiv:1211.3736 [hep-ph], Preprint CERN-PH-TH-2012-313, DFPD-2012-TH-20, CP3-12-47
C. Degrande, F. Maltoni, K. Mimasu, E. Vryonidou, C. Zhang, Single-top associated production with a \(Z\) or \(H\) boson at the LHC: the SMEFT interpretation. JHEP 10, 005 (2018). https://doi.org/10.1007/JHEP10(2018)005. arXiv:1804.07773 [hep-ph], Preprint CERN-TH-2018-092
A. Azatov, R. Contino, G. Panico, M. Son, Effective field theory analysis of double Higgs boson production via gluon fusion. Phys. Rev. D 92(3), 035001 (2015). https://doi.org/10.1103/PhysRevD.92.035001. arXiv:1502.00539 [hep-ph], Preprint CERN-PH-TH-2015-015
A. Azatov, C. Grojean, A. Paul, E. Salvioni, Resolving gluon fusion loops at current and future hadron colliders. JHEP 09, 123 (2016). https://doi.org/10.1007/JHEP09(2016)123. arXiv:1608.00977 [hep-ph]
A. Biekötter, A. Knochel, M. Krämer, D. Liu, F. Riva, Vices and virtues of Higgs effective field theories at large energy. Phys. Rev. D 91, 055029 (2015). https://doi.org/10.1103/PhysRevD.91.055029. arXiv:1406.7320 [hep-ph]
S. Banerjee, C. Englert, R.S. Gupta, M. Spannowsky, Probing electroweak precision physics via boosted Higgs-strahlung at the LHC. arXiv:1807.01796 [hep-ph], Preprint IPPP/18/53, IPPP-18-53
A. Senol, H. Denizli, A. Yilmaz, I. Turk Cakir, K.Y. Oyulmaz, O. Karadeniz, O. Cakir, Probing the effects of dimension-eight operators describing anomalous neutral triple Gauge boson interactions at FCC-hh. Nucl. Phys. B 935, 365–376 (2018). https://doi.org/10.1016/j.nuclphysb.2018.08.018. arXiv:1805.03475 [hep-ph]
C. Grojean, E. Salvioni, M. Schlaffer, A. Weiler, Very boosted Higgs in gluon fusion. JHEP 05, 022 (2014). https://doi.org/10.1007/JHEP05(2014)022. arXiv:1312.3317 [hep-ph], Preprint CERN-PH-TH-2013-292, DESY-13-233
A. Banfi, A. Martin, V. Sanz, Probing top-partners in Higgs+jets. JHEP 08, 053 (2014). https://doi.org/10.1007/JHEP08(2014)053. arXiv:1308.4771 [hep-ph], Preprint CERN-PH-TH-2013-199
A. Azatov, A. Paul, Probing Higgs couplings with high \(p_T\) Higgs production. JHEP 01, 014 (2014). https://doi.org/10.1007/JHEP01(2014)014. arXiv:1309.5273 [hep-ph]
R. Essig, P. Meade, H. Ramani, Y.-M. Zhong, Higgs-precision constraints on colored naturalness. JHEP 09, 085 (2017). https://doi.org/10.1007/JHEP09(2017)085. arXiv:1707.03399 [hep-ph], Preprint YITP-SB-17-25
T. Golling et al., Physics at a 100 TeV pp collider: beyond the Standard Model phenomena, CERN Yellow Report No. 3, pp. 441–634 (2017). arXiv:1606.00947 [hep-ph], Preprint CERN-TH-2016-111, FERMILAB-PUB-16-296-T, https://doi.org/10.23731/CYRM-2017-003.441
T. Cohen, R.T. D’Agnolo, M. Hance, H.K. Lou, J.G. Wacker, Boosting stop searches with a 100 TeV proton collider. JHEP 11, 021 (2014). https://doi.org/10.1007/JHEP11(2014)021. arXiv:1406.4512 [hep-ph], Preprint SLAC-PUB-15987
L. Gouskos, A. Sung, J. Incandela, Search for stop scalar quarks at FCC-hh. CERN-ACC-2019-0036. CERN, Geneva (2018). Preprint CERN-ACC-2019-0036. https://cds.cern.ch/record/2642475
A. Thamm, R. Torre, A. Wulzer, Future tests of Higgs compositeness: direct vs indirect. JHEP 07, 100 (2015). https://doi.org/10.1007/JHEP07(2015)100. arXiv:1502.01701 [hep-ph], Preprint DFPD-2014-TH-03, MITP-14-109
Z. Chacko, H.-S. Goh, R. Harnik, The twin Higgs: natural electroweak breaking from mirror symmetry. Phys. Rev. Lett. 96, 231802 (2006). https://doi.org/10.1103/PhysRevLett.96.231802. arXiv:hep-ph/0506256 [hep-ph]
Z. Chacko, H.-S. Goh, R. Harnik, A twin Higgs model from left-right symmetry. JHEP 01, 108 (2006). https://doi.org/10.1088/1126-6708/2006/01/108. arXiv:hep-ph/0512088 [hep-ph], Preprint SLAC-PUB-11595
G. Burdman, Z. Chacko, H.-S. Goh, R. Harnik, Folded supersymmetry and the LEP paradox. JHEP 02, 009 (2007). https://doi.org/10.1088/1126-6708/2007/02/009. arXiv:hep-ph/0609152 [hep-ph], Preprint SLAC-PUB-12115
J.J. van der Bij, Does low-energy physics depend on the potential of a heavy Higgs particle? Nucl. Phys. B 267, 557–565 (1986). https://doi.org/10.1016/0550-3213(86)90131-8. Preprint NIKHEF-H/85-1
M. McCullough, An indirect model-dependent probe of the Higgs self-coupling. Phys. Rev. D 90(1), 015001 (2014). arXiv:1312.3322 [hep-ph], Preprint MIT-CTP-4521, https://doi.org/10.1103/PhysRevD.90.015001, https://doi.org/10.1103/PhysRevD.92.039903 [Erratum: Phys. Rev. D 92(3), 039903 (2015)]
S. Di Vita, G. Durieux, C. Grojean, J. Gu, Z. Liu, G. Panico, M. Riembau, T. Vantalon, A global view on the Higgs self-coupling at lepton colliders. JHEP 02, 178 (2018). https://doi.org/10.1007/JHEP02(2018)178. arXiv:1711.03978 [hep-ph], Preprint DESY-17-131, FERMILAB-PUB-17-462-T
LHC Higgs cross section working group, HH sub-group. https://twiki.cern.ch/twiki/bin/view/LHCPhysics/LHCHXSWGHH
S. Borowka, N. Greiner, G. Heinrich, S.P. Jones, M. Kerner, J. Schlenk, T. Zirke, Full top quark mass dependence in Higgs boson pair production at NLO. JHEP 10, 107 (2016). https://doi.org/10.1007/JHEP10(2016)107. arXiv:1608.04798 [hep-ph], Preprint MPP-2016-261, ZU-TH-31-16
M. Grazzini, G. Heinrich, S. Jones, S. Kallweit, M. Kerner, J.M. Lindert, J. Mazzitelli, Higgs boson pair production at NNLO with top quark mass effects. JHEP 05, 059 (2018). https://doi.org/10.1007/JHEP05(2018)059. arXiv:1803.02463 [hep-ph], Preprint CERN-TH-2018-044, IPPP/18/15, MPP-2018-30, ZU-TH 10/18, IPPP-18-15, ZU-TH-10-18
DELPHES 3 Collaboration, J. de Favereau, C. Delaere, P. Demin, A. Giammanco, V. Lemaître, A. Mertens, M. Selvaggi, DELPHES 3, a modular framework for fast simulation of a generic collider experiment. JHEP 02, 057 (2014). arXiv:1307.6346 [hep-ex], https://doi.org/10.1007/JHEP02(2014)057
D. Contardo, M. Klute, J. Mans, L. Silvestris, J. Butler, Technical Proposal for the Phase-II Upgrade of the CMS Detector (2015). CERN-LHCC-2015-010, LHCC-P-008, CMS-TDR-15-02
ATLAS Collaboration, Expected performance for an upgraded ATLAS detector at high-luminosity LHC, ATL-PHYS-PUB-2016-026. CERN, Geneva (2016). Preprint ATL-PHYS-PUB-2016-026. https://cds.cern.ch/record/2223839
D. Gonçalves, T. Han, F. Kling, T. Plehn, M. Takeuchi, Higgs boson pair production at future hadron colliders: from kinematics to dynamics. Phys. Rev. D 97(11), 113004 (2018). https://doi.org/10.1103/PhysRevD.97.113004. arXiv:1802.04319 [hep-ph], Preprint PITT-PACC-1802, UCI-TR-2018-1, IPMU-18-0028
S. Homiller, P. Meade, Measurement of the triple Higgs coupling at a HE-LHC. arXiv:1811.02572 [hep-ph], Preprint YITP-SB-18-33
S. Banerjee, C. Englert, M.L. Mangano, M. Selvaggi, M. Spannowsky, \(hh+\text{ jet }\) production at 100 TeV. Eur. Phys. J. C 78(4), 322 (2018). https://doi.org/10.1140/epjc/s10052-018-5788-y. arXiv:1802.01607 [hep-ph], Preprint IPPP/18/10, LAPTH-034/18, CERN-TH-2018-023, IPPP-18-10, LAPTH-034-18, LAPTH-003-18
F. Bishara, R. Contino, J. Rojo, Higgs pair production in vector-boson fusion at the LHC and beyond. Eur. Phys. J. C 77(7), 481 (2017). https://doi.org/10.1140/epjc/s10052-017-5037-9. arXiv:1611.03860 [hep-ph]
A. Papaefstathiou, K. Sakurai, Triple Higgs boson production at a 100 TeV proton-proton collider. JHEP 02, 006 (2016). https://doi.org/10.1007/JHEP02(2016)006. arXiv:1508.06524 [hep-ph], Preprint CERN-PH-TH-2015-205
C.-Y. Chen, Q.-S. Yan, X. Zhao, Y.-M. Zhong, Z. Zhao, Probing triple-Higgs productions via 4b2\(\gamma \) decay channel at a 100 TeV hadron collider. Phys. Rev. D 93(1), 013007 (2016). https://doi.org/10.1103/PhysRevD.93.013007. arXiv:1510.04013 [hep-ph]
B. Fuks, J.H. Kim, S.J. Lee, Scrutinizing the Higgs quartic coupling at a future 100 TeV proton-proton collider with taus and b-jets. Phys. Lett. B 771, 354–358 (2017). https://doi.org/10.1016/j.physletb.2017.05.075. arXiv:1704.04298 [hep-ph]
K. Rummukainen, M. Tsypin, K. Kajantie, M. Laine, M.E. Shaposhnikov, The universality class of the electroweak theory. Nucl. Phys. B 532, 283–314 (1998). https://doi.org/10.1016/S0550-3213(98)00494-5. arXiv:hep-lat/9805013 [hep-lat], Preprint CERN-TH-98-08, NORDITA-98-30-HE
F. Csikor, Z. Fodor, J. Heitger, Endpoint of the hot electroweak phase transition. Phys. Rev. Lett. 82, 21–24 (1999). https://doi.org/10.1103/PhysRevLett.82.21. arXiv:hep-ph/9809291 [hep-ph], Preprint ITP-BUDAPEST-541, KEK-TH-580, KEK-PREPRINT-98-160, MS-TPI-98-16
M. Laine, K. Rummukainen, What’s new with the electroweak phase transition? Nucl. Phys. Proc. Suppl. 73, 180–185 (1999). https://doi.org/10.1016/S0920-5632(99)85017-8. arXiv:hep-lat/9809045 [hep-lat]
M. Gurtler, E.-M. Ilgenfritz, A. Schiller, Where the electroweak phase transition ends. Phys. Rev. D 56, 3888–3895 (1997). https://doi.org/10.1103/PhysRevD.56.3888. arXiv:hep-lat/9704013 [hep-lat], Preprint UL-NTZ-10-97, HUB-EP-97-24, DESY-97-086
A.D. Sakharov, Violation of CP invariance, c asymmetry, and baryon asymmetry of the universe. Pisma Zh. Eksp. Teor. Fiz. 5, 32–35 (1967). https://doi.org/10.1070/PU1991v034n05ABEH002497. [Usp. Fiz. Nauk 161, 61 (1991)]
D.E. Morrissey, M.J. Ramsey-Musolf, Electroweak baryogenesis. New J. Phys. 14, 125003 (2012). https://doi.org/10.1088/1367-2630/14/12/125003. arXiv:1206.2942 [hep-ph], Preprint NPAC-12-08
K. Assamagan et al., The Higgs portal and cosmology. arXiv:1604.05324 [hep-ph], Preprint ACFI-T16-10, FERMILAB-FN-1010-E-PPD, http://inspirehep.net/record/1449094/files/arXiv:1604.05324.pdf
H.H. Patel, M.J. Ramsey-Musolf, Stepping into electroweak symmetry breaking: phase transitions and Higgs phenomenology. Phys. Rev. D 88, 035013 (2013). https://doi.org/10.1103/PhysRevD.88.035013. arXiv:1212.5652 [hep-ph]
H.H. Patel, M.J. Ramsey-Musolf, M.B. Wise, Color breaking in the early universe. Phys. Rev. D 88(1), 015003 (2013). https://doi.org/10.1103/PhysRevD.88.015003. arXiv:1303.1140 [hep-ph]
N. Blinov, J. Kozaczuk, D.E. Morrissey, C. Tamarit, Electroweak baryogenesis from exotic electroweak symmetry breaking. Phys. Rev. D 92(3), 035012 (2015). https://doi.org/10.1103/PhysRevD.92.035012. arXiv:1504.05195 [hep-ph], Preprint IPPP-15-23, DCPT-15-46
A. Katz, M. Perelstein, Higgs couplings and electroweak phase transition. JHEP 07, 108 (2014). https://doi.org/10.1007/JHEP07(2014)108. arXiv:1401.1827 [hep-ph]
A. Katz, M. Perelstein, M.J. Ramsey-Musolf, P. Winslow, Stop-catalyzed baryogenesis beyond the MSSM. Phys. Rev. D 92(9), 095019 (2015). https://doi.org/10.1103/PhysRevD.92.095019. arXiv:1509.02934 [hep-ph], Preprint CERN-PH-TH-2015-217, ACFI-T15-15
A.V. Kotwal, M.J. Ramsey-Musolf, J.M. No, P. Winslow, Singlet-catalyzed electroweak phase transitions in the 100 TeV frontier. Phys. Rev. D 94(3), 035022 (2016). https://doi.org/10.1103/PhysRevD.94.035022. arXiv:1605.06123 [hep-ph], Preprint ACFI-T16-12, FERMILAB-PUB-16-670
J.R. Espinosa, M. Quiros, The electroweak phase transition with a singlet. Phys. Lett. B 305, 98–105 (1993). https://doi.org/10.1016/0370-2693(93)91111-Y. arXiv:hep-ph/9301285 [hep-ph], Preprint IEM-FT-67-93
J. Choi, R.R. Volkas, Real Higgs singlet and the electroweak phase transition in the Standard Model. Phys. Lett. B 317, 385–391 (1993). https://doi.org/10.1016/0370-2693(93)91013-D. arXiv:hep-ph/9308234 [hep-ph], Preprint UM-P-93-80, OZ-93-20
S.W. Ham, Y.S. Jeong, S.K. Oh, Electroweak phase transition in an extension of the standard model with a real Higgs singlet. J. Phys. G 31(8), 857–871 (2005). https://doi.org/10.1088/0954-3899/31/8/017. arXiv:hep-ph/0411352 [hep-ph]
S. Profumo, M.J. Ramsey-Musolf, G. Shaughnessy, Singlet Higgs phenomenology and the electroweak phase transition. JHEP 08, 010 (2007). https://doi.org/10.1088/1126-6708/2007/08/010. arXiv:0705.2425 [hep-ph], Preprint CALTECH-MAP-333, MADPH-07-1489
J.M. Cline, K. Kainulainen, Electroweak baryogenesis and dark matter from a singlet Higgs. JCAP 1301, 012 (2013). https://doi.org/10.1088/1475-7516/2013/01/012. arXiv:1210.4196 [hep-ph]
J.R. Espinosa, T. Konstandin, F. Riva, Strong electroweak phase transitions in the standard model with a singlet. Nucl. Phys. B 854, 592–630 (2012). https://doi.org/10.1016/j.nuclphysb.2011.09.010. arXiv:1107.5441 [hep-ph], Preprint CERN-PH-TH-2011-171
J.M. No, M. Ramsey-Musolf, Probing the Higgs portal at the LHC through resonant di-Higgs production. Phys. Rev. D 89(9), 095031 (2014). https://doi.org/10.1103/PhysRevD.89.095031. arXiv:1310.6035 [hep-ph]
D. Curtin, P. Meade, C.-T. Yu, Testing electroweak baryogenesis with future colliders. JHEP 11, 127 (2014). https://doi.org/10.1007/JHEP11(2014)127. arXiv:1409.0005 [hep-ph], Preprint YITP-SB-14-33
T. Brauner, T.V.I. Tenkanen, A. Tranberg, A. Vuorinen, D.J. Weir, Dimensional reduction of the Standard Model coupled to a new singlet scalar field. JHEP 03, 007 (2017). https://doi.org/10.1007/JHEP03(2017)007. arXiv:1609.06230 [hep-ph], Preprint HIP-2016-27-TH
P. Huang, A.J. Long, L.-T. Wang, Probing the electroweak phase transition with Higgs factories and gravitational waves. Phys. Rev. D 94(7), 075008 (2016). https://doi.org/10.1103/PhysRevD.94.075008. arXiv:1608.06619 [hep-ph]
C.-Y. Chen, J. Kozaczuk, I.M. Lewis, Non-resonant collider signatures of a singlet-driven electroweak phase transition. JHEP 08, 096 (2017). https://doi.org/10.1007/JHEP08(2017)096. arXiv:1704.05844 [hep-ph], Preprint ACFI-T17-07, SLAC-PUB-16951
T. Huang, J.M. No, L. Pernié, M. Ramsey-Musolf, A. Safonov, M. Spannowsky, P. Winslow, Resonant di-Higgs boson production in the \(b{\bar{b}}WW\) channel: probing the electroweak phase transition at the LHC. Phys. Rev. D 96(3), 035007 (2017). https://doi.org/10.1103/PhysRevD.96.035007. arXiv:1701.04442 [hep-ph]
V. Barger, P. Langacker, M. McCaskey, M.J. Ramsey-Musolf, G. Shaughnessy, LHC phenomenology of an extended standard model with a real scalar singlet. Phys. Rev. D 77, 035005 (2008). https://doi.org/10.1103/PhysRevD.77.035005. arXiv:0706.4311 [hep-ph], Preprint MAD-PH-07-1492
M. Jiang, L. Bian, W. Huang, J. Shu, Impact of a complex singlet: electroweak baryogenesis and dark matter. Phys. Rev. D 93(6), 065032 (2016). https://doi.org/10.1103/PhysRevD.93.065032. arXiv:1502.07574 [hep-ph]
C.-W. Chiang, M.J. Ramsey-Musolf, E. Senaha, Standard model with a complex scalar singlet: cosmological implications and theoretical considerations. Phys. Rev. D 97(1), 015005 (2018). https://doi.org/10.1103/PhysRevD.97.015005. arXiv:1707.09960 [hep-ph], Preprint NCTS-PH-1724, ACFI-T17-16
S. Profumo, M.J. Ramsey-Musolf, C.L. Wainwright, P. Winslow, Singlet-catalyzed electroweak phase transitions and precision Higgs boson studies. Phys. Rev. D 91(3), 035018 (2015). https://doi.org/10.1103/PhysRevD.91.035018. arXiv:1407.5342 [hep-ph]
L. Niemi, H.H. Patel, M.J. Ramsey-Musolf, T.V.I. Tenkanen, D.J. Weir, Electroweak phase transition in the \(\Sigma \) SM—I: dimensional reduction. arXiv:1802.10500 [hep-ph]
G.C. Dorsch, S.J. Huber, J.M. No, A strong electroweak phase transition in the 2HDM after LHC8. JHEP 10, 029 (2013). https://doi.org/10.1007/JHEP10(2013)029. arXiv:1305.6610 [hep-ph]
G.C. Dorsch, S.J. Huber, K. Mimasu, J.M. No, Echoes of the Electroweak Phase Transition: Discovering a second Higgs doublet through \(A_0 \rightarrow ZH_0\). Phys. Rev. Lett. 113(21), 211802 (2014). https://doi.org/10.1103/PhysRevLett.113.211802. arXiv:1405.5537 [hep-ph]
D. Curtin, K. Deshpande, O. Fischer, J. Zurita, New physics opportunities for long-lived particles at electron-proton colliders. JHEP 07, 024 (2018). https://doi.org/10.1007/JHEP07(2018)024. arXiv:1712.07135 [hep-ph], Preprint TTP17-053
J. Kozaczuk, A. Long, J.-M. No, M. Ramsey-Musolf, Electroweak phase transition at the FCC (to appear)
E.W. Kolb, M.S. Turner, The early universe. Front. Phys. 69, 1–547 (1990)
K. Griest, M. Kamionkowski, Unitarity limits on the mass and radius of dark matter particles. Phys. Rev. Lett. 64, 615 (1990). https://doi.org/10.1103/PhysRevLett.64.615. Preprint CFPA-TH-89-013, FERMILAB-PUB-89-205-A
K. Blum, Y. Cui, M. Kamionkowski, An ultimate target for dark matter searches. Phys. Rev. D 92(2), 023528 (2015). https://doi.org/10.1103/PhysRevD.92.023528. arXiv:1412.3463 [hep-ph], Preprint UMD-PP-014-022
M. Cirelli, F. Sala, M. Taoso, Wino-like minimal dark matter and future colliders. JHEP 10, 033 (2014). arXiv:1407.7058 [hep-ph], https://doi.org/10.1007/JHEP10(2014)033, https://doi.org/10.1007/JHEP01(2015)041 [Erratum: JHEP 01, 041 (2015)]
D. Curtin et al., Long-lived particles at the energy frontier: the MATHUSLA physics case. arXiv:1806.07396 [hep-ph], Preprint FERMILAB-PUB-18-264-T
K. Terashi, R. Sawada, M. Saito, S. Asai, Search for WIMPs with disappearing track signatures at the FCC-hh, CERN-ACC-2018-0044. CERN, Geneva (2018). Preprint CERN-ACC-2018-0044. https://cds.cern.ch/record/2642474
M. Saito, R. Sawada, K. Terashi, S. Asai, Discovery reach for wino and higgsino dark matter with a disappearing track signature at a 100 TeV \(pp\) collider. arXiv:1901.02987 [hep-ph]
F. Kahlhoefer, K. Schmidt-Hoberg, T. Schwetz, S. Vogl, Implications of unitarity and gauge invariance for simplified dark matter models. JHEP 02, 016 (2016). https://doi.org/10.1007/JHEP02(2016)016. arXiv:1510.02110 [hep-ph], Preprint DESY-15-182
K. Petraki, R.R. Volkas, Review of asymmetric dark matter. Int. J. Mod. Phys. A 28, 1330028 (2013). https://doi.org/10.1142/S0217751X13300287. arXiv:1305.4939 [hep-ph], Preprint NIKHEF-2013-016
K.M. Zurek, Asymmetric dark matter: theories, signatures, and constraints. Phys. Rep. 537, 91–121 (2014). https://doi.org/10.1016/j.physrep.2013.12.001. arXiv:1308.0338 [hep-ph]
M. Bauer, M. Heiles, M. Neubert, A. Thamm, Axion-like particles at future colliders. arXiv:1808.10323 [hep-ph]
S. Weinberg, Baryon and lepton nonconserving processes. Phys. Rev. Lett. 43, 1566–1570 (1979). https://doi.org/10.1103/PhysRevLett.43.1566. Preprint HUTP-79-A050
S. Antusch, E. Cazzato, O. Fischer, Sterile neutrino searches at future \(e^-e^+\), \(pp\), and \(e^-p\) colliders. Int. J. Mod. Phys. A 32(14), 1750078 (2017). https://doi.org/10.1142/S0217751X17500786. arXiv:1612.02728 [hep-ph]
P. Minkowski, \(\mu \rightarrow e\gamma \) at a rate of one out of \(10^{9}\) muon decays? Phys. Lett. B 67, 421–428 (1977). https://doi.org/10.1016/0370-2693(77)90435-X. Preprint Print-77-0182 (BERN)
M. Gell-Mann, P. Ramond, R. Slansky, Complex spinors and unified theories. Conf. Proc. C 790927, 315–321 (1979). arXiv:1306.4669 [hep-th], Preprint PRINT-80-0576
T. Yanagida, Horizontal symmetry and masses of neutrinos. Conf. Proc. C 7902131, 95–99 (1979). Preprint KEK-79-18-95
R.N. Mohapatra, G. Senjanovic, Neutrino mass and spontaneous parity violation. Phys. Rev. Lett. 44, 912 (1980). Preprint MDDP-TR-80-060, MDDP-PP-80-105, CCNY-HEP-79-10, https://doi.org/10.1103/PhysRevLett.44.912 [231 (1979)]
D. Wyler, L. Wolfenstein, Massless neutrinos in left-right symmetric models. Nucl. Phys. B 218, 205–214 (1983). https://doi.org/10.1016/0550-3213(83)90482-0. Preprint CERN-TH-3435
M. Shaposhnikov, A possible symmetry of the nuMSM. Nucl. Phys. B 763, 49–59 (2007). https://doi.org/10.1016/j.nuclphysb.2006.11.003. arXiv:hep-ph/0605047 [hep-ph], Preprint CERN-PH-TH-2006-079
J. Kersten, AYu. Smirnov, Right-handed neutrinos at CERN LHC and the mechanism of neutrino mass generation. Phys. Rev. D 76, 073005 (2007). https://doi.org/10.1103/PhysRevD.76.073005. arXiv:0705.3221 [hep-ph]
M.B. Gavela, T. Hambye, D. Hernandez, P. Hernandez, Minimal flavour seesaw models. JHEP 09, 038 (2009). https://doi.org/10.1088/1126-6708/2009/09/038. arXiv:0906.1461 [hep-ph], Preprint FTUAM-09-09, IFT-UAM-CSIC-09-27, ULB-TH-09-15, IFIC-09-22, FTUV-09-0607
M. Malinsky, J.C. Romao, J.W.F. Valle, Novel supersymmetric SO(10) seesaw mechanism. Phys. Rev. Lett. 95, 161801 (2005). https://doi.org/10.1103/PhysRevLett.95.161801. arXiv:hep-ph/0506296 [hep-ph], Preprint IFIC-05-28
S. Antusch et al., Probing leptogenesis at future colliders. JHEP 124 (2018). https://link.springer.com/content/pdf/10.1007%2FJHEP09%282018%29124.pdf
LHCb Collaboration, R. Aaij et al., Test of lepton universality with \(B^{0} \rightarrow K^{*0}\ell ^{+}\ell ^{-}\) decays. JHEP 08, 055 (2017). arXiv:1705.05802 [hep-ex], Preprint LHCB-PAPER-2017-013, CERN-EP-2017-100, https://doi.org/10.1007/JHEP08(2017)055
B. Capdevila, A. Crivellin, S. Descotes-Genon, J. Matias, J. Virto, Patterns of new physics in \(b\rightarrow s\ell ^+\ell ^-\) transitions in the light of recent data. JHEP 01, 093 (2018). https://doi.org/10.1007/JHEP01(2018)093. arXiv:1704.05340 [hep-ph], Preprint PSI-PR-17-05, LPT-ORSAY-17-19
W. Altmannshofer, P. Stangl, D.M. Straub, Interpreting hints for lepton flavor universality violation. Phys. Rev. D 96(5), 055008 (2017). https://doi.org/10.1103/PhysRevD.96.055008. arXiv:1704.05435 [hep-ph]
G. Hiller, I. Nisandzic, \(R_K\) and \(R_{K^{\ast }}\) beyond the standard model. Phys. Rev. D 96(3), 035003 (2017). https://doi.org/10.1103/PhysRevD.96.035003. arXiv:1704.05444 [hep-ph], Preprint DO-TH-17-04
L.-S. Geng, B. Grinstein, S. Jäger, J. Martin Camalich, X.-L. Ren, R.-X. Shi, Towards the discovery of new physics with lepton-universality ratios of \(b\rightarrow s\ell \ell \) decays. Phys. Rev. D 96(9), 093006 (2017). https://doi.org/10.1103/PhysRevD.96.093006. arXiv:1704.05446 [hep-ph], Preprint CERN-TH-2017-085
M. Ciuchini, A.M. Coutinho, M. Fedele, E. Franco, A. Paul, L. Silvestrini, M. Valli, On flavourful easter eggs for new physics hunger and lepton flavour universality violation. Eur. Phys. J. C 77(10), 688 (2017). https://doi.org/10.1140/epjc/s10052-017-5270-2. arXiv:1704.05447 [hep-ph]
A. Celis, J. Fuentes-Martin, A. Vicente, J. Virto, Gauge-invariant implications of the LHCb measurements on lepton-flavor nonuniversality. Phys. Rev. D 96(3), 035026 (2017). https://doi.org/10.1103/PhysRevD.96.035026. arXiv:1704.05672 [hep-ph], Preprint LMU-ASC-25-17, IFIC-17-20
G. D’Amico, M. Nardecchia, P. Panci, F. Sannino, A. Strumia, R. Torre, A. Urbano, Flavour anomalies after the \(R_{K^*}\) measurement. JHEP 09, 010 (2017). https://doi.org/10.1007/JHEP09(2017)010. arXiv:1704.05438 [hep-ph], Preprint CERN-TH-2017-086, CP3-ORIGINS-2017-014
L. Di Luzio, M. Nardecchia, What is the scale of new physics behind the \(B\)-flavour anomalies? Eur. Phys. J. C 77(8), 536 (2017). https://doi.org/10.1140/epjc/s10052-017-5118-9. arXiv:1706.01868 [hep-ph], Preprint IPPP-17-50, CERN-TH-2017-126
B.C. Allanach, B. Gripaios, T. You, The case for future hadron colliders from \(B \rightarrow K^{(*)} \mu ^+ \mu ^-\) decays. JHEP 03, 021 (2018). https://doi.org/10.1007/JHEP03(2018)021. arXiv:1710.06363 [hep-ph], Preprint CAVENDISH-HEP-2017-11, DAMTP-2017-39
B.C. Allanach, T. Corbett, M.J. Dolan, T. You, Hadron collider sensitivity to fat flavourful \(Z^\prime \)s for \(R_{K^{(\ast )}}\). arXiv:1810.02166 [hep-ph], Preprint Cavendish-HEP-2018-14, DAMTP-2018-33
A. Greljo, D. Marzocca, High-\(p_T\) dilepton tails and flavor physics. Eur. Phys. J. C 77(8), 548 (2017). https://doi.org/10.1140/epjc/s10052-017-5119-8. arXiv:1704.09015 [hep-ph], Preprint ZU-TH-12-17
M. Kramer, T. Plehn, M. Spira, P.M. Zerwas, Pair production of scalar leptoquarks at the CERN LHC. Phys. Rev. D 71, 057503 (2005). https://doi.org/10.1103/PhysRevD.71.057503. arXiv:hep-ph/0411038 [hep-ph], Preprint CERN-PH-TH-2004-207, DESY-04-200, EDINBURGH-2004-28, FERMILAB-PUB-04-298-T, PSI-PR-04-12
I. Doršner, A. Greljo, Leptoquark toolbox for precision collider studies. JHEP 05, 126 (2018). https://doi.org/10.1007/JHEP05(2018)126. arXiv:1801.07641 [hep-ph], Preprint MITP-18-005
P. Arnan, L. Hofer, F. Mescia, A. Crivellin, Loop effects of heavy new scalars and fermions in \(b\rightarrow s\mu ^+\mu ^-\). JHEP 04, 043 (2017). https://doi.org/10.1007/JHEP04(2017)043. arXiv:1608.07832 [hep-ph], Preprint ICCUB-16-031, PSI-PR-16-12
L. Di Luzio, M. Kirk, A. Lenz, Updated \(B_s\)-mixing constraints on new physics models for \(b\rightarrow s\ell ^+\ell ^-\) anomalies. Phys. Rev. D 97(9), 095035 (2018). https://doi.org/10.1103/PhysRevD.97.095035. arXiv:1712.06572 [hep-ph], Preprint IPPP-17-106
J. Kumar, D. London, R. Watanabe, Combined Explanations of the \(b \rightarrow s \mu ^+ \mu ^-\) and \(b \rightarrow c \tau ^- {\bar{\nu }}\) Anomalies: a General Model Analysis, arXiv:1806.07403 [hep-ph], Preprint UdeM-GPP-TH-18-264, UDEM-GPP-TH-18-264
Z. Liu, L.-T. Wang, H. Zhang, Exotic decays of the 125 GeV Higgs boson at future \(e^+e^-\) lepton colliders. Chin. Phys. C 41(6), 063102 (2017). https://doi.org/10.1088/1674-1137/41/6/063102. arXiv:1612.09284 [hep-ph], Preprint FERMILAB-PUB-16-608-T
D. Curtin, C.B. Verhaaren, Discovering uncolored naturalness in exotic Higgs decays. JHEP 12, 072 (2015). https://doi.org/10.1007/JHEP12(2015)072. arXiv:1506.06141 [hep-ph]
J. Liu, L.-T. Wang, X.-P. Wang, W. Xue, Exposing dark sector with future Z-factories. Phys. Rev. D 97(9), 095044 (2018). https://doi.org/10.1103/PhysRevD.97.095044. arXiv:1712.07237 [hep-ph], Preprint CERN-TH-2017-278, EFI-17-28, MITP-17-102, MIT-CTP-4972
CMS Collaboration, A.M. Sirunyan et al., Search for low mass vector resonances decaying into quark–antiquark pairs in proton–proton collisions at \( \sqrt{s}=13 \) TeV. JHEP 01, 097 (2018). arXiv:1710.00159 [hep-ex], Preprint CMS-EXO-17-001, CERN-EP-2017-235, https://doi.org/10.1007/JHEP01(2018)097
ATLAS Collaboration, M. Aaboud et al., Search for light resonances decaying to boosted quark pairs and produced in association with a photon or a jet in proton–proton collisions at \(\sqrt{s}=13\) TeV with the ATLAS detector. arXiv:1801.08769 [hep-ex], Preprint CERN-EP-2017-280
R.M. Harris, K. Kousouris, Searches for dijet resonances at hadron colliders. Int. J. Mod. Phys. A 26, 5005–5055 (2011). https://doi.org/10.1142/S0217751X11054905. arXiv:1110.5302 [hep-ex], Preprint FERMILAB-PUB-11-567, CERN-OPEN-2011-044
G. Salam, A. Weiler, Collider Reach. http://collider-reach.web.cern.ch/collider-reach/
C. Helsens, D. Jamin, M.L. Mangano, T.G. Rizzo, M. Selvaggi, Heavy resonances at energy-frontier hadron colliders. arXiv:1902.11217 [hep-ph], Preprint CERN-TH-2019-020, SLAC-PUB-17408
T.G. Rizzo, Exploring new gauge bosons at a 100 TeV collider. Phys. Rev. D 89(9), 095022 (2014). https://doi.org/10.1103/PhysRevD.89.095022. arXiv:1403.5465 [hep-ph], Preprint SLAC-PUB-15917
T. Han, P. Langacker, Z. Liu, L.-T. Wang, Diagnosis of a new neutral gauge boson at the LHC and ILC for Snowmass 2013. arXiv:1308.2738 [hep-ph]
L. Randall, R. Sundrum, A large mass hierarchy from a small extra dimension. Phys. Rev. Lett. 83, 3370–3373 (1999). https://doi.org/10.1103/PhysRevLett.83.3370. arXiv:hep-ph/9905221 [hep-ph], Preprint MIT-CTP-2860, PUPT-1860, BUHEP-99-9
U. Baur, I. Hinchliffe, D. Zeppenfeld, Excited quark production at hadron colliders. Int. J. Mod. Phys. A 2, 1285 (1987). https://doi.org/10.1142/S0217751X87000661. Preprint FERMILAB-CONF-87-102-T, MAD-PH-354, LBL-23645
U. Baur, M. Spira, P.M. Zerwas, Excited quark and lepton production at hadron colliders. Phys. Rev. D 42, 815–824 (1990). https://doi.org/10.1103/PhysRevD.42.815. Preprint MAD-PH-534, PITHA-89-26
C.T. Hill, Topcolor assisted technicolor. Phys. Lett. B 345, 483–489 (1995). https://doi.org/10.1016/0370-2693(94)01660-5. arXiv:hep-ph/9411426 [hep-ph], Preprint FERMILAB-PUB-94-395-T
J. Jowett, HL-LHC physics workshop. CERN (2017). https://indico.cern.ch/event/647676/contributions/2721134/
L. Apolinário, J.G. Milhano, G.P. Salam, C.A. Salgado, Probing the time structure of the quark-gluon plasma with top quarks. arXiv:1711.03105 [hep-ph], Preprint CERN-TH-2017-237
D. d’Enterria, K. Krajczár, H. Paukkunen, Top-quark production in proton-nucleus and nucleus-nucleus collisions at LHC energies and beyond. Phys. Lett. B 746, 64–72 (2015). https://doi.org/10.1016/j.physletb.2015.04.044. arXiv:1501.05879 [hep-ph]
D. d’Enterria, Top-quark and Higgs boson perspectives at heavy-ion colliders. Nucl. Part. Phys. Proc. 289–290, 237–240 (2017). https://doi.org/10.1016/j.nuclphysbps.2017.05.053. arXiv:1701.08047 [hep-ex]
D. d’Enterria, C. Loizides, Higgs boson suppression in quark-gluon matter. arXiv:1809.06832 [hep-ph]
Y. Liu, C.-M. Ko, Thermal production of charm quarks in heavy ion collisions at future circular collider. J. Phys. G 43(12), 125108 (2016). https://doi.org/10.1088/0954-3899/43/12/125108. arXiv:1604.01207 [nucl-th]
K. Zhou, Z. Chen, C. Greiner, P. Zhuang, Thermal charm and charmonium production in quark gluon plasma. Phys. Lett. B 758, 434–439 (2016). https://doi.org/10.1016/j.physletb.2016.05.051. arXiv:1602.01667 [hep-ph]
G.S. Denicol, C. Gale, S. Jeon, J.F. Paquet, B. Schenke, Effect of initial-state nucleon-nucleon correlations on collective flow in ultra-central heavy-ion collisions. arXiv:1406.7792 [nucl-th]
CMS Collaboration, S. Chatrchyan et al., Multiplicity and transverse momentum dependence of two- and four-particle correlations in pPb and PbPb collisions. Phys. Lett. B 724, 213–240 (2013). arXiv:1305.0609 [nucl-ex], Preprint CMS-HIN-13-002, CERN-PH-EP-2013-077, https://doi.org/10.1016/j.physletb.2013.06.028
ALICE Collaboration, B.B. Abelev et al., Long-range angular correlations of \(\pi \), K and p in p-Pb collisions at \(\sqrt{s_{\rm NN}}\) = 5.02 TeV. Phys. Lett. B 726, 164–177 (2013). arXiv:1307.3237 [nucl-ex], Preprint CERN-PH-EP-2013-115, https://doi.org/10.1016/j.physletb.2013.08.024
ALICE Collaboration, B. Abelev et al., Long-range angular correlations on the near and away side in \(p-\text{ Pb }\) collisions at \(\sqrt{s_{NN}}=5.02\) TeV. Phys. Lett. B 719, 29–41 (2013). arXiv:1212.2001 [nucl-ex], Preprint CERN-PH-EP-2012-359, https://doi.org/10.1016/j.physletb.2013.01.012
ATLAS Collaboration, G. Aad et al., Measurement of long-range pseudorapidity correlations and azimuthal harmonics in \(\sqrt{s_{NN}}=5.02\) TeV proton–lead collisions with the ATLAS detector. Phys. Rev. C 90(4), 044906 (2014). arXiv:1409.1792 [hep-ex], Preprint CERN-PH-EP-2014-201, https://doi.org/10.1103/PhysRevC.90.044906
STAR Collaboration, L. Adamczyk et al., Long-range pseudorapidity dihadron correlations in \(d+\text{ Au }\) collisions at \(\sqrt{s_{\rm NN}}=200\) GeV. Phys. Lett. B 747, 265–271 (2015). arXiv:1502.07652 [nucl-ex], https://doi.org/10.1016/j.physletb.2015.05.075
PHENIX Collaboration, A. Adare et al., Measurements of elliptic and triangular flow in high-multiplicity \(^{3}\text{ He }+\text{ Au }\) collisions at \(\sqrt{s_{_{NN}}}=200\) GeV. Phys. Rev. Lett. 115(14), 142301 (2015). arXiv:1507.06273 [nucl-ex], https://doi.org/10.1103/PhysRevLett.115.142301
J.M. Campbell, R.K. Ellis, MCFM for the tevatron and the LHC. Nucl. Phys. Proc. Suppl. 205–206, 10–15 (2010). https://doi.org/10.1016/j.nuclphysbps.2010.08.011. arXiv:1007.3492 [hep-ph], Preprint FERMILAB-CONF-10-244-T
A.V. Baskakov, E.E. Boos, L.V. Dudko, I.P. Lokhtin, A.M. Snigirev, Single top quark production in heavy ion collisions at energies available at the CERN Large Hadron Collider. Phys. Rev. C 92(4), 044901 (2015). https://doi.org/10.1103/PhysRevC.92.044901. arXiv:1502.04875 [hep-ph]
J. Ghiglieri, U.A. Wiedemann, Thermal width of the Higgs boson in hot QCD matter. arXiv:1901.04503 [hep-ph], Preprint CERN-TH-2019-003
J. Casalderrey-Solana, Y. Mehtar-Tani, C.A. Salgado, K. Tywoniuk, New picture of jet quenching dictated by color coherence. Phys. Lett. B 725, 357–360 (2013). https://doi.org/10.1016/j.physletb.2013.07.046. arXiv:1210.7765 [hep-ph], Preprint CERN-PH-TH-2012-291, LU-TP-12-37
A. Andronic et al., Heavy-flavour and quarkonium production in the LHC era: from proton-proton to heavy-ion collisions. Eur. Phys. J. C 76(3), 107 (2016). https://doi.org/10.1140/epjc/s10052-015-3819-5. arXiv:1506.03981 [nucl-ex]
ALICE Collaboration, J. Adam et al., Differential studies of inclusive \(\text{ J }/\psi \) and \(\psi \)(2S) production at forward rapidity in Pb–Pb collisions at \( \sqrt{s_{{\rm NN}}}=2.76 \) TeV. JHEP 05, 179 (2016). arXiv:1506.08804 [nucl-ex], Preprint CERN-PH-EP-2015-157, https://doi.org/10.1007/JHEP05(2016)179
ALICE Collaboration, J. Adam et al., Inclusive, prompt and non-prompt \(\text{ J }/\psi \) production at mid-rapidity in Pb–Pb collisions at \(\sqrt{s_{{\rm NN}}} = 2.76\) TeV. JHEP 07, 051 (2015). arXiv:1504.07151 [nucl-ex], Preprint CERN-PH-EP-2015-092, https://doi.org/10.1007/JHEP07(2015)051
CMS Collaboration, S. Chatrchyan et al., Suppression of non-prompt \(\text{ J }/\psi \), prompt \(\text{ J }/\psi \), and \(\Upsilon \) in PbPb collisions at \(\sqrt{s_{{\rm NN}}}\) = 2.76 TeV. JHEP 05, 063 (2012). arXiv:1201.5069 [nucl-ex], Preprint CMS-HIN-10-006, CERN-PH-EP-2011-170, https://doi.org/10.1007/JHEP05(2012)063
Y.-P. Liu, Z. Qu, N. Xu, P.-F. Zhuang, \(J/\psi \) transverse momentum distribution in high energy nuclear collisions at RHIC. Phys. Lett. B 678, 72 (2009). https://doi.org/10.1016/j.physletb.2009.06.006. arXiv:0901.2757 [nucl-th]
X. Zhao, R. Rapp, Medium modifications and production of charmonia at LHC. Nucl. Phys. A 859, 114 (2011). https://doi.org/10.1016/j.nuclphysa.2011.05.001. arXiv:1102.2194 [hep-ph]
A. Andronic, P. Braun-Munzinger, K. Redlich, J. Stachel, The thermal model on the verge of the ultimate test: particle production in Pb-Pb collisions at the LHC. J. Phys. G 38, 124081 (2011). https://doi.org/10.1088/0954-3899/38/12/124081. arXiv:1106.6321 [nucl-th]
P. Braun-Munzinger, Workshop on heavy ions at FCC (2015). https://indico.cern.ch/event/382529/contribution/6
A. Andronic, Workshop on heavy ions at FCC (2013). https://indico.cern.ch/event/288576/contribution/7
M.L. Mangano, P. Nason, G. Ridolfi, Heavy quark correlations in hadron collisions at next-to-leading order. Nucl. Phys. B 373, 295–345 (1992). https://doi.org/10.1016/0550-3213(92)90435-E. Preprint IFUP-TH-32-91, UPRF-91-308, GEF-TH-10-1991A
L.V. Gribov, E.M. Levin, M.G. Ryskin, Semihard processes in QCD. Phys. Rep. 100, 1–150 (1983). https://doi.org/10.1016/0370-1573(83)90022-4
A.H. Mueller, J.-W. Qiu, Gluon recombination and shadowing at small values of x. Nucl. Phys. B 268, 427 (1986). https://doi.org/10.1016/0550-3213(86)90164-1. Preprint CU-TP-322
M. Arneodo, Nuclear effects in structure functions. Phys. Rep. 240, 301–393 (1994). https://doi.org/10.1016/0370-1573(94)90048-5. Preprint CERN-PPE-92-113
F. Gelis, E. Iancu, J. Jalilian-Marian, R. Venugopalan, The color glass condensate. Annu. Rev. Nucl. Part. Sci. 60, 463–489 (2010). https://doi.org/10.1146/annurev.nucl.010909.083629. arXiv:1002.0333 [hep-ph]
A. Accardi et al., Electron ion collider: the next QCD frontier. Eur. Phys. J. A 52(9), 268 (2016). https://doi.org/10.1140/epja/i2016-16268-9. arXiv:1212.1701 [nucl-ex], Preprint BNL-98815-2012-JA, JLAB-PHY-12-1652
A.H. Rezaeian, Semi-inclusive photon-hadron production in pp and pA collisions at RHIC and LHC. Phys. Rev. D 86, 094016 (2012). https://doi.org/10.1103/PhysRevD.86.094016. arXiv:1209.0478 [hep-ph]
A.H. Rezaeian, CGC predictions for p+A collisions at the LHC and signature of QCD saturation. Phys. Lett. B 718, 1058–1069 (2013). https://doi.org/10.1016/j.physletb.2012.11.066. arXiv:1210.2385 [hep-ph]
J.L. Albacete, C. Marquet, Azimuthal correlations of forward di-hadrons in d+Au collisions at RHIC in the color glass condensate. Phys. Rev. Lett. 105, 162301 (2010). https://doi.org/10.1103/PhysRevLett.105.162301. arXiv:1005.4065 [hep-ph]
A. van Hameren, P. Kotko, K. Kutak, C. Marquet, S. Sapeta, Saturation effects in forward-forward dijet production in \(\text{ p }+\text{ Pb }\) collisions. Phys. Rev. D 89(9), 094014 (2014). https://doi.org/10.1103/PhysRevD.89.094014. arXiv:1402.5065 [hep-ph], Preprint CERN-PH-TH-2014-029, CPHT-RR005.0214, IFJPAN-IV-2014-2
P. Kotko, K. Kutak, C. Marquet, E. Petreska, S. Sapeta, A. van Hameren, Improved TMD factorization for forward dijet production in dilute-dense hadronic collisions. JHEP 09, 106 (2015). https://doi.org/10.1007/JHEP09(2015)106. arXiv:1503.03421 [hep-ph], Preprint CERN-PH-TH-2015-045, CPHT-RR005.0315, IFJPAN-IV-2015-2
K.J. Eskola, H. Paukkunen, C.A. Salgado, EPS09: a new generation of NLO and LO nuclear parton distribution functions. JHEP 04, 065 (2009). https://doi.org/10.1088/1126-6708/2009/04/065. arXiv:0902.4154 [hep-ph]
H. Paukkunen, P. Zurita, PDF reweighting in the Hessian matrix approach. JHEP 12, 100 (2014). https://doi.org/10.1007/JHEP12(2014)100. arXiv:1402.6623 [hep-ph]
C.F. von Weizsacker, Radiation emitted in collisions of very fast electrons. Z. Phys. 88, 612–625 (1934). https://doi.org/10.1007/BF01333110
E.J. Williams, Nature of the high-energy particles of penetrating radiation and status of ionization and radiation formulae. Phys. Rev. 45, 729–730 (1934). https://doi.org/10.1103/PhysRev.45.729
E. Fermi, On the theory of collisions between atoms and electrically charged particles. Nuovo Cim. 2, 143–158 (1925). arXiv:hep-th/0205086 [hep-th], https://doi.org/10.1007/BF02961914, [243 (1925)]
D. d’Enterria, M. Klasen, K. Piotrzkowski, High-energy photon collisions at the LHC. Nucl. Phys. Proc. Suppl. B 179, 1 (2008). https://doi.org/10.1016/S0920-5632(08)00090-X. Preprint PHOTON-LHC-2008
A.J. Baltz, The physics of ultraperipheral collisions at the LHC. Phys. Rep. 458, 1–171 (2008). https://doi.org/10.1016/j.physrep.2007.12.001. arXiv:0706.3356 [nucl-ex]
H1 Collaboration, A. Atkas et al., Elastic photoproduction of \(J/\psi \) and \(\Upsilon \) mesons at HERA. Phys. Lett. B 483, 23 (2000). arXiv:hep-ex/0003020 [hep-ex], https://doi.org/10.1016/S0370-2693(00)00530-X
ZEUS Collaboration, S. Chekanov et al., Exclusive photoproduction of \(\Upsilon \) mesons at HERA. Phys. Lett. B 680, 4 (2009). arXiv:0903.4205 [hep-ex], https://doi.org/10.1016/physlettb.2009.07.066
P. Jones, D. Martin, M.G. Ryskin, T. Teubner, Probes of the small x gluon via exclusive \(J/\psi \) and \(\Upsilon \) production at HERA and LHC. JHEP 1311, 085 (2013). https://doi.org/10.1007/JHEP11(2013)085. arXiv:1307.7099 [hep-ph]
G. Sampaio, M.V.T. Machado, Exclusive photoproduction of quarkonium in proton–nucleus collisions at the LHC. arXiv:1312.0770 [hep-ph]
N. Armesto, Nuclear PDFs, Talk at the 2nd FCC Physics Week (2018). https://indico.cern.ch/event/618254/contributions/2833211/
N. Armesto, Future of nuclear PDFs, Proceedings of DIS2018 (2018). https://indico.cern.ch/event/656250/contributions/2889208/
N. Armesto, Nuclear physics in eA collisions. POS DIS2017, 107 (2017)
K.J. Eskola, P. Paakkinen, H. Paukkunen, C.A. Salgado, EPPS16: nuclear parton distributions with LHC data. Eur. Phys. J. C 77(3), 163 (2017). https://doi.org/10.1140/epjc/s10052-017-4725-9. arXiv:1612.05741 [hep-ph]
L. Frankfurt, V. Guzey, M. Strikman, Leading twist nuclear shadowing phenomena in hard processes with nuclei. Phys. Rep. 512, 255–393 (2012). https://doi.org/10.1016/j.physrep.2011.12.002. arXiv:1106.2091 [hep-ph], Preprint JLAB-THY-11-1379
T. Lappi, H. Mantysaari, Incoherent diffractive J/Psi-production in high energy nuclear DIS. Phys. Rev. C 83, 065202 (2011). https://doi.org/10.1103/PhysRevC.83.065202. arXiv:1011.1988 [hep-ph], Preprint INT-PUB-10-061
M. Klein, Nuclear parton distributions with the LHeC. EPJ Web Conf. 112, 03002 (2016). https://doi.org/10.1051/epjconf/201611203002
H. Mantysaari, B. Schenke, Confronting impact parameter dependent JIMWLK evolution with HERA data. arXiv:1806.06783 [hep-ph]
D. d’Enterria, D.E. Martins, P. Rebello Teles, Prospects for \(\gamma \gamma \rightarrow \) Higgs observation in ultraperipheral ion collisions at the future circular collider. arXiv:1712.10104 [hep-ph]
CMS Collaboration, S. Chatrchyan et al., Search for exclusive or semi-exclusive photon pair production and observation of exclusive and semi-exclusive electron pair production in \(pp\) collisions at \(\sqrt{s}=7\) TeV. JHEP 11, 080 (2012). arXiv:1209.1666 [hep-ex], Preprint CMS-FWD-11-004, CERN-PH-EP-2012-246, https://doi.org/10.1007/JHEP11(2012)080
CMS Collaboration, S. Chatrchyan et al., Study of exclusive two-photon production of \(W^+W^-\) in \(pp\) collisions at \(\sqrt{s} = 7\) TeV and constraints on anomalous quartic gauge couplings. JHEP 07, 116 (2013). arXiv:1305.5596 [hep-ex], Preprint CMS-FSQ-12-010, CERN-PH-EP-2013-084, https://doi.org/10.1007/JHEP07(2013)116
ALICE Collaboration, E. Abbas et al., Charmonium and \(e^+e^-\) pair photoproduction at mid-rapidity in ultra-peripheral Pb-Pb collisions at \(\sqrt{s_{\rm NN}}=2.76\) TeV. Eur. Phys. J. C 73(11), 2617 (2013). arXiv:1305.1467 [nucl-ex], Preprint CERN-PH-EP-2013-066, https://doi.org/10.1140/epjc/s10052-013-2617-1
ATLAS Collaboration, G. Aad et al., Measurement of exclusive \(\gamma \gamma \rightarrow \ell ^+\ell ^-\) production in proton–proton collisions at \(\sqrt{s} = 7\) TeV with the ATLAS detector. Phys. Lett. B 749, 242–261 (2015). arXiv:1506.07098 [hep-ex], Preprint CERN-PH-EP-2015-134, https://doi.org/10.1016/j.physletb.2015.07.069
ATLAS Collaboration, M. Aaboud et al., Evidence for light-by-light scattering in heavy-ion collisions with the ATLAS detector at the LHC. Nat. Phys. 13(9), 852–858 (2017). arXiv:1702.01625 [hep-ex], Preprint CERN-EP-2016-316, https://doi.org/10.1038/nphys4208
CMS Collaboration, Measurement of light-by-light scattering in ultraperipheral PbPb collisions at \(\sqrt{s_{{\rm NN}}} = 5.02\) TeV. CMS-PAS-FSQ-16-012, CERN, Geneva, 2018, Preprint CMS-PAS-FSQ-16-012, https://cds.cern.ch/record/2319158
D. d’Enterria, G.G. da Silveira, Observing light-by-light scattering at the large hadron collider. Phys. Rev. Lett. 111, 080405 (2013). https://doi.org/10.1103/PhysRevLett.111.080405. arXiv:1305.7142 [hep-ph]
D. d’Enterria, G.G. da Silveira, Measuring light-by-light scattering at the LHC and FCC, in Proceedings, 16th conference on Elastic and Diffractive Scattering (EDS BLOIS 2015) (2016). arXiv:1602.08088 [hep-ph], https://inspirehep.net/record/1424257/files/arXiv:1602.08088.pdf
G.J. Gounaris, P.I. Porfyriadis, F.M. Renard, The \(\gamma \gamma \) to \(\gamma \gamma \) process in the standard and SUSY models at high-energies. Eur. Phys. J. C 9, 673–686 (1999). https://doi.org/10.1007/s100529900079. arXiv:hep-ph/9902230 [hep-ph], Preprint PM-99-04, THES-TP-99-01
I.F. Ginzburg, A. Schiller, Search for a heavy magnetic monopole at the Tevatron and CERN LHC. Phys. Rev. D 57, 6599–6603 (1998). https://doi.org/10.1103/PhysRevD.57.6599. arXiv:hep-ph/9802310 [hep-ph], Preprint UL-NTZ-02-98
D. Bernard, On the potential of light by light scattering for invisible axion detection. Nuovo Cim. A 110, 1339–1346 (1997). Preprint X-LPNHE-97-12
D. Bernard, On the potential of light by light scattering for invisible axion detection. Nucl. Phys. Proc. Suppl. 72, 201 (1999)
T. Kikuchi, N. Okada, M. Takeuchi, Unparticle physics at the photon collider. Phys. Rev. D 77, 094012 (2008). https://doi.org/10.1103/PhysRevD.77.094012. arXiv:0801.0018 [hep-ph], Preprint KEK-TH-1202
K.-M. Cheung, Diphoton signals for low scale gravity in extra dimensions. Phys. Rev. D 61, 015005 (2000). https://doi.org/10.1103/PhysRevD.61.015005. arXiv:hep-ph/9904266 [hep-ph], Preprint UCD-HEP-99-8
J.L. Hewett, F.J. Petriello, T.G. Rizzo, Signals for noncommutative interactions at linear colliders. Phys. Rev. D 64, 075012 (2001). https://doi.org/10.1103/PhysRevD.64.075012. arXiv:hep-ph/0010354 [hep-ph], Preprint SLAC-PUB-8635, FERMILAB-PUB-00-286-T
J.P. Lansberg, R.E. Mikkelsen, U.I. Uggerhoej, Near-threshold production of \(W^\pm \), \(Z^0\) and \(H^0\) at a fixed-target experiment at the future ultra-high-energy proton colliders. Adv. High Energy Phys. 2015, 249167 (2015). https://doi.org/10.1155/2015/249167. arXiv:1507.01438 [hep-ex]
S.J. Brodsky, F. Fleuret, C. Hadjidakis, J.P. Lansberg, Physics opportunities of a fixed-target experiment using the LHC beams. Phys. Rep. 522, 239–255 (2013). https://doi.org/10.1016/j.physrep.2012.10.001. arXiv:1202.6585 [hep-ph], Preprint SLAC-PUB-14878
P. Azzurri et al., Physics behind precision. arXiv:1703.01626 [hep-ph]
M. Mangano, Physics at the FCC-hh, a 100 TeV pp collider. arXiv:1710.06353 [hep-ph], Preprint CERN-2017-003-M, https://doi.org/10.23731/CYRM-2017-003
Acknowledgements
We would like to thank the International Advisory Committee members: R. Assmann, DESY, Germany; C. Biscari, CELLS-ALBA, Spain; M. Diemoz, INFN, Italy; G. Dissertori (Chair), ETH Zurich, Switzerland; V. Egorychev, ITEP, Russia; W. Fischer, BNL, USA; G. Herten, University Freiburg, Germany; P. Lebrun, JUAS, France; J. Minervini, MIT, USA; A. Mosnier, CEA, France; A. Parker, University of Cambridge, UK; C. Quigg, Fermilab, USA; M. Ross, SLAC, USA; M. Seidel, PSI, Switzerland; V. Shiltsev, Fermilab, USA; T. Watson, ITER, IEIO; A. Yamamoto, KEK, Japan and the International Steering Committee members: S. Asai, University of Tokyo, Japan; F. Bordry, CERN, IEIO; P. Campana (ECFA and Chair from 2016), INFN, Italy; P. Chomaz, CEA, France; E. Colby, DOE, USA; G. Dissertori, ETH Zurich, Switzerland; E. Elsen, CERN, IEIO M. Krammer (Chair 2014–2016); HEPHY/CERN, Vienna, Austria; A. Lankford, UCI, USA; S. Peggs, DOE/BNL, USA; L. Rivkin, PSI, Switzerland; J. Womersley, ESS, Sweden for the continued and careful reviewing that helped to successfully complete this report.
The editors wish to thank all the scientific, engineering and technical personnel, the students and early stage researchers and all members of personnel involved in the investigations, designs and prototyping for their invaluable contributions that made this work possible. We also want to express our thanks to the administration officers who prepared the ground and created a framework in which this work could be carried out efficiently. The FCC study management team thanks in particular John Poole for his enthusiastic dedication during the editing phase, contributing significantly to deliver a coherent, consistent and readable set of report volumes. Finally, we wish to thank the CERN management for their strong support and encouragement.
 The research, which led to this publication has received funding from the European Union’s Horizon 2020 research and innovation programme under the Grant numbers 654305 (EuroCirCol), 764879 (EASITrain), 730871 (ARIES), 777563 (RI-Paths) and from FP7 under grant number 312453 (EuCARD-2). The information herein only reflects the views of its authors. The European Commission is not responsible for any use that may be made of the information.
The research, which led to this publication has received funding from the European Union’s Horizon 2020 research and innovation programme under the Grant numbers 654305 (EuroCirCol), 764879 (EASITrain), 730871 (ARIES), 777563 (RI-Paths) and from FP7 under grant number 312453 (EuCARD-2). The information herein only reflects the views of its authors. The European Commission is not responsible for any use that may be made of the information.
Trademark notice All trademarks appearing in this report are acknowledged as such.
Author information
Authors and Affiliations
Consortia
Additional information
Volume Editors: M. Mangano, P. Azzi, M. Benedikt, A. Blondel, D. Britzger, A. Dainese, M. Dam, J. de Blas, D. D’Enterria, O. Fischer, C. Grojean, J. Gutleber, C. Gwenlan, C. Helsens, P. Janot, M. Klein, M. McCullough, S. Monteil, J. Poole, M. Ramsey-Musolf, C. Schwanenberger, M. Selvaggi, T. You, F. Zimmermann.
CERN Accelerator Reports. Published by CERN, CH-1211 Geneva 23, Switzerland.
Knowledge transfer is an integral part of CERN’s mission. CERN publishes this volume Open Access under the Creative Commons Attribution 4.0 license (http://creativecommons.org/licenses/by/4.0/) in order to permit its wide dissemination and use. The submission of a contribution to a CERN Yellow Reports series shall be deemed to constitute the contributor’s agreement to this copyright and license statement. Contributors are requested to obtain any clearances that may be necessary for this purpose. This volume is indexed in: CERN Document Server (CDS)
FCC physics workshops and reports
FCC physics workshops and reports
The major physics meetings organised so far in the course of the FCC study are listed below. In addition to the following extended events, a multitude of shorter, periodic working group meetings have taken place. They can be found at the Indico meeting categories listed below. FCC physics has also been the subject of many events organised worldwide outside of the FCC study proper, which will not be documented here.
1.1 Physics workshops organised within the FCC study
1.1.1 FCC-ee
Starting in 2012, LEP3, then TLEP workshops took place under the umbrella of EUCARD; starting in July 2013 they become integrated in the FCC design study.
-
5th TLEP Workshop “TLEP physics and technology”, Fermilab, 25–26 July 2013 (Org.: P. Azzi, M. Carena, A. Gritsan, M. Klute, S. Malik, F. Piccinini, C. Quigg, M. Schmitt, C. Tully, M. Zanetti, F. Zimmermann), https://indico.cern.ch/event/246137/.
-
6th TLEP Workshop, CERN, 16–18 October 2013, (Org: R. Aleksan, P. Azzi, A. Blondel, J. R. Ellis, P. Janot, M. Koratzinos, F. Zimmermann), https://indico.cern.ch/event/257713/.
-
FCC-ee/TLEP physics workshop (TLEP7), CERN, 19–21 June 2014, (Org: A. Blondel, J. Ellis, C. Grojean, P. Janot). https://indico.cern.ch/event/313708/.
-
FCC-ee (TLEP) Physics Workshop (TLEP8), LPNHE Paris, 27–29 October 2014, (Org: R. Aleksan, S. Laplace, L. Marquet, L. Roos, P. Slavich, D. Varouchas), https://indico.cern.ch/event/337673/.
-
FCC-ee (TLEP) Physics Workshop (TLEP9), SNS Pisa, 3–5 February 2015, (Org: G. Rolandi, R. Tenchini), https://indico.cern.ch/event/357188/.
-
1st FCC-ee mini-workshop on Detector Requirements, CERN, 17–18 June 2015, (Org: C. Leonidopoulos, G. Rolandi, M. Dam), https://indico.cern.ch/event/393093/.
-
FCC-ee mini-workshop on “Precision Observables and Radiative Corrections”, CERN, 13–14 July 2015, (Org: J. Ellis, C. Grojean, S. Heinemeyer), https://indico.cern.ch/event/387296/.
-
First FCC-ee workshop on Higgs physics, CERN, 24–25 Sept. 2015, (Org: K. Peters, M. Klute), https://indico.cern.ch/event/401590/.
-
Workshop on high-precision \(\alpha _s\) measurements: from LHC to FCC-ee, 12–13 October 2015, (Org: D. d’Enterria, P. Skands), https://indico.cern.ch/event/392530/.
-
FCC-ee Mini-Workshop: “Physics Behind Precision”, CERN, 2–3 February 2016, (Org: P. Azzi, F. Blekman, E. Locci, F. Piccinini, R. Tenchini), https://indico.cern.ch/event/469561/.
-
10th FCC-ee Physics Workshop, CERN, CERN, 2–3 February 2016, (Org: P. Azzi, F. Blekman, A. Blondel, J. Ellis, C. Grojean, P. Janot, E. Locci, F. Piccinini, R. Tenchini), https://indico.cern.ch/event/469576/.
-
Parton Radiation and Fragmentation from LHC to FCC-ee, CERN, 21–22 Nov 2016, (Org: P. Skands, D. d’Enterria), https://indico.cern.ch/event/557400/.
-
2nd mini-workshop on FCC-ee detector requirements CERN, 23–24 November 2016, (Org: A. Cattai, G. Rolandi, M. Dam), https://indico.cern.ch/event/570415/.
-
Mini workshop: Precision EW and QCD calculations for the FCC studies: methods and tools, CERN 12–13 January 2018, (Org: A. Blondel, J. Gluza, P. Janot), https://indico.cern.ch/event/669224/.
-
FCC-ee mini-workshop on Flavours, CERN, 31 Jan.–1 Feb. 2018, (Org: J. F. Kamenik S. Monteil), https://indico.cern.ch/event/687191/.
-
11th FCC-ee workshop: Theory and Experiments, CERN, 8–11 Jan 2019, (Org: A. Blondel, M. Dam, J. Gluza, C. Grojean, P. Janot), https://indico.cern.ch/event/766859/.
1.1.2 FCC-hh
-
Ions at the Future Hadron Collider, Dec 16–17 2013, https://indico.cern.ch/event/288576/.
-
BSM physics opportunities at 100 TeV, Febr 10–11 2014, https://indico.cern.ch/event/284800/.
-
1st Future Hadron Collider Workshop, May 26–28 2014, https://indico.cern.ch/event/304759.
-
Ions at the Future Circular Collider, Sept 22–23 2014, https://indico.cern.ch/event/331669/.
-
Higgs & BSM at 100 TeV, March 11–13 2015, https://indico.cern.ch/event/352868/.
-
QCD, EW and tools at 100 TeV, Oct 7–9 2015, https://indico.cern.ch/event/437912/.
-
Dark Matter at a future hadron collider, Dec 4–6 2015, https://indico.cern.ch/event/445743/.
1.1.3 FCC-eh
-
LHeC and FCC-eh, CERN and Chavanne-de-Bogis, 24–26.6.2015, https://indico.cern.ch/event/356714/.
-
Deep Inelastic Scattering, Birmingham, 3–7.4.2017, https://indico.cern.ch/event/568360/.
-
LHeC and FCC-eh, CERN, 11-13.9.2017, https://indico.cern.ch/event/639067/.
-
Deep Inelastic Scattering, Kobe, 16–20.4.2018, https://indico.cern.ch/event/698368/.
-
Electrons for the LHC – LHeC/FCC-eh and PERLE, Orsay, 27–29.6.2018, https://indico.cern.ch/event/698368/.
1.1.4 Common FCC physics events
-
LHC, FCC-ee, FCC-hh Interplay, 25 November 2016, https://indico.cern.ch/event/573689/.
-
1st FCC Physics Workshop, January 16–20 2017, https://indico.cern.ch/event/550509/.
-
2nd FCC Physics Workshop, January 15–19 2018, https://indico.cern.ch/event/618254/.
1.2 Physics reports published during the FCC study
1.2.1 FCC-ee
-
First Look at the Physics Case of TLEP, Journal Publication [8].
-
High-Precision \(\alpha _s\) Measurements from LHC to FCC-ee, Workshop report [43].
-
Physics Behind Precision, Workshop report [465].
-
Parton Radiation and Fragmentation from LHC to FCC-ee, Workshop report [103].
-
Standard Model Theory for the FCC-ee: The Tera-Z, Workshop report [46].
1.2.2 FCC-hh
-
“Physics at 100 TeV”, CERN Yellow Report [466], including:
1.3 Indico categories of the FCC physics groups
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Abada, A., Abbrescia, M., AbdusSalam, S.S. et al. FCC Physics Opportunities. Eur. Phys. J. C 79, 474 (2019). https://doi.org/10.1140/epjc/s10052-019-6904-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-019-6904-3