Noncommutative Schwarzschild geometry and generalized uncertainty principle

Abstract

We discuss a possible link between the deformation parameter $\Theta ^{\mu \nu }$ arising in the framework of noncommutative geometry and the parameter $\beta$ of the generalized uncertainty principle (GUP). We compute the shift of the Hawking temperature induced by the $\Theta ^{\mu \nu }$-deformed Schwarzschild geometry, and then we relate it to one obtained by GUP. Results suggest a granular structure of specetime at the Planck scales. The current bounds on $\beta$ allow to constraint the noncommutative parameter $\Theta ^{\mu \nu }$.

1 Introduction

The possibility to describe spacetime in noncommutive frameworks was noted long time ago [1], and its interest renewed recently owing to the discovery of Seiberg-Witten map [2], which relates noncommutative to commutative gauge theories. Since then there has been a more and more interest to understand the impact of noncommutativity on fundamental issues. From a side by studying the the space-time symmetry¹ and unitary properties of these theories [3,4,5,6,7,8,9,10,11], from the other side, investigate on possible experimental evidences [12,13,14] (see the review [19, 20] and references therein). Moreover, the interest increased also thanks to the fact that the low-energy limit of string theory with an antisymmetric B-field background provides a quantized structure of the spacetimes [2, 19,20,21].

The idea of noncommutativity of spacetime might provide deep indications about the quantum nature of spacetime at very high energy scales, where (gravitational) singularities are inevitable. In fact, the noncommutativity of space-time could be intrinsically connected with gravity [2, 6, 7], and several studies have been proposed in literature to conciliate General Relativity with noncommutative space-time models. The general idea is to define the fields over phase space by replacing the ordinary product of fields with the Gronewald-Moyal product and then map (via the Seiberg-Witten) this theory in the equivalent commutative theory with expansion of the fields in terms of the noncommutative parameter. This approach has been extensively used to study many gauge theories [22,23,24,25,26,27,28] (see also [29,30,31,32]), and since gravity can be considered as a gauge theory, the commutative equivalent approach appears to be a promising formulation² [33, 48, 62,63,64,65,66,67,68,69,70,71,72].

Here we shall confine ourselves to the case in which the noncommutative coordinate product is given by

$$\begin{aligned} {[}x^\mu , x^\nu ] = i\Theta ^{\mu \nu }\,. \end{aligned}$$

(1.1)

The (antisymmetric) tensor $\Theta ^{\mu \nu }$ is a c-number, with $\mu ,\nu = 0,\ldots , n$, where $n+1$ is the dimension of the space-time,³ and accounts for the degree of quantum fuzziness of space-time. Although the canonical form (1.1) is the simplest case, it has the advantage to account for the basic features of noncommutativity. Hereafter we shall take 4-dimensional spacetimes. Limits on the noncommutative scale have been inferred in different frameworks, such as low-energy precision measurements [34, 35, 37], Lorentz symmetry violation [38, 39], early Universe [40,41,42], black holes and gravitational physics [43, 44]. In addition, several approaches of noncommutative theories of gravitation have been suggested [43,44,45,46,47,48,49,50,51, 62], and all these models show that the $\Theta$-corrections occur only at the second order. More specifically, in [39], for example, it has been found that the scale of noncommutativity is limited to be smaller than the inverse TeV scale. Yet, the upper bounds derived from Lamb shift corrections and from cosmology (CMB physics) give $\Theta <10^{-8}$ GeV$^{-2}$ [35] and $\Theta < 10^{-7}$ GeV$^{-2}$ [37], respectively.

The aim of this paper is to relate the parameter $\Theta ^{\mu \nu }$ to the deforming parameter $\beta$ of the generalized uncertainty principle (GUP) [58,59,60,61]. More precisely, we consider the (backreaction) effects of tiny modifications of the Schwarzschild geometry induced noncommutative geometry, which in turn affect the Hawking temperature, to the deformation of the Heisenberg uncertainty principle, that is the GUP, referring in particular to one widely studied in literature

$$\begin{aligned} \Delta x\, \Delta p \ge \frac{\hbar }{2}\left[ 1 + \beta \left( \frac{\Delta p}{M_{Pl}} \right) ^2\right] \,, \end{aligned}$$

(1.2)

where $M_{Pl}=1.2\times 10^{19}\,\text {GeV}$ is the Planck mass ($M_{Pl}^2=G^{-1}$ in natural units $\hbar =c=1$, where G is the universal gravitational constant). The dimensionless parameter $\beta$ is not fixed by the theory (even if it must be pointed out that in some models of string theories it is generally assumed that $\beta \sim \mathcal{O}(1)$ [52,53,54,55,56]). Typically, studies in this context are mainly focalized to understand how gravity may affect the Heisenberg Uncertainty Principle, and it is therefore not surprising that the most relevant modifications have been derived in fundamental (unification) theories, such as string theory, loop quantum gravity, deformed special relativity, and black hole physics [52,53,54,55,56, 73,74,75,76,77,78, 80,81,82, 94,95,99, 107,108,112]. Our target is to use the GUP to compute the Hawking temperature of a given black hole, which however can be also computed by using the effective potential inferred by $\Theta$-deforming the Schwarzschild metric. This provides a relationship between the two parameters, $\beta \propto \Theta ^{\mu \nu }$, that in turn allows to infer, by making use of the most stringent bound on the parameter $\beta$, an upper bound on the deformation parameter $\Theta ^{\mu \nu }$.

2 GUP and Hawking temperature

The relationship between Hawking temperature and GUP has been derived in [78, 83,84,85,86,87,88,89,90, 94]. Let’s shortly summarize here the main points. From Heisenberg uncertainty principle [79] it follows that the size $\delta x$ of the smallest detail of an object detectable with a beam of photons is of the order $\delta x \simeq \frac{\hbar }{2\, E}$, where E is the energy of photon (larger energies allow to explore smaller regions). Inserting into Eq. (1.2) one gets (for $\Delta p \simeq E$)

$$\begin{aligned} \delta x \simeq \frac{\hbar }{2\, E} + 2\,\beta \,l_{Pl}^2\, \frac{E}{\hbar } \end{aligned}$$

(2.1)

This equation allows to relate the mass M and the temperature T of a Schwarzschild black hole. In fact, the position uncertainty of an ensemble of unpolarized photons of Hawking radiation (just outside the event horizon of a Schwarzschild black hole $R_S\equiv 2GM$) is of the order of $R_S$, and therefore the uncertainty on the photon position is $\delta x \simeq 2\mu R_S$ (the constant $\mu$ is fixed in such a way to obtain the correct Hawking temperature, $\mu =\pi$). According to the equipartition principle, the temperature of unpolarized photons of the Hawking radiation is related to the average energy E as $E = T$, so that Eq. (2.1) can be cast in the form

$$\begin{aligned} M =\frac{\hbar }{8\pi G T} + \beta \, \frac{T}{2\pi }\,. \end{aligned}$$

(2.2)

The semiclassical limit $\beta \rightarrow 0$ reproduces the standard semiclassical Hawking temperature $T_H=\frac{\hbar }{8\pi GM}$. The relation (2.2) is the black hole mass-temperature relation derived by making use of the GUP for a Schwarzschild black hole. By inverting (2.2) (typically $\beta \, T \ll 1$, in particular for solar mass black holes) one gets

$$\begin{aligned} T = T_H \left( 1 + \frac{\beta }{4\pi ^2}\,\frac{M_{Pl}^2}{\,M^2} + \cdots \right) , \end{aligned}$$

(2.3)

with $M_{Pl}^2=\hbar /G$ (we set $c=1$). Results here derived rely on the assumption that the correction induced by the GUP has a thermal character, and, as a consequence, it can be cast in the form of a shift of $T_H$ (notice, however, that there exist in literature different approaches in which the corrections do not respect the exact thermality of the spectrum, as, for example, in the corpuscular model of a black hole [91]).

3 Temperature from a $\Theta ^{\mu \nu }$-Schwarzschild metric

In this section, we shall derive the relation between the parameters $\Theta ^{\mu \nu }$ and $\beta$. To this aim, we first recall the modifications to the Schwarzschild metric induced by the noncommutative geometry. Then we compute the correction/shift to the Hawking temperature.

3.1 $\Theta ^{\mu \nu }$-Schwarzschild metric

The question concerning the possible to find new solutions of the deformed Einstein field equations has been faced in many papers (see for example [29, 30, 43, 44, 71, 72] and references therein). For our aim, we shall refer in particular to Chaichian-Tureanua-Zet paper [72], where the authors have been able to derive the noncommutative corrections ($\Theta$-expansion) to the exact Schwarzschild solution. Essentially, the basic idea in this work is that to obtain the deformed Schwarzschild solution, one has to compute the deformed tetrad fields ${\hat{e}}^a_\mu (x, \Theta )$ by contracting the noncommutative gauge group SO(4, 1) to the Poincaré group ISO(3, 1). In short, consider the gauge theory of de Sitter group SO(4, 1) on a commutative spacetime with spherical symmetry $ds^2=g_{\mu \nu }dx^\mu dx^\nu =dr^2 + r^2 d\theta ^2+r^2\sin ^2\theta d\phi ^2-dt^2$. Here we are using the notation $\mu =1, 2, 3, 0$, so that $x^\mu =(r, \theta , \phi , t)$. The non-deformed gauge potentials are denoted with $\omega ^{AB}_\mu (x)$, where hereafter $A, B = 1, 2, 3, 0, 5$, and are identified with the spin connection $\omega _\mu ^{ab}(x)=-\omega _\mu ^{ba}$, and the tetrad fields $\omega ^{a5}_\mu (x)=k e^a_\mu (x)$, with $a, b = 1, 2, 3, 0$ and k is the contraction parameter. The strength of the gauge potential $\omega ^{AB}_\mu (x)$ is defined as

$$\begin{aligned} F_{\mu \nu }^{AB}= & {} \partial _\mu {\hat{\omega }}^{AB}_\nu (x, \Theta )- \partial _\nu {\hat{\omega }}^{AB}_\nu (x, \Theta ) \nonumber \\&\quad + \left[ {\hat{\omega }}^{AC}_\mu (x, \Theta ) {\hat{\omega }}^{DB}_\nu (x, \Theta ) \right. \nonumber \\&\quad \left. - {\hat{\omega }}^{AC}_\nu (x, \Theta ){\hat{\omega }}^{DB}_\mu (x,\Theta )\right] \eta _{CD}\,, \end{aligned}$$

(3.1)

where $\eta _{AB}=(1,1,1,-1,1)$. By defining $F_{\mu \nu }^{a5}=kT^a_{\mu \nu }$ and $F_{\mu \nu }^{ab}\equiv R^{ab}_{\mu \nu }$, the Poincaré gauge theory assumes the geometric structure of Riemann–Cartan space U(4), in which $T^a_{\mu \nu }$ and $R^{ab}_{\mu \nu }$ are interpreted as the torsion and curvature tensors of the Riemann–Cartan spacetime. The commutative Poincaré group theory, the ISO(3, 1) groups, follows for $k=0$.

In the non-commutative case, in which the structure (1.1) determines the noncommutative structure of the spacetime, the noncommutative gauge theory is developed by defining the $*$-product of fields, i.e.

$$\begin{aligned} \phi (x) *\chi (x) \equiv e^{\frac{i}{2}\Theta ^{\mu \nu }\partial _{x^\mu }\partial _{y^\nu }}\phi (x) \chi (y)\Big |_{y\rightarrow x}\,. \end{aligned}$$

(3.2)

The deformed gauge potentials are denoted with ${\hat{\omega }}^{AB}_\mu (x, \Theta )$, that fulfill the reality conditions. Expanding in terms of $\Theta ^{\mu \nu }$ and using the Seiberg-Witten map, one gets

$$\begin{aligned} {\hat{\omega }}^{AB}_\mu (x, \Theta )= & {} \omega ^{AB}_\mu (x)-i \Theta ^{\nu \rho }\omega _{\mu \nu \nu \rho }^{AB}(x) \\&\quad +\Theta ^{\nu \rho }\Theta ^{\alpha \sigma }\omega _{\mu \nu \rho \alpha \sigma }^{AB}(x)+\mathcal{O}(\Theta ^3)\,, \end{aligned}$$

where the coefficient $\omega _{\mu \nu \nu \rho }^{AB}(x)$ is given by

$$\begin{aligned}&\omega _{\mu \nu \nu \rho }^{AB}(x)=\frac{1}{4}\left[ \omega _\nu ^{AC} (\partial _\rho \omega _\mu ^{CB} \right. \\&\quad \left. +R_{\rho \mu }^{CB})+(\partial _\rho \omega _\mu ^{AC}+R_{\rho \mu }^{AC})\omega _\nu ^{CB}\right] \,, \end{aligned}$$

and similar expressions for $\omega _{\mu \nu \rho \alpha \sigma }^{AB}(x)$ and other terms of the expansion, but much more involved. The limit $k\rightarrow 0$ corresponds to the ISO(3, 1) gauge groups (hence a torsionless spacetime), and the spin connection are determined by tetrads. The deformed metric reads

$$\begin{aligned} {\hat{g}}_{\mu \nu }(x, \Theta )=\frac{1}{2}\left( {\hat{e}}_\mu ^a * {\hat{e}}_\nu ^{b \, \dagger }+{\hat{e}}_\mu ^b * {\hat{e}}_\nu ^{a \, \dagger }\right) \eta _{ab}\,, \end{aligned}$$

(3.3)

where the ”${}^\dagger$” is the complex conjugation. As for the gauge fields, the tetrads can be expanded

$$\begin{aligned}& {\hat{e}}^a_\mu (x, \Theta )=e^a_\mu (x)-i\Theta ^{\nu \rho }e^a_{\mu \nu \rho }(x) \\&\quad +\Theta ^{\nu \rho }\Theta ^{\alpha \sigma }e^{a}_{\nu \rho \alpha \sigma }(x)+\mathcal{O}(\Theta ^3)\,, \end{aligned}$$

with $e^a_{\mu \nu \rho }(x)=\frac{1}{4}[\omega ^{ac}_\nu \partial _\rho e^d_\mu +(\partial _\rho \omega _\mu ^{ac}+R_{\rho \mu }^{ac})e^d_\nu ]\eta _{cd}$, and similarly for the other terms of the expansion.

The noncommutative structure allows to derive $\Theta ^{\mu \nu }$-corrections to a given geometry, in particular to the Schwarzschild geometry, to which we are interested in [71].

Following the deformation quantisation discussed in [117,118,119,120] for the Schwarzschild metric, one has to specify a Moyal algebra. Since $x^\mu = (r, \theta , \phi , t)$, the algebra of the functions in these variables is deformed by imposing the Moyal product (3.2) with

$$\begin{aligned} \Theta ^{\mu \nu }= \Upsilon \begin{pmatrix} 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ -1 &{}\quad 0 &{}\quad 0 &{} \quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}\!. \end{aligned}$$

(3.4)

Here $\Upsilon$ is the deformation parameter (the ansatz (3.4) gives rise to the simplest model of noncommutativity spacetime). In the coordinate system in which $\Theta ^{\mu \nu }$ assumes the form (3.4), the non vanishing component $\Upsilon$ has dimensions⁴ L or $E^{-1}$. Considering the non-deformed Schwarzschild geometry $ds^2=g_{\mu \nu }^{(S)}dx^\mu dx^\nu$, with $g_{\mu \nu }^{(S)}=\text {diag}(A^{-1}(r), r^2, r^2\sin ^2\theta , -A(r))$, $A(r)=1-\frac{\alpha }{r}$ ($\alpha \equiv 2GM$ and M is the mass of the gravitational source), with associated vierbein fields $e_\mu ^1=(A^{-1}, 0, 0, 0)$, $e_\mu ^1=(0, r, 0, 0)$, $e_\mu ^3=(0, 0, r\sin \theta , 0)$, and $e_\mu ^0=(0, 0, 0, A)$, one infers the components of the $\Theta$-Schwarzschild metric (see (3.3))

$$\begin{aligned} {\hat{g}}_{\mu \nu }=g_{\mu \nu }^{(S)}+h_{\mu \nu }^{(NC)}\,, \end{aligned}$$

(3.5)

where $h_{\mu \nu }^{(NC)}$ represents the noncommutative corrections to the Schwarzschild geometry

$$\begin{aligned} h_{00}^{(NC)}= & {} -\frac{\alpha (8r-11\alpha )}{16r^4}\Upsilon ^2+\mathcal{O}(\Upsilon ^4)\,, \end{aligned}$$

(3.6)

$$\begin{aligned} h_{rr}^{(NC)}= & {} -\frac{\alpha (4r-3\alpha )}{16r^2(r-\alpha )^2}\Upsilon ^2 + \mathcal{O}(\Upsilon ^4)\,, \end{aligned}$$

(3.7)

$$\begin{aligned} h_{\theta \theta }^{(NC)}= & {} \frac{2r^2-17\alpha (r-\alpha )}{32r(r-\alpha )}\Upsilon ^2+\mathcal{O}(\Upsilon ^4)\,, \end{aligned}$$

(3.8)

$$\begin{aligned} h_{\phi \phi }^{(NC)}= & {} \frac{(r^2+\alpha r-\alpha ^2)\cos ^2\theta -\alpha (2r-\alpha )}{16r(r-\alpha )}\Upsilon ^2 \nonumber \\&\quad +\mathcal{O}(\Upsilon ^4)\,. \end{aligned}$$

(3.9)

The limit $\Upsilon \rightarrow 0$ reproduces the standard Schwarzschild solution. Moreover, as pointed out in the Introduction, all corrections are of the second order in the deformation parameter $\Upsilon$. This is a general feature of noncommutative theories of gravitation (see for example [43,44,45,46,47,48,49,50,51, 62]). Results here obtained are at the order $L^2$ due to the fact that calculations are performed in spherical coordinates⁵ [72, 118, 120,121,122,123] (in Cartesian coordinates,⁶ hence in the standard canonical quantization, the non-commutative parameter $\Theta ^2$ has dimensions $L^4$).

3.2 Temperature shift from the deformed Schwarzschild metric

We can now compute the shift of the Hawking temperature induced by $\Theta$-deformation algebra (3.4) (we follow the procedure delineated in [90, 94, 95]). Consider

$$\begin{aligned} {\hat{g}}_{00} =- 1 + \frac{2GM}{r} - h_{00}^{(NC)}(r)\,, \end{aligned}$$

(3.10)

with $|h_{00}^{(NC)}(r)| \ll 2GM/r$ for any $r\ge 2GM$. The horizon’s equation, i.e., ${\hat{g}}_{00} (r_H)=0$, is given by $r_H - 2 \,G\, M + r_H\, h_{00}^{(NC)}(r_H) = 0$, and the solution is $r_H = \alpha - \frac{\alpha \, h_{00}^{(NC)}(\alpha )}{1 \ + \ [h_{00}^{(NC)}(\alpha ) \ + \ a\, h_{00}^{(NC)\, \prime }(\alpha )]}$. The ”deformed” Hawking temperature is given by

$$\begin{aligned} T= & {} -\hbar \frac{{\hat{g}}_{00}^\prime (r_H)}{4\pi } = T_H \left\{ 1 + \left[ 2h_{00}^{(NC)}(r) + \alpha h_{00}^{(NC)\, \prime }(r)\right] _{r=\alpha } \right\} \nonumber \\&\quad +\mathcal{O}(h_{00}^{(NC)\, 2}). \end{aligned}$$

(3.11)

where the expansion is understood in terms of $\Theta ^2$-parameter and the symbol ${}^\prime$ stands for the derivative with respect to r (${}^\prime \equiv \displaystyle {\frac{\partial }{\partial r}}$). By comparing the temperature (3.11) with the GUP-deformed Hawking temperature given by Eq. (2.3), one finally obtains

$$\begin{aligned} \beta = \frac{4\pi ^2 M^2}{M_{Pl}^2}\, \left[ 2h_{00}^{(NC)}(\alpha ) + \alpha h_{00}^{(NC)\prime }(\alpha )\right] \,, \end{aligned}$$

(3.12)

that, by using (3.6), assumes the form

$$\begin{aligned} \beta = \frac{4\pi ^2 M^2}{M_{Pl}^2}\left[ -\frac{7\Upsilon ^2}{8\alpha ^2}\right] =-\frac{7\pi ^2}{2}(\Upsilon M_{Pl})^2\,. \end{aligned}$$

(3.13)

This is the wanted result, i.e. the interplay between the noncommutative deformation parameter $\Upsilon$ and the deformation parameter $\beta$ of GUP. The relation presents several interesting features:

• Remarkably, the relation between $\beta$ and $\Upsilon$ does not depend on gravitational mass M. This is particularly important because, as Eq. (3.13) shows, it is related to the universal character of the deformation parameter $\Theta$, suggesting its deep connection to Planck scale, then to quantum gravity.

• The above point is corroborated by the fact that $\beta \simeq -(M_{Pl}\Upsilon )^2<0$. A negative value of the GUP parameter typically arises in non-trivial space-time structures such as a (fundamental) discreteness of space, see for example [74, 75, 93]. Interestingly, a similar result has been also obtained in the framework of the crystal lattice [93], providing therefore a further hint that the physical space-time could have a lattice or granular structure at the level of Planck scale.

• To infer bounds on the parameter $\Upsilon$, we require that the $\Upsilon$-correction is smaller or equal to the $\beta$-term, hence

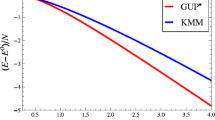
  $$\begin{aligned} \Upsilon \leqslant \frac{2}{7\pi ^2}\frac{\sqrt{|\beta |}}{M_{Pl}}< \frac{2}{7\pi ^2}\frac{\sqrt{\beta _{exp}}}{M_{Pl}}\,, \end{aligned}$$

  (3.14)

  where $\beta _{exp}$ is the experimental upper bound on $|\beta |$. For the sake of completeness, in Tables 1 and 2 are reported experimental bounds on $\beta$ obtained in different frameworks. Using the the more stringent upper bound $\beta _{exp}= 10^{21}$, obtained in the gravitational sector, it follows $\Upsilon < 10^{-10}$GeV$^{-1}$. Such a bound improves one order of magnitude, $\Upsilon <10^{-11}$GeV$^{-1}$, for $\beta$ bounded from non-gravitational experiments.

• As pointed out in the Introduction, the deformation parameter $\beta$ is not fixed by the theory, and it is generally assumed that $\beta \sim \mathcal{O}(1-10)$, as suggested by some models of string theory [52,53,54,55,56]. It is hence interesting to observe that if the parameter $\Upsilon$ is of the order of the Planck scale, $\Upsilon \sim M_{Pl}^{-1}$ (the quantum gravity scale), then the GUP deformation parameter $\beta$ can be fixed to the value $|\beta |\sim \frac{7\pi ^2}{2}\sim \mathcal{O}(1-10)$.

Table 1 Upper bounds on $\beta$ derived from gravitational experiments

Table 2 Upper bounds on $\beta$ derived from non-gravitational experiments

4 Conclusions

In this paper we have derived an upper bound on the deformation parameter $\Upsilon$ of the noncommutative geometry (referring in particular to the gravitational sector of noncommutative geometry), by relating $\Upsilon$ to the coefficients $\beta$ of GUP. The shift of the Hawking temperature, for which the GUP is relevant, is derived by means of pure quantum mechanics principles, and no specific representations of canonical commutator relation is postulated. On the other hand, the same temperature is derived geometrically for a deformed Schwarzschild metric, allowing to link the deformed uncertainty relation with the $\Theta$-deformed metric. We have found that the $\Theta ^2$-correction to the canonical commutation relations of Heisenberg algebra is negative, suggesting a discrete nature of spacetime at the Planck scales, and that the more stringent bound that the current experiments allow to obtain is $\Upsilon <10^{-11}-10^{-10}$ (here $\Upsilon \equiv \Theta ^{12}=\Theta ^{r\theta }$).

Here we focused on noncommutative geometry putting attention to the gravitational sector, but understanding whenever other algebras may affect GUP, or specific representations of canonical operators, is certainly a non trivial task, especially for the possible links with quantum gravity. There is indeed a wide discussion on the implications of various models yielding GUPs, and a common aspect of all these models is related to test the size of these modifications. These aspects appear particularly interesting in perspective of laboratory-scale imitation of the black hole horizon, with the subsequent possible emission of an analogue Hawking radiation [115, 116].