Abstract
A search for weakly interacting massive dark-matter particles produced in association with bottom or top quarks is presented. Final states containing third-generation quarks and missing transverse momentum are considered. The analysis uses \(36.1 \; \mathrm {fb}^{-1}\) of proton–proton collision data recorded by the ATLAS experiment at \(\sqrt{s}=13\) TeV in 2015 and 2016. No significant excess of events above the estimated backgrounds is observed. The results are interpreted in the framework of simplified models of spin-0 dark-matter mediators. For colour-neutral spin-0 mediators produced in association with top quarks and decaying into a pair of dark-matter particles, mediator masses below 50 GeV are excluded assuming a dark-matter candidate mass of 1 GeV and unitary couplings. For scalar and pseudoscalar mediators produced in association with bottom quarks, the search sets limits on the production cross-section of 300 times the predicted rate for mediators with masses between 10 and \(50\; \hbox {GeV}\) and assuming a dark-matter mass of \(1 \;\hbox {GeV}\) and unitary coupling. Constraints on colour-charged scalar simplified models are also presented. Assuming a dark-matter particle mass of \(35\; \hbox {GeV}\), mediator particles with mass below \(1.1\; \hbox {TeV}\) are excluded for couplings yielding a dark-matter relic density consistent with measurements.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Astrophysical observations have provided compelling evidence for the existence of a non-baryonic dark component of the universe: dark matter (DM) [1, 2]. The currently most accurate, although somewhat indirect, determination of DM abundance comes from global fits of cosmological parameters to a variety of observations [3, 4], while the nature of DM remains largely unknown. One of the candidates for a DM particle is a weakly interacting massive particle (WIMP) [5]. At the large hadron collider (LHC), one can search for WIMP DM (\(\chi \)) pair production in pp collisions. WIMP DM would not be detected and its production leads to signatures with missing transverse momentum. Searches for the production of DM in association with Standard Model (SM) particles have been performed at the LHC [6,7,8,9,10,11,12].
Recently proposed simplified benchmark models for DM production assume the existence of a mediator particle which couples both to the SM and to the dark sector [13,14,15]. The searches presented in this paper focus on the case of a fermionic DM particle produced through the exchange of a spin-0 mediator, which can be either a colour-neutral scalar or pseudoscalar particle (denoted by \(\phi \) or a, respectively) or a colour-charged scalar mediator (\(\phi _b\)). The couplings of the mediator to the SM fermions are severely restricted by precision flavour measurements. An ansatz that automatically relaxes these constraints is Minimal Flavour Violation [16]. This assumption implies that the interaction between any new neutral spin-0 state and SM matter is proportional to the fermion masses via Yukawa-type couplings.Footnote 1 It follows that colour-neutral mediators would be sizeably produced through loop-induced gluon fusion or in association with heavy-flavour quarks. The characteristic signature used to search for the former process is a high transverse momentum jet recoiling against missing transverse momentum [7, 11].
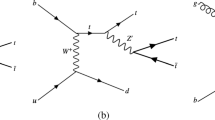
Representative diagrams at the lowest order for spin-0 mediator associated production with top and bottom quarks: a colour-neutral spin-0 mediator associated production with bottom quarks \(b\bar{b}\) +\(\phi /a\); b colour-neutral spin-0 mediator associated production with top quarks \(t\bar{t}\) +\(\phi /a\); c colour-charged scalar mediator model decaying into a bottom quark and a DM particle \(b\)-FDM
This paper focuses on dark matter produced in association with heavy flavour (top and bottom) quarks. These final states were addressed by the CMS Collaboration in Ref. [17]. For signatures with two top quarks (\(t\bar{t}\) +\(\phi /a\)), final states where both W bosons decay into hadrons or both W bosons decay into leptons are considered in this paper. They are referred to as fully hadronic and dileptonic \(t\bar{t}\) decays, respectively. Searches in final-state events characterised by fully hadronic or dileptonic top-quark pairs have been carried out targeting supersymmetric partners of the top quarks [18, 19]. Due to the different kinematics of the events under study, those searches are not optimal for the DM models considered in this paper. The search in the channel where one W boson decays into hadrons and one W boson decays into leptons (semileptonic \(t\bar{t}\) decays) is presented together with the searches for top squarks in the same channel [20]. Signatures with bottom quarks in the final state are denoted \(b\bar{b}\) +\(\phi /a\) in the following. Representative diagrams for tree-level production of these models are shown in Fig. 1a, b. Processes with similar kinematic properties might also occur in two-Higgs-doublet models [21]. Following the notation of Ref. [14], the model has four parameters: the mass of the mediator \(m_\phi \) or \(m_a\), the DM mass \(m_\chi \), the DM–mediator coupling \(g_\chi \), and the flavour-universal SM–mediator coupling \(g_q\). The mediator width is assumed to be the minimal width, which is the one calculated from the masses and couplings assumed by the model [13]. The mediator can decay into SM particles or into DM particles. This search is sensitive to decays of the mediator into a pair of DM particles. Off-shell DM production is also taken into account. The effective production cross-section of DM particles at pp colliders is a function of the production cross-section of the mediator, depending on \(g_q\), and on the branching ratio for the mediator to decay into a pair of DM particles, which is a function of \(g_q\) and \(g_\chi \) [13]. The cross-section for DM production is therefore proportional to the squared product of the couplings (\(g_q\;\cdot g_\chi \))\(^2\), and an additional assumption of \(g_q = g_\chi = g\) is made to reduce the number of parameters. Since the cross-section of annihilation and scattering from nucleons has the same functional dependence on the couplings, the same assumption is made when the results are compared to non-collider experiments.
The second category of models considered in this search is the case of colour-charged scalar mediators [22]. The model assumes bottom-flavoured dark matter (\(b\)-FDM) and was proposed to explain the excess of gamma rays from the galactic centre observed by the Fermi Gamma-ray Space Telescope, if this excess is to be interpreted as a signal for DM annihilation [23], while alternative conjectures without DM are also discussed [24]. A representative diagram for the production of this signal is shown in Fig. 1c. In this model, a new scalar field, \(\phi _b\), mediates the interaction between DM and quarks. Dark matter is assumed to be the lightest Dirac fermion that belongs to a flavour-triplet coupling to right-handed, down-type quarks. The cosmological DM is the third component of the triplet and couples preferentially to bottom quarks. It explains the galactic-centre excess if a DM mass around \(35\;\hbox {GeV}\) is assumed. The other Dirac fermions in the flavour-triplet are heavy and couple weakly, and are therefore neglected. The \(b\)-FDM model has three parameters: the mediator and the DM masses (\(m(\phi _b)\) and \(m(\chi )\), respectively), and the coupling strength between the mediator and the DM particle, \(\lambda _b\) [22]. For each pair of mass values considered, \(\lambda _b\) is set to the value, generally larger than one, predicting a DM relic density compatible with the astrophysical observations as detailed in Ref. [22]. Strong-interaction pair production of \(\phi _b\), which does not depend on the coupling, is equivalent to the pair production of the lightest supersymmetric partner of the bottom quark (bottom squark, \(\tilde{b}_1\)) assuming that it decays exclusively into a bottom quark and the lightest neutralino (\(\tilde{\chi }^0_1\)). Exclusion limits on \(m(\tilde{b}_1)\), which depend on \(m(\tilde{\chi }^0_1)\), are set in dedicated searches by the ATLAS and CMS collaborations [25, 26]. The target of this search is the single production mode represented in Fig. 1(c), which can dominate the production rate of the \(\phi _b\) mediator due to the relatively large values assumed for \(\lambda _b\). The parameter space considered corresponds to \(\phi _b\) masses of a few hundred GeV. A search by the ATLAS Collaboration with the \(\sqrt{s} = 8\; \hbox {TeV}\) LHC Run-1 dataset has already excluded \(m(\phi _b) < 600\;\hbox {GeV}\) for \(m(\chi ) = 35\;\hbox {GeV}\) [27].
Four experimental signatures are considered in this paper. The first two signatures consist of event topologies with large missing transverse momentum and either one or two bottom quarks, while the other two consist of events with large missing transverse momentum and two top quarks, decaying either dileptonically or fully hadronically. The search presented in this paper is based on a set of independent analyses optimised for these four experimental signatures and searches for dark-matter production via colour-charged and colour-neutral mediators.
2 Detector description and event reconstruction
The ATLAS experiment [28] is a multi-purpose particle detector with a forward-backward symmetric cylindrical geometry and nearly \(4\pi \) coverage in solid angle.Footnote 2 It consists of an inner tracking detector (ID) surrounded by a superconducting solenoid, electromagnetic and hadronic calorimeters, and an external muon spectrometer incorporating large superconducting toroidal magnets. The inner tracking detector consists of pixel and silicon microstrip detectors covering the pseudorapidity region \(|\eta |<2.5\), surrounded by a transition radiation tracker which provides electron identification in the region \(|\eta |<2.0\). Between Run 1 and Run 2, a new inner pixel layer, the insertable B-layer [29, 30], was inserted at a mean sensor radius of 3.3 cm. The inner detector is surrounded by a thin superconducting solenoid providing an axial 2 T magnetic field and by a fine-granularity lead/liquid-argon (LAr) electromagnetic calorimeter covering \(|\eta |<3.2\). A steel/scintillator-tile calorimeter provides hadronic coverage in the central pseudorapidity range (\(|\eta |<1.7\)). The end-cap and forward regions (\(1.5<|\eta |<4.9\)) of the hadronic calorimeter are made of LAr active layers with either copper or tungsten as the absorber material. A muon spectrometer with an air-core toroid magnet system surrounds the calorimeters. Three stations of high-precision tracking chambers provide coverage in the range \(|\eta |<2.7\), while dedicated chambers allow triggering in the region \(|\eta |<2.4\). The ATLAS trigger system consists of a hardware-based level-1 trigger followed by a software-based high-level trigger [31].
The events used in this analysis are required to pass either an online trigger requiring a minimum of two electrons, two muons or an electron and a muon, or an online missing transverse momentum trigger selection. The trigger thresholds are such that a plateau of the efficiency is reached for events passing the analysis requirements presented in Sect. 4. The events are also required to have a reconstructed vertex [32] with at least two associated tracks with transverse momentum (\(p_{\text {T}}\)) larger than \(400\;\hbox {MeV}\) which are consistent with originating from the beam collision region. The vertex with the highest scalar sum of the squared transverse momenta of the associated tracks is considered to be the primary vertex of the event.
This analysis requires the reconstruction of jets, muons, electrons, photons and missing transverse momentum. Jets are reconstructed from three-dimensional energy clusters in the calorimeter [33] using the anti-\(k_t\) jet clustering algorithm [34] with a radius parameter \(R=0.4\) implemented in the FastJet package [35]. Jets are calibrated as described in Ref. [36], and the expected average energy contribution from clusters resulting from additional pp interactions in the same or nearby bunch crossings (pile-up interactions) is subtracted according to the jet area [37]. Only jet candidates (baseline jets) with \(p_{\text {T}} >20\;\hbox {GeV}\) and \(|\eta |<2.8\) are considered in the analysis. Quality criteria identify jets arising from non-collision sources or detector noise and any event containing such a jet is removed [38, 39]. Additional selection requirements are imposed on jets with \(p_{\text {T}} < 60\;\hbox {GeV}\) and \(|\eta |<2.4\) in order to reject jets produced in pile-up interactions [40]. Jets are also reclustered into larger-radius jets (\(R=0.8\) or 1.2) by applying the anti-\(k_t\) clustering algorithm to the \(R=0.4\) jets. These jets are exploited to identify W-boson decays into a pair of quarks and also to identify top-quark candidates.
Jets containing b-hadrons (\(b\text {-jets}\)) and which are within the inner detector acceptance (\(|\eta |<2.5\)) are identified (\(b\text {-tagged}\)) with a multivariate algorithm that exploits the impact parameters of the charged-particle tracks, the presence of secondary vertices and the reconstructed flight paths of b- and c-hadrons inside the jet [41, 42]. Depending on the signal region requirements detailed in Sect. 4, a “medium” or “tight” working-point is used for the \(b\text {-jet}\) identification, corresponding to an average efficiency for b-quark jets in simulated \(t\bar{t}\) events of 77 and 60%, respectively. An additional “loose” working-point with 85% efficiency for b-quark jets in simulated \(t\bar{t}\) events is used to resolve ambiguities in the reconstruction of physics objects, as described at the end of this section.
Muon candidates are reconstructed in the region \(|\eta |<2.7\) from muon spectrometer tracks matching ID tracks (where applicable). The pseudorapidity requirements are restricted to \(|\eta |<2.4\) for events passing the muon online trigger criteria, due to the coverage of the muon triggering system. Events containing one or more muon candidates that have a transverse (longitudinal) impact parameter with respect to the primary vertex larger than 0.2 mm (1 mm) are rejected to suppress muons from cosmic rays. Baseline candidate muons, used for the definition of vetoes in all signal regions but those searching for fully hadronic top decays, must have \(p_{\text {T}} >{10}{\hbox {GeV}}\) and pass the “medium” identification requirements defined in Ref. [43]. The baseline candidate muons used in fully hadronic \(t\bar{t} \) final states are instead required to pass the “loose” identification requirements [43] and to have \(p_{\text {T}} >{6}{\hbox {GeV}}\), in order to strengthen the veto definition. Baseline electron candidates are reconstructed from isolated electromagnetic calorimeter energy deposits matched to ID tracks and are required to have \(|\eta |<2.47\) and \(p_{\text {T}} >{10}{\hbox {GeV}}\), and must pass a “loose” likelihood-based identification requirement [44, 45].
Stricter requirements are imposed on the baseline lepton (electron or muon) definitions for the selection criteria requiring leptons in the final state. Signal muon candidates, used for all selection requirements with leptons in the final state, must have \(p_{\text {T}} > 20\;\hbox {GeV}\) and satisfy “medium” identification criteria [43]. Furthermore, they are required to be isolated using a “loose” criterion designed to be 99% efficient for muons from Z-boson decays [43]. Signal electron candidates are required to pass “tight” requirements on the likelihood-based identification [44] and must have \(p_{\text {T}} > 20\;\hbox {GeV}\). In order to improve signal acceptance, the requirement on the likelihood-based identification is relaxed to “medium” for the signal region optimised for the two-lepton final state. Like the muons, signal electrons are required to be isolated from other activity using a “loose” isolation criterion [46]. Signal electrons (muons) are matched to the primary vertex (PV) of the event (see Sect. 4) by requiring their transverse impact parameter \(d^{\mathrm P \mathrm V}_0\), with respect to the primary vertex, to have a significance \(|d^{\mathrm P \mathrm V}_0/\sigma (d^{\mathrm P \mathrm V}_0)| < 5\; (3)\). In addition, for both the electrons and muons the longitudinal impact parameter \(z^{\mathrm P \mathrm V}_0\) and the polar angle \(\theta \) are required to satisfy \(|z^{\mathrm P \mathrm V}_0 \sin \theta | < 0.5\) mm. In the following, the combination of signal electrons and muons optimised for the two-lepton final state is referred to as the medium-lepton requirement. Similarily, the combination of the signal electrons and muons passing the “tight” identification criteria is referred to as the tight-lepton requirement. The number of leptons passing the medium and tight requirements is denoted by \(\mathcal {N}^{\mathrm M}_{\ell }\) and \(\mathcal {N}^{\mathrm T}_{\ell }\), respectively.
Photons are reconstructed from clusters of energy deposits in the electromagnetic calorimeter measured in projective towers [47, 48]. Photon candidates are required to have \(p_{\text {T}} > 10\; \hbox {GeV}\) and \(|\eta |<2.37\), whilst being outside the transition region \(1.37< |\eta | < 1.52\) between the barrel and end-cap calorimeters, and to satisfy “tight” identification criteria [48]. The photons used in this analysis are further required to have \(p_{\text {T}} > 130\; \hbox {GeV}\) and to be isolated [47].
To resolve reconstruction ambiguities, an overlap removal algorithm is applied to loose candidate leptons and jets. Jet candidates with \(p_{\text {T}} >20\;\hbox {GeV}\) and \(|\eta |<2.8\) are removed if they are not b-tagged when employing the loose working-point and are within \(\Delta R =\sqrt{(\Delta y)^2+(\Delta \phi )^2} = 0.2\) of an electron candidate. The same is done for jets which lie close to a muon candidate and have less than three associated tracks or a ratio of muon \(p_{\text {T}}\) to jet \(p_{\text {T}}\) greater than 0.5. Finally, any lepton candidate within \(\Delta R = 0.4\) of the direction of a surviving jet candidate is removed, in order to reject leptons from the decay of a b- or c-hadron. Electrons which share an ID track with a muon candidate are also removed.
The missing transverse momentum vector, \(\vec {p}_{\text {T}}^{\text {miss}}\), whose magnitude is denoted by \(E_{\text {T}}^{\text {miss}}\), is defined as the negative vector sum of the transverse momenta of all identified physics objects (electrons, photons, muons, jets) and an additional soft term. The soft term is constructed from all tracks that originate from the primary vertex but are not associated with any physics object. In this way, the \(E_{\text {T}}^{\text {miss}}\) is adjusted for the calibration of the jets and the other identified physics objects above, while maintaining pile-up independence in the soft term [49, 50].
3 Data and simulated event samples
The dataset used in this analysis consists of pp collision data recorded at a centre-of-mass energy of \(\sqrt{s} = 13~\hbox {TeV}\) with stable beam conditions. The integrated luminosity of the combined 2015 + 2016 dataset after requiring that all detector subsystems were operational during data recording is \(36.1 \; \mathrm {fb}^{-1}\). The uncertainty in the total integrated luminosity is 3.2%, derived following a methodology similar to that detailed in Ref. [51].
Monte Carlo (MC) simulated event samples are used to aid in the estimation of the background from SM processes and to model the dark-matter signal. All simulated events were processed through an ATLAS detector simulation [52] based on Geant4 [53] or through a fast simulation using a parameterisation of the calorimeter response and Geant4 for the other parts of the detector [54]. The simulated events are reconstructed with the same reconstruction algorithms used for data. Correction factors are applied to the simulated events to compensate for differences between data and MC simulation in the b-tagging efficiencies and mis-tag rates, lepton and photon identification, reconstruction and trigger efficiencies. The MC samples are reweighted so that the pile-up distribution matches the one observed in the data.
The matrix element (ME) generator, parton shower (PS), cross-section normalisation, parton distribution function (PDF) set and the set of tuned parameters (known as tune) describing the underlying event for these samples are given in Table 1, and more details of the generator configurations can be found in Refs. [55,56,57,58]. The generation of \(t\bar{t}\) pairs and single-top-quark processes in the Wt- and s-channels was performed using the Powheg-Box v2 generator with the CT10 PDF set for the matrix element calculations. Electroweak t-channel single-top-quark events were generated using the Powheg-Box v1 generator. For all processes, a top-quark mass of 172.5 GeV is assumed. The PS and the underlying event were simulated using Pythia 6.428 with the CT10 PDF set. Samples of single-top-quark and \(t\bar{t}\) production are normalised to their NNLO cross-section including the resummation of soft gluon emission at next-to-next-to-leading-log (NNLL) accuracy using Top++2.0 [59,60,61].
Events containing W or Z bosons with associated jets, including jets from the hadronisation of b- and c-quarks, were simulated using the Sherpa v2.2.1 generator. Matrix elements were calculated for up to two additional partons at next-to-leading order (NLO) and four partons at leading order (LO) using the Comix [62] and Open Loops [63] matrix element generators and merged with the Sherpa PS [64] using the ME+PS@NLO prescription [65]. The NNPDF30NNLO [66] PDF set was used in conjunction with the dedicated PS tune developed by the Sherpa authors.
Diboson and triboson processes were also simulated using the Sherpa generator using the NNPDF30NNLO PDF set in conjunction with a dedicated PS tune developed by the Sherpa authors. Matrix elements for these samples were calculated for up to one (diboson processes) or zero (triboson processes) additional partons at NLO and up to three (diboson processes) or two (triboson processes) additional partons at LO. Additional contributions to the SM backgrounds in the signal regions arise from the production of \(t\bar{t}\) pairs in association with W/Z/h bosons and possibly additional jets. These processes were modelled by event samples generated at NLO using the MadGraph5_aMC NLO [67] v2.2.3 generator and showered with the Pythia v8.186 PS.
In all MC samples, except those produced by Sherpa, the EvtGen v1.2.0 program [85] was used to model the properties of the bottom and charm hadron decays. All Pythia v6.428 samples used the PERUGIA2012 [83] tune for the underlying event, while Pythia v8.186 and Herwig++ showering were run with the A14 and UEEE5 [86] underlying-event tunes, respectively. To simulate the effects of additional pp collisions in the same and nearby bunch crossings, additional interactions were generated using the soft QCD processes of Pythia 8.186 with the A2 tune [87] and the MSTW2008LO PDF [88], and overlaid onto each simulated hard-scatter event.
Alternative samples are employed to derive systematic uncertainties associated with the specific configuration of the MC generators used for the nominal SM background samples, as detailed in Sect. 6. They include variations of the renormalisation and factorisation scales, the CKKW-L matching [89] scale, as well as different PDF sets and hadronisation models.
The event generation for the dark-matter signal samples followed the prescriptions in Ref. [13]. Events were generated from leading-order (LO) matrix elements using the MadGraph generator v2.3.3 interfaced to Pythia v8.212 with the A14 tune for the modelling of the top-quark decay chain (when applicable), parton showering, hadronisation and the description of the underlying event. The renormalisation and factorisation scale choice adopted is the default MadGraph dynamical scale as documented in Ref. [90]. For the \(b\bar{b}\) +\(\phi /a\) and \(t\bar{t}\) +\(\phi /a\) models the events were generated with up to one additional parton, while for the \(b\)-FDM models the events were generated with up to two additional partons. The \(t\bar{t}\) +\(\phi /a\) and \(b\)-FDM samples were generated in the 5-flavour scheme, while the \(b\bar{b}\) +\(\phi /a\) samples were generated in the 4-flavour scheme. Following Ref. [13], the minimum \(p_{\text {T}}\) requirement for \(b\text {-jets}\) in the final state in MadGraph was set to \(30\;\hbox {GeV}\) for the \(b\bar{b}\) +\(\phi /a\) model, in order to increase the number of events in the relevant phase space for the analysis. This requirement does not affect the MC signal sample passing the event selection. The PDF set NNPDF23LO was used, adopting \(\alpha _{\text {S}} = 0.130\) and either the 5-flavour or the 4-flavour scheme consistently with the choice made for generating the events. The jet–parton matching was realised following the CKKW-L prescription. For the \(t\bar{t}\) +\(\phi /a\) model the matching scale was set to one quarter of the mass of the particle mediating the interaction between the SM and DM sectors. For the \(b\bar{b}\) +\(\phi /a\) and \(b\)-FDM models the matching scale was set to 30 GeV. The coupling g between the colour-neutral mediator for the \(t\bar{t}\) +\(\phi /a\) and \(b\bar{b}\) +\(\phi /a\) models and both the SM and the dark sector was assumed to be one, which implies pure Yukawa-type couplings between the mediator and the SM quarks. This choice impacts the mediator width and cross-section calculation for these models, but it was shown to have no significant impact on the kinematic properties [13].
For the \(t\bar{t}\) +\(\phi /a\) and \(b\bar{b}\) +\(\phi /a\) models the production cross-section was computed at NLO accuracy in the strong coupling constant \(\alpha _{\text {S}} \) using the MadGraph5_aMC@NLO generator with the NNPDF30NLO PDF set using \(\alpha _{\text {S}} = 0.118\). For this procedure a dynamical scale equal to \(P_\mathrm {T}/2\) was adopted, with \(P_\mathrm {T}\) being the scalar sum of the transverse momenta of all final-state particles. The flavour scheme adopted is consistent with that used for event generation. For the mass range in which this analysis is sensitive, the NLO value of the cross-sections for the \(t\bar{t}\) +\(\phi /a\) model is about 25% larger than the corresponding LO value [69, 70]. For the \(b\bar{b}\) +\(\phi /a\) samples the NLO value of the cross-section is between 56% and 75% of the corresponding LO value. This is driven by the MadGraph minimum \(b\text {-jet}\) \(p_{\text {T}}\) requirement due to the strong dependence of the NLO cross-section on this parameter. For the \(b\)-FDM signal models, the cross-section was computed at LO accuracy using the MadGraph5_aMC@NLO generator and the same flavour scheme used for the event generation.
4 Event selection
Five signal regions (SR) are defined and optimised to detect dark-matter production via spin-0 mediators. Two signal regions, SRb1 and SRb2, are optimised for models in which dark matter is produced in conjunction with one or two b-quarks, respectively. Specifically, SRb1 is designed to optimally select candidate signal events of the colour-charged scalar mediator models (bFDM) introduced in Sect. 1. SRb2 focuses instead on scalar and pseudoscalar colour-neutral mediators and was specifically optimised for low mediator masses (below \(200\;\hbox {GeV}\)). These SRs require events with no leptons and low jet multiplicity. SRt1, SRt2 and SRt3 are optimised to detect events in which DM is produced in association with a \(t\bar{t}\) pair, which either decays fully hadronically (SRt1 and SRt2) or dileptonically (SRt3). The SRt1 and SRt2 SRs are optimised for low (\(< 100\;\hbox {GeV}\)) and high (between 100 and \(350\;\hbox {GeV}\)) mediator mass assumptions, respectively, and are assigned fully hadronic events with high jet multiplicity. The regions SRt1 and SRt2 overlap in terms of their selection criteria. The region SRt3 focuses on mediator masses below \(100\;\hbox {GeV}\) and contains events with two leptons in the final state.
4.1 Signatures with b-quarks and \(E_{\text {T}}^{\text {miss}}\)
Events assigned to SRb1 and SRb2 are required to pass the missing transverse momentum trigger and to have at least one jet (\(\mathcal {N}_j\)). A minimum azimuthal angle between the directions of the missing transverse momentum and any of the jets in the event (\(\Delta \phi (\mathrm {j}, \vec {p}_{\text {T}}^{\text {miss}})\)) is required, in order to reduce the contamination by multi-jet events where fake \(E_{\text {T}}^{\text {miss}}\) arises from jet energy mismeasurements or semileptonic decays of hadrons inside jets. Events with at least one baseline muon or electron (\(\mathcal {N}^{\mathrm B}_{\ell }\)) are discarded to reject leptonic decays of W and Z bosons. The dominant background processes for the events passing these requirements are \(t\bar{t}\) and \(Z \text {\,+\,jets}\) processes.
Events with at least one tight \(b\text {-tagged}\) jet (\(\mathcal {N}^{\mathrm T}_{b}\)) and which pass the kinematic requirements specified in Table 2 are assigned to SRb1. The high-\(E_{\text {T}}^{\text {miss}}\) selection required is essential to discriminate the signal from the background in this SR. An upper limit on the scalar sum of the transverse momenta of the baseline jets in the events excluding the leading and subleading jets (\(H_\mathrm {T3}\) [25]) is used in this SR to reduce the contributions from top-quark pair-production processes.
Events assigned to SRb2 have instead at least two tight \(b\text {-tagged}\) jets. When the \(b\text {-tagged}\) jet multiplicity is different from two, the \(b\text {-tagged}\) jets are sorted in descending order according to their b-tagging probability. For this SR, a requirement of low jet multiplicity was found to be more effective in reducing the \(t\bar{t}\) background. The jet multiplicity of candidate signal events is required to not exceed three, and the transverse momentum of the third jet in the event must not exceed \(60\;\hbox {GeV}\). For the same purpose, the ratio of the transverse momentum of the leading jet to \(H_\mathrm {T}\), the scalar sum of the transverse momenta of all jets in the events, (\(H_\mathrm {T}^\mathrm {ratio}= p_{\text {T}} (j_1) / H_\mathrm {T}\)) is required to be larger than 75%.
The azimuthal separations between the \(b\text {-tagged}\) jets (\(\Delta \phi _{bb}\)) and the \(\Delta \phi (\mathrm {j}, \vec {p}_{\text {T}}^{\text {miss}})\) are exploited to enhance the separation between the signal and the irreducible background in this channel (\(Z(\nu \bar{\nu })\)+\(b\bar{b}\)), as the latter is characterised by small \(\Delta \phi _{bb}\) values when the \(b\text {-jets}\) originate from the gluon-splitting process. Linear combinations of these two variables are used to define the selection criteria in Table 2:
An additional handle to discriminate between the \(b\bar{b}+\phi \) and \(b\bar{b}+a\) signal models and the background is the spin of the particle decaying into invisible decay products. It was shown in Ref. [91] that it is possible to discriminate between such scalar, pseudoscalar and vector particles by exploiting information about the production angle of the visible particles with respect to the proton beam axis. A convenient variable to exploit this feature, proposed in Ref. [92] relies on the pseudorapidity difference between the two \(b\text {-tagged}\) jets (\(\Delta \eta _{bb}\)):
The variable \(\cos {\theta }^*_{bb}\), evaluated in the laboratory frame, is the key observable used in SRb2 to discriminate the signal from the background. The distribution of \(\cos {\theta }^*_{bb}\) is approximately flat for \(b\text {-jets}\) produced in association with scalar or vector particles with masses below \(100\;\hbox {GeV}\), while it exhibits a pronounced enhancement at values near one for pseudoscalar particles in the same mass range. In order to further enhance the sensitivity to the signal, the signal region SRb2 is divided into four independent bins in \(\cos {\theta }^*_{bb}\): SRb2-bin1 (0, 0.25), SRb2-bin2 (0.25, 0.5), SRb2-bin3 (0.5, 0.75), SRb2-bin4 (0.75, 1.0), which are statistically combined in the final result.
4.2 Signatures with top quarks and \(E_{\text {T}}^{\text {miss}}\)
Events assigned to SRt1 and SRt2 are required to contain at least four jets. At least two jets in every event must be \(b\text {-tagged}\) at the medium working-point (\(\mathcal {N}^{\mathrm M}_{b}\)). Events containing baseline electrons and muons are discarded. Furthermore, events with a \(\tau \)-candidate are also rejected (\(\mathcal {N}_\tau = 0\)). The \(\tau \)-candidate is defined as a jet with less than four associated tracks which has not passed the medium b-tagging requirement and which has a \(\phi \) separation from the \(\vec {p}_{\text {T}}^{\text {miss}}\) of no more than \(\pi /5\) radians. Events are required to pass the missing transverse momentum trigger and to satisfy \(E_{\text {T}}^{\text {miss}} > 300\; \hbox {GeV}\). Also in this SRs, a minimum \(\Delta \phi (\mathrm {j}, \vec {p}_{\text {T}}^{\text {miss}})\) requirement is applied in order to reject events with \(E_{\text {T}}^{\text {miss}}\) arising from mismeasurements and semileptonic decays of hadrons inside jets. Further rejection of such events is achieved by additional requirements on the missing transverse momentum computed using only the information from the tracking system (\(\vec {p}_{\text {T}}^{\text {miss,track}}\), with magnitude \(E_{\text {T}}^{\text {miss,track}}\)) and its angle with respect to the \(\vec {p}_{\text {T}}^{\text {miss}}\) (\(\Delta \phi (\vec {p}_{\text {T}}^{\text {miss}},\vec {p}_{\text {T}}^{\text {miss,track}})\)). The dominant backgrounds for these signal regions are top-quark pair production, Z+jets, and the production of a Z boson in association with \(t\bar{t}\). Four main observables are exploited to discriminate DM signal events from the SM background processes: \(m_{\mathrm {T}}^{b,\mathrm {min}}\), \(m_{\mathrm {T}}^{b,\mathrm {max}}\), \(E_{\text {T}}^{\text {miss, sig}}\), and \(\Delta R_{bb}\). The variables \(m_{\mathrm {T}}^{b,\mathrm {min}}\) and \(m_{\mathrm {T}}^{b,\mathrm {max}}\) are defined as the transverse massFootnote 3 of the \(\vec {p}_{\text {T}}^{\text {miss}}\) vector and \(b\text {-tagged}\) jet with the smallest and largest angular distanceFootnote 4 from it, respectively. The \(m_{\mathrm {T}}^{b,\mathrm {min}}\) variable is designed to be bounded from above by the top-quark mass for semileptonic \(t\bar{t}\) decays, because the closest \(b\text {-tagged}\) jet to the \(\vec {p}_{\text {T}}^{\text {miss}}\) vector usually belongs to the leg of the decay where the \(W\) boson decays into leptons. The variable \(m_{\mathrm {T}}^{b,\mathrm {max}}\) recovers the discriminating power in the case of wrong pairing. The \(E_{\text {T}}^{\text {miss, sig}}\) variable is defined as the ratio of the \(E_{\text {T}}^{\text {miss}}\) to the square-root of the scalar sum of the transverse momenta of all jets in the events (\(H_\mathrm {T}\)) to discriminate the high-mediator-mass signal models in SRt2 from the SM background. Finally, the angular distance between the two \(b\text {-tagged}\) jets in the event (\(\Delta R_{bb}\)) is exploited to suppress \(Z(\nu \nu )\)+\(b\bar{b}\) events where the two b-quarks arise from gluon-splitting and are characterised by a small angular separation.
The SRt1 selection is optimised for low-mass spin-0 mediators (\(m(\phi /a) < 100\;\hbox {GeV}\)). Requirements on the two leading reclustered jet masses with radius 0.8 (\(m^{\mathrm {jet\;1}}_{\mathrm {R=0.8}}\), \(m^{\mathrm {jet\;2}}_{\mathrm {R=0.8}}\)) exploit the presence of boosted hadronic decays of \(W\) bosons from top quarks in the event. The requirements applied in SRt1 are such that both reclustered jets are compatible with a W-boson candidate. The SRt2 signal region is optimised instead for high-mass spin-0 mediators (\(100\;\hbox {GeV}< m(\phi /a) < 350\;\hbox {GeV}\)). Requirements on the two leading reclustered jet masses with radius 1.2 (\(m^{\mathrm {jet\;1}}_{\mathrm {R=1.2}}\), \(m^{\mathrm {jet\;2}}_{\mathrm {R=1.2}}\)) are used to exploit the more boosted topology of these signal events compared to the backgrounds. The requirements applied in SRt2 are such that the leading large-radius jet is compatible with a top-quark candidate and the subleading large-radius jet is compatible with a W-boson candidate. The specific requirements for each discriminating observable in SRt1 and SRt2 are summarised in Table 3.
Finally, events assigned to SRt3 are required to have exactly two opposite-sign leptons (\(\mathcal {N}^{\mathrm M}_{\ell } = 2\) OS), electrons or muons, either same- or different-flavour, with an invariant mass (regardless of the flavours of the leptons in the pair), \(m_{\ell \ell }\), being larger than \(20\;\hbox {GeV}\). In addition, for same-flavour lepton pairs, events with \(m_{\ell \ell }\) within \(20\; \hbox {GeV}\) of the \(Z\)-boson mass are vetoed. Furthermore, candidate signal events are required to have at least one medium \(b\text {-tagged}\) jet. Events are required to pass the two-lepton triggers and the leading and subleading lepton transverse momenta in the event are required to be at least 25 and \(20 \;\hbox {GeV}\), respectively, which also guarantees that the plateau of efficiency of the triggers is reached. The main reducible backgrounds for this analysis are dileptonic \(t\bar{t}\) decays, \(Z \text {\,+\,jets}\) and dibosons. The main handle for the rejection of these backgrounds is the lepton-based “stransverse mass”, \(m_{\mathrm {T2}}^{\ell \ell }\) [93,94,95], which is a kinematic variable with an endpoint at the W-boson mass for events containing two \(W\) bosons decaying into leptons. In this selection it is used in linear combination with the \(E_{\text {T}}^{\text {miss}}\), in order to maximise the discrimination power of the two variables [91]:
Further requirements are placed on \(\Delta \phi _{\mathrm {boost}}\) [93], the azimuthal angular distance between \(\vec {p}_{\text {T}}^{\text {miss}}\) and the vector sum of \(\vec {p}_{\text {T}}^{\text {miss}}\) and the transverse momentum of the leptons, and on \(m^{\mathrm {min}}_{b2\ell }\), which is the smallest invariant mass computed between the \(b\text {-tagged}\) jet and each of the two leptons in the event. Both variables are used to further reject residual contamination from reducible backgrounds for this selection. The variable \(\Delta \phi _{\mathrm {boost}}\), can be interpreted as the azimuthal angular difference between the \(\vec {p}_{\text {T}}^{\text {miss}}\) and the opposite of the vector sum of all the transverse hadronic activity in the event. The requirement on this variable reject \(Z(\ell ^+\ell ^-)\)+jets events where the \(E_{\text {T}}^{\text {miss}}\) arises from jet mismeasurements, while retaining a large fraction of the signal. In events with two top quarks decaying dileptonically such as in the signal topology, at least one of the two mass combinations must be bounded from above by \(m^{\mathrm {min}}_{b2\ell }< \sqrt{m_t^2 - m_W^2}\). This variable helps to reject residual reducible backgrounds, while retaining 99% of the signal. The specific requirements for SRt3 are summarised in Table 3.
5 Background estimation
The SM backgrounds contributing to each of the five SRs are estimated with the aid of the MC simulation and using control regions (CRs) constructed to enhance a particular background and to be kinematically similar but orthogonal to the SRs. The expected background is determined separately in each SR through a profile likelihood fit based on the HistFitter package [96]. The CR yields constrain the normalisation of the dominant SM background processes. Such normalisation factors are treated as free fit parameters and are uncorrelated between fits of different SRs. The systematic uncertainties are included as nuisance parameters in the fit. In the case of a “background-only” fit set-up, only the CRs are considered and the signal contribution is neglected. The number of background events predicted by simulation in the SRs is normalised according to the results of the fit. When computing exclusion limits as described in Sect. 7, the SRs are also used to constrain the background predictions. The non-dominant SM backgrounds are determined purely from MC simulation, except fake or non-prompt lepton backgrounds (arising from jets misidentified as leptons or produced in either hadron decays or photon conversions) and the multi-jet background, both of which are estimated using a data-driven method described below. The background estimates in the SRs are validated by extrapolating the results of the likelihood fit in the CRs to dedicated validation regions (VRs), which are designed to be orthogonal to both the signal and control regions. In all CRs and VRs used in this analysis the signal contamination was found to be negligible.
An important source of background for all 0-lepton signal regions is Z bosons decaying into neutrinos when produced in conjunction with one or more jets emanating from heavy-flavour quarks. Production of top-quark pairs is a substantial background source for all selections except for SRb1, where the very high \(E_{\text {T}}^{\text {miss}}\) requirement rejects this background. More specifically, top-quark pairs with at least one of the W bosons decaying into leptons (where the lepton is either a non-identified electron or muon, or a hadronically decaying \(\tau \) lepton) enter SRb2, SRt1 and SRt2, while events with both W-bosons decaying into leptons enter SRt3. Events from \(t\bar{t} \text {+}Z \) production, when the Z boson decays into neutrinos, are an irreducible background for the three SRs targeting dark matter produced in association with top quarks.
The normalisation factor for the background arising from \(Z\rightarrow \nu \bar{\nu }\) events is estimated from data in CRs with two tight same-flavour opposite-sign (SFOS) leptons (\(\ell = (e, \mu )\)) and an invariant mass compatible with the Z-boson mass. For these CRs, labelled in the following as CRZt1, CRZt2, CRZb1 and CRZb2, the \(p_{\text {T}}\) of the leptons is added vectorially to the \(\vec {p}_{\text {T}}^{\text {miss}}\) to mimic the expected missing transverse momentum spectrum of \(Z\rightarrow \nu \bar{\nu }\) events, and is denoted in the following by \(E_{\mathrm {T,\ell \ell }}^{\mathrm {miss}}\). Observables that make use of \(E_{\text {T}}^{\text {miss}}\) in their definition are recalculated for these regions by using \(E_{\mathrm {T,\ell \ell }}^{\mathrm {miss}}\) instead. These variables are \(\delta ^-_{\ell \ell }\), \(\delta ^+_{\ell \ell }\), \(\Delta \phi (\mathrm {j}, \vec {p}_{\mathrm {T,\ell \ell }}^{\text {miss}})\), \(m_{\mathrm {T,\ell \ell }}^{b,\mathrm {min}}\), \(m_{\mathrm {T,\ell \ell }}^{b,\mathrm {max}}\) and \(E_{\mathrm {T,\ell \ell }}^{\text {miss, sig}}\).
Single tight-lepton CRs, denoted by CRTb2, CRTt1 and CRTt2, are used to estimate the background from top-quark pairs in SRb2, SRt1 and SRt2. The transverse massFootnote 5 (\(m_\mathrm {T}\)) of the lepton and the \(\vec {p}_{\text {T}}^{\text {miss}}\), and the angular distance between the lepton and the \(b\text {-tagged}\) jet closest to it (\(\Delta R^{\mathrm {min}}_{b\ell }\)) are used to enhance the purity of top-quark events. In CRTt1 and CRTt2 the lepton is treated as a jet, in order to better mimic the type of background events that contaminate the corresponding SR. The dileptonic top background, which contaminates SRt3, is instead estimated in a two-medium-leptons CR composed of events that fail the \(\xi ^+\) requirement (CRTt3).
Finally, \(t\bar{t}\) +\(V\) events, and in particular \(t\bar{t} \text {+}Z \) events where the Z boson decays into neutrinos, represent the irreducible background for the three SRs targeting dark matter produced in association with top quarks. This background is estimated from data using two CRs. To estimate the normalisation factor for the \(t\bar{t} \text {+}Z \) background in SRt1 and SRt2 a control region of \(t\bar{t}\) +\(\gamma \) events (CR\(\gamma \)) is used. Events with \(p_{{\mathrm {T}}\gamma } > m_{\mathrm Z}\) are selected, for which the kinematic properties resemble those of \(t\bar{t} \text {+}Z (\nu \nu )\). The CR\(\gamma \) contains events with exactly one energetic tight photon (\(\mathcal {N}_\gamma = 1\)) and at least one lepton from the decay of the \(t\bar{t}\) system. This strategy substantially increases the number of events at large missing transverse momentum and allows CR\(\gamma \) to better mimic the hard kinematic requirements of SRt1 and SRt2. Furthermore, the \(p_{\text {T}}\) of the photon is added vectorially to the \(\vec {p}_{\text {T}}^{\text {miss}}\) to mimic the expected missing transverse momentum spectrum of \(Z\rightarrow \nu \bar{\nu }\) events. The variable obtained with this procedure is referred to as \(E_{\mathrm {T,\gamma }}^{\mathrm {miss}}\) in the following.
Comparison of the data with the post-fit Monte Carlo prediction of some kinematic distributions in control and validation regions. The bottom panel shows the ratio of the data to the Monte Carlo prediction. The band includes all systematic uncertainties defined in Sect. 6. The last bins include overflows, where applicable. The top left panel shows the \(E_{\mathrm {T,\ell \ell }}^{\mathrm {miss}}\) distribution in CRZb1. The \(E_{\mathrm {T,\ell \ell }}^{\mathrm {miss}}\) requirement is relaxed to \(100\;\hbox {GeV}\). The other panels show the \(\cos {\theta }^*_{bb}\) distribution in VRb2 (top right), the \(m^{\mathrm {jet\;1}}_{\mathrm {R=1.2}}\) distribution in VRTt2 (middle left), the \(\xi ^+\) distribution the VRTt3 (middle right), the \(E_{\mathrm {T,\ell \ell }}^{\mathrm {miss}}\) distribution in CR\(\gamma \) (bottom left) and the \(E_{\mathrm {T,\ell \ell }}^{\mathrm {miss}}\) distribution in CR\(3\ell \) (bottom right)
Comparison of the data with the post-fit SM prediction of the background in each control and validation region. The different background components are denoted by the colour specified in the legend. All systematic uncertainties defined in Sect. 6 and statistical uncertainties are included in the shaded band. The lower panel shows the pulls in each VR. The total uncertainty \(\sigma _{\hbox {tot}}\) includes systematic and Poisson uncertainties for each given region
A second control region (CR\(3\ell \)), is used for the background normalisation of SRt3. It makes use of \(t\bar{t} \text {+}Z \) events with \(Z \rightarrow \ell ^+\ell ^-\) and semileptonic decays of the \(t\bar{t}\) system (e or \(\mu \)). CR\(3\ell \) is obtained by selecting three medium leptons out of which one SFOS pair is compatible with a Z-boson decay. This strategy allows the modelling of the lower \(E_{\text {T}}^{\text {miss}}\) part of the SRt3 signal region. Additionally, the momenta of the leptons compatible with the \(Z\)-boson decay are added vectorially to the \(\vec {p}_{\text {T}}^{\text {miss}}\) to define \(\vec {p}_{\mathrm {T,\ell \ell }}^{\text {miss}}\) and \(E_{\mathrm {T,\ell \ell }}^{\mathrm {miss}}\) for this control region. The transverse mass of the \(\vec {p}_{\mathrm {T,\ell \ell }}^{\text {miss}}\) and the lepton not associated with the \(Z\)-boson decay, \(m_{\mathrm {T}}^{\ell \ell }\), is combined with the \(E_{\mathrm {T,\ell \ell }}^{\mathrm {miss}}\) to define a corrected \(\xi ^+\): \(\xi ^{+}_{\ell \ell }= m_{\mathrm {T}}^{\ell \ell }+ 0.2\cdot E_{\mathrm {T,\ell \ell }}^{\mathrm {miss}}\). A requirement is placed on this variable in CR\(3\ell \) in order to approximate the kinematic properties of the signal region. The \(m^{\mathrm {min}}_{b2\ell }\) variable is redefined in this region (\(m^{\mathrm {min}}_{2b\ell }\)) as the smaller of the two transverse masses calculated when combining the lepton not associated with the Z-boson decay and each of the two \(b\text {-tagged}\) jets in the event.Footnote 6 All CR selections are summarised in Table 4.
The relatively small contamination of SRt3 and CR\(3\ell \) from events with fake or non-prompt (NP) leptons is estimated from data with a method similar to that described in Refs. [97, 98]. Different processes contribute to this background for the two selections. The dominant fake or non-prompt lepton contribution for SRt3 comes from semileptonic \(t\bar{t}\) and \(W \text {+\,jets}\) processes, while for CR\(3\ell \) it comes from dileptonic \(t\bar{t}\) and Z+bb processes. The method makes use of the number of observed events containing baseline–baseline, baseline–medium, medium–baseline and medium–medium lepton pairs (see definitions in Sect. 2) in a given selection. The probability for prompt leptons satisfying the baseline selection criteria to also pass the medium selection is measured using a \(Z \rightarrow \ell \ell \) sample. The equivalent probability for fake or non-prompt leptons is measured from multi-jet- and \(t\bar{t}\)-enriched control samples. The number of events containing a contribution from one or two fake or non-prompt leptons is calculated from these probabilities.
The background from multi-jet production for the regions with no leptons is estimated from data using a procedure described in detail in Ref. [99] and modified to account for the heavy flavour of the jets. The contribution from multi-jet production in all regions is found to be very small.
Minor background contributions to each signal region are collectively called “Others” in the following. For SRb1 and SRb2, this category contains the contributions from multi-jet, single top-quark production, diboson production, \(t\bar{t}\) +\(V\) and \(W \text {+\,jets}\). For SRt1 and SRt2, multi-jet, \(V+\gamma \), diboson, single top-quark and \(t\bar{t}\) production in association with Higgs or \(W\) boson(s) collectively define “Others”. Finally, for SRt3 the “Others” category contains the contributions from \(t\bar{t}\) +W / h / WW, \(t\bar{t}\) \(t\bar{t}\), \(t\bar{t} t\), Wh, (gg)h and Zh production.
In summary, one scaling factor is used to normalise the \(Z \text {\,+\,jets}\) background in SRb1, while two scaling factors are used to normalise the \(Z \text {\,+\,jets}\) and \(t\bar{t}\) backgrounds in SRb2. For SRt1 and SRt2, three scaling factors for each region are used to independently normalise the \(Z \text {\,+\,jets}\), \(t\bar{t}\) and \(t\bar{t} \text {+}Z \) backgrounds. Finally, in SRt3 the \(t\bar{t}\) and \(t\bar{t} \text {+}Z \) predictions are adjusted by a floating normalisation for each of the two backgrounds. The background scaling factors are treated as fully uncorrelated between the different SRs. In all selections, it is found that the normalisation of the \(Z \text {\,+\,jets}\) background is larger than unity. This may be related to the fact that in the default Sherpa v2.2.1 generator the heavy-flavour production fractions are not consistent with the measured values [100]. The normalisation factors for \(t\bar{t}\) processes in the SRtX regions are found to be compatible with unity, while they are found to be considerably smaller than unity for SRb2. This is due to the angular separation requirements in this region, which select \(t\bar{t}\) events in a specific corner of the phase space. Finally, the different normalisations of the \(t\bar{t} \text {+}Z \) background processes found in the CR\(\gamma \) and CR\(3\ell \) regions (larger and smaller than unity, respectively) are due to the different kinematic requirements on the jet momenta and the corrected \(E_{\text {T}}^{\text {miss}}\) in the two regions, which are designed to mimic the topology of the respective signal regions.
Dedicated validation regions are used to validate the background prediction for each of the SRs and evaluate the reliability of the MC extrapolation of the SM background estimates from CRs to SRs. The background estimates in SRb2 are validated in a single VR (VRb2) which has a background composition similar to that of the SR. Selected key distributions in the control and validation regions are shown in Fig. 2. The prediction of the \(Z \text {\,+\,jets}\) background in SRb1 relies on an extrapolation over a large interval of missing transverse momentum. As CRZb1 is designed to be kinematically as close as possible to SRb1 and given the low yield in this region, it was not possible to construct a selection to validate this extrapolation. Nevertheless, the use of the same kinematic selection in control and signal region, together with the good agreement between the data and the post-fit SM prediction in CRZb1 in the whole \(E_{\mathrm {T,\ell \ell }}^{\mathrm {miss}}\) spectrum (Fig. 2) gives confidence in the accuracy of the estimate. Two validation regions, VRZt1 and VRZt2, are designed to validate the \(Z \text {\,+\,jets}\) estimate in SRt1 and SRt2. Furthermore, the top background estimate in these SRs is validated in two additional VRs: VRTt1 and VRTt2. Finally, VRTt3 is designed to validate the top background prediction in SRt3. All requirements for each validation region are summarised in Table 5. The data and the post-fit Monte Carlo background prediction yields in each CR and VR are compared in Fig. 3. The background yields in the control regions match the observed data by construction. In the validation regions, the background prediction is compatible with the observed data within two standard deviations of the total systematic uncertainty.
6 Systematic uncertainties
Experimental and theoretical sources of systematic uncertainty in the signal and background estimates are considered in this analysis. Their impact is constrained overall through the normalisation of the dominant backgrounds in the control regions defined with kinematic selections resembling those of the corresponding signal region.
The dominant sources of detector-related systematic uncertainty are the jet energy scale, the jet energy resolution, the b-tagging efficiency and mis-tagging rates, and the scale and resolution of the \(E_{\text {T}}^{\text {miss}}\) soft term. The jet energy scale and resolution uncertainties are derived as a function of the \(p_{\text {T}}\) and \(\eta \) of the jet, as well as of the pile-up conditions and the jet flavour composition of the selected jet sample [37]. Uncertainties associated with the modelling of the b-tagging efficiencies for b-jets, c-jets and light-flavour jets [101, 102] are derived as a function of \(\eta \), \(p_{\text {T}}\) and flavour of each jet. The systematic uncertainties related to the modelling of \(E_{\text {T}}^{\text {miss}}\) in the simulation are estimated by propagating the uncertainties in the energy and momentum scale of all identified electrons, photons, muons and jets, as well as the uncertainties in the soft-term scale and resolution [49]. Other detector-related systematic uncertainties, such as those in the lepton and photon reconstruction efficiency, energy scale and energy resolution, and in the modelling of the trigger [43], are found to have a small impact on the results.
Uncertainties in the theoretical modelling of the SM background processes from MC simulation are also taken into account. The uncertainties in the modelling of the \(t\bar{t} \) process are estimated by varying the renormalisation and factorisation scales, as well as the amount of initial- and final-state radiation used to generate the samples [55]. The uncertainty connected with the parton-shower modelling is estimated as the difference between the predictions from Powheg showered with Pythia or Herwig. Additionally, the uncertainty related to the choice of event generator is evaluated by comparing the Powheg and MadGraph5_aMC@NLO predictions [55] for SRb1, SRb2 and SRt3. Due to the higher jet multiplicity required in SRt1 and SRt2 the generator uncertainty is evaluated instead by comparing the Powheg and Sherpa predictions. The uncertainties in the modelling of the \(Z\) background are accounted for by varying the default renormalisation, factorisation, resummation and matching scales of the Sherpa samples. For SRt1 and SRt2 an additional uncertainty is included to account for effects on the \(\Delta R_{bb}\) modelling not captured by the scale variations. This is estimated as the difference between the observed yield in data and the post-fit background prediction plus one times its uncertainty in each of the VRZs. The theoretical uncertainty connected with the \(t\bar{t} Z\) background in SRt1 and SRt2 is estimated by varying independently the renormalisation, factorisation, resummation and matching scales in the \(t\bar{t} Z\) and \(t\bar{t} \gamma \) samples in signal and control regions, respectively. PDF uncertainties (estimated by varying the parametrisation of the PDF set used to generate the simulated background samples) are found to have a non-negligible impact for this background component and are treated as correlated between signal and control regions. An additional uncertainty in the extrapolation between control and signal region is derived as the difference between the ratio of the \(t\bar{t} \gamma \) and \(t\bar{t} Z\) cross-section predictions obtained with the nominal MC generator and with the alternative MC generator Sherpa interfaced to OpenLoops. For SRt3, SRb1 and SRb2 the uncertainty connected with the \(t\bar{t} Z\) background estimation is assessed by varying the renormalisation, factorisation, resummation and matching scales.
Systematic uncertainties are assigned to the estimated background from fake or non-prompt leptons in SRt3 to account for potentially different compositions (heavy flavour, light flavour or conversions) between the signal regions and the control regions used for the fake-rate extraction, as well as the contamination from prompt leptons in the regions used to measure the probabilities for loose fake or non-prompt leptons to satisfy the tight signal criteria. Table 6 summarises the contributions from the different sources of systematic uncertainty in the total SM background predictions for the different signal regions after the fit to the control regions described in Sect. 5. As can be seen, the contribution from the theoretical uncertainty in the \(t\bar{t} \) background and the contribution from the statistical uncertainty connected with the use of Monte Carlo simulations are higher in SRt1 than in SRt2. The reason for the higher contribution from the theoretical uncertainty in the \(t\bar{t} \) background is primarily due to the larger relative importance of this source of background in SRt1. The reason for the higher contribution from the statistical uncertainty is connected with the W-boson background, which is predicted with low statistical precision in SRt1.
The impact of theoretical and detector-related uncertainties on the dark-matter signal acceptance is considered. The same procedure used to evaluate background uncertainties is applied for the detector-related uncertainties. The theoretical uncertainties in the acceptance are assessed by varying the factorisation, renormalisation, matching scales and parton shower parameters. For SRb1 the total theoretical uncertainty in the acceptance is 6%, for SRb2 it is below 8%, and for SRt1, SRt2 and SRt3 it ranges from 10 to 12%. The theoretical uncertainties in the production cross-section of the signal are evaluated only for the colour-neutral mediator models, for which an NLO computation of the cross-section is available. It is estimated by considering the same scale variations used to assess the uncertainties in the acceptance, and by varying the parametrisation of the PDF set used to generate the simulated signal samples. An additional uncertainty due to the different scale adopted to evaluate the NLO cross-section and to generate the signal samples is also considered. The total theoretical uncertainty in the cross-section amounts to 9% for the on-shell regime in the mass range of \(t\bar{t} +\phi /a\) signals to which the analysis is sensitive, and ranges from 9 to 30% for the off-shell regime. For the \(b\bar{b} +\phi /a\) signals this uncertainty varies between 5 and 13%.
7 Results
The expected and observed yields in each of the five signal regions of this analysis are reported in Tables 7 and 8. The background-only fit to the control regions described in Sect. 5 is compared to the predictions based on the MC normalisation. The observed data is found to be compatible with the background prediction in each one of the SRs. The expected signal yields for selected benchmark models for colour-neutral and colour-charged mediators are also shown. In each SR the observed yield in data is above the expected background but within 1.3 standard deviations of its uncertainty.
Figure 4 shows a comparison between the SM predictions and the observed data for some relevant kinematic distributions in each signal region prior to the selection on the variable. The four bins of SRb2 are statistically combined in the final result. A model-independent fit set-up [96] where both the control and signal regions are included in the fit is used to derive 95% confidence level (CL) upper limits on the visible cross-section \(\langle \epsilon \mathcal {A}\mathrm{\sigma }\rangle _{95}\) of new physics beyond-the-SM (BSM) processes, defined as cross-section times acceptance times efficiency and obtained as the upper limit on the number of BSM events divided by the total integrated luminosity. The 95% CL exclusion limits are derived with the CL\(_\mathrm {s}\) method [103] and summarised in Table 9 for each SR. These limits are calculated assuming no systematic uncertainties for the signal and neglecting any possible signal contamination in the control regions.
Comparison of the data with the post-fit SM prediction of the \(E_{\text {T}}^{\text {miss}}\) distribution in SRb1 (top left), \(\cos {\theta }^*_{bb}\) distribution in SRb2 (top right), \(m_{\mathrm {T}}^{b,\mathrm {min}}\) distribution in SRt1 (middle left), \(E_{\text {T}}^{\text {miss, sig}}\) distribution in SRt2 (middle right) and \(\xi ^+\) distribution in SRt3 (bottom). The last bins include overflows, where applicable. All signal region requirements except the one on the distribution shown are applied. The signal region requirement on the distribution shown is indicated by an arrow. The bottom panel shows the ratio of the data to the prediction. The band includes all systematic uncertainties defined in Sect. 6
The results are also used to set limits on the production cross-section of colour-neutral and colour-charged mediator models decaying into dark-matter particles. An independent fit is used for each of the five signal regions. When deriving model-dependent limits, the expected signal yield in each fit region is considered.
For the signal, the experimental systematic uncertainties and theoretical systematic uncertainties in the acceptance are taken into account for this calculation. The experimental uncertainties are assumed to be fully correlated with those in the SM background. The theoretical systematic uncertainties in the signal cross-section are instead shown separately in the final exclusion result for the colour-neutral mediator models.
Figures 5 and 6 show upper limits at 95% CL on the signal cross-section scaled to the signal cross-section for coupling \(g=1\), denoted by \(\sigma /\sigma (g=1.0)\). These are the most stringent limits to date on \(t\bar{t} +\phi /a\) models and the first ATLAS results for the \(b\bar{b} +\phi /a\) models. To derive the results for the fully hadronic \(t\bar{t}\) final state the region SRt1 or SRt2 providing the better expected sensitivity is used. The SRt1 was originally optimised for low-mass scalar mediators, while SRt2 was optimised for high-mass scalar mediators and pseudoscalar mediators. However, SRt1 is strongly affected by systematic uncertainties in the \(t\bar{t}\) modelling and therefore SRt2 sets more stringent limits for the whole parameter space. These limits are obtained both as a function of the mediator mass, assuming a specific DM mass of \(1\; \hbox {GeV}\) (Fig. 5), and as a function of the DM mass, assuming a specific mediator mass of \(10\;\hbox {GeV}\) (Fig. 6). Both the scalar and pseudoscalar mediator cases are considered. The sensitivity for \(t\bar{t} +\phi /a\) on-shell decays is approximately constant for masses below \(100\;\hbox {GeV}\), with SRt3 excluding the \(g=1\) assumption for scalar mediator masses up to \(50\;\hbox {GeV}\). For a given mediator mass the acceptance of the analysis is independent of the value of the DM mass as long as \(m(\phi /a) > 2\cdot m(\chi )\) is fulfilled and width effects can be neglected. Under these conditions, exclusion limits for DM masses differing from the one presented can be inferred from the result shown in Fig. 5. Due to the smaller Yukawa enhancement of \(b\bar{b} +\phi /a\) final states, it is possible to exclude cross-sections 300 times the nominal values for \(g=1\).
Exclusion limits for colour-neutral \(t\bar{t}/b\bar{b} +\phi \) scalar (top) and \(t\bar{t}/b\bar{b} +a\) pseudoscalar (bottom) models as a function of the mediator mass for a DM mass of \(1\;\hbox {GeV}\). The limits are calculated at 95% CL and are expressed in terms of the ratio of the excluded cross-section to the nominal cross-section for a coupling assumption of \(g = g_q = g_\chi = 1\). The solid (dashed) lines shows the observed (expected) exclusion limits for the different signal regions, according to the colour code specified in the legend. To derive the results for the fully hadronic \(t\bar{t}\) final state the region SRt1 or SRt2 providing the better expected sensitivity is used
Exclusion limits for colour-neutral \(t\bar{t} +\phi \) scalar (top) and \(t\bar{t} +a\) pseudoscalar (bottom) models as a function of the DM mass for a mediator mass of \(10\;\hbox {GeV}\). The limits are calculated at 95% CL and are expressed in terms of the ratio of the excluded cross-section to the nominal cross-section for a coupling assumption of \(g = g_q = g_\chi = 1\). The solid (dashed) lines shows the observed (expected) exclusion limits for the different signal regions, according to the colour code specified in the legend. To derive the results for the fully hadronic \(t\bar{t}\) final state the region SRt1 or SRt2 providing the better expected sensitivity is used
Comparison of the 90% CL limits on the spin-independent DM–nucleon cross-section as a function of DM mass between these results and the direct-detection experiments, in the context of the colour-neutral simplified model with scalar mediator. The black line indicates the exclusion contour derived from the observed limits of SRt3. Values inside the contour are excluded. The exclusion limit is compared with limits from the LUX [104], PandaX-II [105], XENON [106], SuperCDMS [107] and CRESST-II [108] experiments
Exclusion limits for colour-charged scalar mediators (\(b\)-FDM) as a function of the mediator and DM masses for \(36.1 \; \mathrm {fb}^{-1}\) of data. The limits are calculated at 95% CL. The solid (dashed) line show the observed (expected) exclusion contour for a coupling assumption \(\lambda _b\) yielding the measured relic density. No uncertainties on the LO cross-sections are considered for this model. The results are compared with the ATLAS search for \(b\)-FDM models [27], represented by the blue contour, and the ATLAS search for direct sbottom pair production [25], represented by the red contour
For each dark-matter and mediator mass pair, the exclusion limit on the production cross-section of colour-neutral scalar mediator particles can be converted into a limit on the spin-independent DM–nucleon scattering cross-section using the procedure described in Ref. [109]. The results can thus be compared with the results from direct-detection experiments. The most stringent limits, provided by SRt3, are used for this purpose. Figure 7 shows the constraints from this analysis expressed as exclusion limits at 90% CL in the plane defined by the dark-matter mass and the scattering cross-section. The black line indicates the exclusion contour derived from the observed limits in the top part of Fig. 5, where mediator masses between 10 GeV and 500 GeV are considered. The maximum value of the DM–nucleon scattering cross-section displayed corresponds to the result obtained for a mediator mass of 10 GeV. The results of this analysis are compared with the results from the LUX [104], PandaX-II [105], XENON [106], SuperCDMS [107] and CRESST-II [108] experiments. The comparison is model-dependent, and therefore valid only for the specific models considered in this paper. For pseudoscalar mediator models, the predicted dark-matter cross-sections in these direct-detection experiments is suppressed by velocity-dependent terms. As a result, direct-detection limits on spin-independent DM–nucleon scattering cross-section are several orders of magnitude worse than the ones obtained in this analysis, and therefore not presented.
Finally, Fig. 8 shows the exclusion contour for the \(b\)-FDM model as a function of the mediator and DM masses. In this model, the cross-section and therefore also the final sensitivity strongly depends on the coupling choice, \(\lambda _b\), which is set to fulfil the relic density constraints, and determines the decrease of the sensitivity for higher DM masses. For a DM particle of approximately \(35\; \hbox {GeV}\), as suggested by the interpretation of data recorded by the Fermi-LAT Collaboration, mediator masses below \(1.1\; \hbox {TeV}\) are excluded at 95% CL.
8 Conclusion
This article reports a search for dark-matter pair production in association with bottom or top quarks. The analysis is performed using \(36.1 \; \mathrm {fb}^{-1}\) of pp collisions collected at a centre-of-mass energy of \(\sqrt{s} = 13~\hbox {TeV}\) by the ATLAS detector at the LHC. The results are interpreted in the framework of simplified models of spin-0 mediators to the dark sector decaying into pairs of DM particles. The data are found to be consistent with the Standard Model expectations, and limits are set on the signal strength for a coupling assumption of \(g=1.0\) or on the DM and mediator masses. The results represent the most stringent limits to date for colour-neutral spin-0 mediator models for a DM mass assumption of \(1\;\hbox {GeV}\) in top-quark final states. It excludes at 95% CL mediator masses between 10 and \(50\; \hbox {GeV}\) for scalar mediators assuming couplings equal to unity and a dark-matter mass of \(1\;\hbox {GeV}\). Although the analysis is expected to be sensitive to models with pseudoscalar mediators with masses between 10 and 100 GeV, no observed exclusion limit can be set for this model for the coupling assumption of \(g=1.0\) because of a small excess in the observed data. Limits of 300 times the nominal cross section for couplings equal to unity are placed for scalar and pseudoscalar mediator masses between 10 and \(50\; \hbox {GeV}\) for a dark-matter mass of \(1\;\hbox {GeV}\) in bottom-quark final states. Constraints on \(b\)-FDM models are also presented. The excluded region depends on \(m(\phi _b)\) and \(m(\chi )\); for \(m(\chi ) = 35\; \hbox {GeV}\), mediator particles with \(m(\phi ) < 1.1\; \hbox {TeV}\) are excluded.
Notes
Following Ref. [14], couplings to W and Z bosons, as well as explicit dimension-4 \(\phi \)–h or a–h couplings, are set to zero in this simplified model. In addition, the coupling of the mediator to the dark sector are not taken to be proportional to the mass of the DM candidates.
ATLAS uses a right-handed coordinate system with its origin at the nominal interaction point (IP) in the centre of the detector and the z-axis along the beam pipe. The x-axis points from the IP to the centre of the LHC ring, and the y-axis points upward. Cylindrical coordinates (r, \(\phi \)) are used in the transverse plane, \(\phi \) being the azimuthal angle around the beam pipe. The pseudorapidity is defined in terms of the polar angle \(\theta \) as \(\eta = -\ln \tan (\theta /2)\). Rapidity is defined as \(y=0.5 \ln \left[ (E + p_z )/(E - p_z )\right] \) where E denotes the energy and \(p_z\) is the component of the momentum along the beam direction.
The transverse mass of two particles a and b is defined as \(m_{\mathrm T}(a,b) = \sqrt{(E_{\mathrm T,a}+E_{\mathrm T,b})^2 - (\vec {p}_{\mathrm T,a}+\vec {p}_{\mathrm T,b})^2}\)
The angular separation between two particles a, b used in all quantities described in this section is defined as \(\Delta R_{ab} = \sqrt{(\Delta \phi _{ab})^2+(\Delta \eta _{ab})^2}\).
The transverse mass in this case is calculated by neglecting the lepton masses.
When the \(b\text {-tagged}\) jet multiplicity is different from two, the two jets with the highest b-tagging probabilities are chosen, independently of whether they are \(b\text {-tagged}\) or not.
References
F. Zwicky, Die Rotverschiebung von extragalaktischen Nebeln. Helv. Phys. Acta. 6, 110–127 (1933)
G. Bertone, D. Hooper, J. Silk, Particle dark matter: evidence, candidates and constraints. Phys. Rep. 405, 279 (2005). arXiv:hep-ph/0404175
E. Komatsu et al., Seven-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: cosmological interpretation. Astrophys. J. Suppl. 192, 18 (2011). arXiv:1001.4538 [astro-ph.CO]
P.A.R. Ade, Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. A 594, 13 (2016). arXiv:1502.01589 [astro-ph.CO]
G. Steigman, M.S. Turner, Cosmological constraints on the properties of weakly interacting massive particles. Nucl. Phys. B 253, 375 (1985)
CMS Collaboration, Search for associated production of dark matter with a Higgs boson decaying to \(b\bar{b}\) or \(\gamma \gamma \) at \(\sqrt{s} = 13\;\text{TeV}\). (2017). arXiv:1703.05236 [hep-ex]
CMS Collaboration, Search for dark matter produced with an energetic jet or a hadronically decaying \(W\) or \(Z\) boson at \(\sqrt{s} = 13\;\text{ TeV }\). JHEP 07, 014 (2017). arXiv:1703.01651 [hep-ex]
CMS Collaboration, Search for new physics in the monophoton final state in proton-proton collisions at \(\sqrt{s} =\) 13 TeV. (2017). arXiv:1706.03794 [hep-ex]
ATLAS Collaboration, Search for dark matter in association with a Higgs boson decaying to two photons at \(\sqrt{s}\)= 13 TeV with the ATLAS detector. (2017). arXiv:1706.03948 [hep-ex]
ATLAS Collaboration, Search for dark matter at \(\sqrt{s} = 13\;\text{ TeV }\) in final states containing an energetic photon and large missing transverse momentum with the ATLAS detector. Eur. Phys. J. C 77, 393 (2017). arXiv:1704.03848 [hep-ex]
ATLAS Collaboration, Search for new phenomena in final states with an energetic jet and large missing transverse momentum in \(pp\) collisions at \(\sqrt{s} = 13\;\text{ TeV }\) using the ATLAS detector. Phys. Rev. D 94, 032005 (2016). arXiv:1604.07773 [hep-ex]
ATLAS Collaboration, Search for dark matter produced in association with a Higgs boson decaying to \(b\bar{b}\) using 36 fb\(^{-1}\) of \(pp\) collisions at \(\sqrt{s}=13\) TeV with the ATLAS detector. (2017). arXiv:1707.01302 [hep-ex]
D. Abercrombie et al., Dark matter benchmark models for early LHC run-2 searches: report of the ATLAS/CMS Dark Matter Forum. (2015). arXiv:1507.00966 [hep-ex]
M.R. Buckley, D. Feld, D. Goncalves, Scalar simplified models for dark matter. Phys. Rev. D 91, 015017 (2015). arXiv:1410.6497 [hep-ph]
U. Haisch, E. Re, Simplified dark matter top-quark interactions at the LHC. JHEP 06, 078 (2015). arXiv:1503.00691 [hep-ph]
G. D’Ambrosio, G.F. Giudice, G. Isidori, A. Strumia, Minimal flavor violation: an effective field theory approach. Nucl. Phys. B 645, 155 (2002). arXiv:hep-ph/0207036
CMS Collaboration, Search for dark matter produced in association with heavy-flavor quarks in proton–proton collisions at \(\sqrt{s}=13\) TeV. (2017). arXiv:1706.02581 [hep-ex]
ATLAS Collaboration, Search for a scalar partner of the top quark in the jets plus missing transverse momentum final state at \(\sqrt{s} = 13\) TeV with the ATLAS detector. (2017). arXiv:1709.04183 [hep-ex]
ATLAS Collaboration, Search for direct top squark pair production in final states with two leptons in \(\sqrt{s} = 13\) TeV \(pp\) collisions with the ATLAS detector. (2017). arXiv:1708.03247 [hep-ex]
ATLAS Collaboration, Search for top-squark pair production in final states with one lepton, jets, and missing transverse momentum using 36 fb\(^{-1}\) of \(\sqrt{s}=13\) TeV pp collision data with the ATLAS detector. (2017). arXiv:1711.11520 [hep-ex]
M. Bauer, U. Haisch, F. Kahlhoefer, Simplified dark matter models with two Higgs doublets: I. Pseudoscalar mediators. JHEP 05, 138 (2017). arXiv:1701.07427 [hep-ph]
P. Agrawal, B. Batell, D. Hooper, T. Lin, Flavored dark matter and the galactic center gamma-ray excess. Phys. Rev. D 90, 063512 (2014). arXiv:1404.1373 [hep-ph]
T. Daylan et al., The characterization of the gamma-ray signal from the central Milky Way: a compelling case for annihilating dark matter. Phys. Dark Univ. 12, 1 (2016). arXiv:1402.6703 [astro-ph.HE]
M. Ajello et al., Characterizing the population of pulsars in the galactic bulge with the \(Fermi\) large area telescope. Submitted to: Astrophys. J. (2017). arXiv:1705.00009 [astro-ph.HE]
ATLAS Collaboration, Search for supersymmetry in events with \(b\)-tagged jets and missing transverse momentum in \(pp\) collisions at \(\sqrt{s}=13\) TeV with the ATLAS detector. (2017). arXiv:1708.09266 [hep-ex]
CMS Collaboration, Searches for pair production of third-generation squarks in \(\sqrt{s}=13\) \(\,\text{ TeV }\) pp collisions. Eur. Phys. J. C 77, 327 (2017). arXiv:1612.03877 [hep-ex]
ATLAS Collaboration, Search for dark matter in events with heavy quarks and missing transverse momentum in \(pp\) collisions with the ATLAS detector. Eur. Phys. J. C 75, 92 (2015). arXiv:1410.4031 [hep-ex]
ATLAS Collaboration, The ATLAS experiment at the CERN large hadron collider. JINST 3, S08003 (2008)
ATLAS Collaboration, ATLAS insertable B-layer technical design report, ATLAS-TDR-19. (2010). https://cds.cern.ch/record/1291633
ATLAS insertable B-layer technical design report addendum, ATLAS-TDR-19-ADD-1. (2012). https://cds.cern.ch/record/1451888
ATLAS Collaboration, Performance of the ATLAS trigger system in 2015. Eur. Phys. J. C 77, 317 (2017). arXiv:1611.09661 [hep-ex]
ATLAS Collaboration, Vertex reconstruction performance of the ATLAS detector at\(\sqrt{s} = 13\;\text{ TeV }\), ATL-PHYS-PUB-2015-026. (2015). https://cds.cern.ch/record/2037717
ATLAS Collaboration, Topological cell clustering in the ATLAS calorimeters and its performance in LHC Run 1. (2016). arXiv:1603.02934 [hep-ex]
M. Cacciari, G.P. Salam, G. Soyez, The anti-\(k_T\) jet clustering algorithm. JHEP 04, 063 (2008). arXiv:0802.1189 [hep-ph]
M. Cacciari, G.P. Salam, G. Soyez, FastJet user manual. Eur. Phys. J. C 72, 1896 (2012). arXiv:1111.6097 [hep-ph]
ATLAS Collaboration, Jet energy scale measurements and their systematic uncertainties in proton–proton collisions at \(\sqrt{s} = 13\;\text{ TeV }\) with the ATLAS detector. (2017). arXiv:1703.09665 [hep-ex]
ATLAS Collaboration, Jet calibration and systematic uncertainties for jets reconstructed in the ATLAS detector at \(\sqrt{s} = 13\;\text{ TeV }\), ATL-PHYS-PUB-2015-015. (2015). https://cds.cern.ch/record/2037613
ATLAS Collaboration, Selection of jets produced in \(13\;\text{ TeV }\) proton–proton collisions with the ATLAS detector, ATLAS-CONF-2015-029. (2015). https://cds.cern.ch/record/2037702
ATLAS Collaboration, Data-quality requirements and event cleaning for jets and missing transverse energy reconstruction with the ATLAS detector in proton–proton collisions at a center-of-mass energy of \(\sqrt{s} = 7\;\text{ TeV }\), ATLAS-CONF-2010-038. (2010). https://cds.cern.ch/record/1277678
ATLAS Collaboration, Performance of pile-up mitigation techniques for jets in \(pp\) collisions at \(\sqrt{s} = 8\;\text{ TeV }\) using the ATLAS detector. Eur. Phys. J. C 76, 581 (2016). arXiv:1510.03823 [hep-ex]
ATLAS Collaboration, Performance of \(b\)-jet identification in the ATLAS experiment. JINST 11, P04008 (2016). arXiv:1512.01094 [hep-ex]
ATLAS Collaboration, Optimisation of the ATLAS \(b\)-tagging performance for the 2016 LHC Run, ATL-PHYS-PUB-2016-012. (2016). https://cds.cern.ch/record/2160731
ATLAS Collaboration, Muon reconstruction performance of the ATLAS detector in proton–proton collision data at \(\sqrt{s} = 13\;\text{ TeV }\). Eur. Phys. J. C 76, 292 (2016). arXiv:1603.05598 [hep-ex]
ATLAS Collaboration, Electron efficiency measurements with the ATLAS detector using 2012 LHC proton–proton collision data. Eur. Phys. J. C 77, 195 (2017). arXiv:1612.01456 [hep-ex]
ATLAS Collaboration, Electron identification measurements in ATLAS using \(\sqrt{s} = 13\;\text{ TeV }\) data with \(50\;\text{ ns }\) bunch spacing, ATL-PHYS-PUB-2015-041. (2015). https://cds.cern.ch/record/2048202
ATLAS Collaboration, Electron efficiency measurements with the ATLAS detector using the 2015 LHC proton–proton collision data, ATLAS-CONF-2016-024. (2016). https://cds.cern.ch/record/2157687
ATLAS Collaboration, Electron and photon energy calibration with the ATLAS detector using LHC Run 1 data. Eur. Phys. J. C 74, 3071 (2014). arXiv:1407.5063 [hep-ex]
ATLAS Collaboration, Measurement of the photon identification efficiencies with the ATLAS detector using LHC Run-1 data. (2016). arXiv:1606.01813 [hep-ex]
ATLAS Collaboration, Expected performance of missing transverse momentum reconstruction for the ATLAS detector at \(\sqrt{s} = 13\;\text{ TeV }\), ATL-PHYS-PUB-2015-023. (2015). https://cds.cern.ch/record/2037700
ATLAS Collaboration, Performance of missing transverse momentum reconstruction with the ATLAS detector in the first proton–proton collisions at \(\sqrt{s} = 13\;\text{ TeV }\), ATL-PHYS-PUB-2015-027. (2015). https://cds.cern.ch/record/2037904
ATLAS Collaboration, Luminosity determination in \(pp\) collisions at \(\sqrt{s} = 8\;\text{ TeV }\) using the ATLAS detector at the LHC. Eur. Phys. J. C 76, 653 (2016). arXiv:1608.03953 [hep-ex]
ATLAS Collaboration, The ATLAS simulation infrastructure. Eur. Phys. J. C 70, 823 (2010). arXiv:1005.4568 [physics.ins-det]
S. Agostinelli et al., GEANT4: a simulation toolkit. Nucl. Instrum. Methods A 506, 250 (2003)
ATLAS Collaboration, The simulation principle and performance of the ATLAS fast calorimeter simulation FastCaloSim, ATL-PHYS-PUB-2010-013. (2010). https://cds.cern.ch/record/1300517
ATLAS Collaboration, Simulation of top-quark production for the ATLAS experiment at \(\sqrt{s} = 13\;\text{ TeV }\), ATL-PHYS-PUB-2016-004. (2016). https://cds.cern.ch/record/2120417
ATLAS Collaboration, Monte Carlo generators for the production of a \(W\) or \(Z/\gamma ^*\) boson in association with jets at ATLAS in Run 2, ATL-PHYS-PUB-2016-003. (2016). https://cds.cern.ch/record/2120133
ATLAS Collaboration, Multi-boson simulation for \(13\;\text{ TeV }\) ATLAS analyses, ATL-PHYS-PUB-2016-002. (2016). https://cds.cern.ch/record/2119986
ATLAS Collaboration, Modelling of the \(t\bar{t} H\) and \(t\bar{t}V (V = W, Z)\) processes for \(\sqrt{s} = 13\;\text{ TeV }\) ATLAS analyses, ATL-PHYS-PUB-2016-005. (2016). https://cds.cern.ch/record/2120826
N. Kidonakis, Next-to-next-to-leading-order collinear and soft gluon corrections for \(t\)-channel single top quark production. Phys. Rev. D 83, 091503 (2011). arXiv:1103.2792 [hep-ph]
N. Kidonakis, NNLL resummation for \(s\)-channel single top quark production. Phys. Rev. D 81, 054028 (2010). arXiv:1001.5034 [hep-ph]
N. Kidonakis, Two-loop soft anomalous dimensions for single top quark associated production with a \(W\)- or \(H\)-. Phys. Rev. D 82, 054018 (2010). arXiv:1005.4451 [hep-ph]
T. Gleisberg, S. Höche, Comix, a new matrix element generator. JHEP 12, 039 (2008). arXiv:0808.3674 [hep-ph]
F. Cascioli, P. Maierhofer, S. Pozzorini, Scattering amplitudes with open loops. Phys. Rev. Lett. 108, 111601 (2012). arXiv:1111.5206 [hep-ph]
S. Schumann, F. Krauss, A Parton shower algorithm based on Catani–Seymour dipole factorisation. JHEP 03, 038 (2008). arXiv:0709.1027 [hep-ph]
S. Höche, F. Krauss, M. Schönherr, F. Siegert, QCD matrix elements + parton showers: the NLO case. JHEP 04, 027 (2013). arXiv:1207.5030 [hep-ph]
R.D. Ball et al., Parton distributions with LHC data. Nucl. Phys. B 867, 244 (2013). arXiv:1207.1303 [hep-ph]
J. Alwall et al., The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations. JHEP 07, 079 (2014). arXiv:1405.0301 [hep-ph]
T. Sjöstrand, M. Mrenna, P.Z. Skands, A brief introduction to PYTHIA 8.1. Comput. Phys. Commun. 178, 852 (2008). arXiv:0710.3820 [hep-ph]
O. Mattelaer, E. Vryonidou, Dark matter production through loop-induced processes at the LHC: the \(s\)-channel mediator case. Eur. Phys. J. C 75, 436 (2015). arXiv:1508.00564 [hep-ph]
M. Backovic et al., Higher-order QCD predictions for dark matter production at the LHC in simplified models with \(s\)-channel mediators. Eur. Phys. J. C 75, 482 (2015). arXiv:1508.05327 [hep-ph]
H.-L. Lai et al., New parton distributions for collider physics. Phys. Rev. D 82, 074024 (2010). arXiv:1007.2241 [hep-ph]
ATLAS Collaboration, ATLAS Pythia8 tunes to 7 TeV data, ATL-PHYS-PUB-2014-021. (2014). https://cds.cern.ch/record/1966419
T. Gleisberg et al., Event generation with SHERPA 1.1. JHEP 02, 007 (2009). arXiv:0811.4622 [hep-ph]
S. Catani, L. Cieri, G. Ferrera, D. de Florian, M. Grazzini, Vector boson production at hadron colliders: a fully exclusive QCD calculation at NNLO. Phys. Rev. Lett. 103, 082001 (2009). arXiv:0903.2120 [hep-ph]
S. Alioli, P. Nason, C. Oleari, E. Re, A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX. JHEP 06, 043 (2010). arXiv:1002.2581 [hep-ph]
T. Sjöstrand, S. Mrenna, P.Z. Skands, PYTHIA 6.4 physics and manual. JHEP 05, 026 (2006). arXiv:hep-ph/0603175
M. Czakon, P. Fiedler, A. Mitov, Total top-quark pair-production cross section at hadron colliders through \(O(\alpha _{S}^{4})\). Phys. Rev. Lett. 110, 252004 (2013). arXiv:1303.6254 [hep-ph]
M. Czakon, A. Mitov, NNLO corrections to top pair production at hadron colliders: the quark–gluon reaction. JHEP 01, 080 (2013). arXiv:1210.6832 [hep-ph]
M. Czakon, A. Mitov, NNLO corrections to top-pair production at hadron colliders: the all-fermionic scattering channels. JHEP 12, 054 (2012). arXiv:1207.0236 [hep-ph]
P. Bärnreuther, M. Czakon, A. Mitov, Percent level precision physics at the tevatron: first genuine NNLO QCD corrections to \(q \bar{q} \rightarrow t \bar{t} + X\). Phys. Rev. Lett. 109, 132001 (2012). arXiv:1204.5201 [hep-ph]
M. Cacciari, M. Czakon, M. Mangano, A. Mitov, P. Nason, Top-pair production at hadron colliders with next-to-next-to-leading logarithmic soft-gluon resummation. Phys. Lett. B 710, 612 (2012). arXiv:1111.5869 [hep-ph]
M. Czakon, A. Mitov, Top++: a program for the calculation of the top-pair cross-section at hadron colliders. Comput. Phys. Commun. 185, 2930 (2014). arXiv:1112.5675 [hep-ph]
P.Z. Skands, Tuning Monte Carlo generators: the Perugia tunes. Phys. Rev. D 82, 074018 (2010). arXiv:1005.3457 [hep-ph]
LHC Higgs Cross Section Working Group, Handbook of LHC Higgs cross sections: 2. Differential distributions, CERN-2012-002. (2012). arXiv:1201.3084 [hep-ph]
D.J. Lange, The EvtGen particle decay simulation package. Nucl. Instrum. Methods A 462, 152 (2001)
S. Gieseke, C. Rohr, A. Siodmok, Colour reconnections in Herwig++. Eur. Phys. J. C 72, 2225 (2012). arXiv:1206.0041 [hep-ph]
ATLAS Collaboration, Summary of ATLAS Pythia 8 tunes, ATL-PHYS-PUB-2012-003. (2012). https://cds.cern.ch/record/1474107
A.D. Martin, W.J. Stirling, R.S. Thorne, G. Watt, Parton distributions for the LHC. Eur. Phys. J. C 63, 189 (2009). arXiv:0901.0002 [hep-ph]
L. Lönnblad, S. Prestel, Matching tree-level matrix elements with interleaved showers. JHEP 03, 019 (2012). arXiv:1109.4829 [hep-ph]
V. Hirschi, O. Mattelaer, Automated event generation for loop-induced processes. JHEP 10, 146 (2015). arXiv:1507.00020 [hep-ph]
U. Haisch, P. Pani, G. Polesello, Determining the CP nature of spin-0 mediators in associated production of dark matter and \( t\overline{t} \) pairs. JHEP 02, 131 (2017). arXiv:1611.09841 [hep-ph]
A.J. Barr, Measuring slepton spin at the LHC. JHEP 02, 042 (2006). arXiv:hep-ph/0511115
ATLAS Collaboration, Search for direct top-squark pair production in final states with two leptons in pp collisions at \(\sqrt{s} = 8\) TeV with the ATLAS detector. JHEP 06, 124 (2014). arXiv:1403.4853 [hep-ex]
A. Barr, C. Lester, P. Stephens, A variable for measuring masses at hadron colliders when missing energy is expected; m(T2): the truth behind the glamour. J. Phys. G 29, 2343 (2003). arXiv:hep-ph/0304226
C.G. Lester, D.J. Summers, Measuring masses of semi-invisibly decaying particles pair produced at hadron colliders. Phys. Lett. B 463, 99 (1999). arXiv:hep-ph/9906349
M. Baak et al., HistFitter software framework for statistical data analysis. Eur. Phys. J. C 75, 153 (2015). arXiv:1410.1280 [hep-ex]
ATLAS Collaboration, Measurement of the top quark-pair production cross section with ATLAS in \(pp\) collisions at \(\sqrt{s} = 7\;\text{ TeV }\). Eur. Phys. J. C 71, 1577 (2011). arXiv:1012.1792 [hep-ex]
ATLAS Collaboration, Measurement of the top quark pair production cross section in \(pp\) collisions at \(\sqrt{s} = 7\;\text{ TeV }\) in dilepton final states with ATLAS. Phys. Lett. B 707, 459 (2012). arXiv:1108.3699 [hep-ex]
ATLAS Collaboration, Search for bottom squark pair production in proton–proton collisions at \(\sqrt{s} = 13\;\text{ TeV }\) with the ATLAS detector. Eur. Phys. J. C 76, 547 (2016). arXiv:1606.08772 [hep-ex]
ATLAS Collaboration, Studies on top-quark Monte Carlo modelling with Sherpa and MG5_aMC@NLO, ATL-PHYS-PUB-2017-007. (2017). https://cds.cern.ch/record/2261938
ATLAS Collaboration, Calibration of \(b\)-tagging using dileptonic top pair events in a combinatorial likelihood approach with the ATLAS experiment, ATLAS-CONF-2014-004. (2014). https://cds.cern.ch/record/1664335
ATLAS Collaboration, Calibration of the performance of \(b\)-tagging for \(c\) and light-flavour jets in the 2012 ATLAS data, ATLAS-CONF-2014-046. (2014). https://cds.cern.ch/record/1741020
A.L. Read, Presentation of search results: the \(CL_S\) technique. J. Phys. G 28, 2693 (2002)
LUX Collaboration, Results from a search for dark matter in the complete LUX exposure. Phys. Rev. Lett. 118, 021303 (2017). arXiv:1608.07648 [astro-ph.CO]
PandaX-II Collaboration, Dark matter results from first 98.7 days of data from the PandaX-II experiment. Phys. Rev. Lett. 117, 121303 (2016). arXiv:1607.07400 [hep-ex]
XENON Collaboration, First dark matter search results from the XENON1T experiment. (2017). arXiv:1705.06655 [astro-ph.CO]
SuperCDMS Collaboration, New results from the search for low-mass weakly interacting massive particles with the CDMS low ionization threshold experiment. Phys. Rev. Lett. 116, 071301 (2016). arXiv:1509.02448 [astro-ph.CO]
CRESST Collaboration, Results on light dark matter particles with a low-threshold CRESST-II detector. Eur. Phys. J. C 76, 25 (2016). arXiv:1509.01515 [astro-ph.CO]
A. Boveia et al., Recommendations on presenting LHC searches for missing transverse energy signals using simplified \(s\)-channel models of dark matter. (2016). arXiv:1603.04156 [hep-ex]
ATLAS Collaboration, ATLAS computing acknowledgements 2016–2017, ATL-GEN-PUB-2016-002. https://cds.cern.ch/record/2202407
Acknowledgements
We thank CERN for the very successful operation of the LHC, as well as the support staff from our institutions without whom ATLAS could not be operated efficiently. We acknowledge the support of ANPCyT, Argentina; YerPhI, Armenia; ARC, Australia; BMWFW and FWF, Austria; ANAS, Azerbaijan; SSTC, Belarus; CNPq and FAPESP, Brazil; NSERC, NRC and CFI, Canada; CERN; CONICYT, Chile; CAS, MOST and NSFC, China; COLCIENCIAS, Colombia; MSMT CR, MPO CR and VSC CR, Czech Republic; DNRF and DNSRC, Denmark; IN2P3-CNRS, CEA-DSM/IRFU, France; SRNSF, Georgia; BMBF, HGF, and MPG, Germany; GSRT, Greece; RGC, Hong Kong SAR, China; ISF, I-CORE and Benoziyo Center, Israel; INFN, Italy; MEXT and JSPS, Japan; CNRST, Morocco; NWO, Netherlands; RCN, Norway; MNiSW and NCN, Poland; FCT, Portugal; MNE/IFA, Romania; MES of Russia and NRC KI, Russian Federation; JINR; MESTD, Serbia; MSSR, Slovakia; ARRS and MIZŠ, Slovenia; DST/NRF, South Africa; MINECO, Spain; SRC and Wallenberg Foundation, Sweden; SERI, SNSF and Cantons of Bern and Geneva, Switzerland; MOST, Taiwan; TAEK, Turkey; STFC, United Kingdom; DOE and NSF, United States of America. In addition, individual groups and members have received support from BCKDF, the Canada Council, CANARIE, CRC, Compute Canada, FQRNT, and the Ontario Innovation Trust, Canada; EPLANET, ERC, ERDF, FP7, Horizon 2020 and Marie Skłodowska-Curie Actions, European Union; Investissements d’Avenir Labex and Idex, ANR, Région Auvergne and Fondation Partager le Savoir, France; DFG and AvH Foundation, Germany; Herakleitos, Thales and Aristeia programmes co-financed by EU-ESF and the Greek NSRF; BSF, GIF and Minerva, Israel; BRF, Norway; CERCA Programme Generalitat de Catalunya, Generalitat Valenciana, Spain; the Royal Society and Leverhulme Trust, United Kingdom. The crucial computing support from all WLCG partners is acknowledged gratefully, in particular from CERN, the ATLAS Tier-1 facilities at TRIUMF (Canada), NDGF (Denmark, Norway, Sweden), CC-IN2P3 (France), KIT/GridKA (Germany), INFN-CNAF (Italy), NL-T1 (Netherlands), PIC (Spain), ASGC (Taiwan), RAL (UK) and BNL (USA), the Tier-2 facilities worldwide and large non-WLCG resource providers. Major contributors of computing resources are listed in Ref. [110].
Author information
Authors and Affiliations
Consortia
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Aaboud, M., Aad, G., Abbott, B. et al. Search for dark matter produced in association with bottom or top quarks in \(\sqrt{s}=13\) TeV pp collisions with the ATLAS detector. Eur. Phys. J. C 78, 18 (2018). https://doi.org/10.1140/epjc/s10052-017-5486-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-017-5486-1