1 Introduction

Gravitational phase transitions, in particular the ones connected to black hole thermodynamics, are essential constituents of many open problems in modern theoretical physics. The Hawking–Page phase transition [1] of black holes in anti-de Sitter space is one of the most important ones due to its role in the AdS/CFT correspondence [2, 3] and also in related phenomena of confinement/deconfinement transitions at finite temperature in various gauge theories [4, 5]. Because of the different background geometry, asymptotically flat black holes have different stability properties than AdS ones, and in the standard black hole thermodynamic picture [6,7,8,9], they mostly tend to be unstable for any large masses when surrounded by an infinite bath of thermal radiation. A Hawking–Page transition does not occur under these conditions, and a cosmic black hole nucleation is not present in asymptotically flat spacetimes. Apart from the gravity interest, the above phenomenon is interesting from a thermodynamic viewpoint as well, and for a clear understanding of the physics behind, the underlying theory of black hole thermodynamics is also necessary to be well understood. In the past 40 years, after the foundations of the standard thermodynamic theory of black holes [6,7,8,9], numerous achievements have been made in the field. In spite of the active research and successes however, there still are some unsettled and important issues which could not be resolved satisfactorily so far. From a classical thermodynamic perspective, one of the most interesting ones is the non-extensive nature of black holes and the corresponding problem of thermodynamic stability.

A basic group of physical quantities in classical thermodynamics is the group called extensive variables X (like energy, entropy, etc.), where it is assumed that these quantities are additive for composition, i.e. \(X_{12}=X_1+X_2\) when thermodynamic systems are joined together [10]. On the other hand, it is also customary to assume that these quantities characterize the system down to the smallest scales [11], i.e. when working with finite densities:

$$\begin{aligned} \varrho _X = \lim _{n\rightarrow \infty }\frac{1}{n}\sum _{i=1}^n X_i < \infty , \end{aligned}$$
(1)

where the system is divided into n different parts. This property is called extensivity. The two properties: additivity and extensivity are not equivalent. An additive quantity is extensive, but extensive quantities can be non-additive too [12, 13]. Black holes are very peculiar creatures in this respect because they cannot be described as the union of some constituent subsystems which are endowed with their own thermodynamics, and therefore black holes are non-extensive objects.

Looking from a different perspective, phenomenological thermodynamics of macroscopic objects has a well-understood theory from statistical physics where the macroscopic properties of a given body (described by the thermodynamic parameters e.g. total energy, entropy, temperature, etc.) can be uniquely obtained from the microscopic description of the system. Standard statistical descriptions, on the other hand, usually assume that long-range type interactions are negligible, i.e. that the (linear) size of the system in question is much larger than the range of the relevant interaction between the elements of the system. Under these conditions the standard local notions of mass, energy and other extensive quantities are well defined, and by applying the additive (and therefore extensive) Boltzmann–Gibbs formula: \(S_{\text {BG}}=-\sum p_i\ln p_i\), for defining the system’s entropy function, the classical thermodynamic description is recovered in the macroscopic limit.

In the presence of strong gravitational fields however, and in particular when black holes are considered, the assumption of negligible long-range type interactions cannot hold, and consequently the usual definition of mass and other extensive quantities is not possible locally. Non-locality is indeed a fundamental feature of general relativity, and corresponding non-extensive thermodynamic phenomena have been known in cosmology and gravitation theory for a long time (see e.g. [14,15,16,17,18,19,20,21,22,23] and the references therein). In fact, even as early as 1902, Gibbs already pointed out in his statistical mechanics book [24], that systems with divergent partition function lie outside the validity of Boltzmann–Gibbs theory. He explicitly mentions gravitation as an example (see e.g. [25] for more details). Therefore, the standard Boltzmann-Gibbs statistics may not be the best possible choice for defining the entropy function in strongly gravitating systems, and other statistical approaches, which could also take into account the long-range type property of the relevant interaction (i.e. gravitation) and the non-extensive nature of the problem, are also relevant and important to study.

The non-extensive nature of the Bekenstein–Hawking entropy of black hole event horizons has been noticed [26] very early on after the thermodynamic theory of black holes had been formulated [6,7,8,9], and the corresponding thermodynamic and stability problem has been investigated several times with various approaches (see e.g. [14, 25, 27,28,29,30,31,32,33,34] and the references therein). The general theory of non-additive thermodynamics has also advanced significantly in the past few decades (see e.g. [12, 35] and the references therein), and it has been shown, that by relaxing the additivity requirement in the axiomatic approach to the entropy definition (given by Shannon [36, 37] and Khinchin [38]) to the weaker composability requirement, new possible functional forms of the entropy may arise [39]. As a consequence, there exist certain parametric extensions of the Boltzmann–Gibbs statistical entropy formula, which seem to be more appropriate to describe systems with long-range type interactions. One such statistical entropy definition has been proposed by Tsallis [40] as

$$\begin{aligned} S_T=\frac{1}{1-q}\sum _i(p^q_i-p_i), \end{aligned}$$
(2)

where \(p_i\) are the probabilities of the microscopic states of the system, and \(q\in \mathbb {R}\) is the so-called non-extensivity parameter. In the limit of \(q\rightarrow 1\), \(S_T\) reproduces the standard Boltzmann–Gibbs result, however, in the case when \(q\ne 0\), the Tsallis entropy is not additive, and the parameter can be attributed to measure the effects of non-localities in the system. The q-parameter is usually constant in different physical situations, and its explicit value is part of the problem to be solved.

The Tsallis statistics to the black hole problem has been investigated with various approaches (see e.g. [25] and the references therein), however, it has been a long-standing problem in non-extensive thermodynamics that non-additive entropy composition rules (in general) cannot be compatible with the most natural requirement of thermal equilibrium in the system [10]. They usually do not satisfy the zeroth law of thermodynamics, which requires the existence of a well-defined, unique, empirical temperature in thermal equilibrium which is constant all over the system. For resolving these issues, Biró and Ván developed a method [10], called the “formal logarithm approach”, which maps the original, non-additive entropy composition rule of a given system to an additive one by a simple transformation. This procedure results a new, but also well-defined entropy function for the system, which in turn, also satisfies both the equilibrium and the zeroth law compatibility requirements of thermodynamics. In case of the non-extensive Tsallis statistics, this new entropy turns out to be the well-known Rényi formula [42, 43], defined as

$$\begin{aligned} S_R=\frac{1}{1-q}\ln \sum _ip^q_i, \end{aligned}$$
(3)

which had been proposed earlier by the Hungarian mathematician Alfréd Rényi in 1959 [42].

Recently, motivated by the non-extensive and non-local nature of black hole thermodynamics, we proposed and studied an alternative approach to the black hole entropy problem [41]. In this model, in order to satisfy both the equilibrium the zeroth law compatibility, instead of the Tsallis description, we considered its formal logarithm, the Rényi statistics (2) to describe the thermodynamic entropy of black hole event horizons. The explicit details of this approach is presented in the next section, and by applying the Rényi model to Schwarzschild black holes [41], we found that the temperature-horizon radius relation of the black hole has the same form as the one obtained from a black hole in anti-de Sitter space by using the original Boltzmann–Gibbs statistics. In both cases the temperature has a minimum. By using a semi-classical estimate on the horizon radius at this minimum, we obtained a Bekenstein bound [44] for the q-parameter value in the Rényi entropy of micro black holes (\(q \ge 1 + 2/\pi ^2\)), which was surprisingly close to other q-parameter fits from very distant and unrelated physical phenomena, e.g. cosmic ray spectra [45, 46], and power-law distribution of quarks coalescing to hadrons in high energy accelerator experiments [47].

Besides the statistical approach, another fundamental problem of applying standard thermodynamic methods to black holes arises from the question of stability. In ordinary thermodynamics of extensive systems, the local thermodynamic stability (defined as the Hessian of the entropy has no positive eigenvalues) is linked to the dynamical stability of the system. This stability criterion, however, strongly relies on the additivity of the entropy function, which is a property that clearly does not hold for black holes. The simplest example of this discrepancy is the Schwarzschild black hole which is known to be perturbatively stable but has a negative specific heat (positive Hessian). Black hole phase transitions are also strongly related to the stability properties of the system (in particular the Hawking–Page transition), and since the standard methods are not reliable in non-extensive thermodynamics, one has to be very careful when considering stability and phase transitions in strongly gravitating systems.

Avoiding the complications arising from the Hessian approach to the stability problem of black holes, an alternative technique was proposed in a series of paper by Kaburaki et al. [48,49,50]. In this work the so-called “Poincaré turning point method of stability” [51] has been applied to the problem, which is a topological approach and does not depend on the additivity of the entropy function. More recently this method has also been used to study the critical phenomena of higher dimensional black holes and black rings [52] and to determine the conditions of stability for equilibrium configurations of charged black holes surrounded by quintessence [53]. In Sect. 4 we present an overview of this method.

By considering the Rényi model in the black hole problem, we also investigated the thermodynamic stability question of Schwarzschild black holes [54]. First we considered the question of pure, isolated black holes in the microcanonical approach, and showed that these configurations are stable against spherically symmetric perturbations, just like in the Boltzmann picture. However, in considering the case when the black holes are surrounded by a heat bath in the canonical treatment, we found that – in contrast to the Boltzmann approach – Schwarzschild black holes can be in stable equilibrium with thermal radiation at a fixed temperature. This results a stability change at a certain value of the mass-energy parameter of the black hole which belongs to the minimum temperature solution. Black holes with smaller masses are unstable in this model, however, larger black holes become stable. These findings are essentially identical to the ones obtained by Hawking and Page in AdS space within the standard Boltzmann entropy description [1]. According to this similarity, we also analyzed the question of a possible phase transition in the canonical picture and found that a Hawking–Page black hole phase transition occurs in a very similar fashion as in AdS space in the Boltzmann statistics. We showed that the corresponding critical temperature depends only on the q-parameter of the Rényi formula, just like it depends only on the curvature parameter in AdS space. For the stability analysis we considered both the Poincaré and the Hessian methods. The latter one could also be applied since the Rényi entropy is additive for composition (see the next section), and therefore the standard stability analysis is also reliable in this case. Both approaches confirmed the same stability results.

These findings might have some relevant consequences in black hole physics. In particular, if an effective physical model could be constructed on how to compute the q-parameter value for the Rényi entropy of black holes (or other strongly gravitating systems) in order to parametrize the non-local effects of the gravitational field, the Rényi statistics can provide a well-behaving and additive entropy description of the system which is also compatible with the requirements of equilibrium and the zeroth law of thermodynamics. In [55], a Tsallis model has been considered to black hole thermodynamics from a loop quantum gravity approach, and a specific correlation has been found between the Barbero-Immirzi parameter \(\gamma \) and the non-extensivity parameter q of the Tsallis entropy. Interestingly, in the explicit form of the expression determining \(\gamma \), it is the Rényi entropy formula for black holes [as defined in (22)] which arises. In another recent work [56], our Tsallis–Rényi model has been considered in a cosmological setup describing the difference between the degrees of freedom on the surface and in the bulk in a closed region of space. It has been found that the corresponding Padmanabhan’s “holographic equipartition law” [57] can result an effective cosmological constant in the model. Similar considerations have also been applied to describe the relative information entropy measure inside compact domains of an inhomogeneous universe [58], and an explicit geometric model has been proposed to compute the q-parameter of the Rényi entropy in order to measure the effects of the gravitational entanglement problem.

In the case of black hole thermodynamics, we showed that large, asymptotically flat, Schwarzschild black holes can be in stable equilibrium with a thermal heath bath in the Rényi picture, and a Hawking–Page transition can occur in the system. This result offers a possible explanation for the problem of cosmic black hole nucleation in the early universe, and this mechanism might be the origin of large or super massive black holes that can be found in most galaxy centers. Many other interesting consequences can be deduced from the Rényi approach, but in this work we aim to achieve a more modest goal. In the present paper, by extending our previous investigations, we study the thermodynamic, stability and phase transition properties of Kerr black holes within the Rényi model and analyze whether similar results can be obtained to what we have found in the Schwarzschild case. In this analysis the turning point method is applied to the stability problem in both the microcanonical and the canonical ensembles, and we will show that stability changes appear in the latter case, which suggests that a Hawking–Page transition and a first order small black hole/large black hole phase transition occur in the system, similar to the one observed for charged and rotating black holes in AdS space [59,60,61,62,63]. This result provides a correspondence between the Kerr–Rényi and the Kerr–AdS–Boltzmann pictures, analogous to the one we reported in the Schwarzschild problem [41, 54].

The plan of the paper is as follows. In Sect. 2 we discuss the foundations and motivation of the Rényi approach arising from non-extensive thermodynamics to the black hole problem. In Sect. 3 we introduce the Kerr solution and calculate its thermodynamic quantities within the Rényi statistics. In Sect. 4 we investigate the thermodynamic stability problem of Kerr black holes in the Rényi model by the Poincaré turning point method both in the microcanonical and canonical treatments. We also discuss the question of possible phase transitions in this section. In Sect. 5 the thermodynamic stability problem of Kerr–AdS black holes in the standard Boltzmann case is also presented by the turning point method, and the correspondence between the Kerr–Rényi and the Kerr–AdS–Boltzmann approaches is discussed. In Sect. 6 we summarize our results and draw our conclusions. Throughout this paper we use units such as \(c=G=\hbar =k_B=1\).

2 Rényi approach from non-additive thermodynamics

By replacing the additivity axiom to the weaker composability in the Shannon–Khinchin axiomatic definition of the entropy function, new type of entropy expressions arise. The composability axiom asserts, roughly speaking, that the entropy \(S_{12}\) of a compound system consisting of two independent systems should be computable only in terms of the individual entropies \(S_{1}\) and \(S_{2}\). This means that there is a function f(x, y) such that

$$\begin{aligned} S_{12} = f (S_1, S_2), \end{aligned}$$
(4)

for any independent systems. This property is of fundamental importance, since it implies that an entropic function is properly defined on macroscopic states of a given system, and it can be computed without having any information on the underlying microscopic dynamics. Composability is a key feature to ensure that the entropy function is physically meaningful. In Ref. [64], based on the concept of composability alone, Abe recently derived the most general functional form of those non-additive entropy composition rules that are compatible with homogeneous equilibrium. Assuming that \(f(S_1, S_2)\) is a \(C^2\) class symmetric function, he has shown that the most general, equilibrium compatible composition rule takes the form

$$\begin{aligned} H_{\lambda }(S_{12})=H_{\lambda }(S_1)+H_{\lambda }(S_2)+\lambda H_{\lambda }(S_1)H_{\lambda }(S_2), \end{aligned}$$
(5)

where \(H_{\lambda }\) is a differentiable function of S and \(\lambda \in \mathbb {R}\) is a constant parameter. Later on, this result has been extended to non-homogeneous systems as well [10], where not only the entropy, but the energy function is also considered to be non-additive.

The simplest and perhaps the best-known non-additive entropy composition rule can be obtained from (5) by setting \(H_{\lambda }(S)\) to be the identity function, i.e. \(H_{\lambda }(S)=S\). In this case Abe’s equation becomes

$$\begin{aligned} S_{12}=S_1+S_2+\lambda S_1 S_2, \end{aligned}$$
(6)

which results the familiar Tsallis composition rule with \(\lambda =1-q\) [40], and the corresponding entropy definition is given in (2). The non-extensive Tsallis statistics is widely investigated in many research fields from natural to social sciences, an updated bibliography on the topic can be found in [65]. This approach has also been studied in the problem of black hole thermodynamics (see e.g. [25] and the references therein), and our starting point in considering a more general entropy definition for black holes than the one based on the Boltzmann–Gibbs statistics is also the Tsallis formula.

Generalized, non-additive entropy definitions has been investigated in various problems from high energy physics [13] to DNA analysis [66], and it has been a longstanding problem that the zeroth law of thermodynamics (i.e. the existence of a well-defined temperature function in thermal equilibrium) cannot be compatible with non-additive entropy composition rules. A possible resolution to this problem has been proposed recently by Biró and Ván in [10], where they developed a formulation to determine the most general functional form of those non-additive entropy composition rules that are compatible with the zeroth law of thermodynamics. They found that the general form is additive for the formal logarithms of the original quantities, which in turn, also satisfy the familiar relations of standard thermodynamics. In particular, for homogeneous systems, they showed that the most general, zeroth law compatible entropy function takes the form

$$\begin{aligned} L(S)=\frac{1}{\lambda }\ln [1+\lambda H_{\lambda }(S)], \end{aligned}$$
(7)

which is additive for composition, i.e.,

$$\begin{aligned} L(S_{12})=L(S_{1})+L(S_{2}), \end{aligned}$$
(8)

and the corresponding zeroth law compatible temperature function can be obtained:

$$\begin{aligned} \frac{1}{T}=\frac{\partial L(S(E))}{\partial E}, \end{aligned}$$
(9)

where E is the energy of the system.

In the case of the Tsallis statistics, it is easy to show that by taking the formal logarithm (7) of the Tsallis entropy (2), i.e.

$$\begin{aligned} L(S_T)=\frac{1}{1-q}\ln \left[ 1+(1-q)S_T\right] \equiv S_R, \end{aligned}$$
(10)

the Rényi expression in Eq. (3) is reproduced, which, unlike the Tsallis formula, is additive for composition. In the limit of \(q\rightarrow 1\) (\(\lambda \rightarrow 0\)), both the Tsallis and the Rényi entropies recovers the standard Boltzmann–Gibbs description.

According to these results, in the present paper, in order to describe the non-Boltzmannian nature of Kerr black holes, we consider the Tsallis statistics as the simplest, non-additive, parametric but equilibrium compatible extension of the Boltzmann–Gibbs theory which also satisfies Abe’s formula. On the other hand, in order to satisfy the zeroth law of thermodynamics, we follow the formal logarithm method of Biró and Ván, and rather the Tsallis description, we consider the Rényi entropy for the thermodynamics of the problem. Since the Rényi definition is additive, it satisfies all laws of thermodynamics, and compared to the Boltzmann picture, it has the advantage of having a free parameter which can be accounted to describe the effects of non-locality in our approach. The thermodynamics of Schwarzschild black holes in this model has been studied in [41], and the corresponding stability problem has been investigated in [54].

3 Kerr black holes

The spacetime metric that describes the geometry of a rotating black hole is given by the Kerr solution

$$\begin{aligned} \text {d}s^2= & {} -\text {d}t^2 + \frac{2 M r}{\varSigma } \left( \text {d}t -a \sin ^2 \theta \text {d} \phi \right) ^2 + \frac{\varSigma }{\varDelta } \text {d}r^2 + \varSigma \text {d} \theta ^2 \nonumber \\&+ (r^2 +a^2) \sin \theta \text {d} \phi ^2, \end{aligned}$$
(11)

where

$$\begin{aligned} \varSigma = r^2 + a^2 \cos ^2 \theta , ~~~ \varDelta = r^2 + a^2 - 2Mr . \end{aligned}$$
(12)

Here, M is the mass-energy parameter of the black hole and a is its rotation parameter. The thermodynamic quantities of a Kerr black hole can be expressed in terms of its horizon radius \(r_{+} = M + \sqrt{M^2 - a^2}\), which is defined by taking \(\varDelta = 0\). The Hawking temperature of the black hole horizon is

$$\begin{aligned} T_H = \frac{1}{2\pi }\left[ \frac{r_{+}}{r_{+}^2 + a^2} - \frac{1}{2 r_{+}} \right] , \end{aligned}$$
(13)

the Bekenstein–Hawking entropy is

$$\begin{aligned} S_{\text {BH}} = \pi (r_{+}^2 + a^2), \end{aligned}$$
(14)

the angular momentum of the black hole is

$$\begin{aligned} J = \frac{a}{2 r_{+}}(r_{+}^2 + a^2), \end{aligned}$$
(15)

the angular velocity of the horizon is

$$\begin{aligned} \varOmega = \frac{a}{r_{+}^2 + a^2}, \end{aligned}$$
(16)

and the mass-energy parameter can also be written as

$$\begin{aligned} M = \frac{r_{+}^2 + a^2}{2 r_{+}}. \end{aligned}$$
(17)

The heat capacity at constant angular velocity is given by

$$\begin{aligned} C_{\varOmega } = T_H \left( \frac{\partial S_{\text {BH}}}{\partial T_H} \right) _\varOmega = \frac{2 \pi r_{+}^2(a^2 - r_{+}^2)}{r_{+}^2 +a^2}, \end{aligned}$$
(18)

and the heat capacity at constant angular momentum is

$$\begin{aligned} C_J = T_H \left( \frac{\partial S_{\text {BH}}}{\partial T_H} \right) _J = \frac{2 \pi (r_{+}^2 -a^2)(r_{+}^2 + a^2)^2}{3 a^4 + 6 r_{+}^2 a^2 - r_{+}^4}\ . \end{aligned}$$
(19)

\(C_\varOmega \) and \(C_J\) can be written in simpler forms if we normalize them by \(r_{+}^2\), i.e.

$$\begin{aligned} \frac{C_{\varOmega }}{r_{+}^2} = - \frac{2 \pi (1 - h^2)}{h^2 + 1 } \end{aligned}$$
(20)

and

$$\begin{aligned} \frac{C_{J}}{r_{+}^2} = \frac{2 \pi (1 - h^2 )(h^2 + 1)^2}{3 h^4 + 6 h^2 - 1}, \end{aligned}$$
(21)

where we also introduced the normalized rotation parameter h [67] as

$$\begin{aligned} h \equiv \frac{|a|}{r_{+}} . \end{aligned}$$

The \(r_{+}\) horizon radius exists only for \(|a| \le M\), which corresponds to \(0 \le h \le 1\). The \(h=0\) value describes a Schwarzschild black hole, while the limiting value \(h=1\) belongs to the extreme Kerr black hole case. The heat capacities as functions of h are plotted on Fig. 1. It can be seen that \(C_\varOmega \) is negative for \( 0\le h<1\) and \(C_J\) diverges at \(h_c = \sqrt{\frac{2}{3}\sqrt{3} - 1}\), where a pole occurs. \(C_J\) is negative for \(h<h_c\) and positive for \(h>h_c\) values. The heat capacities coincide at the limit values \(h=0\) and 1.

Fig. 1
figure 1

Plots of the heat capacities \(C_J\) (red solid line) and \(C_\varOmega \) (blue dotted line) against h. \(C_J\) diverges at \(h_c\) where a pole occurs

Full size image

The Rényi entropy function of black holes can be obtained by taking the formal logarithm of the Bekenstein–Hawking entropy, which in our non-Boltzmannian approach follows the non-additive Tsallis statistics. The physical meaning of the \(\lambda \) parameter is connected to the non-extensive and non-local nature of the problem, and the Rényi entropy of a general black hole in this picture is given by

$$\begin{aligned} S_R = \frac{1}{\lambda } \ln (1 + \lambda S_{\text {BH}}). \end{aligned}$$
(22)

The zeroth law compatible Rényi temperature is then defined as

$$\begin{aligned} T_R = \frac{1}{\partial S_R / \partial M} = T_H ( 1 + \lambda S_{\text {BH}} ). \end{aligned}$$
(23)

For the case of a Kerr black hole, the Rényi entropy and the corresponding temperature take the forms

$$\begin{aligned} S_R = \frac{1}{\lambda } \ln ( 1 + \pi \lambda (r_{+}^2 + a^2) ) \end{aligned}$$
(24)

and

$$\begin{aligned} T_R = \frac{(1 + \pi \lambda (r_{+}^2 + a^2))(r_{+}^2 - a^2)}{4 \pi r_{+} (r_{+}^2 + a^2)}. \end{aligned}$$
(25)

The heat capacities can be obtained:

$$\begin{aligned} C_{R} = T_R \left( \frac{\partial S_R}{\partial T_R} \right) = \frac{C_{\text {BH}}}{1 + \lambda (S_{\text {BH}} + C_{\text {BH}})}, \end{aligned}$$
(26)

where \(C_{\text {BH}} = T_H \left( \frac{\partial S_{\text {BH}}}{\partial T_H} \right) \). The heat capacity at constant angular velocity is then

$$\begin{aligned} C_{\varOmega R} = \frac{2 \pi r_{+}^2(a^2 - r_{+}^2)}{r_{+}^2 + a^2 + \pi \lambda (a^4 - r_{+}^4 + 4 a^2 r_{+}^2)}, \end{aligned}$$
(27)

while the heat capacity at constant angular momentum takes the form

$$\begin{aligned} C_{JR} \!= \!\frac{2 \pi (r_{+}^2 \!-\! a^2)(a^2 \!+ \!r_{+}^2)^2}{3 a^4 +6 a^2 r_{+}^2 \!- \!r_{+}^4 \!+ \!\pi \lambda (a^2 \!+ \!r_{+}^2)(a^4 \!+\!6 r_{+}^2 a^2 +r_{+}^4)}. \end{aligned}$$
(28)

\(C_{\varOmega R}\) and \(C_{JR}\) can also be written in the simpler, normalized forms as before, i.e.

$$\begin{aligned} \frac{C_{\varOmega R}}{r_{+}^2} = \frac{2 \pi (h^2 -1)}{h^2 + 1 + \pi k (h^4+ 4 h^2 -1)} \end{aligned}$$
(29)

and

$$\begin{aligned} \frac{C_{JR}}{r_{+}^2} = - \frac{2 \pi (h^2 - 1)(h^2 + 1)^2}{3 h^4 + 6 h^2 - 1 + \pi k (h^2 + 1)(h^4 + 6 h^2 + 1)}, \end{aligned}$$
(30)

where we also introduced the parameter

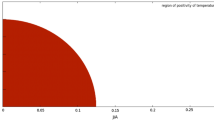
$$\begin{aligned} k = \lambda r_{+}^2. \end{aligned}$$

The heat capacities change their sign depending on the parameter values as plotted on Fig. 2.

Fig. 2
figure 2

Phase diagram of Kerr black holes with Rényi entropy. On the dashed curve \(C_{JR}\) diverges while on the dotted curve \(C_{\varOmega R}\) diverges. In region I, \(C_{\varOmega R}<0\) and \(C_{JR} <0\), in region II, \(C_{\varOmega R}<0\) and \(C_{JR} >0\), while in region III, \(C_{\varOmega R}>0\) and \(C_{JR} >0\)

Full size image

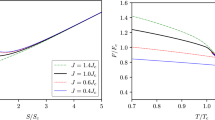
For fixed angular momentum, both the Rényi and the Boltzmann entropies of a Kerr black hole are monotonically increasing functions of the mass parameter (Fig. 3). An important difference however, is that while the standard Boltzmann entropy is asymptotically convex (being proportional to \(M^2\) as approaching the static Schwarzschild solution in the large M limit), the Rényi entropy is asymptotically concave, since it increases only logarithmically.

Fig. 3
figure 3

Plots of the Rényi entropy as a function of the mass-energy parameter at fixed \(J = J_0\) for the parameter values \(\lambda J_0 = 0.05\), 0.04, 0.03, 0.02 and 0.01 starting from the bottom curve, respectively. The top, bold curve belongs to the standard Boltzmann entropy of the Kerr black hole

Full size image

On Fig. 4, we also plotted the temperature-energy relations for fixed angular momentum \(J = J_0\). As is well known, there is a maximum temperature in the case of the standard Boltzmann approach. In the smaller mass (low entropy) region of the \(T_H(M)\) curve, the heat capacity \(C_J\) is positive, while at larger masses (high entropy) region it is negative. The two regions correspond to the phases of \(h>h_c\) and \(h<h_c\) on Fig. 1. In the Rényi approach, the \(T_R(M)\) curve has different behavior depending on the actual parameter values of the angular momentum and \(\lambda \). It has a local maximum and a local minimum when \(\lambda J_0\) is smaller than some critical value. In this case three black holes with different masses can coexist at a given temperature. The \(C_{JR}\) heat capacity is negative in the phase between the two local extrema and positive otherwise (see also Fig. 7 in Sect. 4). Above the critical value of \(\lambda J_0\), the local extrema disappear and the Rényi temperature becomes a monotonically increasing function of the energy. From these properties one can expect a stability change and a thermodynamic phase transition of Kerr black holes in the canonical ensemble. We will investigate this question in the next section.

Fig. 4
figure 4

Plots of the Rényi temperature against the mass-energy parameter of Kerr black holes at fixed \(J = J_0\) with \(\lambda J_0 = 0.05\), 0.04, 0.03, 0.02 and 0.01 parameter values starting from the top, respectively. The bottom, bold curve belongs to the standard Hawking temperature of the black hole in the Boltzmann model

Full size image

4 Stability analysis

Kaburaki et al. [48] have shown that isolated Kerr black holes are stable against axisymmetric perturbations in the standard picture of black hole thermodynamics. They also investigated the effects of thermal radiation around Kerr black holes from the standpoint of a canonical ensemble. They concluded that slowly rotating black holes (just like Schwarzschild black holes) are unstable in a heat bath, but rapidly rotating holes are less unstable and may even be stable.

As we pointed out, the standard thermodynamic stability criterion based on the Hessian analysis fails when it is applied to black holes because of the non-additivity of the entropy function and of the impossibility to define extensive thermodynamic quantities (see e.g. [52]). These problems can be mainly avoided by the Poincaré turning point method [51], which can divide a linear series of equilibrium into subspaces of unstable and less unstable states of equilibria solely from the properties of the equilibrium sequence without solving any eigenvalue equation. The method has been widely applied to problems in astrophysical and gravitating systems, in particular for the study of the thermodynamic stability of black holes in four and in higher dimensions [48,49,50, 52, 53]. A well-organized review of the method has been given by Arcioni and Lozano-Tellechea in [52], which we will mainly follow in the next brief description. Formal proofs of the results can be found in the previous work of Katz [68, 69] and Sorkin [70], and a more intuitive interpretation has also been given in [71].

Suppose \(\mathscr {M}\) is the space of possible configurations of a system in which a given configuration is specified by a point X. The set of independent thermodynamic variables \({\mu ^i}\) specifies a given ensemble. Let Z be the corresponding Massieu function. Both \({\mu ^i}\) and Z are functions on \(\mathscr {M}\). Equilibrium states occur at points in \(\mathscr {M}\) which are extrema of Z under displacements dX for which \(d \mu ^i = 0\). At equilibrium the Massieu function depends only on the values of the thermodynamic variables \(\mu ^i\). We can define conjugate variables \(\beta _i\) such that

$$\begin{aligned} \text {d}S = \beta _i \text {d} \mu ^i \end{aligned}$$
(31)

for all displacements dX. The set of equilibria is a submanifold \(\mathscr {M}_{\text {eq}}\) of the configuration space. Points in \(\mathscr {M}_{\text {eq}}\) can be labeled by the corresponding values of \(\mu _i\), which are called control parameters. Usually all that we know is the explicit expression of the equilibrium Massieu function

$$\begin{aligned} Z_{\text {eq}} = Z (\mu ^i), \end{aligned}$$
(32)

which is the integral of Eq. (31). The explicit expressions for the conjugate variables at equilibrium are calculated as

$$\begin{aligned} \beta _i (\mu ^i) = \frac{\partial Z_{\text {eq}}}{\partial \mu ^i}. \end{aligned}$$
(33)
Fig. 5
figure 5

Example of stability curves. A conjugate variable \(\beta _a\) against a control parameter \(\mu _a\) is plotted. The point A is a turning point, where a stability change can occur. At point B a stability change does not occur even if the slope changes its sign there

Full size image

The entropy maximum postulate is a statement about the behavior of the entropy function along off-equilibrium curves in \(\mathscr {M}\), not along equilibrium sequences \(\mathscr {M}_{\text {eq}}\). Therefore we need an expression for an extended Massieu function \(\hat{Z} = \hat{Z}(X^\rho , \mu ^i)\) where \(X^\rho \) denote a set of off-equilibrium variables. The equilibrium configurations occur at the values \(X^\rho _{\text {eq}} = X^\rho _{\text {eq}}(\mu ^i)\) which are solutions of

$$\begin{aligned} \frac{\partial \hat{Z}}{\partial X^\rho } = 0. \end{aligned}$$
(34)

A stable equilibrium takes place at the point \(X^\rho _{\text {eq}}\) if and only if it is a local maximum of \(\hat{Z}\) at fixed \(\mu ^i\). Therefore stable solutions have a matrix

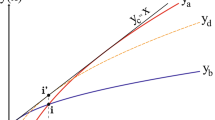
$$\begin{aligned} \left. \frac{\partial ^2 \hat{Z}(X^\tau , \mu ^i)}{\partial X^\rho \partial X^\sigma }\right| _{X^\tau = X^\tau _{\text {eq}}(\mu ^i)} \end{aligned}$$
(35)

with a negative spectrum of eigenvalues. A change of stability takes place when one of these eigenvalues become zero and changes sign. It has been shown that we can obtain information as regards the sign of an eigenvalue near a point where it vanishes without computing the spectrum of the matrix (35). What we have to do is to plot a conjugate variable \(\beta _a (\mu ^a) = \frac{\partial Z_{\text {eq}}}{\partial \mu ^a}\) against a control parameter \(\mu ^a\) along an equilibrium sequence for some fixed a. When a change of stability occurs, called a turning point, the plot of the stability curve \(\beta _a (\mu ^a)\) has a vertical tangent. Figure 5 shows an example of stability curves with a turning point A. The branch with negative slope near this point is always unstable, since one can prove that at least one eigenvalue of the matrix (35) is positive. The branch with positive slope near A is more stable. If the spectrum of zero modes is non-degenerate, only one of the eigenvalues changes its sign at the turning point. Therefore the positive slope branch has one unstable mode less than the negative slope branch. Note that what we can see with this method is the existence of instabilities because there can be positive eigenvalues which do not change sign at the turning point. If there is a point in the equilibrium sequence which is fully stable, all equilibria in the sequence are fully stable until the first turning point is reached.

4.1 Pure black holes

The case of a black hole isolated from its surroundings can be described in the microcanonical emsemble. The Massieu function is the Rényi entropy (24) and the control parameters are M and J. The conjugate variables are \(\beta \) and \(-\alpha \), where \(\beta \) is the inverse of the Rényi temperature (25) and \(\alpha = \frac{\varOmega }{T_R}\). To study the stability of the black hole we need to plot the stability curves \(\beta (M)\) at constant J and \(-\alpha (J)\) at constant M.

Fig. 6
figure 6

Curves of the conjugate variable \(\beta (M)\) at fixed J in the microcanonical treatment. The \(\lambda = 0\) (black) curve represents the stability curve of the black hole in the standard thermodynamic approach, while the \(\lambda J_0 = 0.01\) (green), \(\lambda J_0 = 0.02\) (red) and \(\lambda J_0 =0.1\) (blue) curves are the stability curves within the Rényi approach. No vertical tangent occurs in either case. By rotating the figure clockwise with \(\frac{\pi }{2}\), the stability curves of the canonical treatment can be obtained, i.e. \(-M(\beta )\) at fixed J. In this case, the \(\lambda J_0 = 0.01\) (green) curve has two vertical tangents denoting the loss and the recovery of stability. In this scenario, up to three black holes with different mass-energy parameters can coexist at a given temperature

Full size image

When \(J=J_0\) is a constant, the variables \(\beta /\sqrt{J_0}\) and \(M/\sqrt{J_0}\) can be written as functions of the normalized parameter h with constant \(\lambda J_0\). On Fig. 6 we plotted the stability curves \(\beta (M)\) for different values of \(\lambda J_0\). For comparison, the stability curve of the standard Kerr black hole (\(\lambda = 0\)) is also plotted on the figure. It can be seen that no curves of the Kerr–Rényi case have a vertical tangent (similar to the standard Kerr result analyzed by Kaburaki, Okamoto and Katz in [48]), and therefore there is no stability change for any M. Like in the \(\lambda = 0\) case, the \(\lambda >0\) curves also diverge asymptotically as we consider the extreme black hole limit \(h\rightarrow 1\). In the large M limit the black holes approach the static Schwarzschild solution (\(h=0\)). It can also be seen that the \(\lambda > 0\) stability curves are similar to the Schwarzschild-Rényi case in the large M region (see Fig. 3 of [54]).

For the standard case, it has been shown that isolated Kerr holes are thermodynamically stable with respect to axisymmetric perturbations. Also, the isolated Schwarzschild black holes have been found to be stable against spherically symmetric perturbations in the Rényi approach. Based on these results, since no turning point occurs on the stability curves in between these two extrema, we can conclude that isolated Kerr black holes are thermodynamically stable against axisymmetric perturbations in the Rényi approach as well.

By looking at Fig. 6, we can also see that there are two points where the tangent of the stability curves with smaller \(\lambda \) (or small angular momentum \(J_0\)) becomes horizontal. These correspond to the points where the heat capacity at constant J changes its sign through an infinite discontinuity, similar to the Davies point [26] of the standard Kerr black hole case. On Fig. 7 we plotted the lines of constant J in the normalized parameter space of (h, k). Here the \(\lambda J_0 = 0.01\) line crosses the line where \(C_{JR}\) diverges. Along this line the heat capacity \(C_{JR}\) changes its sign two times on the way from the \((h=0)\) Schwarzschild limit to \((h = 1)\) extremality.

Fig. 7
figure 7

Plots of \(J = \text{ const. }\) curves for \(\lambda J_0 = 0.01\) (green), \(\lambda J_0 = 0.02\) (red) and \(\lambda J_0 =0.1\) (blue) parameter values on the (h, k) space

Full size image

When \(M=M_0\) is a constant, \(\alpha \) and \(J/M_0^2\) become functions of h with a constant \(\lambda M_0^2\). On Fig. 8, we plotted the \(-\,\alpha (J)\) stability curves for different values of \(\lambda M_0^2\). There is no vertical tangent and hence no stability change occurs at any point for any \(\lambda \). The \(M=const.\) lines in the parameter space of (h, k) are plotted on Fig. 9.

Fig. 8
figure 8

Curves of the conjugate variable \(-\alpha (J)\) at fixed M. The \(\lambda = 0\) (black) curve represents the stability curve of a Kerr black hole in the standard approach within the microcanonical treatment. The \(\lambda M_0^2 = 0.01\) (green), \(\lambda M_0^2 = 0.08\) (red) and \(\lambda M_0^2 =0.3\) (blue) curves are the stability curves of the Rényi approach. No vertical tangents occurs

Full size image
Fig. 9
figure 9

Plots of \(M = \text{ const. }\) curves for \(\lambda M_0^2 = 0.01\) (green), \(\lambda M_0^2 = 0.08\) (red) and \(\lambda M_0^2 =0.3\) (blue) parameter values on the (h, k) space

Full size image

4.2 Black holes in a heat bath

Let us now consider the black hole in the canonical approach. The canonical ensemble describes the system of a black hole in equilibrium with an infinite reservoir of thermal radiation at constant temperature. The Massieu function in this case is

$$\begin{aligned} \varPsi (\beta ,J) = S_R - \beta M = -\beta F, \end{aligned}$$
(36)

where \(F = M - T_R S_R\) is the Helmholtz free energy. The conjugate variables of the control parameters are \(-M\) and \(-\,\alpha \). To study the stability of the black hole we need to plot the stability curves \(-M(\beta )\) at constant J and \(-\,\alpha (J)\) at constant \(\beta \).

The stability curves of \(-M(\beta )\) at constant J are simply the \(\frac{\pi }{2}\) clockwise rotated versions of Fig. 6. We can see that there is a vertical tangent along the stability curve in the standard Boltzmann treatment (\(\lambda = 0\)). The heat capacity \(C_J\) diverges at this turning point where \(h=h_c\). The \(0<h<h_c\) branch of this curve is less stable than the \(h>h_c\) branch. As Kaburaki, Okamato and Katz have shown [48], one can conclude from this result that since Schwarzschild black holes (\(h=0\)) are unstable in an infinite bath, so are the slowly rotating holes until the \(h_c\) turning point is reached. Rapidly rotating Kerr black holes, on the other hand, can become stable if the slowly rotating (unstable) holes have only one negative eigenmode, which changes sign at \(h_c\).

For the parametrized Rényi case, the behavior of the stability curves changes depending on the value of \(\lambda J_0\). We can see that there are two turning points on the \(\lambda J_0 = 0.01\) stability curve when we rotate the plots of Fig. 6 with \(\pi /2\) clockwise. These turning points disappear when the value of \(\lambda J_0\) is larger than a critical value. As a consequence, stability change occurs only when the parameter \(\lambda \) and/or \(J_0\) is sufficiently small. In this case, there are three phases of black holes; small, intermediate unstable and large black holes. The stability property of a rapidly rotating, small black hole is the same as of a slowly rotating, large black hole, which is expected to be stable from continuity requirements to the static solution in the Rényi approach [54].

The stability curves of \(-\alpha (J)\) at constant \(\beta \) are plotted on Fig. 10, while the lines of constant \(\beta \) in the parameter space of (h, k) are plotted on Fig. 11. One can see again that the stability curves have no vertical tangent when the \(\lambda \) parameter is sufficiently large, similar to the case of \(\beta (M)\) with constant J. Vertical tangents to the stability curves appear, however, when \(\lambda \) and/or \(\beta _0\) are smaller than some critical value. When a curve has two vertical tangents, there are two turning points where the heat capacity \(C_{JR}\) diverges and changes its sign. The black hole changes its stability there in the order from a less unstable state to unstable state and back to a less unstable state again, where the less unstable states may even be stable but not guaranteed.

When \(\lambda \beta _0^2\) is less than some critical value, there are two branches of the stability curves \(-\alpha (J)\) at constant \(\beta _0\). This result is consistent with the fact that in the Schwarzschild-Rényi case there are two black holes with the same \(\beta \), as can be seen on Fig. 1 in [54]. The lower branch of the \(\lambda \beta _0^2=9\) curve terminates at the \(h = 0\) small, static black hole limit. The behavior of this branch is similar to the curve of the \(\lambda = 0\) Kerr–Boltzmann case. According to these results, we can conclude that small, static or slowly rotating black holes in the Rényi approach are unstable in a heat bath, but fast rotation can stabilize them in a similar way as is done in the Kerr–Boltzmann case, which has been shown by Kaburaki, Okamoto and Katz [48]. The upper branch of the \(\lambda \beta _0^2=9\) stability curve belongs to larger mass black holes and terminates at the large, static black hole limit when \(h \rightarrow 0\). There is no vertical tangent in this branch so the corresponding rotating black holes have the same stability property as the large, static black holes in a heat bath, i.e. they are stable.

Fig. 10
figure 10

Curves of the conjugate variable \(-\alpha (J)\) at fixed \(\beta \) in the canonical approach. The \(\lambda = 0\) (black) curve describes the standard thermodynamic approach. The \(\lambda \beta _0^2 = 9\) (brown), \(\lambda \beta _0^2 = 12.7\) (green), \(\lambda \beta _0^2 = 13.4\) (red) and \(\lambda \beta _0^2 = 20\) (blue) curves are the stability curves of the Rényi model. The \(\lambda \beta _0^2 = 12.7\) (green) curve has two turning points, while the stability curve of \(\lambda \beta _0^2 = 9\) (brown) exhibits two branches with a single turning point in the lower branch

Full size image
Fig. 11
figure 11

Plots of \(\beta = \text{ const. }\) curves on the (h, k) space for \(\lambda \beta _0^2 = 9\) (brown), \(\lambda \beta _0^2 = 12.7\) (green), \(\lambda \beta _0^2 = 13.4\) (red) and \(\lambda \beta _0^2 = 20\) (blue)

Full size image

4.3 Phase Transitions

We have shown in Ref. [54] that a Hawking–Page transition can be observed for static black holes in the Rényi approach. Previously, it had also been shown [61,62,63] that Kerr–AdS black holes exhibit a first order small black hole/large black hole (SBH/LBH) phase transition in the canonical ensemble. In this subsection we will study the question of possible phase transitions of Kerr black holes in the Rényi model.

The behavior of the free energy function \(F = M - T_R S_R\) for \(\lambda J_0 =\) 0.01, 0.02 and 0.1 at constant J is displayed on Fig. 12. We can see that all curves cross the horizontal axis. Small black holes with lower temperature possess positive free energy, while larger black holes with higher temperature possess negative free energy. One can, therefore, expect a Hawking–Page transition between the thermal gas phase with angular momentum, and the large black hole state, which would be locally stable according to our analysis in Sect. 4.2. It is generally assumed that \(F\approx 0\) for a thermal gas, so the phase transition occurs around the temperature where the free energy of the black hole becomes zero.

Fig. 12
figure 12

Free energy of a Kerr black hole in the Rényi model against the temperature for various angular momenta \(J_0\), \(\lambda J_0 = 0.01\) (green), \(\lambda J_0 = 0.02\) (red) and \(\lambda J_0 = 0.1\) (blue). Characteristic swallowtail behavior is observed for \(\lambda J_0 = 0.01\) (green), which corresponds to a SBH/LBH phase transition

Full size image

An SBH/LBH phase transition can also be observed for Kerr black holes in the Rényi model when we enlarge the \(\lambda J_0 =\) 0.01 curve of Fig. 12 on Fig 13. The swallowtail behavior of the free energy function is a typical sign of a first order transition between the SBH and LBH phases. There are three branches on the picture: small, lower temperature holes; large, higher temperature holes; and intermediate, unstable black holes. There is a coexistence point of small and large black holes where the SBH/LBH transition occurs. The mass and entropy functions are discontinuous at this point which indicates that the phase transition is a first order kind. By increasing \(\lambda \), the swallowtail behavior disappears, as it can be seen on the \(\lambda J_0 =\) 0.02 curve on Fig. 12. This suggests the existence of a critical point where the phase transition becomes second order.

Fig. 13
figure 13

Close up figure of the free energy of a Kerr black hole in the Rényi model for \(\lambda J_0 = 0.01\) on Fig. 12. The intermediate, unstable branch is displayed with a dashed line

Full size image

5 Kerr–AdS black holes

In order to compare the obtained stability results of the Kerr–Rényi model to the Kerr–AdS–Boltzmann case in the Poincaré approach (analogous to the Schwarzschild problem), in this section we present the Poincaré stability analysis of the Kerr–AdS–Boltzmann case as well. The Kerr–AdS black hole metric is described by

$$\begin{aligned} ds^2= & {} - \frac{\varDelta _r}{\rho ^2} \left( dt - \frac{a \sin ^2 \theta }{\varXi } d \phi \right) ^2 + \frac{\rho ^2}{\varDelta _r} dr^2 + \frac{\rho ^2}{\varDelta _\theta } d \theta ^2 \nonumber \\&+ \frac{\varDelta _\theta \sin ^2 \theta }{\rho ^2} \left( a dt - \frac{r^2 + a^2}{\varXi } d\phi \right) ^2, \end{aligned}$$
(37)

where

$$\begin{aligned} \varDelta _r= & {} (r^2 + a^2) \left( 1 + \frac{r^2}{l^2} \right) - 2 m r, \quad \varDelta _\theta = 1 - \frac{a^2 \cos ^2 \theta }{l^2}, \\ \rho ^2= & {} r^2 + a^2 \cos ^2 \theta , \quad \varXi = 1 - \frac{a^2}{l^2}. \end{aligned}$$

The thermodynamic quantities are written in terms of a, l and the horizon radius \(r_{+}\), which is obtained by solving \(\varDelta = 0\). The Hawking temperature of the horizon is given by

$$\begin{aligned} T = \frac{1}{2 \pi r_{+}} \left( \frac{(a^2 +3 r_{+}^2)(r_{+}^2/l^2+1)}{2(a^2 + r_{+}^2)} -1\right) , \end{aligned}$$
(38)

while the Bekenstein–Hawking entropy of the black hole is

$$\begin{aligned} S =\pi \frac{a^2 + r_{+}^2}{1 -a^2/l^2}. \end{aligned}$$
(39)

The angular momentum of a Kerr–AdS black hole is

$$\begin{aligned} J = \frac{(r_{+}^2 + a^2)(1 + r_{+}^2/l^2)}{2 r_{+}} \frac{a}{(1 - a^2/l^2)^2}, \end{aligned}$$
(40)

the angular velocity of the horizon is

$$\begin{aligned} \varOmega = \frac{a}{l^2} \frac{r_{+}^2 + l^2}{r_{+}^2 + a^2}, \end{aligned}$$
(41)

and the mass-energy parameter of the black hole can be re-expressed as

$$\begin{aligned} M = \frac{(r_{+}^2 + a^2)(1 + r_{+}^2/l^2)}{2 r_{+}} \frac{1}{(1 - a^2/l^2)^2}. \end{aligned}$$
(42)

The heat capacity at constant angular velocity can be computed as

$$\begin{aligned} C_\varOmega = \frac{2 \pi l^2 r_{+}^2( 3 r_{+}^4 +( a^2 + l^2) r_{+}^2 - a^2 l^2)}{(l^2 - a^2)(3 r_{+}^4 -(a^2 + l^2) r_{+}^2 - a^2 l^2)}, \end{aligned}$$
(43)

and the heat capacity at constant angular momentum takes the form

$$\begin{aligned} C_J = \frac{2 \pi l^4 \left( a^2+r_{+}^2\right) ^2 \left( -a^2 l^2+\left( a^2+l^2\right) r_{+}^2 +3 r_{+}^4\right) }{(l^2 -a^2) X}, \end{aligned}$$
(44)

where

$$\begin{aligned} X&= -l^4 r_{+}^4+3 l^2 r_{+}^6+a^6 \left( l^2+r_{+}^2\right) +a^4 \Big (3 l^4+13 l^2 r_{+}^2\\&\quad +\,6 r_{+}^4\big ) +a^2 \left( 6 l^4 r_{+}^2+23 l^2 r_{+}^4+9 r_{+}^6\right) . \end{aligned}$$

Here we introduced the normalized parameters

$$\begin{aligned} p \equiv \frac{|a|}{r_{+}}, ~\text{ and }~~ s \equiv \frac{l}{r_{+}}. \end{aligned}$$
(45)

The heat capacities \(C_\varOmega \) and \(C_J\) change their signs depending on the values of p and s. The parameter space of (p, s) can be divided into four regions depending on the signs of \(C_\varOmega \) and \(C_J\) as shown on Fig. 14.

Fig. 14
figure 14

Phase diagram of Kerr–AdS black holes in the standard model. On the dashed curve \(C_J\), while on the dotted curve \(C_\varOmega \) diverges. In region I, \(C_{\varOmega }<0\) and \(C_{J} <0\), in region II, \(C_{\varOmega }<0\) and \(C_{J} >0\), and in region III, \(C_{\varOmega }>0\) and \(C_{J} >0\). In region IV, there is no physical solution because \(|a| > l\)

Full size image
Fig. 15
figure 15

Stability curves of \(\beta (M)\) at fixed J for Kerr–AdS black holes in the microcanonical treatment. The curves of \(\tilde{J} = 0.01\) (green), \(\tilde{J} = 0.025\) (red), and \(\tilde{J} =0.05\) (blue) are plotted. No vertical tangent occurs in either case. The figure rotated by \(\frac{\pi }{2}\) clockwise represents the stability curves of \(-M(\beta )\) at fixed J for the canonical ensemble, in which case the \(\tilde{J} = 0.01\) (green) curve has two vertical tangents

Full size image
Fig. 16
figure 16

Plots of \(J = \text{ const. }\) curves for \(\tilde{J} = 0.01\) (green), \(\tilde{J} = 0.025\) (red) and \(\tilde{J} =0.05\) (blue) on the (p, s) space

Full size image

Similarly to the Kerr–Rényi case in Sect. 4, the thermodynamic stability problem of Kerr–AdS black holes can also be analyzed by the Poincaré turning point method. The stability curves of the two systems are qualitatively similar. For the study of the Kerr–AdS black hole problem we will use the following normalized variables:

$$\begin{aligned} \tilde{\beta } = \frac{\beta }{l},~~ \tilde{J} = \frac{J}{l^2}, ~~ \tilde{M} = \frac{M}{l}. \end{aligned}$$
(46)

First we consider the microcanonical ensemble. The stability curves \(\beta (M)\) at constant J are plotted on Fig. 15, while the curves of constant J in the parameter space of (p, s) are plotted on Fig. 16. Just like in the Kerr–Rényi case, we can see that there is no turning point of stability. The stability curves \(-\,\alpha (J)\) at constant M and the curves of constant M in the (p, s) space are depicted on Fig. 17 and Fig. 18, respectively. The behavior of the stability curves is almost identical to the one of the Kerr–Rényi case.

Fig. 17
figure 17

Curves of the conjugate variable \(-\alpha (J)\) at fixed \(\beta \) for Kerr–AdS black holes in the canonical treatment. The stability curves of \(\tilde{M} = 0.3\) (green), \(\tilde{M} = 0.4\) (red) and \(\tilde{M} = 0.6\) (blue) are plotted. There are no turning points on the diagram

Full size image
Fig. 18
figure 18

Plots of \(M = \text{ const. }\) curves for \(\tilde{M} = 0.3\) (green), \(\tilde{M} = 0.4\) (red) and \(\tilde{M} = 0.6\) (blue) on the (p, s) plane

Full size image
Fig. 19
figure 19

Curves of the conjugate variable \(-\alpha (J)\) at fixed \(\beta \) for Kerr–AdS black holes in the canonical ensemble. The curves of \(\tilde{\beta } = 3\) (brown), \(\tilde{\beta } = 3.63\) (green), \(\tilde{\beta } = 3.7\) (red) and \(\tilde{\beta } = 4\) (blue) are plotted. The \(\tilde{\beta } = 3.63\) (green) curve has two turning points, while the \(\tilde{\beta } = 3\) (brown) curve has two branches and the lower branch has a turning point

Full size image
Fig. 20
figure 20

Plots of \(\beta = \text{ const. }\) curves on the (p, s) space for \(\tilde{\beta } = 3\) (brown), \(\tilde{\beta } = 3.63\) (green), \(\tilde{\beta } = 3.7\) (red) and \(\tilde{\beta } = 4\) (blue)

Full size image

For the canonical system, the stability curves of \(-M(\beta )\) at constant J can be seen on Fig. 15 if we rotate it by \(\frac{\pi }{2}\) clockwise. The figure shows the existence of a critical temperature, above which the Kerr–AdS black holes allow a first order SBH/LBH phase transition in the canonical ensemble. On Fig. 19 we plotted the stability curves of \(-\alpha (J)\) at constant \(\beta \). The curves of constant \(\beta \) on the (p, s) space are plotted on Fig. 20. There are no turning points on the lower temperature (larger \(\beta \)) curves, but higher temperature curves exhibit turning points. Therefore, a stability change of Kerr–AdS black holes occurs only when the temperature is higher than a certain critical value. Black holes with slightly higher temperature than the critical one have an unstable branch between two, more stable branches. There is another critical temperature above which a cusp appears on the stability curve at \((\tilde{J},-\alpha ) = (0,0)\), where the Kerr–AdS black hole reduces to the Schwarzschild–AdS case. A vertical tangent occurs in the small black hole branch only, and no vertical tangent exists in the large black hole branch. From this result we can conclude that small and slowly rotating Kerr–AdS black holes are unstable in the canonical ensemble.

As it can be clearly seen from the analysis above, the thermodynamic properties of the Kerr–Rényi and the Kerr–AdS–Boltzmann models are very similar. In the static case, we have obtained a simple relation between the entropy parameter \(\lambda \) and the AdS curvature parameter l for black holes with identical horizon temperatures [41]. By assuming the same condition for stationary black holes augmented with the assumption of identical horizon angular velocity, we can derive analogous relations between the (h, k) and (p, s) parameters for rotating black holes by solving the following equations:

$$\begin{aligned} \hat{T}_R (h,k) = \hat{T}_{\text {AdS}} (p,s), ~~~ \hat{\varOmega }_R (h,k) = \hat{\varOmega }_{\text {AdS}} (p,s), \end{aligned}$$
(47)

where we normalized the quantities by the horizon radius \(r_{+}\) as

$$\begin{aligned} \hat{T} = T r_{+}, ~~~ \hat{\varOmega } = \varOmega r_{+}. \end{aligned}$$
(48)

As a result, a quantitative analogy between the Kerr–Rényi and Kerr–AdS–Boltzmann pictures of black hole thermodynamics can be given by the parameter equations

$$\begin{aligned} p= & {} \frac{3+h^2+k \pi -h^4 k \pi -Y}{2 h}, \end{aligned}$$
(49)
$$\begin{aligned} s= & {} \sqrt{\frac{3(1+h^2)}{3-h^2+2 k \pi -2 h^4 k \pi -Y}}, \end{aligned}$$
(50)

where

$$\begin{aligned} Y = \sqrt{\left( 3-h^2\right) ^2+2 \left( 3+h^2-3 h^4-h^6\right) k \pi +\left( 1-h^4\right) ^2 k^2 \pi ^2}. \end{aligned}$$

These equations provide a very interesting correspondence between the two approaches.

6 Summary and conclusions

In this paper we investigated the thermodynamic and stability properties of Kerr black holes described by the parametric, equilibrium- and zeroth law compatible Rényi entropy function. The corresponding problem of static Schwarzschild black holes has been analyzed in [41, 54], where interesting similarities have been found to the picture of standard black hole thermodynamics in asymptotically AdS space. In particular, a stability change and a Hawking–Page transition have been identified, which motivated us to extend our investigations to the present (3 + 1)-dimensional, rotating problem as well.

The novel results of this work are the following. We derived the temperature and heat capacities of a Kerr black hole in the Rényi approach, and found that the global maximum of the temperature-energy curve at a fixed angular momentum in the standard description becomes only a local maximum in the Rényi model. In the thermodynamic stability analysis we investigated both the microcanonical and the canonical ensembles. We have plotted the stability curves of the Boltzmann–Gibbs and Rényi entropy models, and showed that no stability change occurs for isolated black holes in either case. From this result, we concluded that, similarly to the standard Boltzmann case, isolated Kerr black holes are thermodynamically stable with respect to axisymmetric perturbations in the Rényi approach.

In case when the black holes are surrounded by a bath of thermal radiation in the canonical picture, we found that, in contrast to the standard Boltzmann case, slowly rotating Kerr black holes can be in stable equilibrium with thermal radiation at a fixed temperature if the number of negative eigenmodes of the stability matrix is one. We showed that fast rotating black holes have similar stability properties to slowly rotating ones, and there may also exist intermediate size, unstable black holes. We also analyzed the question of possible phase transitions in the canonical picture, and found that, in addition to a Hawking–Page transition, a first order small black hole/large black hole phase transition occurs in a very similar fashion as in AdS space. These findings indicate that there is a similarity between the Kerr–Rényi and Kerr–AdS–Boltzmann models, analogous to the one that we found in the static case. Based on this result we also investigated the Poincaré stability curves of Kerr–AdS black holes in the standard Boltzmann picture, and confirmed this similarity by obtaining simple algebraic relations between the parameters of the two approaches with identical surface temperature and angular velocity.

The above results may be relevant in many aspects of black hole physics. Our main motivation in the first place was to consider a statistical model to the non-extensive and non-local nature of black hole thermodynamics, where we do not assume a priori that the classical, additive Boltzmann statistics can describe this strongly gravitating system. The Rényi form of the black hole entropy includes a parameter \(\lambda \), which seems to be a good candidate to incorporate the effects of the long-range type behavior of the gravitational field, while also being additive and satisfying both the equilibrium compatibility and the zeroth law’s requirements. Specific models on how to compute the \(\lambda \) parameter value for various gravitational problems are actively investigated; see e.g. [55] for a quantum geometric approach to the black hole problem, and [58] for the case of the problem of information entropy in cosmology. In the latter work, as an effective model, the \(\lambda \) parameter of the Tsallis/Rényi relative entropy has been defined in a geometric way in order to describe the causal connection between a cosmological domain and its surroundings during the cosmic evolution. Since black holes are essentially the final states of cosmic structure formation, one can expect that the two directions might be connected somehow in the nonlinear regime of matter collapse.

As a different direction, it is also interesting to mention that by considering the Boltzmann picture in the standard description, the Bekenstein–Hawking entropy has a nontrivial non-additive property which also satisfies Abe’s formula. In the case of Schwarzschild black holes this non-additivity reads \(H_{\lambda }(S)=\sqrt{S}\) and for Kerr black holes \(H_{\lambda }(S)=\frac{S}{\sqrt{S-a^2\pi }}\) with \(\lambda = 0\). The corresponding thermodynamic and stability problems (by also applying the formal logarithm method) has been studied in [72] and [73], respectively.

In the present parametric approach however, the most important result is the confirmation of a stability change and the Hawking–Page transition of Kerr black holes in the Rényi model. As we discussed in the introduction, this phenomenon has many interesting connections with other open problems in theoretical physics, e.g. the cosmic nucleation of matter into black holes in the early universe, or due to the similarity to the AdS–Boltzmann problem, it may also be connected to the AdS/CFT correspondence and related phenomena. Parametric corrections to the black hole entropy problem also arise from quantum considerations, e.g. from string theory, loop quantum gravity or other semi-classical theories (see e.g. [74] and the references therein), and we expect that other parametric situations are also possible which might be connected to the Rényi description. In this paper, we did not aim to consider any quantum aspects of the Rényi model to black hole thermodynamics, rather our goal was to show that by accepting the Rényi formula as a physically reasonable statistical approach to the problem, the corresponding phenomenological thermodynamics provides a consistent and physical picture for black holes not only in the Schwarzschild but also in the rotating Kerr case. Nevertheless, let us briefly mention one quantum aspect where the Rényi approach may also serve as a useful model.

In the standard picture of black hole thermodynamics, Hawking found [9] that (except under very special circumstances): “black holes cannot be in stable thermal equilibrium, which means that the standard statistical-mechanical canonical ensemble cannot be applied when gravitational interactions are important.” In his other famous paper with Gibbons [75], Hawking investigated action integrals and partition functions in quantum gravity by evaluating the action for a gravitational field on a section of the complexified spacetime which avoids the singularities. In that paper, in the path-integral approach to the quantization of a field \(\phi \), they found that

$$\begin{aligned} Tr \exp [-i(t_2-t_1)H] = \int \text {d}[\phi ] \exp (iI[\phi ]), \end{aligned}$$
(51)

where H is the Hamiltonian, I is the Euclidean action, and the action integral is taken over all fields which are periodic with period \(t_2-t_1\). By introducing the notation \(t_2-t_1=-i\beta \), the left hand side of (51) can be rewritten as

$$\begin{aligned} Tr \exp [-\beta H], \end{aligned}$$
(52)

which formula looks identical to a partition function Z (in the Boltzmann–Gibbs statistics) for the canonical ensemble consisting of the field \(\phi \) at a temperature defined as \(T=\beta ^{-1}\). In evaluating the right hand side of (51), they considered a Taylor series about the background fields as

$$\begin{aligned} I[g,\phi ]= I[g_0,\phi _0]+I_2[\delta g] +I_2[\delta \phi ] + \text{ higher } \text{ order } \text{ terms, } \end{aligned}$$
(53)

and by keeping only the first term in the action integral, they argued that one can regard \(iI[g_0,\phi _0]\) as the contribution of the background to the partition function. Based on these findings, they showed that by applying this analysis to the Kerr–Newman solutions where the points \((t,r,\theta ,\varphi )\) and \((t+2\pi i \kappa ^{-1},r,\theta ,\varphi +2\pi i \varOmega \kappa ^{-1})\) are identified, the corresponding temperature T of the background (i.e. black hole) field becomes \(\kappa /2\pi \), which is the Hawking temperature.

The above result has been commonly considered as an independent confirmation of the standard model of BH thermodynamics, however there is a hidden inconsistency in its derivation, and “the essentially classical (i.e., “zero-loop”) nature of the Euclidean path-integral derivation of the formula \(S_{\text {BH}}=A/4\) remains somewhat mysterious” as Wald calls it in his discussion of the subject [76]. The main problem is that black holes cannot be in stable thermal equilibrium (in the Boltzmann–Gibbs picture as shown in [9]), however, such an equilibrium should be necessary in order to justify the use of the canonical ensemble in the calculation above. Another manifestation of the problem is that the corresponding partition function Z defined in (52), is divergent, which can easily be seen already for the simplest, Schwarzschild black hole case. Furthermore, even if one accepts that the total action integral is a canonical partition function with the Hawking temperature, the “zero-loop approximation” which describes the background contribution to Z is just a part of the total integral, so one can expect that higher-loop corrections also contribute to Z and therefore the background field alone cannot have the black body spectrum itself with \(T_H\).

In the above problem, the Rényi entropy approach can also be looked at as a possible way to avoid the inconsistency in applying the canonical ensemble. Indeed, one of our main results in the paper is to show that the canonical picture exists for black holes in the Rényi model, so the corresponding partition function also exists and is meaningful. In fact we also showed that due to a Hawking–Page transition effect, stable and large black holes are the thermodynamically preferred state similarly to asymptotically AdS black holes in the Boltzmann–Gibbs description. Of course, the explicit form of Z in this case shall be different from (52), but it is reasonable to assume that the action integral in (51) is a monotonic function of it, and therefore a consistent Rényi temperature could also be derived from this calculation which is again related to the imaginary time period, although possibly not as simply as in the Boltzmann picture.

This result is important as various Rényi entropy approaches are investigated frequently in different contexts connected to curved backgrounds, black holes and cosmology, and our findings can provide support for further investigations in this field by confirming that this approach has a physically meaningful macroscopic behavior while also reproducing the standard results in the appropriate parameter limit.

A further motivation for our approach arises from a different possible interpretation of the parametric Rényi picture originating from finite size reservoir effects in the canonical ensemble. In [77] Wald showed that “If a black hole were placed in a thermal cavity at exactly the same temperature, there would be no way of determining where the black hole is by observing particle emission, since the black hole would emit exactly as much thermal radiation by spontaneous quantum particle creation as it would absorb by classical processes”. For a thermal system like this, in Ref. [78], Biró showed that by requiring zero mutual information between a finite subsystem and a finite reservoir in thermodynamic equilibrium, the Tsallis- and Rényi entropy formulas arise very naturally. Although we have not worked out the details of this approach yet, it provides a nice possible interpretation of our findings as placing a black hole into a finite heat bath in the canonical approach instead of an infinite reservoir (which is an idealistic model) and require zero mutual information between the black hole and the reservoir in thermal equilibrium. In this situation the system is dominated by the bath, and Biró showed that the entropy parameter is proportional to the heat capacity of the bath as \(\lambda =1/C_0\), where instead of the classical infinite approximation, the heat capacity of the bath is a large but finite constant \(C_0\). This approach has been investigated e.g. for the case when a quark–gluon plasma system is connected to a finite heat bath in [79].

In conclusion, several interesting consequences can be deduced from the Rényi approach to black hole thermodynamics which is motivated by various physical considerations, and our present results provide further support for investigations in this interesting topic.