INTRODUCTION

Storage of adsorbed methane, which is the principal constituent of natural gas, in microporous adsorbents offers promise in developing gas automotive energy storage systems and mobile systems of natural gas transportation to remote consumers, as well as creating local natural gas storage facilities for heavy consumers. Unlike gasoline, diesel fuel, propane–butane motor mixtures, and liquefied natural gas (LNG), methane has a low density [1]. Therefore, the compressed natural gas (CNG) technique is currently used to increase the natural gas density in the storage system [2]. The LNG technique is also one of the main methods for methane storage [3, 4].

However, these techniques have some disadvantages. The CNG method is associated with high energy consumptions for gas compression. Compressed gas storage requires heavy tanks made of metal or expensive composite materials, and the risks of fire and explosion are high. LNG storage, which is possible at cryogenic temperatures and pressures close to atmospheric, can be implemented only using specialized equipment. This method is the most efficient and widely explored in the storage and transportation of extralarge amounts of natural gas. However, it is impractical for small consumers, as strict safety requirements are imposed on LNG systems [4, 5].

Natural gas has significant environmental benefits compared to conventional petroleum-based fuels. The use of natural gas methane as motor fuel needs no additives based on lead or other heavy metals to increase the octane number, which results in an absence of their emission into the atmosphere. There is no particulate matter from additives and soot in the exhaust gases, inhalation of which by human beings leads to the development of respiratory and cardiovascular diseases. There are no sulfur compounds in natural gas, and, as a result, there is no emission of sulfur dioxide, a typical component of exhaust gases [6].

A major problem that is holding back the widespread use of natural gas by remote consumers is a lack of energy-efficient, fire- and explosion-safe systems of storage and transportation, providing a high density of accumulated gas. In this regard, efforts are underway to develop competitive storage systems of adsorbed natural gas [7]. In addition to requirements for adsorption properties, an adsorbent intended for the adsorbed methane storage systems should meet a target value for volumetric adsorption methane density of no less than 263 m3 (NTP)/m3 Footnote 1 [8].

Among the essential properties of this adsorbent are its hydrophobicity, sufficiently high strength, and low cost.

Microporous carbon adsorbents best meet all the listed technological and economic conditions.

Consequently, it is relevant to synthesize adsorbents with an optimal porous structure so as to have a high methane adsorption capacity.

OBJECTS OF STUDY

Adsorbents

The EC-103 carbon adsorbent was synthesized by carbonization of waste from wood processing at 673‒1073 K with subsequent chemical activation at 1273°С in the presence of Н3РО4 and reduction followed by washing and drying. The structural and energy characteristics of the adsorbent were determined from the isotherm of nitrogen adsorption at 77 K measured on an Autosorb iQ analyzer (Quantachrome Instruments) and interpreted in terms of the theory of volume filling of micropores (TVFM) [9], BET, and Kelvin equations [10]. Figure 1 shows the isotherm of standard nitrogen vapors at 77 K.

Fig. 1.
figure 1

Isotherm of nitrogen adsorption on the EC-103 microporous carbon adsorbent at 77 K.

Full size image

As follows from Fig. 1, the isotherm of nitrogen adsorption–desorption at 77 K is reversible at the initial fillings of micropores. However, there is a hysteresis loop observed at high micropore fillings, which is indicative of the presence of micro- and mesopores in the adsorbent. Table 1 summarizes the structural and energy characteristics of the adsorbent.

Table 1.   The structural and energy characteristics of the ЕС-103 microporous carbon adsorbent.
Full size table

Affinity coefficient \({{\beta }_{{{{{\text{N}}}_{{\text{2}}}}}}}\) = Е/Е0 = 0.33 is used to convert the nitrogen adsorption data to the standard benzene vapor adsorption data [11]; the effective half-width (radii) of micropores was evaluated as х0 = 12/Е0 (nm) [11]. The affinity coefficient for methane was calculated from the ratio between the parachors for benzene and methane using the Sugden increments: \({{\beta }_{{{\text{C}}{{{\text{H}}}_{4}}}}}\) = 0.35. Specific surface SBET was determined from the initial section of the nitrogen adsorption isotherm at relative pressures up to p/ps = 0.1.

The preliminary estimations of methane adsorption onto activated carbons by molecular dynamics numerical simulation [12] revealed three characteristic maxima of methane density observed for the pore widths of (I) 0.7‒0.9, (II) 1.0‒1.1, and (III) 1.4‒1.5 nm, which are associated with the formation of methane adsorption associates in micropores. For these porous structure parameters, the energy of adsorbent–adsorbate interactions is maximal due to the formation of adsorption associates in pores, which results in an additional increase in the adsorption value. As follows from Table 1, the microporous structure of the EC-103 adsorbent is similar to type III structures.

Adsorbate

High purity (99.999%) methane was used in the experiments. Methane has the following physicochemical properties: molecular mass μ = 16.0426 g/mol, boiling temperature Т0 = 111.66 K, critical temperature Тсr = 190.77 K, and critical pressure pсr = 4.626 MPa [1].

DISCUSSION

Isotherms of Adsorption

Methane adsorption was studied within the pressure range from 0.2 to 40 MPa at the temperatures of 303, 313, 323, and 333 K by the volumetric–gravimetric method on the basis of changes in the mass of an ampoule with the adsorbent due to adsorption [13].

The value of methane adsorption was determined as the total content of the adsorbed substance in micropores:

$$a = {{(V - {{V}_{a}}){{\rho }_{g}}} \mathord{\left/ {\vphantom {{(V - {{V}_{a}}){{\rho }_{g}}} {{{m}_{0}}}}} \right. \kern-0em} {{{m}_{0}}}}.$$
(1)

Here, V is the total volume of the system, Vа is the volume of an adsorbent with micropores, ρg is the density of a gaseous phase at given pressure Р and temperature Т, and m0 is the mass of a regenerated adsorbent. The pressure, temperature, and adsorption were measured with the errors of ±0.015 MPa, ±0.3 K, and ±4 × 10–4 g, respectively.

As follows from Table 1, the specific surface of mesopores was insignificant, no more than 10% of the total specific surface. Therefore, adsorption in mesopores can be neglected in comparison with that in micropores. Volume of the adsorbent Vа was determined as a sum of skeletal volume of the adsorbent evaluated from the helium pycnometry experiments VHe and micropore volume W0 calculated from the isotherm of adsorption of benzene vapors at 293 K using the Dubinin–Radushkevich (D–R) equation.

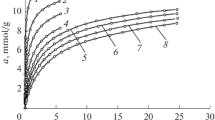
Figure 2 shows the dependences of methane adsorption onto EC-103 on pressure at the temperatures of 303, 313, 323, and 333 K.

Fig. 2.
figure 2

Isotherms of methane adsorption on the EC-103 microporous carbon adsorbent at the temperature, K: (1) 303, (2) 313, (3) 323, and (4) 333 K. Symbols are experimental data. Lines are results of approximation.

Full size image

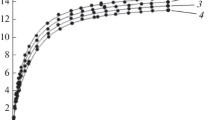
As follows from Fig. 2, methane adsorption increases rapidly at a pressure as low as 10 MPa, and, at higher pressures, a tendency to saturation is observed. At the temperature of 303 K and pressure of 40 MPa, the value of methane adsorption amounts to ~14.5 mmol/g (23.2 wt %). The isotherm of methane adsorption on EC-103 is reversible. The value of methane adsorption drops with the increase in temperature. The isosteres of methane adsorption were plotted from the experimental isotherms of adsorption (see Fig. 3).

Fig. 3.
figure 3

Isosteres of methane adsorption on the EC-103 microporous carbon adsorbent at different values of methane adsorption, a, mmol/g: (1) 1, (2) 2, (3) 3, (4) 4, (5) 5, (6) 6, (7) 7, (8) 8, (9) 9, (10) 10, (11) 11, (12) 12, and (13) 13. Symbols are experimental data. Lines are results of approximation.

Full size image

Figure 3 shows that the isosteres of methane adsorption on the EC-103 microporous adsorbent are well approximated by a linear function within the entire range of temperatures and pressures.

The obtained isosteres were employed for calculating the differential molar isosteric heat of methane adsorption on EC-103 as the difference between molar enthalpy of the gaseous phase hg and differential molar enthalpy of the adsorption system ha:

$${{q}_{{st}}} = {{h}_{g}}-{{h}_{a}}.$$

DIFFERENTIAL MOLAR ISOSTERIC HEAT OF ADSORPTION

The heat of adsorption was calculated using the general equation [14, 15], which takes into account the nonideality of a gaseous phase at high pressures Z(P, Vg, T) ≠ 1 and noninertness of an adsorbent upon adsorption, i.e., the dependence V = V(a, T):

$$\begin{gathered} {{q}_{{st}}} = - RZ{{\left( {\frac{{\partial (\ln P)}}{{\partial \left( {\frac{1}{T}} \right)}}} \right)}_{a}}\left\{ {1 - {{{{{\left( {\frac{{\partial V\left( a \right)}}{{\partial a}}} \right)}}_{T}}} \mathord{\left/ {\vphantom {{{{{\left( {\frac{{\partial V\left( a \right)}}{{\partial a}}} \right)}}_{T}}} {{{V}_{g}}}}} \right. \kern-0em} {{{V}_{g}}}}} \right\} \\ - \,\,{{\left( {\frac{{\partial P}}{{\partial a}}} \right)}_{T}}\left[ {V\left( {a,T} \right) - T{{{\left( {\frac{{\partial V\left( a \right)}}{{\partial T}}} \right)}}_{a}}} \right]. \\ \end{gathered} $$
(3)

In [16], it was shown that the relative adsorption deformation of adsorbents during methane adsorption in the temperature range of 303−333 K did not exceed 1%, while the contributions from the intensities of adsorption and temperature deformations of carbon adsorbents were negligible. Therefore, the heat of methane adsorption on EC-103 was calculated from the formula

$${{q}_{{st}}} = - RZ{{\left( {\frac{{\partial (\ln P)}}{{\partial \left( {\frac{1}{T}} \right)}}} \right)}_{a}} - {{\left( {\frac{{\partial P}}{{\partial a}}} \right)}_{a}}V,$$
(4)

where Z = PV/RT is the coefficient of compressibility of the gaseous equilibrium phase at pressure P and temperature T, R is the universal gas constant, V is the volume of the adsorbent with micropores, and a is the equilibrium value of adsorption at defined pressure and temperature. From the heat of methane adsorption estimated at the initial fillings of micropores (up to ~0.5 mmol/g), we evaluated the initial isosteric heat of adsorption: \(q_{{st}}^{0}\) = 15.8 kJ/mol.

Figure 4 shows the calculated molar differential isosteric heat of methane adsorption as a function of the value of methane adsorption on EC-103.

Fig. 4.
figure 4

Dependence of differential molar isosteric heat of methane adsorption on the EC-103 microporous carbon adsorbent at the temperatures, K: (1) 303, (2) 313, (3) 323, and (4) 333. Symbols are experimental data. Lines are results of approximation.

Full size image

As follows from Eq. (3), the isosteric heat of adsorption is determined by the slope of isosteres of adsorption, nonideality of a gaseous phase (Z), and curvature of isotherm of adsorption (dp/da)T. Figure 4 shows that, with an increase in methane adsorption, the isosteric heat of adsorption slightly decreases from the initial value of 15.7 to 12 kJ/mol at a = 10 mmol/g. According to Eq. (3), at high values of adsorption, the nonideality of the gaseous phase Z ≠ 1 and adsorption intensity factor (dP/da)T become more significant, resulting in a fan of the temperature-dependent curves of qst = f(a). At the temperature of 303 K and methane adsorption up to 10‒12 mmol/g, the slow decline in the heat of adsorption is probably associated with the volume filling of micropores, accompanied by an increasing contribution from the adsorbate–adsorbate intermolecular interactions, which leads to the formation of adsorption associates. A subsequent sharp drop in the heat of adsorption at 12‒14.5 mmol/g is caused by an increase in the repulsive energy between the adsorbed molecules in the associates [17].

An increase in the energy of attraction between adsorbate molecules results in the formation of methane associates at high micropore fillings. These processes blur with increasing temperature, and the drop of the heat of adsorption described by curves 2, 3, and 4 at the adsorption values between ~10 and ~14 mmol/g can be attributed to a decrease in the coefficient of compressibility Z with the increase in pressure according to Eq. (3) [18].

CALCULATION OF METHANE ADSORPTION AT SUPERCRITICAL TEMPERATURES

In many cases, the Dubinin TVFM allows one to calculate gas adsorption equilibria on microporous adsorbents in the subcritical and supercritical temperature ranges. The D–R thermal equation [9] is often used for this purpose:

$$a = {{a}_{0}}{\text{exp}}\left[ { - {{{\left\{ {R{\text{ }}T{{{\text{ ln}}\left( {{{fs} \mathord{\left/ {\vphantom {{fs} f}} \right. \kern-0em} f}} \right)} \mathord{\left/ {\vphantom {{{\text{ ln}}\left( {{{fs} \mathord{\left/ {\vphantom {{fs} f}} \right. \kern-0em} f}} \right)} E}} \right. \kern-0em} E}} \right\}}}^{2}}} \right],~$$
(5)

where а0 is the limited value of methane adsorption, mmol/g; Е is the characteristic energy of adsorption, kJ/mol; А = RTln(fs/f) is the differential molar work of adsorption, kJ/mol; fs is the fugacity of saturated pressure (fugacity of the standard state), Pa; f is the equilibrium fugacity, Pa; and R is the universal gas constant, kJ/mol⋅K.

The condition of linear extrapolation of lnps = f(1/T) was used to evaluate fs in the range of supercritical temperatures.

The limited adsorption is calculated from the Dubinin-Nikolaev equation [9]:

$${{a}_{0}} = a_{0}^{0}\exp [ - \alpha (T - {{T}_{0}})],$$
(6)

where \(a_{0}^{0}\), [mmol/g] is the limiting adsorption at the boiling temperature T0, K, and α, 1/K, is the thermal coefficient of the limiting adsorption. For methane, α= 1.52 × 10–3 K–1 [13].

In the region of supercritical temperatures, the value of limiting adsorption is evaluated using Eq. (6) provided that (dlna0/dT)fs = const [13]. The characteristic energy of adsorption E of a given gas is determined through the affinity coefficient β = E/E0. For methane, β = 0.35 [13].

The linear extrapolations of lnps = f(1/Т) and lna0 = f(Т) to the supercritical region were used for calculating the isotherm of methane adsorption on EC-103. Figure 5 shows the calculated isotherms of methane adsorption on EC-103.

Fig. 5.
figure 5

Dependence of methane adsorption on the EC-103 microporous carbon adsorbent at the temperatures, K: (1) 303, (2) 313, (3) 323, and (4) 333. Symbols are experimental data. Solid lines are results of calculations using the D–R equation.

Full size image

As follows from Fig. 5, the calculations of methane adsorption equilibria on the EC-103 adsorbent by using the D–R equation gave satisfactory results. The largest deviations of the calculated values from the experimental data were less than 10% at lnP = 8.5.

CONCLUSIONS

Thermochemical activation with Н3РО4 was used to synthesize the EC-103 microporous carbon adsorbent, which exhibited a high methane adsorption capacity (23.2 wt %) at 303 K and 40 MPa. The structural and energy characteristics and differential molar heats of methane adsorption were calculated for EC-103. The dependence of the differential molar isosteric heats of methane adsorption on the methane adsorption value was built. This dependence indicates that an enhancement of methane adsorption capacity requires such structures, which allow an additional increase in the energy of adsorption through the energy of adsorbate association in micropores. The methane adsorption equilibria in the supercritical temperature region were calculated using the structural and energy characteristics of the adsorbent and the thermal D–R equation within the framework of the TVFM.