Abstract
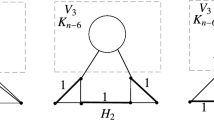
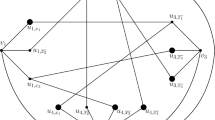
Let \( G=(V,E,w) \) be a simple weighted undirected graph with nonnegative edge weights. Let \( D \) be a minimal dominating set in \( G \). The cutset induced by \( D \) is the set of edges with one vertex in the set \( D \) and the other in \( V\setminus D \). The weight of the cutset is the total weight of all its edges. The paper deals with the problem of finding a cutset with the maximum weight among all minimal dominating sets. In particular, the nonexistence of a polynomial approximation algorithm with a ratio better than \( |V|^{-\frac {1}{2}} \) in the case of \( \text {P}\ne \text {NP} \) is proved.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
REFERENCES
R. Yu. Simanchev, I. V. Urazova, V. V. Voroshilov, V. V. Karpov, and A. A Korableva, “Selection of a key indicator system of the region economic security with use of the (0,1)-programming model,” Vestn. Omsk. Univ. Ser. Ekon. 17 (3), 170–179 (2019).
G. A. Cheston, G. Fricke, S. T. Hedetniemi, and D. P. Jacobs, “On the computational complexity of upper fractional domination,” Discrete Appl. Math. 27 (3), 195–207 (1990).
N. Boria, F. D. Croce, and V. Th. Paschosdef, “On the max min vertex cover problem,” Discrete Appl. Math. 196, 62–71 (2015).
V. V. Voroshilov, “A maximum dicut in a digraph induced by a minimal dominating set,” Diskretnyi Anal. Issled. Oper. 27 (4), 5–20 (2020) [J. Appl. Ind. Math. 14, 792–801 (2020)].
N. Christofides, Graph Theory. An algorithmic approach (Academic Press, New York, 1978; Mir, Moscow, 1978).
R. M. Karp, “Reducibility among combinatorial problems,” in Complexity of Computer Computations. The IBM Research Symposia Series, Ed. by R. R. Miller, J. W. Thatcher, and J. D. Bohlinger (Springer, Boston, MA, 1972).
J. Lee, N. Viswanath, and X. Shen, “Max-cut under graph constraints,” in Integer Programming and Combinatorial Optimization. IPCO 2016, Ed. by Q. Louveaux and M. Skutella, (Springer, Cham, 2016) Lect. Notes Comput. Sci. Vol. 9682, pp. 50–62.
M. R. Garey and D. S. Johnson, Computers and Intractability: A Guide to the Theory of NP-Completeness, (Freeman, San Francisco, 1979; Mir, Moscow, 1982).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated by V. Potapchouck
Rights and permissions
About this article
Cite this article
Voroshilov, V.V. Complexity of the max cut Problem with the Minimal Domination Constraint. J. Appl. Ind. Math. 16, 168–174 (2022). https://doi.org/10.1134/S1990478922010161
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S1990478922010161