INTRODUCTION

Modern technologies impose high requirements on materials, especially in terms of ecology and safety for humans. Therefore, attempts are made to replace synthetic polymers by natural polymers capable of biodegradation accompanied by the formation of harmless products [1]. An alternative approach can be the use of supramolecular chains formed by the noncovalent interactions of small molecules instead of polymer chains formed by covalent bonds. The simplest example of such chains is the wormlike micelles of surfactants [2–7]. The contour length of the chains can reach tens of micrometers [8], while their persistence length is usually 15–40 nm [2] at a cross-section size of 4–5 nm [3, 9]. They are similar to polymer chains, in particular, they can interlace and form a network of topological entanglements which imparts viscoelastic properties to solutions. But, as opposed to polymer chains, living micellar chains constantly break up and recombine [9, 10] and they can be easily destroyed, for example, by adding a small amount of nonpolar substances [11].

Wormlike surfactant micelles are widely used as thickening agents in the oil production [12, 13], cosmetics, and household chemicals [14] and drag reducing additives promoting the laminarity of a flow at its high velocities [15]. Wormlike micelles replace polymers in many practical applications. However, a wider use of micellar systems is prevented by relatively low values of the viscosity and elastic modulus of surfactant solutions.

One of the most promising approaches to increase the viscosity and elastic modulus of the networks proposed in recent years consists in the addition of inorganic nanoparticles to wormlike surfactant micelles [16]. Micellar chains can attach by their ends to the surface of nanoparticles covered with a surfactant layer; as a result, the nanoparticles act as a crosslinking agent in the micellar network. It was shown that just end-caps of wormlike micelles participate in interaction with the nanoparticles because they are the energy unfavorable micelle regions. Surfactant molecules have a spherical packing in them, as opposed to the cylindrical packing in the central part of a micelle which is optimum in the formation of wormlike micelles. It was shown that the addition of nanoparticles induces a significant increase in the viscosity of surfactant solutions. The most substantial growth in viscosity (by orders of magnitude) is observed at the concentration of surfactants in the vicinity of the overlap concentration C* of micellar chains [17–19]. In this case, the introduction of nanoparticles leads to transition from a viscous fluid to a viscoelastic solution. At a higher surfactant concentration when the micelles are already significantly entangled, the introduction of nanoparticles increases viscosity moderately by 1.5–3 times [20–22].

Most studies of the effect of nanoparticles on the rheological properties of the solutions of wormlike micelles were performed using cationic [17, 22] and anionic surfactants [18, 20, 23] and their mixtures [19]. At the same time, zwitterionic surfactants, which are low-toxic, biodegradable, and safe even for the sensitive child skin, are more promising in environmental terms [24]. However, just one work devoted to the effect of nanoparticles on the rheological properties of the solutions of zwitterionic surfactants has been published so far [25]. It was shown that the addition of negatively charged silica nanoparticles (0.3–0.8 wt %) with a radius of 12 nm to a solution of the wormlike micelles of erucyl amidopropyl dimethyl betaine with a long C22 tail increases the viscosity of the system twofold. At higher concentrations of the nanoparticles (above 1 wt %) a two-phase system is formed. No structural studies of these suspensions are available.

The aim of this work is to study the effect of nanoparticles on the rheological properties and structure of wormlike micelles based on a biodegradable zwitterionic surfactant with a long C18 tail, oleyl amidopropyl dimethyl carboxybetaine (OAB), obtained from biorenewable resources, vegetable oils, with a small addition of an anionic surfactant, sodium dodecyl sulfate (SDS). As opposed to the overwhelming majority of previous works on nanocomposite systems based on wormlike surfactant micelles [17–23, 25], platelike nanoparticles with a high specific surface compared with commonly used spherical particles were used as a filler. This provided a larger surface for interaction with micellar chains. Moreover, the platelike nanoparticles of bentonite clay chosen for studies are a nontoxic material of natural origin. It is shown in this work that the addition of bentonite nanoparticles to the dense network of micellar chains increases the viscosity and relaxation time by an order of magnitude. Therefore, the clay nanoparticles are an efficient and eco-friendly filler for micellar networks.

EXPERIMENTAL

Materials

The anionic surfactant sodium dodecyl sulfate (SDS) (a molecular weight of 288 g/mol) (Helicon, Russia) (>97%) and sodium hydroxide (>85%) (Riedel-de Haën) were used without additional purification. The zwitterionic surfactant oleyl amidopropyl dimethyl carboxybetaine (OAB)

was provided by OOO NPO NIIPAV (Russia) in the form of a solution containing 33 wt % OAB (including sodium and chloride ions), 0.5 wt % oleyl amidopropyl dimethyl amine (OA), 17.0 wt % isopropanol, and 49.5 wt % water. OAB was synthesized in two stages.

Oleyl amidopropyl dimethyl amine was first obtained from oleic acid and dimethylaminopropylamine (160°C, under vacuum). Oleyl amidopropyl carboxybetaine was then synthesized from oleyl amidopropyl dimethyl amine and sodium monochloroacetate at 80°C. Sodium chloride was the side reaction product.

To remove isopropanol the initial solution of the surfactant diluted fivefold with distilled water was frozen in liquid nitrogen and lyophilized. The absence of isopropanol was confirmed by 1H NMR spectroscopy. In experiments, pH was maintained in the range of 11.0–11.2. Under these conditions, OA was not charged and OAB was in the zwitterionic form (pKa of OAB is 2 [26]).

Natural bentonite clay was purchased from Sigma-Aldrich. The size of clay nanoplates was in the range of 30–200 nm, and the average size was estimated as 100 nm [27]. The specific surface area of the nanoplates was 63 m2/g [28]. Al–OH, Mg–OH, and Si‒OH functional groups were present on the surface [29], so that the nanoparticles had a negative charge in an alkaline medium [29].

Solutions were prepared using bidistilled deionized water obtained on a Milli-Q Millipore Waters unit (United States) as well as deuterated water (>99%) provided by Astrakhim (Russia).

Preparation of Nanocomposite Networks

Clay nanoparticles were dispersed in an aqueous medium using a SonoPuls ColePalmer 350 ultrasonic disperser with a power of 350 W for 30–60 min. The time was increased with an increase in the amount of the clay. Afterwards, the surfactants were added, and the resulting mixture was stirred for 1 day. The amount of surfactants (OAB, SDS) adsorbed on bentonite nanoparticles was earlier determined by thermogravimetry and elemental analysis. It is as low as 1 wt % in terms of the clay amount [27]. Since the amount of the clay in the samples did not exceed 0.3 wt %, the amount of the adsorbed surfactant (up to 0.003 wt %) was extremely small in comparison with the total amount of the surfactant in the system under study (2.1 wt %). As was shown by transmission electron microscopy, elemental analysis, and X-ray diffraction [30], in the presence of OAB and SDS, bentonite mainly occurs in the form of tactoids consisting of five to ten plates and the interplanar distance insignificantly increases (by 5%). The small amount of the adsorbed surfactant almost does not change the charge of the nanoplates, the zeta potential of which is −27 mV, which is equal to the zeta potential of the initial nanoplates of −26 mV within the error of the measurements [27]. The prepared suspensions were stable and retained the initial viscoelastic properties for at least 1 year.

Research Methods

Rheometry. Rotational rheometry was used to study the viscoelastic properties of the solutions and suspensions. The measurements were performed on a Physica MCR301 rheometer (Anton Paar, Austria). Shear stress was applied to the sample, and a change in the strain with time was measured. The viscosity of the samples during flow was determined in the constant shear stress mode. In order to measure each point in the graph of the dependence of viscosity on the shear rate the shear stress was applied to the sample during the time comparable to the inverse value of the corresponding shear rate. Frequency dependences of the viscous and elastic components of the complex elastic modulus G *, the storage modulus G ' and the loss modulus G ", were obtained in the oscillatory shear stress mode. The specified experiments were carried out at low stress amplitudes after the preliminary determination of the linear region of viscoelasticity. All the measurements were performed at 25°C in a thermostatted cone–plate measurement cell with a cone diameter of 49.93 mm and an angle of 1°.

Small-angle neutron scattering. Small-angle neutron scattering was used to study the structure of the samples. The experiments were performed on a time-of-flight YuMO spectrometer with a two-detector system [31] of the IBR-2 reactor at the Frank Laboratory of Neutron Physics, Joint Institute of Nuclear Research (Dubna, Russia) in the dynamic range of scattering vectors q = 0.006–0.7 Å−1 in a thermostatted cell at 25°C. D2O was used as a solvent to obtain scattering from the entire structure, while a mixture of water and deuterated water (85%/15%), which makes it possible to “hide” scattering from surfactant micelles, was used to obtain scattering only from clay nanoplates in the nanocomposite network. The intensity curves measured by small-angle neutron scattering were normalized to a vanadium scatterer and corrected for sample transmission and thickness and background scattering using the SAS program [32].

Cryogenic transmission electron microscopy (cryo-TEM). Cryo-TEM was used to visualize the structure of the networks. The sample was studied in the frozen hydrated state. This is a direct method for visualizing objects of self-organizing systems in almost the same form as that in which they exist in solution. The samples were studied on a Titan Krios 60-300 TEM/STEM microscope (FEI, United States) with a spherical aberration corrector (Cs corrector), a direct electron detector (DDE Falcon II), and a phase plate (Volta phase plates). TEM images were obtained at an accelerating potential of 300 kV in the parallel beam mode; the radiation dose was no more than 100 e/Å2. Images were processed using Digital Micrograph and TIA programs. The samples for the cryo-TEM measurements were prepared by applying the solution or suspension under study through the side port of Vitrobot (Vitrobot Mark IV, FEI, United States) directly onto a three-millimeter microscopic copper grid covered with a carbon layer [33]. After applying the sample onto the grid, it was immersed into liquid ethane for fast freezing.

RESULTS AND DISCUSSION

Wormlike micelles of surfactants based on a mixture of OAB and SDS at a total surfactant concentration of 0.048 mol/L (2.03 vol %) and a molar ratio of OAB : SDS = 10 were used to prepare nanocomposite networks. This ratio provides the formation of long wormlike surfactant micelles owing to the large size of the hydrophobic tail of OAB and the addition of the anionic surfactant [27, 34], which shields repulsion between the cationic fragments of OAB. The concentration of the filler, bentonite nanoplates (0–0.13 vol %), did not exceed the overlap concentration of bentonite plates (1 vol %) to ensure the predominant interaction of the nanoparticles with the micelles rather than with each other (Fig. 1). The overlap concentration of the plates which corresponds to percolation was experimentally determined. It was shown that clay suspensions without surfactants exhibit the yield point at concentrations above 1 vol % which is associated with formation of a three-dimensional structure of clay nanoplates [35].

Fig. 1.
figure 1

Photographic images of the viscoelastic samples containing 0.044 mol/L (1.93 vol %) OAB and 0.004 mol/L (0.1 vol %) SDS in (a) the absence and (b, c) presence of (b) 0.03 and (c) 0.1 vol % bentonite clay. Color drawings can be viewed in the electronic version.

Full size image

Rheological Properties

Figure 2 presents the viscosity curve and the frequency dependences of the storage modulus G '(ω) and the loss modulus G "(ω) for the initial micellar network without nanoparticles. It is seen that, in the region of low shear rates, a Newtonian plateau is observed in the flow curve which makes it possible to determine the viscosity at the zero shear rate η0. The value of the zero-shear viscosity η0 is 2 × 102 Pa s, which is by five orders of magnitude higher than the viscosity of water. With an increase in the shear rate viscosity decreases which is associated with the extension of micelles along the shear direction [36]. A wide elastic response region is seen in the frequency dependences of G '(ω) and G "(ω) in which G ' > G ". In addition, there is a plateau in the dependence G '(ω) which indicates formation of a network structure owing to topological entanglements of the micelles [2, 37]. The plateau of the storage modulus G0 is proportional to the amount of elastically active chains in the network [10, 37]. Therefore, in the absence of the nanoparticles, the micellar chains entangle with each other and form a network structure exhibiting the viscoelastic behavior.

Fig. 2.
figure 2

(a) Frequency dependences of (closed symbols) the storage modulus and (open symbols) the loss modulus as well as (b) dependences of viscosity on the shear rate for solutions of wormlike surfactant micelles containing 0.044 mol/L OAB and 0.004 mol/L SDS (1) before and (2, 3) after addition of (2) 0.07 and (3) 0.13 vol % dispersed clay. The dependences of the complex viscosity modulus on frequency for solutions (opened triangles) without clay and (open circles) containing 0.07 vol % clay. The arrows in (a) indicate the values of the minimum of the loss modulus \(G_{{{\text{min}}}}^{{''}}\), and the solid lines in (b) refer to data approximation by the Carreau model.

Full size image

Figure 2 illustrates how the rheological properties of the network of entangled surfactant micelles change upon the addition of clay nanoparticles. It is seen that, in the presence of the nanoplates, the zero-shear viscosity of the system η0 increases by an order of magnitude and the frequency region of the elastic response G ' > G " expands but the value of the storage modulus G ' remains almost unchanged. The observed changes can be explained by the incorporation of the nanoplates into the network of the interlaced surfactant micellar chains as multifunctional physical crosslinks between the micelles. This incorporation may occur by the attachment of energy unfavorable semispherical ends of wormlike micelles to the layer of surfactants on the surface of the particles, as was shown in recent theoretical and experimental studies and computer simulation using particles of different nature [17, 19, 20, 27, 38–40]. The binding of the micelles with clay nanoparticles slows down their reptation, which leads to an increase in the viscosity of the system during flow (Fig. 2b) and to a decrease of the nonelastic response (loss modulus) of the network under oscillatory shear (Fig. 2a). It should be noted that at high shear rates (Fig. 2b) during the extension of chains along the direction of deformation the value of viscosity does not depend on the presence of the particles. This can be explained by breakage of the bonds of micelles with particles under these conditions. A weak effect of the nanoparticles on the storage modulus of the system is associated with a small number of new elastically active entanglements formed by the nanoparticles in comparison with the total number of entanglements formed by the interlaced chains, as was earlier demonstrated for spherical nanoparticles [41].

Therefore, it is shown that bentonite clay nanoplates can effectively increase viscosity and expand the region of the elastic response of the network of entangled micellar chains of surfactants. We assume that this effect results from the binding of the ends of wormlike micelles to the surface of the nanoplates covered with the surfactant layer.

Structure

The structure of the nanocomposite network was studied by small-angle neutron scattering. For the interpretation of the results, the scattering curves of the nanocomposite network were compared to the curves of scattering from the nanoparticles in the micellar network which were obtained by the contrast variation method and the scattering curves for the micellar network without the clay (Fig. 3).

Fig. 3.
figure 3

(1, 2) Small-angle neutron scattering curves of the nanocomposite network of wormlike surfactant micelles containing 0.044 mol/L OAB, 0.004 mol/L SDS, and 0.04 vol % bentonite clay nanoplates in (1) D2O and (2) D2O/H2O mixture (volume parts, 15/85) which reveals scattering from clay nanoplates only as well as (3) the small-angle neutron scattering curve of the corresponding micellar network of OAB/SDS without the clay in D2O.

Full size image

It follows from Fig. 3 that the curve of scattering from the bentonite clay nanoparticles in the region of medium q has a slope of q2 which is characteristic for randomly orientated platelike objects [42]. In the region of small q values, a small deviation from this slope can be observed which indicates the interaction of charged nanoplates with each other (a weak structural peak [42]). For the micellar network without the clay the dependence of q−1 traditional for cylindrical objects is observed in the region of small q values. There is no structural peak of electrostatic interaction which is associated with a relatively weak charge of OAB/SDS micellar chains [27] containing just 10% anionic surfactant.

As for the curve of scattering from the nanocomposite network in deuterated water, it is close to the scattering curve of the nanoplates in the region of small q (which characterizes large scattering objects), while, in the region of large q (which characterizes small scattering objects), it agrees with the curve of scattering from the micellar network. Therefore, it can be assumed that upon the addition of nanoparticles the micellar chains retain the local cylindrical structure and the nanoparticles are uniformly distributed over the network; i.e., there is no additional structuring or strong electrostatic interaction between the nanoplates in the network.

The micellar network before the addition of the nanoplates and the nanocomposite network were visualized by cryo-TEM. It follows from Figs. 4a and 4b that, in both systems, the surfactant forms wormlike micelles with a micron length which interlace and form a dense network of entanglements.

Fig. 4.
figure 4

Cryo-TEM images of (a) the micellar network without nanoparticles and (b) the corresponding nanocomposite network containing 0.044 mol/L OAB, 0.004 mol/L SDS, and 0.04 vol % bentonite clay nanoplates as well as (c) the schematic representation of nanocomposite network consisting of micellar chains and clay nanoplates and the schematic representation of attachment of a micelle to a particle (crosslink formation). The arrows in (b) indicate the regions of attachment of the micellar chains to the surface of the particles.

Full size image

Bentonite clay nanoplates with sizes of 100–200 nm are observed in the cryo-TEM image of the nanocomposite network (Fig. 4b). Note that the network of interlaced micelles is not deformed near the nanoparticles although the size of the latter is much larger than the size of the unit cell of the network. This can be explained by the fact that owing the ability for rearrangement and self-organization the network of living micelles “adapts” to the nanoparticles. The image clearly shows points (denoted by the arrows in Fig. 4b), in which the micelles attach by the end parts to the surface of the nanoplates covered by the surfactant shell; this confirms the earlier proposed model for the interaction of wormlike micelles with nanoparticles [17, 27, 40, 43]. To the best of our knowledge, crosslinks between nanoparticles and micellar chains were earlier experimentally demonstrated only for the network filled with spherical silica nanoparticles [19, 41]. This binding provides explanation for the increase in the zero-shear viscosity, as shown above.

Let us compare the size of the unit cell of the network ξ from the rheological data and the results of cryo-TEM studies. The value of ξ calculated from the elasticity modulus as \(\xi = {{\left( {\frac{{kT}}{{{{G}_{0}}}}} \right)}^{{1/3}}}\) [10] is 80 nm. The density of the network in the cryo-TEM images seems to be much higher than the calculated value (Fig. 5). This may be associated with the fact that we observe a two-dimensional picture from several layers of the network which visually increases the density of the entanglement network.

Fig. 5.
figure 5

Size of the unit cell of the network ξ calculated from the cryo-TEM images of the nanocomposite network containing 0.044 mol/L OAB, 0.004 mol/L SDS, and 0.04 vol % bentonite clay nanoplates.

Full size image

Thus, the clay nanoplates are uniformly distributed in the network and do not deform it owing to the rearrangement of living micellar chains. The points of crosslinking of wormlike micelles and clay nanoplates which provide the increase in the viscosity of the systems under study are visualized.

Role of the Concentration of Nanoparticles

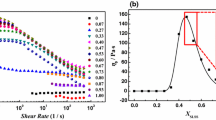
Let us consider how the rheological properties change with increasing amount of the added nanoparticles. The value of the zero-shear viscosity was determined through approximation of the dependences of viscosity on the shear rate using the Carreau model [44, 45]. As is seen from Fig. 6a, with an increase in the concentration of bentonite from 0 to 0.04 vol % the zero-shear viscosity first grows intensely and then the growth noticeably weakens. Here, the value of the plateau storage modulus remains almost unchanged (Fig. 6c).

Fig. 6.
figure 6

Dependence of (a) zero-shear viscosity, (b) terminal relaxation time, and (c) plateau storage modulus on the concentration of bentonite clay nanoparticles in networks containing 0.044 mol/L OAB and 0.004 mol/L SDS.

Full size image

Figure 6b presents the dependence of the terminal relaxation time on the concentration of bentonite. To estimate the terminal relaxation time in this system, the inverse value of the shear rate, at which transition from the plateau of viscosity to the drop region is observed in the graph of the dependence of viscosity on the shear rate, was calculated. It is known [46, 47] that this transition occurs at the frequency that corresponds to the intersection of the frequency dependences of the storage modulus G ' and the loss modulus G " [48]. In our case, the corresponding shear rate was determined via approximation using the Carreau model (Fig. 2b) [44, 45]. This method for estimation of the terminal relaxation time is based on the fact that the Cox–Merz rule is fulfilled for the system under study like for most solutions of wormlike surfactant micelles [46, 47]; i.e., the frequency dependence of the complex viscosity modulus is in good agreement with the dependence of viscosity on the shear rate (Fig. 2b). Therefore, estimation of the terminal relaxation time from the dependence of viscosity on the shear rate corresponds to estimation of this relaxation time from the frequency dependence of the storage and loss moduli.

It was shown (Fig. 6b) that the character of the dependence of the relaxation time on the concentration of clay nanoparticles Cn generally repeats the character of the dependence of viscosity on Cn, which is consistent with the formula η = G0τ [10] valid for most viscoelastic solutions of wormlike surfactant micelles. Thus, this ratio is also valid for the nanocomposite system.

Hence, the significant increase in viscosity which is accompanied by an increase in the relaxation time can be explained by the growth in the number of crosslinks between the nanoplates and wormlike surfactant micelles and slowdown of the reptation of the micelles at Cn from 0 to 0.04 vol %.

At higher concentrations Cn the effect of the nanoparticles on the rheological parameters weakens noticeably. The attainment of saturation by the rheological characteristics with an increase in the concentration of nanoparticles Cn was earlier predicted within the interaction model proposed by N.J. Wagner [17] and was experimentally observed upon adding silica nanoparticles to the network of wormlike micelles of cationic [17] and anionic surfactants [20] as well as upon adding submicron magnetite particles to the micellar network of the cationic surfactant [43]. In this work, this effect was first observed for a system with nonspherical nanoparticles. The reason for this effect can be explained by the fact that, at a certain concentration of bentonite, all the end parts of the micelles are bound to the surface of the nanoparticles; as a result, further increase in the amount of the nanoparticles does not induce the formation of additional crosslinks but leads to the redistribution of the end-caps of the micelles between the nanoparticles which weakly affects the viscosity and relaxation time. Note that, in this system, saturation is attained at lower concentrations of clay nanoparticles in comparison with spherical silica nanoparticles [17, 20]. This makes it possible to assume that much more micellar chains attach to one nanoplate than to a spherical nanoparticle.

Let us estimate the number of the end-caps of the micelles attached to one nanoparticle in the network under saturation when all the ends of the micelles are attached to clay nanoplates. The total number of the end-caps of micellar chains can be calculated knowing the concentration of micelles in the network. For this purpose, let us determine the average length of the micelles L from the rheological data using the Granek–Cates formula [37]

$$\frac{L}{{{{l}_{e}}}} \approx \frac{{{{G}_{0}}}}{{G_{{{\text{min}}}}^{{''}}}},$$

where G0 is the plateau storage modulus, \(G_{{{\text{min}}}}^{{''}}\) is the minimum loss modulus in the region of the plateau storage modulus (Fig. 2a), and le is the contour length of the micelle between two entanglements.

It is found that the average length of the micelles is 2000 nm. Taking into account these data and knowing the weight of the surfactants in solution and the volume of one surfactant molecule, it is possible to estimate the concentration of the micelles in the network as 3.5 × 1017 1/L. Consequently, the concentration of the end-caps will twice as much, 7 × 1017 1/L. The amount of the clay nanoplates can be calculated knowing the concentration of the nanoplates and their average size (it is 100 nm according to [27]). The as-calculated concentration of the nanoplates is 1.1 × 1016 1/L. When the network is saturated with the nanoparticles about 60 ends of the micelles are attached to each nanoplate. Note that in the case of 30-nm silica nanoparticles no more than three end-caps of wormlike micelles are attached to one particle [41]. Therefore, the use of clay nanoplates with a large surface area (the plate size is 30–200 nm) in comparison with spherical silica nanoparticles (a diameter of 30 nm) makes it possible to increase the functionality of the crosslinks in the system by more than an order of magnitude. Assuming that the clay is uniformly distributed in the network the distance between the nanoparticles can be estimated as about 500 nm, which is several times shorter than the contour length of the micelles. This provides conditions for the attachment of all end-caps of the micelles to the clay particles.

In addition, the rheological data make it possible to assess the characteristic breaking time of wormlike micelles τbr (the time between the successive chain scission and recombination) from the frequency ω* of the minimum in the frequency dependence of the loss modulus \(G_{{{\text{min}}}}^{{''}}\) as τbr = 1/ω* [10, 36, 49]. The breaking time of the micelles τbr characterizes the intensity of renewal of the network owing to the reversible scission of living chains and determines the relaxation time of the system together with the reptation time of the micelles [2, 9]. Since the characteristic breaking time of wormlike micelles is usually 0.01–1 s [9, 27], the minimum of the loss modulus \(G_{{{\text{min}}}}^{{''}}\) often occurs in the region of 1–100 rad/s in the frequency dependence. The breaking time is 0.8 s for the network of the surfactant micelles without nanoparticles under study (Fig. 2a). Upon adding the clay the minimum of \(G_{{{\text{min}}}}^{{''}}\) shifts to lower frequencies (Fig. 2a) which provides evidence for an increase in the breaking time. In the nanocomposite system, the renewal of the network occurs not only owing to the reversible scission of the chains but also due to the reversible scission of the crosslinks. Therefore, the observed increase in the breaking time may be associated with the fact that the breaking time of crosslinks of the micelles with the nanoparticles is longer than the breaking time of the micelles.

Figure 7 presents the dependence of breaking time on the amount of nanoplates in the network. It is seen that in the region of the intense increase in the relaxation time (0–0.04 vol % clay), the breaking time increases in agreement with the increase in the number of crosslinks in the network. Thus, the increase in the relaxation time of the nanocomposite network can be explained by the formation of crosslinks with the breaking time longer than the one of the micelles. As a result, the micellar network strengthens. Note that if the breaking time of the crosslinks was shorter than the breaking time of the micelles, the effect of the addition of the nanoparticles would be insignificant.

Fig. 7.
figure 7

Dependence of breaking time characterizing the intensity of renewal of the network on the concentration of bentonite clay nanoparticles added to solution containing 0.044 mol/L OAB and 0.004 mol/L SDS.

Full size image

Our assumption about the role of the breaking time of the crosslinks in comparison with the breaking time of the micelles was not earlier discussed in literature. It can make a significant contribution to explanation of the effects of addition of nanoparticles to a micellar network because regularities of the change in the properties of nanocomposite micellar networks available in the literature cannot always be explained within the existing model [16].

Thus, nanocomposite networks of OAB/SDS micellar chains and natural bentonite clay nanoplates were created and studied in this work. It was shown that the nanoplates, acting as physical crosslinks, can effectively increase the zero-shear viscosity and expand the region of the elastic response of the network of the entangled micellar chains of surfactants. Nanoplates of natural bentonite clay are a promising filler for the networks of living micellar chains of surfactants, and the obtained nanocomposite networks based on eco-friendly components show promise for practical application, in particular, in cosmetics and oil production.