On the Parametric Stability of the Isosceles Triangular Libration Points in the Planar Elliptical Charged Restricted Three-body Problem

Abstract

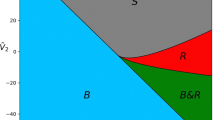
We consider the planar charged restricted elliptic three-body problem (CHRETBP). In this work we consider the parametric stability of the isosceles triangle equilibrium solution denoted by $L_{4}^{iso}$. We construct the boundary surfaces of the stability/instability regions in the space of the parameters $\mu$, $\beta$ and $e$, which are parameters of the mass, charges associated to the primaries and the eccentricity of the elliptic orbit, respectively.

APPENDIX A. COEFFICIENTS OF HAMILTONIAN FUNCTIONS FOR THE CASE OF COMBINED RESONANCE $$\omega_{1}-\omega_{2}=0$$

Coeficientes of $\mathcal{H}_{1}$ and $\mathcal{H}_{2}$

$$\displaystyle h^{(1)}_{2000}=\frac{-3\sqrt{8\beta_{0}^{4}+10\beta_{0}^{2}-3}}{4\beta_{0}\Delta_{1}^{7/2}\Delta_{2}^{3/2}}((-80\beta_{0}^{8}+992\beta_{0}^{6}-3160\beta_{0}^{4}+2040\beta_{0}^{2}-333\beta_{1}+4\beta_{0}(16\beta_{0}^{8}-164\beta_{0}^{6}+172\beta_{0}^{4}$$

$$\displaystyle-69\beta_{0}^{2}+9)\cos\nu),$$

$$\displaystyle h^{(1)}_{1100}=\frac{-\sqrt{-64\beta_{0}^{8}+496\beta_{0}^{6}+600\beta_{0}^{4}-396\beta_{0}^{2}+54}}{4\beta_{0}\Delta_{2}^{7/2}\Delta_{2}^{3/2}}\left((2(80\beta_{0}^{6}-748\beta_{0}^{4}+960\beta_{0}^{2}-171)\beta_{1}+\beta_{0}(16\beta_{0}^{6}+620\beta_{0}^{4}\right.$$

$$\displaystyle\left.-552\beta_{0}^{2}+99)\cos\nu)\right),$$

$$\displaystyle h^{(1)}_{1010}=\frac{\sqrt{-32\beta_{0}^{8}+248\beta_{0}^{6}+300\beta_{0}^{4}-198\beta_{0}^{2}+27}}{2\beta_{0}\Delta_{1}^{5/2}\Delta_{2}^{3/2}}\left((\beta_{0}(40\beta_{0}^{4}-22\beta_{0}^{2}+3)\cos\nu-2(16\beta_{0}^{4}-86\beta_{0}^{2}+33)\beta_{1})\right)$$

$$\displaystyle h^{(1)}_{1001}=\frac{\sqrt{16\beta_{0}^{4}+20\beta_{0}^{2}-6}}{2\beta_{0}\Delta_{1}^{5/2}\Delta_{2}^{3/2}}\left(((-56\beta_{0}^{6}+484\beta_{0}^{4}-642\beta_{0}^{2}+135)\beta_{1}+\beta_{0}(16\beta_{0}^{6}-196\beta_{0}^{4}+156\beta_{0}^{2}-27)\cos\nu)\right),$$

$$\displaystyle h^{(1)}_{0200}=\frac{-\left(\left(80\beta_{0}^{8}-1360\beta_{0}^{6}+6072\beta_{0}^{4}-1764\beta_{0}^{2}+81\right)\beta_{1}+2\beta_{0}(16\beta_{0}^{8}-100\beta_{0}^{6}-1236\beta_{0}^{4}+639\beta_{0}^{2}-81)\cos\nu\right)}{2\beta_{0}\Delta_{1}^{3}\Delta_{2}},$$

$$\displaystyle h^{(1)}_{0110}=-\frac{3\sqrt{2}\left(\left(8\beta_{0}^{6}-84\beta_{0}^{4}+106\beta_{0}^{2}-21\right)\beta_{1}+\beta_{0}\left(40\beta_{0}^{4}-22\beta_{0}^{2}+3\right)\cos\nu\right)}{\beta_{0}\left(2\beta_{0}^{2}+3\right)^{2}\left(4\beta_{0}^{2}-1\right)},$$

$$\displaystyle h^{(1)}_{0101}=\frac{\sqrt{-16\beta_{0}^{6}+148\beta_{0}^{4}-72\beta_{0}^{2}+9}\left(2\left(16\beta_{0}^{4}-98\beta_{0}^{2}+15\right)\beta_{1}+\beta_{0}\left(8\beta_{0}^{4}+82\beta_{0}^{2}-21\right)\cos\nu\right)}{2\beta_{0}\left(2\beta_{0}^{2}+3\right)^{2}\left(4\beta_{0}^{2}-1\right)^{3/2}},$$

$$\displaystyle h^{(1)}_{0020}=\frac{\left(4\beta_{0}^{4}-32\beta_{0}^{2}+9\right)\beta_{1}+\left(2\beta_{0}^{3}-8\beta_{0}^{5}\right)\cos\nu}{-8\beta_{0}^{5}-10\beta_{0}^{3}+3\beta_{0}},$$

$$\displaystyle h^{(1)}_{0011}=\frac{\sqrt{-16\beta_{0}^{6}+148\beta_{0}^{4}-72\beta_{0}^{2}+9}\left(2\left(4\beta_{0}^{2}-5\right)\beta_{1}+\left(\beta_{0}-4\beta_{0}^{3}\right)\cos\nu\right)}{\sqrt{2}\beta_{0}\left(2\beta_{0}^{2}+3\right)\left(4\beta_{0}^{2}-1\right)^{3/2}},$$

$$\displaystyle h^{(1)}_{0002}=\frac{3\left(\left(4\beta_{0}^{4}-20\beta_{0}^{2}+5\right)\beta_{1}+2\beta_{0}\left(4\beta_{0}^{2}-1\right)\cos\nu\right)}{2\beta_{0}\left(8\beta_{0}^{4}+10\beta_{0}^{2}-3\right)},$$

$$\displaystyle h^{(2)}_{2000}=\frac{1}{4\beta_{0}^{2}\left(2\beta_{0}^{2}+3\right)^{7/2}\left(4\beta_{0}^{2}-1\right)^{5/2}}\left(3\sqrt{8\beta_{0}^{4}+10\beta_{0}^{2}-3}(256\beta_{0}^{12}+640\beta_{0}^{11}\beta_{2}-640\beta_{0}^{10}\beta_{1}^{2}-2688\beta_{0}^{10}\right.$$

$$\displaystyle\left.-8096\beta_{0}^{9}\beta_{2}+7248\beta_{0}^{8}\beta_{1}^{2}+3408\beta_{0}^{8}+27264\beta_{0}^{7}\beta_{2}-19296\beta_{0}^{6}\beta_{1}^{2}-1792\beta_{0}^{6}-22640\beta_{0}^{5}\beta_{2}\right.$$

$$\displaystyle\left.+4152\beta_{0}^{4}\beta_{1}^{2}+420\beta_{0}^{4}+6744\beta_{0}^{3}\beta_{2}+1872\beta_{0}^{2}\beta_{1}^{2}-36\beta_{0}^{2}-666\beta_{0}\beta_{2}-459\beta_{1}^{2}+4(1-4\beta_{0}^{2})^{2}(4\beta_{0}^{6}\right.$$

$$\displaystyle\left.-40\beta_{0}^{4}+33\beta_{0}^{2}-9)\beta_{0}^{2}\cos 2\nu-2(320\beta_{0}^{10}-4048\beta_{0}^{8}+13632\beta_{0}^{6}-11320\beta_{0}^{4}+3372\beta_{0}^{2}\right.$$

$$\displaystyle\left.-333)\beta_{0}\beta_{1}\cos\nu)\right),$$

$$\displaystyle h^{(2)}_{1100}=\frac{1}{4\beta_{0}^{2}\left(2\beta_{0}^{2}+3\right)^{7/2}\left(4\beta_{0}^{2}-1\right)^{5/2}}\left(\sqrt{-64\beta_{0}^{8}+496\beta_{0}^{6}+600\beta_{0}^{4}-396\beta_{0}^{2}+54}(64\beta_{0}^{10}-1280\beta_{0}^{9}\beta_{2}\right.$$

$$\displaystyle\left.+1280\beta_{0}^{8}\beta_{1}^{2}+2464\beta_{0}^{8}+12288\beta_{0}^{7}\beta_{2}-10080\beta_{0}^{6}\beta_{1}^{2}-2828\beta_{0}^{6}-18352\beta_{0}^{5}\beta_{2}+6360\beta_{0}^{4}\beta_{1}^{2}+948\beta_{0}^{4}\right.$$

$$\displaystyle\left.+6576\beta_{0}^{3}\beta_{2}-1008\beta_{0}^{2}\beta_{1}^{2}-99\beta_{0}^{2}-684\beta_{0}\beta_{2}+54\beta_{1}^{2}+(1-4\beta_{0}^{2})^{2}(4\beta_{0}^{4}+156\beta_{0}^{2}-99)\beta_{0}^{2}\cos 2\nu\right.$$

$$\displaystyle\left.+4(320\beta_{0}^{8}-3072\beta_{0}^{6}+4588\beta_{0}^{4}-1644\beta_{0}^{2}+171)\beta_{0}\beta_{1}\cos\nu)\right),$$

$$\displaystyle h^{(2)}_{1010}=-\frac{1}{2\beta_{0}^{2}\left(8\beta_{0}^{4}+10\beta_{0}^{2}-3\right)^{5/2}}\left(\sqrt{-32\beta_{0}^{8}+248\beta_{0}^{6}+300\beta_{0}^{4}-198\beta_{0}^{2}+27}(160\beta_{0}^{8}+256\beta_{0}^{7}\beta_{2}\right.$$

$$\displaystyle\left.-256\beta_{0}^{6}\beta_{1}^{2}-128\beta_{0}^{6}-1440\beta_{0}^{5}\beta_{2}+1152\beta_{0}^{4}\beta_{0}^{2}+34\beta_{0}^{4}+872\beta_{0}^{3}\beta_{2}+132\beta_{0}^{2}\beta_{1}^{2}-3\beta_{0}^{2}-132\beta_{0}\beta_{2}\right.$$

$$\displaystyle\left.-126\beta_{1}^{2}+(10\beta_{0}^{2}-3)(1-4\beta_{0}^{2})^{2}\beta_{0}^{2}\cos 2\nu-4(64\beta_{0}^{6}-360\beta_{0}^{4}+218\beta_{0}^{2}-33)\beta_{0}\beta_{1}\cos\nu)\right),$$

$$\displaystyle h^{(2)}_{1001}=\frac{1}{\sqrt{2}\beta_{0}^{2}\left(8\beta_{0}^{4}+10\beta_{0}^{2}-3\right)^{2}}\left(-64\beta_{0}^{10}-448\beta_{0}^{9}\beta_{2}+448\beta_{0}^{8}\beta_{1}^{2}+800\beta_{0}^{8}-27\beta_{0}^{2}-3288\beta_{0}^{6}\beta_{1}^{2}-820\beta_{0}^{6}\right.$$

$$\displaystyle\left.-6104\beta_{0}^{5}\beta_{2}+2388\beta_{0}^{4}\beta_{1}^{2}++264\beta_{0}^{4}+2364\beta_{0}^{3}\beta_{2}-81\beta_{1}^{2}+3984\beta_{0}^{7}\beta_{2}-270\beta_{0}\beta_{2}-90\beta_{0}^{2}\beta_{1}^{2}\right.$$

$$\displaystyle\left.-(1-4\beta_{0}^{2})^{2}(4\beta_{0}^{4}-48\beta_{0}^{2}+27)\beta_{0}^{2}\cos 2\nu+2(224\beta_{0}^{8}-1992\beta_{0}^{6}+3052\beta_{0}^{4}-1182\beta_{0}^{2}+135)\beta_{0}\beta_{1}\cos\nu\right),$$

$$\displaystyle h^{(2)}_{0200}=\frac{1}{2(2\beta_{0}^{2}+3)^{3}(\beta_{0}-4\beta_{0}^{3})^{2}}\left(128\beta_{0}^{12}-640\beta_{0}^{11}\beta_{2}+640\beta_{0}^{10}\beta_{1}^{2}-832\beta_{0}^{10}+7584\beta_{0}^{6}-8784\beta_{0}^{8}\beta_{1}^{2}\right.$$

$$\displaystyle\left.-9688\beta_{0}^{8}-51296\beta_{0}^{7}\beta_{2}+30000\beta_{0}^{6}\beta_{1}^{2}+11040\beta_{0}^{9}\beta_{2}+26256\beta_{0}^{5}\beta_{2}-8712\beta_{0}^{4}\beta_{1}^{2}-1926\beta_{0}^{4}\right.$$

$$\displaystyle\left.-4176\beta_{0}^{3}\beta_{2}-540\beta_{0}^{2}\beta_{1}^{2}+162\beta_{0}^{2}+162\beta_{0}\beta_{2}+243\beta_{1}^{2}+2(1-4\beta_{0}^{2})^{2}(4\beta_{0}^{6}-24\beta_{0}^{4}-315\beta_{0}^{2}\right.$$

$$\displaystyle\left.+81)\beta_{0}^{2}\cos 2\nu+2(320\beta_{0}^{10}-5520\beta_{0}^{8}+25648\beta_{0}^{6}-13128\beta_{0}^{4}+2088\beta_{0}^{2}-81)\beta_{0}\beta_{1}\cos\nu\right),$$

$$\displaystyle h^{(2)}_{0110}=\frac{1}{\beta_{0}^{2}(8\beta_{0}^{4}+10\beta_{0}^{2}-3)^{2}}\left(3\sqrt{2}(-64\beta_{0}^{9}\beta_{2}+64\beta_{0}^{8}\beta_{1}^{2}+160\beta_{0}^{8}+34\beta_{0}^{4}+688\beta_{0}^{7}\beta_{2}-128\beta_{0}^{6}-616\beta_{0}^{6}\beta_{1}^{2}\right.$$

$$\displaystyle\left.-1016\beta_{0}^{5}\beta_{2}+276\beta_{0}^{4}\beta_{1}^{2}+380\beta_{0}^{3}\beta_{2}-66\beta_{0}^{2}\beta_{1}^{2}-3\beta_{0}^{2}+9\beta_{1}^{2}+(10\beta_{0}^{2}-3)(1-4\beta_{0}^{2})^{2}\beta_{0}^{2}\cos 2\nu\right.$$

$$\displaystyle\left.-42\beta_{0}\beta_{2}+2(32\beta_{0}^{8}-344\beta_{0}^{6}+508\beta_{0}^{4}-190\beta_{0}^{2}+21)\beta_{0}\beta_{1}\cos\nu),\right)$$

$$\displaystyle h^{(2)}_{0101}=\frac{1}{2\beta_{0}^{2}(2\beta_{0}^{2}+3)^{2}(4\beta_{0}^{2}-1)^{5/2}}\left(\sqrt{-16\beta_{0}^{6}+148\beta_{0}^{4}-72\beta_{0}^{2}+9}(32\beta_{0}^{8}+21\beta_{0}^{2}-256\beta_{0}^{7}\beta_{2}+256\beta_{0}^{6}\beta_{1}^{2}\right.$$

$$\displaystyle\left.+320\beta_{0}^{6}+1632\beta_{0}^{5}\beta_{2}-960\beta_{0}^{4}\beta_{1}^{2}-166\beta_{0}^{4}-632\beta_{0}^{3}\beta_{2}+84\beta_{0}^{2}\beta_{1}^{2}+(2\beta_{0}^{2}+21)(1-4\beta_{0}^{2})^{2}\beta_{0}^{2}\cos 2\nu\right.$$

$$\displaystyle\left.+60\beta_{0}\beta_{2}+18\beta_{1}^{2}+4(64\beta_{0}^{6}-408\beta_{0}^{4}+158\beta_{0}^{2}-15)\beta_{0}\beta_{1}\cos\nu)\right),$$

$$\displaystyle h^{(2)}_{0020}=\frac{1}{(2\beta_{0}^{2}+3)(\beta_{0}-4\beta_{0}^{3})^{2}}\left(-32\beta_{0}^{8}-32\beta_{0}^{7}\beta_{2}+32\beta_{0}^{6}\beta_{1}^{2}+16\beta_{0}^{6}+264\beta_{0}^{5}\beta_{2}-2\beta_{0}^{4}-228\beta_{0}^{4}\beta_{1}^{2}-136\beta_{0}^{3}\beta_{2}\right.$$

$$\displaystyle\left.-48\beta_{0}^{2}\beta_{1}^{2}+18\beta_{0}\beta_{2}+27\beta_{1}^{2}-2(1-4\beta_{0}^{2})^{2}\beta_{0}^{4}\cos 2\nu+2(16\beta_{0}^{6}-132\beta_{0}^{4}+68\beta_{0}^{2}-9)\beta_{0}\beta_{1}\cos\nu\right),$$

$$\displaystyle h^{(2)}_{0011}=\frac{1}{\sqrt{2}\beta_{0}^{2}(2\beta_{0}^{2}+3)(4\beta_{0}^{2}-1)^{5/2}}\left(\sqrt{-16\beta_{0}^{6}+148\beta_{0}^{4}-72\beta_{0}^{2}+9}(16\beta_{0}^{6}+6\beta_{1}^{2}-64\beta_{0}^{4}\beta_{0}^{2}+64\beta_{0}^{5}\beta_{2}\right.$$

$$\displaystyle\left.-8\beta_{0}^{4}-96\beta_{0}^{3}\beta_{2}+24\beta_{0}^{2}\beta_{1}^{2}+\beta_{0}^{2}+20\beta_{0}\beta_{2}+(1-4\beta_{0}^{2})^{2}\beta_{0}^{2}\cos 2\nu-4(16\beta_{0}^{4}-24\beta_{0}^{2}+5)\beta_{0}\beta_{1}\cos\nu)\right),$$

$$\displaystyle h^{(2)}_{0002}=-\frac{3}{2(2\beta_{0}^{2}+3)(\beta_{0}-4\beta_{0}^{3})^{2}}\left(-32\beta_{0}^{7}\beta_{2}+32\beta_{0}^{6}\beta_{1}^{2}+32\beta_{0}^{6}+168\beta_{0}^{5}\beta_{2}-16\beta_{0}^{4}-100\beta_{0}^{4}\beta_{1}^{2}-80\beta_{0}^{3}\beta_{2}\right.$$

$$\displaystyle\left.+12\beta_{0}^{2}\beta_{1}^{2}+2\beta_{0}^{2}+10\beta_{0}\beta_{2}+3\beta_{1}^{2}+2(1-4\beta_{0}^{2})^{2}\beta_{0}^{2}\cos 2\nu+2(16\beta_{0}^{6}-84\beta_{0}^{4}+40\beta_{0}^{2}-5)\beta_{0}\beta_{1}\cos\nu\right).$$

where $\Delta_{1}=\sqrt{-32\beta_{0}^{8}+248\beta_{0}^{6}+300\beta_{0}^{4}-198\beta_{0}^{2}+27}$, $\Delta_{2}=\sqrt{-\left(2\beta_{0}^{2}+3\right)\left(16\beta_{0}^{6}-148\beta_{0}^{4}+72\beta_{0}^{2}-9\right)^{3}}$.

APPENDIX B. COEFFICIENTS OF HAMILTONIAN FUNCTIONS FOR THE CASE OF BASIC RESONANCE $$2\omega_{2}=1$$

Coefficients of $\mathrm{H_{2}}$,$\mathrm{H_{3}}$ and $\mathrm{H_{4}}$

$$\displaystyle\mathrm{h}^{(2)}_{2000}=-\frac{3}{4\beta_{0}^{4}}\left(\beta_{0}^{2}\cos^{2}\nu+2\beta_{0}\beta_{1}\cos\nu-2\beta_{0}\beta_{2}+3\beta_{1}^{2}\right),$$

$$\displaystyle\mathrm{h}^{(2)}_{1100}=\frac{1}{2\beta_{0}^{4}\left(4\beta_{0}^{2}-1\right)^{5/2}}\sqrt{3}\sqrt{-4\beta_{0}^{6}+49\beta_{0}^{4}-24\beta_{0}^{2}+3}\left(16\beta_{0}^{6}\cos^{2}\nu-\beta_{0}^{5}\beta_{2}+\beta_{0}^{5}\beta_{1}\cos\nu+16\beta_{0}^{4}\beta_{1}^{2}\right.$$

$$\displaystyle\left.-8\beta_{0}^{4}\cos^{2}\nu-12\beta_{0}^{3}\beta_{1}\cos\nu+12\beta_{0}^{3}\beta_{2}-18\beta_{0}^{2}\beta_{1}^{2}+\beta_{0}^{2}\cos^{2}\nu+2\beta_{0}\beta_{1}\cos\nu-2\beta_{0}\beta_{2}+3\beta_{1}^{2}\right),$$

$$\displaystyle\mathrm{h}^{(2)}_{0200}=-\frac{3}{4\beta_{0}^{4}}\left(4\beta_{0}^{4}\cos^{2}\nu-\beta_{0}^{2}\cos^{2}\nu-2\beta_{0}\beta_{1}\cos\nu+2\beta_{0}\beta_{2}-3\beta_{1}^{2}\right),$$

$$\displaystyle\mathrm{h}^{(3)}_{2000}=\frac{9}{4\beta_{0}^{5}}\left(\beta_{0}^{3}\cos^{3}\nu+2\beta_{0}^{2}\beta_{1}\cos^{2}\nu-2\beta_{0}^{2}\beta_{2}\cos\nu+2\beta_{0}^{2}\beta_{3}+3\beta_{0}\beta_{1}^{2}\cos\nu\beta_{0}\beta_{1}\beta_{2}+4\beta_{1}^{3}\right),$$

$$\displaystyle\mathrm{h}^{(3)}_{1100}=\frac{3\sqrt{3}}{2\beta_{0}^{5}\left(4\beta_{0}^{2}-1\right)^{7/2}}\sqrt{-4\beta_{0}^{6}+49\beta_{0}^{4}-24\beta_{0}^{2}+3}\left(2\beta_{0}^{2}\left(2\beta_{0}^{2}-1\right)\left(1-4\beta_{0}^{2}\right)^{2}\beta_{3}+4\left(16\beta_{0}^{6}-30\beta_{0}^{4}\right.\right.$$

$$\displaystyle\left.\left.+10\beta_{0}^{2}-1\right)\beta_{1}^{3}+\beta_{0}\cos\nu\left(\beta_{0}\left(1-4\beta_{0}^{2}\right)^{2}\cos\nu\left(2\left(2\beta_{0}^{2}-1\right)\beta_{1}+\beta_{0}\left(4\beta_{0}^{2}-1\right)\cos\nu\right)\right.\right.$$

$$\displaystyle\left.\left.{-}2\beta_{0}\left(2\beta_{0}^{2}{-}1\right)\left(1{-}4\beta_{0}^{2}\right)^{2}\beta_{2}{+}\left(64\beta_{0}^{6}{-}\beta_{0}^{4}{+}30\beta_{0}^{2}{-}3\right)\beta_{1}^{2}\right){+}2\beta_{0}\left({-}64\beta_{0}^{6}{+}88\beta_{0}^{4}{-}30\beta_{0}^{2}{+}3\right)\beta_{1}\beta_{2}\right),$$

$$\displaystyle\mathrm{h}^{(3)}_{0200}=-\frac{9}{4\beta_{0}^{5}}\left(\beta_{0}\cos\nu\left(\beta_{0}\cos\nu\left(\left(\beta_{0}-4\beta_{0}^{3}\right)\cos\nu+2\beta_{1}\right)-2\beta_{0}\beta_{2}+3\beta_{1}^{2}\right)+\beta_{0}^{2}\beta_{3}-6\beta_{0}\beta_{1}\beta_{2}+4\beta_{1}^{3}\right),$$

$$\displaystyle\mathrm{h}^{(4)}_{2000}=-\frac{9}{\beta_{0}^{6}}\left(\beta_{0}^{4}\cos^{4}\nu+2\beta_{0}^{3}\beta_{1}\cos^{3}\nu+2\beta_{0}\cos\nu\left(\beta_{0}^{2}\beta_{3}-3\beta_{0}\beta_{1}\beta_{2}+2\beta_{1}^{3}\right)-\beta_{0}^{2}\cos^{2}\nu\left(2\beta_{0}\beta_{2}-3\beta_{1}^{2}\right)\right.$$

$$\displaystyle\left.+6\beta_{0}^{2}\beta_{1}\beta_{3}+\beta_{0}^{2}\left(3\beta_{2}^{2}-2\beta_{0}\beta_{4}\right)-12\beta_{0}\beta_{1}^{2}\beta_{2}+5\beta_{1}^{4}\right),$$

$$\displaystyle\mathrm{h}^{(4)}_{1100}=-\frac{6\sqrt{3}}{\beta_{0}^{6}\left(4\beta_{0}^{2}-1\right)^{9/2}}\sqrt{-4\beta_{0}^{6}+49\beta_{0}^{4}-24\beta_{0}^{2}+3}\left(-\beta_{0}^{2}\left(1-4\beta_{0}^{2}\right)^{2}\cos^{2}\nu\left(\left(-16\beta_{0}^{4}+18\beta_{0}^{2}-3\right)\beta_{1}^{2}\right.\right.$$

$$\displaystyle\left.\left.+2\beta_{0}\left(8\beta_{0}^{4}-6\beta_{0}^{2}+1\right)\beta_{2}\right)+2\beta_{0}^{2}\left(1-4\beta_{0}^{2}\right)^{2}\left(16\beta_{0}^{4}-\beta_{0}^{2}+3\right)\beta_{1}\beta_{3}+\beta_{0}^{4}\left(1-4\beta_{0}^{2}\right)^{4}\cos^{4}\nu\right.$$

$$\displaystyle\left.+2\beta_{0}^{3}\left(2\beta_{0}^{2}-1\right)\left(4\beta_{0}^{2}-1\right)^{3}\beta_{1}\cos^{3}\nu+\beta_{0}\left(4\beta_{0}^{2}-1\right)\cos\nu\left(\beta_{0}^{2}\left(2\beta_{0}^{2}-1\right)\left(1-4\beta_{0}^{2}\right)^{2}\beta_{3}+\left(32\beta_{0}^{6}\right.\right.\right.$$

$$\displaystyle\left.\left.\left.-60\beta_{0}^{4}+20\beta_{0}^{2}-2\right)\beta_{1}^{3}+\beta_{0}\left(-64\beta_{0}^{6}+88\beta_{0}^{4}-30\beta_{0}^{2}+3\right)\beta_{1}\beta_{2}\right)+\left(\beta_{0}-4\beta_{0}^{3}\right)^{2}\left(\left(16\beta_{0}^{4}-\beta_{0}^{2}+3\right)\beta_{2}^{2}\right.\right.$$

$$\displaystyle\left.\left.-2\beta_{0}\left(8\beta_{0}^{4}-6\beta_{0}^{2}+1\right)\beta_{4}\right)+\left(256\beta_{0}^{8}-704\beta_{0}^{6}+350\beta_{0}^{4}-70\beta_{0}^{2}+5\right)\beta_{1}^{4}-12\beta_{0}\left(64\beta_{0}^{8}-136\beta_{0}^{6}\right.\right.$$

$$\displaystyle\left.\left.+70\beta_{0}^{4}-14\beta_{0}^{2}+1\right)\beta_{1}^{2}\beta_{2}\right),$$

$$\displaystyle\mathrm{h}^{(4)}_{0200}=-\frac{9}{\beta_{0}^{6}}\left(4\beta_{0}^{6}\cos^{4}\nu-\beta_{0}^{4}\cos^{4}\nu-2\beta_{0}^{3}\beta_{1}\cos^{3}\nu+2\beta_{0}^{3}\beta_{2}\cos^{2}\nu-\beta_{0}^{3}\beta_{3}\cos\nu+2\beta_{0}^{3}\beta_{4}\right.$$

$$\displaystyle\left.-3\beta_{0}^{2}\beta_{1}^{2}\cos^{2}\nu+6\beta_{0}^{2}\beta_{1}\beta_{2}\cos\nu-6\beta_{0}^{2}\beta_{1}\beta_{3}-3\beta_{0}^{2}\beta_{2}^{2}-\beta_{0}\beta_{1}^{3}\cos\nu+12\beta_{0}\beta_{1}^{2}\beta_{2}-5\beta_{1}^{4}\right).$$

$$\displaystyle h^{(1)}_{2000}=\frac{\sqrt{3}}{28\beta_{0}^{5}-11\beta_{0}^{3}+\beta_{0}}\left(2\left(6\beta_{0}^{4}-21\beta_{0}^{2}+5\right)\beta_{1}+\beta_{0}\left(4\beta_{0}^{4}+3\beta_{0}^{2}-1\right)\cos\nu\right),$$

$$\displaystyle h^{(1)}_{1100}=\frac{8\sqrt[4]{3}}{\beta_{0}\left(4\beta_{0}^{2}-1\right)\sqrt{7\beta_{0}^{2}-1}\sqrt{37\beta_{0}^{2}-9}}\left(2\left(5\beta_{0}^{4}-13\beta_{0}^{2}+3\right)\beta_{1}+\left(4\beta_{0}^{2}-1\right)\beta_{0}^{3}\cos\nu\right).$$