Abstract
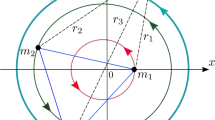
We present a geometric interpretation of the spectral stability of the triangular libration points in the charged three-body problem. We obtain that the spectral stability varies with the position of the center of mass of the three charges with respect to the circumcenter of the triangle configuration, which does not depend directly of the charges. If the center of mass is outside or on the circumference of a well defined radius ρ, then spectral stability occurs. In addition, we analyze the existence of resonances within the spectral region of stability under this geometric interpretation, determining resonance curves of order 2, 3, 4, . . ., some of them with multiple resonances.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Alfaro F., Perez-Chavela E.: Linear stability of relative equilibria in the charged three-body problem. J. Differ. Equ. 245(7), 1923–1944 (2008)
Hogan, E., Schaub, H.: Collinear invariant shapes for three-craft Coulomb formations. In: AAS/AIAA Astrodynamics Specialist Conference, Toronto, Canada, 2–5 August 2010. Paper no. AIAA-2010-7954
Hogan, E., Schaub, H.: Linear stability and shape analysis of spinning three-craft Coulomb formations. In: AAS Spaceflight Mechanics Meeting, New Orleans, Louisiana, 13–17 February 2011. Paper No. AAS 11-225-I
Hogan E., Schaub H.: Linear stability and shape analysis of spinning three-craft Coulomb formations. Celest. Mech. Dyn. Astron. 112, 131–148 (2012)
Hussein I., Schaub H.: Invariants shape solutions of the spinning three craft Coulomb tether problem. Celest. Mech. Dyn. Astron. 96(2), 137–157 (2006)
Ivanov A.P.: Investigation of stability of constant lagrange solutions of the unrestricted three-body problem. PMM 43(5), 787–795 (1979)
Kunitsyn, A.L.: Geometric interpretation of necessary conditions of stability of the triangular libration point of the general three-body problem. In: Celestial Mechanics, vol. 3, pp. 222–226. (in Russian) (1971)
Mansilla J.E.: Stability of Hamiltonian systems with three degrees of freedom and the three body-problem. Celest. Mech. Dyn. Astron. 94(3), 249–269 (2006)
Pérez-Chavela E., Saari D., Susin A., Yan Z.: Central configuration in the charged three body problem. Contemp. Math. 198, 137–155 (1996)
Routh, E.J.: On Laplace’s three particles, with a supplement on the stability of stead motion. In: Proceedings of London Mathematical Society, vol. 6 (1875)
Wintner A.: The Analytical Foundations of Celestial Mechanics. Princeton University Press, Princeton (1941)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Mansilla, J.E., Vidal, C. Geometric interpretation for the spectral stability in the charged three-body problem. Celest Mech Dyn Astr 113, 205–213 (2012). https://doi.org/10.1007/s10569-012-9405-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10569-012-9405-3