INTRODUCTION

The study of the electron density (ED) distribution is an important tool for the solution of theoretical and practical problems of the modern chemical science [1–3]. The high-resolution X-ray diffraction (XRD) studies make it possible to obtain the experimental ED distribution, calculate the electrostatic potential and energy of intra- and interatomic interactions in the crystal, reveal structure-forming factors determining the structure, and establish the fragments that weakly change in related compounds [4]. This study is especially important for the correlation of the properties of compounds to the structure. However, a number of requirements is imposed on the sample in order to carry out high-resolution XRD experiments, and it is rather labor consuming to obtain a suitable single crystal. This fact substantially restricts the experimental study of the ED in practically significant compounds. A compromise solution is to obtain the ED distribution in compounds from theoretical calculations by the density functional (DFT) method [5–7].

The procedure based on the invariom (invariant atom) was developed for the study of the ED distribution in organic and organoelement compounds with relatively light atoms (Periods 1–3) [8, 9]. This experimental–theoretical approach makes it possible to obtain the ED distribution on the basis of data of routine XRD studies and theoretical calculations. The improved method based on the determination of the molecular invariom was applied for the organometallic compounds [10–12]. The use of this method provides an information about the topology of the ED in molecules with good accuracy [13, 14]. However, the majority of studies in this area is devoted to the transferability of the topological characteristics in the coordination sphere of the metal atom [15–17].

Intramolecular weak nonvalent interactions are significant among structural features of many biologically active compounds for the determination of the molecular conformation and physicochemical properties manifested by the molecule [18]. Intramolecular nonvalent interactions in organometallic complexes are also important. For example, the C–F → Ln interactions are possible in the lanthanide complexes with the fluorinated ligands, due to which, in particular, these complexes are catalytically active [19, 20]. It is also significant that these interactions determine the thermal stability of the complexes [21, 22].

Some lanthanide complexes with hexafluoroisopropoxide ligands manifest the promising luminescence properties [23, 24]. Our recent study of the ED topology in the trimeric europium complex demonstrated numerous intramolecular interactions involving the fluorine atoms F···X (X = Eu, F, H, O) [25].

This work is devoted to the study of the principal possibility to obtain an information about the topological characteristics of the ED at the critical points (CP) corresponding to the interactions involving the fluorine atoms in the {\({\text{Yb}}_{{\text{2}}}^{{{\text{II}}}}\)(μ2-OCH(CF3)2)3(μ3-OCH(CF3)2)2YbIII(OCH(CF3)2)2(THF)(Et2O)} com-plex (I) using the molecular invariom model.

EXPERIMENTAL

The full optimization of the geometry of complex I was performed by the DFT method implemented in the Gaussian 09 [26] program package using the B3LYP hybrid functional. The 6-31 + G* basis set was used for the organic moiety [27–31], and the ECP28MWB pseudopotential was used for the lanthanide atoms [32]. The electron density function for the ECP (effective core potential) was calculated using the Molden2aim program.

The topological analysis of the theoretical function of the ED distribution obtained by the DFT calculation was performed using the AIMALL program [33].

The routine set of experimental XRD data was used for the experimental–theoretical refinement. The one-point calculation of an isolated molecule of complex I was performed by the DFT method (B3LYP/DZP) [34] using the Gaussian 09 program [26]. Then the complex molecule was placed in the pseudocubic cell (а = 30 Å). The structural amplitudes (sinθ/λ = 1.155 Å–1) were calculated using the Tonto program [35]. The populations of the spherically symmetric valent shell (Pval) and the multipole parameters (Plm) describing its deformation together with the corresponding expansion–compression coefficients (k, k') for each atom in complex I were obtained from the structural amplitudes for the cubic cell using the MoPro program [36]. The calculated values of Pval, Plm, k, and k' were used (but they themselves were not refined) for the refinement of the atomic coordinates and their thermal parameters by the experimental reflections of the routine data in the real symmetry of complex I. The topological analysis of the experimental–theoretical function of the ED distribution was performed using the WinXPRO program [37].

An analysis of the deformation electron density (DED) distribution in the region of nonvalent interactions between the fluorine atoms in complex I was performed using the MoPro [36] and Multiwfn v. 3.3.8 [38] programs.

RESULTS AND DISCUSSION

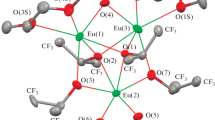
The crystal structure of complex I was determined by XRD and described in detail previously [23]. The molecular structure of the complex is presented in Fig. 1. An analysis of the geometric characteristics assumes (by analogy to the related europium complex [25]) that the structure contains many intramolecular nonvalent interactions involving the fluorine atoms.

Fig. 1.
figure 1

Molecular structure of complex I. Thermal ellipsoids are given with 30% probability. Hydrogen atoms are omitted for clarity.

Full size image

To check this hypothesis, we performed the quantum-chemical (DFT) study of complex I by the DFT method (B3LYP/6-31+G*, ECP28MWB) with geometry optimization. Then the model of complex I obtained by the DFT calculation will be named Iisol for convenience. The molecular invariom of complex I was simultaneously calculated using the known methodology, and the refinement was performed by the routine experimental data (Iinv). Thus, the experimental–theoretical ED distribution in complex Iinv was obtained. The molecular graphs for the Iisol and Iinv models demonstrating all interactions in the coordination sphere of the ytterbium atoms are presented in Fig. 2.

Fig. 2.
figure 2

(a) Theoretical (Iisol) and (b) experimental–theoretical (Iinv) molecular graphs of complex I. Only selected CP (3, –1) corresponding to the valent interactions and nonvalent contacts C–F → Ln in the coordination sphere of the ytterbium atoms are presented for clarity. Hydrogen atoms are omitted.

Full size image

It should be mentioned that the molecular invariom model more precisely reproduces the main geometric characteristics of complex I obtained by the routine XRD method than those calculated by the theoretical quantum-chemical DFT study (Table 1). The average deviation of the Yb–O and Yb···F bonds for Iinv is 0.003 Å, whereas for Iisol this value is 0.024 Å. The highest changes do not exceed 0.009 and 0.094 Å, respectively. Interestingly, in the cases of both Iisol and Iinv, the highest deviations from the XRD data are observed for the coordination bonds with the neutral solvents Yb(2)–O(8)THF and Yb(3)–O(9)EtOEt.

Table 1. Distances of the Yb–O bonds and Yb···F contacts in complex I according to the routine XRD data, theoretical DFT calculations (Iisol), and experimental–theoretical (with molecular invariom) (Iinv) studies
Full size table

The atomic charges on the organic fragment of complex I obtained from the theoretical (Iisol) and experimental–theoretical (Iinv) ED distributions are well consistent (Table 2). All fluorine and oxygen atoms are characterized by a negative charge. The highest difference in the charges is observed on the atoms of the neutral coordinated solvents THF and Et2O. The Yb(2) and Yb(3) ytterbium atoms in complex I are divalent, whereas Yb(1) has the formal charge +3. This representation is well consistent with the theoretical atomic charges in Iisol. The charges on the ytterbium atoms in Iinv coincide with the DFT data at the semiquantitative level. The proportional difference between the charge on the formally trivalent Yb(1) atom and divalent Yb(2, 3) atoms is retained. An analysis of the published data showed that the theoretically calculated values of charges on the metal atoms in the isolated molecules were more positive than the values obtained by the high-resolution XRD studies [16, 39]. Thus, less positive charges on the ytterbium atoms in Iinv are quite expected.

Table 2. Atomic charges in complex I obtained on the basis of Iisol and Iinv of the ED distribution
Full size table

The topology of the theoretical and experimental–theoretical ED distributions in complex I was studied in the framework of R. Bader’s theory “Atoms in Molecules” [40]. The main topological characteristics of Iisol and Iinv are compared in Table 3. The main topological characteristics corresponding to the interactions of the ytterbium atoms in the coordination sphere are well consistent. All interactions Yb(II)–O, Yb(II)···F, and Yb(III) with the μ3-bridging hexafluoroisopropoxide ligands correspond to the closed shell type (∇2ρ(r)) > 0, he(r) > 0) in both Iisol and Iinv. In turn, all bonds of trivalent Yb(1) with the terminal and μ2-bridging hexafluoroisopropoxide ligands are classified as intermediate interactions (∇2ρ(r)) > 0, he(r) < 0) (Table 3). It is important that both models (theoretical and experimental–theoretical) make it possible to reveal four intramolecular C–F → Yb interactions (Fig. 2). According to the Espinosa–Molins–Lecomte correlation [41], the energy of these interactions lies in ranges of 6.26–7.90 and 5.71–8.44 kcal/mol for Iisol and Iinv, respectively. The presented values are only insignificantly lower than the corresponding values for the Yb(2)–O(8)THF and Yb(3)–O(9)EtOEt coordination bonds and interactions with the μ3-bridging hexafluoroisopropoxide ligands. The energy of Yb‒O(iso-PrF) increases systematically from the μ3‑bridging to terminal ligands in both Iisol and Iinv. This ED distribution in the coordination sphere of the lanthanide atoms in compound I also agrees well with the rela-ted europium complex {\({\text{Eu}}_{{\text{2}}}^{{{\text{II}}}}\)(μ2-OCH(CF3)2)3(μ3-OCH(CF3)2)2EuIII(OCH(CF3)2)2(DME)2} [25].

Table 3. Selected topological characteristics of the Yb–O bonds and Yb···F contacts in Iisol and Iinv
Full size table

The difference in ρ(r) and ∇2ρ(r) at the CP (3, –1) corresponding to the Yb–O and Yb···F interactions between models Iisol and Iinv does not exceed 0.009 and 0.046 a.u., respectively. Thus, the main topological characteristics for the interactions of the ytterbium atoms in the coordination sphere lie within the transferability index range for these values (ρ(r) = 0.1 e Å–3 (0.015 a.u.), ∇2ρ(r) = 4 e Å–5 (0.17 a.u.)) [42] (Fig. 3).

Fig. 3.
figure 3

Graphical representation of the deviation modules in the values of ρ(r) and ∇2ρ(r) at the CP (3, –1) corresponding to the interactions of the ytterbium atoms in the coordination sphere between Iisol and Iinv. The gray region demonstrates the boundary of the transferability index.

Full size image

The both methods (theoretical and experimental–theoretical) expectedly allow numerous intramolecular nonvalent interactions F···F, F···H, and F···O to be found in the structure of complex I (Fig. 4). The following interactions were revealed totally by the study of the topology of the theoretical ED: 24 F···F, 24 F···H, and 14 F···O. It should be mentioned that the study of the topology of the experimental–theoretical ED makes it possible to reveal much less interactions involving fluorine atoms: 11 F···F, 13 F···H, and 6 F···O. The absolute values of the energy of these interactions and the total energies of all interactions involving the fluorine atoms in Iinv are lower than those in the Iisol model (Table 4). The distances corresponding to the F···F, F···H, and F···O interactions in complex I vary in rather wide ranges regardless of the method of obtaining the ED distribution. However, the range of determination of the interactions involving fluorine atoms is somewhat broader in Iisol, and the maximum distances at which the interacting atoms are remote are longer (Table 4). The energy scatter for the corresponding interactions is also significant (0.65–4.11, 0.23–2.25, and 0.48–2.23 kcal/mol in Iisol and 0.53–1.67, 0.33–1.54, and 0.86–1.66 kcal/mol in Iinv).

Fig. 4.
figure 4

(a, c, e) Theoretical (Iisol) and (b, d, f) experimental–theoretical (Iinv) molecular graphs for complex I. Only selected CP (3, –1) corresponding to the (a, b) F···F, (c, d) F···H, and (e, f) F···O interactions are presented separately for clarity. Hydrogen atoms are omitted.

Full size image
Table 4. Intramolecular interactions involving fluorine atoms in Iisol and Iinv
Full size table

This difference in the number and energy of intramolecular nonvalent interactions involving the fluorine atoms in complex I is determined by geometry optimization in the theoretical study of the ED distribution in the molecule. An analysis of the geometry of the F···X interactions (X = F, H, O) showed that the Iinv model much more precisely reproduced the geometric characteristics determined in the routine XRD experiment than the Iisol model. The average deviations in the F···F, F···H, and F···O distances are 0.112, 0.184, and 0.062 Å in Iisol and 0.005, 0.047, and 0.009 Å in Iinv. The optimization of the molecular structure in the quantum-chemical calculation leads to the most energetically favorable conformation and ignores an intermolecular interaction in the crystal. Interestingly, during geometry optimization the highest changes are characteristic of the Fδ–···Hδ+ interactions. The distances between these atoms decrease considerably due to the optimization. Therefore, it should be expected that the Iisol model somewhat overestimates the energy of these interactions. The overall contribution of all interactions Fδ–···Fδ– plays an important role in the stabilization of the molecular structure of complex I regardless of the approach to the study of the ED distribution. This conclusion is well consistent with the previously performed quantum-chemical study of the related europium complex [25].

In spite of such a significant difference in the energies of interactions, the main topological characteristics for the interactions involving the fluorine atoms, which can be localized in terms of both approaches to the study of the ED distribution in complex I, are in rather good agreement. The difference in ρ(r) and ∇2ρ(r) does not exceed 0.005 and 0.022 a.u., respectively. Thus, the main topological characteristics for the nonvalent interactions, which can be localized in the framework of both theoretical and experimental–theoretical approaches, lie within the transferability index range of these values [42] (Fig. 5). The least average deviation in the values of ρ(r) and ∇2ρ(r) is observed for the F···O interactions, while the largest is observed for the F···H interactions in strict accordance with the difference in bond lengths. The absolute values of the topological characteristics corresponding to the nonvalent interactions of the fluorine atoms are well consistent with the published data on the F···F interactions [43].

Fig. 5.
figure 5

Graphical representation of the deviation modules in the values of ρ(r) and ∇2ρ(r) at the CP (3, –1) corresponding to the intramolecular interactions F···X (X = F, H, O) between Iisol and Iinv. The gray region demonstrates the boundary of the transferability index.

Full size image

The studies of the experimental [44] and theoretical [25] DED distributions in the region of the halogen contacts Fδ–···Fδ– showed that fluorine···fluorine interactions are possible due to the donation of the ED from the region of its concentration on one of the atoms to the region of ED depletion on the second atom. The DED map was constructed for the Iinv model in the framework of the applicability of the experimental–theoretical approach to the study of the interactions involving the fluorine atoms in the structure of complex I. As can be seen from Fig. 6a, in the area where the F(28)···F(33) interaction occurs, the region of ED accumulation on F(28) rigidly corresponds to the region of ED depletion on the F(33) atom. Note that the molecule of complex I contains the shortened pairs of atoms F···F for which CP (3, –1) were not localized either in the case of the theoretical approach, or when using the experimental–theoretical approach to obtaining the ED distribution. For example, the F(33)···F(36) distance in Iinv is 2.774(4) Å. This value lies in the range of interactions characteristic of F···F (Table 4), but the CP and bonding route for this pair of atoms were not localized (Fig. 4b). In order to determine the principal distinction of such noninteracting pairs of atoms, we constructed the DED distribution in Iinv in the C(17)–F(33)···F(36) plane (Fig. 6b). Unlike the F(28)···F(33) interaction, the F(33) and F(36) atoms are arranged relative to each other in such a way that the region of ED accumulation on one of the atoms corresponds to the ED accumulation region on the second atom. This is the reason for the absence of interactions between the atoms F(33)···F(36). The distribution of the theoretical DED in the region of nonvalent interactions of fluorine in the molecule of Iisol excellently reproduces the data of the Iinv model.

Fig. 6.
figure 6

Distribution of the DED (0.05 a.u.) in complex Iinv in the (a) С(15)–F(28)···F(33) and (b) C(17)–F(33)···F(36) planes. The regions of ED concentration are marked by solid lines, and the regions of ED depletion are indicated by dashed lines.

Full size image

In addition to the nonvalent interactions involving the fluorine atoms F···F, F···O, F···H, and C–F → Yb in the structure of the Iisol model, the following intramolecular contacts are localized: three O···H and two O···O. The energy of the O···H interactions is 0.93, 1.33, and 1.65 kcal/mol, and that of O···O is 3.36 and 4.24 kcal/mol. An analysis of the topology of the ED in Iinv did not allow localizing the O···H interaction in the molecule. However, one of two O···O interactions found in Iisol is reproduced in Iinv. The CP (3, –1) is localized between the oxygen atoms of the μ3-bridging hexafluoroisopropoxide ligands. The energy of this interaction calculated by the Espinosa–Molins–Lecomte equation [41] is 4.24 and 4.96 kcal/mol in Iisol and Iinv, respectively.

To conclude, the topology of the ED distribution in complex I obtained by the theoretical (quantum-chemical DFT calculation) and experimental–theoretical (molecular invariom) methods was studied. The main topological characteristics corresponding to the interactions of the ytterbium atoms in the coordination sphere range within the transferability index between Iisol and Iinv. This assertion is valid, in particular, for the intramolecular interactions C–F → Yb in complex I. Geometry optimization leads to a stronger change in the geometry compared to the use of the molecular invariom model. As a result, the number of intramolecular interactions involving the fluorine atoms and their energy in Iisol are much higher than those in Iinv. However, the main topological characteristics (ρ(r) and ∇2ρ(r)) corresponding to the F···X interactions (X = F, H, O), which can be localized in terms of both studied approaches, lie within the transferability indices of these values. The study of the DED distribution in Iinv showed that the Fδ–···Fδ– interactions can occur due to the correspondence of the region of ED concentration on one of the atoms to the region of ED depletion on another atom regardless of the method of obtaining the ED distribution in the molecule.