INTRODUCTION

Crack dynamics in rocks was studied from acoustic emissions (AE) (Zhurkov et al., 1981; Lockner et al., 1992; Sobolev and Ponomarev, 2003). This technique provides information about cracks whose sizes are comparable to the wavelength of acoustic waves and is poorly sensitive to cracks less than a few microns.

A few years ago, smaller cracks in rocks have come to be studied by a fractoluminescence method (Vettegren et al., 2020a; 2020b; 2021). This method is based on the detection and analysis of fractoluminescence signals emitted from the fracture of mineral crystals.

The analysis of signals recorded with a time resolution of 2 ns allowed detecting the crack initiation time and tracking the crack growth, deceleration, and arrest under fracture of some rocks. It was established that crack sizes are from a few nm to a few dozens of nm and the time from the initiation to the arrest of crack is a few ns. These cracks are likely to be smallest: all the larger cracks are formed by their coalescence; therefore, they were called primary (Vettegren et al., 2020a).

However, until recently it was unclear how these cracks are formed. There are several models of the formation of “primary” cracks in metal crystals which attribute crack initiation to the breakthrough of the barriers that prevent the motion of dislocations along slip planes (Cottrell, 1964; Vladimirov, 1984; Gottstein, 2004).

The analysis of the FL signals from the fracture of quartz and low albite (Vettegren et al., 2020a; 2020b; 2021) has shown that “primary” cracks in these minerals are also formed under the breakthrough of these barriers.

The purpose of this work is to investigate the formation mechanism and dynamics of “primary” cracks under fracture of oligoclase—a widespread rock-forming mineral using the FL method. The interest in studying this mineral is due to the fact that, on one hand, oligoclase is a solid solution of albite and anorthite (Betekhtin, 2008; Bulakh et al., 2008) and, on the other hand, it is a crystal whose lattice parameters have long been well known (Phillips, 1971).

STUDY OBJECT AND METHODS

A photo of the studied oligoclase sample is shown in Fig. 1. Its fracture was studied on the laboratory setup described in (Vettegren et al., 2020a). The measurement procedure was as follows. The sample was pressed against a steel disk with diamond microcrystals with a size of ~7 μm glued to its surface. The disk is fixed on the axis of the electric motor. As the motor was switched on, the disk began to rotate and the diamond microcrystals damaged the surface. The fracture excited the FL emission (Fig. 2) and its spectrum was recorded by the AvaSpec-ULSi2048L-USB2 OE spectrometer.

Fig. 1.
figure 1

Photo of oligoclase sample studied in this work.

Full size image
Fig. 2.
figure 2

FL of oligoclase under fracture of sample.

Full size image

To study the time dependence of the FL signals, the emitted radiation was focused by a quartz lens onto the detector window of the photomultiplier PEM-136. The PEM-136 output electric voltage was fed to the input of the ADC-3106 analog-to-digital converter (ACTACOM) and the ADC output voltage was recorded to the computer memory every 2 ns.

OLIGOCLASE FL SPECTRUM

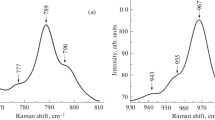
The analysis of the FL spectrum (Fig. 3) has shown that the observed emission band was formed by the superposition of three Gaussian bands 1.4, 1.7, and 2 eV. The band with the maximum at 2 eV corresponds to electronically excited free radicals ≡Si−O• (Götze, 2012), and the 1.7 eV band corresponds to the excited Fe3+• ions (Götze, 2012) substituting Si4+ ions in the crystal cells of oligoclase. Fracture of rocks causes emission of free electrons (Kawaguchi, 1988; Shuldiner and Zakrevskii, 1996) part of which fall into the conduction zone and from it into the empty traps formed during under the destruction of the oligoclase crystal. Under filling of traps, the FL spectrum displays yet another maximum that appears at 1.4 eV (Andersen et al., 2012; Baril and Huntley, 2003).

Fig. 3.
figure 3

FL spectrum upon destruction of oligoclase. Solid lines are FL bands. Dashed line is summary band formed by overlapping FL bands.

Full size image

What is the mechanism of formation of excited radicals, ions, and electron traps? It is known that plagioclases contain dislocations (Hull and Bacon, 2011; Shaocheng and Mainprice, 1988; Yongsheng and Hangrong, 2015). Motion of dislocations in oligoclase and quartz requires breaking the strong Si-O-Si bonds between the atoms, therefore under mechanical stresses used in the creep tests and at temperatures below 700°C, dislocations in dry oligoclase do not move. However, Trépied and Doukhan (1978) established that under mechanical stresses developing due to indentation of quartz, dislocations in the latter glide over a few µm. The theoretical calculations (Shavva and Grubiy, 2015) show that stresses causing movement of dislocations can also arise at diamond grinding of surfaces of other minerals. At the intersections of planes, barriers are formed that prevent dislocation motion (Vladimirov, 1984; Orlov, 1983). When barriers are broken, the Si–O–Si bonds break, and excited free radicals ≡Si–O• (Shuldiner, Zakrevskii, 1996), Fe3+• ions, and free electrons are formed.

The relaxation of excitation of these radicals and electrons as well as the filling of electron traps is accompanied by energy release in the FL form.

MECHANISM OF NANOCRACK FORMATION UPON OLIGOCLASE FRACTURE

The oligoclase crystal has a trigonal crystal system and four main systems of dislocation slip planes. Using transmission electron microscopy, Shaocheng and Mainprice (1988) studied the compression deformation of oligoclase at temperatures above 850°C. They established the existence of two dislocation slip planes (010)(001) and (010)(100). Simultaneously, deformation of oligoclase macrocrystals was studied also using electron microscopy at temperatures from 800 to 1000°C by Kramer (1988). Kramer found that four systems of slip planes exist: (010)[001], (010)[101], (001)1/2[110], and (110)[001].

According to (Cottrell, 1964; Vladimirov, 1984; Orlov, 1983), under the intersection of four slip planes, four barriers are formed that impede the dislocation motion. The destruction of these barriers should lead to the formation of four “primary” cracks. In turn, the emergence of each crack should produce a maximum in the FL signals (Turro et al., 2010) whereas the formation of a cluster of four cracks should result in the appearance of four maxima in these signals. As said above, the FL signals do indeed contain four maxima (Fig. 4). This result allows each maximum to be interpreted as corresponding to the formation of one of the four “primary” cracks.

Fig. 4.
figure 4

Typical FL sygnal of oligoclase. τ1 is time when first maximum reaches peak intensity.

Full size image

DYNAMICS OF FL SIGNALS

The time dependence of FL is a sequence of signals appearing with a time gap between them from 0.1 to a few µs despite the fact that that the disk with diamonds glued on its surface rotates at a constant speed of 10 nm/ns. This type of the time dependences was observed in our previous experiments on the destruction of the surface of quartz, quartz diorite, and other minerals (Vettegren et al., 2011; 2020b; 2021). The cause of this pattern of time behavior is unclear. It can be hypothesized that dislocations in the surface layer of minerals are not distributed continuously but as separate “tangles.” Mechanical stresses in these tangles can cause movement and breakthrough of the barriers. This initiates the formation of “primary” cracks which leads to the emission of the FL signals.

This hypothesis explains the pattern of the time dependence of the FL signal intensity: the first maximum in these FL signals is approximately twice as high as the other three maxima. The force acting on the dislocations is proportional to the product cosα·cosβ where α and β are the angles between the direction of the applied force, the slip plane, and slip plane normal (the Schmid factor) (Schmid and Boas, 1938). Apparently, the first peak in the FL signals corresponds to the cracks that are initiated by the breakthrough of the barriers under the intersection of the slip planes for which the product cosα·cosβ is maximal. Other signals correspond to the cracks formed under the intersection of the slip planes for which cosα·cosβ is smaller and, therefore, the intensity of the emitted FL signals is also lower.

The intensity of the maxima in the FL signals is proportional to the total number of emission sources (i.e., excited radicals ≡S–O•, Fe3+• ions, and electron traps) on the crack walls. Therefore, by examining the time dependence of signal intensity, it is in principle possible to obtain information about the dynamics of crack growth. However, the maxima so strongly overlap that we were able to do this only for the first maximum (Fig. 4). Indeed, at time t < τ1 where τ1 is the time of formation of the first maximum, the change in its intensity (I1) due to the superposition of the other maxima can be neglected. Its intensity exclusively depends on the rates of two processes: on one hand, it increases due to the crack growth, and on the other hand, it decreases due to the decrease in the number of the FL sources because of their being “extinguished” after the release of energy in the form of fractoluminescence.

In the general case, the number of the FL sources I1 depends on time t in the following form (Emanuel and Knorre, 1984):

$${{I}_{1}}(t) = q\left[ {\left( {N - n} \right)\exp \left( {{{k}_{i}}t} \right) - n\exp \left( {{{k}_{r}}t} \right)} \right],$$

where N is the initial number of the FL sources, n is the number of the “extinguished” spources, ki and kr are constants of the rates of the growth and reduction of the number of these sources (the constants are defined as k≡ (dn/ndt)).

At time t ≤ 0.5τ , the decrease in the intensity of the first maximum due to the “extinction” of the FL sources can be neglected, and, therefore,

$$I(t) \approx qN\exp \left( {{{k}_{i}}t} \right).$$

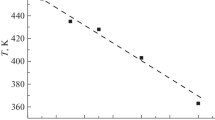
Figure 5 shows (in semi-logarithmic coordinates) a fragment of the initial interval of the time dependence of intensity I1 in an arbitrarily selected signal under the destruction of the surface of oligoclase. It can be seen that the dependence of intensity I1 on time t has the following form:

$$\ln {{I}_{1}}\left( t \right) = B + \ln {{I}_{d}}\left( 0 \right) + {{k}_{i}}t,$$
(1)

where B is the logarithm of the intensity of the noise signal, \({{I}_{d}}\left( 0 \right)\) is the intensity of the emission under the breakthrough of the barrier and coalescence of two dislocations.

Fig. 5.
figure 5

Fragment of time dependence of log intensity of first maximum (I1).

Full size image

The same linear dependence of log intensity of the first maximum on time was also observed for other FL signals emitted upon the destruction of the surface of oligoclase. Coefficient ki was determined by measuring the b-value of the linear segment of these dependences for the signals whose intensity I1 was at least 54 μV. (At lower I1, noise impedes reliable b-value determination.) It was established that at I1 = 54 μV, ki ≈ 0.016 ns–1, and for the signals having maximum intensity, –570 μV, ki is twice as high, ~0.03 ns–1.

The FL intensity is proportional to the number of the FL emission sources on the crack wall surface. Therefore, an important conclusion follows from (1): the area Scr of the walls of “primary” cracks grows exponentially with time:

$${{S}_{{cr}}}(t) = {{S}_{0}}\exp {{k}_{i}}t,$$
(2)

where S0 is the area of the source of the future “primary” crack under the coalescence of two dislocations.

What is the cause of this form of dependence \({{S}_{{cr}}}(t)?\) The first dislocations probably pass through the barrier when it only begins to break down; the resistance to their coalescence is still substantial, and the rate of nucleation of the “primary” crack is low. Subsequently, as the degree of barrier destruction increases, the rate of coalescence of dislocations and the growth rate of the “primary” crack increases. When the barrier is broken, the rate of gliding of dislocations is exclusively determined only by the rate of change of the applied force, i.e. by the velocity of motion of diamond crystals 10 m/s.

It was established that the time of growth of the intensity of the first maximum in all signals does not depend on the intensity of its maximum and is tcr ≈ (16 ± 1) ns. The cause of this constancy of tcr is currently not known. Then, in 16 ns, the fastest primary cracks will reach a size of ~10 nm and the slowest ones will growth to ~5 nm.

DISTRIBUTION OF FL SIGNALS BY INTENSITY

Crack distribution in loaded rocks was previously studied in detail using acoustic emission measurements. It was established that the dependence of the number N of acoustic events on their amplitude А is described by the power-law function (Lockner et al., 1991; Amitrano, 2003):

$$N( > {\kern 1pt} A) = a{{A}^{{ - b}}},$$

where a and b are the constants.

In seismology, a similar equation is known as the Gutenberg–Richter law (Gutenberg and Richter, 1954) and is one of the fundamental empirical relationships in the physics of the Earth which represents the frequency of occurrence of the earthquakes as a function of earthquake magnitude M:

$$\log N = a - bM,$$

where N is the number of the earthquakes with magnitudes higher than M and a and b are constants; for the distribution of acoustic signals, b ≈ 1.

This law is observed on the fracture scales ranging from mm for laboratory experiments to dozens of km typical in seismology (Wiemer and Wyss, 2002; Scholz, 2019).

It would be interesting to find out whether this scaling is observed for nanometer cracks in oligoclase.

Since the FL intensity is proportional to the area of a crack surface, we believe that this parameter can serve as the energy characteristic of the signal source.

Figure 6 shows the log-log plot of the distribution of the logarithmic intensity logI1 of the first maximum in 4000 FL signals. Only the signals whose intensity was at least twice as high as the noise level were taken into account.

Fig. 6.
figure 6

Distribution of intensities of first maximum in FL signals.

Full size image

It can be seen that in the interval of logI1 values from 1.7 to 2.4, the experimental points fall on a straight line, i.e., the crack distribution has a form of the power law:

$$\log N({{I}_{1}}) = \log {{N}_{0}} - \beta \log {{I}_{{1,}}}$$

where N0 is the parameter of the experiment which depends on the location of the receiver of the FL signals—photomultiplier, its sensitivity, etc. At the same time, the exponent β does not depend on these parameters and is 1.9 ± 0.2. At the logI1 values above 2.4, the layout of the experimental points deviates from the straight line.

Remarkably, the β values for nanocracks are higher than for the distribution of the acoustic signals and earthquakes (β ≈ 1). Why this is so is currently unclear.

CONCLUSIONS

The above results show that under the destruction of the surface of oligoclase crystal, clusters of the smallest (“primary”) cracks with the sizes ranging from ~5 to ~10 nm are formed. It is supposed that cracks are formed under the breakthrough of the barriers that prevent dislocations from sliding on the slip planes. The crack distribution by sizes (surface areas of the crack walls) obeys the power law with the exponent β = 1.9.