Abstract
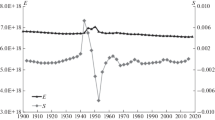
The possibility of determining parameters of complex geophysical processes is considered in terms of nonlinear dynamics. In accordance with modern approaches in the theory of nonlinear dynamic systems, the number of independent parameters controlling the behavior of a nonlinear system can be estimated from the available time realization of only one of these parameters. Model calculations showed that the dimension of the phase space of a dynamic system can be estimated from a sample of one variable. Experimental data on variations in the apparent electric resistivity (AER) and the relative vertical movement of the surface (RVMS) in a seismically active region are analyzed and the dimension of the dynamic system determining its behavior in the phase space is estimated. The resulting estimates of the embedding dimension m = 7−8 for AER variations and m = 6 for RVMS variations possibly characterize the complexity of the dynamic system describing the given fields. The method presented in the paper is also applied to the analysis of the degree of connectivity of different dynamic systems and their parameters. By the connectivity we mean the number of independent parameters simultaneously involved in the formation of the dynamic behavior of various physical fields. The model estimates demonstrate the possibility of such an approach. It is shown that variations in the AER in perpendicular directions are described by a general system of dynamic equations, whereas dynamic systems controlling the AER field and the RVMSs are interconnected only partially. The resulting dimension m = 12 estimated for the AER-RVMS system provides an estimate for the number of common controlling parameters: n = (8 + 6)−12 = 2. The methods and results presented in the paper are applicable to the construction of models of complex geophysical processes and the development and the development of new approaches and methods of identification of prognostic characteristics for the behavior of physical fields of various origins.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
A. Afifi and S. Eizen, Statistical Analysis: A Computer-Based Approach (Mir, Moscow, 1982) [in Russian].
I. Likesh and I. Lyaga, Main Tables of Mathematical Statistics (Finansy i Statistika, Moscow, 1985) [in Russian].
G. G. Malinetskii and A. B. Potapov, Current Problems in Nonlinear Dynamics (Editorial URSS, Moscow, 2002) [in Russian].
T. Parker and L. Chua, Practical Numerical Algorithms for Chaotic Systems (Springer, New York, 1989), p. 348.
H. G. Shuster, Deterministic Chaos (Springer, Heidelberg, 1982; Mir, Moscow, 1988) [in Russian].
V. B. Smirnov, A. V. Ponomarev, Qian Jiadong, and A. S. Cherepantsev, “Rhythms and Deterministic Chaos in Geophysical Time Series,” Fiz. Zemli, No. 6, 6–28 (2005) [Izvestiya, Phys. Solid Earth 41, 428–448 (2005)].
S. Sternberg, Lectures on Differential Geometry (Prentice-Hall, New Jersey, 1964; Mir, Moscow, 1970).
M. Tabor, Chaos and Integrability in Nonlinear Dynamics: An Introduction (Wiley, New York, 1989; Editorial URSS, Moscow, 2001).
F. Takens, “Detecting Strange Attractors in Turbulence,” in Lecture Notes in Mathematics (Springer, Berlin, 1981), Vol. 898, pp. 336–381.
Author information
Authors and Affiliations
Additional information
Original Russian Text © A.S. Cherepantsev, 2007, published in Fizika Zemli, 2007, No. 12, pp. 72–81.
Rights and permissions
About this article
Cite this article
Cherepantsev, A.S. Dimension of the phase space of a dynamic system from geophysical data. Izv., Phys. Solid Earth 43, 1047–1055 (2007). https://doi.org/10.1134/S1069351307120075
Received:
Issue Date:
DOI: https://doi.org/10.1134/S1069351307120075