An Inverse Problem for a Semilinear Wave Equation

Abstract

For the equation ${{u}_{{tt}}} - \Delta u - f(x,u) = 0, (x,t) \in {{\mathbb{R}}^{4}},$ where $f(x,u)$ is a smooth function of its variables and is compact in x, the inverse problem of recovering this function from given information on solutions of Cauchy problems for the differential equation is studied. Plane waves with a strong front that propagate in a homogeneous medium in the direction of the unit vector ν and then impinge on an inhomogeneity localized inside some ball B(R) are considered. It is supposed that the solutions of the Cauchy problems can be measured on the boundary of this ball for all ν at times close to the arriving time of the front. The forward Cauchy problem is studied, and the existence of a unique bounded solution in a neighborhood of a characteristic wedge is stated. An amplitude formula for the derivative of the solution with respect to t on the front of the wave is derived. It is demonstrated that the solution of the inverse problem reduces to a series of X-ray tomography problems.

Consider the Cauchy problem

$$\begin{gathered} {{u}_{{tt}}} - \Delta u - f(x,u) = 0, (x,t) \in {{\mathbb{R}}^{4}}; \\ u{{{\text{|}}}_{{t < 0}}} = g(t + {{t}_{0}} - x \cdot \nu ), \\ \end{gathered} $$

(1)

where $f(x,u)$ is a smooth function of x and u that is compactly supported with respect to $x \in {{\mathbb{R}}^{3}}$ and g(t) has a discontinuity at t = 0 such that $g( + 0) = \alpha > 0$ and $g(t) = 0$ for $t < 0.$ Additionally, we assume that the structure of g(t) is such that $g(t) = \alpha > 0$ for $t \in [0,\varepsilon ]$, where $\varepsilon > 0,$ while, for $t > \varepsilon$, g(t) is arbitrary (specifically, it is possible that $g(t) = 0$ for $t > \varepsilon$). The parameter α can vary, running over a set of values. In (1) $\nu = ({{\nu }_{1}},{{\nu }_{2}},{{\nu }_{3}})$ is a vector belonging to the unit sphere ${{\mathbb{S}}^{2}}$. The parameter t₀ will be interpreted later. In  problem (1), $\nu$ and α are parameters. Accordingly, its solution is denoted by $u(x,t,\alpha ,\nu )$ to emphasize its dependence on these parameters. However, in the study of problem (1), the dependence of the solution on $\nu$ and α will be omitted for brevity.

In what follows, we consider the problem of determining the function $f(x,u)$ from some information on the solutions of problem (1). In this context, we make some assumptions about $f(x,u)$ to be used in the subsequent consideration.

Assumptions.

(i) For any $u \geqslant 0,$ the support of the function $f(x,u)$ is contained in the ball B(R) = $\{ x \in {{\mathbb{R}}^{3}}\,{\text{|}}\,{\text{|}}x{\text{|}} < R\}$, R > 0.

(ii) $f(x,u)$ and ${{f}_{u}}(x,u)$ are continuous functions for $(x,u) \in B(R) \times {{\mathbb{R}}_{ + }}$, ${{\mathbb{R}}_{ + }} = \{ t \in \mathbb{R}\,{\text{|}}\,t \geqslant 0\}$.

(iii) ${\text{|}}f(x,u){\text{|}} \leqslant {{f}_{0}}(u)$, where ${{f}_{0}} \in C({{R}_{ + }})$, ${{f}_{0}}(0) = 0$, and ${{f}_{0}}(u) > 0$ for $u > 0$.

(iv) For any $K \in (0,\infty ),$ there exists a positive constant $M = M(K)$ such that

$${\text{|}}{{f}_{u}}(x,u){\text{|}} \leqslant M(K), \quad (x,u) \in B(R) \times [0,K].$$

(2)

Define ${{S}_{ + }}(R,\nu ) = \{ x \in {{\mathbb{R}}^{3}}\,{\text{|}}\,{\text{|}}x{\text{|}} = R,x \cdot \nu > 0\}$. In (1) we set ${{t}_{0}} = {{\inf }_{{x \in B(R)}}} = (x \cdot \nu ) = - R$. The equation $u = g(t + {{t}_{0}} - x \cdot \nu )$ describes a plane wave propagating in the direction of the vector ν through homogeneous space (for $f(x,u) \equiv 0$). At the time t = 0, the front of this wave touches the domain $B(R)$ occupied by an inhomogeneity.

Inverse problem. Find $f(x,u)$ in the domain $x \in B(R)$, $u \in (0,U]$ from the following information on the solutions of problem (1):

$$\begin{gathered} u(x,t,\nu ,\alpha ) = h(x,t,\nu ,\alpha )\quad {\text{for all}}\quad \nu \in {{\mathbb{S}}^{2}}, \\ x \in {{S}_{ + }}(R,\nu ),\quad t \in (0,x \cdot \nu - {{t}_{0}} + \varepsilon , \alpha \in (0,U], \\ \end{gathered} $$

(3)

where $h(x,t,\nu ,\alpha )$ is a given function and ε is an arbitrary small positive number.

Inverse problems of determining coefficients in nonlinear hyperbolic equations have been intensively studied in recent years (see [1–9]). This work is based on the idea of expanding the solution in terms of singularities in a neighborhood of the wavefront; this idea was used, for example, in [10–13].

Theorem 1. Suppose that $\nu \in {{\mathbb{S}}^{2}}$, $\alpha > 0$, and the functions $f(x,u)$ and g(t) satisfy the assumptions made above. Then, near the characteristic wedge t = $x \cdot \nu - {{t}_{0}}$, problem (1) has a unique weak solution and it can be represented in the form

$$\begin{gathered} u(x,t) = \alpha H(t + {{t}_{0}} - x \cdot \nu ) \\ \, + [\beta (x,\nu ,\alpha ) + \bar {u}(x,t)]{{H}_{1}}(t + {{t}_{0}} - x \cdot \nu ), \\ \end{gathered} $$

(4)

where H(t) is the Heaviside step function defined as $H(t) = 1$ for $t \geqslant 0$ and $H(t) = 0$ for t < 0, H₁(t) = $tH(t)$, and the function $\beta (x,\nu ,\alpha )$ is given by the formula

$$\beta (x,\nu ,\alpha ) = \frac{1}{2}\int\limits_0^\infty f(x - s\nu ,\alpha )ds.$$

(5)

Here, ds is the element of the Euclidean length and the function $\bar {u}(x,t)$ in (4) is continuous in its arguments and infinitesimal as $t \to x \cdot \nu - {{t}_{0}} + 0$.

This theorem is proved using a series of lemmas.

In a homogeneous medium (i.e., for $f(x,u) \equiv 0$), the solution of problem (1) has the form u(x, t) = $g(t + {{t}_{0}} - x \cdot \nu )$. The Kirchhoff formula for an inhomogeneous wave equation implies that the solution of problem (1) satisfies the integral equation

$$\begin{gathered} u(x,t) = g(t + {{t}_{0}} - x \cdot \nu ) \\ \, + \frac{1}{{4\pi }}\int\limits_{|\xi - x| \leqslant t} \frac{{f(\xi ,u(\xi ,t\; - \;{\text{|}}\xi - x{\text{|}}))}}{{{\text{|}}\xi - x{\text{|}}}}{\kern 1pt} d\xi , \quad t \geqslant 0. \\ \end{gathered} $$

(6)

Since $g(t + {{t}_{0}} - x \cdot \nu ) = 0$ for $t < x \cdot \nu - {{t}_{0}}$ and $f(x,0)$ = 0, it follows that $u(x,t)$ = 0 for $0 \leqslant t < x$ · ν – t₀. Therefore, (6) implies the equation

$$\begin{gathered} u(x,t) = g(t + {{t}_{0}} - x \cdot \nu ) \\ \, + \frac{1}{{4\pi }}\int\limits_{D(x,t,\nu )} \frac{{f(\xi ,u(\xi ,t\; - \;{\text{|}}\xi - x{\text{|}}))}}{{{\text{|}}\xi - x{\text{|}}}}{\kern 1pt} d\xi \,, \\ t \geqslant x \cdot \nu - {{t}_{0}}, \\ \end{gathered} $$

(7)

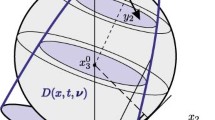
where $D(x,t,\nu )$ is the domain bounded by the axisymmetric paraboloid

$$P(x,t,\nu ) = \{ \xi \in {{\mathbb{R}}^{3}}\,{\text{|}}\,\xi \cdot \nu \; + \;{\text{|}}\xi - x{\text{|}} = t + {{t}_{0}}\} $$

with the central axis passing through $x$ in the direction of the vector –ν.

Consider the family of paraboloids

$$P(x,\tau ,\nu ) = \{ \xi \in {{\mathbb{R}}^{3}}\,{\text{|}}\,\xi \cdot \nu \; + \;{\text{|}}\xi - x{\text{|}} = \tau + {{t}_{0}}\} $$

for $\tau \in (x \cdot \nu - {{t}_{0}},t]$.

Along with the Cartesian coordinates ${{\xi }_{1}},{{\xi }_{2}},{{\xi }_{3}}$, we consider a system of coordinates ${{y}_{1}},{{y}_{2}},{{y}_{3}}$ with the origin placed at the point $x = ({{x}_{1}},{{x}_{2}},{{x}_{3}})$ and with basis vectors ${{e}_{1}},\;{{e}_{2}},\;{{e}_{3}}$:

$${{e}_{3}} = \nu = (\sin \theta \cos \varphi ,\sin \theta \sin \varphi ,\cos \theta ),$$

$${{e}_{1}} = (\cos \theta \cos \varphi ,\cos \theta \sin \varphi , - \sin \theta ),$$

$${{e}_{2}} = ( - \sin \varphi ,\cos \varphi ,0).$$

In these formulas, $\theta \in [0,\pi ]$ and $\varphi \in [0,2\pi )$. Additionally, we introduce cylindrical coordinates $z,\;r,\;\psi$ related to ${{y}_{1}},\;{{y}_{2}},\;{{y}_{3}}$ by the equalities ${{y}_{1}} = r\cos \psi$, ${{y}_{2}} = r\sin \psi$, and ${{y}_{3}} = z$, where $\psi \in [0,2\pi )$. Then

$$\xi = x + y,\quad y = {{e}_{2}}r\cos \psi + {{e}_{3}}r\sin \psi + {{e}_{3}}z,$$

(8)

and the equation defining the paraboloid $P(x,\tau ,\nu )$ becomes

$$P(x,\tau ,\nu ) = \{ \left( {r,z} \right):z + {{({{z}^{2}} + {{r}^{2}})}^{{1/2}}} = \tau + {{t}_{0}} - x \cdot \nu \} $$

or

$$r = \sqrt {(\tau + {{t}_{0}} - x \cdot \nu )(\tau + {{t}_{0}} - x \cdot \nu - 2z)} .$$

(9)

Therefore, as $\tau \to x \cdot \nu - {{t}_{0}} + 0$, the paraboloid $P(x,\tau ,\nu )$ degenerates into the ray L(x, ν) =: $\{ \xi \in {{\mathbb{R}}^{3}}\,{\text{|}}\,\xi = x + z\nu ,z \leqslant 0\}$.

In Eq. (7), instead of the variables of integration ${{\xi }_{1}},\;{{\xi }_{2}},\;{{\xi }_{3}}$, we introduce curvilinear coordinates $\tau ,z,\psi$. Then

$$\frac{{d\xi }}{{{\text{|}}x - \xi {\text{|}}}} = \frac{{dy}}{{{\text{|}}y{\text{|}}}} = d\tau dzd\psi .$$

Therefore, Eq. (7) becomes

$$\begin{gathered} u(x,t) = g(t + {{t}_{0}} - x \cdot \nu ) \\ \, + \frac{1}{{4\pi }}\int\limits_{x \cdot \nu - {{t}_{0}}}^t \int\limits_{P(x,\tau ,\nu )} f(\xi ,u(\xi ,t - \,{\text{|}}\xi - x{\text{|}})){\kern 1pt} d\psi dzd\tau \\ \end{gathered} $$

$$\, = g(t + {{t}_{0}} - x \cdot \nu )$$

(10)

$$\begin{gathered} \, + \frac{1}{{4\pi }}\int\limits_{x \cdot \nu - {{t}_{0}}}^t \int\limits_{ - \infty }^{(\tau + {{t}_{0}} - x \cdot \nu )/2} \int\limits_0^{2\pi } u(\xi ,u(\xi ,t\; - \;{\text{|}}\xi - x{\text{|}})){\kern 1pt} d\psi dzd\tau , \\ t \geqslant x \cdot \nu - {{t}_{0}}, \\ \end{gathered} $$

where the variable ξ is defined by formulas (8) and (9).

The sequence ${{u}_{k}}(x,t)$, $k = 0,1, \ldots$, is defined as

$${{u}_{0}}(x,t) = g(t + {{t}_{0}} - x \cdot \nu ),$$

$$\begin{gathered} {{u}_{k}}(x,t) = g(t + {{t}_{0}} - x \cdot \nu ) \\ \, + \frac{1}{{4\pi }}\int\limits_{x \cdot \nu - {{t}_{0}}}^t \int\limits_{P(x,\tau ,\nu )} f(\xi ,{{u}_{{k - 1}}}(\xi ,t\; - \;{\text{|}}\xi - x{\text{|}})){\kern 1pt} d\psi dzd\tau , \\ \end{gathered} $$

(11)

$$k = 1,2, \ldots , \quad t \geqslant x \cdot \nu - {{t}_{0}}.$$

Let $F(u)$ be a fixed antiderivative for the function $1{\text{/}}{{f}_{0}}(u)$. Here, $F{\kern 1pt} '(u) = \frac{1}{{{{f}_{0}}(u)}}$. Let ${{F}^{{ - 1}}}(p)$ denote the inverse of the function $p = F(u)$ for u > 0. Then

$$\frac{d}{{dp}}{{F}^{{ - 1}}}(p) = {{f}_{0}}({{F}^{{ - 1}}}(p)).$$

(12)

Let ε be a fixed number from the interval $(0,(F(2\alpha ) - F(\alpha )))$. Define

$$G(\nu ,\varepsilon ) = \{ (x,t)\,{\text{|}}\,0 \leqslant R(t + {{t}_{0}} - x \cdot \nu ) \leqslant \varepsilon \} .$$

Lemma 1. Suppose that $g(t) = \alpha > 0$ for $t \in [0,\varepsilon {\text{/}}R]$ and the function $f(x,u)$ satisfies the assumptions made above. Then, in the domain $G(\nu ,\varepsilon )$, the sequence ${{u}_{k}}(x,t)$ satisfies the estimate

$$\begin{gathered} 0 < {{u}_{k}}(x,t) \leqslant {{F}^{{ - 1}}}(F(\alpha ) + R(t + {{t}_{0}} - x \cdot \nu )), \\ (x,t) \in G(\nu ,\varepsilon ), \quad k = 0,1,2, \ldots . \\ \end{gathered} $$

(13)

Indeed, since the function $F(u)$ is monotone, we have

$$\begin{gathered} 0 < {{u}_{0}}(x,t) = g(t + {{t}_{0}} - x \cdot \nu ) \\ \, = \alpha \leqslant {{F}^{{ - 1}}}(F(\alpha ) + R(t + {{t}_{0}} - x \cdot \nu )), \\ (x,t) \in G(\nu ,\varepsilon ). \\ \end{gathered} $$

Furthermore,

$$\begin{gathered} {{u}_{1}}(x,t) \leqslant \alpha + \frac{1}{{4\pi }}\int\limits_{x \cdot \nu - {{t}_{0}}}^t \int\limits_{P(x,\tau ,\nu ) \cap B(R)} {{f}_{0}}({{F}^{{ - 1}}}(F(\alpha ) \\ \, + R(t\; - \;{\text{|}}\xi - x{\text{|}} + {{t}_{0}} - \xi \cdot \nu ))){\kern 1pt} d\psi dzd\tau \\ \end{gathered} $$

$$\begin{gathered} \, = \alpha + \frac{1}{{4\pi }}\int\limits_{x \cdot \nu - {{t}_{0}}}^t \int\limits_{P(x,\tau ,\nu ) \cap B(R)} {{f}_{0}}({{F}^{{ - 1}}}(F(\alpha ) \\ \, + R(t - \tau ))){\kern 1pt} d\psi dzd\tau \\ \end{gathered} $$

$$\begin{gathered} \, \leqslant \alpha + R\int\limits_{x \cdot \nu - {{t}_{0}}}^t {{f}_{0}}({{F}^{{ - 1}}}(F(\alpha ) + R(t - \tau ))){\kern 1pt} d\tau \\ \, = {{F}^{{ - 1}}}(F(\alpha ) + R(t + {{t}_{0}} - x \cdot \nu )), \quad (x,t) \in G(\nu ,\varepsilon ). \\ \end{gathered} $$

The last equality in this chain of relations is derived by changing τ to the new variable s = F^–1(F(α) + $R(t - \tau ))$ and checking, with the help of (12), that

$$R{{f}_{0}}({{F}^{{ - 1}}}(F(\alpha ) + R(t - \tau ))){\kern 1pt} d\tau = - ds.$$

Using similar calculations, we check that ${{u}_{1}}(x,t)$ is positive in $G(\nu ,\varepsilon )$:

$$\begin{gathered} {{u}_{1}}(x,t) \geqslant \alpha - \frac{1}{{4\pi }}\int\limits_{x \cdot \nu - {{t}_{0}}}^t \int\limits_{P(x,\tau ,\nu ) \cap B(R)} {{f}_{0}}({{F}^{{ - 1}}}(F(\alpha ) \\ \, + R(t\; - \;{\text{|}}\xi - x{\text{|}} + {{t}_{0}} - \xi \cdot \nu ))){\kern 1pt} d\psi dzd\tau \\ \end{gathered} $$

$$\, \geqslant \alpha - R\int\limits_{x \cdot \nu - {{t}_{0}}}^t {{f}_{0}}({{F}^{{ - 1}}}(F(\alpha ) + R(t - \tau ))){\kern 1pt} d\tau $$

$$\begin{gathered} \, = 2\alpha - {{F}^{{ - 1}}}(F(\alpha ) + R(t + {{t}_{0}} - x \cdot \nu )) \\ \, > 2\alpha - {{F}^{{ - 1}}}(F(\alpha ) + \varepsilon )) > 0,\quad (x,t) \in G(\nu ,\varepsilon ). \\ \end{gathered} $$

Entirely similar calculations show that estimates (13) hold for any k.

Corollary 1. Under the conditions of Lemma 1, the sequence ${{u}_{k}}(x,t)$ is uniformly bounded in the domain $G(\nu ,\varepsilon )$; moreover, for all k,

$$\begin{gathered} 0 < {{u}_{k}}(x,t) \leqslant 2\alpha ,\quad (x,t) \in G(\nu ,\varepsilon ), \\ k = 0,1,2, \ldots . \\ \end{gathered} $$

(14)

Lemma 2. Under the conditions of Lemma 1, the sequence ${{u}_{k}}(x,t)$ converges uniformly in the domain $G(\nu ,\varepsilon )$ and defines a continuous limit function $u(x,t)$ in this domain.

Consider the differences

$${{{v}}_{k}}(x,t) = {{u}_{k}}(x,t) - {{u}_{{k - 1}}}(x,t),\quad k = 1,2, \ldots .$$

It follows from (11) that

$${{v}_{1}}(x,t) = \frac{1}{{4\pi }}\int\limits_{x \cdot \nu - {{t}_{0}}}^t \int\limits_{P(x,t,\nu )} f(\xi ,{{u}_{0}}(\xi ,t\; - \;{\text{|}}\xi - x{\text{|}}))d\varphi dzd\tau ,$$

$${{v}_{k}}(x,t) = \frac{1}{{4\pi }}\int\limits_{x \cdot \nu - {{t}_{0}}}^t \int\limits_{P(x,t,\nu )} {{v}_{{k - 1}}}(\xi ,t\; - \;{\text{|}}\xi - x{\text{|}})$$

(15)

$$\begin{gathered} \, \times Q({{u}_{{k - 1}}}(\xi ,t\; - \;{\text{|}}\xi - x{\text{|}}),{{u}_{{k - 2}}}(\xi ,t\; - \;{\text{|}}\xi - x{\text{|}}))d\varphi dzd\tau , \\ k = 2,3, \ldots . \\ \end{gathered} $$

In formula (15), the function $Q({{u}_{{k - 1}}},{{u}_{{k - 2}}})$ is defined by the equality

$$Q({{u}_{{k - 1}}},{{u}_{{k - 2}}}) = \int\limits_0^1 {{f}_{u}}(\xi ,{{u}_{{k - 1}}}s + {{u}_{{k - 2}}}(1 - s))ds.$$

(16)

It follows from (11) that

$$\begin{gathered} {\text{|}}{{v}_{1}}(x,t){\text{|}} \leqslant R{{f}_{0}}(\alpha )\int\limits_{x \cdot \nu - {{t}_{0}}}^t d\tau = R{{f}_{0}}(\alpha )(t + {{t}_{0}} - x \cdot \nu ), \\ (x,t) \in G(\nu ,\varepsilon ). \\ \end{gathered} $$

The quantity $Q({{u}_{{k - 1}}},{{u}_{{k - 2}}})$ can easily be estimated by applying Corollary 1 and inequality (2):

$${\text{|}}Q({{u}_{{k - 1}}},{{u}_{{k - 2}}}){\text{|}} \leqslant M(2\alpha ).$$

Setting k = 2 in formula (15), we find that

$$\begin{gathered} {\text{|}}{{v}_{2}}(x,t){\text{|}} \leqslant \frac{{R{{f}_{0}}(\alpha )M(2\alpha )}}{{4\pi }} \\ \, \times \int\limits_{x \cdot \nu - {{t}_{0}}}^t \int\limits_{P(x,\tau ,\nu ) \cap B(R)} (t + {{t}_{0}} - \xi \cdot \nu \; - \;{\text{|}}\xi - x{\text{|}}){\kern 1pt} d\varphi dzd\tau \\ \end{gathered} $$

$$\begin{gathered} \, \leqslant {{R}^{2}}{{f}_{0}}(\alpha )M(2\alpha )\int\limits_{x \cdot \nu - {{t}_{0}}}^t (t - \tau )d\tau \\ \, = {{R}^{2}}{{f}_{0}}(\alpha )M(2\alpha )\frac{{{{{(t + {{t}_{0}} - x \cdot \nu )}}^{2}}}}{{2!}},\quad (x,t) \in G(\nu ,\varepsilon ). \\ \end{gathered} $$

Continuing the process of estimating the differences ${{v}_{k}}(x,t)$ yields

$$\begin{gathered} {\text{|}}{{v}_{k}}(x,t){\text{|}} \leqslant {{R}^{k}}{{f}_{0}}(\alpha ){{M}^{{k - 1}}}(2\alpha )\frac{{{{{(t + {{t}_{0}} - x \cdot \nu )}}^{k}}}}{{k!}}, \\ k = 2,3, \ldots ,\quad (x,t) \in G(\nu ,\varepsilon ). \\ \end{gathered} $$

(17)

Estimate (17) implies that the series $\sum\nolimits_{k = 1}^\infty {{v}_{k}}(x,t)$ converges uniformly in $G(\nu ,\varepsilon )$. This proves the uniform convergence of the sequence ${{u}_{k}}(x,t)$ in the same domain. Since all ${{u}_{k}}(x,t)$ are obviously positive and continuous in $G(\nu ,\varepsilon )$, the limit of this sequence defines a positive function $u(x,t)$ that is a continuous solution of problem (1) for $(x,t) \in G(\nu ,\varepsilon )$.

Corollary 2. The limit function $u(x,t)$ of the sequence ${{u}_{k}}(x,t)$ is a continuous solution of Eq. (10) in the domain $G(\nu ,\varepsilon )$ and satisfies the inequality

$$0 < u(x,t) \leqslant 2\alpha , \quad (x,t) \in G(\nu ,\varepsilon ).$$

(18)

Lemma 3. Equation (10) has a unique continuous solution in the domain $G(\nu ,\varepsilon )$.

Assume that there are two solutions ${{u}_{k}}(x,t)$, k = 1, 2, that are positive, continuous, and bounded in $G(\nu ,\varepsilon )$ by a constant K. Consider w(x, t) = ${{u}_{1}}(x,t) - {{u}_{2}}(x,t,(x,t\nu ))$. Writing equality (10) for ${{u}_{1}}(x,t)$ and ${{u}_{2}}(x,t)$ and representing their difference with the help of (16), we obtain

$$\begin{gathered} w(x,t) = \frac{1}{{4\pi }}\int\limits_{x \cdot \nu - {{t}_{0}}}^t \int\limits_{ - \infty }^{(\tau + {{t}_{0}} - x \cdot \nu )/2} \int\limits_0^{2\pi } w(\xi ,t\; - \;{\text{|}}\xi - x{\text{|}}) \\ \, \times Q({{u}_{1}}(\xi ,t\; - \;{\text{|}}\xi - x{\text{|}},{{u}_{2}}(\xi ,t\; - \;{\text{|}}\xi - x{\text{|}}){\kern 1pt} d\psi dzd\tau . \\ \end{gathered} $$

(19)

In view of (16), ${\text{|}}Q({{u}_{1}},{{u}_{2}}){\text{|}} \leqslant M(K)$. Since |w(x, $t){\text{|}} \leqslant K$ and the interval of integration with respect to z does not exceed 2R because $f(x,u)$ is compactly supported, it follows from (19) that

$$\begin{gathered} {\text{|}}w(x,t){\text{|}} \leqslant KRM(K)\int\limits_{x \cdot \nu - {{t}_{0}}}^t d\tau \\ \, = KRM(K)(t + {{t}_{0}} - x \cdot \nu ),\quad (x,t) \in G(\nu ,\varepsilon ). \\ \end{gathered} $$

(20)

Substituting (20) into (19) yields the new estimate

$$\begin{gathered} {\text{|}}w(x,t){\text{|}} \leqslant K{{R}^{2}}{{M}^{2}}(K)\int\limits_{x \cdot \nu - {{t}_{0}}}^t (t - \tau )d\tau \\ \, = K{{R}^{2}}{{M}^{2}}(K)\frac{{{{{(t + {{t}_{0}} - x \cdot \nu )}}^{2}}}}{{2!}},\quad (x,t) \in G(\nu ,\varepsilon ). \\ \end{gathered} $$

Repeating this iteration process n times, we obtain the estimate

$$\begin{gathered} {\text{|}}w(x,t,\nu ){\text{|}} \leqslant K{{R}^{n}}{{M}^{n}}(K)\frac{{(t + {{t}_{0}} - x \cdot \nu {{{))}}^{n}}}}{{n!}}, \\ (x,t) \in G(\nu ,\varepsilon ). \\ \end{gathered} $$

(21)

Since the right-hand side of (21) tends uniformly to zero in $G(\nu ,\varepsilon )$ as $n \to \infty$, we have $w(x,t) = 0$ in this domain. Therefore, ${{u}_{1}}(x,t) = {{u}_{2}}(x,t)$ for all (x, $t) \in G(\nu ,\varepsilon )$.

Lemma 4. Under the conditions of Lemma 1, the solution of problem (1) can be represented in the domain $G(\nu ,\varepsilon )$ in the form of (3).

We introduce the new function ${v}(x,t) = u(x,t) - \alpha$. It satisfies the equation

$$\begin{gathered} v(x,t) = \frac{1}{{4\pi }}\int\limits_{x \cdot \nu - {{t}_{0}}}^t \int\limits_{ - \infty }^{(\tau + {{t}_{0}} - x \cdot \nu )/2} \,\int\limits_0^{2\pi } f(\xi ,\alpha \\ \, + {v}(\xi ,t\; - \;{\text{|}}\xi - x{\text{|}})){\kern 1pt} d\psi dzd\tau , \\ (x,t) \in G(\nu ,\varepsilon ). \\ \end{gathered} $$

(22)

In the integral, we change the variable τ to ${{\tau }_{1}}$:

$$\tau = x \cdot \nu - {{t}_{0}} + (t + {{t}_{0}} - x \cdot \nu ){{\tau }_{1}}.$$

Then Eq. (22) becomes

$$\begin{gathered} v(x,t) = \frac{{(t + {{t}_{0}} - x \cdot \nu )}}{{4\pi }}\int\limits_0^1 \int\limits_{ - \infty }^{(t + {{t}_{0}} - x \cdot \nu ){{\tau }_{1}}/2} \,\int\limits_0^{2\pi } f(\xi ,\alpha \\ \, + {v}(\xi ,t\; - \;{\text{|}}\xi - x{\text{|}})){\kern 1pt} d\psi dzd{{\tau }_{1}}, \\ (x,t) \in G(\nu ,\varepsilon ). \\ \end{gathered} $$

As $t \to x \cdot \nu - {{t}_{0}} + 0$, we have the limit relations $\xi = x + z\nu$ and the paraboloid $P(x,\tau ,\nu )$ degenerates into the ray

$$L(x,\nu ) = \{ \xi \in {{\mathbb{R}}^{3}}\,{\text{|}}\,\xi = x + z\nu ,{\kern 1pt} z \leqslant 0\} .$$

Thus, the function ${v}(x,t)$ tends uniformly to zero as $t \to x \cdot \nu - {{t}_{0}} + 0$. Therefore,

$$\int\limits_0^1 \int\limits_{ - \infty }^{(t + {{t}_{0}} - x \cdot \nu ){{\tau }_{1}}/2} \,\int\limits_0^{2\pi } f(\xi ,\alpha + v(\xi ,t\; - \;{\text{|}}\xi - x{\text{|}}){\kern 1pt} d\psi dzd{{\tau }_{1}}$$

$$\, = 2\pi \int\limits_{ - \infty }^0 f(x + z \cdot \nu ,\alpha ){\kern 1pt} dz + o(t + {{t}_{0}} - x \cdot \nu ),$$

(23)

$$t \to x \cdot \nu - {{t}_{0}} + 0.$$

By using (23), Eq. (22) can be rewritten as

$$\begin{gathered} v(x,t) = (t + {{t}_{0}} - x \cdot \nu ) \\ \, \times \left( {\frac{1}{2}\int\limits_{L(x,y)} f(x + z \cdot \nu ,\alpha ){\kern 1pt} dz + \bar {v}(x,t)} \right), \\ t \geqslant x \cdot \nu - {{t}_{0}}, \\ \end{gathered} $$

where $\bar {v}(x,t) = o(t + {{t}_{0}} - x \cdot \nu )$ as $t \to x \cdot \nu - {{t}_{0}} + 0$.

Since $u(x,t) = v(x,t) + \alpha$ and $u(x,t) = 0$ for $t \leqslant x \cdot \nu - {{t}_{0}}$, we obtain representation (3), in which

$$\begin{gathered} \bar {u}(x,t,\nu ) = \bar {v}(x,t,\nu ) = o(t - x \cdot \nu ) \\ {\text{as}}\quad t \to x \cdot \nu - {{t}_{0}} + 0. \\ \end{gathered} $$

By Theorem 1 and formulas (4) and (5), information (3) determines the integrals

$$\begin{gathered} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\int\limits_0^\infty f(x - s \cdot \nu ,\alpha )ds = p(x,\nu ,\alpha ) \hfill \\ {\text{for all}}\quad \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\nu \in {{\mathbb{S}}^{2}},\quad x \in S_{R}^{ + }(\nu ), \alpha \in (0,U], \hfill \\ \end{gathered} $$

(24)

in which the function $p(x,\nu .\alpha )$ is given by the formula

$$\begin{gathered} p(x,\nu ,\alpha ) = 2\mathop {\lim }\limits_{t \to x \cdot \nu - {{t}_{0}} + 0} \frac{{\partial h}}{{\partial t}}(x,t,\nu ,\alpha ) \\ \, = 2{{h}_{t}}(x,x \cdot \nu - {{t}_{0}} + 0,\nu ,\alpha ). \\ \end{gathered} $$

Thus, for any fixed $\alpha \in (0,U]$, the integrals over all straight lines crossing the domain B(R) are known. As a result, the problem of determining $f(x,\alpha )$ for every fixed α from information (3) is reduced to an X‑ray tomography problem (see, e.g., [14]). This problem is known to be uniquely solvable. Accordingly, the following uniqueness theorem holds.

Theorem 2. Suppose that the conditions of Theorem 1 are satisfied. Then the inverse problem has a unique solution.