INTRODUCTION

Data uncertainty upon long-term monitoring of organic carbon stocks. Currently, monitoring of soil carbon stocks is one of the priority areas in soil and ecological studies, since the soil acts as a reservoir that can both conserve carbon and release it in the form of greenhouse gases, the presence of which in the atmosphere is believed to contribute to global warming. For information support of strategic decisions at the national level, high-quality monitoring of the carbon budget at the regional and local scales is necessary. Issues of monitoring carbon in natural environments, in soils, in particular, have been considered at several workshops of the European and worldwide level over the past 20 years. In a review on the state of soil carbon monitoring in Europe [30], the authors showed that the minimum detectable changes in carbon concentration differ significantly between the soil monitoring networks in different countries.

Information about the potential and actual ability of soils to sequester carbon requires clear protocols for assessing soil organic carbon stocks [26]. This was confirmed at the Global Symposium on Soil Organic Carbon held in Rome in 2017, where “Measuring, mapping, monitoring and reporting soil organic carbon” was one of the main topics (FAO website https://www.fao.org/about/meetings/soil-organic-carbon-symposium/about/).

Any data on the properties of the environment, including soil, are inherently uncertain due to both the heterogeneity of soil properties at different scales and the methods of obtaining information [7, 9, 23]. Often, the number obtained as a result of the analysis is attributed to objects whose dimensions are several orders of magnitude larger than the dimensions of analyzed sample. For monitoring the natural environment, information on the degree of data uncertainty becomes especially important now, since actions aimed at preventing certain possible adverse phenomena depend on the result of observations.

The property variability is usually characterized by its variance, which may be represented as a sum of populations variances \(~\sigma _{i}^{2},~\)due to different sources of variability [6, 12, 28].

For a particular study, populations variances are replaced by estimates

$$s_{{{\text{tot}}}}^{2} = s_{{{\text{analyt}}}}^{2} + s_{{{\text{nat}}}}^{2},$$
(1)

where \(s_{{{\text{tot}}}}^{2}\), \(s_{{{\text{analyt}}}}^{2}\), and \(s_{{{\text{nat}}}}^{2}\) are estimates of the total, analytical and natural variance.

The contributions of each of the variance estimates, in turn, may be taken into account by setting up special experiments. Both estimates include either a random, or a systematic component. Estimation of the random component requires constant experimental conditions (object of study, sampling scheme, and sampling method (samples size and shape), similar sample preparation and analysis method [6, 13]. The systematic component should be studied at different ranges of influencing factors, for example, for different sizes of samples, different territories, different analytical methods, etc.

Analysis of uncertainty sources in soil organic carbon stocks. General equation. The organic carbon content in the arable layer of agricultural lands varies from 7 to 27% [1, 2, 5, 14]; therefore, monitoring its reserves requires knowledge in the variation reasons.

The standard method for calculating the soil organic carbon (SOC) stocks M (t/ha) in a layer takes into account С, soil carbon content, %; dv, the soil bulk density, g/cm3; and h, the layer thickness, cm (2):

$$M = Cdvh.$$
(2)

For stony soils, the volume of large rocky fragments containing no carbon should be taken into account [27, 32]; therefore, the final equation looks like (3):

$$M = Cdvhf,$$
(3)

where f is the fine earth percent in the regarded soil volume. Since each of the variables represents a random value, its variability at each soil space point contributes to the overall uncertainty of the final result. Standard uncertainty is measured in standard deviations. The paper [25] provides an example of calculating the standard uncertainty of SOC stocks in the 0–30 cm layer, proceeding from the standard uncertainty of organic carbon content, bulk density, and stoniness. For the carbon content equal to 5%, bulk density equal to 1.5 g/cm3, and stoniness 10%, with the corresponding standard deviations of these indices 1%, 0.1 g/cm3, and 5%, respectively, the carbon stock constituted 203 ± 44 t/ha, i.e., the relative uncertainty amounted to 44/ 203 × 100 ≈ 22%. Such a high uncertainty surely requires increasing time intervals between recurrent monitoring observations, and it also testifies to the necessity to study the uncertainty sources in order to reduce them. Let us consider the uncertainty sources upon assessing the SOC stocks.

Uncertainty in measuring the soil organic carbon by the Tyurin method. To determine the soil carbon content, many authors recommend dry combustion using an automatic C–N analyzer according to ISO 10694-1995 [21, 29]. However, other methods are also applied: for example, the wet ashing method in two modifications, differing in time and duration of soil treatment with potassium dichromate solution. In English-speaking countries, this is the Walkley-Black method [21]. In Russia, the Tyurin method is used, regulated by GOST 26213-2021 and recommended by FAO [17]. In [29], four methods for determining the soil carbon content were compared to find out that not only they give different results for different soils, but also the correspondence between them (expressed in correlation coefficients) turns out to be unstable for the same soil. An experimental series was performed to compare the dry combustion methods and two methods of wet ashing for soils in the Russian Federation [31], proving their good comparability and the possibility of recalculating the results.

The role of sample preparation. Analytical variance has long been considered as the variance of analytical process, i.e., the parameter determination in the laboratory. However, the situation began to change in the second half of the 20th century. The works by Pierre Gy and his followers [11, 12, 24, 28] showed that sample preparation inputs significantly to the total variation, i.e., the share related to the sampling method and preliminary sample preparation for analysis should be recorded in the natural parameter variability.

Thus, equation (2) is transformed to:

$$s_{{{\text{tot}}}}^{2} = s_{{{\text{analyt}}}}^{2} + s_{{{\text{sample}}\,\,{\text{prep}}}}^{2} + \,~s_{{{\text{nat}}}}^{2}.$$
(4)

So, analytical measurement uncertainty turns out to be the sum of analytical error and sample preparation uncertainty. For instance, [33] shows that upon monitoring the total SOC content within an agricultural plot, the sample pretreatment (sifting, grinding), the studied sample volume, and the analytical method chosen appear to be the main factors controlling the total uncertainty in carbon monitoring. The expanded monitoring uncertainty, i.e., a 95% confidence interval for organic carbon content obtained from the interlaboratory tests (including sampling) amounted to ±20%.

Uncertainty in soil bulk density measurement. Soil bulk density is assessed by sampling a fixed soil volume [20]. The measurement accuracy is known to depend on bulk density, e.g., larger augers are used in arable layers, whereas 100 cm3 soil augers are most often used in the lower horizons. Determination is recommended to repeat up to 10 replicates in arable layers, and 2–3 replicates is recommended in the underlying ones [4, 18]. The initial procedure does not specify the replicates locations. Quantitative data on the magnitude of soil bulk density uncertainty are scarce, being usually limited to average values and most often referring to uncultivated soils. For example, as shown in [15], the spatial variability of bulk density approximates to 9% of the total bulk density variation at a depth of 10–14 cm in a forest biogeocenosis; and in [3], the variation coefficient of arable soil bulk density does not exceed 5% within the agricultural land area. Another study [10] provides the variation coefficient value equal to 7% for a structural-metamorphic agrozem.

Uncertainty in measuring the soil layer thickness. The error in measuring the layer thickness depends on sampling scheme and type. If the carbon content and bulk density are analyzed in separate layers, with their thickness registered beforehand, this error can be disregarded, since the parameter values are attributed to the predetermined layer center. All variation caused by unequal sampling depths is attested for in the properties variability.

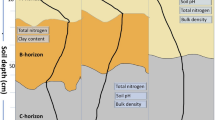
However, if the entire layer thickness is sampled, the layer thickness measurement may contribute significantly to the result uncertainty, since sampling inaccuracies will lead to the fact that the sample may characterize different layers. The sampled layer thickness contributes to uncertainty most noticeably in the soils with contrasting horizons, e.g., podzolic and soddy-podzolic soils. When sampling these soils with an auger, for example, to a depth of 30 cm, a 1 cm change in the horizon thickness may add up to 3% of soil mass with a substantially lower content of organic matter. This underestimates the organic carbon content and, therefore, requires more careful averaging of the primary soil sample.

Finally, the sample volume effect may depend on soil moistening. This effect will be higher in swelling soils.

Uncertainty related to the fine earth percentage. This source of uncertainty is acute for soils containing large hard rock or moraine fragments. These soils require special sampling methods, since the size of rock fragments can be comparable to that of routine soil samplers designed for non-stony soils. The estimation error of fine earth percentage may be insignificant in a particular point; however, the overall uncertainty will be strongly affected by the pattern of spatial distribution of large fragments. Spatial variation of stoniness parameter is almost unstudied, although in some cases it may be the principal factor controlling the uncertainty in soil carbon estimates.

Calculation of carbon stock uncertainty. Since the soil carbon stock represents a multiple indirect measurement uniting several direct measurements, its uncertainty must account for the uncertainties in each of these measurements. The final result equation is a product; we may also assume that the properties obey normal distribution and are uncorrelated to each other. The standard uncertainty can be found from a fairly complex formula based on the Taylor series expansion [25]. Here is a simplified version for the case not taking into account the measurement uncertainty of layer h (5):

$${{\Delta }_{m}} = h\sqrt {s_{c}^{2}~d{{v}^{2}}{{f}^{2}} + {{C}^{2}}s_{{dv}}^{2}~{{f}^{2}} + ~{{C}^{2}}~d{{v}^{2}}s_{f}^{2}} ,$$
(5)

where Δm (t/ha) is the standard uncertainty in layer h; С is the soil carbon content, %; dv is the soil bulk density, g/cm3; h is the layer thickness, cm; and sС, sdv, sf are the corresponding standard deviations.

It is easier to calculate the relative uncertainty of the carbon stock εM expressed in %, which essentially appears to be an analogue of the variation coefficient (5):

$${{\varepsilon }_{M}} = \sqrt {\varepsilon _{C}^{2} + \varepsilon _{{dv}}^{2} + \varepsilon _{h}^{2} + \varepsilon _{f}^{2}} ,$$
(6)

where εС, εdv, εh, and εf are the relative measurement uncertainties (%) of carbon content, bulk density, layer thickness and stoniness, respectively. Then the standard uncertainty (Δm) can be found from equation (7):

$${{\Delta }_{m}} = M{{\varepsilon }_{M}},$$
(7)

where M is the average carbon stock.

For example, the calculations are as follows in [25]. Stocks can be found from equation (3), whereas standard and relative uncertainties are derived according to formulas (5–7),

$$\begin{gathered} M = {\text{ }}5\left[ \% \right] \times 1.5{\text{ }}\left[ {{{\text{g}} \mathord{\left/ {\vphantom {{\text{g}} {{\text{c}}{{{\text{m}}}^{{\text{3}}}}}}} \right. \kern-0em} {{\text{c}}{{{\text{m}}}^{{\text{3}}}}}}} \right] \times {\text{ }}30{\text{ }}\left[ {{\text{cm}}} \right] \\ \times \,\,{{\left( {100-10} \right)} \mathord{\left/ {\vphantom {{\left( {100-10} \right)} {100}}} \right. \kern-0em} {100}} = 202.5{\text{ }}\left[ {{{\text{t}} \mathord{\left/ {\vphantom {{\text{t}} {{\text{ha}}}}} \right. \kern-0em} {{\text{ha}}}}} \right], \\ \end{gathered} $$
$$\begin{gathered} {{\Delta }_{m}} = 30 \times \sqrt {{{{0.1}}^{2}}~{{{1.5}}^{2}}{{{0.9}}^{2}} + {{5}^{2}}~{{{0.1}}^{2}}{{{0.9}}^{2}} + ~{{5}^{2}}~{{{1.5}}^{2}}{{{0.05}}^{2}}} \\ = 44.1\,\,\left[ {{\text{t/ha}}} \right], \\ \end{gathered} $$
$${{\varepsilon }_{Z}} = \sqrt {{{{\left( {\frac{5}{1}} \right)}}^{2}} + {{{\left( {\frac{{1.5}}{{0.1}}} \right)}}^{2}} + {{{\left( {\frac{{\left( {100 - 10} \right)}}{5}} \right)}}^{2}}} = 21.8~\left[ \% \right],$$
$${{\Delta }_{m}} = 202.5 \times 21.8 = 44.1\,\,[{\text{t/ha}}].$$

The purpose of this study is to evaluate, using a case study, the accuracy of determining the stocks of soil organic carbon at the experimental plot under repeatability, with the maximum possible constancy of determination conditions and interlaboratory reproducibility, with changing analytical laboratory and operator.

OBJECTS AND METHODS

The experimental plot. General characteristics. The experimental plot was located on one of the fields belonging to the Educational and Experimental Soil and Ecological Center, Lomonosov Moscow State University (56.0400° N, 37.1662° E). The soil was sampled in September 2022. For the last three years (2019–2022), the field has been a regularly plowed fallow; and before that it was an unplowed fallow for many years. The relief is hilly-undulating, and microrelief shows plowing furrows. According to the 1977 Russian classification, the soils belong to cultivated soddy-podzolic soils (Albic Glossic Retisol (Aric, Loamic, Cutanic, Ochric)).

The sampling schemes. Soil samples were taken within a 100 × 100 m plot in five points (Fig. 1). Two sampling schemes were used, i.e., in pits and with an auger. According to the first scheme, sampling combined the samples for the analysis of soil bulk density and organic carbon content. The soil bulk density was measured in pits in two parallel columns (20 cm between samples) in the centers of layers 0–10, 10–20, and 20–30 cm using a 100 cm3 ring auger. The ring height was equal to 5 cm. After weighing and sampling for moisture, the soil mass was used for the analysis of soil carbon content. The carbon content and bulk density determined in such a sample were attributed to the entire 10-cm-thick layer.

Fig. 1.
figure 1

Characteristics of sampling: (a) location of sampling points at the site; (b) ratio between the samples from pits and those taken with an 0–30 cm auger in respect to soil horizons.

Full size image

Samples with an auger (4 cm in diameter and 30 cm long) were taken near the pits to a depth as a single sample in 3 replicates. Figure 1 shows the arrangement of samples from the pits and those taken by the auger in respect to the soil horizons.

Sample preparation and carbon content analysis. For all samples, sample preparation was carried out in the same way. The soil mass was brought to an air-dry state, crushed and sieved through a 2-mm sieve, large roots were removed, and small roots were collected with an electrified glass rod.

The organic carbon content in the samples was analyzed by the Tyurin method modified by Nikitin (heated not in a water bath, but in an oven at 140°C) and Orlov-Grindel (spectrophotometry instead of titration as a final procedure).

The samples taken for bulk density determination from three depths (30 samples) as well as those taken with an auger (15 samples) according to the double sampling scheme [12, 22] were analyzed. To rule out the systematic errors in the carbon content estimation, the samples were examined in a random order. To control the reproducibility, the samples from three pits (18 items) were analyzed in the testing laboratory of the Bryansk State Agrarian University (GAU). The same modification of the Tyurin method was used for the analysis.

Statistical processing of data and calculation of carbon stocks. The main difference in the carbon stock calculation in the 0–30 cm layer between the samples from pits and those taken with an auger was the following. In the first case, the soil carbon stock in the 0–30 cm layer was obtained from summing the values in layers; whereas in the second case, the resultant value corresponded to the soil mass obtained from physical averaging of the entire sample. We took the average bulk density for the entire sample.

The results were processed by nested analysis of variance [6, 16]. For bulk density, the point—depth—replicates (error) levels were considered. For the carbon content, the number of levels was greater: point—depth—field sample replicates—sample preparation—analytical error. The significance level for testing statistical hypotheses was equal to 0.05.

RESULTS

Analysis of uncertainty in the bulk density estimate. Since the samples were taken in September, the soil bulk density reached a quasi-equilibrium state, because more than 3 months had already passed since the spring plowing (Table 1). The bulk density increased with the depth to reach relatively high values at 30 cm. The variability degree was low within the 100 × 100 m plot. However, the presence of outliers both of high and low values (Table 1) increases noticeably the variation coefficients related to different depths.

Table 1.   Bulk density of the soddy-podzolic soil in the experimental site
Full size table

The registered extreme low bulk density values can be explained by sampling the sod; whereas extreme high values in the lower part of profile may result partly from gravel grains occurring in the sample, since the thickness of mantle loam covering moraine deposits varies in the area of Chashnikovo Educational and Experimental Soil and Ecological Center, and the moraine even outcrops the day surface somewhere.

The normal probability plot for bulk density values shows that all the data, except for the two extreme values on the left and right, fit a straight line (Fig. 2). Applying the Dixon test [8] to these data, we find that they do not fit the general distribution and may be removed from the sample (the significance level α < 0.05). Since the sample was small, the removal of two values may have affected the final results. Therefore, for these data, a winsoring operation was performed, i.e., replacement with the values corresponding to the minimum and maximum values in the normal distribution with the relevant parameters for a given sample size.

Fig. 2.
figure 2

Normal probability plot of soil bulk density values (dv). Q(N) are quantiles of the normal distribution. The unfilled points correspond to the original values that were winzored.

Full size image

For the bulk density, the total average was equal to 1.31 g/cm3, and the variation coefficient amounted to 5.8%. As proceeds from the results of nested analysis of variance, the influence of both sampling points and depths appears to be insignificant, since the probability of exceeding (p-value) is α > 0.05. However, the average values change with depth, and if the possible spatial variability of bulk density is not taken into account, a complete illusion appears of this change regularity. A general trend in bulk density change with the depth can be observed (Fig. 3), but each individual bulk density profile differs from the others, and the diversity of these “individuals” prevents from elucidating a common dependency between bulk density and depth. This group of profiles fits the calculated data obtained from the pedotransfer function proposed for soddy-podzolic soils [19].

Fig. 3.
figure 3

Change in soil bulk density (dv) with depth (h). The dashed line shows the calculated values according to [19].

Full size image

Since the analysis of variance reveals the influence of neither depth nor location of the sampling point, we may assume that random causes control the total variation. Then the best estimate of the standard uncertainty (standard deviation of the analytical error) for the bulk density will be the root of the error mean square from the ANOVA table (Table 2):

$${{s}_{{{\text{analyt}}}}} = \sqrt {0.0056} = 0.075\,\,\left( {{{\text{g}} \mathord{\left/ {\vphantom {{\text{g}} {{\text{c}}{{{\text{m}}}^{{\text{3}}}}}}} \right. \kern-0em} {{\text{c}}{{{\text{m}}}^{{\text{3}}}}}}} \right).$$
Table 2.   Results of nested analysis of variance of bulk density determination
Full size table

Thus, the relative uncertainty will be equal to 0.075/1.32 × 100 = 5.7 ≈ 6%.

Comparing with the results obtained by other authors [3, 10, 15], we can see that this value is comparable with the coefficients of variation obtained from the analysis of different soils.

Analysis of SOC content uncertainty (laboratory at Moscow State University). The statistical characteristics of the organic matter content in the 0–30 cm layer studied at the 100 × 100 m plot using different sampling schemes differ somewhat. Thus, the samples from pits show the mean value and variance equal to 1.48% and 0.032(%)2, respectively; and for samples taken with an auger, they are 1.28% and 0.038(%)2.

The results of nested analysis of variance for organic carbon in the samples taken for bulk density in pits show that all the considered factors, except for replicate at the sampling point, affect the final results of determining the organic carbon content (Table 3). More than a half of value variability is controlled by the sampling point location at the site. As expected, the sampling depth exerts a strong effect. Replication at the sampling point does not affect the final result. But the variance of sample preparation is three times higher than the variance due to randomness.

Table 3.   Results of nested analysis of variance of organic carbon content for samples taken in pits
Full size table

The results of nested analysis of variance for organic carbon in samples taken by the auger show that all the considered factors, including replication at the sampling point, affect the final results of determining the organic carbon content (Table 4).

Table 4.   Results of nested analysis of variance of organic carbon content for samples taken by an auger
Full size table

Comparison of the results of different sampling schemes. This comparison (Fig. 4) shows that the input of random factors is almost the same, but the effect of sample preparation turned out to differ. The random variance standing for the analytical error is close in both cases.

Fig. 4.
figure 4

Contribution of factors (1—analysis, 2—sample preparation, 3—replication at the sampling point, and 4—location of the sampling point) to the total variance in the content of organic carbon in the samples taken (a) from the pits at depths of 0–10, 10–20, and 20–30 cm and (b) with an auger from a depth of 0–30 cm.

Full size image

The analytical schemes used for the samples in pits and those taken with an auger differ in the variability aggregation levels. In case of pits, the depth of sampling layer is taken into account; whereas for the samples taken by an auger this factor is implicitly included in the replication at the sampling point. But if to assume the repeatability factor at the sampling point from pits to be insignificant, then the sampling depth must be probably considered implicitly in the samples taken by the auger. This is also evidenced by the closeness of variances corresponding to these factors.

Analyzing the ratio of variances due to laboratory replication and random causes for samples taken by the auger, it can be seen that the estimates of the uncertainty associated with the sample preparation specifics twice exceed the analytical error of the method. This confirms the need to pay special attention to the standardization of sample preparation, which will help to reduce the overall uncertainty of the estimate.

A comparison of values corresponding to different sampling methods (sampling in pits and with an auger) at particular points proves that the samples taken by an auger show lower values at four out of five points (Table 5). The probability of this result due to random reasons can be calculated from the binomial distribution. Let us assume that the probability of positive and negative deviations of the difference of results is the same, being equal to p = 0.5. Then the probability of obtaining four negative results out of five tests will be equal to 16%:

$${{P}_{4}} = \frac{{5!}}{{4!~1!}}{{0.5}^{4}}~{{0.5}^{1}} = 0.1562,$$

which does not give grounds to believe these discrepancies being unlikely. That means that a deviation in one direction of the results obtained from different sampling methods seems to occur purely by chance. Note that upon such a comparison, only the deviation sign rather than its absolute value is taken into account. However, negative values are very likely to appear, since the samples taken by the auger covered the entire 30-cm thickness, whereas the samples from pits were attributed to the horizon centers. On one hand, sampling in the horizon centers aimed at bulk density estimation should give more correct results; however, it does not take into account the contrast to the over- and underlying horizons in the organic carbon content, which is manifested in Fig. 2. This could be taken into account by determining the organic carbon content in the underlying horizon and interpolating this value to the total depth.

Table 5.   Average values of organic carbon content in individual sampling points for a layer of 0–30 cm
Full size table

A comparison of the results shows that the influence of laboratories on the average level of values can be significant, since the laboratory of the Bryansk State Agrarian University produced overestimated results for three points on average. However, the number of samples co-analyzed is small to conclude unambiguously, since an accidental excess probability is (0.5)3 = 0.125. Nevertheless, the possible shifting of estimates should be always taken into consideration.

Analysis of SOC content uncertainty (Bryansk State Agrarian University). The nested analysis of variance of a sample part passed to the laboratory at the Bryansk State Agrarian University shows a good agreement with the analytical results obtained for the samples from pits, which attests to the stability of uncertainty estimates. However, upon the study of organic carbon content at the laboratory of Bryansk State Agrarian University, the factor “location of the sampling point” turned out to be insignificant (Table 6). The other factors (as in the cases described above) appeared to be significant, their variances being comparable with the previous cases.

Table 6. Nested analysis of variance for the results of repeated sample analysis
Full size table

To increase the degrees of freedom in the analytical error estimation, we may average the variances standing for random factors. Thus, the average analytical error of the organic carbon content sanalyt is:

$${{s}_{{{\text{analyt}}}}} = \sqrt {{{\left( {0.0033 \times 60 + 0.0021 \times 30 + 0.0022 \times 18} \right)} \mathord{\left/ {\vphantom {{\left( {0.0033 \times 60 + 0.0021 \times 30 + 0.0022 \times 18} \right)} {\left( {60 + 30 + 18} \right)}}} \right. \kern-0em} {\left( {60 + 30 + 18} \right)}}} = 0.052\left( \% \right),$$

which is below the standard uncertainty upon interlaboratory reproducibility, GOST 26213-2021, approximating to about 0.1% for different ranges of content.

The total variance due to sample preparation and error can be estimated by averaging the sums of analytical variance and sample preparation, namely 0.0130, 0.0070, 0.0099 (%2). This value can be av-eraged with the corresponding degrees of freedo-m:

$${{s}_{{{\text{sample}\_\text{prep}}}}} = \sqrt {{{\left( {0.0130 \times 30 + 0.0070 \times 15 + 0.0099 \times 9} \right)} \mathord{\left/ {\vphantom {{\left( {0.0130 \times 30 + 0.0070 \times 15 + 0.0099 \times 9} \right)} {\left( {30 + 15 + 9} \right)}}} \right. \kern-0em} {\left( {30 + 15 + 9} \right)}}} = 0.089\left( \% \right),$$

which also fits the standard uncertainty upon interlaboratory reproducibility.

Comparison of stock calculations according to different schemes with the same soil bulk density. Assuming the average bulk density and relative bulk density uncertainty being the same for the entire 30-cm layer, we come up with different organic carbon stocks on the test plot calculated by different schemes (Table 7). If we disregard the errors in determination of the layer thickness and the content of large fragments, the relative uncertainty of soil carbon stocks may be calculated from equation (5).

Table 7.   Comparison of the results of determination of carbon stock variation upon using different sampling methods
Full size table

The relative uncertainties of the averages should be smaller in \(\sqrt 5 \)times, since the number of sampling points was 5. Multiplying the averages by the relative uncertainty, we get the standard uncertainties, and after multiplying by a factor of 2, we get the relative probabilistic uncertainties (expanded uncertainties) with a confidence level of 95%. Thus, the final result of calculations of the average stocks of organic matter at the site will be 58.2 ± 7.0 t/ha for samples from pits and 50.3 ± 7.4 t/ha for samples taken by an auger.

DISCUSSION

As proceeds from our investigation, the “sample preparation” source, which includes drying the samples, grinding them and sifting through a 2-mm sieve, eliminating roots, grinding the soil mass and taking samples for analysis, stands for 11–26% of the total variability in soil carbon content (analyzed by the Tyurin method), which exceeds the analytical error proper. Therefore, the techniques providing for more thorough sample preparation can reduce significantly the influence of this uncertainty source. Removal of fine roots appears to be the key point. This procedure is often ignored; however, note that upon sample preparation, fragile dry roots are crushed to become hardly noticeable. Therefore, the use of a glass (ebonite) rod for root selection stabilizes the values of organic carbon content.

If the study is aimed at estimating the carbon content in a certain layer only, then calculating the values in thinner layers with subsequent summing them up creates the illusion of accuracy, although summing the values in the resultant layer raises uncertainty. The time spent for collecting a column of three samples by depth from pits (if sampling is performed according to the scheme described above) is 5–7 times longer the time spent for taking one sample with an auger. Analytical uncertainties when using samples of different shapes are comparable. This is also true for the assessment of total variation in soil carbon content at the site. However, if pure determination of the studied parameter is accompanied by additional analyses, e.g., assessment of soil respiration in different soil layers or investigation of biota species composition, then expenses for digging pits and sampling soil by layers will be quite justified.

The uncertainty of bulk density value, its variation coefficient not exceeding 6% at test plots of 1 ha in size, contributes insignificantly to the carbon stock estimate uncertainty; hence, just practically, knowledge on the bulk density values at each sampling point reduces insignificantly the carbon stock calculation uncertainty. Expenses for bulk density analysis upon sampling for carbon stocks study are incomparable with calculation error mitigation.

The analytical errors of the Tyurin method turned out to be practically the same in two laboratories, but the average values of organic matter content calculated in the laboratory at the Bryansk State Agrarian University were systematically higher than those obtained in the laboratory of the Faculty of Soil Science, Moscow State University. However, this fact can only be considered as the field for further research, since the since the number of replications was insufficient for making a statistical conclusion.

The study of organic carbon content in certified laboratories, a random order of analyzed samples, the control samples in analytical series, and the control over repeatability in each sample series by adding anonymous duplicate samples are mandatory conditions for monitoring soil properties.

Any, even very precise determination of a soil property, may turn out to be incorrect, if sampling, a method (or a laboratory) introduces systematic errors. A systematic error is always more difficult to discover.

Structuring uncertainties allows us to estimate the natural variation at a study area. Assessing it using different sampling schemes appears to give close results. This may possibly permit researchers to compare different landscapes by the value of natural variation of the analyzed property by specifying its portion in the total variability; and thus, to learn more about the processes causing this variation.

CONCLUSIONS

Spatial variation of a soil property over a certain area can be structured depending on the determining factors. Since information about the soil body is obtained from the analysis of soil samples (single or mixed), the first level of factors represents the possible errors proceeding from implementation of a particular protocol of soil mass analysis, which may be basically named analytical error. The maximum relative uncertainty for each analysis can usually be found in the corresponding GOST. Errors of this level for routine analyses do not exceed 10–15% and are often taken into account when interpreting the results.

The second level is errors associated with sample preparation. This uncertainty factor can contribute a lot, but as often assumed, it is already taken into account in the block of analytical errors. For example, selection of roots in the analysis of organic matter content, the degree of preliminary grinding and the method of taking an analytical sample from the prepared specimen can result in a wide scattering of values. This factor is usually disregarded completely, although, as shown above, it can cause 10% or more of the total variation.

The third level is sampling in the field. Depending on whether the samples were taken in soil profiles, or the soil sample was formed by mixing several subsamples either at fixed depths or by soil horizons, etc., errors may be different and, hence, the results obtained may be incomparable. For instance, comparison of data obtained in one pit with a mixed sample obtained over the whole site can lead to erroneous conclusions, since a single pit cannot reflect the entire variety of land properties.

The next level is the territorial one. It can be an agricultural field, several fields, a region, and so on.

The influence of each factor can be taken into account by nested analysis of variance; however, its applicability is limited by the requirements of independent data, same variances in factor levels, and obeying the law of normal population distribution for a property. At least, these requirements should be verified prior to analysis or known from previous studies.

Since such properties as layer thickness, bulk density and stoniness are used in carbon stock calculations they also contribute to the overall result uncertainty. Therefore, the total uncertainty of the result can be large. The use of mixed samples and special sampling schemes can significantly reduce these uncertainties sometimes.

Thus, the idea about the soil depends on the method of obtaining information about the object.

However, this fact is not always taken into account in soil studies. To assess the influence of factors of different origin, it is necessary to discriminate clearly between the scales of possible analytical errors and actual changes. The analysis of uncertainty sources associated with obtaining primary information should be an integral part of any soil research.