Quadratic Method of the Angular Resolution of Two Closely Spaced Targets

Abstract

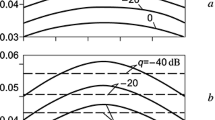
A method for the formation of measurements of the angular coordinates of two closely spaced point targets by four independent receivers located at the same distance from each other is proposed. It is shown that the target angles are determined by the fixed points of some linear fractional transformation and can be found by solving a quadratic equation with complex coefficients. A method for calculating the accuracy of measuring the angular coordinates and a criterion for target resolution are substantiated. Results of numerical analysis on a model example are given. The method is designed for measuring the angular coordinates of two closely spaced targets and the elevation angle of a low-flying target against the background of the underlying surface (marine or terrestrial), as well as for measuring the coordinates of the target under the conditions of active interference.

APPENDIX

Proof of assertion 1. From the first three equations of system (4), it follows that ${{z}_{1}}$ and ${{z}_{2}}$ are symmetric with respect to the linear fractional transformation [10]

$${\varsigma } = \frac{{S_{1}^{*}z - S_{2}^{*}}}{{S_{0}^{*}z - S_{1}^{*}}},$$

i.e., ${{z}_{1}} = \varsigma ({{z}_{2}})$ and ${{z}_{2}} = \varsigma ({{z}_{1}}).$ Similarly, from the last three equations (4), it follows that ${{z}_{1}}$ and ${{z}_{2}}$ are symmetric with respect to the linear fractional transformation

$$\omega = \frac{{S_{2}^{*}\varsigma - S_{3}^{*}}}{{S_{1}^{*}\varsigma - S_{2}^{*}}}.$$

Therefore, the points ${{z}_{1}}$ and ${{z}_{2}}$ are fixed points of a linear fractional transformation $\rho = \omega (\varsigma (z)),$ which, as is easily seen, is given in (5), and Eq. (6) is obtained from the condition $z = \rho (z)$ by elementary transformations.

Proof of assertion 2. First, let us establish the following fact. Given a complex number $z = {{z}_{x}} + i{{z}_{y}}.$ Consider the function $\mu (z) = \arg z.$ Impart a small increment $\varepsilon = {{\varepsilon }_{x}} + i{{\varepsilon }_{y}}$ to the number z: ${{z}_{1}} = z + \varepsilon ,$$\left| \varepsilon \right| \ll \left| z \right|.$ Then, for the increment of the argument, we have

$$\begin{gathered} \Delta \mu = \mu ({{z}_{1}}) - \mu (z) \approx \frac{1}{{{{{\left| z \right|}}^{2}}}}( - {{\varepsilon }_{x}}{{z}_{y}} + {{\varepsilon }_{y}}{{z}_{x}}) \\ = \frac{1}{{{{{\left| z \right|}}^{2}}}}\operatorname{Im} \left( {\varepsilon \bar {z}} \right). \\ \end{gathered} $$

((A.1))

Consider the functions ${{z}_{1}}({\mathbf{S}}{\text{*}})$ and ${{z}_{2}}({\mathbf{S}}{\text{*}})$ defined implicitly by the system of equations (4) in a small neighborhood of the solution. Impart a small increment to the variable $S_{j}^{*}.$ Let $\tilde {S}_{j}^{*} = S_{j}^{*} + {{\xi }_{j}}.$ Denote the elements of the matrix ${\mathbf{H}}$with the numbers $(2,j)$ and $(4,j)$ by ${{a}_{j}}$ and ${{b}_{j}}\,:$

$${{a}_{j}} = \frac{{\partial {{z}_{1}}}}{{\partial S_{j}^{*}}},\,\,\,\,{{b}_{j}} = \frac{{\partial {{z}_{2}}}}{{\partial S_{j}^{*}}}.$$

Then, in accordance with formula (A.1), for the increments of the arguments of the functions ${{z}_{1}}({\mathbf{S}}{\text{*}})$ and ${{z}_{2}}({\mathbf{S}}{\text{*}})$, we obviously have

$$\Delta {{\mu }_{1}} = \frac{1}{{{{{\left| {{{z}_{1}}} \right|}}^{2}}}}\operatorname{Im} \left( {{{a}_{j}}\varepsilon {{{\bar {z}}}_{1}}} \right),\,\,\,\,\Delta {{\mu }_{2}} = \frac{1}{{{{{\left| {{{z}_{2}}} \right|}}^{2}}}}\operatorname{Im} \left( {{{b}_{j}}\varepsilon {{{\bar {z}}}_{2}}} \right).$$

This proves formulas (10) and (11).