Skip to main content
SpringerLink
Log in

On the capillary stability of a cylindrical dielectric liquid jet in a longitudinal electrostatic field

  • Gases and Liquids
  • Published:
Technical Physics Aims and scope Submit manuscript

Abstract

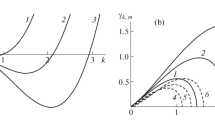
A dispersion relation is derived for capillary waves with arbitrary symmetry (with arbitrary azimuthal numbers) on the surface of a cylindrical jet of an ideal incompressible dielectric liquid subjected to an electrostatic field aligned with the symmetry axis of the jet. It is shown that only long axisymmetric waves can experience capillary instability in such a system. The wavenumber range into which unstable waves fall begins with a zero value, and its width depends on the permittivities of the liquid and ambient and on the electrostatic field strength squared. As the field strength grows, the wavenumber range for unstable waves rapidly narrows and the capillary instability growth rate, as well as the wavenumber of the wave with the greatest growth rate, decreases.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. J. W. Strutt (Lord Rayleigh), Proc. London Math. Soc. 10, 4 (1878).

    Article  Google Scholar 

  2. J. W. Strutt (Lord Rayleigh), The Theory of Sound (Dover, New York, 1945; Gostekhizdat, Moscow, 1955), Vol. 2.

    MATH  Google Scholar 

  3. V. M. Entov and A. L. Yarin, Itogi Nauki Tekh., Ser.: Mekh. Zhidk. Gaza 17, 112 (1984).

    Google Scholar 

  4. E. V. Ametistov, V. V. Blazhenkov, A. K. Gorodov, et al., Monodispersion of Matter: Principles and Applications, Ed. by V. A. Grigor’ev (Energoatomizdat, Moscow, 1991) [in Russian].

    Google Scholar 

  5. S. O. Shiryaeva, A. I. Grigor’ev, and M. V. Volkova, Spontaneous Capillary Disintegration of Charged Jets (Yaroslavsk. Gos. Univ., Yaroslavl’, 2007) [in Russian].

    Google Scholar 

  6. J. Eggers and E. Willermaux, Rep. Prog. Phys. 71, 036601 (2008).

    Article  ADS  Google Scholar 

  7. Ya. I. Frenkel’, Zh. Eksp. Teor. Fiz. 6, 348 (1936).

    Google Scholar 

  8. N. K. Nayyar and G. S. Murty, Proc. Phys. Soc. 75, 369 (1960).

    Article  Google Scholar 

  9. G. A. Glonti, Zh. Eksp. Teor. Fiz. 34, 1328 (1958) [Sov. Phys. JETP 7, (1958)].

    Google Scholar 

  10. R. J. Raco, AIAA J. 6, 979 (1968).

    Article  ADS  Google Scholar 

  11. D. A. Saville, J. Fluid. Mech. 48, 815 (1971).

    Article  MATH  ADS  Google Scholar 

  12. A. J. Mestel, J. Fluid. Mech. 312, 311 (1996).

    Article  MATH  MathSciNet  ADS  Google Scholar 

  13. A. A. Shutov, Izv. Ross. Akad. Nauk, Mekh. Zhidk. Gaza, No. 6, 52 (2006).

    MathSciNet  Google Scholar 

  14. D. F. Belonozhko and A. I. Grigor’ev, Zh. Tekh. Fiz. 74(11), 22 (2004) [Tech. Phys. 49, 1422 (2004)].

    Google Scholar 

  15. V. G. Levich, Physicochemical Hydrodynamics (Fizmatgiz, Moscow, 1959; Prentice Hall, Englewood Cliffs, 1962).

    Google Scholar 

  16. M. Cloupeau and B. Prunet Foch, J. Electrost. 25, 165 (1990).

    Article  Google Scholar 

  17. A. Jaworek and A. Krupa, J. Aerosol Sci. 30, 873 (1999).

    Article  Google Scholar 

  18. S. O. Shiryaeva and A. I. Grigor’ev, J. Electrost. 34, 51 (1995).

    Article  Google Scholar 

  19. S. O. Shiryaeva, A. I. Grigor’ev, and A. A. Svyatchenko, RF Preprint No. 25, IMI RAN (Institute of Microelectronics and Informatics RAN, Yaroslavl’, 1993).

  20. A. I. Grigor’ev, Zh. Tekh. Fiz. 77(2), 31 (2007) [Tech. Phys. 52, 173 (2007)].

    MathSciNet  Google Scholar 

  21. A. I. Grigor’ev and D. M. Pozharitskii, Zh. Tekh. Fiz. 78(10), 40 (2008) [Tech. Phys. 53, 1289 (2008)].

    Google Scholar 

  22. A. F. Aleksandrov, V. L. Bychkov, L. P. Grachev, et al., Zh. Tekh. Fiz. 76(3), 38 (2006) [Tech. Phys. 51, 330 (2006)].

    Google Scholar 

  23. A. I. Grigor’ev and S. O. Shiryaeva, Zh. Tekh. Fiz. 62(12), 9 (1992) [Sov. Phys. Tech. Phys. 37, 1136 (1992)].

    Google Scholar 

  24. N. B. Zolotoi, G. V. Karpov, and V. E. Skurat, Zh. Tekh. Fiz. 58, 315 (1988) [Sov. Phys. Tech. Phys. 33, 193 (1988)].

    Google Scholar 

  25. S. O. Shiryaeva and A. I. Grigor’ev, Zh. Tekh. Fiz. 63(8), 162 (1993) [Tech. Phys. 38, 715 (1993)].

    Google Scholar 

  26. S. O. Shiryaeva, A. I. Grigor’ev, T. V. Levchuk, and M. V. Rybakova, Zh. Tekh. Fiz. 73(5), 5 (2003) [Tech. Phys. 48, 527 (2003)].

    Google Scholar 

  27. S. O. Shiryaeva, A. I. Grigor’ev, and T. V. Levchuk, Zh. Tekh. Fiz. 73(11), 22 (2003) [Tech. Phys. 48, 1380 (2003)].

    Google Scholar 

  28. A. I. Grigor’ev, N. V. Voronina, and S. O. Shiryaeva, Zh. Tekh. Fiz. 78(2), 33 (2008) [Tech. Phys. 53, 173 (2008)].

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Demidov State University, Sovetskaya ul. 14, Yaroslavl, 150000, Russia

    S. O. Shiryaeva

Authors
  1. S. O. Shiryaeva
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. O. Shiryaeva.

Additional information

Original Russian Text © S.O. Shiryaeva, 2010, published in Zhurnal Tekhnicheskoǐ Fiziki, 2010, Vol. 80, No. 2, pp. 45–50.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Shiryaeva, S.O. On the capillary stability of a cylindrical dielectric liquid jet in a longitudinal electrostatic field. Tech. Phys. 55, 204–209 (2010). https://doi.org/10.1134/S1063784210020076

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S1063784210020076

Keywords

Search

Navigation