1 INTRODUCTION

Pulses of electromagnetic field are often used to heat plasma (see, for example, [1, 2]). Herewith, the patterns of heating depend on how field of the pulse penetrates into the plasma. At the same time, heating of particles is accompanied by a change in plasma conductivity, as a result of which field penetration changes. Thus, under conditions of strong heating of electrons and ions, the problem of field penetration into the plasma becomes essentially nonlinear. Consistent description of field penetration implies a joint solution of the coupled system of nonlinear equations for temperatures of electrons and ions and an equation for electric field strength. The explicit form of these equations depends on plasma density, particle temperatures, pulse duration and field strength. Due to the large number of parameters acting the penetration of the field, penetration modes of the heating pulse into plasma are very diverse. Field penetration into plasma with varying particle temperatures over time has been considered in a number of papers. In [3–7], skin effect is described under conditions of turbulent heating of electrons. Nonlinear penetration of monochromatic field into plasma with ion-acoustic turbulence was studied in [8, 9]. Penetration of strong quasistationary electric field into nonisothermal plasma was studied in [6, 10, 11]. A number of works are devoted to consideration of penetration of relatively weak electric field into turbulent [12–14] or laminar [15] plasma with time-varying electron and ion temperatures. Herewith, a time limit of electromagnetic pulse effect was taken into account [14, 15]. Effect of a strong heating electromagnetic pulse on laminar plasma was studied in [16]. In [16], a numerical solution of the coupled system of equations for electric field strength and temperatures of electrons and ions was given, which allowed us to describe the effect of electron heat transfer on field penetration. The present communication is devoted to further study of penetration of a heating electromagnetic pulse into laminar plasma under conditions similar to those considered in [16], but taking into account effect of constant magnetic field on heat transfer by electrons and ions.

Below we consider effect of an electromagnetic pulse on plasma in constant magnetic field directed along its surface. Electric field of the acting pulse is directed along the magnetic field. As field penetrates into plasma, electrons and ions are heated inhomogeneously, which is accompanied by heat transfer into the depth of plasma across the magnetic field. Presence of an electron temperature gradient across the magnetic field leads to appearance of current and field strength components in the direction orthogonal to the polarization direction of the acting pulse. This article gives derivation of a coupled system of nonlinear equations for temperatures of electrons and ions and components of electric field strength directed along and across the magnetic field. For the parameters of relatively cold rarefied plasma, which are close to those in facilities with magnetic confinement, a numerical solution of mentioned nonlinear equations is obtained under effect of a quite strong millisecond pulse on the plasma. A detailed analysis of time evolution and distribution over width of the plasma layer of electron and ion temperatures is given. It is shown to what extent heating of electrons worsens penetration of the field into the plasma. The degree of influence of inhomogeneous heating on the field skinning depends on magnitude of the constant magnetic field, which changes heat transfer by electrons and ions. It is found that strong magnetic field leads to suppression the “inverse” skin effect [17]. Nonmonotonic influence of the magnetic field on polarization of electric field inside plasma is described. It is shown that with an increase in magnitude of the magnetic field, a state of plasma with large difference of electron and ion temperatures occurs.

2 CURRENT AND HEAT FLUX DENSITY

Let us consider fully ionized plasma in constant magnetic field \({\mathbf{B}} = (0,0,B)\). Let us accept that the electric field \({\mathbf{E}} = {\mathbf{E}}(x,t)\) and electron temperature and density gradients lead to small deviations of the distribution function of electrons \(\delta f = \delta f({\mathbf{v}},x,t)\) from the Maxwell distribution \({{f}_{m}} = n{{(2\pi {{v}_{T}})}^{{ - 3}}}\exp ( - {{v}^{2}}{\text{/}}2v_{T}^{2})\), where \({{v}_{T}} = \sqrt {\varkappa T{\text{/}}m} \), \(\varkappa \) is the Boltzmann constant, m is the electron mass, \(n = n(x,t)\) and \(T = T(x,t)\) are electron density and temperature. To determine \(\delta f\), we use the kinetic equation of the form

$$\begin{gathered} \frac{1}{2}\nu (v)\frac{\partial }{{\partial {{v}_{\alpha }}}}({{v}^{2}}{{\delta }_{{\alpha \beta }}} - {{v}_{\alpha }}{{v}_{\beta }})\frac{\partial }{{\partial {{v}_{\beta }}}}\delta f \\ \, - \Omega ([{\mathbf{v}} \times {\mathbf{b}}]\frac{\partial }{{\partial {\mathbf{v}}}})\delta f = ({\mathbf{d}} \cdot {\mathbf{v}}){{f}_{m}}. \\ \end{gathered} $$
(1)

Here, \(\nu (v)\) is the frequency of electron–ion collisions, \(\nu (v) = 4\pi {{Z}^{2}}{{e}^{4}}n\Lambda {{m}^{{ - 2}}}{{v}^{{ - 3}}}\), e is the charge of electron, Λ is the Coulomb logarithm, \( - Ze = {{e}_{i}}\) is the charge of ion, \(\Omega = eB{\text{/}}mc\) is the cyclotron frequency, c is the speed of light, \({\mathbf{b}} = {\mathbf{B}}{\text{/}}B = (0,0,1)\) is the unit vector along the magnetic field,

$${\mathbf{d}} = - \frac{{e{\mathbf{E}}}}{{\varkappa T}} + \nabla \ln n + \left( {\frac{{m{{v}^{2}}}}{{2\varkappa T}} - \frac{3}{2}} \right)\nabla \ln T.$$
(2)

In Eq. (1), the electron–ion collision integral is written in the Fokker–Planck form. The term containing the cyclotron frequency describes the effect of the Lorentz force on electrons, and the right-hand side of Eq. (1) is the result of the effect of electric field and spatial gradients on the Maxwell distribution function.

Equation (1) is written taking into account several assumptions. In addition to the smallness of \(\delta f\) compared to \({{f}_{m}}\), this equation does not take into account the term \(\partial \delta f{\text{/}}\partial t\), which is certainly justified for \(\nu (v)t \gg 1\). Furthermore, the collision integral in Eq. (1) takes into account only elastic collisions of electrons with ions. The last approximation leads to small corrections \( \lesssim {\kern 1pt} 1{\text{/}}\sqrt 2 Z\) when calculating electron fluxes (see, for example, [18]). In the problem of nonlinear penetration of a heating pulse into plasma considered below, the use of a more complex collision integral seems premature. In these approximations, the solution of the equation for \(\delta f\) has the form

$$\begin{gathered} \delta f = - \frac{1}{{\nu (v)}}({\mathbf{b}} \cdot {\mathbf{v}})({\mathbf{b}} \cdot {\mathbf{d}}){{f}_{m}} \\ \, + \frac{\Omega }{{{{\Omega }^{2}} + {{\nu }^{2}}(v)}}({\mathbf{v}} \cdot [{\mathbf{b}} \times {\mathbf{d}}]){{f}_{m}} \\ \, + \frac{{\nu (v)}}{{{{\Omega }^{2}} + {{\nu }^{2}}(v)}}({\mathbf{v}} \cdot [{\mathbf{b}} \times [{\mathbf{b}} \times {\mathbf{d}}]]){{f}_{m}}. \\ \end{gathered} $$
(3)

Equation (3) allows us to see under what restrictions on the value d the condition \({\text{|}}\delta f{\text{|}} \ll {{f}_{m}}\) is satisfied. Further, using Eq. (3), we find the current density

$$\begin{gathered} {\mathbf{j}} = e\int d{\mathbf{v}}\,{\mathbf{v}}\delta f = \frac{{en}}{\nu }v_{T}^{2}\left\{ {\mathop {I(1,10)[{\mathbf{b}} \times {{{\mathbf{d}}}_{0}}]}\limits_{} } \right. \\ \, + I(1,12)[{\mathbf{b}} \times {{{\mathbf{d}}}_{1}}] + I(0,7)[{\mathbf{b}} \times [{\mathbf{b}} \times {{{\mathbf{d}}}_{0}}]] \\ \, + I(0,9)[{\mathbf{b}} \times [{\mathbf{b}} \times {{{\mathbf{d}}}_{1}}]] - \left. {\frac{{32}}{{\sqrt {2\pi } }}{\mathbf{b}}({\mathbf{b}} \cdot ({{{\mathbf{d}}}_{0}} + 8{{{\mathbf{d}}}_{1}}))} \right\}. \\ \end{gathered} $$
(4)

When writing expression (4), next notations are used:

$$\begin{gathered} {{{\mathbf{d}}}_{0}} = - \frac{{e{\mathbf{E}}}}{{\varkappa T}} + \nabla \ln n - \frac{3}{2}\nabla \ln T, \\ {{{\mathbf{d}}}_{1}} = \frac{1}{2}\nabla \ln T,\quad \nu \equiv \nu ({{v}_{T}}), \\ \end{gathered} $$
(5)

and also \(I(s,p)\), where s and p are integers. The explicit form of the integrals \(I(s,p)\) depends on the ratio of the cyclotron frequency to the collision frequency:

$$I(s,p) = \frac{2}{{3\sqrt {2\pi } }}\int\limits_0^\infty {du} \frac{{{{u}^{p}}{{{(\Omega {\text{/}}\nu )}}^{s}}}}{{1 + {{u}^{6}}{{{(\Omega {\text{/}}\nu )}}^{2}}}}\exp \left( { - \frac{{{{u}^{2}}}}{2}} \right).$$
(6)

A similar calculation makes it possible to represent the heat flux density \({\mathbf{q}}\) in the form

$$\begin{gathered} {\mathbf{q}} = \frac{m}{2}\int d{\mathbf{v}}{\kern 1pt} {\mathbf{v}}{{v}^{2}}\delta f = \frac{{nm}}{{2\nu }}v_{T}^{4}\left\{ {\mathop {I(1,12)[{\mathbf{b}} \times {{{\mathbf{d}}}_{0}}]}\limits_{} } \right. \\ \, + I(1,14)[{\mathbf{b}} \times {{{\mathbf{d}}}_{1}}] + I(0,9)[{\mathbf{b}} \times [{\mathbf{b}} \times {{{\mathbf{d}}}_{0}}]] \\ \, + I(0,11)[{\mathbf{b}} \times [{\mathbf{b}} \times {{{\mathbf{d}}}_{1}}]] - \left. {\frac{{256}}{{\sqrt {2\pi } }}{\mathbf{b}}({\mathbf{b}} \cdot ({{{\mathbf{d}}}_{0}} + 10{{{\mathbf{d}}}_{1}}))} \right\}. \\ \end{gathered} $$
(7)

Formulas (4)–(7) form the basis for further consideration of the effect of charge and energy transfer of electrons on the nonlinear penetration of a heating pulse into plasma.

3 EQUATIONS FOR FIELD STRENGTH AND TEMPERATURES OF PARTICLES

Let us assume that a plasma layer with thickness L occupies domain \(0 < x < L\), and the constant magnetic field is directed along the layer surface along the \(Oz\) axis. This layer is affected by an electromagnetic pulse, whose the electric field strength has the form \({{{\mathbf{E}}}_{0}}(x,t) = (0,0,{{E}_{0}}(x,t)),\)

$${{E}_{0}}(x,t) = {{E}_{0}}\exp \left[ { - {{{\left( {\frac{{x - ct}}{{c{{t}_{{\text{p}}}}}}} \right)}}^{{2g}}}} \right],$$
(8)

where the parameter g determines the rate of switching on and off the pulse, the time \({{t}_{{\text{p}}}}\) determines full duration at half maximum according to the expression \(2{{t}_{{\text{p}}}}{{(\ln 2)}^{{1/2g}}}\). The pulse acting on the plasma layer creates the electromagnetic field inside plasma, which is inhomogeneous along the \(Ox\) axis. Let us consider such conditions under which the time of inhomogeneous field variation is much longer than the reciprocal conductivity of the plasma. Under these conditions, the displacement current can be neglected in Maxwell’s equations. Since the field is inhomogeneous only along the \(Ox\) axis, \({\mathbf{E}} = {\mathbf{E}}(x,t)\), \({\mathbf{B}} = {\mathbf{B}}(x,t)\), then \({{(\nabla \times {\mathbf{B}})}_{x}} = 0\). Herewith, taking into account the smallness of the displacement current from the equation \(\nabla \times {\mathbf{B}} = (4\pi {\text{/}}c){\mathbf{j}}\) we approximately have \({{j}_{x}} \simeq 0\). It follows from this and from the continuity equation that change of density can be neglected. We neglect the slow directed motion of ions, since \({{m}_{i}} \gg m{\text{/}}Z\), \({{m}_{i}}\) is the ion mass. In this approximation, the current density is mainly determined by the electrons, and from formulas \({{j}_{x}} \simeq 0\) and (4), (5) we obtain the electric field strength component \({{E}_{x}}\):

$$\begin{gathered} {{E}_{x}} = \frac{1}{{I(0,7)}} \\ \, \times \left\{ { - I(1,10){{E}_{y}} + \frac{1}{2}\left[ {I(0,9) - 3I(0,7)} \right]\frac{1}{e}\frac{\partial }{{\partial x}}\varkappa T} \right\}. \\ \end{gathered} $$
(9)

Taking into account formula (9) and the smallness of the displacement current from the Maxwell’s equations we obtain two equations for the components \({{E}_{y}}\) and \({{E}_{z}}\) of the electric field strength

$$\begin{gathered} \frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}}{{E}_{y}} = \frac{{\omega _{{\text{p}}}^{2}}}{{{{c}^{2}}}}\frac{\partial }{{\partial t}}\left[ {\left( {I(0,7) + \frac{{{{I}^{2}}(1,10)}}{{I(0,7)}}} \right)\frac{{{{E}_{y}}}}{\nu }} \right] \\ \, + \frac{{\omega _{{\text{p}}}^{2}}}{{{{c}^{2}}}}\frac{\partial }{{\partial t}}\left\{ {\left[ {I(1,12) - \frac{{I(0,9)}}{{I(0,7)}}I(1,10)} \right]\frac{1}{{2e\nu }}\frac{\partial }{{\partial x}}\varkappa T} \right\}, \\ \end{gathered} $$
(10)
$$\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}}{{E}_{z}} = \frac{{\omega _{{\text{p}}}^{2}}}{{{{c}^{2}}}}\frac{\partial }{{\partial t}}\left[ {\frac{{32}}{{\sqrt {2\pi } }}\frac{{{{E}_{z}}}}{\nu }} \right],$$
(11)

where \({{\omega }_{{\text{p}}}} = (4\pi {{e}^{2}}n{\text{/}}m{{)}^{{1/2}}}\) is the Langmuir electron frequency.

There is no field inside plasma layer at the instant the acting pulse is switched on. Therefore the initial conditions for Eqs. (10), (11) have the form

$${{E}_{y}}(x,t \to - \infty ) = 0,\quad {{E}_{z}}(x,t \to - \infty ) = 0.$$
(12)

The boundary conditions are derived from the continuity conditions for the tangential field components at the layer boundaries. Taking into account the smallness of the displacement current the boundary conditions have the form:

$$\begin{gathered} {{\left. {\frac{\partial }{{\partial x}}{{E}_{y}}(x,t)} \right|}_{{x = 0,L}}} = 0, \\ {{\left. {\frac{\partial }{{\partial x}}{{E}_{z}}(x,t)} \right|}_{{x = 0}}} = - \frac{{2{{E}_{0}}}}{c}\frac{d}{{dt}}\exp \left[ { - {{{\left( {\frac{t}{{{{t}_{{\text{p}}}}}}} \right)}}^{{2g}}}} \right], \\ {{\left. {\frac{\partial }{{\partial x}}{{E}_{z}}(x,t)} \right|}_{{x = L}}} = 0. \\ \end{gathered} $$
(13)

According to Eqs. (10), (11), the evolution of the field components depends on how the electron temperature changes. In turn, the heating of electrons is due to the absorption of the electric field and is described by the equation

$$\frac{3}{2}n\varkappa \frac{\partial }{{\partial t}}T + \frac{\partial }{{\partial x}}{{q}_{x}} = {\mathbf{j}} \cdot {\mathbf{E}} - \frac{3}{2}{{\nu }_{T}}n\varkappa (T - {{T}_{i}}),$$
(14)

where \({{T}_{i}} = {{T}_{i}}(x,t)\), \({{\nu }_{T}} = (2m{\text{/}}{{m}_{i}}){{\nu }_{{ei}}}\) is the frequency of electron temperature relaxation, \({{\nu }_{{ei}}} = (\sqrt 2 {\text{/}}3\sqrt \pi )\nu \), \({{q}_{x}}\) and j are defined by formulas (4)−(7). Taking into account these formulas and formula (9), which allows to eliminate the field strength component \({{E}_{x}}\), we represent Eq. (14) as

$$\begin{gathered} \frac{3}{2}n\varkappa \frac{\partial }{{\partial t}}T \\ \, + \varkappa T\frac{\partial }{{\partial x}}\left\{ {\frac{{en}}{{2m\nu }}{{E}_{y}}\left[ {I(1,12) - \frac{{I(0,9)}}{{I(0,7)}}I(1,10)} \right]} \right\} \\ \end{gathered} $$
$$\, - \frac{\partial }{{\partial x}}\left\{ {\frac{{n\varkappa T}}{{4m\nu }}\left[ {I(0,11) - \frac{{{{I}^{2}}(0,9)}}{{I(0,7)}}} \right]\frac{\partial }{{\partial x}}\varkappa T} \right\}$$
(15)
$$\begin{gathered} \, = \frac{{32}}{{\sqrt {2\pi } }}\frac{{{{e}^{2}}n}}{{m\nu }}E_{z}^{2} + \frac{{{{e}^{2}}n}}{{m\nu }}\left[ {I(0,7) + \frac{{{{I}^{2}}(1,10)}}{{I(0,7)}}} \right]E_{y}^{2} \\ \, - \frac{3}{2}{{\nu }_{T}}n\varkappa (T - {{T}_{i}}). \\ \end{gathered} $$

The last term in Eq. (15) determines the energy density that is transferred to the ions per unit time, which is accompanied by their heating. Herewith, the evolution of the ion temperature is described by the eq-uation

$$\frac{3}{2}{{n}_{i}}\varkappa \frac{\partial }{{\partial t}}{{T}_{i}} + \frac{\partial }{{\partial x}}{{q}_{{ix}}} = \frac{3}{2}{{\nu }_{T}}{{n}_{i}}\varkappa (T - {{T}_{i}}).$$
(16)

In Eq. (16) for the density of the \(x\)-component of the ion heat flux, we use the expression obtained in the thirteen-moment approximation of the Grad method [19]:

$${{q}_{{ix}}} = - \frac{5}{2}\frac{{{{n}_{i}}\varkappa {{T}_{i}}}}{{{{m}_{i}}}}\frac{{{{\nu }_{{ii}}}}}{{\nu _{{ii}}^{2} + \Omega _{i}^{2}}}\frac{\partial }{{\partial x}}\varkappa {{T}_{i}},$$
(17)

where \({{\Omega }_{i}} = {{e}_{i}}B{\text{/}}{{m}_{i}}c\) is the ion cyclotron frequency. \({{\nu }_{{ii}}} = (16\sqrt \pi {\text{/}}15){{Z}^{3}}{{e}^{4}}n\Lambda {\text{/}}\sqrt {{{m}_{i}}} {{(\varkappa {{T}_{i}})}^{{3/2}}}\) is the effective frequency of ion–ion collisions. The equations for the temperatures of electrons and ions correspond to the initial conditions

$$T(x,t \to - \infty ) = {{T}_{i}}(x,t \to - \infty ) = {{T}_{0}},$$

and the boundary conditions ensuring the absence of heat flux at the layer boundaries:

$$\begin{gathered} \left\{ {\frac{\varkappa }{2}\left[ {I(0,11) - \frac{{{{I}^{2}}(0,9)}}{{I(0,7)}}} \right]} \right.\frac{\partial }{{\partial x}}T \\ {{\left. {\left. {\, - e{{E}_{y}}\left[ {I(1,12) - \frac{{I(0,9)}}{{I(0,7)}}I(1,10)} \right]} \right\}} \right|}_{{x = 0,L}}} = 0, \\ {{\left. {\frac{{\partial {{T}_{i}}}}{{\partial x}}} \right|}_{{x = 0,L}}} = 0, \\ \end{gathered} $$
(18)

where \({{T}_{0}}\) is the plasma temperature before the electromagnetic pulse effect. Note that the boundary condition including the electron temperature gradient takes into account the influence of the \({{E}_{y}}\) electric field strength component on the heat flux. Equations (10), (11), (15), and (16) allow us to consider the patterns of penetration of a heating electromagnetic pulse into the plasma, placed in constant magnetic field.

4 DIMENSIONLESS VARIABLES AND MAIN PARAMETERS

In order to solve numerically the equations for the electric field strength components and temperatures of particles, we introduce dimensionless time and coordinate variables

$$\tau = {{\nu }_{T}}(0)t,\quad \xi = \frac{{8{{\omega }_{{{\text{L}}i}}}}}{{c\sqrt {3\pi Z} }}x,$$
(19)

where \({{\omega }_{{{\text{L}}i}}} = \sqrt {4\pi Zn{{e}^{2}}{\text{/}}{{m}_{i}}} \) is the Langmuir ion frequency, \({{\nu }_{T}}(0)\) is the frequency of temperature relaxation before the electromagnetic pulse effect, i.e., when \(t \to - \infty \). As units for temperature and field strength we choose \({{T}_{0}}\) and \({{E}_{0}}\sqrt {3\pi Z} {\text{/}}2{{\omega }_{{{\text{L}}i}}}{{t}_{{\text{p}}}}\), respectively:

$$u = \frac{T}{{{{T}_{0}}}},\quad v = \frac{{{{T}_{i}}}}{{{{T}_{0}}}},\quad {{\mathcal{E}}_{{y,z}}} = \frac{{2{{\omega }_{{{\text{L}}i}}}{{t}_{{\text{p}}}}}}{{{{E}_{0}}\sqrt {3\pi Z} }}{{E}_{{y,z}}}.$$
(20)

In the new variables, Eqs. (10), (11) take the form

$$\begin{gathered} \frac{{{{\partial }^{2}}}}{{\partial {{\xi }^{2}}}}{{\mathcal{E}}_{y}} = \frac{{\sqrt {2\pi } }}{{32}}\frac{\partial }{{\partial \tau }}\left\{ {\left[ {I(0,7) + \frac{{{{I}^{2}}(1,10)}}{{I(0,7)}}} \right]{{u}^{{3/2}}}{{\mathcal{E}}_{y}}} \right\} \\ \, + {{\beta }_{T}}\frac{\partial }{{\partial \tau }}\left\{ {\left[ {I(1,12) - \frac{{I(0,9)}}{{I(0,7)}}I(1,10)} \right]{{u}^{{3/2}}}\frac{{\partial u}}{{\partial \xi }}} \right\}, \\ \end{gathered} $$
(21)
$$\frac{{{{\partial }^{2}}}}{{\partial {{\xi }^{2}}}}{{\mathcal{E}}_{z}} = \frac{\partial }{{\partial \tau }}[{{u}^{{3/2}}}{{\mathcal{E}}_{z}}],$$
(22)

where the parameter \({{\beta }_{T}}\) characterizes generation efficiency of the \({{\mathcal{E}}_{y}}\) electric field strength component due to inhomogeneity of the electron temperature,

$${{\beta }_{T}} = \frac{1}{{6\sqrt {2\pi } }}\frac{{\varkappa {{T}_{0}}}}{{Ze{{E}_{0}}c}}\omega _{{Li}}^{2}{{t}_{p}}.$$
(23)

The integrals \(I(s,p)\) (6) in the new variables take the form

$$I(s,p) = \frac{2}{{3\sqrt {2\pi } }}\int\limits_0^\infty {dy} \frac{{{{y}^{p}}{{b}^{s}}{{u}^{{3s/2}}}(\xi ,\tau )}}{{1 + {{y}^{6}}{{b}^{2}}{{u}^{3}}(\xi ,\tau )}}\exp \left( { - \frac{{{{y}^{2}}}}{2}} \right),$$
(24)

where the parameter b determines the degree of magnetic field effect on the electron transport

$$b = \frac{{\sqrt 2 \Omega }}{{3\sqrt \pi {{\nu }_{{ei}}}(0)}},$$
(25)

\({{\nu }_{{ei}}}(0)\) is the frequency of electron–ion collisions when \(t \to - \infty \). The initial and boundary conditions take the form

$${{\mathcal{E}}_{{y,z}}}(\xi ,\tau \to - \infty ) = 0,$$
(26)
$$\begin{gathered} {{\left. {\frac{{\partial {{\mathcal{E}}_{y}}(\xi ,\tau )}}{{\partial \xi }}} \right|}_{{\xi = 0,\mathcal{L}}}} = 0,\quad {{\left. {\frac{{\partial {{\mathcal{E}}_{z}}(\xi ,\tau )}}{{\partial \xi }}} \right|}_{{\xi = \mathcal{L}}}} = 0, \\ {{\left. {\frac{{\partial {{\mathcal{E}}_{z}}(\xi ,\tau )}}{{\partial \xi }}} \right|}_{{\xi = 0}}} = \mu (\tau ) = g{{\left( {\frac{\tau }{{{{\tau }_{{\text{p}}}}}}} \right)}^{{2g - 1}}}{{e}^{{ - {{{(\tau /{{\tau }_{{\text{p}}}})}}^{{2g}}}}}}, \\ \end{gathered} $$
(27)

where \({{\tau }_{{\text{p}}}} = {{\nu }_{T}}(0){{t}_{{\text{p}}}}\) and \(\mathcal{L} = 8{{\omega }_{{{\text{L}}i}}}L{\text{/}}c\sqrt {3\pi Z} \). In turn, Eqs. (15), (16) for the temperatures of particles take the form

$$\frac{{\partial u}}{{\partial \tau }} = \alpha \frac{\partial }{{\partial \xi }}\left\{ {{{u}^{{5/2}}}\left[ {I(0,11) - \frac{{{{I}^{2}}(0,9)}}{{I(0,7)}}} \right]\frac{{\partial u}}{{\partial \xi }}} \right\}$$
$$\begin{gathered} \, - \beta u\frac{\partial }{{\partial \xi }}\left\{ {{{u}^{{3/2}}}\left[ {I(1,12) - \frac{{I(0,9)}}{{I(0,7)}}I(1,10)} \right]{{\mathcal{E}}_{y}}} \right\} \\ \, + \gamma {{u}^{{3/2}}}\left\{ {\mathcal{E}_{z}^{2} + \frac{{\sqrt {2\pi } }}{{32}}\left[ {I(0,7) + \frac{{{{I}^{2}}(1,10)}}{{I(0,7)}}} \right]\mathcal{E}_{y}^{2}} \right\} \\ \end{gathered} $$
(28)
$$\, - \frac{{u - v}}{{{{u}^{{3/2}}}}},$$
$$\frac{{\partial v}}{{\partial \tau }} = {{\alpha }_{i}}\frac{\partial }{{\partial \xi }}\left[ {\frac{{{{v}^{{5/2}}}}}{{1 + b_{i}^{2}{{v}^{3}}}}\frac{{\partial v}}{{\partial \xi }}} \right] + Z\frac{{u - v}}{{{{u}^{{3/2}}}}}.$$
(29)

Here next notations are used: \({{b}_{i}} = {{\Omega }_{i}}{\text{/}}{{\nu }_{{ii}}}(0)\),

$$\begin{gathered} \alpha = \frac{{32}}{{27\pi \sqrt {2\pi } }}\frac{{\omega _{{\text{p}}}^{2}v_{T}^{2}(0)}}{{{{c}^{2}}\nu _{{ei}}^{2}(0)}},\quad \beta = \frac{8}{{9\sqrt {2\pi } }}\frac{{e{{E}_{0}}}}{{{{\tau }_{{\text{p}}}}{{\nu }_{{ei}}}(0)mc}}, \\ \gamma = \frac{8}{{3\pi }}\frac{1}{{\tau _{{\text{p}}}^{2}}}\frac{{E_{0}^{2}}}{{n\varkappa {{T}_{0}}}},\quad {{\alpha }_{i}} = \frac{{80}}{{9\pi }}\frac{{{{\nu }_{T}}(0)}}{{{{\nu }_{{ii}}}(0)}}\frac{{\omega _{{\text{p}}}^{2}v_{T}^{2}(0)}}{{{{c}^{2}}\nu _{{ei}}^{2}(0)}}, \\ \end{gathered} $$
(30)

where \({{v}_{T}}(0)\) and \({{\nu }_{{ii}}}(0)\) are the thermal velocity of electrons and the frequency of ion–ion collisions respectively when \(t \to - \infty \). Parameters α and \({{\alpha }_{i}}\) characterize the degree of influence of heat transfer by electrons and ions on the evolution of electron and ion temperatures, respectively. The parameter γ determines Joule heating efficiency, and the parameter β characterizes the degree of influence of the electron temperature inhomogeneity and the electric field strength component orthogonal to the magnetic field on the evolution of the electron temperature.

Herewith, the initial and boundary conditions take the form

$$u(\xi ,\tau \to - \infty ) = v(\xi ,\tau \to - \infty ) = 1,$$
(31)
$$\begin{array}{*{20}{c}} \begin{gathered} \left\{ {\left[ {I(0,11) - \frac{{{{I}^{2}}(0,9)}}{{I(0,7)}}} \right]} \right.\frac{{\partial u(\xi ,\tau )}}{{\partial \xi }} - {{\beta }_{E}}\left[ {\mathop {I(1,12)}\limits_{}^{} } \right. \\ \, - {{\left. {\left. {\left. {\frac{{I(0,9)}}{{I(0,7)}}I(1,10)} \right]{{\mathcal{E}}_{y}}(\xi ,\tau )} \right\}} \right|}_{{\xi = 0,\mathcal{L}}}} = 0, \\ \end{gathered} \\ {{{{\left. {\frac{{\partial v(\xi ,\tau )}}{{\partial \xi }}} \right|}}_{{\xi = 0,\mathcal{L}}}} = 0,} \end{array}$$
(32)

where \({{\beta }_{E}} = (3{\text{/}}32)({{E}_{0}}{{m}_{i}}c{\text{/}}en\varkappa {{T}_{0}}{{t}_{{\text{p}}}})\).

Further we discuss numerical solution of Eqs. (21), (22) and (28), (29) in next conditions. It is accepted that the electromagnetic pulse with \({{t}_{{\text{p}}}} = \) 10‒3 s, \(g = 4\) and \({{E}_{0}} = 5\) kV/cm acts on argon plasma with \(Z = 1\) and \(A = 40\), electron density \(n{{ = 10}^{{13}}}\) cm–3 and initial particle temperature \({{T}_{0}} = 0.3\) eV. Main physical parameters of such plasma are \({{v}_{T}}(0) = \) 2.3 × 107 cm/s, \({{\omega }_{{\text{p}}}} = 1.8 \times {{10}^{{11}}}\) s–1, \(\Lambda \) = 5.6, \({{\omega }_{{{\text{L}}i}}} = \) 6.6 × 108 s–1, \({{\nu }_{{ei}}}{{(0) = 10}^{9}}\) s–1, \({{\nu }_{{ii}}}(0) = 2.1 \times {{10}^{6}}\) s–1, \({{\nu }_{T}}(0) = \) 2.8 × 104 s–1, \(\nu (0) = (3{\text{/}}2)\sqrt {2\pi } {{\nu }_{{ei}}}(0) = 3.8 \times {{10}^{9}}\) s–1, \(l = {{v}_{T}}(0){\text{/}}\nu (0) = 0.6 \times {{10}^{{ - 2}}}\) cm. Herewith, for the coefficients α, β, \({{\beta }_{E}}\), γ, \({{\alpha }_{i}}\) and \({{\beta }_{T}}\), which are included in the equations for the electric field strength component \({{\mathcal{E}}_{y}}\) and temperatures of particles, one gets next values: \(\alpha = 2.9 \times {{10}^{{ - 3}}}\), \(\beta = 3.7 \times {{10}^{{ - 3}}}\), \({{\beta }_{E}} = 1.3\), \(\gamma = 6.2 \times {{10}^{{ - 2}}}\), \({{\beta }_{T}} = 6.0 \times {{10}^{{ - 2}}}\), \({{\alpha }_{i}} = 7.2 \times {{10}^{{ - 4}}}\). The calculations were carried out for several values of the magnetic field strength: \(B = \) 5, 25, 100, 1000 G. As the magnetic field strength increases, the ratio of the cyclotron frequency to the collision frequency increases. For electrons the parameter b (25), of which the integrals \(I(s,p)\) (24) depend on, takes values: \(b = \Omega {\text{/}}\nu (0) = 2.4 \times {{10}^{{ - 2}}}\); 1.2 × 10–1; 4.8 × 10–1; 4.8. That is, as B increases, the cyclotron frequency becomes higher than the frequency of electron–ion collisions even before the electromagnetic pulse effect. The similar parameter for ions \({{b}_{i}}\) (29) varies in the interval: \({{b}_{i}} = 5.9 \times {{10}^{{ - 4}}}\); 2.9 × 10–3; 1.2 × 10–2; 1.2 × 10–1. Note that in the calculations the time \({{\tau }_{{\text{p}}}}\) was quite large: \({{\tau }_{{\text{p}}}} = 28\). Under these conditions, the effect of particles heating on the field penetration was fully manifested.

5 RESULTS OF NUMERICAL CALCULATIONS

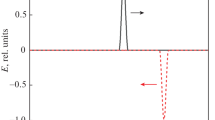
At first, in order to disclose the effect of plasma heating on field penetration, we present the electric field in the plasma under the assumption that electron temperature is constant. Figure 1 shows a plot of the function \({{\mathcal{E}}_{z}}(\xi ,\tau )\)

$$\begin{gathered} {{\mathcal{E}}_{z}}(\xi ,\tau ) \\ \, = - \frac{1}{{\sqrt \pi }}\sum\limits_{n = - \infty }^{ + \infty } \int\limits_{ - \infty }^\tau d\tilde {\tau }\frac{{\mu (\tilde {\tau })}}{{\sqrt {\tau - \tilde {\tau }} }}\exp \left[ { - \frac{{{{{(\xi + 2n\mathcal{L})}}^{2}}}}{{4(\tau - \tilde {\tau })}}} \right], \\ \end{gathered} $$
(33)

that is a solution of Eq. (22) for \(u(\xi ,\tau ) = 1\). In addition to \({{\mathcal{E}}_{z}}(\xi ,\tau )\), Fig. 1 also shows the function \(\mu (\tau )\), which creates the field in plasma. Figure 1 shows time dependencies \({{\mathcal{E}}_{z}}(\xi ,\tau )\), which are plotted for the following values of the dimensionless coordinate \(\xi = 0,\;1.5,\;3\). On the boundary \(\xi = 0\), the electric field strength component \({{\mathcal{E}}_{z}}(0,\tau )\) reaches its maximum near the minimum of the function \(\mu (\tau )\). Further, \({{\mathcal{E}}_{z}}(0,\tau )\) decreases monotonically to a minimum in the region of the maximum \(\mu (\tau )\), and then increases monotonically. The sharpest change of \({{\mathcal{E}}_{z}}(0,\tau )\) occurs at the moments of switching on and off the electromagnetic pulse. Strictly speaking, the pulse switches on infinitely far from the plasma layer at \(\tau \to - \infty \). However, due to a sharp increase in the pulse field, the effective effect of the field on the plasma surface begins at τ close to –27, and ends at τ close to 27. Therefore, the dimensionless time close to the moment –27 corresponds to the “switching on” the pulse or the beginning of the impact of the pulse, and the time close to the moment 27 corresponds to the “switching off” the impact on the illuminated surface of the plasma layer. Due to the sharp switching on the pulse, the results of the calculations differ negligibly if the distance to the past from the time point –27 is sufficient. In turn, after the pulse is switched off, that is, at a sufficient distance into the future from time 27, the evolution of the field proceeds in accordance with the initial equations for the field and temperatures. In the depth of the layer and at the far boundary, the field first increases, reaches a plateau, which persists during the impact of the pulse, and then rapidly decreases (see the curves corresponding to \(\xi = 1.5,3\)). Since the electric field strength component \({{\mathcal{E}}_{z}}(0,\tau )\) takes negative values at the moment of switching off the pulse, while in the depth of the layer at \(\xi = 1.5\) and \(\xi = 3\) it takes values close to zero (see Fig. 1), then the “inverse” skin effect [17] is realized. The “inverse” skin effect is a phenomenon of electric field strength increasing with increasing a distance from the boundary \(\xi = 0\). The effect of electron heating on field penetration is shown in Figs. 2a, 2b. For \(\xi = 0\) the heating of electrons leads to a decrease in the absolute value of \({{\mathcal{E}}_{z}}(0,\tau )\). The extent of the decrease depends on the magnitude of the constant magnetic field. The stronger the magnetic field, the worse heat transfer across the layer and the higher electron temperature in the region of \(\xi = 0\). With increasing temperature, the plasma conductivity increases and the field penetrates the layer worse. The tendency of \({{\mathcal{E}}_{z}}(0,\tau )\) to decrease with increasing magnetic field strength is observed in Fig. 2a. The heating of electrons has a particularly strong effect on the “inverse” skin effect, which appears at the stage of switching off the pulse. As the magnetic field leads to a decrease of heat flux, in strong magnetic field the electron temperature near the surface \(\xi = 0\) is especially high, and the field penetrates poorly deep into the layer at the moment of switching off the pulse. As a consequence, as can be seen in Fig. 2b, on the boundary \(\xi = 3\), i.e., on the back side of the layer, there is no sign change of the field at all. These patterns are clearly seen in Figs. 3a, 3b, which show the electric field strength component \({{\mathcal{E}}_{z}}\) at the moments \(\tau = - 27\) and \(\tau = 27\). When the pulse is switched on, the electric field strength component \({{\mathcal{E}}_{z}}(\xi ,\; - {\kern 1pt} 27)\) monotonically decreases with increasing ξ. An increase of the magnetic field is accompanied (see Fig. 3a) by a relative decrease of \({{\mathcal{E}}_{z}}(\xi ,\; - {\kern 1pt} 27)\) for small ξ, and, vice versa, an increase for large ξ. Figure 3b shows how significant impact of the magnetic field is on the “inverse” skin effect. According to Fig. 3b, the stronger the magnetic field, the weaker the “inverse” skin effect is. Such changes in the structure of the electric field strength component \({{\mathcal{E}}_{z}}\) are related to the evolution of the electron temperature. Dependencies of the dimensionless electron temperature \(u(\xi ,\tau )\) are presented in Figs. 4a, 4b. Figure 4a shows distribution of dimensionless electron temperature over width of the plasma layer \(u(\xi , - 27)\) at the moment of switching on the pulse. It can be seen from Fig. 4a that an increase in the magnetic field is accompanied by an increase in \(u(\xi , - 27)\) for small ξ and a decrease in \(u(\xi , - 27)\) for large ξ. At the moment of switching off the pulse \(\tau = 27\), the behavior of \(u(\xi ,27)\) is similar with the only exception that the absolute values of temperature are higher. It can be seen in Fig. 4b, where the plot of the function \(u(0,\tau )\) is presented. The slowdown in decrease of \(u(0,\tau )\) at \(\tau \sim 27\) is due to additional heating of electrons because of the “inverse” skin effect, when the maximum of negative values \({{\mathcal{E}}_{z}}(0,\tau )\) is realized (see Fig. 2a). Simultaneously with the heating of electrons, heating of ions occurs.

Fig. 1.
figure 1

Time evolution of electric field strength on the layer boundaries and in the middle of the plasma layer in the absence of electron heating. The dotted curve corresponds to the function \(\mu (\tau )\).

Full size image
Fig. 2.
figure 2

(a) Time evolution of electric field strength component \({{\mathcal{E}}_{z}}(0,\tau )\) on the front boundary of the plasma layer. (b) The same as in Fig. 2a, but on the back boundary of the plasma layer.

Full size image
Fig. 3.
figure 3

(a) Distribution of electric field strength component \({{\mathcal{E}}_{z}}(\xi , - 27)\) over width of the plasma layer at the stage of switching on the pulse. (b) The same as in Fig. 3a, but at the stage of switching off the pulse.

Full size image
Fig. 4.
figure 4

(a) Distribution of electron temperature \(u(\xi , - 27)\) over width of the plasma layer at the stage of switching on the pulse. (b) Evolution in time of electron temperature \(u(0,\tau )\) on the front boundary of the plasma layer.

Full size image

Figures 5a, 5b show plots of dimensionless ion temperature. Figure 5a shows \(v(\xi , - 27)\), and Fig. 5b shows \(v(0,\tau )\). Increase of ion temperature is less than increase of electron temperature. However, in not very strong magnetic field electron and ion temperatures do not diverge much due to the relatively high thermal conductivity of electrons and quite fast energy transfer to ions (see Figs. 4a, 4b, 5a, 5b). If the magnetic field is very strong, then a large difference of electron and ion temperatures occurs at small ξ due to the suppression of electron heat flux. In strongly nonisothermal plasma, ion-acoustic instability can develop under the effect of the electric field strength component \({{\mathcal{E}}_{z}}\). This may be a reason for change in both heating of electrons and ions and heat transfer. Therefore, the calculation in strong magnetic field (under discussed conditions at \(B = \) 103 G), strictly speaking, requires additional analysis associated with going beyond the range of applicability of the equations used. Note that, as can be seen from Fig. 5b, unlike electron temperature, values of ion temperature \(v(0,\tau )\) in strong magnetic field are comparable to its values in weaker magnetic fields. The absence of very strong heating of ions is due to relatively high thermal conductivity of ions, which is not strongly suppressed by the magnetic field. As already noted, inhomogeneous heating of electrons across the magnetic field leads to an electron current in the direction orthogonal to both the magnetic field and the temperature gradient. As a consequence, the electric field strength component \({{\mathcal{E}}_{y}}\) appears. In Figs. 6a, 6b\({{\mathcal{E}}_{y}}(0,\tau )\) and \({{\mathcal{E}}_{y}}(\xi , - 27)\) are plotted, respectively. The maximum values of \({{\mathcal{E}}_{y}}(0,\tau )\) are approximately an order of magnitude smaller than \({{\mathcal{E}}_{z}}(0,\tau )\) (see Fig. 2a) and are reached at the stage of switching on the pulse, when the electron temperature gradients are maximum. In weak magnetic field, the maximum of \({{\mathcal{E}}_{y}}(0,\tau )\) increases proportionally to B0. On the contrary, in strong magnetic field, when the cyclotron frequency of electrons exceeds their effective collision frequency, the maximum of \({{\mathcal{E}}_{y}}(0,\tau )\) decreases with increasing B. This tendency is observed in Fig. 6a. After reaching the maximum, the function \({{\mathcal{E}}_{y}}(0,\tau )\) decreases. The monotonic decrease is violated at the moment of switching off the pulse (see Fig. 6a), when due to the “inverse” skin effect, a relatively sharp change in heating of electrons occurs, which is accompanied by a change in their temperature gradient. The nonmonotonic change in \({{\mathcal{E}}_{y}}\) described above with increasing magnetic field is clearly illustrated in Fig. 6b, which shows the function \({{\mathcal{E}}_{y}}(\xi , - 27)\) at the moment of switching on the pulse. Since the electric field strength component \({{\mathcal{E}}_{y}}\) is continuous on the plasma surface, its measurement in vacuum allows one to extract information about heat transfer into the plasma. Unlike the incident pulse, the reflected pulse contains two components of the electric field strength: \({{\mathcal{E}}_{z}}\) and \({{\mathcal{E}}_{y}}\), i.e., it has a different polarization.

Fig. 5.
figure 5

(a) Distribution of ion temperature \(v(\xi , - 27)\) over width of the plasma layer at the stage of switching on the pulse. (b) Evolution in time of ion temperature \(v(0,\tau )\) on the front boundary of the plasma layer.

Full size image
Fig. 6.
figure 6

(a) Evolution in time of electric field strength component \({{\mathcal{E}}_{y}}(0,\tau )\) on the front boundary of the plasma layer. (b) Distribution of electric field strength component \({{\mathcal{E}}_{y}}(\xi , - 27)\) over width of the plasma layer at the stage of switching on the pulse.

Full size image

6 CONCLUSIONS

Above, using relatively simple expressions for plasma conductivity, thermal conductivity of electrons and ions, and energy exchange between electrons and ions, the effect of plasma heating on the nonlinear penetration of a heating pulse into plasma in constant magnetic field is analyzed. It is shown how patterns of the field penetration into the plasma change as the magnetic field strength increases. It is established that in strong magnetic field the “inverse” skin effect is significantly suppressed. It is demonstrated how inhomogeneous heating of electrons across the magnetic field leads to generation of the electric field strength component orthogonal to both the magnetic field and the electron temperature gradient. As a result, polarization of the field changes. The analysis of evolution of the field and particle temperatures is given under conditions where it is possible not to involve the concepts of anomalous charge and heat transfer and turbulent plasma heating. This analysis may be useful for interpreting and planning experiments on additional pulsed heating of plasma in magnetic traps like TUMAN-3. In addition, the given study allows us to see the path of transition to pulsed plasma heating under less theoretically studied conditions.