1 INTRODUCTION

In recent years, the interest in spacecraft-based lunar studies has been considerably increased all over the world. In Russia, the Luna-25, Luna-26, and Luna-27 lunar missions are being prepared (see, for example, [1]). Important contribution to the development of lunar programs is made by the People’s Republic of China and the United States of America (see, for example, [2–4]), etc. The issues concerning dust and dusty plasma in the lunar exosphere are the subjects of research in considerable part of the studies of the Moon [5, 6]. The source of dust on the Moon is the lunar regolith, the formation of which was considerably affected by the bombardment of the surface of the Earth’s natural satellite by meteoroids of different sizes over billions of years. The side of the Moon facing the Sun is exposed to the solar wind and radiation. Of great importance is the photoelectric effect, due to which the surface of the Moon illuminated by sunlight acquires positive charge [7].

Under certain conditions, the forces of electrostatic repulsion can cause the levitation of submicro- and microsized dust grains above the lunar surface [8–10]. In this case, we can speak of “dusty” exosphere of the Moon, which, in addition to solar wind electrons and ions, contains levitating charged dust grains, as well as photoelectrons incoming to the exosphere from the lunar surface and surfaces of levitating dust grains as a result of photoemission. We emphasize that the role of photoelectrons in the process of charging dust grains is decisive. The parameters of “dusty” exosphere of the Moon are shown in Fig. 1; they were the results of numerical calculations based on the model described in [9].

Fig. 1.
figure 1

Parameters of “dusty” exosphere of the Moon as functions of height h above lunar surface (ne and nd are electron density and concentration of dust grains, and Zd is charge of dust grain) for angle θ = 82° between local normal and direction to the Sun.

Full size image

Studies of linear and nonlinear wave structures, for example, solitons, are an important part of plasma physics (see, e.g., [11–14]).

As in any plasma system, linear and nonlinear waves can exist in the exosphere of the Moon [15–19]. In [20], dust acoustic solitons are described, propagating in plasma of the dusty exosphere of the Moon. In this study, the simplified description was used, in which the lunar surface was assumed to be smooth, and anisotropy, associated, for example, with the presence of magnetic field, was not taken into account, which made it possible to use one-dimensional (in space) equations. At the same time, it is well known that approximately a quarter of the lunar orbit passes through the tail of the Earth’s magnetosphere. Typical magnetic fields in the magnetosphere tail are on the order of 10–5–10–4 G [21, 22]. In addition, there are the magnetic field regions of the Moon’s crust, known as regions of magnetic anomalies. The surface fields measured by the magnetometers of the Apollo 12, 14, 15, and 16 missions were 3.8 × 10–4, 1.03 × 10–3, 3 × 10–5, and 3.27 × 10–3 G, respectively [23]. We note that all the Apollo moonfall sites were on the visible side of the Moon. There are satellite observations [24], which showed that the highest magnetic fields are located on the invisible side of the Moon.

Due to the action of magnetic fields in the tail of the Earth’s magnetosphere, charged dust grains can be transported above the lunar surface over long distances [25]. The transport of dust grains over long distances occurs due to the uncompensated magnetic part of the Lorentz force and is an important qualitative effect. For the fields in the regions of magnetic anomalies, the magnetic part of the Lorentz force acting on dust grain is either less than or comparable to the similar force calculated for the magnetic fields in the tail of the Earth’s magnetosphere at the Moon’s orbit. However, due to the localization of the regions of magnetic anomalies, their effect on the dynamics of charged dust grains above the Moon surface does not lead to new qualitative effects [26]. At the same time, the magnetic fields can determine the nature of plasma turbulence [14, 19].

For dusty plasma above the illuminated surface of the Moon, the main contribution is made by photoelectrons and positively charged dust grains, which play the role of ions in ordinary plasma. In [14], the situation was considered when the gyrofrequency \({{\omega }_{{Bd}}}\) of dust grains is so low that for the frequencies ω of dust-acoustic waves, the relation \(\omega \gg {{\omega }_{{Bd}}}\) is satisfied. In this case, on the one hand, the action of the magnetic field can be neglected, but on the other hand, there is the anisotropy associated with the magnetic field vector, which can affect the structure of the nonlinear wave. In this case, if there is almost one-dimensional wave packet, in which localization along the magnetic field vector is much more pronounced than in other directions, then, as shown in [14], nonlinear waves could be described by the modified Kadomtsev–Petviashvili equation. In this paper, we consider the opposite situation, when the frequencies of dust-acoustic waves do not exceed the \({{\omega }_{{Bd}}}\) frequency. In ordinary plasma, in the case of low frequencies and the pancake-shaped wave packet stretched-out along the external magnetic field, nonlinear waves can be described by the well-known Zakharov–Kuznetsov equation (see, for example, [27]). At the same time, the circumlunar dusty plasma considerably differs from ordinary plasma, and these differences consist in not only the replacement of ions by positively charged dust grains. Therefore, the equation describing the dust acoustic solitons under similar conditions will differ from the Zakharov–Kuznetsov equation. The goal of this paper is to derive this equation, find its one-dimensional solutions, and study the stability of these solutions.

2 FUNDAMENTAL EQUATIONS

The formation of nonlinear dust-acoustic structures near the illuminated surface of the Moon can be caused, for example, by the dust-acoustic instability, which can be quite easily excited in plasma in the region of interaction between the tail of the Earth’s magnetosphere and the Moon [17, 18]. If the amplitude oscillations (or waves), excited due to the development of instability, become so large that the linear consideration is no longer possible, then the nonlinear dust-acoustic waves of different types can arise in the plasma, one of which are solitons.

With allowance for the magnetic field B directed along the z-axis, the dynamics of dust grains in the plasma of the dusty exosphere of the Moon can be described by the continuity equation and the Euler equation:

$$\frac{{\partial {{n}_{d}}}}{{\partial t}} + \frac{{\partial {{n}_{d}}{{v}_{{d,x}}}}}{{\partial x}} + \frac{{\partial {{n}_{d}}{{v}_{{d,y}}}}}{{\partial y}} + \frac{{\partial {{n}_{d}}{{v}_{{d,z}}}}}{{\partial z}} = 0,$$
(1)
$$\begin{gathered} \frac{{\partial {{v}_{{d,x}}}}}{{\partial t}} + {{v}_{{d,x}}}\frac{{\partial {{v}_{{d,x}}}}}{{\partial x}} + {{v}_{{d,y}}}\frac{{\partial {{v}_{{d,x}}}}}{{\partial y}} + {{v}_{{d,z}}}\frac{{\partial {{v}_{{d,x}}}}}{{\partial z}} \\ \, + \frac{{{{q}_{d}}}}{{{{m}_{d}}}}\frac{{\partial \varphi }}{{\partial x}} = \frac{{{{q}_{d}}B}}{{{{m}_{d}}c}}{{v}_{{d,y}}}, \\ \end{gathered} $$
(2)
$$\begin{gathered} \frac{{\partial {{v}_{{d,y}}}}}{{\partial t}} + {{v}_{{d,x}}}\frac{{\partial {{v}_{{d,y}}}}}{{\partial x}} + {{v}_{{d,y}}}\frac{{\partial {{v}_{{d,y}}}}}{{\partial y}} + {{v}_{{d,z}}}\frac{{\partial {{v}_{{d,y}}}}}{{\partial z}} \\ \, + \frac{{{{q}_{d}}}}{{{{m}_{d}}}}\frac{{\partial \varphi }}{{\partial y}} = - \frac{{{{q}_{d}}B}}{{{{m}_{d}}c}}{{v}_{{d,x}}}, \\ \end{gathered} $$
(3)
$$\begin{gathered} \frac{{\partial {{v}_{{d,z}}}}}{{\partial t}} + {{v}_{{d,x}}}\frac{{\partial {{v}_{{d,z}}}}}{{\partial x}} + {{v}_{{d,y}}}\frac{{\partial {{v}_{{d,z}}}}}{{\partial y}} \\ \, + {{v}_{{d,z}}}\frac{{\partial {{v}_{{d,z}}}}}{{\partial z}} + \frac{{{{q}_{d}}}}{{{{m}_{d}}}}\frac{{\partial \varphi }}{{\partial z}} = 0. \\ \end{gathered} $$
(4)

Here, \({{n}_{d}}\), \({{m}_{d}}\), \({{q}_{d}} = e{{Z}_{d}}\) are the concentration, mass and charge of dust grains (\({{Z}_{d}}\) is the electric charge of dust grain, expressed in the number of electrons); \(B = \left| {\mathbf{B}} \right|\), \( - e\) is the electron charge; \({{v}_{{d,x}}}\), \({{v}_{{d,y}}}\), and \({{v}_{{d,z}}}\) are the velocity components of dust grains, and φ is the self-consistent electrostatic potential of the plasma.

The Poisson equation has the following form:

$$\frac{{{{\partial }^{2}}\varphi }}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}\varphi }}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}\varphi }}{{\partial {{z}^{2}}}} = 4\pi \left( {e{{n}_{e}} - {{q}_{d}}{{n}_{d}}} \right),$$
(5)

where \({{n}_{e}}\) is the electron density.

On the scale of space–time changes characteristic of the dust-acoustic waves, electrons have time to form the statistical distribution. Since dust grains above the illuminated surface of the Moon can acquire the positive charge as a result of the photoelectric effect, the dust-acoustic solitons will create the positive electrostatic potential [16, 20], which will form the potential well for electrons. Electrons will be adiabatically captured when the following inequality is satisfied:

$${{\tau }_{{\text{S}}}} \geqslant {{{{l}_{{\text{S}}}}} \mathord{\left/ {\vphantom {{{{l}_{{\text{S}}}}} {{{v}_{{Te}}}}}} \right. \kern-0em} {{{v}_{{Te}}}}},$$
(6)

where \({{\tau }_{{\text{S}}}}\) and \({{l}_{{\text{S}}}}\) are the characteristic space–time scales of soliton, and \({{v}_{{Te}}}\) is the thermal velocity of electrons above the illuminated surface of the Moon. We note that \({{\tau }_{{\text{S}}}} \propto \omega _{{pd}}^{{ - 1}}\), where \({{\omega }_{{pd}}} = \sqrt {{{4\pi {{n}_{{e0}}}{{Z}_{d}}{{e}^{2}}} \mathord{\left/ {\vphantom {{4\pi {{n}_{{e0}}}{{Z}_{d}}{{e}^{2}}} {{{m}_{d}}}}} \right. \kern-0em} {{{m}_{d}}}}} \) is the dust plasma frequency. The soliton spatial size \({{l}_{{\text{S}}}}\) is usually equal to several Debye lengths λDe = \(\sqrt {{{{{T}_{e}}} \mathord{\left/ {\vphantom {{{{T}_{e}}} {4\pi {{n}_{{e0}}}{{e}^{2}}}}} \right. \kern-0em} {4\pi {{n}_{{e0}}}{{e}^{2}}}}} \). So, \({{l}_{S}}{\text{/}}{{v}_{{Te}}}\, \propto \,\omega _{{pe}}^{{ - 1}}\), where \({{\omega }_{{pe}}}\, = \,\sqrt {4\pi {{n}_{{e0}}}{{e}^{2}}{\text{/}}{{m}_{e}}} \) is the electron plasma frequency (here, \({{m}_{e}}\) is the electron mass, \({{n}_{{e0}}}\) is the unperturbed electron density, and \({{T}_{e}}\) is the electron temperature). Therefore, for the dust-acoustic solitons, inequality (6) is usually satisfied. That is why, when describing the dust-acoustic waves, one should take into account the adiabatic capture of electrons [28] by the potential well formed by the dust-acoustic soliton. In this case, electrons can be described using the Gurevich distribution:

$${{n}_{e}}(\varphi ) = \left[ {\left( {1 - \frac{2}{{\sqrt \pi }}\int\limits_0^{\sqrt {{{e\varphi } \mathord{\left/ {\vphantom {{e\varphi } {{{T}_{e}}}}} \right. \kern-0em} {{{T}_{e}}}}} } {{{e}^{{ - {{u}^{2}}}}}du} } \right)\exp \left( {\frac{{e\varphi }}{{{{T}_{e}}}}} \right) + \frac{2}{{\sqrt \pi }}\sqrt {\frac{{e\varphi }}{{{{T}_{e}}}}} } \right].$$
(7)

We introduce the dimensionless variables \(t \to \omega _{{pd}}^{{ - 1}}\tilde {t}\); \(\left( {x,\;y,\;z} \right) \to \left( {\tilde {x},\;\tilde {y},\;\tilde {z}} \right){{\lambda }_{{{\text{De}}}}}\); \(({{v}_{{d,x}}},{{v}_{{d,y}}},{{v}_{{d,z}}}) \to ({{\tilde {v}}_{{d,x}}},{{\tilde {v}}_{{d,y}}},\) \({{\tilde {v}}_{{d,z}}}){\kern 1pt} {{C}_{{{\text{S}}d}}}\); \(\varphi \to {{{{T}_{e}}\tilde {\varphi }} \mathord{\left/ {\vphantom {{{{T}_{e}}\tilde {\varphi }} e}} \right. \kern-0em} e}\); and \({{n}_{d}} \to {{\tilde {n}}_{d}}{\kern 1pt} {{n}_{{d0}}}\); here, ωpd = \(\sqrt {{{4\pi {{n}_{{e0}}}{{Z}_{d}}{{e}^{2}}} \mathord{\left/ {\vphantom {{4\pi {{n}_{{e0}}}{{Z}_{d}}{{e}^{2}}} {{{m}_{d}}}}} \right. \kern-0em} {{{m}_{d}}}}} \) is the dust plasma frequency, λDe = \(\sqrt {{{{{T}_{e}}} \mathord{\left/ {\vphantom {{{{T}_{e}}} {4\pi {{n}_{{e0}}}{{e}^{2}}}}} \right. \kern-0em} {4\pi {{n}_{{e0}}}{{e}^{2}}}}} \) is the electron Debye length CSd = \({{\omega }_{{pd}}}{{\lambda }_{{{\text{De}}}}}\) is the characteristic velocity of dust-acoustic perturbations, and \({{n}_{{d0}}}\) is the unperturbed concentration of dust grains. In these dimensionless variables, the set of equations takes the following form (hereinafter, we omit the “~” sign above all dimensionless variables):

$$\frac{{\partial {{n}_{d}}}}{{\partial t}} + \frac{{\partial {{n}_{d}}{{v}_{{d,x}}}}}{{\partial x}} + \frac{{\partial {{n}_{d}}{{v}_{{d,y}}}}}{{\partial y}} + \frac{{\partial {{n}_{d}}{{v}_{{d,z}}}}}{{\partial z}} = 0,$$
(8)
$$\begin{gathered} \frac{{\partial {{v}_{{d,x}}}}}{{\partial t}} + {{v}_{{d,x}}}\frac{{\partial {{v}_{{d,x}}}}}{{\partial x}} + {{v}_{{d,y}}}\frac{{\partial {{v}_{{d,x}}}}}{{\partial y}} \\ \, + {{v}_{{d,z}}}\frac{{\partial {{v}_{{d,x}}}}}{{\partial z}} + \frac{{\partial \varphi }}{{\partial x}} = \frac{{{{\omega }_{{Bd}}}}}{{{{\omega }_{{pd}}}}}{{v}_{{d,y}}}, \\ \end{gathered} $$
(9)
$$\begin{gathered} \frac{{\partial {{v}_{{d,y}}}}}{{\partial t}} + {{v}_{{d,x}}}\frac{{\partial {{v}_{{d,y}}}}}{{\partial x}} + {{v}_{{d,y}}}\frac{{\partial {{v}_{{d,y}}}}}{{\partial y}} \\ \, + {{v}_{{d,z}}}\frac{{\partial {{v}_{{d,y}}}}}{{\partial z}} + \frac{{\partial \varphi }}{{\partial y}} = - \frac{{{{\omega }_{{Bd}}}}}{{{{\omega }_{{pd}}}}}{{v}_{{d,x}}}, \\ \end{gathered} $$
(10)
$$\frac{{\partial {{v}_{{d,z}}}}}{{\partial t}} + {{v}_{{d,x}}}\frac{{\partial {{v}_{{d,z}}}}}{{\partial x}} + {{v}_{{d,y}}}\frac{{\partial {{v}_{{d,z}}}}}{{\partial y}} + {{v}_{{d,z}}}\frac{{\partial {{v}_{{d,z}}}}}{{\partial z}} + \frac{{\partial \varphi }}{{\partial z}} = 0,$$
(11)

where the dust Larmor frequency has the form \({{\omega }_{{Bd}}} = {{\left( {{{q}_{d}}B} \right)} \mathord{\left/ {\vphantom {{\left( {{{q}_{d}}B} \right)} {\left( {{{m}_{d}}c} \right)}}} \right. \kern-0em} {\left( {{{m}_{d}}c} \right)}}\).

The Poisson equation (6) in the dimensionless form (under the assumption of \(\varphi \ll 1\)) has the following form with an accuracy up to the terms \(o({{\varphi }^{3}})\):

$$\frac{{{{\partial }^{2}}\varphi }}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}\varphi }}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}\varphi }}{{\partial {{z}^{2}}}} = 1 + \varphi - \frac{4}{3}\frac{{{{\varphi }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}{{\sqrt \pi }} + \frac{{{{\varphi }^{2}}}}{2} - {{n}_{d}}.$$
(12)

3 MODIFIED ZAKHAROV–KUZNETZSOV EQUATION

Set of Eqs. (1)–(7) or the similar dimensionless set of Eqs. (8)–(12) is used to describe the dust-acoustic solitons in the dusty exosphere above the illuminated lunar surface. In the linear approximation, set of Eqs. (8)–(12) gives the following well-known dispersion law (in dimensionless form):

$${{{\mathbf{k}}}^{2}} + 1 = \frac{{{\mathbf{k}}_{{{\mathbf{||}}}}^{2}}}{{{{\omega }^{2}}}} + \frac{{{\mathbf{k}}_{ \bot }^{2}}}{{{{\omega }^{2}} - \omega _{{Be}}^{2}}},$$
(13)

where \({\mathbf{k}}_{{{\mathbf{||}}}}^{{}}\) and \({\mathbf{k}}_{ \bot }^{{}}\) are the components of the wave vector k along and across the magnetic field, respectively; and \({{\omega }_{{Be}}} = {{{{\omega }_{{Bd}}}} \mathord{\left/ {\vphantom {{{{\omega }_{{Bd}}}} {{{\omega }_{{pd}}}}}} \right. \kern-0em} {{{\omega }_{{pd}}}}}\) is the dimensionless dusty Larmor frequency.

For example, for the wavelengths considerably exceeding the Larmor radius, at small angles between the direction of wave propagation and the magnetic field, dispersion law (13) takes the following form [27]:

$$\omega \left( {\mathbf{k}} \right) = \left| {{{{\mathbf{k}}}_{{{\mathbf{||}}}}}} \right|\left[ {1 - \frac{{{{{\left| {{{{\mathbf{k}}}_{{{\mathbf{||}}}}}} \right|}}^{2}}}}{2} - \frac{{\left( {1 + \omega _{{Be}}^{2}} \right){\mathbf{k}}_{ \bot }^{2}}}{{\omega _{{Be}}^{2}}}} \right]$$
(14)

or in dimensional form, it looks as follows:

$$\omega \left( {\mathbf{k}} \right) = {{C}_{{{\text{S}}d}}}\left| {{{{\mathbf{k}}}_{{{\mathbf{||}}}}}} \right|\left[ {1 - \frac{{{{{\left| {{{{\mathbf{k}}}_{{{\mathbf{||}}}}}} \right|}}^{2}}\lambda _{{{\text{De}}}}^{2}}}{2}\left( {1 + \frac{{\omega _{{pd}}^{2} + \omega _{{Bd}}^{2}}}{{\omega _{{Bd}}^{2}}}\frac{{{\mathbf{k}}_{ \bot }^{2}}}{{{\mathbf{k}}_{{{\mathbf{||}}}}^{2}}}} \right)} \right].$$
(15)

In the coordinate space, the following equation corresponds to dispersion law (15):

$$\begin{gathered} \frac{{\partial \Phi }}{{\partial t}} + {{C}_{{{\text{S}}d}}}\frac{{\partial \Phi }}{{\partial z}} + \frac{{{{C}_{{{\text{S}}d}}}\lambda _{{{\text{De}}}}^{2}}}{2}\frac{{{{\partial }^{3}}\Phi }}{{\partial {{z}^{3}}}} \\ \, + \frac{{{{C}_{{{\text{S}}d}}}\lambda _{{{\text{De}}}}^{2}}}{2}\frac{{\omega _{{pd}}^{2} + \omega _{{Bd}}^{2}}}{{\omega _{{Bd}}^{2}}}\frac{\partial }{{\partial z}}\left( {\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}}} \right)\Phi = 0, \\ \end{gathered} $$
(16)

where \(\Phi = {{e\varphi } \mathord{\left/ {\vphantom {{e\varphi } {{{T}_{e}}}}} \right. \kern-0em} {{{T}_{e}}}}\).

Equation (16) is an equation of linear type. It coincides in form with similar equation for ion–acoustic waves obtained in [27] in the case of ordinary plasma, when electrons have the Boltzmann distribution. Accounting for the higher orders of smallness in set of Eqs. (8)–(12) results in the appearance of nonlinear equation. However, the nonlinear equation obtained from set of Eqs. (8)–(12) will differ from the similar nonlinear equation for ion–acoustic waves in ordinary plasma in nonlinear term. To derive the nonlinear equation, we will use the standard method of expansion in small parameter \(\varepsilon \) [29, 30]. Using the method of asymptotic representation based on the classical dimensional analysis, the new variables can be represented in the following form:

$$\tau = {{\varepsilon }^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}}}}t,$$
(17)
$$\xi = {{\varepsilon }^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}x,$$
(18)
$$\eta = {{\varepsilon }^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}y,$$
(19)
$$\xi = {{\varepsilon }^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}z - M{{\varepsilon }^{{1/4}}}t.$$
(20)

In this case, the expansions in small parameter ε will take the following form:

$${{n}_{d}} = 1 + \varepsilon {{n}_{1}} + {{\varepsilon }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{n}_{2}},$$
(21)
$${{v}_{{d,x}}} = {{\varepsilon }^{{{5 \mathord{\left/ {\vphantom {5 4}} \right. \kern-0em} 4}}}}{{v}_{{1\;d,x}}} + {{\varepsilon }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{v}_{{2\;d,x}}},$$
(22)
$${{v}_{{d,y}}} = {{\varepsilon }^{{{5 \mathord{\left/ {\vphantom {5 4}} \right. \kern-0em} 4}}}}{{v}_{{1\;d,y}}} + {{\varepsilon }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{v}_{{2\;d,y}}},$$
(23)
$${{v}_{{d,z}}} = \varepsilon {{v}_{{1\;d,z}}} + {{\varepsilon }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{v}_{{2\;d,z}}},$$
(24)
$$\varphi = \varepsilon {{\varphi }_{1}} + {{\varepsilon }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{\varphi }_{2}}.$$
(25)

We will obtain in this way the nonlinear equation for dust-acoustic disturbances near the illuminated surface of the Moon. With allowance for the effect of the magnetic field, for the wavelengths considerably exceeding the Larmor radius, and at small angles between the direction of wave propagation and the magnetic field, after performing the change of variables \({{\varphi }_{1}} \to \varphi \), we will obtain this equation in the following dimensional form:

$$\begin{gathered} \frac{{\partial \phi }}{{\partial t}} + {{C}_{{{\text{S}}d}}}\sqrt {\frac{{e\phi }}{{\pi {{T}_{e}}}}} \frac{{\partial \phi }}{{\partial z}} + \frac{{{{C}_{{{\text{S}}d}}}\lambda _{{{\text{De}}}}^{2}}}{2}\frac{{{{\partial }^{3}}\phi }}{{\partial {{z}^{3}}}} \\ \, + \frac{{{{C}_{{{\text{S}}d}}}\lambda _{{{\text{De}}}}^{2}}}{2}\frac{{\omega _{{pd}}^{2} + \omega _{{Bd}}^{2}}}{{\omega _{{Bd}}^{2}}}\frac{\partial }{{\partial z}}\left( {\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}}} \right)\phi = 0. \\ \end{gathered} $$
(26)

Equation (26) is the modified Zakharov–Kuznetsov equation (cf. the Zakharov–Kuznetsov equation [27]) obtained for the ion–acoustic waves in ordinary plasma that does not contain dust grains.

4 SOLITON SOLUTIONS AND THEIR STABILITY

We will try the solution to the modified Zakharov–Kuznetsov equation (26) in the form of dust-acoustic waves horizontally propagating at heights h that considerably exceed the Debye length \({{\lambda }_{{{\text{De}}}}}\). To do this, we go to the coordinate system, in which the \(z{\kern 1pt} '\)-axis is oriented along the direction of the wave packet propagation. Introducing the \(\vartheta \) angle between the \(z{\kern 1pt} '\)-direction and the magnetic field B, we go to the new coordinate system in accordance with the following change of variables:

$$x{\kern 1pt} ' = x\cos \vartheta - z\sin \vartheta ,$$
(27)
$$y{\kern 1pt} ' = y,$$
(28)
$$z{\kern 1pt} ' = x\sin \vartheta + z\cos \vartheta .$$
(29)

In the new coordinate system, Eq. (26) takes the following form:

$$\begin{gathered} \frac{{\partial \phi }}{{\partial t}} + {{\gamma }_{1}}\sqrt \phi \frac{{\partial \phi }}{{\partial z{\kern 1pt} '}} + {{\gamma }_{2}}\frac{{{{\partial }^{3}}\phi }}{{\partial z{\kern 1pt} {{'}^{3}}}} + {{\gamma }_{3}}\sqrt \phi \frac{{\partial \phi }}{{\partial x{\kern 1pt} '}} + {{\gamma }_{4}}\frac{{{{\partial }^{3}}\phi }}{{\partial x{\kern 1pt} {{'}^{3}}}} \\ \, + {{\gamma }_{5}}\frac{{{{\partial }^{3}}\phi }}{{\partial x{\kern 1pt} '\partial z{\kern 1pt} {{'}^{2}}}} + {{\gamma }_{6}}\frac{{{{\partial }^{3}}\phi }}{{\partial z{\kern 1pt} '\partial x{\kern 1pt} {{'}^{2}}}} + {{\gamma }_{7}}\frac{{{{\partial }^{3}}\phi }}{{\partial z{\kern 1pt} '\partial y{\kern 1pt} {{'}^{2}}}} \\ \, + {{\gamma }_{8}}\frac{{{{\partial }^{3}}\phi }}{{\partial x{\kern 1pt} '\partial y{\kern 1pt} {{'}^{2}}}} = 0, \\ \end{gathered} $$
(30)

where

$${{\gamma }_{1}} = {{C}_{{{\text{S}}d}}}\sqrt {\frac{e}{{\pi {{T}_{e}}}}} \cos \vartheta ,$$
(31)
$$\begin{gathered} {{\gamma }_{2}} = \frac{{{{C}_{{{\text{S}}d}}}\lambda _{{{\text{De}}}}^{2}}}{2}{{\cos }^{3}}\vartheta \\ + \;\frac{{{{C}_{{{\text{S}}d}}}\lambda _{{{\text{De}}}}^{2}}}{2}\frac{{\omega _{{pd}}^{2} + \omega _{{Bd}}^{2}}}{{\omega _{{Bd}}^{2}}}\cos \vartheta {{\sin }^{2}}\vartheta , \\ \end{gathered} $$
(32)
$${{\gamma }_{3}} = - {{C}_{{{\text{S}}d}}}\sqrt {\frac{e}{{\pi {{T}_{e}}}}} \sin \vartheta ,$$
(33)
$$\begin{gathered} {{\gamma }_{4}} = - \frac{{{{C}_{{{\text{S}}d}}}\lambda _{{{\text{De}}}}^{{\text{2}}}}}{2}{{\sin }^{3}}\vartheta \\ - \;\frac{{{{C}_{{{\text{S}}d}}}\lambda _{{{\text{De}}}}^{{\text{2}}}}}{2}\frac{{\omega _{{pd}}^{2} + \omega _{{Bd}}^{2}}}{{\omega _{{Bd}}^{2}}}\sin \vartheta {{\cos }^{2}}\vartheta , \\ \end{gathered} $$
(34)
$$\begin{gathered} {{\gamma }_{5}} = - \frac{{3{{C}_{{{\text{S}}d}}}\lambda _{{{\text{De}}}}^{2}}}{2}{{\cos }^{2}}\vartheta \sin \vartheta \\ \, + \frac{{{{C}_{{{\text{S}}d}}}\lambda _{{{\text{De}}}}^{{\text{2}}}}}{2}\frac{{\omega _{{pd}}^{2} + \omega _{{Bd}}^{2}}}{{\omega _{{Bd}}^{2}}}\left( {2{{{\cos }}^{2}}\vartheta \sin \vartheta - {{{\sin }}^{3}}\vartheta } \right), \\ \end{gathered} $$
(35)
$$\begin{gathered} {{\gamma }_{6}} = \frac{{3{{C}_{{{\text{S}}d}}}\lambda _{{{\text{De}}}}^{2}}}{2}\cos \vartheta {{\sin }^{2}}\vartheta \\ \, - \frac{{{{C}_{{{\text{S}}d}}}\lambda _{{{\text{De}}}}^{2}}}{2}\frac{{\omega _{{pd}}^{2} + \omega _{{Bd}}^{2}}}{{\omega _{{Bd}}^{2}}}\left( {2\cos \vartheta {{{\sin }}^{2}}\vartheta - {{{\cos }}^{3}}\vartheta } \right), \\ \end{gathered} $$
(36)
$${{\gamma }_{7}} = \frac{{{{C}_{{{\text{S}}d}}}\lambda _{{{\text{De}}}}^{2}}}{2}\frac{{\omega _{{pd}}^{2} + \omega _{{Bd}}^{2}}}{{\omega _{{Bd}}^{2}}}\cos \vartheta ,$$
(37)
$${{\gamma }_{8}} = \frac{{{{C}_{{{\text{S}}d}}}\lambda _{{{\text{De}}}}^{2}}}{2}\frac{{\omega _{{pd}}^{2} + \omega _{{Bd}}^{2}}}{{\omega _{{Bd}}^{2}}}\sin \vartheta .$$
(38)

There is a solution to Eq. (30) in the form of one-dimensional solitons propagating along the \(z{\kern 1pt} '\)-axis at the velocity \({{u}_{0}}\):

$${{\phi }_{{{\text{Sol}}}}} = {{\left( {\frac{{15{{u}_{0}}}}{{8{{\gamma }_{1}}}}} \right)}^{2}}{{\cosh }^{{ - 4}}}\left[ {\frac{1}{2}\sqrt {\frac{{{{u}_{0}}}}{{4{{\gamma }_{2}}}}} \left( {z{\kern 1pt} '\; - {{u}_{0}}t} \right)} \right].$$
(39)

The amplitude of soliton (39) is positive, i.e., the assumption is justified that takes into account the adiabatic capture of electrons by the potential well formed by the dust-acoustic soliton.

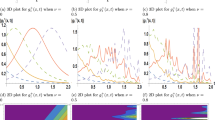
The amplitudes \({{\phi }_{0}}\) of soliton solutions (39) as functions of the height h above the lunar surface and velocity \({{u}_{0}}\) of the soliton propagation are shown in Fig. 2 for different \(\vartheta \) angles: \(\vartheta \) = 1°, 3°, and 5° correspond to Figs. 2a, 2b, and 2c, respectively. All calculations were performed for the parameters of dusty exosphere above the lunar surface corresponding to the solar declination angle is \(\theta = 82^\circ \). The corresponding parameters are shown in Fig. 1.

Fig. 2.
figure 2

Amplitudes of soliton solutions as functions of height h above lunar surface and velocity \({{u}_{0}}\) of soliton propagation for (a) \(\vartheta = 1^\circ \), (b) 3° and (c) 5°.

Full size image

For studying the stability of soliton solutions, we use the standard method [27] of linearization of Eq. (30) with respect to small perturbations \(\delta \phi \left( {x{\kern 1pt} ',y{\kern 1pt} ',\tilde {z}{\kern 1pt} ',t} \right)\) of the exact solution (39). Here, \(\tilde {z}{\kern 1pt} ' = z{\kern 1pt} ' - {{u}_{0}}t\) and \(\delta \phi = {{\phi }_{{{\text{Sol}}}}}\). Substituting the expression \(\phi = {{\phi }_{{{\text{Sol}}}}} + \delta \phi \left( {x{\kern 1pt} ',y{\kern 1pt} ',\tilde {z}{\kern 1pt} ',t} \right)\) into relation (31), we obtain the following equation:

$$\begin{gathered} \frac{{\partial \delta \phi }}{{\partial t}} - {{u}_{0}}\frac{{\partial \delta \phi }}{{\partial \tilde {z}{\kern 1pt} '}} + {{\gamma }_{1}}\sqrt \phi \frac{{\partial \sqrt {{{\phi }_{{{\text{Sol}}}}}} \delta \phi }}{{\partial \tilde {z}{\kern 1pt} '}} + {{\gamma }_{2}}\frac{{{{\partial }^{3}}\delta \phi }}{{\partial \tilde {z}{\kern 1pt} {{'}^{3}}}} \\ \, + {{\gamma }_{3}}\sqrt {{{\phi }_{{{\text{Sol}}}}}} \frac{{\partial \delta \phi }}{{\partial x{\kern 1pt} '}} + {{\gamma }_{4}}\frac{{{{\partial }^{3}}\delta \phi }}{{\partial x{\kern 1pt} {{'}^{3}}}} + {{\gamma }_{5}}\frac{{{{\partial }^{3}}\delta \phi }}{{\partial x{\kern 1pt} '\partial \tilde {z}{\kern 1pt} {{'}^{2}}}} \\ \, + {{\gamma }_{6}}\frac{{{{\partial }^{3}}\delta \phi }}{{\partial \tilde {z}{\kern 1pt} '\partial x{\kern 1pt} {{'}^{2}}}} + {{\gamma }_{7}}\frac{{{{\partial }^{3}}\delta \phi }}{{\partial \tilde {z}{\kern 1pt} '\partial y{\kern 1pt} {{'}^{2}}}} + {{\gamma }_{8}}\frac{{{{\partial }^{3}}\delta \phi }}{{\partial x{\kern 1pt} '\partial y{\kern 1pt} {{'}^{2}}}} = 0. \\ \end{gathered} $$
(40)

We note that when deriving Eq. (40), we used the condition of smallness of the perturbation \(\delta \phi \ll {{\phi }_{{{\text{Sol}}}}}\). In this case, generally speaking, the inequality \(\delta \phi + {{\phi }_{{{\text{Sol}}}}} > 0\) should be satisfied. The fulfillment of this inequality can be achieved by choosing the \(\delta \phi \) perturbation, for example, in the form \(\delta \phi = \sigma {{\phi }_{{{\text{Sol}}}}}\), where \(0 < \sigma \ll 1\). Such consideration makes it possible to study the stability of the soliton solution in the vicinity of any point from the definitional domain of the soliton.

We try the solution in the following form:

$$\begin{gathered} \delta \phi \left( {x{\kern 1pt} ',y{\kern 1pt} ',\tilde {z}{\kern 1pt} ',t} \right) \\ \, = \psi \left( {\tilde {z}{\kern 1pt} '} \right)\exp \left[ {ik\left( {{{l}_{{x{\kern 1pt} '}}}x{\kern 1pt} '\; + {{l}_{{y{\kern 1pt} '}}}y{\kern 1pt} '\; + {{l}_{{\tilde {z}{\kern 1pt} '}}}\tilde {z}{\kern 1pt} '} \right) - i\omega t} \right], \\ \end{gathered} $$
(41)

where \(\left( {{{l}_{{x{\kern 1pt} '}}},{{l}_{{y{\kern 1pt} '}}},{{l}_{{\tilde {z}{\kern 1pt} '}}}} \right)\) are the direction cosines of the wave vector k. For the small wave vectors k, the following expansion is valid:

$$\psi \left( {\tilde {z}{\kern 1pt} '} \right) \approx {{\psi }_{0}} + k{{\psi }_{1}} + {{k}^{2}}{{\psi }_{2}} + ...,$$
(42)
$$\omega \approx k{{\omega }_{1}} + {{k}^{2}}{{\omega }_{2}} + ....$$
(43)

Substituting expression (41) into Eq. (40) with allowance for expansions (42) and (43) and equating the terms of the same order of smallness, we obtain the following chain of equations:

$$ - {{u}_{0}}\frac{{\partial {{\psi }_{0}}}}{{\partial \tilde {z}{\kern 1pt} '}} + {{\gamma }_{1}}\frac{{\partial \sqrt {{{\phi }_{{{\text{Sol}}}}}} {{\psi }_{0}}}}{{\partial \tilde {z}{\kern 1pt} '}} + {{\gamma }_{2}}\frac{{{{\partial }^{3}}{{\psi }_{0}}}}{{\partial \tilde {z}{\kern 1pt} {{'}^{3}}}} = 0,$$
(44)
$$\begin{gathered} - {{u}_{0}}\frac{{\partial {{\psi }_{1}}}}{{\partial \tilde {z}{\kern 1pt} '}} + {{\gamma }_{1}}\frac{{\partial \sqrt {{{\phi }_{{{\text{Sol}}}}}} {{\psi }_{1}}}}{{\partial \tilde {z}{\kern 1pt} '}} + {{\gamma }_{2}}\frac{{{{\partial }^{3}}{{\psi }_{1}}}}{{\partial \tilde {z}{\kern 1pt} {{'}^{3}}}} \\ \, = i\left( {{{\omega }_{1}} + {{u}_{0}}{{l}_{{\tilde {z}{\kern 1pt} '}}}} \right){{\psi }_{0}} - i{{v}_{1}}\sqrt {{{\phi }_{{{\text{Sol}}}}}} {{\psi }_{0}} - i{{v}_{2}}\frac{{{{\partial }^{2}}{{\psi }_{0}}}}{{\partial \tilde {z}{\kern 1pt} {{'}^{2}}}}, \\ \end{gathered} $$
(45)
$$\begin{gathered} - {{u}_{0}}\frac{{\partial {{\psi }_{2}}}}{{\partial \tilde {z}{\kern 1pt} '}} + {{\gamma }_{1}}\frac{{\partial {{\phi }_{{{\text{Sol}}}}}{{\psi }_{2}}}}{{\partial \tilde {z}{\kern 1pt} '}} + {{\gamma }_{2}}\frac{{{{\partial }^{3}}{{\psi }_{2}}}}{{\partial \tilde {z}{\kern 1pt} {{'}^{3}}}} = i{{\omega }_{2}}{{\psi }_{0}} \\ \, + i\left( {{{\omega }_{1}} + {{u}_{0}}{{l}_{{\tilde {z}{\kern 1pt} '}}} - {{v}_{1}}\sqrt {{{\phi }_{{{\text{Sol}}}}}} } \right){{\psi }_{1}} + {{v}_{3}}\frac{{\partial {{\psi }_{0}}}}{{\partial \tilde {z}{\kern 1pt} '}} - i{{v}_{2}}\frac{{{{\partial }^{2}}{{\psi }_{1}}}}{{\partial \tilde {z}{\kern 1pt} {{'}^{2}}}}, \\ \end{gathered} $$
(46)

where \({{v}_{1}} = {{\gamma }_{1}}{{l}_{{\tilde {z}{\kern 1pt} '}}} + {{\gamma }_{3}}{{l}_{{x{\kern 1pt} '}}}\), \({{v}_{2}} = 3{{\gamma }_{2}}{{l}_{{\tilde {z}{\kern 1pt} '}}} + {{\gamma }_{5}}{{l}_{{x{\kern 1pt} '}}}\), \({{v}_{3}} = 3{{\gamma }_{2}}l_{{\tilde {z}{\kern 1pt} '}}^{2} + \) \(2{{\gamma }_{5}}{{l}_{{x{\kern 1pt} '}}}l_{{\tilde {z}{\kern 1pt} '}}^{{}} + {{\gamma }_{6}}l_{{x{\kern 1pt} '}}^{2} + {{\gamma }_{7}}l_{{y{\kern 1pt} '}}^{2}\).

There is the solution to Eq. (44) in the following form:

$${{\psi }_{0}} = {{C}_{1}}\frac{{\partial {{\phi }_{{{\text{Sol}}}}}}}{{\partial \tilde {z}{\kern 1pt} '}},$$
(47)

where \({{C}_{1}}\) is some arbitrary constant. Substituting sol-ution (47) into Eq. (45), we find the next-order solution \({{\psi }_{1}}\)

$$\begin{gathered} {{\psi }_{1}} = {{C}_{2}}\frac{{\partial {{\phi }_{{{\text{Sol}}}}}}}{{\partial \tilde {z}{\kern 1pt} '}} \\ \, + \frac{{i{{C}_{1}}{{\gamma }_{2}}}}{{2{{u}_{0}}\beta }}\left[ {\left( {a + b} \right)\tilde {z}{\kern 1pt} '{{C}_{1}}\frac{{\partial {{\phi }_{{{\text{Sol}}}}}}}{{\partial \tilde {z}{\kern 1pt} '}} + \frac{4}{5}\left( {5a + b} \right){{\phi }_{{{\text{Sol}}}}}} \right], \\ \end{gathered} $$
(48)

where \({{C}_{2}}\) is some arbitrary constant, and the other parameters are as follows:

$$a = {{\omega }_{1}} + {{u}_{0}}{{l}_{{\tilde {z}{\kern 1pt} '}}} - \frac{{5{{v}_{1}}{{u}_{0}}}}{{4{{\gamma }_{1}}}} + \frac{{{{v}_{2}}{{u}_{0}}}}{{4{{\gamma }_{2}}}},$$
(49)
$$b = \frac{{5{{v}_{1}}{{u}_{0}}}}{{4{{\gamma }_{1}}}} - \frac{{5{{v}_{2}}{{u}_{0}}}}{{4{{\gamma }_{2}}}}.$$
(50)

Solution to Eq. (46) exists if the right-hand side of this equation is orthogonal to the kernel of the operator adjoint to the following operator:

$$ - {{u}_{0}}\frac{\partial }{{\partial \tilde {z}{\kern 1pt} '}} + {{\gamma }_{1}}\frac{{\partial \sqrt {{{\phi }_{{{\text{Sol}}}}}} }}{{\partial \tilde {z}{\kern 1pt} '}} + {{\gamma }_{2}}\frac{{{{\partial }^{3}}}}{{\partial \tilde {z}{\kern 1pt} {{'}^{3}}}}.$$
(51)

Thus, since the \({{\phi }_{{{\text{Sol}}}}}\) function is the solution to operator (51), the existence condition for the solution to Eq. (46) has the following form:

$$\begin{gathered} \int\limits_{ - \infty }^\infty {{{\phi }_{{{\text{Sol}}}}}\left[ {\mathop {i{{\omega }_{2}}{{\psi }_{0}}}\limits_{_{{_{{_{{_{{}}}}}}}}} } \right. + i\left( {{{\omega }_{1}} + {{u}_{0}}{{l}_{{\tilde {z}{\kern 1pt} '}}} - {{v}_{1}}\sqrt {{{\phi }_{{{\text{Sol}}}}}} } \right){{\psi }_{1}}} \\ \, + \left. {{{v}_{3}}\frac{{\partial {{\psi }_{0}}}}{{\partial \tilde {z}{\kern 1pt} '}} - i{{v}_{2}}\frac{{{{\partial }^{2}}{{\psi }_{1}}}}{{\partial \tilde {z}{\kern 1pt} {{'}^{2}}}}} \right]d\tilde {z}{\kern 1pt} ' = 0. \\ \end{gathered} $$
(52)

With allowance for expressions (47) and (48), expression (52) can be easily integrated, and we obtain the following dispersion law:

$${{\omega }_{1}} = \Omega - {{u}_{0}}{{l}_{{z'}}} + \sqrt {{{\Omega }^{2}} - \Lambda } ,$$
(53)

where

$$\Omega = \frac{{16}}{{25}}\left( {\sqrt {{{\phi }_{0}}} {{v}_{1}} - \frac{{3{{v}_{2}}{{u}_{0}}}}{{16{{\gamma }_{2}}}}} \right),$$
(54)
$$\begin{gathered} \Lambda = \frac{{512}}{{945}}\left( {{{{\left( {\frac{{15{{u}_{0}}}}{{8{{\gamma }_{1}}}}} \right)}}^{2}}v_{1}^{2} - \frac{{75u_{0}^{2}{{v}_{1}}{{v}_{2}}}}{{128{{\gamma }_{1}}{{\gamma }_{2}}}}} \right. \\ \left. {\mathop {\, - }\limits_{_{{_{{_{{_{{_{{}}}}}}}}}}} \frac{{15}}{{512}}\frac{{v_{2}^{2}u_{0}^{2}}}{{\gamma _{2}^{2}}} + \frac{{15u_{0}^{2}{{v}_{3}}}}{{128{{\gamma }_{2}}}}} \right). \\ \end{gathered} $$
(55)

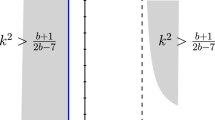
It can be seen from Eq. (53) that in the case of \(\Lambda < {{\Omega }^{2}}\), the dispersion law is real and the solution is stable. The instability occurs at \(\Lambda > {{\Omega }^{2}}\). The analysis of Eq. (53) leads to the following threshold value \(\omega _{{Be,\;{\text{th}}}}^{2}\) for the instability development:

$$\omega _{{Be,\;{\text{th}}}}^{2} = \frac{{1 + \frac{{l_{{x{\kern 1pt} '}}^{2}}}{{l_{{y'}}^{2}}}\left( {1 - \frac{9}{7}{\text{ta}}{{{\text{n}}}^{2}}\vartheta } \right)}}{{{{{\sin }}^{2}}\vartheta - \frac{9}{7}\frac{{l_{{x{\kern 1pt} '}}^{2}}}{{l_{{y{\kern 1pt} '}}^{2}}}{{{\tan }}^{2}}\vartheta }},$$
(56)

the instability growth rate being as follows:

$$\Gamma = \frac{2}{{\sqrt {63} }}\frac{{{{u}_{0}}\sqrt {\left( {1 + \omega _{{Be}}^{2}} \right)P} }}{{{{{\sin }}^{2}}\vartheta + \omega _{{Be}}^{2}}},$$
(57)

where

$$\begin{gathered} P = \left[ {1 + \frac{{l_{{x{\kern 1pt} '}}^{2}}}{{l_{{y{\kern 1pt} '}}^{2}}}\left( {1 - \frac{9}{7}{{{\tan }}^{2}}\vartheta } \right)} \right]\omega _{{Be}}^{2} \\ + \;{{\sin }^{2}}\vartheta - \frac{9}{7}\frac{{l_{{x{\kern 1pt} '}}^{2}}}{{l_{{y{\kern 1pt} '}}^{2}}}{{\tan }^{2}}\vartheta . \\ \end{gathered} $$
(58)

5 CONCLUSIONS

The nonlinear equation was obtained that describes the dynamics of nonlinear wave structures in dusty plasma above the illuminated surface of the Moon in the case of low frequencies and pancake-like shape of wave packet stretched out along the external magnetic field. This equation is the modified Zakharov–Kuznetsov equation. The resulting equation differs from the ordinary Zakharov–Kuznetsov equation. Its nonlinear term contains the factor \(\sqrt \phi \), while the analogous term in the ordinary equation contains the factor ϕ, the exponent of which is equal to 1. The analytical formula for the one-dimensional soliton solution was obtained. This solution differs from the well-known one-dimensional soliton solutions of the Korteweg–de Vries and Zakharov–Kuznetsov equations. The analysis was performed of the stability of the one-dimensional soliton solution, which shows that this solution is stable.

The non-analyticity of the nonlinear term makes it difficult to find two-dimensional solutions to the modified Zakharov–Kuznetsov equation, which can be obtained analytically in the case of the ordinary equation. In this regard, for the two-dimensional analysis of solutions to the modified Zakharov–Kuznetsov equation, apparently, numerical methods should be used, which is the goal of future research. From the point of view of the possible applications of the considered solitons, as in the case described in [14], the so-called transient lunar phenomena are of interest.