Simulation of a Positive Corona Discharge from a Plane-Parallel System of Horizontal Grounded Wires in the Electric Field of a Thundercloud

Abstract

We study theoretically a non-stationary positive corona developing in free space from a system of grounded wires suspended at the same height and placed in a uniform thundercloud electric field growing with time. To calculate the corona characteristics, a two-dimensional computer model has been developed. The discharge is described by an equation for the density of positive ions of a single species and Poisson’s equation for the electric field. It is assumed for simplicity that the wires are identical and the neighboring wires are separated by the same distance. The two-dimensional calculations are performed for the system composed of infinite number of parallel wires, when the problem is reduced to studying the corona from one wire, and for the system consisting of eight parallel wires. The corona current, the distribution of the space charge generated by the corona, and the electric field about the wires are found. In the case of the corona from the infinite number of the wires, the calculated corona current reaches saturation and depends only on the growth rate of the thundercloud electric field and the distance between the wires. The results may be of interest for subsequent assessments of the reliability of multi-wire lightning protection.

APPENDIX

1.1 POTENTIAL INDUCED BY THE PERIODIC SYSTEM OF PARALLEL WIRES IN EMPTY SPACE ABOVE THE GROUND

This potential $\varphi {\kern 1pt} '(x,y)$ is given by the formula

$$\begin{gathered} \varphi {\kern 1pt} '(x,y) \\ \, = \frac{q}{{4\pi {{\varepsilon }_{{\text{0}}}}}}\sum\limits_{k = - \infty }^\infty {\int\limits_{ - \infty }^{ + \infty } {\left( {\frac{{dz}}{{\sqrt {{{{\left( {x - {{x}_{{\text{k}}}}} \right)}}^{2}} + {{{(y - h)}}^{2}} + {{z}^{2}}} }}} \right.} } \\ \, - \left. {\frac{{dz}}{{\sqrt {{{{\left( {x - {{x}_{{\text{k}}}}} \right)}}^{2}} + {{{(y + h)}}^{2}} + {{z}^{2}}} }}} \right), \\ \end{gathered} $$

(A.1)

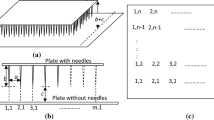
where x_k = D/2 + kD are the coordinates of the centers of the wires, k = 0, ±1, ±2, etc. (see Fig. 1a), and q = 2πr₀ε₀E(r₀) is the charge per unit length of each wire.

Evaluating the integrals in (A.1), we obtain

$$\varphi {\kern 1pt} '(x,y) = \frac{q}{{4\pi {{\varepsilon }_{{\text{0}}}}}}\sum\limits_{k = - \infty }^\infty {\ln \left[ {\frac{{{{{\left( {x - {{x}_{k}}} \right)}}^{2}} + {{{(y + h)}}^{2}}}}{{{{{\left( {x - {{x}_{k}}} \right)}}^{2}} + {{{(y - h)}}^{2}}}}} \right]} {\kern 1pt} {\kern 1pt} .$$

(A.2)

Transforming (A.2) to the summation over positive k, we find

$$\begin{gathered} \varphi {\kern 1pt} '(x,y) = \frac{q}{{4\pi {{\varepsilon }_{{\text{0}}}}}}\ln \left[ {\frac{{{{{\left( {x - D{\text{/}}2} \right)}}^{2}} + {{{(y + h)}}^{2}}}}{{{{{\left( {x - D{\text{/}}2} \right)}}^{2}} + {{{(y - h)}}^{2}}}}} \right] \\ \, + \frac{q}{{4\pi {{\varepsilon }_{{\text{0}}}}}}\sum\limits_{k = 1}^\infty {\ln \left\{ {\left[ {\frac{{{{{\left( {x - D{\text{/}}2 + kD} \right)}}^{2}} + {{{(y + h)}}^{2}}}}{{{{{\left( {x - D{\text{/}}2 + kD} \right)}}^{2}} + {{{(y - h)}}^{2}}}}} \right]} \right.} \\ \, \times \left. {\left[ {\frac{{{{{\left( {x - D{\text{/}}2 - kD} \right)}}^{2}} + {{{(y + h)}}^{2}}}}{{{{{\left( {x - D{\text{/}}2 - kD} \right)}}^{2}} + {{{(y - h)}}^{2}}}}} \right]} \right\}. \\ \end{gathered} $$

(A.3)

Introducing the variable ξ = x – D/2 in (A.3) and replacing in the last term the sum of logarithms by the product under the sign of logarithm, we have

$$\begin{gathered} \varphi {\kern 1pt} '(x,y) = \frac{q}{{4\pi {{\varepsilon }_{{\text{0}}}}}}\ln \left[ {\frac{{{{\xi }^{2}} + {{{(y + h)}}^{2}}}}{{{{\xi }^{2}} + {{{(y - h)}}^{2}}}}} \right] \\ \, + \frac{q}{{4\pi {{\varepsilon }_{{\text{0}}}}}}\ln \prod\limits_{k = 1}^\infty {\left\{ {\left[ {\frac{{{{{\left( {\xi + kD} \right)}}^{2}} + {{{(y + h)}}^{2}}}}{{{{{\left( {\xi + kD} \right)}}^{2}} + {{{(y - h)}}^{2}}}}} \right]} \right.} \\ \, \times \left. {\left[ {\frac{{{{{\left( {\xi - kD} \right)}}^{2}} + {{{(y + h)}}^{2}}}}{{{{{\left( {\xi - kD} \right)}}^{2}} + {{{(y - h)}}^{2}}}}} \right]} \right\}. \\ \end{gathered} $$

(A.4)

Introducing the complex variables ${{z}_{1}} = \frac{\xi }{D} + i\frac{{(y + h)}}{D}$, ${{z}_{2}} = \frac{\xi }{D} + i\frac{{(y - h)}}{D}$ and their complex conjugates ${{\bar {z}}_{1}}$ and ${{\bar {z}}_{2}}$, we rewrite the product in (A.4) as

$$\begin{gathered} \prod\limits_{k = 1}^\infty {\left[ {\frac{{{{{\left( {\xi + kD} \right)}}^{2}} + {{{(y + h)}}^{2}}}}{{{{{\left( {\xi + kD} \right)}}^{2}} + {{{(y - h)}}^{2}}}}} \right]\left[ {\frac{{{{{\left( {\xi - kD} \right)}}^{2}} + {{{(y + h)}}^{2}}}}{{{{{\left( {\xi - kD} \right)}}^{2}} + {{{(y - h)}}^{2}}}}} \right]} \\ \, = \prod\limits_{k = 1}^\infty {\left[ {\frac{{\left( {1 + {{z}_{1}}{\text{/}}k} \right)\left( {1 - {{z}_{1}}{\text{/}}k} \right)\left( {1 + {{{\bar {z}}}_{1}}{\text{/}}k} \right)\left( {1 - {{{\bar {z}}}_{1}}{\text{/}}k} \right)}}{{\left( {1 + {{z}_{2}}{\text{/}}k} \right)\left( {1 - {{z}_{2}}{\text{/}}k} \right)\left( {1 + {{{\bar {z}}}_{2}}{\text{/}}k} \right)\left( {1 - {{{\bar {z}}}_{2}}{\text{/}}k} \right)}}} \right]} {\kern 1pt} {\kern 1pt} . \\ \end{gathered} $$

Transforming the last expression by using the well-known sine expansion $\frac{{\sin z}}{z} = \prod\nolimits_{k = 1}^\infty {\left( {1 - \frac{z}{{k\pi }}} \right)} \left( {1 + \frac{z}{{k\pi }}} \right)$ [57], we find

$$\begin{gathered} \prod\limits_{k = 1}^\infty {\left[ {\frac{{\left( {1 + {{z}_{1}}{\text{/}}k} \right)\left( {1 - {{z}_{1}}{\text{/}}k} \right)\left( {1 + {{{\bar {z}}}_{1}}{\text{/}}k} \right)\left( {1 - {{{\bar {z}}}_{1}}{\text{/}}k} \right)}}{{\left( {1 + {{z}_{2}}{\text{/}}k} \right)\left( {1 - {{z}_{2}}{\text{/}}k} \right)\left( {1 + {{{\bar {z}}}_{2}}{\text{/}}k} \right)\left( {1 - {{{\bar {z}}}_{2}}{\text{/}}k} \right)}}} \right]} \\ \, = \frac{{{{z}_{2}}{{{\bar {z}}}_{2}}}}{{{{z}_{1}}{{{\bar {z}}}_{1}}}}\frac{{\sin \pi {{z}_{1}}\sin \pi {{{\bar {z}}}_{1}}}}{{\sin \pi {{z}_{2}}\sin \pi {{{\bar {z}}}_{2}}}}. \\ \end{gathered} $$

Returning back to the variables ξ and y in the right-hand side of the last expression and using the formula for the product of sines, we obtain that the infinite product under the sign of logarithm in (A.4) is equal to the following expression:

$$\begin{gathered} \frac{{{{z}_{2}}{{{\bar {z}}}_{2}}}}{{{{z}_{1}}{{{\bar {z}}}_{1}}}}\frac{{\sin \pi {{z}_{1}}\sin \pi {{{\bar {z}}}_{1}}}}{{\sin \pi {{z}_{2}}\sin \pi {{{\bar {z}}}_{2}}}} = \left[ {\frac{{{{\xi }^{2}} + {{{(y - h)}}^{2}}}}{{{{\xi }^{2}} + {{{(y + h)}}^{2}}}}} \right]{\kern 1pt} \\ \times \;\frac{{\cosh {\kern 1pt} \left[ {2\pi (h + y){\text{/}}D} \right] - \cos {\kern 1pt} \left( {2\pi \xi {\text{/}}D} \right)}}{{\cosh {\kern 1pt} \left[ {2\pi (h - y){\text{/}}D} \right] - \cos {\kern 1pt} \left( {2\pi \xi {\text{/}}D} \right)}}. \\ \end{gathered} $$

(A.5)

Replacing the infinite product in (A.4) by the right-hand side of (A.5) and combining two terms in the right-hand side of (A.4), finally we have

$$\begin{gathered} \varphi {\kern 1pt} '(x,y) = \frac{q}{{4\pi {{\varepsilon }_{{\text{0}}}}}} \\ \times \;\ln \left\{ {\frac{{\cosh \left[ {2\pi (h + y){\text{/}}D} \right] - \cos \left( {2\pi \xi {\text{/}}D} \right)}}{{\cosh \left[ {2\pi (h - y){\text{/}}D} \right] - \cos \left( {2\pi \xi {\text{/}}D} \right)}}} \right\}. \\ \end{gathered} $$

(A.6)

Formula (A.6) is similar to that given in the book [58], in which a similar problem is considered, namely, the distribution of the potential induced by a periodic system of charged lines is found. However, the formula of [58] contains the factor $2\pi {{\varepsilon }_{{\text{0}}}}$ rather than $4\pi {{\varepsilon }_{{\text{0}}}}$ in the denominator. Besides in the mentioned formula, the value of the argument of the cosine and hyperbolic cosine contains the factor π, as opposed to our factor 2π.

Returning from ξ = x – D/2 to the initial variable x and expressing the charge per unit length q = 2πr₀ε₀E(r₀) in terms of the potential U by using (20), we can rewrite (A.6) in the form:

$$\begin{gathered} \varphi {\kern 1pt} '(x,y) = \frac{U}{{2\ln \left[ {\frac{{\sinh (\pi 2h{\text{/}}D)}}{{\pi {{r}_{0}}{\text{/}}D}}} \right]}} \\ \, \times \ln \left\{ {\frac{{\cosh \left[ {2\pi (h + y){\text{/}}D} \right] + \cos \left( {2\pi x{\text{/}}D} \right)}}{{\cosh \left[ {2\pi (h - y){\text{/}}D} \right] + \cos \left( {2\pi x{\text{/}}D} \right)}}} \right\}. \\ \end{gathered} $$

(A.7)

Note finally that the formula given in the book [59] for the potential about a grating composed of parallel wires, if r₀ ≪ D, h, can be transformed to (A.7) after expanding the potential as a series in the small parameter (r₀/D)² and neglecting the high-order terms.