Spectral Methods of Control of Impurities, Their Flows and Localization in an Equilibrium Low-Temperature Plasma of Low Pressure

Abstract

The state-of-art of studies of processes involving small fractions of particles formed as a result of chemical transformations of the source gas or appearing from the outside as an impurity is discussed. Various high-sensitivity methods for measuring the low concentrations of particles are considered. The main focus is on spectral methods, both classical and laser ones. The main modern fields of the application of non-equilibrium plasma, features, and achievements of the diagnostic tools used in them are highlighted. The emphasis is on spectroscopic studies of plasma purity in the low-temperature near-wall layers of thermonuclear reactors. In this case, the issue of the penetration of water molecules into the plasma chamber from the cooling circuits is of particular importance. In view of the limited accessibility to the reactors, new remote versions of spectral emission methods are being developed that are focused on the diagnostics of the ITER near-wall plasma. A new method of multispectral optical actinometry is discussed, in which intermediate chemically unstable particles can play the role of actinometers. This broadens the range of possibilities for quantitative measurements of concentrations of particles of different kinds, and increases the sensitivity. Effective actinometric pairs were found for the objects under consideration, e.g., hydrogen and deuterium atoms. The schemes are worked out on laboratory facilities, and kinetic models of plasma-chemical processes are developed. Scaling of the results of model experiments makes it possible to predict the measurement of the impurity flows at the level (10^–9–10^–13) Pa m³ s^–1 with the localization of sources determined by the spatial resolution of the optical system.

1 INTRODUCTION

According to estimates, more than 90% of matter known in nature is in a plasma state [1], being, naturally, one of the most common and traditional objects of the studies and applications. A significant fraction of it is the low-temperature plasma (LTP) with partial ionization. For a long time, the main applications were associated and continue to be associated with heating during combustion or the passage of current through gas media (light sources, cutting, welding, processing, hardening of materials, analysis of the composition of the substance, etc.). In recent decades, the center of gravity has noticeably shifted to the applications where plasma effects are not limited to thermal effects and exhibit selective properties. This was stimulated by the tasks of the interpretation and formation of line spectra, the development of laser technology, the implementation of directed chemical reactions, and required a more detailed description of plasma states [2, 3].

The forms and manifestations of LTP are classified, first of all, with respect to the state of its equilibrium [4–6]. At the thermodynamic equilibrium (TE), the plasma is closed, uniform and the only parameter—temperature—fully describes its properties, including the composition and energy distribution of neutral and charged chemical particles of matter. However, it almost does not occur in this state, mainly due to the violation of the closed condition. Various approximations to the TE are described by the models of: the local (LTE) and partially local (PLTe) thermodynamic equilibrium, coronal (CEM), collisional-radiation (CRM), etc. [4–8]. They usually maintain the main parameter—temperature Т, at least with respect to individual kinds of particles, their states, degrees of freedom, etc.: kinetic (translational, gas) for neutral particles T_t, electron T_e, vibrational T_V, rotational T_R, excitation temperature of electron levels T_exc, and ionization T_i ones. Despite the conventionality, such models are useful because, in particular, they make it possible to consider certain Boltzmann–Maxwell ensembles of particles using partial temperatures, although there can be several such ensembles for the plasma as a whole. Such nonequilibrium models consider the energy distribution of particles, but it is not known about proposals for models of the chemical composition, which replenishing the detailed-equilibrium Arrhenius rules to some extent.

Along with the development of the analytical models, the kinetic approach becomes the main one in modern practice, which as much as possible takes into account particles of all kinds, their states, and interactions. The difficulty is associated with a large number of processes. The book [9] describes the concept of limiting the number of reactions according to the principle of eliminating less probable and significant ones. The involvement, starting in the 1970s, of computing tools with special software packages and the accumulation of experimental data support this logic. The problem of the concept, however, is to develop criteria for the completeness of the selection of processes from among those in a real object. A description of the kinetics in the form of equilibrium equations also implies the availability of information on the rates of the processes, if known but with errors, and it is often difficult to estimate the reliability of the calculation results as a whole. For example, the review [10] considers a detailed level kinetics scheme for interpreting the spectrum of discharge radiation in nitrogen at low pressure. The data on the reaction rates involving more than 500 levels are used. Moreover, the number of bound states only in N₂ is on the order of 2 × 10⁴, and the completeness of the description of the plasma state is difficult to estimate. Information about the chemical composition of the plasma, which differs significantly from the gases from which it is formed, is important.

In this article, we consider problems associated with small components in the nonequilibrium plasma. In addition to the indicated difficulties, some may arise not only due to the chemical transformations of the source gases, but also due to their final purity, emissions from structural elements, and their appearance from outside through wall defects. In these cases, the important question is not only about the presence and quantity of particles, but also about sources, their localization, flows of emitted particles and their transformations. In the analysis of processes and, as mentioned, the forced limitation of their number, the consideration is sometimes used that it is allowed to exclude some of them, if the number of reacting particles in them is small at the intermediate stages. However, it is known that many cases confirmed in practice when particles in small quantities play an important role. For example, OH radicals (~10¹³ cm^–3) slow down the decomposition of CO₂ molecules in the discharge, and this affects the operation of CO₂ lasers [11]. In CO lasers, energy transfer from vibrationally excited CO molecules to electronically excited CN molecules (~10¹² cm^–3) leads to radiation quenching of laser levels [12], the presence of oxygen atoms О (~10¹⁴ cm^–3) affects the chain of transformations of working CO molecules [12, 13], and burning of carbon atoms C (~10¹³–10¹⁴ cm^–3) contributes to the population of laser levels [14]. Small (~10¹⁰ cm^–3) quantities of Н₂О molecules in the wall layer of a large plasma nuclear reactor violate the mode of its operation [15].

In many cases, it is small components and radical, in particular, that determines the results of targeted plasma applications. F, Cl atoms (~10¹⁰–10¹⁴ cm^–3) and HF_x, HCl_x radicals (~10⁹–10¹² cm^–3) play a key role in the manufacturing technology of electronics elements [16–20]. Small fractions of hydrocarbon radicals play a decisive role in various chemical industries and ecology [21]. The ratio of the amounts of C, H, and CF₃ radicals in the plasma, which depends on the composition of the gas and the energy inlet, affects the morphology of the growth of nanotubes, graphene [22], and diamond-like films [23].

As a rule, deviations from equilibrium in the stationary plasma of a self-sustained discharge increase with decreasing pressure of the plasma-forming gases due to the deceleration of relaxation processes at a relatively low kinetic temperature of the neutral component in the bulk and participation in reactions on the surface. In the pulsed mode, however, deep violations in the equilibrium can also be observed both at atmospheric and at higher pressures. This is used, in particular, in high-power pulsed gas lasers with planar discharges and transverse breakdown. Often, the necessary result is achieved by the fact that there is excitation and production of particles in the plasma, which are then introduced into the medium separated from the plasma. The design of the first high-power molecular lasers by mixing vibrationally excited N₂ molecules in a high-frequency discharge with a flow of CO₂ and CO molecules can be emphasized among the most well-known examples [11]. In iodine–oxygen lasers, the generation occurs when iodine vapors are mixed with a flow of metastable oxygen О₂(¹Δ) from a gas discharge, and in this case, an important role is played by techniques for controlling the electron energy [24]. In recent years, great interest has been shown in plasma objects in which gas is continuously pumped under increased pressure through a discharge of small sizes (typically millimeters) and its subsequent expansion in the nozzle or free space. In this case, the jet has a kinetic temperature close to room temperature at a distance of several centimeters but its composition is dramatically different from the original one, it contains vibrationally and electronically excited particles, radicals. In this state, the jets have pronounced bactericidal properties, are studied and applied in biomedical technologies and food processing with minimal thermal effects [25–27]. Expansion occurs in vacuum in procedures such as etching of materials. The inlet of energy to the discharge is increased for some other applications in surface treatment, and the nonequilibrium plasma jet at the same stages of outflow has a kinetic temperature of ~1500 K [28]. There are many similar practically important results, and their number is growing.

Even from such individual examples it is clear that when developing methods for the measurement and simulation of the composition of the nonequilibrium plasma of various objects and the problems solved with their help, it is hardly possible now and at least in the near future to count on a universal answer. It is also clear that the logic of the development of physics and technology of non-equilibrium plasma does not provide an alternative in favor of calculations or measurements, they should be complementary.

Experimental research methods for small components should have high detection sensitivity. One of the latest books on plasma spectral studies [4] describes various methods for measuring the composition and properties of particles. However, the arsenal of these tools, on the one hand, is constantly replenished, and, on the other hand, the already known methods are adapting to new conditions for their application. These non-disturbing plasma methods and their applications are emphasized in this review.

We take into account that interest in the problem is extremely great and that the works performed in the last 20 years in this direction are difficult to cover sufficiently and, moreover, to analyze them compactly. Specific reviews are devoted to separate cycles related to notable advances in the selected problems. Some of them are mentioned, others will be indicated in the subsequent sections of the article. This applies to the emergence of new objects, and the results of the scientific and technical nature obtained with their help. However, they have in common that the objects are relatively compact, such as discharges for etching the surfaces of the bases of large electron circuits [19], synthesis of nanostructures [22], electron-beam facilities [29], “cold” plasma jets [25], etc. The studies in order to optimize the technology are carried out directly on them. A number of reviews are devoted to new diagnostic methods, including laser applications [30–33].

In addition to a number of general issues of the research technique, we describe the state-of-the-art of the problem of the chemical composition of the nonequilibrium near-wall zone of plasma power reactors. Typically, these are large cooled facilities with large loads on the shell of the working chamber, and the problems of vacuum insulation, the possible inlet of impurities, their control and localization of sources are urgent. On the basis of the experience of previous generations of reactors, these problems attract particular attention in the design of the largest (~1000 m³) ITER reactor [15]. The problem has been discussed for over 10 years and includes the development of physically and technically adequate control methods, their testing on model facilities and a description of physicochemical processes in order to scale the results.

2 FEATURES OF APPLICATION OF METHODS RELATED TO THE SAMPLING FOR THE STUDY OF PLASMA-CHEMICAL TRANSFORMATIONS

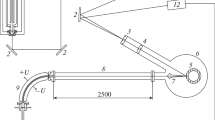
In the 1960s, the works on powerful gas-discharge CO₂, CO, N₂O lasers started, and the mechanisms of their action and the possibility of designing devices with a long service life under the conditions of chemical reactions were studied. This stimulated the deployment of systematic works on nonequilibrium plasma chemistry. The applicable quantitative methods were developed, and attempts were made to use experience and instruments for gas analysis based on chromatography, mass spectrometry, EPR, and IR analysis. They meant working with gases formed after exposure to plasma—sampling, analysis of the gas flow that passed through the plasma or after the discharge was turned off. In the simplest versions, gas was sampled into removable ampoules on a discharge tube, followed by the analysis on remote instruments [34–36]. To develop these versions, the methods were proposed when the analytical instruments were integrated with plasma objects. Figure 1 shows sketches of some of the first such schemes.

Fig. 1.

Examples of schemes: (а) facility with a mass spectrometer chamber using a discharge tube [37]; (b) EPR measurements [13]; and (c) infrared analyzer [38]. Notations are given in the text.

Figure 1a shows a fragment of a circuit with a mass spectrometer. Here, 1 is a cooled discharge tube passing through the chamber of the device pumped out through the aperture 2. The inlet and pumping of the laser–gas mixture was carried out through channels 3. The first differential pumping chamber of the spectrometer 4 is connected with the internal volume of the tube through a small opening of a diaphragm 5. An aperture 6 separated the first chamber from the analyzer chamber with pumping through a port 8, ionization chamber 9 and quadrupole mass spectrometer sensor 10. Particular attention in this method is required by the organization of sampling through the diaphragm 5. It should be a small hole in a thin film, the choice of dimensions and materials is associated with minimization of distortion the composition of the particles passing through it depends on the conditions in the plasma and was discussed in [37].

Figure 1b shows a scheme for analyzing the composition of the gas flow passing through a discharge 1 using an EPR spectrometer. The poles of a magnet 2 and a microwave cavity are indicated. Figure 2c shows a schematic diagram of an optical gas analyzer. Len-ses 2–4 collimate and focus IR radiation from a heat source 1 on a detector 5 after passing through the gas medium in a cuvette 6. The radiation is modulated by a disk 7 rotated by a motor 8. Two holes on the disk are closed by interference filters 9, 10. The passband of one of the filters corresponds to the absorption band of the analyzed molecules, the band of the other lies in the transparency window. The absorption and concentration of molecules was determined by synchronous detection using electronic units 11 and 12 with a reference signal from the photoresistance. The response time of facilities (a) and (c) was about 10 s, the time of flight of particles from the plasma to the  microwave cavity in the facility (b) varied from 0.2 to 5 s.

Fig. 2.

Change in the СО₂ concentration in the discharge in the СО₂–N₂–He mixture. (1 and 4) Measurements with the gas analyzer (Fig. 1c [39]), (2) data from the remote mass spectrometric analysis of samples [36], and (3) data from the remote chromatographic analysis [35]. Inset shows the initial section of the dependence (4) at the short-term exposure to the discharge. In the case (4), Ni electrodes, in the case (1), Pt electrodes.

An important result of these early experiments with integrated circuits was that it was possible to separate the transformations occurring in different phases of the action of the nonequilibrium plasma. It was shown that in the cases of CO₂ and CO lasers, the stationary composition of particles is established quite quickly, in times on the order of seconds, and the slower displacements of this dynamic equilibrium are associated with the effect of surfaces: particle adsorption, desorption of impurities, and catalytic processes. Figure 2 shows examples of the dynamics of CO₂ concentration in measurements by various methods.

This determined the strategy for the development of the design of sealed-off CO₂ and CO lasers with a long service life without changing the filling of active elements. On the contrary, in the case of N₂O lasers, already at the first stage, the dynamic equilibrium is achieved with the complete decay of the working N₂O molecules, and the creation of such sealed-off systems is impossible.

In the subsequent period and until now, as mentioned in the Introduction, the studies of the composition of plasma have expanded significantly but the analysis with sampling has not lost its relevance. The measurement principles contained in circuits (Fig. 1) are constantly used and modified.

The methods for mass spectrometry of the nonequilibrium plasma have developed as the most universal ones with respect to the kind and charge of particles. Although the prototype (Fig. 1) and the methodology as a whole are preserved, their improvement and elimination of the disadvantages noted already at the initial stage of application are carried out. In modern facilities, the principle of the molecular beam formation using a system of two diaphragms is implemented using three diaphragms (skimmers), three-stage differential pumping, and beam modulation [40]. This makes it possible to a greater extent to exclude the occurrence of secondary reactions on the way from the plasma boundary to the ionization chamber of the spectrometer, which was noted when working with the scheme (Fig. 1a) [37]. Such a modification is called molecular beam mass spectrometry (MBMS). Another proposal is aimed at minimizing the effect of fragmentation particles in the ionization chamber. This difficulty was also noted in [37] and is related to the fact that the appearance of a particle in the ion mass spectrum can be associated with either direct or dissociative ionization. The second process has a higher threshold. The proposal is reduced to measuring the ion peak intensity for mass (M/Z) of the corresponding particle depending on the electron energy in the ionization chamber. The emerging features make it possible to separate the contributions of processes. Similar features can be observed if dissociative ionization occurs with the participation of metastable molecules, this lowers the threshold, and their concentration can be determined. This technique is now called threshold ionization mass spectrometry (TIMS) [41]. Both approaches are used in a number of works [17]. The absolute calibration of concentrations n_X of the measured particles X in mass spectrometric measurements can be carried out in the presence of inert gas atoms A with the known concentration n_A in the composition of the plasma-forming gases, which do not participate in reactions,

$${{n}_{X}} = {{n}_{A}}{{I}_{X}}{{\sigma }_{A}}{\text{/}}{{I}_{A}}{{\sigma }_{X}},$$

(1)

here, I and σ are mass peak intensities and ionization cross section, respectively.

Plasma ions can be fixed when the electron beam is turned off or when its energy is below the minimum ionization threshold. This was also demonstrated in [42], which describes the ionic composition of plasma of CO and N₂O lasers. In particular, a homologous series ${{{\text{C}}}_{k}}{\text{O}}_{l}^{ + }$ at l = 2, 2 ≤ k ≤ 10 was found. At the same time, it is still problematic to speak about absolute ion concentrations due to the complexity of calibrations.

The docking of the mass spectrometer with a real plasma object in combination with the need to select a substance with the minimal distortion of its composition remains one of the central problems. These circumstances distinguish this technique from modern commercially available mass spectrometric complexes for determining the elemental composition of samples, including atomizers, the role of which is played by the equilibrium plasma (flame, inductively coupled plasma with a high gas temperature).

Although the applicability of the EPR technique is limited by the particles paramagnetic in the ground electron state, the circuit (Fig. 1b) is used to diagnose plasma flows and determine the content of not only oxygen atoms in them (as in [13]), but also of other radicals [43]. If necessary to study the interaction of these radicals with various media, the EPR technique is supplemented by the spin trap technique [44].

The technique of infrared absorption spectroscopy of high sensitivity, implemented according to the scheme Fig. 1c has also been modified. In [38], the metal–ceramic array was used as the source in the diagram of Fig. 1c, and measurements were carried out after the discharge was switched off or during continuous pumping from an external discharge. In [37], for the purpose of plasma pyrometry, a heated multi-cavity graphite structure with a blackbody spectrum at temperatures up to 2500 K was used as the source 1. At such temperatures exceeding the molecular vibrational temperatures, the contribution of the own IR radiation of the discharge to the total intensity is small, and the concentration of molecules can be measured not only after turning off the discharge but also directly in the plasma. Subsequently, with the advent of frequency tunable lasers, IR analysis methods were transferred to a new base, which will be discussed in more detail in the following sections.

In summary, it is possible say that the methods for studying the composition of the non-equilibrium plasma using sampling having been under way for a long time are well developed to the level of current needs using special mass spectrometers, EPR and IR analysis. The characteristic sensitivity is ~10¹²–10¹³ cm^–3. It is common to these methods that the localization of measurements is almost impossible. Information on the composition of the plasma, depending on the conditions, refers either to the values averaged due to diffusion or to the vicinity of the place of sampling of the substance (in the diagram Fig. 1a).

3 STUDIES OF THE PLASMA COMPOSITION BY CLASSICAL OPTICAL SPECTROSCOPY METHODS

These methods are currently widely developed and used for various purposes. For plasma, they, in particular, make it possible to conduct studies of the chemical composition directly in the object under study without significant disturbances. In the absence of equilibrium, however, such measurements are also not direct, since they provide information about the selected energy state or their group. This leads to the necessity to establish a relationship between the level populations and the total concentration based on the physics of the processes and, often, to use several independent methods. The methods are divided into emission (radiation), absorption (absorption), and scattering ones. We briefly focus on the main aspects.

3.1 Spontaneous Plasma Emission

The intensity of the I_Xul line of X-ray emission at the u–l transition is related to the measured concentration N_X at the u–l transition at the frequency ν_X of an optically thin homogeneous layer by the ratio [4]

$${{I}_{{Xul}}} = {{C}_{X}}h{{\nu }_{{Xul}}}{{A}_{{Xul}}}{{k}_{{Xu}}}{{N}_{X}}{{\left( {{{Q}_{{Xu}}} + {{{\left( {{{\tau }_{{Xu}}}} \right)}}^{{ - 1}}}} \right)}^{{ - 1}}},$$

(2)

where С_Х are coefficients determined by aperture optics and detection sensitivity; h is the Planck constant; A_Xul is the Einstein coefficient; k_Xu and τ_Xu are excitation rates and radiative lifetime of the radiating state u; Q_Xu is the decay frequency of the upper level in processes other than radiation. If the listed values are known, and I_Xul is measured in the absolute measure, then relation (2) gives the desired value N_X.

Technically, this is one of the simplest methods for determining particle concentrations. The С_Х coefficients are determined for a particular facility, A_Xul and Q_Xu values for a large number of particles, transitions and states are available in spectroscopic databases, the same as τ_Xu values, which take into account the branching factors of radiation transitions. The absolute intensities of I_Xul are measured by a reference lamp with a continuous spectrum and a known brightness temperature. This is also a well-established procedure [45].

Difficulties are associated with the lack of equilibrium in the object under consideration. Level populations, including the emitting level u, can be determined by various mechanisms with the participation of other levels i with populations N_Xi and rates k_Xiu. Sometimes, taking into account the experience of previous studies and evaluations of their compliance with the conditions of measurements, simplifying assumptions are made. It is assumed that the overwhelming number of particles is in the ground electron state ΣN_Xi = N_X. If, based on the type of spectrum, we select the strongest optical transitions from the excited and radiating states under consideration, then (τ_Xu)^–1 = A_Xul. In the case of electronically excited molecules, transitions to other repulsive states (pre-dissociation) can contribute to Q_Xu. If this is excluded by the structure of the terms or atoms with a radiating state remote from the boundary of the continuous spectrum are considered, then the frequencies Q_Xu can be attributed to quenching collisions with other particles Y with N_Y concentrations and with each other with rate constants q_XY, q_XX:

$${{Q}_{{Xu}}} = {{q}_{{XX}}}{{N}_{X}} + \sum\limits_Y {{{q}_{{XY}}}{{N}_{Y}}} ,$$

(3)

$${{q}_{{XX,Y}}} = \left\langle {{{v}_{{X,Y}}}\sigma _{{XX,Y}}^{q}} \right\rangle ,$$

(4)

where $v$ and σ^q are particle velocities and quenching cross sections. Such assumptions are indeed often justified and significantly simplify the use of Eq. (2). It is also accepted that the excitation of levels occurs by the direct electron impact and the excitation rate in Eq. (2) depends on the electron density n_e and their distribution f over energies ε

$$\left\{ \begin{gathered} {{k}_{{Xu}}} = \sqrt {\frac{2}{{{{m}_{e}}}}} {{n}_{e}}\int {\sigma (\varepsilon )} f(\varepsilon )\sqrt \varepsilon d\varepsilon , \hfill \\ \int {f(\varepsilon )d\varepsilon } = 1, \hfill \\ \end{gathered} \right.$$

(5)

where σ(ε) is the excitation cross section of the level u from the ground state. The last assumption introduces certainty into the excitation mechanism, and information on the cross sections σ (ε) can be taken from databases on elementary processes. This, however, does not eliminate the need to define n_e and f (ε) under co-nditions of the measurements. To this end, in the theoretical approach, it is necessary to solve the system of equations of kinetics and electrostatics with the involvement of a large amount of additional information. In the experimental approach, information on the electron component can be obtained by scattering methods [4] for n_e > (10¹⁴–10¹⁵) cm^–3 that greatly limits the range of objects and complicates the measurements as a whole, or using probe methods. The latter, however, violates not only the simplicity but also another important advantage of emission methods, lack of contact, which greatly narrows the scope of their application as independent ones. It is stated in a recent very detailed and useful review of plasma radical spectroscopy [33], e.g., that the emission methods cannot be considered as quantitative ones. We can only partially agree with this, bearing in mind the reservations made above.

This simple method, on the contrary, is one of the most popular in quantitative measurements. From the point of view of the topic under discussion—determination of particle concentrations—it is often used as accompanying other methods that are not associated with such serious premises and limitations. With rare exceptions, almost all highly sensitive spectral methods, as noted, provide information on the population of the selected energy level of the particle. They are focused on the fact that this level belongs to the main electron state, which is sometimes metastable, if we consider its population. For atoms, in most cases this condition is fulfilled. Any spectral method for analyzing the results for the nonequilibrium plasma requires additional information. To know the temperature of a neutral gas is important. Spontaneous emission at low densities provides the necessary information from the Doppler broadening [4]. The same information can be obtained from the distribution of intensities in   the rotational structure of electron-vibrational bands [4, 220]. From the distribution of intensities in the vibrational structure of the transition bands between electronically excited states, it is possible to recover the vibrational temperatures of diatomic molecules in the ground electron states. They are used to find the complete internal statistical sums of molecules necessary for the application of any spectral methods for measuring their concentrations.

3.2 Actinometry of Spontaneous Plasma Emission

The indicated difficulties of emission methods associated with the necessity to know the parameters of the electron component of the plasma can be significantly reduced by applying the optical actinometry (OA) method [4, 46]. The OA method does not use absolute optical measurements and is based on a comparison of the intensities of the spectra of two particles of various kinds. If the concentration of some particles (X) should be determined, and the concentration of others (A) is known, then particle A is called an actinometer. If we write expressions (2) for each of the particles and compose their ratio, then the concentration N_X is

$${{N}_{X}} = {{N}_{A}}\frac{{{{I}_{{Xul}}}}}{{{{I}_{{Aul}}}}}\frac{{{{\lambda }_{{Xul}}}}}{{{{\lambda }_{{Aul}}}}}\frac{{{{C}_{A}}}}{{{{C}_{X}}}}\frac{{{{k}_{{Au}}}}}{{{{k}_{{Xu}}}}}\frac{{{{A}_{{Aul}}}}}{{{{A}_{{Xul}}}}}\frac{{{{Q}_{{Xu}}} + {{A}_{{Xul}}}}}{{{{Q}_{{Au}}} + {{A}_{{Aul}}}}}.$$

(6)

The electron density is not included in (6), and instead of the absolute excitation rates of the emitting states, their ratio is included. The attractiveness of the OA method is associated with this last circumstance; it is important that we could choose pairs of cross sections with close threshold values ε_t and similar energy dependences. The similarity of the cross-sectional shapes at close thresholds is not accidental, since in the Born approximation they are related to the oscillator strength f_gu of the optically allowed transition between the ground g and excited u states [4]:

$$\sigma (\varepsilon ) = 4\pi a_{0}^{2}{{\left( {\frac{{{\text{Ry}}}}{{{{\varepsilon }_{t}}}}} \right)}^{2}}\frac{{{{\varepsilon }_{t}}}}{\varepsilon }\ln \left( {\frac{\varepsilon }{{{{\varepsilon }_{t}}}}} \right){{f}_{{gu}}},$$

(7)

where Ry is the ionization potential of a hydrogen atom, а₀ is the Bohr radius. For the excitation at optically forbidden transitions, the cross section maxima are grouped near the ε/ε_t ≈ 1.2–1.6 values, and section shapes are also close [4]. It is possible to set:

$${{\sigma }_{{Au}}}(\varepsilon ) \approx \Gamma {{\sigma }_{{Xu}}}(\varepsilon ),$$

(8)

where Г = const. The additional correction is introduced to account for the effect of f (ε) by introducing the factor (1 + δ_X). It is calculated by formulas (5) taking into account real f (ε). In [47], such calculations were performed for several actinometric pairs for the Maxwell distribution functions with different average energies ε* for combinations Х–А with differences ε_t,А – ε_t,X = (0.1–5) eV and are confirmed by measurements for O, H, Ar, and Xe atoms when processing the results taking into account and disregarding this factor. At the real value ε* = 9 eV the quantities δ_X = 0.01…±0.3. At the variations in calculations 6 < ε∗ [eV] < 12 the quantities |δ_X| < 0.6. In [48], the close results were obtained for f (ε), which differ from Maxwellian ones due to the effect of nonlocal formation mechanisms.

Examples of the form of cross sections used in measuring the concentrations of H₂O molecules and its fragments in plasma are shown in Fig. 3 [49]. It also shows the form of the electron energy distribution function (EEDF) measured by the probe method in a discharge with a hollow cathode in a He + Xe + Ar + H₂O mixture at the pressure of 0.8 mbar [49]. The inert gas partial pressure He : Xe : Ar = 99 : 1 : 1 is 0.6 mbar; that of water vapors is 0.2 mbar. The discharge current is 280 mA.

Fig. 3.

Cross sections of the excitation of atoms, dissociation of the H₂O molecule, and EEDF [49]: OH-dissociative excitation of H₂O; Xe 823 nm; O 777 nm and 844 nm; H 656 nm; and Ar 751 nm.

Thus, the actinometric approach completely eliminates the effect of n_e on the measurements of particle concentrations and reduces the effect of f(ε) to relatively small estimated corrections. Given these factors, the desired particle concentration is determined by a simple formula

$$N_{X}^{\Gamma } = {{N}_{A}}\frac{{{{I}_{{Xul}}}}}{{{{I}_{{Aul}}}}}\frac{{{{\lambda }_{{Xul}}}}}{{{{\lambda }_{{Aul}}}}}\frac{{{{C}_{A}}}}{{{{C}_{X}}}}\Gamma (1 + {{\delta }_{X}})\frac{{{{A}_{{Aul}}}}}{{{{A}_{{Xul}}}}}\frac{{{{Q}_{{Xu}}} + {{A}_{{Xul}}}}}{{{{Q}_{{Au}}} + {{A}_{{Aul}}}}}.$$

(9)

Table 1 presents X and A selected taking into account the comments on the excitation cross sections in the works of different authors. The combinations of wavelengths in these pairs are also indicated there. The references therein contain data on excitation cross sections Х and А.

Table 1. Approved actinometric pairs

Table 2 contains data on particles and optical transitions that are potentially suitable for compiling actinometric pairs with information on threshold values of excitation cross sections for various terms, designations, and configurations of terms. For heavy inert gases, two types of notations used in the literature are indicated (due to the intermediate type of coupling), Einstein’s coefficients A and lifetimes τ_u of the upper transition levels.

Table 2. Some parameters of particle for actinometric pairing. Data from database [89] for atoms and from [4, 90] for molecules. Symbols in the text

3.3 Localization of Emission of Heterogeneous Sources

If the plasma is nonuniform, then even for an optically thin layer expression (2) is valid only in its small region. Actually, the intensities are summed over the line of sight. To localize intensities in the general case, a tomographic problem is required to be solved with the profile recovery from plasma observations at different angles. This is a mathematically complex inverse problem [4]. In practice, they are usually limited to cases where the plasma has an axis of symmetry. Experimentally, the recovery without the complex mathematical processing is possible if the optical imaging system on the plane of the inlet slot of the spectrometer allows the selection and movement of rather narrow regions parallel to the axis. This is not always feasible for extended objects, and observations of emission along chords across the plasma column are used (Fig. 4). If ${{I}_{\nu }}$ is the intensity along the line of sight, and $I_{\nu }^{1}$ is the intensity from the unit length, then solving such a particular recovery problem of $I_{\nu }^{1}$ over ${{I}_{\nu }}$ is given by the Abel formula

$$\begin{gathered} I_{\nu }^{1}(x,y) = I_{\nu }^{1}(r) = - \frac{1}{\pi }\int\limits_r^R {\frac{{d{{I}_{\nu }}(x)}}{{dx}}\frac{{dx}}{{\sqrt {{{x}^{2}} - {{r}^{2}}} }}} \\ \, = - \frac{1}{{\pi r}}\frac{d}{{dr}}\int\limits_r^R {{{I}_{\nu }}(x)\frac{{xdx}}{{\sqrt {{{x}^{2}} - {{r}^{2}}} }}} . \\ \end{gathered} $$

(10)

Fig. 4.

Intensity profile in a cylindrical source recovered from chord measurements.

For recovered $I_{\nu }^{1}$formula (2) is valid for the localization region. If such measurements and procedures were performed for particles A and X, then the actinometry method can be applied with the spatial resolution.

Formula (10) illustrates the sensitivity of a solution to the accuracy of integral measurements general for inverse problems. In this case, differentiation of ${{I}_{\nu }}(x)$ is required in the presence of a singularity at the lower limit. Practice shows that at typical normally distributed experimental errors of 1–2%, the errors of such a recovery are 10–15%, and it is advisable to test the results on model problems. An alternative is the development of methods of three-dimensional localization by experimental means based on other physical measurement principles.

3.4 Continuous Spectral Absorption

Figure 5а shows a case when plasma Р is illuminated by a continuous spectral source E. The spectral device S_in separates the frequency interval $\Delta \nu$ including the plasma absorption line. In the simplest case, one line is separated and Δν > Δν_ul, where Δν_ul is the half-linewidth. The detector Det has a large linear range, operates at a frequency determined by the modulator M, and plasma intrinsic radiation is not detected.

Fig. 5.

Absorption measurements: (a) using a point source of continuous spectrum and (b) in the version with two tubes.

The change in the light intensity from I₀ to I after passing through the plasma is characterized by complete absorption at the transition u–l:

$${{A}_{G}} = \Delta \nu \frac{{{{I}_{0}} - I}}{{{{I}_{0}}}} = \Delta \nu {{A}_{L}}.$$

(11)

The dimensionless quantity A_L is the function of absorption. For the uniform plasma

$${{A}_{G}} = \int\limits_{\Delta \nu } {\left( {1 - \exp \left\{ { - {{\chi }_{{lu}}}(\nu )l} \right\}} \right)d\nu } .$$

(12)

For the Doppler and Lorentz broadening, integral (12) is expressed through the tabulated Ladenburg–Levi function S(χ_0,luL) and Ladenburg–Reiche function S ′(χ_0,luL), respectively [4]. At mixed broadening, the A_G values are calculated numerically (growth curves) as a function of the optical density in the center of the line χ_0,lu l.

From the measured total absorption A_G, either the integral absorption coefficient

$${{\chi }_{{lu}}} = \int {{{\chi }_{{lu}}}(v)d\nu } ,$$

(13)

or the absorption coefficient associated with it in the center of the line χ_0,lu is determined. the particle c-oncentrations on the lower absorbing level l are found from these values. At the Doppler or Lorentz broadening

$${{\chi }_{{lu}}} = \frac{1}{2}{{\left( {\frac{\pi }{{\ln 2}}} \right)}^{{1/2}}}{{\chi }_{{0,lu}}}\Delta {{\nu }_{D}},$$

(14)

$${{\chi }_{{lu}}} = \frac{\pi }{2}{{\chi }_{{0,lu}}}\Delta {{\nu }_{L}}.$$

(15)

If the wavelength λ is measured in nanometers, A_lu in s^–1, N_l in cm^–3, χ in cm^–1, then, neglecting induced radiation, at the Doppler broadening, the quantity

$${{\chi }_{{0,lu}}} = 1.23 \times {{10}^{{ - 33}}}\frac{{{{g}_{u}}}}{{{{g}_{l}}}}\frac{{{{A}_{{ul}}}}}{{\Delta {{\lambda }_{D}}}}\lambda _{{lu}}^{4}{{N}_{l}},$$

(16)

and at the Lorentz broadening

$${{\chi }_{{0,lu}}} = 0.84 \times {{10}^{{ - 33}}}\frac{{{{g}_{u}}}}{{{{g}_{l}}}}\frac{{{{A}_{{ul}}}}}{{\Delta {{\lambda }_{D}}}}\lambda _{{lu}}^{4}{{N}_{l}}.$$

(17)

Here, g_u and g_l are statistical weights of levels.

Speaking about the concentration sensitivity of this method, it should be noted that:

—at given quantities χ_lu and χ_0,lu, it increases with the length of the optical path l; integration (12) shows that A_G ~ Δν_D and A_G ~ Δν_L, and the A_L quantity measured from the intensity decreases is the smaller, the larger the Δν/Δν_D,lu and Δν/Δν_L,lu ratio. This corresponds to the decrease in the measured relative absorption and, ultimately, limits the concentration sensitivity of measurements against the background of the continuous spectrum;

—measurements at small Δν ≪ Δν_ul go beyond the assumptions made above but are possible. To this end, the high spectral resolution accompanied by the drop in the level of the detected signal from the source transmitting through the plasma is required. For physical reasons, the key circumstance here is the fact that the heat sources of the continuous spectrum have a relatively low brightness temperature Т_В ≤ (2–2.5) × 10³ K.

To overcome these difficulties, other versions of the absorption method have been developed.

3.5 Absorption of Emission with the Line Spectrum

In Fig. 5b, the source E with a continuous spectrum is replaced by a source with a line spectrum, the lines of which overlap, at least partially, with absorption lines in the plasma. In this case, the functions of the spectral device are reduced to the separation of these lines. This option is called the linear absorption method (or atomic absorption). There are various options for choosing and using such a source [4, 91]. This can be, e.g., the same discharge tube as the studied P. At low pressure, the emitting levels u of atoms are excited by an electron impact, and even in the presence of, apart from second-kind impacts, quenching by heavy particles is the “excitation temperature” (see Introduction) for a pair of levels u–l is comparable with the electron one—on the order of several eV. Therefore, in addition to the gain in the spectral resolution (and aperture ratio), in this case, the spectral brightness of the transmission radiation will also be much higher than that when using a heat source of a continuous spectrum.

At the accepted definition (11), the absorption function A_L is found from two measurements of I₀ and I. In the case of identical tubes, taking into account self-absorption in an extended source [4], its relationship with the absorption coefficients has the form

$${{A}_{L}} = 2\left( {1 - \frac{{S{\text{*}}\left( {2{{\chi }_{{0,lu}}}l} \right)}}{{S{\text{*}}\left( {{{\chi }_{{0,lu}}}l} \right)}}} \right),$$

(18)

where the same as for the result of integration (12), S* = S ' for the Doppler contour and S* = S ′ for the Lorentz contour. The measurements of A_L establish the absorption value χ_0,luL and, in accordance with Eqs. (16) and (17), the concentration N_l of absorbing particles. Expression (18) refers to the case of the singlet line of the spectra of the source and the studied plasma. The cases of fine-structure lines are considered in [4, 91].

Table 3 shows the A_L(χ_0,luL) values for three cases: A_L is the Doppler broadening; $A_{L}^{'}$ is the Lorentz broadening; $A_{L}^{0}$ is the monochromatic light of the source at the frequency of the center of the plasma absorption line.

Table 3. Absorption functions at different types of line broadening

At fixed χ_0,luL, the A_L values for all cases vary within a factor of 2, and the use of a narrow-line source does not lead to a noticeable increase in sensitivity if the characteristics important for detection (intensity, noise, etc.) are not considered. This characterizes the convenience of the method, since it is often difficult to ensure identical conditions in the transmission source and the plasma under study.

The latter is one of the reasons that the method is widely used in the studies of a wide range of plasma objects, including plasma analyzers. A large number of models of commercial atomic absorption spectrometers for industry have been developed. As a rule, discharges in the hollow cathode with radiation in the visible spectral region are used in them as the source of transmission radiation, and the equilibrium plasma (flame, inductively coupled plasma) serves as an atomizer of samples. Recently, special types of discharges with hollow micro-cathodes have been developed and are used for the studies of the nonequilibrium plasma. At small sizes allowing good collimation of radiation, they can also be used in the VUV spectral region. For example, they can be used to determine the concentrations of H atoms from the line L_α (121.6 nm) [92], oxygen O (130.2 nm) [93], N (120.7 nm) [29], etc.

4 LASER SPECTROSCOPY

Plasma studies, including optical and spectral methods, began to be carried out much earlier than the lasers appeared. Lasers were immediately in demand in this area. As the laser technology developed, the field of plasma laser spectroscopy expanded. Conventionally, laser plasma spectroscopy methods can be divided into three groups. The first group uses the basic principles of classical spectroscopy methods increasing the limits of measurements. The second group implements measurements not available to classical methods. The third group partly uses both of the previous features and adds new possibilities for indirect measurements and detection of optical signals.

As part of the topic of this review, we focus on the methods for determining particle concentrations using lasers, mainly in the ground and metastable states. These problems are solved, as in the classics, by the methods of absorption and, partially, scattering. Given the large number of review papers in this field (see Introduction), we only note the fundamental possibilities, their physical justification, fields of applicability and limitations, referring to the literature for details.

4.1 Track Measurements with Semiconductor Lasers

Since the 1970s, the development of user-accessible tunable frequency semiconductor lasers in continuous and pulse-periodic modes has been conducted. Lasers based on А²В⁶ and А³В⁵ compounds emit from near UV to near IR region 0.4–2.5 µm at room temperature, and on А⁴В⁶ compounds 4–40 µm when cooled with refrigerants or Peltier elements [30]. Since the 1980s, the use of plasma cascade 3–30 µm lasers operating at room temperature has been expanding in plasma spectroscopy [31]. These ranges correspond to the frequencies of vibrational-rotational transitions of the vast majority of molecules. A typical emission line width is on the order of 10^‒4 cm^–1, and frequency tuning is carried out by the injection current or cooling temperature. The tuning characteristic is piecewise-continuous due to the mode switching but all frequencies from the tuning region become available by combined changes in temperature and current. Miniature lasers are almost point sources. The radiation divergence is diffractional, and at the simple collimation, the transverse dimensions of the beam in the object are on the order of 1 mm; it is possible to localize measurements along coordinates normal to the propagation axis.

Track measurements are measurements, in which the length of the optical path along the propagation axis coincides (up to refraction) with the geometric size of the object. It is shown above (Section 3.4) that narrowing of the transmission line does not give a significant gain in the concentration sensitivity. A marked increase in sensitivity when using lasers is associated with the detection of transmission radiation [4].

The minimum detectable power changes due to absorption, ΔР_min, are determined by quantum fluctuations of the signal (shot noise). At the photoelectric recording and Poisson statistics of photoelectrons

$$\Delta {{P}_{{\min }}} = \xi '\sqrt {\frac{{Ph{{\nu }_{{lu}}}}}{{\Delta t{{\eta }_{D}}}}} .$$

(19)

Here, P is the laser power, Δt is the recording time, η_D is the photodetector quantum yield, and ξ' ~ 1. Let A be the beam cross section, I the power density (intensity), L the length of the absorbing object, σ_lu the absorption cross section. The number of particles on the level l at their concentrations on the low level l in the region of the laser beam is N ' = N_l  AL. Taking into account Eq. (19) for small absorption, neglecting induced transitions, and saturating power density I_s the minimum detectable number of molecules N ' (maximum sensitivity) is

$$N_{{\min }}^{'} = \sqrt {\frac{{Ph{{\nu }_{{lu}}}}}{{\Delta t{{\eta }_{D}}}}} \frac{{1 + I{\text{/}}{{I}_{s}}}}{{I{{\sigma }_{{lu}}}}}.$$

(20)

The lowest $N_{{\min }}^{'}$ value is achieved at I = I_s. The saturation power density for a two-level system is expressed in terms of the lifetime τ_u of the upper level I_s = hν_lu/(σ_luτ_u), and for estimating the sensitivity, the following ratio can be used

$$N_{{\min }}^{'} = 2\sqrt {\frac{{A{{\tau }_{u}}}}{{\Delta t{{\eta }_{D}}{{\sigma }_{{lu}}}}}} .$$

(21)

To go from the number of particles at the absorbing ground level to the total number of particles, one should use in Eqs. (20) and (21) not $N_{{\min }}^{'}$ but N_min = $N_{{\min }}^{'}{{Q}_{{{\text{in}}}}}$, where Q_in is the internal statistical sum. If at the determination of the concentrations of atoms from the resonance transitions σ_lu ~10^–12 cm², τ_u ~10^–8 s, almost all atoms are in the ground state and Q_in ~ 1, Δt ~ 1 s, then N_min ~ 10². For the concentration of molecules total over the levels, the sensitivity decreases to the typical N_min ~ 10⁸ value due to the increase in τ_u ~10^–4 s and Q_in ~ 10² typical for molecules.

Achieving the maximum sensitivity at the transmission radiation power equal to the saturation one leads to the nonlinear dependence of ΔР on Р and violation of the level distributions of particles. It is more correct to choose the mode I ≪ I_s [94], and the sensitivity does not worsen appreciably: according to formula (20) for I = 10^–2 × I_s the $N_{{\min }}^{'}$ value increases five times. In this case, the absolute laser power values remain high, their power and spectral brightness significantly exceed the corresponding parameters of classical sources. The typical saturation intensity for resonant transitions in atoms I_s ~ 10 W cm^–2. It is sufficient that at the beam cross section of 1 mm², the corresponding laser power was not higher than 0.1 W. This is many times higher than the typical powers of classical sources after the necessary monochromatization on the order of 10^–6–10^–4 W per spectral interval equal to the absorption line width.

Due to the high (compared to classical sources) power density of laser radiation, the detector response is high, and the intrinsic thermal noise of the photodetector has no critical effect on measurements. This is especially important in the IR spectral region. For λ ~ 10 µm, at modern detectors with η_D ~ 0.4 and detection ability D* ~ 10¹⁰ cm Hz^1/2, thermal noise in such measurements can be neglected at P > 1 mW. For details, see [94–96]. The paper [97] considers the measurement errors of concentrations associated with the finite accuracy of determining the intensities for of various types of noise (in addition to shot ones, Johnson, generation–recombination, and dark ones).

Figure 6 shows an example of the radial distribution of ArH⁺ ions in the positive column of a glow discharge in the tube in argon at the pressure of 6 Torr in the 2-m-long 25-mm-diameter tube at the current of 1.25 А [4, 223]. A 2-mm-diameter beam passed parallel to the discharge axis transitions were recorded: v ''  =  0, J '' = 3 → v ' = 1, J ' = 2 (2525.475 cm^–1) and v '' = 0, J '' = 3 → v ' = 1, J ' = 2 (2525.414 cm^–1). Ions arose due to the appearance of hydrogen impurities in the discharge (probably from the walls).

Fig. 6.

Radial distribution of ArН⁺.

4.2 Schemes with Increasing Optical Path Length

The basic Bouguer–Lambert–Beer (BLB, see Eq. (12)) absorption law includes the product χL. To record small components with small χ, it is desirable to use traces with large L. A number of schemes have been developed to implement this approach.

А. To study the compact objects, mirror optics is used, which provides multiple passes of light between them at a limited aperture. The most famous schemes (cells) are those of White, Erio, and Chernin. These and other schemes are described in detail in the review [98]. Up to 200 passages are possible at a distance between reflectors of 50 cm [99]. The circuits are used with classical and laser sources. At plasma studies with broadband classical sources, White and Erio schemes are combined with high-resolution spectral instruments, e.g., Fourier transform spectrometers. In such a combination, the composition of gases formed at the interaction of a plasma jet flowing from a capillary discharge in argon with air of variable humidity was studied in [100] using absorption in the IR spectral region. Measurements in an 8-pass White cell with a path length L = 19.2 m showed NO₂ variations within (1–8) × 10¹⁴ cm^–3 and О₃ variations within (0.5–3) × 10¹⁴ cm^–3. The localization is almost absent, and the measurement results are averaged over a volume close to the cell volume.

B. Historically, the development of the method of intracavity laser spectroscopy (ICLS) followed the development of the cell method. The object under study and the active laser medium are placed in a common optical cavity. By the beginning of the 1970s, frequency-tunable diode lasers were not yet spread but dye lasers and crystal and glass lasers with a wide spectral gain contour became widely available. Until now, the development of this method is mainly carried out using solid-state, fiber, semiconductor lasers, optical parametric oscillators (OPO) and dye lasers.

Qualitatively, ICLS differs from passive multipass cells in that the losses on the mirrors are compensated by the gain of the active medium, and the selectivity of the absorption of the object is compensated by the presence of many high-quality resonator modes with a wide gain contour. In this case, the effective optical path length is much higher than that in cells and can reach tens of kilometers with a distance between the mirrors on the order of a meter. The spectral resolution is provided by an external spectral device, and the spatial resolution is provided by the overlapping region of the object volumes and the cavity caustic. The fundamental limitation of the sensitivity is associated with the dynamics of the cavity modes, depends on the type of laser used, and, according to the estimates of [101], the effective optical path can reach the values for the Ti laser: sapphire of 1.3 × 10⁹ km and 250 km for the GaAlAs laser. Real limitations are associated with a number of factors: spontaneous emission of a laser medium, Rayleigh scattering, third-order nonlinear interactions, and a number of other reasons. So, for Ti: sapphire, the lengths of 70 000 km are more realistic, 40 km for GaAlAs, and these values are experimentally confirmed, and in the first case, the main factor is nonlinear interaction and, in the second case it is spontaneous emission. The largest path of those studied is achieved for Ti lasers: sapphire, the smallest 1.5 m is for OPO, the latter value is associated with a limitation on the duration of the lasing pulse.

The method as analytical is described in detail in original works, reviews, and monographs [101–105] and continues to develop.

As examples of the application to the study of track particles (newly formed and impurity) in the plasma, one can give the measurements of concentrations of singlet metastable oxygen O₂(a¹Δ_g) on the quadrupole transition a¹Δ_g–${{b}^{1}}\Sigma _{{\text{g}}}^{ + }$ in the region of 1.9 µm. In the afterglow of an RF discharge in oxygen at the pressure of 1.9 Torr, the concentrations varied in the range of (2–5) × 10¹⁴ cm^–3 [105]. Monitoring of metastable nitrogen molecules in a pulsed discharge in СО₂ : N₂ : He at the pressure of 240 Torr on transitions 1⁺ of the system 575–610 nm showed the concentrations [N₂(А³Σ, v = 2–8)] ~ (0.2–2) × 10¹⁴ cm^–3 [104]. The localization region is determined by the resonator caustics.

C. Absorption and decay of light in the resonator. This technique, as a development of the technique of classical multi-pass cells, is focused exclusively on the use of lasers, is actively developing. It can be conditionally divided into several groups.

In the first, multipass cells do not separate the beams in space, but are configured so that the beam experiences multiple reflections propagating along the axis in the form of short time-divided pulses, the intensity of which decreases in time due to dissipative losses with each new reflection by the mirrors. Schematically, this is usually illustrated in a form similar to Fig. 7 [4]. The spectral width of the radiation in such pulses determines the resolution and, as a rule, exceeds the interval c/2d between the axial modes of a cell of length d that also helps to suppress the interference structure of the detected signal. This technique introduced in the 1980s [106] for measurements of reflection coefficients of mirrors, later became widely used in laser spectroscopy and is described in detail, e.g., in the monograph [107] (Cavity Ring Down Spectroscopy—CRDS).

Fig. 7.

Detected signal when a light pulse passes through a cell with dense mirrors.

With each round passage of the cuvette, a part of the pulse energy is lost not only for transmission of the mirrors but also for absorption in the medium between the mirrors. For transmission, this fraction is (1 – R), and for absorption, A = 1–exp(–χct). If the mirrors have the same reflection, then at A, (1 – R) ≪ 1 the pulse intensity decreases in time according to the law

$$I(t) = {{I}_{0}}\exp [ - 2(1 - R + A)t{\text{/}}{{t}_{r}}],$$

(22)

that is fixed as the envelope of the pulse train from the detector. For an empty cuvette, one has A = 0, and the characteristic decay time τ₀ = L/(c(1 – R)). Modern technologies make it possible to manufacture mirrors with reflection coefficients R > 99.99%, so the decay can be quite “slow” convenient for the analysis. At a cuvette length of 50 cm and R = 99.99% the decay τ₀ = 17 µs, and the effective number of light passages of the cuvette is ~5000. The absorption А is determined from Eq. (22) by comparing the decay times of pulses for empty and filled cuvettes:

$$A = \left( {\frac{1}{\tau } - \frac{1}{{{{\tau }_{0}}}}} \right)\frac{{{{\tau }_{r}}}}{2}.$$

(23)

Here, the decay time

$$\tau = L{\text{/}}\left[ {c\left( {1 - R + A} \right)} \right].$$

(24)

The absorption coefficient χ and the particle concentrations at the absorption level are successively determined from τ measurements Eqs. (16), (17). The measurement sensitivity is close to that of the ICLS method. At reflection of mirrors of R = 99.99% and cell length of 50 cm, the effective optical path length is 10 km.

As an example, one can consider measurements of concentrations of silicon atoms by this method [108]. The appearance of impurities of these atoms is associated with the erosion of quartz in the plasma. An RF barrier discharge in argon with a quartz plate in the CRDS scheme was used with a mirror reflection of ~99.7% at the wavelength of 252 nm. Figure 8 shows the results of measurements of the concentrations of Si atoms as a function of the discharge power at different argon pressures. The limits of the observed concentrations were 10⁷–10⁹ cm^–3. The spatial resolution of ~5–10 mm was achieved in the space above the quartz plate up to 100 mm at the displacement of the discharge across the cell axis.

Fig. 8.

Concentration of silicon atoms as a function of the power inlet.

The same group should include the option when not a pulsed but a continuous laser is used, and at the same time an integral signal is detected from the beams that have passed through the cell different numbers of times. This option has several abbreviations used in the literature: CRDS, ICOS, and CEAS. It is also widely used in plasma spectroscopy and is analyzed in detail in the monograph [107].

Other versions are based on the use of the resonance properties of cells in which an increase in the optical path is achieved for the eigen axial longitudinal modes TEM_m0 [107], and the laser line width is less than the intermode distance. These systems are undoubtedly promising, but so far they are used little, are in the research stage, and there are unresolved issues of matching laser modes with modes of the external cavity and taking into account their inevitable mismatches in real systems. One of the promising proposals is the use of a three-beam scheme (RICOS), in which, before being introduced into the cell, the laser beam, after reflection from the inlet mirror, is diverted to a separate detector and is a reference one [109, 110]. When the frequency of the laser radiation is mismatched with the frequency of the axial mode, transmission and reflection of the cell change simultaneously, and the intensities in the beams reflected and transmitted through the cell are anticorrelated. This makes it possible to effectively eliminate the effect of the cavity instability on the measurement results, which was successfully demonstrated by monitoring methane in the atmosphere [109, 110]. This approach has not yet been applied for the plasma research.

The third group of versions includes resonance cells with non-axial radiation inlet by analogy with classical interferometers [111]. The abbreviation used in the literature is “off-axis ICOS.” In this case, a set of transverse modes TEM_mn with m, n ≠ 0 is excited. The spectrum of the excited modes becomes dense enough for the resonance properties of the cell not to be lost, and matching of the laser and cell modes is facilitated. The deviation of the inlet beam from the axis cannot be large, and the cell aperture a_c is sufficient to satisfy the condition of small diffraction losses ${{Z}_{{\text{F}}}} = a_{c}^{2}{\text{/}}\lambda L \gg 1$, where Z_F is the Fresnel number, λ is the light wavelength light, L is the distance between mirrors. As to the ideology, this group is intermediate between the two previous ones. A compromise is most often used when measuring particle concentrations starting with [112] for the gas analysis and as applied to plasma studies (e.g., reviews [30, 31, 33]).

This group of methods is developing most actively supplemented by new techniques. For example, in [113], the increase in the sensitivity is achieved due to the nonstationary current heating of the active element of a diode laser. The technique of phase measurements at deep modulation without loss of resolution was developed in [109, 110, 114]. The studies are underway to measure the concentrations of paramagnetic particles (О₂, ОН, NO, HO₂…) from the difference between the rotation angles of the s- and p-polarizations of radiation in the resonant cells under the application of the magnetic field [115–117]. According to the estimates made in the review [33], in the future such a method can provide the sensitivity of polarization measurements in the magnetic field of ~10–1000 G, e.g., [НО₂] radicals ~10⁷ cm^–3, while the measurements carried out by traditional CRDS methods and its “off-axis ICOS” version showed the sensitivity of ~[НО₂] ~ 10¹⁰ cm^–3 [117]. In this case, it is difficult for now to say how this affects the properties of plasma.

The analysis of the ongoing research shows that at present, most versions of particle concentration measurements using large optical paths in the plasma are conducted using frequency-tunable semiconductor lasers.

When measuring particle concentrations, an alternative to the method of measurements of direct absorption of light may be recording changes in a particular parameter of the object caused by absorption. This can be, e.g., heating an object and the associated refractive and acoustic effects, additional luminescence, conductivity, etc. The measured quantitative characteristics of these manifestations can be related to the absorption and the concentrations that are used in the gas analysis [96]. Unlike gases, for which they do not have their own background, the plasma produces the same phenomena, and it is possible to talk about some effect of absorption on them. In some cases, this can be successfully implemented.

D.1. Laser-induced fluorescence. The LIF method has much in common with the plasma spontaneous emission method. The luminescence intensity is determined by expression (2) with the difference that the glow excitation rate k_Xu of the particle X from the level u is determined by the light absorption. If absorption occurs from the ground state g–u, additional luminescence on the transition u–l (to exclude the scattering noise l ≠ g) can be separated from other numerous possible channels of excitation of the same level in the plasma. In particular, there is no need to know the properties of the electron component, but it remains necessary to take into account quenching Q_Xu.

In this version of the single-photon excitation g–u–l the LIF method is used for the determination of concentrations in the plasma of a series of atoms (F (1–20) × 10¹³ cm^–3 [16]), radicals NO (2–40) × 10¹⁴ cm^–3 [118], СН (1–6) × 10¹² cm^–3 [119], С₂ (1–6) × 10¹⁰ cm^–3 [120], CF (1–6) × 10¹² cm^–3 [16] and a series of other molecules, if lasers are available with a quantum value corresponding to the transition g–u. This is a simple and convenient method that does not require absolute measurements, because it can be calibrated, e.g., by Rayleigh scattering with the same linear dependence of the intensity on the laser intensity as the LIF signal. For most particles, the energy between the ground and excited states lies in the UV or VUV regions, and this simplest version is not suitable due to the absence of radiation (and harmonics) from frequency-tunable lasers. A way out can be associated with the use of synchrotron radiation. In general, with respect to the method under discussion, synchrotron radiation is similar to laser radiation. It has a small spectral width, can be tuned in frequency and collimated. In [121], a study of a high-brightness halogen lamp used synchrotron radiation in the photon energy range (40–100) keV ((0.3–0.12) Å), monochromaticity of Δλ/λ ~10^–3, divergence of ~10^–5 rad, beam cross section of 1 × 1 mm². The locality of measurements was ~1 mm³. The fluorescence spectra excited by such “hard” radiation correspond to atomic transitions involving inner electron shells and contained k_α lines of elements such as I (filler) and Cs, Dy (impurities due to electrode erosion) in the studied object. No calibration was carried out for the concentrations, although for atomic particles this would not be a big problem for using gases or equilibrium atomizers for controlling by other methods. Apparently, the limited study in this field is associated with the complexity of combining an expensive synchrotron with the studied objects. However, with the development of the technology of X-ray sources, this approach has prospects.

In other cases, versions of double optical resonance (DOR LIF) or two-photon excitation (TALIF) are available.

In the first of these, two lasers and an intermediate excitation level i of g–i–u–l are used for excitation. To obtain quantitative results, this case requires an analysis of the processes populating the level i in the plasma, and is technically complicated, and although it allows the localization of measurements at the suppression of focused laser beams, plasma is practically not used in spectroscopy.

The use of the TALIF version is much more common. In this case, the Rayleigh scattering calibration is also not suitable due to the different dependences of the scattering intensities and luminescence on the laser power. In this situation, once again it was proposed to use the experience of classical actinometry and conduct measurements simultaneously for the particles and particles with a known concentration, e.g., atoms of inert gases. Actinometric pairs are selected, similarly to Table 1, but, unlike classical actinometry, where the proximity of the thresholds of electron excitation plays a role, in TALIF the choice is more strictly limited, mainly by the possibilities of the laser selection. This method is used most often in spectroscopy of small plasma components for the measurements of concentrations of H, O, and N atoms. The three-dimensional localization with a linear size of <100 µm is achieved due to the nonlinearity of the process at the beam focusing. This technique has been developed starting with [122–125], where it is possible to find application examples, and the corresponding combinations of pairs are shown in the diagram in Fig. 9.

Fig. 9.

Schemes of the two-photon excitation of Kr, H, N, Xe, and O atoms.

For practical convenience when working with the nonequilibrium plasma, the ratio of the cross sections of the corresponding two-photon excitations were measured in [124] under equilibrium conditions (with accuracy of ±5%):

$$\frac{{\sigma _{u}^{{{\text{Kr}}}}\left( {5p'\,{{{[3{\text{/}}2]}}_{2}}} \right)}}{{\sigma _{u}^{{\text{H}}}(3{}^{2}{{D}_{J}})}} = 0.62,$$

(25)

$$\frac{{\sigma _{u}^{{{\text{Kr}}}}\left( {5p'\,{{{[3{\text{/}}2]}}_{2}}} \right)}}{{\sigma _{u}^{{\text{N}}}(3{}^{2}{{D}_{J}})}} = 0.67,$$

(26)

$$\frac{{\sigma _{u}^{{{\text{Xe}}}}\left( {5p'\,{{{[3{\text{/}}2]}}_{2}}} \right)}}{{\sigma _{u}^{{\text{O}}}(3p{}^{3}{{P}_{J}})}} = 0.36.$$

(27)

D.2. Photodetachment spectroscopy. Negative ions (N I) are formed in the plasma containing particles capable of trapping electrons. Electrons can be released at irradiation. Photodetachment cross sections σ_d for many particles are given in the book [4]. Excess electrons appear in the plasma, and their number can be measured using probes. This number is given by the ratio:

$$\Delta {{n}_{e}}(t) = N_{0}^{ - }\left[ {1 - \exp \left\{ { - \frac{{{{\sigma }_{a}}(\nu )}}{{h\nu }}\int {I(\nu )dt} } \right\}} \right],$$

(28)

where $N_{0}^{ - }$ is the radiation-unperturbed NI density; σ_a is the photoattachment cross section related to σ_d by the detailed equilibrium relation, the integral in Eq. (28) is the pulse energy of the irradiating light. The N I concentrations are found from Δn_e measurements [126–128].

The development of the highly sensitive methods of low-concentration particle spectroscopy discussed in this review has created an alternative to this well-known method. Photodetachment is associated with absorption of light with characteristic cross sections σ_d ~ 10^–18–10^–16 cm² in the spectral region of UV to NIR. The absorption coefficients and the corresponding concentrations can be measured by the methods described in the previous sections. The concentrations of О^– ions in a planar RF discharge in oxygen were measured by the CRDS method in the range of [O^–] ~ (10¹⁰–10¹¹) cm^–3 in [129]. At the discharge in hydrogen in the same system and at the same pressures 0.075–0.4 Torr, the [H^–] concentrations are ~10⁹–10¹⁰ cm^–3. At the discharge in the tube in the magnetic field in hydrogen at the pressure of (0.3–1.8) × 10^–2 Torr using the absorption method, the range of [H^–] concentrations is ~(2–15) × 10⁹ cm^–3 [130].

D.3. Optical-galvanic measurements. This method, the same as the photo-separation method, is associated with the effect of radiation on the ionization equilibrium in the plasma, but its mechanism is more complicated. The optical-galvanic effect (OGE) occurs due to the redistribution of level populations of atoms or molecules at the absorption of light. As a result of various radiation and (or) collisional and (or) collective processes, the densities of charged particles, their mobility and energy that affect the ionization equilibrium and conductivity change. The method is technically simple. Absorption spectra can be recorded as a change in the current or voltage on electrodes or by the probe method. It is possible to localize measurements, as in the case of LIF, when using double optical resonance or two-photon excitation.

For analytical plasma analyzers, where the LTE model is valid, OGE is used as a quantitative method. With its help, the concentrations of most metals having absorption lines in the visible and near UV regions are measured. In this case, its sensitivity in most cases exceeds that of absorption, radiation, and LIF methods.

When working under conditions of the nonequilibrium plasma, OGE is used for the establishment of the structure of the spectra of weak transitions. The problem of quantitative calibrations has not yet been solved; therefore, the OGE can be used as a sensitive indicator of the presence of certain particles in the plasma. A detailed analysis of the method was carried out in the review [131], books [4, 132, 133], and the work is continued (see, e.g., [134]).

5 METHODS OF MEASUREMENTS OF SMALL PARTICLE CONCENTRATIONS IN FACILITIES SIMULATING CONDITIONS SIMILAR TO PLASMA OF NEAR-WALL LAYERS OF REACTORS

5.1 Impurity Problem

Starting from the 1950s, the ideas and projects of designing nuclear fusion reactors with magnetic plasma confinement at temperatures sufficient for the course of controlled nuclear fusion reactions D + T → He (3.5 МeV) + n (14.2 МeV) began to come to life. To date, several generations of such facilities of various sizes and equipment have already been created, a lot of experience has been accumulated, which is expressed, inter alia, in the formulation of a number of problems that need to be solved in the preparation for the design of reactors of subsequent generations. Unlike the previous ones, the experimental ITER reactor [15, 135–147] is planned already as a prototype of an industrial power engineering facility, although, of course, in the process of its creation a number of issues still need to be resolved, the answers to which were not given in the previous experiments. We will touch on the issue of purity of the plasma.

For the course of the specified reaction, the heat released in it should suffice to compensate for the dissipative energy losses of the reactor. This requirement is expressed by the Lawson criterion. It is satisfied if at the ion temperature T_i ~15 keV, electron density n_e and confinement time τ_E the condition T_i n_eτ_E > 6 × 10²⁰ keV s m^–3 is satisfied. At τ_E = 1 s the density should be n_e > 10²⁰ m^–3 = 10¹⁴ cm^–3.

At such high temperatures in the hot plasma zone, all not heaviest atoms are completely ionized, and, according to the condition of the detailed equilibrium, the intense recombination accompanied by radiation occurs. Recombination radiation turns out to be one of the important (if not the most important, along with the removal of energy by neutrons) mechanisms for cooling the plasma contaminated with impurities. The power Р_rad of recombination radiation for ions with a charge Z is expressed by the formula [136–147]

$${{P}_{{{\text{rad}}}}} = 1.78 \times {{10}^{{ - 32}}}{{n}_{e}}{{n}_{Z}}\frac{{{{Z}^{4}}}}{{\sqrt {{{T}_{e}}} \;({\text{keV}})}}{\text{, W}}\;{\text{c}}{{{\text{m}}}^{{ - {\text{3}}}}}.$$

(29)

The radiation power depends sharply on Z, and it is much less for “working” H, D, T elements than that for heavier elements of impurities. If the radiation power makes up a significant fraction of the power in the plasma, the plasma cools down, and the Р_rad increases. The cooling process develops like an avalanche, the plasma cannot exist in a self-sustaining mode, and the so-called radiation collapse occurs. Taking into account such considerations and the features of particle transport (anomalous and neoclassical ones), the “lethal” dose of impurities can be calculated as a fraction of the electron density ξ_d = n_z/n_e. Table 4 presents these values for the operating conditions of the ITER reactor [15]. The real doses ξ_c allowed by project developers are also written there.

Table 4. “Lethal dose” of impurities

For ITER the quantity n_e ~10¹⁴ cm^–3 and the determination of the content of impurities at such a level requires a reasonable choice of the measurement method taking into account the possibilities presented above in Sections 2–4.

5.2 Preceding, Ongoing, and Required Studies

The negative effect of impurities has been noted during the operation of almost all generations of specific facilities with magnetic plasma confinement. The plasma contamination has traditionally been the cause of long downtime in research facilities. The analysis that preceded the formulation of the requirements of the ITER project showed that the “weak point” of a complex construction made of numerous modules (~10³ individual parts) is the appearance of oxygen in the plasma, which can be carried by water molecules.

Water is both a coolant for the walls of the reactor and its working fluid. In the operating mode, the temperature of the cooler is ~450 K, the pressure of the vapor-gas medium is ~4 MPa (~40 atm), and the penetration of water molecules into the multi-element cooled structure is quite real [15, 148]. Monitoring these molecules in the parietal zone has become a challenge for many groups. Taking into account the considerations of Section 5.1, the dimensions of the ITER chamber (1400 m³), the pumping capacity and additional injection of particles instead of those left out at incomplete recycling (the recovery of neutrals at electron–ion recombination on the wall), the project [15] specifies the maximum allowed flow Q of water molecules into the camera. It was 10^–7 Pa m³ s^–1 or 2.65 × 10¹³ s^–1 according to the number of inlet particles (the flow of 2.65 × 10²⁰ s^–1 corresponds to the quantity 1 Pa m³ s^–1 = 10^–2 mbar m³ s^–1 = 10 mbar L s^–1 = 1 W).

This implies the required sensitivity of the concentration measurements. The planned plasma confinement time of 10 s at the discharge duration of 400–3000 s sets the required high-speed performance. An important condition is to find places (localization) of the particle penetration into the chamber from the first wall (680 m², 480 blanket modules in ITER [135–143]). Taken together, this makes the diagnostics problem very complex, which has no known analogues.

The output of the reactor to the operating mode will be carried out in stages over several years. After the facility is built, the vacuum density of the structure should be diagnosed. At the next stage, the inner surface of the first wall will be treated with a discharge, tested with discharges in hydrogen, then in deuterium and in their mixtures, and only then in the D–T mixture. This is due to the checkout of the systems at saving of tritium and the radiation resistance of the facility. In accordance with this, it is necessary to focus on three groups of diagnostic methods and tools. The first is used to control the reactor in the “cold” state, not only after completion of the construction, but also during technological “windows” during repair, maintenance, and the introduction of structural corrections. However, possible defects resulting from the loads determined by the discharge will not be noticed. At the next stage with a discharge in hydrogen and deuterium, the second diagnostics group should already be complete, with the identification of such defects, and although some variations of the conditions are acceptable, after this stage the means of the third group for monitoring the operating mode should be provided. It is likely that the methods of the second and third groups will be close, although the identified possible difficulties should be taken into account. A common feature for all groups is the condition of the remoteness of the measurements. For the second and third groups, this is obvious, for the first group it is dictated by safety requirements even during breaks between starts of a reactor with discharges in hydrogen and deuterium also according to safety requirements.

On the other hand, despite the possibility of such a step-by-step introduction of diagnostics, the specificity complicating the task as a whole is related to the fact that the methods already worked out at the current rectors, although they require adaptation, are focused on measurements in the active hot plasma region. Among them, one can distinguish the classic Thomson scattering method, which has been repeatedly tested on laboratory plasma systems and several generations of reactors, but requiring the use of modern high-power lasers with short pulses, as well as active spectroscopy methods. The first method examines mainly the parameters of the electron component, but since the LTE model is well executed in this zone, other parameters can be extracted from the measurements. The second is based on the injection of a narrow diagnostic beam of hydrogen atoms. At velocities of atoms comparable to the velocities of electrons in atomic orbits, the beam penetrates the center of the plasma and the maximum (resonant) cross section of the charge exchange. The use of an atomic beam with the energy of ~100 keV and capacity of 2.2 MW for ITER is discussed. The spectra of cascade transitions from high levels of the formed ions can be used for the measurement of the concentrations of particles of various kinds, including impurities. Both methods are quantitative and capable to provide a sufficiently sharp locality. However, the plasma region near the wall to the boundary of the transport barrier (the H mode for which ITER is designed) with low energies and the electron densities remains out of sight. In addition to the technical issues related to the sensitivity, attempts to adapt these methods to the near-wall layer meet fundamental difficulties associated with the lack of equilibrium, separating this problem as an independent one.

In the above-mentioned first group, a number of works is carried out with respect to the simulation of the gas dynamics of leaks and the study the chambers for vacuum density. For example, the gas dynamics of gas leaks through a narrow channel in the wall was calculated in [148, 149]. At the wall temperature of 450 K, the external pressure of 40 atm and the channel length of 1 cm, the calculated flow rate of water molecules at a capillary diameter of 1 μm is Q = 1.5 × 10^–4 Pa m³ s^–1, at 0.1 µm it is of 10^–8 Pa m³ s^–1, and at 0.03 µm it is of 10^–10 Pa m³ s^–1, i.e., the allowed leakage occurs when there are 10 identical channels with a diameter of 0.1 µm. In [150], this model was modified for the case of latent leaks, when molecules penetrate through a narrow opening on the outer side of the wall and then migrate into the chamber through a system of channels and blanket cracks. Under some assumptions, the inlet rate of molecules into the chamber can be 2–3 orders of magnitude higher than in the case of a narrow channel of the same diameter as that of the hole in a thin layer of the shell element.

Experiments of the first group were carried out under various conditions, which somewhat simulate the ITER. Adapted tools of the traditional high-sensitivity gas analysis are used in these works.

The development of a multipurpose “robot-arm” carrier [151–153] tested on the Tore Supra tokamak is underway. This facility takes into account the features of the geometry of a particular chamber and can place various devices inside it, e.g., leak detectors, mass spectrometers, laser spectrometers, etc. Another group uses the method of direct measurements of water flows using laser absorption spectroscopy in a track scheme [154]. Experiments are carried out on the TITAN facility designed in 2011. The volume of its vacuum chamber is 18 m³ and the walls can be heated to 250°С. A calibrated leakage was introduced into the system making it possible to produce He or H₂O flows at the level of 10^–5 Pa m³ s^–1, however real measurements were carried out at large flows. The direct measurements of the light absorption by water molecules demonstrate the sensitivity of the method at the level of flows of 10^–2 Pa m³ s^–1, and the extreme extrapolation of the direct measurements gives the result of 10^‒5 Pa m³ s^–1. The planned level of detectable leaks after the proposed modification of the measuring scheme using an external resonator (Section 4) is about 10^–6 Pa m³ s^–1 that is still not enough for ITER.

In [155], a sensor system for signaling the occurrence of a leak based on pressure changes in the reactor cooling system was proposed. A similar system was also tested earlier on the Tore Supra facility [156]. In addition to determining the specific cooling circuit from which the coolant leaks occur, a scheme for the removal of water vapors that have entered the chamber is proposed in [156]. Since the construction provides five cooling circuits, each of which contains several tens of elements of the blanket, a more detailed localization of the place of water leakage into the chamber is problematic.

It was proposed to add small (at the level of 0.1%) markers to the cooling water in an earlier work [157]. They will be detected in the case of a leak using a mass spectrometer in the pumping channel of the reactor chamber. However, the establishment of the marker concentration in water required for the recording takes at best a few hours (for the most acceptable marker Xe), and the localization problem is the same as indicated the above.

The use of traditional methods with helium leak detectors is also difficult, since it requires careful drying of the cooling circuits.

The second group of works is almost entirely focused on spectral methods. As one of the few exceptions, we indicate works [158, 159], where the effect of the emergence of self-oscillations of the discharge in the presence of water molecules is used. This contact method is based on the effect of an oxide film on the emissivity of some cathode materials, and the demonstrated sensitivity (10^–4 Pa m³ s^–1) still does not suffice.

It can be seen from the preceding Sections 3 and 4 that a large number of spectroscopic methods for direct measurements of the concentrations of atoms and molecules with high sensitivity in the plasma at the absence of equilibrium in it for many objects has been developed. A substantive analysis of these and a number of other methods shows, however, that most of them encounter serious problems with regard to their applicability to ITER tokamaks. The main one is the technical complexity, radiation loads and limited accessibility to the active medium. Under these circumstances, the most technically simple methods, using the plasma spontaneous emission spectra, seem to be most preferable. Paradoxically, as noted in Section 3, they require the most detailed physical substantiation to obtain quantitative results when they are used for studying specific nonequilibrium plasma objects. The work in this direction is carried out by a number of groups.

Since ITER is not yet in operation, it will take a long time to determine its regimes, and full-scale experiments are not yet possible, at the preparation stage it is necessary:

—to use and/or specially develop facilities for the experimental simulation of conditions as close as possible to those in the near-wall plasma of the reactor;

—to work out on model facilities the acceptable quantitative spectral methods for determining the concentrations of water molecules and their fragments, to determine the flows of their inlet into the plasma, and to find out the conditions for the localization of measurements;

—since the total recovery of the conditions for a unique reactor under construction on model facilities is problematic, it is necessary to design a calculation model of transformations of particles in the plasma of model facilities, to test it for a combination of as many different particle and experiment conditions as possible in order to scale to the plasma conditions of the reactor.

Several experimental studies on the topic under discussion were carried out on ITER assignments even at the development stage of the project [15]. The concentration of oxygen atoms was measured spectroscopically by the emission of a glow discharge in the IR region (see [150]), and the limiting sensitivity of 10^–6 Pa m³ s^–1 and the spatial resolution of several m² were achieved.

Experiments with discharges were carried out on the PR-2 “mirror cell” facility at pressures of 10^–2–10^–4 Torr in inert gases, hydrogen, deuterium, air and their mixtures [149, 150]. The study of the emission spectra showed that, regardless of the composition of the plasma-forming gas, OH hydroxyl bands dominate in the region of 230–350 nm. The intensities of these bands are compared with the results of parallel mass spectrometric measurements of the concentration of water molecules, and on the basis of extrapolation it is concluded that in these experiments OH bands can be noticeable at pressures of water vapors up to 2 × 10^‒4 Torr. The rest of the estimates were of a qualitative nature. An important conclusion from the results of these studies was that OH bands observed, in particular, in the spectra of inert gases without water additions, can serve as a sensitive indicator of moisture.

The proposal [148–150] was studied in more detail in [160], in which measurements of the glow intensities of the OH radical bands in the discharge with a hollow cathode (1 × 5 × 10 cm³) were carried out with parallel calibrations at using inert gases of the known moisture. The achieved sensitivity to the water flow was 10^–5 Pa m³ s^–1.

A complex of spectroscopic studies was carried out on an L-2M stellarator (the major radius of 1 m, the minor radius of 0.115 m) [161–163]. There were also carried out measurements on the OH luminescence according to the method of [160], which confirmed the sensitivity of 10^–5 Pa m³ s^–1 [162, 163]. The idea [153, 157] on the use of Xe as a marker [161, 163] was tested in parallel but in this case the marker was detected from the emission spectrum. In contrast to [153, 157], xenon did not dissolve in water but was let in directly into the stellarator chamber using a special leakage with a controlled flow through a small hole. The chord measurements showed the sensitivity to the xenon flux Q_Хе ~10^–6 Pa m³ s^–1, the leak localization accuracy of ~5 mm. At the Xe concentration dissolved in cooling water in the amount of 1%, which is close to the possible one, the sensitivity of this technique to the flow of water molecules could be ${{Q}_{{{{{\text{H}}}_{2}}{\text{O}}}}}$ ~10^–4 Pa m³ s^–1. For facilities cooled by a flow of water with a high flow rate, the use of a dissolved noble gas as a marker, in addition to the insufficient sensitivity to water molecules, is costly, requires the special water preparation and the need for technologically complex processing of the walls of the vacuum chamber after each emergency or test run of the diagnostics system due to behind the interaction of the marker with the wall.

Thus, after many experiments with emission spectra, the highest sensitivity was demonstrated by recording the intensities of the hydroxyl bands ОН(Х²П-А²Σ), but the progress stopped at the level of flows Q ~ 10^–5–10^–6 Pa m³ s^–1. Even in this case, the question remained about the adequacy of the correlation of the intensity of these bands with the concentration of the “parent” Н₂О molecules in all previous works.

5.3 Model Facilities

Most of the research was carried out on two facilities. The Tech facility (Figs. 10, 11) simulates the properties of the plasma discharge at the stages of primary treatment of the blanket of the first reactor wall (a glow discharge is planned as well) and in the modes with discharges in hydrogen and deuterium [47, 49, 55–58, 72, 84–86, 164–167]. The blanket structure of the first wall at the junctions of structure elements at burning in the discharge chamber is potentially the most susceptible to leaks either directly through the joints or as a result of the migration of molecules along the internal channels of the structure. The discharge supported by the hollow cathode can be a model for these regions. The second facility with a glow discharge in the tube (Figs. 12, 13) is used to simulate conditions in the positive column and to compare different measurement methods [58, 82, 83, 168–172].

Fig. 10.

Block scheme of the Tech facility. Notations are in the text.

Fig. 11.

One of the views of the Tech vacuum chamber.

Fig. 12.

Scheme of the glow discharge facility. Symbols are in the text.

Fig. 13.

Central part of the facility with a glow discharge in the tube resonator.

The Tech facility. The volume of the stainless steel chamber 1 is 22 L. A heater 2 varied the wall temperature in the range 295–450 К, the residual pressure of 10^‒7 mbar was provided by a vacuum station 3 connected to the chamber by gate 4. Probes 5 and 6 controlled the gas pressure of 10^–9–1000 mbar inlet from baloons 7, 9, and 10 and a container with water 14 through leakages 8, 11, 12, and 15. He, Xe, Ar, Н₂, and D₂ gases were used in addition to water vapor. We used a discharge supported by the hollow cathode 16 with dimensions 100 × 50 × 10 mm³ with an open side of 100 × 10 mm² facing anode 17 in the form of a tungsten wire with a diameter of 1.5 mm or a 100 × 10 mm tungsten mesh at a distance of 10–15 mm from the edge of the cathode. The discharge radiation emerging through a window 22 was collimated and focused by optical system 23 onto the slot of spectrograph 24 with replaceable diffraction gratings and photoelectric recording. The signal from the PMT was fed into a computer 21.

To measure the absolute radiation intensities in spectral lines, the hollow cathode unit (16 and 17 ) was replaced by a calibrated strip lamp. The scheme of a single Langmuir probe 19 made of a tungsten wire with a diameter of 0.04–0.1 mm protruding from the ceramic insulator by 2–3 mm was used for the measurements of the electron parameters. The probe could be installed in various places of the discharge. For methods of processing probe characteristics, see [167]. Figure 11 shows a view of the vacuum chamber.

The facility with a glow discharge (Figs. 12 and 13) is intended to carry out the comparative emission and absorption laser measurements with control of the axial electric field strength. A quartz tube 1 was used as a discharge tube with electrodes 2, 2', 3 and a high-voltage current source 4. Three electrodes were used to exclude near-electrode voltage drops at the control of the axial electric field in the positive column; 5, 6 are channels for pumping out and inlet of gases; 7, 7 ' are water inlet and outlet into the tube cooling jacket; 8 is a diode laser, 9, 10 are mirrors with the reflection of 0.99–0.9998 at the wavelength of 1392 nm; 11—dividing plate; 12 is a Fabry–Perot standard; 13, 16 are ThorLabs PDA10CS-EC detectors; 14 is a lens; 15 is an interference filter for the selection of a spectral section in laser measurements; 17 is a National Instruments PCI-6120 board, which carried out output of laser control signals 8 and input of signals from detectors 13, 16 into a computer 18 with the LabVIEW medium, in which the control signals were generated and signals from detectors were processed. In actinometric measurements, mirror 10 was replaced by a quartz window 10  ', filter 15 was removed, and a monochromator 16  ' (MDR-204) with a photomultiplier tube replaced detector 16, the signal from which was fed into a computer 18. A fragment of the facility is shown in Fig. 13.

5.4 Measurements of Absolute Concentrations of Water Molecules by the Fine Structure of the Emission Electron Spectrum of Hydroxyl

The above-noted problem of ambiguity in correlating the luminescence intensities of water molecules with the H₂O concentration by means of various calibrations [160, 163] was considered in [164] in a fundamentally different way.

In exothermic reactions under nonequilibrium conditions, the excess energy is redistributed between different degrees of products. This situation was studied with respect to the excitation of emitting electron states of atoms and molecules in various elementary processes [4]. This, in particular, applies to the processes of excitation of OH radicals [173–180]. The latter is illustrated in Fig. 14 [164].

Fig. 14.

Two excitation mechanisms of hydroxyl glow by electron impact: I is direct excitation of hydroxyl from the ground state; and II is dissociative excitation of water molecules.

Two main excitation mechanisms of the ОН(A²Σ) state emitting violet bands are known.

I. If free hydroxyl is somehow formed in the ground ОН(Х²П) state in the plasma, it can be excited by electrons into the ОН(A²Σ) state:

$$\begin{gathered} e + {\text{OH(}}{{{\text{X}}}^{2}}{{{\Pi}}}) \to e + {\text{O}}{{{\text{H}}}^{{\text{c}}}}{\text{(}}{{{\text{A}}}^{2}}\Sigma ) \\ \to e + {\text{OH}}({{{\text{X}}}^{2}}{{{\Pi}}}) + h\nu . \\ \end{gathered} $$

(30)

The band structures of the “cold” ОН^с(A²Σ) group with a rotational temperature close to the gas temperature dominate in the electron spectrum at the process (30) [173–176], since in the ground state the rotations of the molecules are in equilibrium with the kinetic motion of the gas, and the electron at the excitation of the electron state of the molecule cannot give it a significant angular momentum. Therefore, the gas temperature can be determined from the line intensities in the rotational structure of the band excited in the process I.

II. During the dissociative excitation of water molecules by electrons the Н₂О molecule transfers from ground the bound Х¹А₁ state into the repulsive В¹А₁ state and decays into a hydrogen atom in the ground state and an excited ОН(A²Σ) molecule followed by radiation.

In the ground state, the water molecule is bent at an angle of 105° (Fig. 14), and the excess deformation energy is transferred to thermal, vibrational and rotational movements at the transition into the linear В¹А₁ state. Light hydrogen takes up most of the kinetic energy. The heavier radical ОН(A²Σ), on the contrary, it changes little speed, but begins to rotate rapidly, forming the so-called “hot” rotation ОН^h(A²Σ) ensembles:

$$\begin{gathered} e + {{{\text{H}}}_{{\text{2}}}}{\text{O(}}{{{\text{X}}}^{{\text{1}}}}{{{\text{A}}}_{{\text{1}}}}{\text{)}} \to e + {{{\text{H}}}_{{\text{2}}}}{\text{O(}}{{{\text{B}}}^{{\text{1}}}}{{{\text{A}}}_{1}}{\text{)}} \\ \to e + {\text{O}}{{{\text{H}}}^{{\text{h}}}}({{{\text{A}}}^{2}}\Sigma ) + H \to e + {\text{OH(}}{{{\text{X}}}^{{\text{2}}}}{{{\Pi})}} \\ + \;H + h\nu . \\ \end{gathered} $$

(31)

This is manifested in the electron spectrum of electron-vibrational bands in the form of a developed rotational structure of OH(A–X) bands—“hot” groups.

Figure 15 shows a fragment of the rotational structure of the spectrum (0, 0) of the transition band ОН(A²Σ–Х²П) obtained on the Tech facility [164]. The discharge is in the Н₂О : Не = 0.075 : 0.925 mixture, at a pressure of 1 mbar, and current of 0.23 А. The lines of the branch Q₁(K) according to data [4, 181] for high-resolution spectra are marked, K is the rotational quantum number of the total angular momentum without spin. The inset shows the semi-log dependence Z = I_K(S_K$\nu _{K}^{4}$)^–1 on the energy of the rotational term F(K) = BK(K + 1) of the ОН(A²Σ) state. Here, I_K are line intensities, S_K are Hönl–London factors, ν_K are transition frequencies (the K values of the lower and upper level coincide for the Q₁ branch), В ~ 18 cm^–1 is the rotational constant.

Fig. 15.

Fragment of the spectrum of the rotational structure of the (0, 0) transition band ОН(A²Σ–Х²П). Lines of the Q₁(K) branch are indicated. Inset shows dependences of the line intensities of the rotational term energy [164].

It can be seen that the ОН(A²Σ) molecules are divided into two Boltzmann groups. The rotational temperature of the “cold” molecules formed in the process (30) corresponds to the kinetic temperature of the plasma neutral gas T ^с ~ 400 К. As indicated above, this is associated with restrictions on the transfer of angular momentum to a molecule by an electron. Levels with K > 10 (310–320 nm) are populated almost by only “hot” molecules with rotational temperatures T ^h ~ 4.5 × 10³ К. In this case, the presence of the partial temperature is explained by the statistical law of the decay of the excited Н₂О(В¹А₁) complex [173–176]. These temperatures varied in experiments [164] with different wet gases: T  ^с ~ 320–500 K and T ^h ~ 4–7 × 10³ K, but always sharply differed among themselves that allowed their reliable separation. It follows from the balance condition for concentrations of excited molecules of the $N_{{{\text{OH}}}}^{h}$ hot group under stationary conditions that

$${{N}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} = \frac{1}{{{{\tau }_{{{{A}^{2}}\Sigma }}}}}\frac{{N_{{{\text{OH}}}}^{h}}}{{{{n}_{e}}\left\langle {{{v}_{e}}{{\sigma }_{{de}}}} \right\rangle }}.$$

(32)

Here, ${{\tau }_{{{{A}^{2}}\Sigma }}}$ is the lifetime of the ОН(A²Σ) state, to which the rotationally hot molecules belong, ${{v}_{e}}$ are electron velocities, σ_de is the cross section of the dissociative excitation in the process (31). The lifetime is determined by radiative decay and quenching:

$$\frac{1}{{{{\tau }_{{{{A}^{2}}\Sigma }}}}} = {{A}_{{{{A}^{2}}\Sigma }}} + \sum\limits_i {{{N}_{i}}\left\langle {{{v}_{i}}{{\sigma }_{{iq}}}} \right\rangle } ,$$

(33)

where ${{v}_{i}}$ are thermal velocities, N_i are concentrations, σ_iq are quenching cross sections of ОН(A²Σ), the subscript i refers to the kind of the gas particles. The Einstein coefficient ${{A}_{{{{A}^{2}}\Sigma }}}$ ~ 3 × 10⁶ s^–1, quenching rate constants at (300, 450) K are given in Table 5.

Table 5. Quenching rate constants

Since the additions of inert gases, hydrogen, and deuterium to the main inert gas (usually helium in experiments) are small, ~1–10%, the same as quenching rate constants with their participation, water molecules can play the main role in quenching at ${{N}_{{{{{\text{H}}}_{2}}{\text{O}}}}}$ > 10¹⁵ cm^–3. For the considered conditions the traces of Н₂О with ${{N}_{{{{{\text{H}}}_{2}}{\text{O}}}}}$ < 10¹⁴–10¹³ cm^–3 are of interest, it is possible to assume ${{({{\tau }_{{{{A}^{2}}\Sigma }}})}^{{ - 1}}} \approx {{A}_{{{{A}^{2}}\Sigma }}}$, and formula (32) has the form

$${{N}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} = \frac{{{{A}_{{{{A}^{2}}\Sigma }}}N_{{{\text{OH}}}}^{h}}}{{{{n}_{e}}\left\langle {{{v}_{e}}{{\sigma }_{{de}}}} \right\rangle }} = \frac{{I_{{}}^{h}}}{{{{n}_{e}}\left\langle {{{v}_{e}}{{\sigma }_{{de}}}} \right\rangle }}\frac{1}{{h\nu }},$$

(34)

where I ^h is the intensity of a part of the band [W/cm³] corresponding to the group of rotational states with the high temperature. At the content of ${{N}_{{{{{\text{H}}}_{2}}{\text{O}}}}}$ > 10¹⁵ cm^–3 in the plasma-forming gas at the initial stage of the decomposition of molecules in the plasma, one should use formula (32) and the data of Table 5.

Thus, to measure the concentrations of water molecules in the plasma, it is required to determine the absolute intensity of the group of lines in the rotational structure of the transition ОН(A²Σ–Х²П), electron density and their energy distribution. These are standard techniques [182, 183], and their implementation is provided on the Tech installation [164, 167]. The measurement results demonstrated the ability to measure concentrations of water molecules at the level of 10¹² cm^–3. In this case, the changes in concentration of molecules of 10¹³ cm^–3 s^–1 are reliably controlled that satisfies the previously unattainable experiment requirements of the ITER project for the detection of the flow of H₂O molecules in the chamber of the level of 10^–7 Pa m³ s^–1 (see Section 5.2).

5.5 Multispectral Actinometry

The method described in Section 5.4 requires the use of contact probe methods and absolute intensity measurements. This is easily accomplished on model facilities but is not always acceptable for real objects. Another difficulty is that the corresponding working spectral range in it is 306–320 nm. In facilities with high background radiation, which is characteristic of nuclear-fusion reactors, optics are subject to the greatest degradation precisely in the short-wave UV region. While keeping the importance of this method as a control and calibration method for other methods, it is possible to consider techniques to minimize these difficulties.

In particular, in this regard, a new version of classical actinometry, multispectral actinometry (MA), was proposed in [49, 55]. As noted in Section 3.2, the actinometric approach does not require knowledge of the electron density and greatly reduces the accuracy requirements for knowledge of their energy spectrum (EEDF). If, however, small concentrations of particles are measured, there remains the problem of taking into account quenching of the emitting states of the detected particle and the actinometer. If in formula (6) the quantity A_Xul ≤ Q_Xu and A_Aul ≤ Q_Au, quenching of radiating states can no longer be neglected.

Quenching rate constants of many particle states are known from literature databases; in the first approximation, the effect of quenching can be estimated based on the Einstein coefficients and the chemical composition of the plasma-forming gas mixture. However, in the real chemically active plasma, it is not known in advance which particles should be taken into account when determining the quenching rate.

To interpret the results of the measurements of intensities I_X,A in chemically active plasma, a procedure is proposed [49], which includes a number of successive iterations, each of which uses two approximations.

In the first approximation, a system consisting of Eqs. (6) is written for each actinometric pair, in which concentrations of measured particle, known concentrations of actinometers and buffer gas are present the terms Q_X,A:

$${{N}_{{{{X}_{i}}}}} = {{N}_{{{{A}_{j}}}}}{{G}_{{{{X}_{i}}{{A}_{j}}}}}{{K}_{{{{X}_{i}}{{A}_{j}}}}}{{I}_{{{{X}_{i}}{{A}_{j}}}}}\frac{{{{Q}_{{{{X}_{i}}}}} + {{A}_{{{{X}_{i}}ul}}}}}{{{{Q}_{{{{A}_{i}}}}} + {{A}_{{{{A}_{j}}ul}}}}},$$

(35)

where

$$\frac{{{{C}_{A}}}}{{{{C}_{X}}}}\frac{{{{\nu }_{A}}}}{{{{\nu }_{X}}}}\frac{{{{A}_{A}}}}{{{{A}_{X}}}} = {{G}_{{AX}}},\quad \frac{{{{k}_{A}}}}{{{{k}_{X}}}} = {{R}_{{AX}}},\quad \frac{{{{I}_{A}}}}{{{{I}_{X}}}} = {{I}_{{XA}}}.$$

(36)

The equations of system (35) are nonlinear, since the quenching rates Q depend on concentrations particle:

$${{Q}_{{{{X}_{i}}}}} = {{q}_{{{{X}_{i}}}}}\sum\limits_{j,l} {({{N}_{{{{X}_{j}}}}} + {{N}_{{{{A}_{l}}}}}} ),$$

(37)

$${{Q}_{{{{A}_{i}}}}} = {{q}_{{{{A}_{i}}}}}\sum\limits_{j,l} {({{N}_{{{{X}_{j}}}}} + {{N}_{{{{A}_{l}}}}})} .$$

(38)

In the first iteration, the concentrations of only those particles, in addition to the buffer gas and actinometers, are determined that make up actinometric pairs. The accuracy of any measurement is finite. If the concentration of particles of one kind is determined independently by several (M) actinometers, and the results differ within the limits allowed by the accuracy of the intensity measurements and the discrepancy between the cross-sectional data in different sources without justified preference, the arithmetic mean is taken

$${{N}_{{{{X}_{i}}}}} = {{\left( {\sum\limits_j {{{N}_{{{{X}_{i}}{{A}_{j}}}}})} } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\limits_j {{{N}_{{{{X}_{i}}{{A}_{j}}}}})} } \right)} M}} \right. \kern-0em} M}.$$

(39)

The second approximation takes into account the fact that, in addition to the initial ones, other particles are also formed (e.g., due to the dissociation of molecules etc.) in the discharge. If one or several “new” particles is detected by the spectrum or the concentration of these particular particles and is measured, the gross chemical balance of the particles [49] is recorded with the preservation of the number of atoms of all kinds. This condition is also included in the system of equations. In this case, it is possible to determine the concentrations of components that are not measured.

The concentrations of all particles after the second approximation are substituted into the Q_X,A terms, then the system is solved again and new concentrations of atoms and molecules are found. Iterations are repeated until the convergence within the required accuracy of the determination of the N_X concentrations. This method was successfully applied in [49] for measuring concentrations of H₂O, O, H, and ОН in the mixture, originally composed of Не and H₂O, in the discharge with a hollow cathode.

A special case of MA is the H/D method for studying plasma containing hydrogen and deuterium, which is important for fusion reactors. In [184] it was noted at the operation of the PR-2 “mirror cell” facility that if the plasma-forming gas contains deuterium, then the ratio of the line intensities Dα (656.09 nm) and Hα (656.27 nm) changes, and it has been suggested that this ratio can be used as an indicator of plasma moisture. Parallel studies on the Tech facility [55] showed that this method becomes quantitative at the multispectral approach. An example of a spectrum recording at the Tech facility is shown in Fig. 16 [55].

Fig. 16.

Spectra of the Dα–Hα doublet. The initial partial pressure D₂ is ${{p}_{{{{{\text{D}}}_{2}}}}}$ = 0.05 mbar ($p_{(\text{He} + \text{Ar} + \text{Xe} + {{{{{\text{D}}}_{2}}}})}$) = 0.65 mbar). Curve 1—without H₂O additives; 2—${{p}_{{{{{\text{H}}}_{2}}{\text{O}}}}}$ = 0.05 mbar; 3—${{p}_{{{{{\text{H}}}_{2}}{\text{O}}}}}$ = 0.1 mbar. The fine structure of lines is not resolved.

A feature of this pair, if it is considered as actinometric within the multispectral approach, is that the excitation cross sections of the corresponding states are almost identical for two atomic isotopes. This means that when measuring concentrations, the parameters of the electron component are completely excluded. In this case, Eq. (6) is further simplified due to the small difference in wavelengths λ_H/λ_D ≈ С_D/С_H ≈ k_D/k_H ≈ 1, and, since the radiative lifetimes of the emitting states (Table 2) ²D_3/2 and ²P_3/2,1/2 are (18–45) ns, quenching can be neglected at pressures of several mbar and less. Then Eq. (6) takes the form

$$\frac{{{{N}_{{\text{H}}}}}}{{{{N}_{{\text{D}}}}}} = \frac{{{{I}_{{\text{H}}}}}}{{{{I}_{{\text{D}}}}}}.$$

(40)

The MA method expands the capabilities of traditional actinometry. In particular:

—the choice of actinometric pairs and the number of particles, the concentrations of which can be measured;

—as actinometers, one can use not only those particles, the concentrations of which do not change in comparison with the plasma-forming gas (mainly inert gases), but also newly formed particles, including unstable ones. They play the role of intermediate actinometers, since their concentration is determined using basic actinometers;

—due to the expansion of the choice of actinometric pairs, the working range of the spectrum may vary;

—the concentration of a number of other particle can be determined from measurements of one actinometric ratio.

Here are some examples.

First, it was required to carry out probe measurements of the electrons parameters in the above method for determining molecules Н₂О from OH radicals with fast rotation. At the introduction of small additions of Xe, the MA method can be used to determine the H₂O concentration without using probe measurements taking advantage of the fact that the cross sections for the Xe excitation (823 nm) and dissociative excitation of H₂O have close thresholds and are similar to each other,. Even at strong EEDF variations, the relevant error does not exceed 10%. In this case, it is possible to additionally determine the concentrations of О, Н, and the total concentration of ОН in the ground state.

Another example. In [55], the actinometric pair H–D was used to measure leakage flow ${{Q}_{{{{{\text{H}}}_{2}}{\text{O}}}}}$ of water molecules under conditions of the Tech facility. To this end, first the calibration is performed at known quantities $N_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{0}$ of water molecules in the initial mixture and the coefficient γ is found in the ratio

$$N_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{0} = \frac{1}{\gamma }{{N}_{{\text{D}}}}\frac{{{{I}_{{\text{H}}}}}}{{{{I}_{{\text{D}}}}}},$$

(41)

and the concentration of deuterium atoms N_D is determined using actinometer Xe from one of the four lines in the region of 750–826 nm (Table 2). Thus, the concentration of molecules in the initial mixture can be recovered from the measurements of intensities in the visible and near-IR regions, without using the UV range problematic for ITER.

The sensitivity to the external flow of water molecules is determined as

$$Q_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{{}} = \frac{{\Delta \left( {N_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{0}} \right)}}{{\Delta t}} = \frac{{\alpha \Delta \left( {N_{{\text{H}}}^{{}}{\text{/}}N_{{\text{D}}}^{{}}} \right)}}{{\Delta t}}.$$

(42)

We also note that calibration (41) is universal and can be done on a laboratory facility, since the ratio I_H/I_D is independent of the conditions in the plasma. The only condition is the control of the atoms deuterium in a real object, but this is done by a simple method of traditional actinometry in a convenient spectral range. It is very important that in this case the MA method can significantly increase the sensitivity at small deuterium concentrations in a model facility to ${{Q}_{{{{{\text{H}}}_{2}}{\text{O}}}}}$ = 5 × 10^–9 Pa m³ s^–1 [55].

5.6 Localization of Measurements in the Discharge Maintained by Hollow Cathode

The scheme of the Tech facility (Fig. 10) shows that the introduction of water vapors into the plasma was carried out from container 14 through capillary 13. The inner diameter of the capillary is 1 mm. In experiments on the effect of water vapors at the pressure of 0.7 Torr at such an injection, the dynamics of the establishment of a homogeneous discharge in helium, supported by a hollow cathode, was manifested [57, 160]. The discharge glow was monitored using a high-speed camera. The entire region of the discharge was photographed. At a closed leakage 15, the weak glow of helium filled the entire region opposite the open side of the cathode cavity, almost repeating its shape. At the rapid opening of the leakage at the initial moment, a brighter glow appeared in the region of injection against the background of the helium glow due to the change in the local composition of the plasma (Fig. 17). The interval between shots is 3 ms. It can be seen in Fig. 17b that already after 6–7 ms the bright glow fills the entire discharge region. This is consistent with the estimated diffusion time of particle. Under the conditions of this experiment, the stationary three-dimensional localization turns out to be impossible due to the small linear plasma dimensions of 10 × 2 × 1 cm³ on the order of the diffusion length. In this case, however, the 2D localization exists in the stationary mode, since the lifetime of the emitting states of the particle is short and the glow stops after the particle leaves the excitation zone. In larger systems, the situation may be different and will be discussed below.

Fig. 17.

Photographs of the discharge glow region opposite the open side of the hollow cathode after injection of water vapor: (a) 3.3 ms after the beginning of the injection and (b) 6.6 ms after the beginning of the injection.

5.7 Measurements of Concentrations of Water Isotopomers in the Discharge Tube

Comparative measurements were carried out using diode laser absorption spectroscopy and emission actinometry using diode laser spectroscopy (Figs. 12 and 13). The initial gas mixture is He : Xe (99 : 1) with Н₂О and D₂ additives [82, 83].

Emission measurements were carried out by the method of isolation of “hot” rotational groups. In the absence of deuterium, the measurements of concentrations of OH molecules in these groups were carried out using Xe as an actinometer (line 823 nm, Table 2) without measurements of the parameters of the electron component. Concentrations of О₂ and Н₂ for taking quenching into account were found from the gross balance $N_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{0}$–$N_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{{}}$ = $N_{{{{{\text{H}}}_{{\text{2}}}}}}^{{}}$= 2$N_{{{{{\text{O}}}_{{\text{2}}}}}}^{{}}$, where $N_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{0}$ is the unitial concentration of water molecules in the chamber before the discharge ignition.

The absorption spectrum of Н₂О recorded on a laser spectrometer (DLS) is shown in Fig. 18.

Fig. 18.

Absorption spectrum of Н₂О in the gas mixture. The pressure is of 0.5 mbar and the discharge current is of 4 mA.

A rather large relative proportion of water molecules H₂O : He : Xe (148 : 99 : 1) was used. At such concentration vibrational relaxation of molecules occurs rapidly, and the internal partition function required for calculating the concentrations can be calculated as equilibrium, when the vibrational temperatures of all H₂O modes coincide with the rotational and gas ones. The gas temperature was measured by Doppler broadening in the case of a laser absorption spectrum and was identified with the temperature of the “cold” OH group at emission measurements. The results matched.

With respect to concentrations of H₂O molecules, both methods also give consistent results within errors (Fig. 19).

Fig. 19.

Results of the measurements of the concentration of water molecules N at different discharge currents. (1) Is the DLS method [82]; (2) is the actinometry method [82, 83]; and (3) is the simulation result [83].

When deuterium molecules are added to the initial gas, the lines of HDO molecules appear in the absorption spectrum (Fig. 20) [168–172].

Fig. 20.

Experimental absorption spectrum of H₂O and HDO in the range of laser tuning [168]. Inset shows an example of the approximation of the transition line of 7181.31 cm^–1 HDO according to Gauss. (1) Is measurements and (2) is approximation.

When processing spectra absorption, we used lines for which the ratio of intensities at the input and output of the resonator was within 0.2 < I/I₀ < 0.4 that provides the best accuracy of measurements [97].

Figure 21 shows the results of measurements of the HDO concentrations as a function of the discharge burning time at the current of 4 mA in helium $N_{{{\text{He}}}}^{0}$ = 8.5 × 10¹⁵ cm^–3 + $N_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{0}$ = 2.1 × 10¹⁴ cm^–3 and different initial concentrations of deuterium molecules $N_{{{\text{D2}}}}^{0}$ [168, 169]. In the absence of the discharge, HDO molecules are not detected, but appear immediately after the discharge is switched on. Further, there is a weak (but noticeable against the background of measurement errors) tendency towards a decrease in the concentrations of heavy water in the plasma. Since this process has a characteristic time of tens of minutes, it is apparently associated with chemisorption.

Fig. 21.

Behavior of HDO molecules after switching on of the discharge at the initial concentration of water molecules $N_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{0}$ = 8.4×10¹⁴ cm^–3 and different initial concentrations of deuterium molecules $N_{{{{{\text{D}}}_{{\text{2}}}}}}^{0}$: 1—1.8 × 10¹⁵ cm^–3; 2—3.6 × 10¹⁵ cm^–3; and 3—5.3 × 10¹⁵ cm^–3 [168].

Similar measurements of the concentrations of water molecules [168] show their rapid decay already at the initial stage (the measurement time of ~30 s) by 20–30% and further stabilization with a trend towards a slow decrease in concentrations (this is close to that observed in early studies on СО₂ dissociation, see Section 2). When comparing these results, it is possible to introduce the ratios k = $N_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{{}}$/N_HDO in the discharge. It turned out to be almost constant k = 3 ± 0.5 and well maintained in time. The results are shown in Fig. 22. It is possible to assume the existence of a mechanism that limits the fraction of H₂O molecules on the wall, capable of overcoming the desorption barrier at the interaction with D₂ molecules [170].

Fig. 22.

Behavior of the ratio of concentrations of H₂O and HDO molecules at different initial concentrations N⁰ of H₂O and D₂ molecules measured in the discharge [168]: 1—$N_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{0}$ = 2.4 × 10¹⁴ cm^–3 and $N_{{{{{\text{D}}}_{{\text{2}}}}}}^{0}$ = 1.8 × 10¹⁵ cm^–3; 2—$N_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{0}$ = 1.7 × 10¹⁴ cm^–3 and $N_{{{{{\text{D}}}_{{\text{2}}}}}}^{0}$ = 1.8 × 10¹⁵ cm^–3; 3—$N_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{0}$ = 2.0 × 10¹⁴ cm^–3 and $N_{{{{{\text{D}}}_{{\text{2}}}}}}^{0}$ = 1.8 × 10¹⁵ cm^–3; 4—$N_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{0}$ = 2.1 × 10¹⁴ cm^–3 and $N_{{{{{\text{D}}}_{{\text{2}}}}}}^{0}$ = 3.6 × 10¹⁵ cm^–3; 5—$N_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{0}$ = 2.7 × 10¹⁶ cm^–3 and $N_{{{{{\text{D}}}_{{\text{2}}}}}}^{0}$ = 3.6 × 10¹⁵ cm^–3; 6—$N_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{0}$ = 1.8 × 10¹⁴ cm^–3 and $N_{{{{{\text{D}}}_{{\text{2}}}}}}^{0}$ = 5.3 × 10¹⁵ cm^–3; 7—$N_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{0}$ = 2.1 × 10¹⁴ cm^–3 and $N_{{{{{\text{D}}}_{{\text{2}}}}}}^{0}$ = 5.3 × 10¹⁵ cm^–3.

6 SIMULATION OF PROCESSES IN THE GLOW DISCHARGE PLASMA WITH WATER AND DEUTERIUM ADDITIVES. COMPARISON WITH EXPERIMENT

The transformations of molecules and plasma composition in a positive column of a glow discharge in helium with additions of H₂O and D₂ were analyzed using a homogeneous kinetic model [172]. The balance equations for neutral and charged particles were solved together with the Boltzmann equation for the electron energy distribution function (EEDF) in the two-term approximation.

The estimate of the electron energy relaxation length λ_u for conditions of the experiment gives the value λ_u = D_T/V_e ∼ 0.3–0.8 cm, where D_T is the transverse diffusion coefficient of electrons, and V_e is their drift velocity. The λ_u value is less than the radius of the discharge tube of 1 cm that justifies the use of the local approximation for EEDF.

The model takes into account processes in volume and on the surface with the participation of atoms, molecules and radicals He, H₂O, O₂, H₂, O, H, OH, H₂O₂, HO₂, D₂O, HDO, D₂, D, OD, DO₂, D₂O, HD, D₂O₂, and HDO₂, positive ions He⁺, H₂O⁺, ${\text{O}}_{2}^{ + }$, ${\text{H}}_{2}^{ + }$, D₂O⁺, HDO⁺, and ${\text{D}}_{2}^{ + }$, and negative ions O^–, H^–, D^–, OH^–, and D^– and electrons. The model includes an equation for an external electrical circuit consisting of a ballast and a voltage source,

$${{U}_{{{\text{disch}}}}} = {{U}_{0}}-{{I}_{{{\text{disch}}}}}{{R}_{b}},$$

(43)

where U_disch is the voltage between the electrodes of the tube, U₀ is the supply voltage, R_b is the ballast resistance; the discharge current I_disch = en_eV_eS, n_e is the electron density, V_e is their drift velocity, S is the area of the cross sections of the tube. The high-voltage voltage source operated in the current stabilization mode, so its effective internal resistance depended on the discharge conditions and the specified current. In Eq. (43), the R_b value includes both components, U_disch was measured independently.

Reactions of the interaction of electrons with helium atom and molecules are given in Table 6 (processes R1–R37).

Table 6. Reactions of the interaction of electrons with the helium atom and molecules

Table 7 lists the processes (R38–R57) involving negative ions and ion–ion recombination.

Table 7. Reactions of detachment of electrons from negative ions, charge exchange of negative ions and ion–ion recombination

Processes (R58–R71) of the decay of repulsive electron singlet and triplet states of hydrogen isotopomers and processes of heterogeneous recombination are given in Table 8.

Table 8. Decay channels of electron states H₂, D₂, and НD, and heterogeneous reactions

The sets of cross sections for the interaction electrons with helium atoms and deuterium molecules were taken from [185] and [186], respectively. The calculation of the drift velocity of electrons, the coefficients of longitudinal and transverse diffusion, the ionization rate of the quantity with a set of these cross sections give results that are in good agreement with the experimental data available in the literature.

Under the conditions of the conducted experiments, the measured steady-state values of the reduced electric field E/N ~ 55–90 Td. Taking this into account, the processes of excitation of rotational and vibrational levels of deuterium molecules (processes R1 and R2, in Table 6), triplet R3 (b³Σ$_{{\text{u}}}^{ + }$, c³П_u, a³Σ$_{{\text{g}}}^{ + }$, …) and singlet R4 (B¹Σ$_{{\text{u}}}^{ + }$, E¹Σ$_{{\text{g}}}^{ + }$, C¹П_u, …) of electron states of deuterium molecules were included in the kinetic model. The dissociative adhesion (R6), ionization of helium atoms (R7) and molecules of deuterium (R5) was taken into account. Taking into account the excitation of electron levels of helium atoms contributes about 5% to the energy equilibrium at E/N = 70 Td, so the data from processes were not taken into account in the calculations. For H₂ and HD molecules, only the processes of excitation of triplet and singlet electron states, as well as dissociative attachment of electrons to molecules in the main vibrational states and ionization (R8–R16), were taken into account due to their noticeably lower concentrations (see below). As follows from the analysis of the database [187], the transport cross sections of electron scattering on D₂, H₂, and НD molecules differ insignificantly. Cross sections of excitation of electron levels and ionization cross sections differ slightly as well. According to the data of [188], the dependence of the form and the size of the cross sections of dissociation on the type of isotope is small. The cross sections for electron level excitation, ionization and dissociative adhesion for molecules H₂, HD, and D₂ were assumed to be equal in the calculations. In this case, the cross sections of dissociative adhesion to H₂, HD, and D₂ molecules were considered equal to the cross section of dissociative adhesion to the H₂ molecule.

It was taken into account that the dissociative attachment to the HD molecule can occur through two channels with equal probability,

$${\text{HD}} + e \to {{{\text{H}}}^{-}} + {\text{D}},$$

(44)

$${\text{HD}} + e \to {\text{H}} + {{{\text{D}}}^{ - }},$$

(45)

and their cross sections σ_1,2(u) are 0.5 of cross sections of the dissociative attachment to the D₂ molecule. The lower b³Σ$_{u}^{ + }$ state is repulsive, and its excitation leads to the dissociation of the molecule. This cross section is the main contributor to the sum of the triplet state cross sections. Therefore, it was believed that the excitation of triplet electron states of H₂ isotopomers leads to the dissociation of molecules (R58, R61, R64). Based on the data recommended in the review [189] for the integral dissociation cross sections of H₂ molecules and recent calculations carried out in [190], it can be concluded that about 10% of the excited molecules are dissociated at the excitation of singlet electron states. Moreover, in the model it was assumed that the dissociation of molecules occurs instantly. The probabilities of channels of dissociation of electron states and heterogeneous reactions are given in Table 8.

The cross sections for dissociation, ionization, and dissociative attachment for H₂O molecules were taken from [191].

For H₂O isotopomers, the cross sections of their dissociation (R17, R22, R27, and R28), ionization (R18, R23, and R29) and dissociative adhesion (R19–R21, R24–R26, and R30–R34) were taken into account. The same as for HD, in the case of the appearance of two channels of dissociation or dissociative adhesion for HDO, the probabilities of these channels were considered equally probable, and the cross-sections themselves were taken by analogy with H₂O (R27–R28, R30–R31, and R32–R34) [191].

For oxygen molecules, their dissociation [192, 193], ionization [193], and dissociative adhesion [193] were taken into account. It was taken into account that for the O₂ molecule there are two electron impact dissociation channels with a threshold of 5.6 eV and 8.4 eV [192]. In the first channel, two O atoms are formed in the ground state, in the second channel, one of the atoms is in the electronically excited O (¹D) state. In the kinetic scheme, the same as in our previous works [49, 56, 57, 72, 82, 83, 171, 172], the dissociation constant was taken equal to the sum of the constants of two channels.

Table 7 shows the detachment processes of electrons from negative ions, charge exchange of negative ions and ion–ion recombination. If there is no reference next to the rate constant, then the constant is taken equal to the rate constant of a similar process [172].

It was believed that singlet and triplet electron states of H₂, D₂, and НD dissociate instantly into atoms. The probabilities of dissociation channels of the electron states and heterogeneous reactions are given in Table 8.

Estimates have shown that, due to the low pressure of the gas mixture, the processes of decay of charged particles on the walls of the discharge tube play the main role. Therefore, the model includes, along with volumetric loss, the processes of ambipolar diffusion of charged particles onto the walls of the discharge tube. In the plasma-forming gas, there are molecules to which electrons (isotopomers of water molecules and molecular hydrogen) adhere dissociatively. The calculation of the plasma charge composition showed that for the conditions under consideration the concentration of negative ions exceeds significantly the electron density. In this case, the high concentration of negative ions affects the diffusion rate of electrons to the wall of the discharge tube. Therefore, to take into account the loss of electrons, negative and positive ions on the walls of the discharge tube, we used the approximation proposed in [197]. The equation for the electron density has the form

$$\frac{{d{{n}_{e}}}}{{dt}} = {{\nu }_{{{\text{ion}}}}}{{n}_{e}} + \sum\limits_k {{{\nu }_{{\det ,k}}}} {{n}_{{n,k}}} - {{\nu }_{{{\text{att}}}}}{{n}_{e}} - {{\nu }_{{\text{D}}}}{{n}_{e}},$$

(46)

where n_e is the electron density, ν_ion is the total ionization frequency, ν_det,k is the frequency of the detachment of electrons from negative ions of the kind k, n_n,k is the concentration of negative ions of the kind k, ν_D is the frequency of ambipolar diffusion of electrons onto the walls of the discharge tube making it possible to take into account the increase in the diffusion rate at a noticeable excess of negative ions over the electron density [197].

The rate constants of processes involving heavy particles: atoms, molecules and radicals,—and their temperature dependences in the gas phase, taken from [56], are given in Table 9.

Table 9. Bulk reactions involving neutral particles

For D₂, HD, D₂O, and HDO molecules, the dissociation rate constants were taken the same as for H₂ and H₂O molecules, respectively. For bulk chemical reactions involving components containing D atoms, the reaction rate constants were taken from the NIST database [215]. In the absence of such processes in the database, their rate constants were taken the same as for similar reactions but with components containing H atoms. The rate constants of reverse processes were calculated from the principle of detailed equilibrium using thermodynamic data [216].

The processes of the heterogeneous particle recombination on surfaces are important under considered conditions,. These processes are taken into account in the model by reactions R67–R71. The calculations are performed in the approximation of the constant gas temperature in the discharge volume (320 K). To solve the described system of equations, we used the Chemical WorkBench software package (CWB 4.1.18411, www.kintech.ru) [217]. The system of equations was solved by the establishment method until stationary values of the concentrations of the plasma components were reached.

The kinetic model described above was used to calculate the characteristics of the glow discharge and the concentrations of the plasma components in the tube. The joint solution of the kinetic equations for the plasma component with the Boltzmann equation for the EEDF and the equation for the external circuit makes it possible to determine the electric field and the electron density in the positive column of e plasma. In experiment, the high-voltage source was operating in the constant current mode and the internal resistance tuning in Eq. (43) is included in the resistance R_b. It was selected from the condition of equality of the established calculated discharge current value to the measured value.

Calculations were carried out for the concentration of He atoms of 8.5 × 10¹⁵ cm^–3, the initial concentrations of H₂O molecules varied in the range from 4.4 × 10¹⁴ cm^–3 to 9.6 × 10¹⁴ cm^–3, and those of D₂ molecules of (1.8–5.3) × 10¹⁵ cm^–3 [172]. The initial concentration of the other molecules, atoms and radicals, included in the model, was set zero. The initial electron density was set 10⁷ cm^–3. The gas temperature was considered constant and equal to that measured in experiment T = 320 K. The inner tube diameter was 2 cm. The calculated dynamics of the behavior of the reduced value of the electric field E/N and the discharge current are shown in Fig. 23. At the initial time, the electron density is low and the voltage U₀ is applied to the discharge tube. There is the increase in the electron density, discharge current and voltage drop on the ballast resistance. As a result, the stationary value of the discharge current and voltage on the discharge tube is established at times of about 1 µs. The markers correspond to the measured steady-state discharge current and E/N. The experimental value of the reduced electric field was found taking into account the cathode voltage drop, the value of which was determined by measuring the voltage across different pairs of electrodes with discharges of different lengths. Initially, the discharge current and E/N are rapidly established at times of about 1 µs, the concentration of water molecules at these times is equal to the initial one. Then the dissociation of water molecules occurs, its concentration decreases in several times and reaches a stationary value at times on the order of 50‒100 s. In this case, the reduced E/N value falls by only 4 Td. This is due to the fact that electrons decay mainly due to their ambipolar diffusion to the walls of the discharge tube. The final steady-state calculation of the reduced electric field is 69 Td, and the average electron energy of 7.43 eV.

Fig. 23.

Time dependence of the reduced electric field and discharge current in the tube. Solid lines are simulation results. Markers are results of changes in the experiment. N_He = 8.5 × 10¹⁵ cm^–3, $N_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{0}$ = 8.8 × 10¹⁴ cm^–3, $N_{{{{{\text{D}}}_{{\text{2}}}}}}^{0}$ = 3.6 × 10¹⁵ cm^–3.

Figure 24 presents the time evolution of the electron density and concentrations of positive and negative ions. The electron density, as well as the discharge current, is set in ~1 µs. The establishment of the ion concentrations occurs in two stages: first, over a time of about 1 ms, then about 10 s. This is due to the fact that at first the ion composition is established when the H₂O molecules are still weakly dissociated, and at the next stage, the formation of the stationary composition for almost all neutral particles is terminated (see Fig. 25). OH and OD radicals have the electron affinity energy of 4.77 eV. For comparison, the electron affinity energy for H and О atoms is 0.754 and 1.47 eV, respectively. The concentration of negative O^–, H^–, and D^– ions is about 250 times lower than the concentration of OH^– and OD^– ions. Concentrations of OH^– and OD^– ions are about an order of magnitude higher than the electron density. Figure 26 shows three dependences of those presented in Fig. 25 corresponding to the behavior of water isotopomers. The measurement data for H₂O, HDO molecules are also shown there. It can be seen that by choosing the constants of heterogeneous reactions it is possible to obtain good agreement between the theory and experiment for these molecules in the stationary stage of the formation of the plasma chemical composition.

Fig. 24.

Calculated time dependence of the electron density and concentrations of positive and negative ions in the discharge in the tube. N_He = 8.5 × 10¹⁵ cm^–3, $N_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{0}$ = 8.8 × 10¹⁴ cm^–3, $N_{{{{{\text{D}}}_{{\text{2}}}}}}^{0}$ = 3.6 × 10¹⁵ cm^–3.

Fig. 25.

Calculated time dependence of concentrations of neutral particles in the discharge in the tube. N_He = 8.5 × 10¹⁵ cm^–3, $N_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{0}$ = 8.8 × 10¹⁴ cm^–3, $N_{{{{{\text{D}}}_{{\text{2}}}}}}^{0}$ = 3.6 × 10¹⁵ cm^–3.

Fig. 26.

Calculated time dependence of H₂O, HDO, and D₂O concentrations in the discharge in the tube. Markers—experiment. N_He = 8.5 × 10¹⁵ cm^–3, $N_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{0}$ = 8.8 × 10¹⁴ cm^–3, $N_{{{{{\text{D}}}_{{\text{2}}}}}}^{0}$ = 3.6 × 10¹⁵ cm^–3.

A simpler kinetic model was used to simulate plasma-chemical processes in helium mixtures and water vapors in the discharge in a hollow cathode [49]. The following components were taken into account: He, H₂O, O₂, H₂, H₂O₂, HO₂, OH, H, and O. The processes of dissociation of H₂O, O₂, and H₂ molecules by plasma electrons, bulk chemical reactions, heterogeneous recombination of O and H atoms were included, and OH radicals on the surface of the chamber walls were taken into account. The dissociation rates by plasma electrons of H₂O, O₂, and H₂ molecules were calculated by averaging with the Maxwellian EEDF with the electron temperature of 9 eV and the electron density of 10⁹ cm^–3 from the results of probe measurements. The gas temperature is 430 K that corresponds to the experimental measurements, the pressure of 0.87 Torr, the initial gas mixture H₂O : He = 1 : 3. It was assumed that small amounts of inert actinometers present in the gas mixture do not affect the chemical transformations.

The simulation results show that in the quasi-stationary state, the main channels of the destruction of H₂O, O₂, and H₂ molecules are associated with dissociation by electrons, and their formation occurs by recombination on the surface. The recombination probabilities of О and Н atoms and ОН radical on the surface depend on its material and the state. They are known with a larger error than the chemical reaction constants in the volume. Therefore, the probabilities of heterogeneous recombination were chosen from the condition that the concentrations of H₂O molecules, ОН radicals and О and Н atoms are equal to the measured values.

In the experiment, the H₂O, OH, O, and H concentrations were measured. The calculations showed that the concentration of HO₂ and H₂O₂ molecules is significantly less than the H₂O, OH, O, and H concentrations. Therefore, the concentrations of H₂ and O₂ molecules were determined from the condition of particle conservation neglecting the HO₂ and H₂O₂ concentration, and the gross chemical equilibrium of particles can be written as

$$\begin{gathered} {\text{A}}(\Delta {{{\text{H}}}_{{\text{2}}}}{\text{O}}) \\ = {\text{B(OH)}} + {\text{C}}({\text{H}}) + {\text{D(O)}} + {\text{E(}}{{{\text{H}}}_{2}}{\text{)}} + {\text{F(}}{{{\text{O}}}_{2}}{\text{)}}, \\ \end{gathered} $$

(47)

where А, B, C, D, E, F is the amount of molecules of the corresponding kind, ΔH₂O = [H₂O]₀ – [H₂O] is the difference between the initial amount of water molecules in the gas mixture and its amount at the time of the measurement. The condition for the elemental equilibrium for oxygen and hydrogen is

$${\text{F}} = ({\text{A}}-{\text{B}}-{\text{D}}){\text{/}}2,$$

(48)

$${\text{E}} = (2{\text{A}}-{\text{B}}-{\text{C}}){\text{/}}2,$$

(49)

and the amount of Н₂ and О₂ molecules was found from the experimental A, B, C, D values.

Figure 27 shows calculation results (solid lines) and measurement results (markers). It can be seen that the model describes the experiment data well, with the exception of the behavior of oxygen atoms. Perhaps this is due to the presence of water molecules on the surface of the chamber walls, which is manifested through the reaction О + H₂O (wall) → Н₂ + О₂ (gas). A detailed explanation of this discrepancy is given in [49, 50].

Fig. 27.

Time behavior of measured concentrations of molecules and atoms in the discharge with a hollow cathode. Markers—experimental data, solid lines—simulation results.

Figure 28 shows simulation results for the initial phase of the discharge. According to the calculation, the characteristic time of the establishment of chemical equilibrium is about 1 s. Figure 28 illustrates the strong dissociation of water molecules up to 97%. Such a strong decomposition of water molecules should be taken into account when diagnosing leaks in electric vacuum devices using plasma spectra.

Fig. 28.

Calculated behavior of particle concentrations in the initial period of the establishment of the stationary chemical composition of the plasma.

7 ON THE EXPECTED SENSITIVITY OF ACTINOMETRIC MEASUREMENTS AND LOCALIZATION OF SOURCES OF IMPURITIES OF WATER MOLECULES UNDER ITER CONDITIONS

Based on the analysis of the performed preliminary and model studies on finding water leaks and determining their flows described in Sections 5 and 6, the methods based on the plasma own emission seem to be a reasonable compromise for a large reactor. In recent years, their capabilities as quantitative methods of the analysis in nonequilibrium plasma have expanded due to a deeper methodological and physical study and focus on such problems. For complex systems, the nonperturbing nature and the possibility of remote measurements are also crucial. Optical actinometry in its new multispectral version of MA with the inclusion of pairs of intermediate actinometers, e.g., hydrogen and deuterium atoms with H_α–D_α lines in the 656 nm range convenient for experiment seems to be preferable. By introducing an additional actinometer Xe, the concentrations of O, H, and D atoms are monitored, as well as the density of the “hot” hydroxyl group, and through it, the concentration of water molecules and their flow into the plasma from outside. The independence of I(H_α)/I(D_α) = N_H/N_D of the electron component parameters makes it possible to perform the necessary checks and calibrations on model facilities. Another important factor is the proven and MA tested model of the formation of a chemical neutral and ionic plasma composition based on gases containing water and deuterium impurities (Section 6). Direct monitoring of the reactor is not yet possible, and either full calculations or extrapolation models are necessary to estimate the capabilities of the impurity control from preliminary experiments.

7.1 Extrapolation of Model Experiment Results, Heterogeneity Factor

Since the kinetic model describes well the results of experiments on two different model facilities, it can be used to predict the results from the concentrations of molecules over an extended range of conditions. Figure 29 shows the calculation results of the concentrations of H₂O molecules and O, H atoms in the discharge plasma and the [H₂O]⁰ value in the initial Не(0.5 Torr) + Н₂О mixture with deuterium additives [57]. The same as in Section 6, experiment results in their measurement region agree well with calculation results. The measurements for a group of particles were carried out using one pair of intermediate actinometers H–D. In particular, it can be seen from the comparison of dependences 4, 4  ' and 7, 7  ' that the decrease in the D concentration (which is achieved by the decrease in the D₂ additives) increases the sensitivity of the concentration measurements. This is a favorable factor for the diagnostics of ITER-type reactors, in some operating modes of which low deuterium concentrations are expected, [D₂] ~(10¹³–10¹¹) cm^–3.

Fig. 29.

Concentrations N of О, Н atoms, Н₂О molecules in the plasma and the concentration of Н₂О in the initial mixture. Markers—experiment, lines—calculation. 1, 1 '—[H₂O]⁰; 2, 2 '—H₂O; 3, 3 '—O; 4, 4 '—H at [D₂]⁰ = 6.75 × 10¹⁴ cm^–3; 5, 5 '—[H₂O]⁰; 6, 6 '—H₂O; 7, 7  '—H at [D₂]⁰ = 1.35 × 10¹⁵ cm^–3 [57].

The measurements on model facilities and simulations were carried out for uniform plasma conditions, while the parameter gradients are characteristic for the plasma near the wall in the reactor. To take into account the effect of this circumstance on the measurements and simulation, we used the results of calculations carried out in a number of works. Table 10 shows the results [218] obtained by the Monte Carlo method in the EIRENE version adapted for tokamaks.

Table 10. Distributions of the concentrations of neutral particles N, electron concentrations n_e, and temperature Т_е in the direction Х normal to the ITER wall

It was noted that neutral particles in the reactor are present only near the wall, no further than 10 cm, after that the plasma becomes completely ionized, and the electron density and temperature increase from 0 to 10¹³ cm^–3 and from units to several tens of eV at this distance, respectively. In this case, the estimate of the temperature of neutrals increases as 430–1200 K.

7.2 Localization of Sources of the Penetration of Water Molecules

The region in which the source of the impurity can be localized is determined by the optical scheme, which detects spontaneous emission, and the processes in the plasma.

The optical system in the ITER diagnostic complex includes a panoramic spectrometer for the operation in the visible and near-IR spectral regions (VisIR [221, 222]) with the inverse linear dispersion of at least 1 nm/mm. This is a sufficient resolution for the discussed methods. The panorama covers about 80% of the area of the inner wall at the spatial resolution of the image R³ ~ 10 × 10 × 10 cm³ = 1 L. To establish the location and flow of the leak, it is necessary that the molecules and their average concentrations in the plasma be measured within this volume.

The controlled [H₂O]⁰ amounts were introduced into the initial mixture in model experiments on determining the sensitivity to the concentration of water molecules. In the case of a real leak and a limited localization area, the density of molecules should be related to their flow, Q = Δ(PV)/Δt. In the absence of the discharge but at the heated wall, the molecules penetrating through the wall do not undergo transformations, and their number in the observation zone is

$${{N}_{0}} = {{\left[ {{{{\text{H}}}_{{\text{2}}}}{\text{O}}} \right]}^{0}} = (dN{\text{/}}dt){{\tau }_{D}},$$

(50)

where τ_D = l²/D, D is the diffusion coefficient of Н₂О in helium, l is the path length of the molecule. If is assumed that the discharge in He (0.5 Torr) with small deuterium additives is used in the testing and leak detection mode, then D ~1500 cm² s^–1 (430 K, D ~ T ^3/2) [219]. The characteristic time for molecules to leave the observation region determined by the spatial resolution of the optical system is τ_D ~6 × 10^–2 s. Table 11 shows the correspondence of flow values, frequencies of molecules penetration into the plasma Ω and concentration N₀ = [H₂O]⁰ in the region of the spatial optical resolution taking into account the volume of the reactor chamber.

Table 11. Ratio of quantities characterizing the leakage of molecules into the observation region

When the discharge is switched on, the chemical processes have different local rates. We calculated the dynamics of transformations of molecules for different combinations of electron densities and temperatures. An example is shown in Fig. 30. It can be seen that stationary concentrations all particles are established during the time ~2 × 10^–2 s, shorter than the time that the particle leaves the localization region due to diffusion. This time is reduced even more at high electron densities and temperatures.

Fig. 30.

Dynamics of the establishment of the chemical composition of the plasma in the near-wall region. Plasma-forming gas He (2.5 × 10¹⁶ cm^–3) + D₂ (10¹² cm^–3) + H₂O (5 × 10¹² cm^–3). T_e = 10 eV, n_e = 10¹¹ cm^–3. 1—H₂O, 2—D₂, 3—O, 4—H₂, 5—D, 6—O₂, 7—H, 8—HD, 9 —OD, 10—OH, 11—D₂O, 12—HDO, 13—HO₂, and 14—H₂O₂.

Two methods were used in averaging the results of actinometric measurements over the localization region. The n_e, T_e values (Table 10) and the neutral gas temperature T in the central region (X = 4 cm) were used in the first of them. The concentrations for various X and the corresponding data from Table 10 were calculated with subsequent averaging over X at another procedure. The results coincided with an accuracy of no worse than 20%.

Figure 31 shows the stationary concentrations of water molecules in the plasma and in the absence of the discharge corresponding to different ratios of densities [H] and [D] (equal to ratios of intensities in the actinometric pair H–D) for the additive N_D2 = 10¹² cm^–3. The examples are given for X = 2 cm and Х = 7 cm. It can be seen that the particles entering the chamber in these regions are deeply dissociated. The change in the H/D ratio from 10^–2 to 10² corresponds to the change in the $N_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{{}}$ concentrations from 10⁷ cm^–3 to 10¹¹ cm^–3 in the case (a) and from 10⁵ cm^–3 to 10⁹ cm^–3 in the case (b). At the same H/D, concentrations N for cases (a) and (b) differ by two orders of magnitude. On the contrary, concentrations $N_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{0}$ almost coincide within errors of measurements and data of Table 10 at the equal H/D. In this case, in the same region of changes of H/D the $N_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{0}$ values vary in both cases from 5 × 10⁹ to 5 × 10¹³ cm^–3. A strong difference between cases (a) and (b) with respect N_H2O and almost independence $N_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}^{0}$ at the same H/D are explained naturally. Changes in N are associated with changes in the cycle of plasma-chemical processes at various electron parameter, while N₀ is determined only by the flow Q of molecules from outside. This result is very important, since it is the determination of the power and localization of leaks in the ITER project that is highlighted.

Fig. 31.

Calculated concentrations of Н₂О molecules in the plasma (N) and in the gas before the discharge ignition (N₀) penetrating in the chamber. (a) X = 2 cm, Т_е = 8 eV, n_e = 6 × 10¹¹ cm^–3, and T = 600 K and (b) X = 7 cm, T_e = 30 eV, n_e = 10¹³ cm^–3, and T = 1000 K.

It can be seen in Fig. 31 and Table 10 that at the measurements of the Н–D pair using multispectral actinometry local measurements of leak flows are possible in the range of Q = (10^–13–10^–9) Pa m³ s^–1. The range can be refined by varying the D₂ additives to the inert gas.

Based on the requirements of the ITER project on the maximum permissible flow of water molecules into the reactor chamber Q < 10^–7 Pa m³ s^–1, it is possible to talk about the possibility of finding localization of up to 100 leaks simultaneously and determining flows, if each leak gives a flow Q < 10^–9 Pa m³ s^–1.

8 CONCLUSIONS

The review considers the development and modern possibilities of the methods of measuring small particle concentrations in the low-temperature plasma. The objects with non-equilibrium plasma are of the greatest scientific and practical interest, and this critically affects the physical substantiation and applicability of their diagnostic methods. The measure of smallness of concentrations in different situations can indicate their different roles in plasma processes.

The importance of analytical mass spectrometry methods is not diminished. The difficulty of their application is associated with the need for sampling, and the correspondence of the number of particles in the sample to their number in the plasma needs justification. This problem is also gradually being solved, but, as a rule, under the control of optical spectroscopy methods.

We are talking often about the particles, the concentrations of which are small due to their high reactivity and, as a consequence, their key role in the formation of the plasma composition, the production of target products in the plasma volume and the active interaction of the plasma with surfaces. As a rule, these are radicals in the form of atoms, di- and polyatomic molecules, including alkali metals, OH, CH, CN, CH₂O₂, etc. These particles are important, in particular, for the selective chemistry of hydrocarbons. Halogens and halides are of interest for applications in microelectronics. The field of research with the use of plasma sources of atmospheric pressure generating jets with active atoms and molecules is under development. It is interesting for many applications, and at the current stage, most in demand for biological and medical applications. An important role in plasma physics and chemistry is played by electronically excited metastable particles, which accumulate plasma energy and spend it on initiating chemical reactions, exciting laser levels, etc. For many of these active particles, there exist transitions that are allowed in the dipole approximation with the participation of the most populated ground electron state. They belong to the near-UV to mid-IR spectral range, which are quite convenient for the use of absorption methods. With the development of frequency tunable lasers, they gradually replace the means of classical absorption spectroscopy and allow the use of both single-photon and multi-photon processes, direct and indirect recording of weak absorption (laser fluorescence, galvanic phenomena, etc.). Each success in the development of these areas is accompanied by numerous publications, reviews, and monographs.

Nevertheless, in many, if not most, works, laser and sampling techniques are complemented by classical absorption and emission techniques. They are simpler in technical terms and they received reliable physical justification for a number of measurements in the nonequilibrium plasma. This applies, e.g., to the measurement of gas, rotational and vibrational temperatures required for the calculation of the internal partition function of the laser absorption measurement.

Finally, laser methods or sampling methods are often difficult to apply for diagnosing real objects because even small disturbances, the introduction of unacceptable additions to a complex design, limited accessibility for reasons of remoteness, safety, etc. are forbidden.

It is known that in a number of cases, the presence of small particle fractions has no positive effect and, on the contrary, hinders the achievement of the desired result in the plasma technologies; they are more often classified as impurities, and they also need monitoring.

In this review, along with the analysis of the general situation with the development of highly sensitive spectroscopy of particles in plasma, we consider a situation in which to the choice of measuring instruments, in addition to the above difficulties, is imposed the requirement of spatial localization of impurity sources. Along with the general interest in the creation of such methods, the immediate applied interest is associated with the upcoming launch of the ITER nuclear fusion reactor, for which it is necessary to provide protection against water vapors in the working chamber, which plays the role of both a cooler and a working fluid. Experience of working with reactors of previous generations made it possible to formulate the level of allowed restrictions on impurities. Over the years, a number of groups, including ours, have been working in this direction. The best current solution is the emission method in a new version of multispectral actinometry. This approach uses not only classical actinometers of inert atoms, but also intermediate unstable particles. This made it possible to increase the sensitivity of measurements and expand the spectrum of detected particles, which are the products of transformations of water molecules. The technique was practiced on model facilities with mutual control, including a laser one. An important result was the creation of a kinetic model of reactions in the plasma, which adequately describes model experiments.

Along with the high sensitivity of the method, the principle of the localization is implemented due to the fact that, already near the first wall, the products of chemical reactions reach stationary concentrations in a time shorter than the time of diffusion escape of a particle from the measurement zone determined by the spatial resolution of the optical system.

This made it possible to make a positive forecast of the possibilities of monitoring impurities in the reactor being put into operation.

It should be said that the results obtained answer the question of controlling impurities at the stage of testing a reactor with discharges in gases containing deuterium. The development of diagnostics in the regime of nuclear fusion reactions, despite the created basis, will require additional research.