Geodesics in the Wormhole Gravitational Field

Abstract

The structure of spacetime near a wormhole (WH) and possible observational consequences are investigated theoretically. In connection with the growing accuracy of observations and the prospects of a new gravitational-wave channel, the problem of distinguishing between astrophysical manifestations of black holes (BHs) and hypothetical WHs is becoming relevant. WHs, along with BHs, naturally arise within general relativity (GR). Observational searches for WHs require knowledge of the characteristic trajectories of bodies in its vicinity, including the trajectories entering its throat. Equations of motion of a test particle in the WH metric are derived, and the most interesting properties of these motions are considered. A general equation of geodesics in the WH metric is derived, and some properties of these geodesics are considered. The exact solution for circular orbits of test particles around a WH, as well as an approximate analytical solution of the geodesic equations, is analyzed. The shift of the pericenter of the orbit of a test particle in the WH field is considered, and possible observational consequences are discussed. Examples of test particle trajectories near a WH are presented that are obtained by numerical simulation.

Appendices

APPENDIX

Simulation of Finite Trajectories

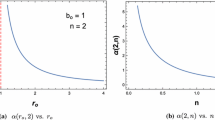
Consider the shape of trajectories for various values of the orbit parameters $\epsilon$ and h or e and p (see (26) and (27)).

The trajectories have the simplest shape when

$$p \geqslant {{r}_{0}}.$$

In this case, a trajectory lies completely in one fold of the space, touching the throat of the WH at a single point; the case when the parameter p = r₀ is illustrated in Fig. 1. In the finite case, the trajectories have the shape of a relativistic ellipse; in other words, they have the shape of an almost elliptical trajectory with a shift of the pericenter of the orbit.

Fig. 1.

The geodesic starts at the green dot, reaches the WH throat, passes to the second fold of the space (the second universe), and ends at the black dot. For such a trajectory, the angular momentum is h = 0; i.e., the test particle moves only along the radius. The total energy is $\epsilon$ ≈ 0.949, and the minimum distance from the center of the WH is r_min = r₀. The trajectory in the first universe is superimposed on the trajectory in the second universe; therefore, in the r–ϕ projection, the two parts of the trajectory merge.

Let us give several examples of finite trajectories near a WH (Figs. 2–7). All the pictures are drawn in the coordinates r and ϕ, except for Fig. 4, which presents a qualitative view of the trajectory when the line of sight lies in the plane of the WH throat. The trajectory parameters are given in units of the gravitational radius (r_g) of the WH. The maximum distance (apocenter) of the trajectory from the WH center is r_max = 10r_g for all trajectories. The black lines denote the BH horizon, and the purple lines show the position of the WH throat. The green dot is the starting point of the geodesic, and the black dot is the endpoint of the geodesic. The green dot corresponds to ϕ = 0.

Fig. 2.

The geodesic starts at the green dot and moves in the first universe. This section of the geodesic is indicated by the red line. It reaches the throat and passes through it. Then the geodesic moves in the second universe, which is indicated by the blue line, returns to the throat, passes through it again, and returns to the first universe (red line). The geodesic stops at the black point. The angular momentum is h = 0.1r_g, and the total energy is $\epsilon$ ≈ 0.949. The minimum distance from the WH center is r_min = r₀.

Fig. 3.

This trajectory is of most interest. It starts, as before, at the green point, reaches the throat, enters the second universe, makes half a revolution, returns to the throat, passes through it, and ends at the black point. A small gap in the trajectory corresponds to the shift of the apocenter. The angular momentum is h = r_g, the total energy is $\epsilon$ ≈ 0.953, and the minimum distance from the WH center is r_min = r₀.

Fig. 4.

The trajectory shown in Fig. 3 is represented in an artificial virtual projection that graphically separates the upper and lower folds of the space.

Fig. 5.

A trajectory similar to those shown in Figs. 1 and 2. The angular momentum is h = 1.9r_g, the total energy is $\epsilon$ ≈ 0.966, and the minimum distance from the WH center is r_min = r₀.

Fig. 6.

A trajectory similar to those shown in Figs. 1 and 2. The angular momentum is h = 2r_g, the total energy is $\epsilon$ ≈ 0.973, and the minimum distance from the WH center is r_min = r₀.

Fig. 7.

A trajectory similar to those shown in Figs. 1 and 2. The angular momentum is h = 2.3r_g, the total energy is $\epsilon$ ≈ 0.973, and the minimum distance from the WH center is r_min = r₀.