Magnetocaloric Effect in Nanosystems Based on Ferromagnets with Different Curie Temperatures

Abstract

The magnetocaloric effect in nanosystems based on exchange-coupled ferromagnets with different Curie temperatures is calculated within the mean-field theory. Good agreement between the results of the mean-field theory and the Landau theory, valid near the critical phase transition temperature, is demonstrated for a flat-layered Fe/Gd/Fe structure. We show that a high magnetic cooling efficiency in this system is attainable in principle and prove the validity of the Maxwell relation, enabling an experimental verification of the predictions made. The theory developed for flat-layered structures is generalized to a granular medium.

1 INTRODUCTION

The magnetocaloric effect consists in a reversible change in the temperature of a magnetic material under its adiabatic magnetization or demagnetization. The effect was discovered more than a hundred years ago [1] and still arouses considerable interest [2]. This interest stems from the possibility of creating a “magnetic” refrigerator in which a magnetic material with a strong magnetocaloric effect will act as a refrigerant. Despite the progress in creating such materials (see, e.g., [3]), the problem of magnetic cooling at room temperature remains, in our view, unsolved. The fundamental difficulty for homogeneous magnetocaloric materials lies in the necessity of applying a very strong (1–10 T) magnetic field to achieve a noticeable (1 K) change in temperature. Thus, the record magnetic cooling efficiencies to date are 10 K/T [2].

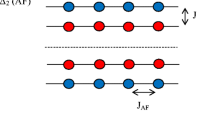
A new approach to the problem of reducing the magnetic field strength and increasing the magnetic cooling efficiency is proposed in [4]. Multilayered structures consisting of films with different Curie temperatures are proposed to be used as a magnetic material. A “strong” ferromagnet with a higher Curie temperature Θ will then magnetize a “weak” ferromagnet (T_C < Θ) due to the magnetic proximity effect [5] even if the latter is in the paramagnetic phase, i.e., T_C < T. Moreover, for a multilayered structure in which a weak ferromagnet is sandwiched between layers of a strong ferromagnet, the demagnetization (magnetization) of the spacer depends on the mutual orientation of the magnetic moments at the edges that can be controlled by applying a magnetic field (Fig. 1). For a parallel orientation of the edge magnetizations, the interlayer has a greater (on average, over the thickness) magnetization than that for an antiparallel orientation. The magnetic field strength needed to switch the mutual orientation of the magnetizations is ~10^–2 T (see Fig. 2b below). The efficiency of this method for changing the magnetization (entropy) of a weak ferromagnet increases with decreasing thickness and can reach huge values. The effect is an “exchange” one in nature and an increase in the cooling efficiency is achieved through a reconfiguration of the exchange fields at the film boundaries. The experiments that confirmed the possibility of amplifying the magnetocaloric effect in multilayered strong/weak ferromagnet structures were carried out in [6–9]. However, the magnitude of the effect is lower than the values predicted by the theory by tens of times.

Fig. 1.

Schematic view of a three-layer structure with an AFM exchange at the interfaces for parallel (a) and antiparallel (b) orientations of the side layer magnetizations: I is a ferromagnetic layer; II is a paramagnetic layer; M_f is the magnetization of the free ferromagnetic layer; M_p is the magnetization of the “pinned” ferromagnetic layer, m_↑↑(z) and m_↑↓(z) are the magnetizations of the spacer.

Fig. 2.

(In color online) (a) Schematic view of a model layered Fe/Gd/Fe structure and the magnetization distributions over the atomic layers of the Gd interlayer. The magnetization curves (b) and the field dependences of the entropy (c) derived in the mean-field model for Fe(35 Å)/Gd(d)/Fe(35 Å) systems with interlayer thicknesses d = 30 Å (1, 2) and 50 Å (3, 4) are shown. The solid and dashed curves correspond to temperatures T = T_C = 200 and 210 K, respectively. Panel (d) demonstrates the fulfilment of the Maxwell relation (dS/dH)_T = (dM/dT)_H.

The central point of the approach being developed by us is the assumption about an exchange interaction at the boundary of the ferromagnets. The magnitude of this interaction is not known in advance and a careful experimental data processing is required, which will allow this exchange constant to be determined. To make a comparison, we need to have a quantitative theory of the magnetocaloric effect in such inhomogeneous systems and this paper is devoted to its construction. As a starting point, we use the mean-field approximation well proven in analyzing the static and dynamic magnetic properties of multilayered Fe/Gd structures [10]. In Section 2 of this paper we present our calculations of the magnetization distribution, entropy, and magnetocaloric effect in three-layer Fe/Gd/Fe structures within the mean-field approximation. In Section 3.1 we use the Landau theory of phase transitions, valid at temperatures close to T_C for which the magnetocaloric effect is maximal, to calculate the system’s thermodynamic characteristics. We make a comparison with the results of Section 2. In addition, we derive the conditions for the applicability of our approximate analytical solutions for parallel and antiparallel orientations of the magnetic moments of the ferromagnetic edges. In Section 3.2 the approximate solutions obtained are used to estimate the magnetocaloric effect in a system of ferromagnetic granules placed in a paramagnetic matrix. In Conclusions we discuss the possibilities for amplifying the magnetocaloric effect in ferromagnetic nanosystems.

2 A FLAT-LAYERED STRUCTURE IN THE MEAN-FIELD MODEL

The idea of applying the mean-field method to calculate the magnetic characteristics of layered structures was proposed by Camley in [11–13]. The studies were aimed primarily at elucidating the magnetism of systems based transition (TM) and rare-earth (REM) ferromagnetic (FM) metals such as Fe/Gd. A characteristic feature of these systems is the possibility of a highly nonuniform magnetization distribution inside the REM layers due to competition between several factors: a strong antiferromagnetic (AFM) exchange at the TM/REM interface, a relatively low Curie temperature, and a small exchange stiffness of the REM layers. The proposed approach allowed the key features of the behavior of layered TM/REM structures to be described qualitatively and even certain quantitative agreement with the experiment to be reached [14–17]. Below we use the mean-field method to estimate the magnitude of the magnetocaloric effect in multilayered structures using a Fe/Gd system, whose magnetic properties have been studied quite well [18, 19], as an example.

Consider a three-layer Fe(d_Fe)/Gd(d)/Fe(d_Fe) structure with layer thicknesses d and d_Fe of the order of a few nanometers at temperatures T near the Curie temperature T_C of gadolinium. Note that in thin Gd layers T_C can be noticeably suppressed compared to its bulk value of 293 K. For example, T_C ≈ 200 K was obtained in [10, 20, 21] for d ≈ 50 Å. In the conditions under consideration the Fe layers can be assumed to be homogeneously magnetized up to saturation. In this case, a large AFM exchange at the Fe–Gd boundaries (an exchange constant J ≈ –200 K per Gd atom [10, 20]) leads to a strong magnetic polarization of near-boundary Gd atoms. At the same time, a significantly weaker FM interaction of Gd atoms inside the interlayer (J_Gd ≈ 13 K [20]) leads to rapid (on scales ~20 Å) decay of the magnetic order away from the Fe‒Gd boundary due to strong thermal fluctuations near T_C. Thus, a highly nonuniform profile of the magnetization distribution with maxima near the Fe‒Gd boundaries and a minimum deep in the layer is formed inside the Gd interlayer. The existence of such a magnetization distribution in Gd layers was experimentally proven while investigating Fe/Gd superlattices by the resonant X-ray magnetic scattering method (see, e.g., [15, 20]).

To theoretically model this distribution by the mean-field method, we consider a partition of the Gd interlayer into “atomic” sublayers of thickness a = 3 Å and with magnetization m_i, where i is the layer number (Fig. 2a). The chosen elementary layer thickness a = 3 Å roughly corresponds to the distance between the atomic (0001) planes of a hexagonal close-packed (HCP) Gd crystal. The effective field H_i acting on the atoms of the ith layer is a sum of the external field H and the exchange “molecular” fields from the nearby atoms of the same layer (γ_iim_i) and the neighboring layers (γ_{ii ± 1}m_{i ± 1}):

$${{{\mathbf{H}}}_{i}} = {\mathbf{H}} + {{\gamma }_{{ii}}}{{{\mathbf{m}}}_{i}} + {{\gamma }_{{ii - 1}}}{{{\mathbf{m}}}_{{i - 1}}} + {{\gamma }_{{ii + 1}}}{{{\mathbf{m}}}_{{i + 1}}},$$

(1)

where γ_ij are the mean-field constants. Note that in the homogeneous case m_i = m and we obtain the standard expression for the Weiss molecular field H + γm, where γ = γ_ii + γ_{ii – 1} + γ_{ii + 1}.

To characterize the distribution of exchange interactions between a Gd atom in a given layer and atoms in the same layer and the neighboring layers, it is convenient to introduce a parameter ζ = γ_{ii ± 1}/γ, which may be considered as the ratio of the number of nearest atoms in the neighboring layers to their total number. For example, for a HCP gadolinium single crystal ζ = 1/4 [15], while in the case of an amorphous structure this parameter can slightly differ [10]. Taking into account this definition of ζ, the expression for the effective field inside Gd can be rewritten as

$${{{\mathbf{H}}}_{i}} = {\mathbf{H}} + \gamma {{{\mathbf{m}}}_{i}} + \gamma \zeta {{a}^{2}}\frac{{{{{\mathbf{m}}}_{{i + 1}}} - 2{{{\mathbf{m}}}_{i}} + {{{\mathbf{m}}}_{{i - 1}}}}}{{{{a}^{2}}}}.$$

(2)

It can be seen from this formula that the first two terms represent the case of a homogeneous magnetization, while the third term specifies the “gradient” contribution to the effective field. This term in the continuum limit is proportional to the second derivative of the magnetization d²m/dz² along the normal to the film z and, thus, gives a relation between the mean-field constants and the exchange stiffness of the material, D = γζa².

It is also necessary to determine the effective fields acting at the Fe–Gd interfaces. The surface energy density of the exchange AFM interaction at the Fe–Gd interface is written as

$${{E}_{{{\text{ex}}}}} = J\frac{{{{{\mathbf{m}}}_{{{\text{Fe}}}}} \cdot {{{\mathbf{m}}}_{{{\text{Gd}}}}}}}{{{{m}_{{{\text{Fe}}}}}{{m}_{s}}}},$$

(3)

where J is the exchange constant, m_Fe and m_Gd are the Fe and near-boundary Gd layer magnetization vectors, m_Fe and m_s are the Fe and Gd saturation magnetizations. Hence we obtain the effective field acting from the Fe layer on the near-boundary Gd layer,

$${{{\mathbf{H}}}_{{{\text{Gd}}}}} = - \frac{{J{{{\mathbf{m}}}_{{{\text{Fe}}}}}}}{{{{m}_{{{\text{Fe}}}}}{{m}_{s}}a}},$$

and the effective field acting from Gd on the Fe layer,

$${{{\mathbf{H}}}_{{{\text{Fe}}}}} = - \frac{{J{{{\mathbf{m}}}_{{{\text{Gd}}}}}}}{{{{m}_{{{\text{Fe}}}}}{{m}_{s}}{{d}_{{{\text{Fe}}}}}}}.$$

The equilibrium direction of the magnetization in each of the atomic Gd layers is defined by the condition

$${{{\mathbf{m}}}_{i}}||{{{\mathbf{H}}}_{i}},$$

(4)

while its absolute value is

$${{m}_{i}} = {{m}_{s}}{{B}_{j}}\left( {\frac{{\mu {{H}_{i}}}}{{{{k}_{{\text{B}}}}T}}} \right),$$

(5)

where B_j is the Brillouin function for the total angular momentum j, μ is the magnetic moment per Gd atom, and k_B is the Boltzmann constant. The magnetization direction for the Fe layers can be specified to be fixed (in the case of a “pinned” layer) or be determined from a condition similar to (4): m_Fe || (H + H_Fe) (in the case of a “free” layer). The resulting equilibrium distribution of the magnitude and direction of the magnetization over the structure layers is calculated numerically at given H and T.

The derived magnetization distribution allows the total magnetic moment M and the entropy S per unit volume of the system to be calculated. Obviously, the total magnetization of the system is defined by the formula

$${\mathbf{M}} = \frac{{{{d}_{{{\text{Fe}}}}}({\mathbf{m}}_{{{\text{Fe}}}}^{{(1)}} + {\mathbf{m}}_{{{\text{Fe}}}}^{{(2)}}) + a\sum\limits_i^{} {{{{\mathbf{m}}}_{i}}} }}{{d + 2{{d}_{{{\text{Fe}}}}}}}$$

(6)

(hence, in particular, we can determine the component of the magnetization M along the magnetic field). To calculate the entropy S, we will take into account the fact that the Fe layers do not contribute to S and that the entropy per unit volume of the ith Gd layer in the mean-field model is [22, 23]

$${{s}_{i}} = \frac{{{{m}_{s}}}}{\mu }{{k}_{{\text{B}}}}\left[ {\ln \left( {\frac{{\sinh \left( {\frac{{2j + 1}}{{2j}}\frac{{\mu {{H}_{i}}}}{{{{k}_{{\text{B}}}}T}}} \right)}}{{\sinh \left( {\frac{1}{{2j}}\frac{{\mu {{H}_{i}}}}{{{{k}_{{\text{B}}}}T}}} \right)}}} \right) - \frac{{{{m}_{i}}}}{{{{m}_{s}}}}\frac{{\mu {{H}_{i}}}}{{{{k}_{{\text{B}}}}T}}} \right].$$

(7)

Thus, the mean entropy of the Gd layer per unit volume is

$$s = \frac{a}{d}\sum\limits_i^{} {{{s}_{i}},} $$

(8)

and the total entropy of the entire Fe/Gd/Fe system per unit volume is

$$S = \frac{a}{{d + 2{{d}_{{{\text{Fe}}}}}}}\sum\limits_i^{} {{{s}_{i}}.} $$

(9)

Figure 2 shows examples of calculating the magnetization curves and the field dependences of the entropy for a Fe/Gd/Fe system in the case where the magnetization of the first Fe layer is fixed in a direction opposite to the field and the second Fe layer is free. In this situation, owing to the interaction through the Gd interlayer, a parallel orientation of the magnetic moments of the Fe layers turns out to be favorable in zero field. However, when applying a certain magnetic field, the free Fe layer is reoriented, leading to an antiparallel orientation of the Fe layers. In this case, the shape of the magnetization profile inside the Gd interlayer changes significantly (see Fig. 3 below). For our calculations we used the parameters derived in [10] for a [Fe(35 Å)/Gd(50 Å)]₁₂ superlattice: m_Fe = 1270 G, m_s = 1150 G, J = 40 erg cm^–2,  j = 7/2, μ = 7μ_B, γ = 870, ζ = 0.33, and T_C = 200 K; for both iron layers d_Fe = 35 Å. Our calculations were performed for d = 30 and 50 Å at T = T_C = 200 and 210 K.

Fig. 3.

Dependences m_↑↑(z) at T = T_C (a), T – T_C = 10 K (b) and m_↑↓(z) at T = T_C (c), T – T_C = 10 K (d) for d = (1) 3, (2) 5, (3) 7, and (4) 15 nm in a Fe/Gd/Fe structure. The solid lines indicate the exact solutions (16) and (17), the dashed lines indicate the approximate solutions (21) and (22), the circles represent our calculations based on the mean-field theory.

The temperature dependences of the change in entropy per unit interlayer volume when the mutual orientation of the Fe layer magnetizations is switched are presented in Section 3.1 (see Fig. 5 below). Interestingly, the Maxwell relation (dS/dH)_T = (dM/dT)_H, on which numerous experiments on measuring the magnetocaloric potential are based (see Fig. 2d), is fulfilled in the problem under consideration. This fact is not trivial. Indeed, the fulfilment of the Maxwell relation for homogeneous materials is obvious. In inhomogeneous systems, to which the three-layer structure considered belongs, the magnetization is a function of coordinates and, therefore, cannot directly enter into the Maxwell relation. However, as we showed, this relation is fulfilled for the magnetization (6) and entropy (9) referring to the entire system.

3 THE LANDAU THEORY FOR SECOND-ORDER PHASE TRANSITIONS

Previously, we applied the Landau theory for phase transitions to a flat-layered Co₉₀Fe₁₀/Ni_xCu_{100 – x}/ Co₄₀Fe₄₀B₂₀ (x ≈ 70 at %) structure [9]. In this paper we make calculations for a Fe/Gd/Fe structure and obtain considerably simpler approximate solutions to compare them with the exact ones and to use this approach for the description of a granular medium (see Section 3.2).

3.1 A Flat-Layered Structure

Within the Landau theory for phase transitions the free energy F per unit area can be written as a functional [9]:

$$\begin{gathered} F[m] = \int\limits_{ - d/2}^{d/2} {\left( {\frac{{l_{0}^{2}}}{2}{{{\left( {\frac{{dm}}{{dz}}} \right)}}^{2}} + \frac{{\alpha \tau }}{2}{{m}^{2}} + \frac{\beta }{{4m_{s}^{2}}}{{m}^{4}}} \right)} dz \\ + \frac{{{{l}_{J}}}}{2}{{(m - \sigma {{m}_{s}})}^{2}}{{{\text{|}}}_{{z = - \frac{d}{2}}}} + \frac{{{{l}_{J}}}}{2}{{(m - {{m}_{s}})}^{2}}{{{\text{|}}}_{{z = \frac{d}{2}}}}. \\ \end{gathered} $$

(10)

Here, α, β, l₀, and l_J are phenomenological constants, τ = (T – T_C)/T_C, σ = 1 for a parallel orientation of the Fe layer magnetizations (|↑↑|), and σ = –1 for an antiparallel one (| ↑↓|). The last two terms in Eq. (10) describe the exchange interaction of the interlayer with the ferromagnetic edges (see Fig. 1). Since the external magnetic field is weak, we neglect the term –H ⋅ m under the integral sign in Eq. (10). The equation corresponding to the extremum of functional (10) and the boundary conditions are

$$\frac{{{{d}^{2}}m}}{{d{{z}^{2}}}} - \frac{1}{{{{l}^{2}}}}m - \frac{\beta }{{l_{0}^{2}m_{s}^{2}}}{{m}^{3}} = 0,$$

(11)

$${{\left. {\frac{{dm}}{{dz}}} \right|}_{{z = \frac{d}{2}}}} = - {{\left. {\frac{{{{l}_{J}}}}{{l_{0}^{2}}}(m - {{m}_{s}})} \right|}_{{z = \frac{d}{2}}}},$$

(12)

$${{\left. {\frac{{dm}}{{dz}}} \right|}_{{z = - \frac{d}{2}}}} = {{\left. {\frac{{{{l}_{J}}}}{{l_{0}^{2}}}(m - \sigma {{m}_{s}})} \right|}_{{z = - \frac{d}{2}}}},$$

(13)

where we introduce the notation l = l₀/$\sqrt {\alpha \tau }$. The Jacobi elliptic functions dn and sn satisfy Eq. (11). These functions have been well studied [24]. We will seek solutions in the form

$${{m}_{{ \uparrow \uparrow }}} = {{a}_{{ \uparrow \uparrow }}}{{m}_{s}}{\text{dn}}\left( {{{c}_{{ \uparrow \uparrow }}}\left( {\frac{{z + z_{0}^{{ \uparrow \uparrow }}}}{{{{l}_{0}}}}} \right),{{k}_{{ \uparrow \uparrow }}}} \right),$$

(14)

$${{m}_{{ \uparrow \downarrow }}} = \frac{{\sqrt {{{a}_{{ \uparrow \downarrow }}}} {{m}_{s}}}}{{{{c}_{{ \uparrow \downarrow }}}}}{\text{sn}}\left( {{{c}_{{ \uparrow \downarrow }}}\left( {\frac{{z + z_{0}^{{ \uparrow \downarrow }}}}{{{{l}_{0}}}}} \right),{{k}_{{ \uparrow \downarrow }}}} \right).$$

(15)

Here, a_{↑↑(↑↓)}, c_{↑↑(↑↓)}, and $z_{0}^{{ \uparrow \uparrow ( \uparrow \downarrow )}}$ are constants, k_↑↑ and k_↑↓ are the elliptic moduli. Since

$${{a}_{{ \uparrow \uparrow }}}{{m}_{s}} = {{m}_{{ \uparrow \uparrow }}}{{{\text{|}}}_{{z = 0}}},\quad {{a}_{{ \uparrow \downarrow }}}m_{s}^{2} = l_{0}^{2}{{(dm{\text{/}}dz{{{\text{|}}}_{{z = 0}}})}^{2}},$$

the constants a_↑↑ and a_↑↓ are real numbers (if $z_{0}^{{ \uparrow \uparrow ( \uparrow \downarrow )}}$ = 0). After the substitution of m_↑↑ and m_↑↓ into Eq. (11), we can express all of the unknown constants via a_{↑↑(↑↓)}. As a result, we obtain

$${{m}_{{ \uparrow \uparrow }}} = {{a}_{{ \uparrow \uparrow }}}{{m}_{s}}{\text{dn}}\left( {i{{a}_{{ \uparrow \uparrow }}}\sqrt {\frac{\beta }{2}} \frac{z}{{{{l}_{0}}}},\sqrt {2\left( {1 + \frac{{\alpha \tau }}{{\beta a_{{ \uparrow \uparrow }}^{2}}}} \right)} } \right),$$

(16)

$$\begin{gathered} {{m}_{{ \uparrow \downarrow }}} = - i{{\left( {\frac{{2{{a}_{{ \uparrow \downarrow }}}}}{\beta }} \right)}^{{1/4}}}{{\eta }_{ \pm }}{{m}_{s}} \\ \times \,{\text{sn}}\left( {i{{{\left( {\frac{{\beta {{a}_{{ \uparrow \downarrow }}}}}{2}} \right)}}^{{1/4}}}\frac{z}{{{{\eta }_{ \pm }}{{l}_{0}}}},\sqrt {2{{\tau }_{0}}\eta _{ \pm }^{2} - 1} } \right), \\ \end{gathered} $$

(17)

where i is the imaginary unit and we introduce the notation

$${{\eta }_{ \pm }} = {{({{\tau }_{0}} \pm {{(\tau _{0}^{2} - 1)}^{{1/2}}})}^{{1/2}}},\quad {{\tau }_{0}} = \alpha \tau {\text{/}}{{(2\beta {{a}_{{ \uparrow \downarrow }}})}^{{1/2}}}.$$

Here, we have taken into account the fact that the constants $z_{0}^{{ \uparrow \uparrow ( \uparrow \downarrow )}}$ may be chosen to be zero. The constants a_↑↑ and a_↑↓ are determined numerically from the boundary conditions. To establish which of the constants η_± should be chosen, let us consider the limiting case of an infinitely thick interlayer (a_↑↓ → 0). In this limit, using the definition of the function y = sn(u, k) [25],

$$u = \int\limits_0^y {\frac{{dx}}{{\sqrt {(1 - {{x}^{2}})(1 - {{k}^{2}}{{x}^{2}})} }}} $$

(18)

and Eqs. (15) and (17), for η₊ we will obtain

$$m = - \sqrt {\frac{{2\alpha \tau }}{\beta }} \frac{{{{m}_{s}}}}{{\sinh \left( {\frac{{\tilde {z} + {{{\tilde {z}}}_{0}}}}{l}} \right)}},$$

(19)

where $\tilde {z}$ = z + d/2 and the constant ${{\tilde {z}}_{0}}$ = $z_{0}^{{ \uparrow \downarrow }}$ – d/2 – lcoth^–1 (1) must be a finite positive number to be determined from the boundary conditions. Equation (19) corresponds to the interlayer magnetization induced only by one ferromagnetic layer located at $\tilde {z}$ < 0. Thus, the magnetization (17) with η₊ gives the correct limiting expression. For our subsequent calculations we will use Eq. (17) with η₊. Note that from the magnetization (16) we can also come to the limit (19), but, of course, with the opposite sign.

Let us now obtain simpler, but approximate solutions of Eq. (11). In the case of a parallel orientation of the side layer magnetizations, we will represent the interlayer magnetization m_↑↑ as

$${{m}_{{ \uparrow \uparrow }}}(z) = {{m}_{0}} + \xi (z),\quad \xi (0) = 0,\quad \xi \ll {{m}_{0}}.$$

Here, m₀ is a constant and ξ(z) is a function of coordinate z. In the linear approximation in ξ Eq. (11) will take the form

$$\frac{{{{d}^{2}}\xi }}{{d{{z}^{2}}}} - {{\kappa }^{2}}(\xi + {{\xi }_{0}}) = 0,$$

(20)

where

$${{\kappa }^{2}} = \frac{1}{{l_{0}^{2}}}\left( {\alpha \tau + \frac{{3\beta m_{0}^{2}}}{{m_{s}^{2}}}} \right),\quad {{\xi }_{0}} = \frac{{{{m}_{0}}(\alpha \tau m_{s}^{2} + \beta m_{0}^{2})}}{{\alpha \tau m_{s}^{2} + 3\beta m_{0}^{2}}}.$$

The solution of this equation is the function

$$\xi = {{\xi }_{0}}(\cosh \kappa z - 1).$$

(21)

The boundary conditions (12) and (13) allow m₀ to be determined numerically. If the magnetizations of the ferromagnetic edges are antiparallel, then the nonlinear term in Eq. (11) may be neglected by assuming β$m_{{ \uparrow \downarrow }}^{2}$/ατ$m_{s}^{2}$ ≪ 1. Given the boundary conditions, we will obtain

$${{m}_{{ \uparrow \downarrow }}} = \frac{{l{{l}_{J}}{{m}_{s}}}}{{l_{0}^{2}\cosh \frac{d}{{2l}} + l{{l}_{J}}\sinh \frac{d}{{2l}}}}\sinh \frac{z}{l}.$$

(22)

The approximate solution (22) can also be obtained from Eq. (17) by formally letting β approach zero. For this purpose, let us express sn(u, k) via dn(u, k) according to the formula dn²(u, k) = 1 – k²sn²(u, k). Next, using the definition of the function y = dn(u, k) [25],

$$u = \int\limits_1^y {\frac{{dx}}{{\sqrt {(1 - {{x}^{2}})({{x}^{2}} - 1 + {{k}^{2}})} }}} ,$$

(23)

we will arrive at Eq. (22). In this case, $z_{0}^{{ \uparrow \downarrow }}$ = 0. Note also that the approximate and exact solutions (21) and (16) have identical expansions into power series (at least to the second-order terms inclusive).

The phenomenological constants α and β have been derived by expressing them via the parameters of the mean-field theory. For a separate Gd film Eq. (5), where the homogeneous magnetization m should be taken instead of m_i, is valid. By expanding B_j(x) into a series at x ≪ 1, we can bring Eq. (5) to the equation ατm + βm³/m_s = 0, which in the Landau theory corresponds to the equation that the magnetization of a separate magnet film satisfies in the absence of an external magnetic field. For the constants α and β we then obtain the following formulas:

$$\alpha = \gamma = \frac{{{{T}_{C}}}}{{{{c}_{C}}}} \approx 870,$$

(24)

$$\beta = \frac{3}{{10}}\gamma \left( {1 + {{{\left( {\frac{j}{{j + 1}}} \right)}}^{2}}} \right) \approx 420,$$

(25)

where c_C is the Curie constant. The constant l₀ can be estimated as l₀ = (γζ)^1/2a ≈ 5.1 nm. We estimate the constant l_J, which characterizes the interaction of the Gd interlayer with the Fe layers, as l_J ~ J/m_sm_Fe ≈ 280 nm.

Figure 3 presents the dependences m_↑↑(z) and m_↑↓(z) for a Fe/Gd/Fe structure at various interlayer thicknesses and temperatures. As would be expected, there is satisfactory agreement between the theories. However, the discrepancies increase as the interlayer magnetization grows, because the absence of the discarded higher-order terms in the free energy (10) begins to have an effect. Our calculations also show that the approximate solutions (21) and (22) for a multilayered Fe/Gd/Fe structure give a fairly large error. Indeed, it can be seen from Fig. 3c that the dependences m_↑↓(z) are significantly nonlinear, while the approximate solution (22) at T = T_C is linear in z. An increase in the correlation length l₀ leads to better results. For example, for a multilayered Co₉₀Fe₁₀/Ni_xCu_{100 – x}/Co₄₀Fe₄₀B₂₀ structure (α = 1300, β = 750, l₀ = 25 nm, l_J = 30 nm, m_s = 180 erg G^–1 cm^–3, T_C = 330 K) [9] the approximate formulas describe correctly the magnetization distribution (Fig. 4).

Fig. 4.

(In color online) Dependences m_↑↑(z) at T = T_C (a), T – T_C = 10 K (b) and m_↑↓(z) at T = T_C (c), T – T_C = 10 K (d) for d = (1) 3, (2) 5, (3) 7, and (4) 15 nm in a Co₉₀Fe₁₀/Ni_xCu_{100 – x}/Co₄₀Fe₄₀B₂₀ structure. The solid lines indicate the exact solutions (16) and (17), the dashed lines indicate the approximate solutions (21) and (22).

Fig. 5.

(In color online) Dependences Δs(T) for d = (1) 3, (2) 5, (3) 7, and (4) 15 nm. The solid lines and circles represent our calculations based on the Landau and mean-field theories, respectively. The presented dependences correspond to the change in magnetic field whereby the mutual orientation of the ferromagnetic edge magnetizations is switched (H ∈ (0, H₀), H₀ ≈ 100 Oe).

Let us now calculate the entropy per unit interlayer volume, s = ‒(∂F/∂T)/∂. The following formula is valid irrespective of the orientation of the ferromagnetic edge magnetizations:

$$s = - \frac{\alpha }{{2{{T}_{C}}}}\frac{1}{d}\int\limits_{ - d/2}^{d/2} {{{m}^{2}}dz = - \frac{{\alpha \overline {{{m}^{2}}} }}{{2{{T}_{C}}}}.} $$

(26)

It can be derived by differentiating the free energy (10) using Eqs. (11)–(13). Here, $\overline {{{m}^{2}}}$ is the mean square of the interlayer magnetization. Note that Eq. (26) can also be derived from the relation between the entropy s, internal, U, and free, F, energies: F = U – Ts. Our subsequent calculations of the entropy for parallel and antiparallel orientations of the ferromagnetic edge magnetizations lead to the following results:

$${{s}_{{ \uparrow \uparrow }}} = - \frac{{\alpha {{l}_{0}}a_{{ \uparrow \uparrow }}^{2}m_{s}^{2}}}{{{{T}_{C}}{{c}_{{ \uparrow \uparrow }}}d}}{\text{E}}\left( {{\text{am}}\left( {\frac{{{{c}_{{ \uparrow \uparrow }}}d}}{{2{{l}_{0}}}},{{k}_{{ \uparrow \uparrow }}}} \right),{{k}_{{ \uparrow \uparrow }}}} \right),$$

(27)

$$\begin{gathered} {{s}_{{ \uparrow \downarrow }}} = - \frac{{\alpha {{a}_{{ \uparrow \downarrow }}}m_{s}^{2}}}{{2{{T}_{C}}c_{{ \uparrow \downarrow }}^{2}k_{{ \uparrow \downarrow }}^{2}}} \\ \times \left( {1 - \frac{{2{{l}_{0}}}}{{{{c}_{{ \uparrow \downarrow }}}d}}{\text{E}}\left( {{\text{am}}\left( {\frac{{{{c}_{{ \uparrow \downarrow }}}d}}{{2{{l}_{0}}}},{{k}_{{ \uparrow \downarrow }}}} \right),{{k}_{{ \uparrow \downarrow }}}} \right)} \right), \\ \end{gathered} $$

(28)

where E(u, k) and am(U, k) are, respectively, an elliptic integral of the second kind and the amplitude of an elliptic integral of the first kind. In the limit of a large exchange (l_J → ∞) at the interlayer boundaries, from Eqs. (27) and (28) at T ~ T_C we derive

$${{s}_{{ \uparrow \uparrow }}} \approx - \frac{{\alpha m_{s}^{2}}}{{2{{T}_{C}}}},\quad {{s}_{{ \uparrow \downarrow }}} \approx 0.$$

(29)

The derived formulas characterize the maximum possible magnetocaloric potential for a given interlayer material, Gd:

$$\Delta {{s}_{{\max }}} = \alpha m_{s}^{2}{\text{/}}2{{T}_{C}} \approx 3 \times {{10}^{6}}\,\,{\text{erg}}\,\,{{{\text{K}}}^{{ - 1}}}\,\,{\text{c}}{{{\text{m}}}^{{ - 3}}}.$$

Note that the estimates of Δs_max can be significantly inaccurate, because the theory being outlined is poorly applicable at great magnetizations m. The solid lines in Fig. 5 indicate the dependences of the magnetocaloric potential Δ_s(T) = s_↑↓(T) – s_↑↑(T) at various interlayer thicknesses calculated based on Eqs. (27) and (28) for Fe/Gd/Fe. The circles represent the corresponding calculations within the mean-field theory based on Eq. (7). It can be seen that the theories agree well between themselves.

Given the magnetocaloric potential, we can estimate the adiabatic change in temperature ΔT for the entire structure when the mutual orientation of the side layer magnetizations changes from parallel to antiparallel (see, e.g., [26]):

$$\Delta T = {{T}_{f}} - T = - \frac{{Td}}{{(d + 2{{d}_{{{\text{Fe}}}}})c}}\Delta s.$$

(30)

Here, T_f is the final temperature, c is the heat capacity per unit volume of the system that, in general, includes the contributions from the lattice and magnetic subsystems. Let us show that the contribution of the magnetic subsystem may be neglected, so that, according to the Dulong–Petit law, c ≈ 1.2 × 10⁷ erg K^–1 cm^–3. Using Eqs. (27) and (28), we will find the magnetic contributions to the heat capacity in a constant field:

$${{c}_{{ \uparrow \uparrow ( \uparrow \downarrow )}}} = T{{\left( {\frac{{\partial {{s}_{{ \uparrow \uparrow ( \uparrow \downarrow )}}}}}{{\partial T}}} \right)}_{H}}.$$

(31)

Figure 6 shows the dependences c_{↑↑(↑↓)}(T) calculated numerically for Fe/Gd/Fe. It can be seen that even at T = T_C the magnetic contributions to the heat capacity c_{↑↑(↑↓)} are smaller than the contribution of the lattice subsystem by almost an order of magnitude. Let us now give our estimates of the adiabatic change in temperature for Fe/Gd/Fe (Fig. 7). Here we will not pay attention to the fact that in the immediate vicinity of the transition point the interlayer can pass to the FM phase as the temperature changes due to the application of an external magnetic field.

Fig. 6.

Dependences c_{↑↑(↑↓)}(T) for d = 3 (1), 5 (2), 7 (3), and 15 (4) nm.

Fig. 7.

Dependences ΔT(T) for d = (1) 3, (2) 5, (3) 7, and (4) 15 nm. The presented dependences correspond to the change in magnetic field whereby the mutual orientation of the ferromagnetic edge magnetizations is switched (H ∈ (0, H₀), H₀ ≈ 100 Oe).

Thus, we have managed to obtain the interlayer magnetization profiles and the magnetocaloric potentials within the two approaches. Both approaches agree well between themselves, despite the fact that at such large interlayer magnetizations the Landau theory, seemingly, should not be used. Our estimates of the change in the system’s temperature under adiabatic demagnetization near the Curie temperature for the interlayer thicknesses under consideration are 0.1–0.3 K. This is an order of magnitude smaller than ΔT ≈ 3 K for bulk Gd under its complete demagnetization beginning from H = 1 T [26]. At the same time, in the case of a Fe/Gd/Fe structure, switching the mutual orientation of the Fe layer magnetizations requires applying a magnetic field with a strength of only a few hundred oersted (see Fig. 2), which gives a gain by one or two orders of magnitude in applied field compared to bulk Gd. Thus, the magnetic cooling efficiency in the system under consideration can increase significantly.

3.2 A Granular Medium

Let us now study the magnetocaloric properties of a medium that is an amorphous matrix made of a weak ferromagnet containing granules made of a strong ferromagnet (Fig. 8). The latter are single crystals with a uniaxial magnetic anisotropy characterized by a constant K. The role of the granules is to magnetize the matrix through an exchange interaction, much as the ferromagnetic edges in a flat-layered structure magnetize the interlayer for a parallel orientation of their magnetizations. The system’s magnetic state can also be controlled by an external field.

Fig. 8.

Schematic view of granules made of a strong ferromagnet in a matrix made of a weak ferromagnet. The two-sided arrows indicate the easy magnetization axes. The dashed circumference indicates a cell of radius λ. The field H is directed along the z axis.

We will assume that all N granules differ from one another only by the directions of the easy magnetization axes and have a spherical shape with a volume V_g = (4/3)πR³. The system is placed in a uniform magnetic field H directed along the z axis. The free energy can then be written as

$$F[{\mathbf{m}}] = {{E}_{A}} + {{E}_{H}} + {{F}_{0}}[{\mathbf{m}}],$$

(32)

$$\begin{gathered} {{F}_{0}}[{\mathbf{m}}] = \int {\left( {\frac{{l_{0}^{2}}}{2}\sum\limits_{a = 1}^3 {{{{\left( {\frac{{\partial {\mathbf{m}}}}{{\partial {{x}_{a}}}}} \right)}}^{2}} + \frac{{\alpha \tau }}{2}{{{\mathbf{m}}}^{2}} + \frac{\beta }{{4m_{s}^{2}}}{{{\mathbf{m}}}^{4}}} } \right)d{{V}_{m}}} \\ + \frac{{{{l}_{J}}}}{2}\sum\limits_{i = 1}^N {\int {{{{({\mathbf{m}} - {{{\mathbf{m}}}_{{si}}})}}^{2}}d{{\sigma }_{i}},} } \\ \end{gathered} $$

(33)

$${{E}_{A}} = - \frac{{K{{V}_{g}}}}{{{{M}^{2}}}}\sum\limits_{i = 1}^N {{{{({{{\mathbf{M}}}_{i}} \cdot {{{\mathbf{n}}}_{i}})}}^{2}},} $$

(34)

$${{E}_{H}} = - {\mathbf{H}} \cdot \sum\limits_{i = 1}^N {{{{\mathbf{M}}}_{i}},} $$

(35)

where E_A and E_H are the anisotropy energy and the Zeeman energy of the granules, respectively; σ_i, n_i, and M_i (|M_i| = M) are the surface area, the unit vector directed along the easy magnetization axis, and the magnetization of the ith granule, respectively. The constant vector m_si is parallel or antiparallel to the vector M_i (depending on the sign of the exchange interaction at the granule boundary), |m_si| = m_s. The integration in the first term of Eq. (33) is over the matrix volume V_m. We again neglect the term –H ⋅ m under the integral sign of the first term in Eq. (33). Within our model the terms (34) and (35) do not depend on the temperature and, therefore, will not contribute to the entropy and the magnetocaloric potential of the system. The equation corresponding to the extremum of functional (33) and the boundary condition are

$$\Delta {\mathbf{m}} - \frac{1}{{{{l}^{2}}}}{\mathbf{m}} - \frac{\beta }{{l_{0}^{2}m_{s}^{2}}}{{{\mathbf{m}}}^{3}} = 0,$$

(36)

$$\sum\limits_{i = 1}^N {\int {\left( {({{{\mathbf{e}}}_{i}} \cdot \nabla ){\mathbf{m}} - \frac{{{{l}_{J}}}}{{l_{0}^{2}}}({\mathbf{m}} - {{{\mathbf{m}}}_{{si}}})} \right)} d{{\sigma }_{i}} = 0.} $$

(37)

Here, the direction of the unit vector e_i coincides with the direction of the outward normal to the surface of the ith granule. A further solution in general form is difficult due to the absence of spherical symmetry and the complex boundary condition (37) relating the matrix magnetization on the surfaces of all granules and the vectors m_si.

To go further, let us divide the system’s volume into Voronoi cells [27]. These are polyhedrons containing one granule inside. All points of the surfaces of these polyhedrons are closer to their inner granules than to all the remaining ones. We will assume that the matrix magnetization m_i inside the ith cell is induced mainly by the ith granule and the boundary conditions that will describe the interaction of the magnetizations of neighboring cells can be introduced at the cell boundaries. This will allow the separate boundary conditions on the granule surfaces for each cell to be derived from Eq. (37). However, these simplifications are not enough. We will replace the Voronoi cells by identical spheres of radius λ equal to half the mean distance between the centers of the nearest granules (Fig. 8). In view of the emerged spherical symmetry, Eq. (36) and the boundary condition (37) will take a simpler form:

$$\frac{{{{d}^{2}}{{{\mathbf{m}}}_{i}}}}{{dR_{i}^{2}}} + \frac{2}{{{{R}_{i}}}}\frac{{d{{{\mathbf{m}}}_{i}}}}{{d{{R}_{i}}}} - \frac{1}{{{{l}^{2}}}}{{{\mathbf{m}}}_{i}} - \frac{\beta }{{l_{0}^{2}m_{s}^{2}}}{\mathbf{m}}_{i}^{3} = 0,$$

(38)

$${{\left. {\frac{{d{{{\mathbf{m}}}_{i}}}}{{d{{R}_{i}}}}} \right|}_{{{{R}_{i}} = R}}} = \frac{{{{l}_{J}}}}{{l_{0}^{2}}}({{{\mathbf{m}}}_{i}} - {{{\mathbf{m}}}_{{si}}}){{{\text{|}}}_{{{{R}_{i}} = R}}},$$

(39)

where we introduce the notation R_i = |r – r_i|, r_i is the radius vector of the center of the ith granule. The condition at the cell boundary will depend on the mutual orientation of the granule magnetizations. If a magnetic field H > K/M, whose value is ~10 Oe [28], is applied to the system, then the granule magnetizations will be aligned with this field. The following condition at the cell boundary can then be introduced:

$${{\left. {\frac{{d{\mathbf{m}}_{i}^{{ \uparrow \uparrow }}}}{{d{{R}_{i}}}}} \right|}_{{{{R}_{i}} = \lambda }}} = 0.$$

(40)

We have designated the magnetization of the ith cell in this case as ${\mathbf{m}}_{i}^{{ \uparrow \uparrow }}$. If there is no external magnetic field, then the matrix magnetization is, on average, zero due to the directions of the granule easy axes being random. The following boundary condition for the magnetization ${\mathbf{m}}_{i}^{{ \uparrow \downarrow }}$ in the ith cell can then be introduced:

$${\mathbf{m}}_{i}^{{ \uparrow \downarrow }}{{{\text{|}}}_{{{{R}_{i}} = \lambda }}} = 0.$$

(41)

Of course, the system under consideration possesses hysteresis and can have a nonzero average magnetization under remagnetization in the state with a switched-off external field. The question about the ways of achieving the system’s complete demagnetization is beyond the scope of this paper (see, e.g., [29]). Clearly, the larger the correlation length of the paramagnetic matrix, the better the “averaged” boundary conditions (40) and (41) are fulfilled. To solve Eq. (38), we will apply the approach described in Section 3.1 for a flat-layered structure. We will seek the magnetization ${\mathbf{m}}_{i}^{{ \uparrow \uparrow }}$ in the form

$${\mathbf{m}}_{i}^{{ \uparrow \uparrow }} = {{{\mathbf{m}}}_{{0i}}} + {{{\boldsymbol{\xi }}}_{i}},\quad {\text{|}}{{{\boldsymbol{\xi }}}_{i}}{\text{|}} \ll {{m}_{s}},\quad {{{\boldsymbol{\xi }}}_{i}}(\lambda ) = 0.$$

Retaining only the linear terms in ξ_i, we will obtain

$$\frac{{{{d}^{2}}{{{\boldsymbol{\xi }}}_{i}}}}{{dR_{i}^{2}}} + \frac{2}{{{{R}_{i}}}}\frac{{d{{{\boldsymbol{\xi }}}_{i}}}}{{d{{R}_{i}}}} - {{\kappa }^{2}}({{{\boldsymbol{\xi }}}_{i}} + {{{\boldsymbol{\xi }}}_{{0i}}}) = 0,$$

(42)

where ξ_0i = m_0i(ατ$m_{s}^{2}$ + β$m_{0}^{2}$)/(ατ$m_{s}^{2}$ + 3β$m_{0}^{2}$), |m_0i| = m₀. The solution of the linear equation (42), given the boundary condition (40), is the following function:

$$\begin{gathered} {{{\boldsymbol{\xi }}}_{i}} = {{{\boldsymbol{\xi }}}_{{0i}}}\left( {\frac{1}{{\kappa {{R}_{i}}}}(\kappa \lambda \cosh \kappa (\lambda - {{R}_{i}})} \right. \\ \left. {_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}} - \sinh \kappa (\lambda - {{R}_{i}})) - 1} \right). \\ \end{gathered} $$

(43)

The constant m_0i is determined numerically from Eq. (39). To find the magnetization ${\mathbf{m}}_{i}^{{ \uparrow \downarrow }}$, we will neglect the nonlinear term in Eq. (38). This can be done if the condition

$$\frac{\beta }{{\alpha \tau }}{{\left( {\frac{{{\mathbf{m}}_{i}^{{ \uparrow \downarrow }}}}{{{{m}_{s}}}}} \right)}^{2}} \ll 1$$

(44)

is fulfilled. Given the boundary conditions, we will then obtain

$${\mathbf{m}}_{i}^{{ \uparrow \downarrow }} = \frac{{{{{\mathbf{m}}}_{{si}}}{{l}_{J}}{{R}^{2}}\sinh \frac{{\lambda - {{R}_{i}}}}{l}}}{{l_{0}^{2}{{R}_{i}}\left( {\left( {1 + \frac{{{{l}_{J}}R}}{{l_{0}^{2}}}} \right)\sinh \frac{{\lambda - R}}{l} + \frac{R}{l}\cosh \frac{{\lambda - R}}{l}} \right)}}.$$

(45)

In this section all of the further calculations will be made for a Ni_xCu_{100 – x} (x ≈ 70 at %) matrix and Co₄₀Fe₄₀B₂₀ granules. For a Gd matrix and Fe granules the presented approximate solutions are improper. This is due to a large interaction at the Fe‒Gd interface, leading to a violation of the applicability conditions for the approximate solutions. We will also assume that all of the phenomenological parameters for flat-layered structures coincide with those for granular media.

Consider the influence of the granule radius on the magnetization in a cell under the condition for the mean distance L between the surfaces of neighboring granules being constant, L = 2(λ – R). If the granule radius is small, so that l_JR/$l_{0}^{2}$ ≪ 1, then $m_{i}^{{ \uparrow \downarrow }}$(R)/m_s ≪ 1 is valid for any L. In the opposite case, l_JR/$l_{0}^{2}$ ≫ 1, two variants are possible. If l₀$\sqrt {\alpha \tau }$ coth(L/2l)/l_J ≪ 1, then $m_{i}^{{ \uparrow \downarrow }}$(R) ≈ m_s. If, on the contrary, l₀$\sqrt {\alpha \tau }$coth(L/2l)/l_J ≫ 1, then $m_{i}^{{ \uparrow \downarrow }}$(R)/m_s ≪ 1. The analysis of $m_{i}^{{ \uparrow \uparrow }}$ is slightly complicated due to the need to resort to numerical calculations of the constant m₀. We give the dependences of $m_{i}^{{ \uparrow \uparrow }}$(R) and m₀ on radius R for various temperatures and mean distances between the granule surfaces (Fig. 9). We see that an increase in the granule sizes while keeping L constant leads both to an increase in $m_{i}^{{ \uparrow \uparrow }}$ and to an increase in $m_{i}^{{ \uparrow \downarrow }}$ at some ratio of other parameters. At this stage it is hard to say what influence this will exert on the system’s magnetocaloric potential. However, it is clear that an increase in the granule size by more than 7–10 nm makes no sense.

Fig. 9.

Dependences $m_{i}^{{ \uparrow \uparrow }}$(R) at T = T_C = 3 (a), 15 (b) K and m₀(R) at T – T_C = 3 (c), 15 (d) K for L = (1) 3, (2) 5, and (3) 7 nm. A structure based on Ni_xCu_{100 – x}/Co₄₀Fe₄₀B₂₀.

Figure 10 shows the dependences $m_{i}^{{ \uparrow \uparrow }}$(R_i) and $m_{i}^{{ \uparrow \downarrow }}$(R_i) at various mean distances between the surfaces of the nearest granules and various temperatures. The granule radius is R = 10 nm. The dependences of the magnetocaloric potential Δs(T) for a granular medium calculated numerically are shown in Fig. 11 for various L and R. As can be seen, an increase in the granule radius R leads to an increase in Δs. Here, we restrict ourselves to constructing the solution outside the neighborhood of the transition point, where the approximate formulas (43) and (45), on which the calculations of Δs are based, can be applied.

Fig. 10.

Dependences $m_{i}^{{ \uparrow \uparrow }}$(R) at T = T_C = 3 (a), 15 (b) K and m₀(R) at T – T_C = 3 (c), 15 (d) K for L = (1) 3, (2) 5, and (3) 7 nm. A structure based on Ni_xCu_{100 – x}/Co₄₀Fe₄₀B₂₀.

Fig. 11.

Dependences Δs(T) for L = (1) 3, (2) 5, and (3) 7 nm at R = 2 (a), 5 (b), and 10 (c) nm. A structure based on Ni_xCu_{100 ‒ x}/Co₄₀Fe₄₀B₂₀. The presented dependences correspond to the change in magnetic field whereby the system is remagnetized (H ∈ (0, H₀), H₀ ≈ 10 Oe [29]).

Let us now present our calculations of the contributions to the heat capacity from the magnetic subsystem per unit matrix volume (Fig. 12). In the absence of an external magnetic field, the heat capacity is lower than that in the state of a parallel orientation of the magnetizations of all granules by four orders of magnitude. This can be explained by a much lower temperature sensitivity of the cell magnetization in the absence of a field. We again see that the magnetic contribution to the heat capacity may be neglected. The adiabatic change in the system’s temperature will then take the form

$$\Delta T = {{T}_{f}} - T = - \frac{{T({{\lambda }^{3}} - {{R}^{3}})}}{{{{\lambda }^{3}}c}}\Delta s.$$

(46)

Fig. 12.

Dependences c_{↑↑(↑↓)}(T) for L = (1) 3, (2) 5, and (3) 7 nm at R = 10 nm. A structure based on Ni_xCu_{100 – x}/Co₄₀Fe₄₀B₂₀.

Figure 13 shows the dependences ΔT(T) at various L and R. At a sufficiently high density of granules (L = 3–5 nm) there is an increase in ΔT with decreasing R, despite the increase in Δs. The presented estimates of ΔT are fairly small due to the comparatively small interaction l_J.

Fig. 13.

Dependences ΔT(T) for L = (1) 3, (2) 5, and (3) 7 nm at R = 2 (a), 5 (b), and 10 (c) nm. A structure based  on Ni_xCu_{100 – x}/Co₄₀Fe₄₀B₂₀. The presented dependences correspond to the change in magnetic field whereby the system is remagnetized (H ∈ (0, H₀), H₀ ≈ 10 Oe [29]).

Thus, the approximate approach developed in Section 3.1 has been generalized to a granular medium. The magnetocaloric potentials calculated for a granular medium are comparable to those for a three-layer structure [9].

4 CONCLUSIONS

Based on the Landau theory and the mean-field theory, we showed that the magnetocaloric potential in a flat-layered Fe/Gd/Fe structure could reach fairly large values. For example, Δs ≈ 10⁵ erg K^–1 cm^–3 for a thin interlayer 3 nm in thickness at the critical temperature, which is a third of the magnetocaloric potential for bulk Gd corresponding to complete demagnetization (beginning from H = 1 T) at T ~ T_C [26]. Our estimates of the adiabatic change in temperature are smaller than those for bulk Gd under the same conditions by an order of magnitude. However, to switch the mutual orientation of the ferromagnetic edge magnetizations, it is necessary to apply a field with a strength of only several hundred oersted, giving a gain by one or two orders of magnitude in applied field. Both theories agree well between themselves. The Landau theory has limitations (for example, there should be τ ≪ 1), but it allows analytical formulas to be derived. We also estimated Δs for a granular medium (Co₄₀Fe₄₀B₂₀ granules, a Ni_xCu_{100 – x} matrix, x ≈ 70 at %). Our estimates turned out to be close to the magnetocaloric potential of a similar flat-layered system [9].

Note that a granular structure has a number of advantages with respect to a flat-layered one. First, it is easier to impart a macroscopic volume to it, which is necessary for use in refrigerators. Second, in real experiments, in addition to the interlayer itself and two ferromagnetic layers adjacent to it, there are also other layers and a substrate. All these elements are “superfluous” in the sense of a decrease in the magnetocaloric potential in terms of the volume of the entire system. The search for pairs of materials with an even larger exchange interaction at the interface is needed to amplify the magnetocaloric effect in exchange-coupled magnetic systems. The solid-state refrigerant itself must possess, on the one hand, a significant internal exchange interaction and, on the other hand, a large saturation magnetization.