Temperature Dependence of the Electrical Resistivity of Electron-Doped Cuprates

Abstract

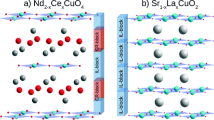
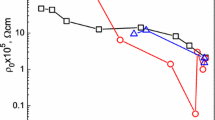
Experimental data on the temperature dependence of electrical resistivity are analyzed for electron-doped Nd_2 – xCe_xCuO_4 – δ cuprates in a wide range of cerium concentrations 0.12 ≤ x ≤ 0.20. It is shown that, in a wide temperature range above the superconducting transition temperature, the electrical resistivity mainly exhibits quadratic temperature dependence and decreases sharply at concentrations of x ≥ 0.17. Theoretical analysis based on the microscopic t – J model for strongly correlated electrons shows that the quadratic temperature dependence of electrical resistivity is attributed to electron scattering by spin excitations. To describe these excitations, a model of antiferromagnetic (AFM) spin fluctuations in the paramagnetic phase is proposed; the intensity of these fluctuations depends on the AFM correlation length. The quadratic temperature dependence of electrical resistivity agrees well with experimental data.

Spectrum of Electronic Excitations

The spectrum of electronic excitations is determined by the one-electron Green’s function for the operators (3). Using the method of equations of motion for the two-time retarded Green’s function [5], we obtain the following equation for the Fourier component of the Green’s function:

$$\begin{gathered} \tilde {G}({\mathbf{k}},\omega ) = {{\langle \langle {{{\tilde {c}}}_{{{\mathbf{k}},\sigma }}}{\text{|}}\tilde {c}_{{{\mathbf{k}},\sigma }}^{\dag }\rangle \rangle }_{\omega }} \\ = \frac{Q}{{\omega - \varepsilon ({\mathbf{k}}) - \Sigma ({\mathbf{k}},\omega )}} \equiv QG({\mathbf{k}},\omega ), \\ \end{gathered} $$

(A.1)

where Q = n/2 = (1 + x)/2 defines the weight of the doubly filled electron band, ε(k) is the electron spectrum (7), and Σ(k, ω) is the mass operator. For the mass operator in the approximation of noncrossing diagrams, we obtain the following equation [5]:

$$\Sigma ({\mathbf{k}},\omega ) = \frac{1}{N}\sum\limits_{\mathbf{q}}^{} {\int\limits_{ - \infty }^\infty {dzK(\omega ,z{\text{|}}{\mathbf{q}},{\mathbf{k}} - {\mathbf{q}})A({\mathbf{q}},z),} } $$

(A.2)

where

$$A({\mathbf{q}},z) = - \frac{1}{\pi }{\text{Im}}G({\mathbf{q}},z)$$

(A.3)

is the spectral density of electronic excitations. The kernel of the integral equation (A.2) has the form

$$\begin{gathered} K(\omega ,z{\text{|}}{\mathbf{q}},{\mathbf{k}} - {\mathbf{q}}) = {\text{|}}t({\mathbf{q}}){{{\text{|}}}^{2}}\frac{1}{\pi }\int\limits_{ - \infty }^\infty {\frac{{d\Omega }}{{\omega - z - \Omega }}} \\ \times \frac{1}{2}\left( {\tanh \frac{z}{{2T}} + \coth \frac{\Omega }{{2T}}} \right)\chi {\kern 1pt} ''({\mathbf{k}} - {\mathbf{q}},\Omega ), \\ \end{gathered} $$

(A.4)

where model (9) is used for the spectral density of spin excitations:

$$\chi {\kern 1pt} ''({\mathbf{k}} - {\mathbf{q}},\Omega ) = {{\chi }_{s}}({\mathbf{k}} - {\mathbf{q}})\chi _{s}^{{''}}(\Omega ).$$

Taking into account that the energy of spin excitations in (A.4) is determined by the frequency Ω ≈ ω_s, which is much lower than the characteristic energy of electronic excitations z ~ 4t, we can neglect the effects of retardation and set Ω = 0 in the denominator of (A.4). In this case, the integral of the odd function $\chi _{s}^{{''}}$(Ω) with respect to frequency Ω does not contribute to the term tanh(z/2T), and for the mass operator we obtain the equation

$$\begin{gathered} \Sigma ({\mathbf{k}},\omega ) = \frac{1}{N}\sum\limits_{\mathbf{q}}^{} {{\text{|}}t({\mathbf{q}}){{{\text{|}}}^{2}}{{\chi }_{s}}({\mathbf{k}} - {\mathbf{q}})\frac{1}{{2\pi }}} \\ \times \,\mathop {\iint\limits_{ - \infty } {\frac{{dzd\Omega }}{{\omega - z}}A({\mathbf{q}},z)\coth \frac{\Omega }{{2T}}\chi _{s}^{{''}}(\Omega )}}\limits^\infty \\ = \frac{1}{N}\sum\limits_{\mathbf{q}}^{} {{\text{|}}t({\mathbf{q}}){{{\text{|}}}^{2}}{{\chi }_{s}}({\mathbf{k}} - {\mathbf{q}})I(T)\int\limits_{ - \infty }^\infty {\frac{{dz}}{{\omega - z}}A({\mathbf{q}},z).} } \\ \end{gathered} $$

(A.5)

Introducing the real Σ′(k, ω) and imaginary Σ′′(k, ω) parts of the mass operator

$$\Sigma ({\mathbf{k}},\omega + i\epsilon ) = \Sigma {\kern 1pt} '({\mathbf{k}},\omega ) - i\Sigma {\kern 1pt} ''({\mathbf{k}},\omega ),$$

we obtain the following expression for the spectral density of electronic excitations (A.3):

$$A({\mathbf{q}},\omega ) = \frac{{\Sigma {\kern 1pt} ''({\mathbf{q}},\omega ){\text{/}}\pi }}{{{{{[\omega - \varepsilon ({\mathbf{q}}) - \Sigma {\kern 1pt} '({\mathbf{q}},\omega )]}}^{2}} + {{{[\Sigma {\kern 1pt} ''({\mathbf{q}},\omega )]}}^{2}}}}.$$

(A.6)

Setting A(q, z) = δ[z – ε(q)], in the first approximation we obtain the following expression for the mass operator (A.5):

$$\begin{gathered} \Sigma ({\mathbf{k}},\omega ) = \frac{1}{N}\sum\limits_{\mathbf{q}}^{} {{\text{|}}t({\mathbf{q}}){{{\text{|}}}^{2}}{{\chi }_{s}}({\mathbf{k}} - {\mathbf{q}})I(T)\frac{1}{{\omega - \varepsilon ({\mathbf{q}})}}} \\ = \frac{{3(1 - x)}}{{4I(\kappa )}}\frac{1}{N}\sum\limits_{\mathbf{q}}^{} {{\text{|}}t({\mathbf{q}}){{{\text{|}}}^{2}}\frac{1}{{{{\kappa }^{2}} + {{{({\mathbf{Q}} - {\mathbf{q}})}}^{2}}}}\frac{1}{{\omega - \varepsilon ({\mathbf{q}})}}} , \\ \end{gathered} $$

(A.7)

where we used formulas (10) and (16).

The spectral density of electronic excitations (A.6) is demonstrated in Fig. 4 for the symmetric directions Γ(0, 0) → X(π, 0) → M(π, π) → Γ(0, 0) for the electron density x = 0.18, the chemical potential μ = –1, and the AFM correlation length ξ = 5.5. We can clearly see the dispersion of the main hole band, which is represented by a curve with high intensity with a minimum at the point Q and a maximum at the point Γ(0, 0) of the Brillouin zone. The shadow band shifted by the AFM vector Q relative to the main hole band is represented by a curve with lower intensity. This band is due to short-range AFM correlations and is determined by the mass operator (A.7). Figure 5 demonstrates the dependence of the chemical potential μ on the density x of doped electrons calculated from Eq. (4) for the spectral density (A.6):

$$\begin{gathered} x = \frac{Q}{{2N}}\sum\limits_{\mathbf{q}}^{} {\langle \tilde {c}_{{{\mathbf{k}},\sigma }}^{\dag }{{{\tilde {c}}}_{{{\mathbf{k}},\sigma }}}\rangle } \\ = \frac{{1 + x}}{{2N}}\sum\limits_{\mathbf{q}}^{} {\int\limits_{ - \infty }^\infty {\frac{{d\omega A({\mathbf{q}},\omega )}}{{\exp (\omega {\text{/}}T) + 1}}.} } \\ \end{gathered} $$

(A.8)

Fig. 4.

Spectral density of electronic excitations (28).

Fig. 5.

Chemical potential μ as a function of doping x.

According to this formula, the density of doped electrons does not exceed x ≤ 1.

As discussed in Subsection 3.3, ARPES experiments and experiments on the study of quantum oscillations show that, as the doping level decreases, the large hole Fermi surface is reconstructed into a small electron and two hole Fermi surfaces due to the formaion of a gap in the electron spectrum. This transformation is usually associated with the appearance of long-range AFM order. However, a similar change in the Fermi surface can also occur due to short-range AFM correlations, as discussed in the theoretical work [4]. The formation of a gap in the electron spectrum for a sufficiently large correlation length ξ at low doping can be described within our approach as follows.

Consider the mass operator (A.7) for a large correlation length ξ, when the static spin susceptibility χ_s(k – q) has a sharp maximum at (k – q) = Q = (π, π). In this case, setting ε(q) = ε(k – Q) in expression (A.7), we can approximate the mass operator by the function

$$\begin{gathered} \Sigma ({\mathbf{k}},\omega ) \approx \frac{1}{{\omega - \varepsilon ({\mathbf{k}} - {\mathbf{Q}})}}\frac{1}{N} \\ \times \,\sum\limits_{\mathbf{q}}^{} {{\text{|}}t({\mathbf{q}}){{{\text{|}}}^{2}}{{\chi }_{s}}({\mathbf{k}} - {\mathbf{q}})I(T) = \frac{1}{{\omega - \varepsilon ({\mathbf{k}} - {\mathbf{Q}})}}\Delta ({\mathbf{k}}).} \\ \end{gathered} $$

(A.9)

Substituting this expression into the Green’s function (A.1), we find the spectrum of electronic excitations determined by the poles of this function:

$$\begin{gathered} {{E}_{{1,2}}} = \frac{1}{2}(\varepsilon ({\mathbf{k}}) + \varepsilon ({\mathbf{k}} - {\mathbf{Q}})) \\ \pm \frac{1}{2}\sqrt {{{{[\varepsilon ({\mathbf{k}}) - \varepsilon ({\mathbf{k}} - {\mathbf{Q}})]}}^{2}} + 4{{\Delta }^{2}}({\mathbf{k}})} \\ = 4t{\kern 1pt} '{\kern 1pt} \gamma {\kern 1pt} '({\mathbf{k}}) + 4t{\kern 1pt} ''{\kern 1pt} \gamma {\kern 1pt} ''({\mathbf{k}}) - \mu \pm \sqrt {{{{[4t\gamma ({\mathbf{k}})]}}^{2}} + {{\Delta }^{2}}({\mathbf{k}})} , \\ \end{gathered} $$

(A.10)

where formula (7) is used for ε(k). A similar spectrum is observed in ARPES experiments [35]. In our approach, the gap Δ(k) in the spectrum arises at the intersection of the main band and the shadow band. The width of the gap depends on the doping level (in our model, on the correlation length ξ). For a small value of ξ, the shadow band has low intensity, and a gap in the spectrum is not observed, which leads to a large Fermi surface determined by the main band.