On the Tactics of Ab Initio Search for the Shape of Protein Particles from Small-Angle X-Ray Scattering Data

Abstract

The determination of 3D particle shapes from the one-dimensional data on small-angle scattering from macromolecule solutions is ambiguous. In addition, due to the poor conditionality of the inverse problem, the determination is unstable and depends on the search algorithm parameters. Consequently, in practice, it is necessary not only to estimate the degree of stability of the solution of the problem but also to select the parameters of both the search method and the model itself. A search tactic is considered which consists in sequential determination of a set of models of particle shape represented in the form of a structure consisting of small close-packed spherical beads. The set of solutions is obtained by varying the relative contributions of objective function terms: the criterion for the deviation of the model scattering curve from the experimental one and the penalties for the looseness and discontinuity of the body structure, and the deviation of the average number of bead contacts from a specified value. Examples of the solution of model problems and the determination of molecular shape from the measurements available in the SASBDB bank of structures are presented.

INTRODUCTION

To date, several techniques of ab initio shape reconstruction using the model of small-volume elements have been developed [1–3]. The 3D shape of a particle is looked for by the minimization of the total quadratic residual between the experimental scattering curve and the theoretical one calculated using the model structure represented by a set of small-volume close-packed elements. Spheres and cubes with sizes such that the diffraction on their packing will affect the scattering curve only outside the experimental angular range are taken as the elements. The cubic elements allow a more uniform space filling. However, in the case of spheres, the nonuniformity can be easily taken into account using the correction factor. The solution (spatial arrangement of spheres in the model) is searched using the global minimization methods [1, 2], e.g., simulated annealing [1, 2, 4] or application of genetic algorithms [3]. The algorithm based on the search by simulated annealing method proved to be extremely effective due to a number of algorithmic decisions, in particular, due to the rejection from the variation at each step of the search for all model parameters (the number of parameters amounts to the number of the sites in real space in which the spheres filling the space and simulating electron density in the model are located). Instead, only a single randomly selected parameter is varied, In this case, the experimental scattering data are approximated with restrictions (concerning, first of all, the density and continuity of the structure) imposed on the solution.

THEORY

Briefly, the basic idea of the simulation implemented in the DAMMIN program [1] is as follows. The search domain (e.g., the sphere with the diameter equal to the maximum particle size D_max) is partitioned into N (∼10³–10⁵) close-packed sites. The value of D_max is determined from the pair distance function p(r) calculated from the experimental data I(s), e.g., using the GNOM program [5] from the ATSAS package [6] by the formula

$$p(r) = \frac{1}{{2{{\pi }}_{{}}^{{\text{2}}}}}\int\limits_{s = 0}^\infty {I(s)\frac{{\sin (sr)}}{{sr}}ds} ,$$

(1)

where r is the length of the distance in the structure, s = $4\pi \sin \theta {\text{/}}\lambda$ is the scattering vector modulus, 2θ is the scattering angle, and λ is the radiation wavelength. An index X_j is assigned to each jth site. This index denotes the phase to which a site belongs: X_j = 0 for the solvent and X_j = 1 for the particle. Thus, the model structure is described by the configuration vector X of length N. In the DAMMIN method, the scattering intensity from such model is rapidly calculated using the multipole expansion of the scattering amplitude function from a volume element. The tactic of the simulated annealing method implies the start from an arbitrary model, followed by its random modifications until the theoretical scattering from the model approximates the data. In the conventional Monte Carlo method, two models are used at each step: the best and the trial ones. The latter is obtained by a random variation of the best model. The trial model is rejected if it proves to be worse than the best one and is taken as the best in the opposite case. Then the cycle is repeated. However, this method, despite its stochastic nature, cannot find a solution for an acceptable time interval owing to the trapping in wide local minima of the objective function. In the simulated annealing method, the model that is better than the previous one is not necessarily taken as the current structure. A random variation is performed relative to the current model and a trial one is obtained. The probability to accept the worse model as the new current one depends on a certain parameter called the “temperature” T in literature. High temperature implies a high probability (calculated as exp(–Δ/T)) to take the worse model as the new current one if Δ (the trial value of the objective function minus the current one) is positive (the solution is worse). If the trial model proves to be better, i.e., Δ < 0, it is always taken as the new current one. At the beginning of the search, the temperature is chosen to be sufficiently high to make the rate of acceptance of worse solutions as current ones be larger than the rate of renewal of better models. This makes the program walk over the search domain and, in the case of the model falling into the vicinity of another local minimum, eventually get out of the current one. With an increase in the number of trials, the temperature is periodically lowered. Most often the multiplicative law T_next = T_currF is used, where F is the annealing factor, equal to 0.9–0.98 in the DAMMIN program. The objective function value decreases by analogy with the decrease in the internal system energy with lowering the temperature, for which reason the method was called “the simulated annealing” [4].

Since the shape determination uses scattering data whose range corresponds to a low spatial resolution, the model sought must also have a lower resolution relative to the size of the volume element. For this reason, the connectivity and density conditions are imposed on the model. The complete objective function used in this study has the form of a penalty function dependent on the elements of the configuration vector:

$${{\Phi}}(\text{X}) = {{w}_{R}}R + {{w}_{D}}{{P}_{D}} + {{w}_{L}}{{P}_{L}} + {{w}_{C}}{{P}_{C}} + ...\,.$$

(2)

Here, the quantity R is the criterion of similarity between the model and experimental scattering curves

$$R = \left\{ {\frac{{\sum\limits_{i = 1}^N {{{{[({{I}_{{\exp }}}({{s}_{i}}) - \xi {{I}_{{\bmod }}}({{s}_{i}}))W({{s}_{i}})]}}^{2}}} }}{{\sum\limits_{i = 1}^N {[I_{{\exp }}^{2}({{s}_{i}}){{W}^{2}}({{s}_{i}})]} }}} \right\},$$

(3)

where ${{\xi }} = \frac{{({{{\mathbf{I}}}_{{\exp }}} \cdot {{{\mathbf{I}}}_{{mod}}})}}{{{{{\left\| {{{{\mathbf{I}}}_{{exp}}}} \right\|}}^{2}}}}$ is the least-squares method (LSM) factor superposing the scattering curves multiplied by the weight function W(s), which is assigned in the form

$$W(s) = \left\{ \begin{gathered} {{s}^{n}},\quad n = 0,1,2,3,4 \hfill \\ {\text{if}}\quad s > s\left| {_{{\max [{{I}_{{\exp }}}(s){{s}^{n}}]}}} \right. \hfill \\ 0.5\left\{ {{{s}^{n}} + \frac{{\max [{{I}_{{\exp }}}(s){{s}^{n}}]}}{{{{I}_{{\exp }}}(s)}}} \right\} \hfill \\ {\text{if}}\quad s \leqslant s\left| {_{{\max [{{I}_{{\exp }}}(s){{s}^{n}}]}}\,.} \right. \hfill \\ \end{gathered} \right.$$

(4)

Multiplying by W(s) allows one to equalize the contribution of the deviations along the scattering curve: at n = 0 the residual (3) is calculated at the initial scale of the data (this makes sense when the intensity decreases by no more than an order of magnitude); as n increases, the intensity curve transforms into a contour passing through the maximum value at a certain value $s = s\left| {_{{\max [{{I}_{{\exp }}}(s){{s}^{n}}]}}} \right.$ and decreasing to a certain value, which is the larger the higher n is. Thus, it becomes possible to weaken the contribution to the total residual of the initial portion of data, which is most susceptible to the effect of scattering by particle aggregates, and, at the same time, increase the contribution of the low-intensity portion at large s. The lower line in (4) serves to ensure that the reduction of the initial portion is not too large. In practice, it is recommended to choose n at which the quantity $\frac{{\max [{{I}_{{\exp }}}(s){{s}^{n}}]}}{{\min [{{I}_{{\exp }}}(s){{s}^{n}}]}}$ falls in the range of 10–50. At such weighing, the division of residuals by the standard deviation of experimental noise, which is common in LSM, is not applied.

To adequately describe the particle shape and exclude the influence of bead packing on the scattering curve, the sphere diameter should be sufficiently small. To ensure this, the number of sites in the search domain is chosen to be at least 2000–5000 for compact particles and up to 10 000–30 000 for anisometric bodies. In this case, the bead size appears to be 5–10 times smaller than the spatial resolution of the structural model; to describe homogeneous areas of the structure, they should be in a close-packed state. To this end, penalty terms reflecting the requirement of continuity of the structure (w_DP_D) and its diffusivity (w_LP_L) are added to the objective function. The quantity P_D is calculated as the ratio of the total number of structure beads to the number of beads comprising the maximally connected domain. The value of P_L (the penalty for “looseness”) is calculated as ${{P}_{L}} = 1 - {{\left\langle {1 - \exp ( - {{N}_{e}}) + \exp ( - 12)} \right\rangle }_{N}}$, where 12 is the maximum number of contacts with neighbors, N_e is the actual number of contacts, and ${{\left\langle {} \right\rangle }_{N}}$ means averaging of the number of contacts over the structure reduced to one bead. Values from the range of 0.01–0.001 are recommended for the w_D and w_L weight coefficients, based on the consideration that the contributions from R and the penalties at the point of the minimum of functional (2) should be approximately equal. The quantity P_C is the penalty for the relative displacement of the particle centroid from the search domain center. This term prevents the “adhesion” of the model to the domain boundary and thus excludes the boundary influence on the shape.

A much more efficient algorithm of searching for spherical models is implemented in the DAMMIF program [2]. While the DAMMIN program performs a search for the model in a finite space region and senselessly scans many sites located far from the formed structural cluster, the DAMMIF program always operates with a singly connected structure in the infinite space. One can say that DAMMIN “assembles” the particle, whereas DAMMIF “grows” it, operating 5–10 times faster and making much more random modifications. Nevertheless, the constant connectivity of the structure graph can restrict its variability during the search procedure. For this reason, to determine the variety of possible models, the DAMMIF program (as well as DAMMIN) should be launched several times with different parameters: the number of modifications in a constant-temperature cycle, the number of accepted modifications before passing to the next temperature, the starting temperature and the factor of its lowering, and the balance of penalty weights. This work is too time-consuming and requires a wealth of experience in the solution of model problems.

In this study, we consider the modified DAMMINV algorithm, which automates the setting of search parameters. In some cases, similar results can be obtained using DAMMIN and DAMMIF programs at a suitable preparation of a series of text files of assignments or when the programs are run again in the dialog mode. The modified vrsion of DAMMINV is focused on the sequential search for 10–15 solutions in the mode of varying values of weight coefficients at the penalty terms (“alternating mode”). An additional penalty for the presence of beads not contacting with the main structure is introduced in DAMMINV (similarly to the DAMMIF algorithm, but the contact radius can be increased to enhance the model variability; see details below). An additional penalty for the deviation of the average number of sphere contacts from a specified value was also introduced to simulate the diffuse structures. This penalty replaces the penalty for the looseness (e.g., the penalty for the deviation of the contact number from 2 facilitates the search for a structure in the form of a loose coil).

EXPERIMENTAL PART

Proposed Sequence of Steps in the Search for Particle Shape

1. Select the rule of weighing the scattering intensity W (Eq. (4)). To this end, it is possible to use the SASPLOT program from [6], in which the areas of the left and right halves of the scattering curve can be evaluated. In most cases, the exponent n in formula (4) should provide 3 to 10 times domination for the area of the left (initial) half of the weighted curve; the wider the angular range of scattering data, the higher this domination is. In the DAMMINV program, the selection is automatic.

An important note: when calculating the pairwise distance function in the presence of weak particle aggregation, one should not groundlessly decrease D_max in order to prevent artifacts in the solution. The artifacts manifest themselves as the structure spreading near the search domain surface. Instead, it is better to increase the initial angle in the data by dropping the region distorted by the scattering from large formations. In this case, the artifacts in the shape models are often seen as easily distinguishable individual domains or “tails.”

2. To implement a rapid preliminary search for the model, one can set the spherical bead radius larger than the default one: 3000–5000 sites in the search domain (or, e.g., the doubled radius in the DAMMIF program). Since the resolution of the small-angle scattering (SAS) data is low, the model details smaller than 1/5–1/10 of the maximum particle diameter reflect only the presence of small-size internal inhomogeneities but not their actual structure. We should also note that the number of successful model modifications (the criterion of the transition to the next temperature) in the DAMMIF program can be increased. By default, their fraction comprises 0.1 of the maximum modification number at a constant temperature; it can be increased to 0.3–0.5. It will be shown below that such an increase results in finding a more adequate structure in some cases.

3. It is possible not to vary the default starting temperature T_init and the factor T_F of its decrease when using the DAMMIN and DAMMIF programs. However, the too high temperature T_init in the DAMMIN program results in a larger number of initial temperature cycles in which the structure remains in the form of a random diffuse cloud without any significant decrease in the residual R. In the DAMMINV program, the initial temperature is set to be T_init = 2.5σ_Φ(X), where σ_Φ(X) is the standard deviation of the changes in the objective function (2), calculated using the difference table from the Φ(X), values obtained by 100–300 variations of the starting model (usually this is the randomly filled search domain). Such a choice of T_init ensures the beginning of Φ(X) decrease already at the second–third temperature cycle during the search. In the course of the search, the program can additionally decrease the temperature in the case where the criterion of similarity of the shapes of experimental and model scattering curves (the angle between the data vectors) is larger than 3°. This technique avoids transforming the model formed to this point into a completely random arrangement of beads.

4. To search for the solution at w_R = 1.0 (Eq. (2)). In the DAMMINV program, the Skip Bulk Solvent (SBS) mode is used to increase the search efficiency. In this mode, the modifications placing a new bead in a site not contacting with the beads of the current model are skipped if the relative number of detached beads in the model becomes less than 3%. This allows the program to implement a larger number of variations of singly connected structures without increasing their maximum admissible number and the penalty for the presence of separately located beads. This mode is almost similar to that implemented in the DAMMIF algorithm, but the contact radius can exceed the radius of bead packing in the site network (in this case, the penalty for separate beads remains zero). To ensure higher variability of the model when searching in the switched-on SBS mode, the temperature is increased by a factor of 1.5.

5. Before searching for the next solution, the weight w_R is increased by a factor of 10, and the temperature T_init is set to be 1.5–2 times lower than that at step 3. The weight of the penalty for the centroid displacement from the search domain center w_C is increased by a factor of 4. The annealing procedure starts from the obtained model. The found solution has a somewhat worse value of R but better values of penalties. The result obtained at step 4 is usually not considered as the solution if the residual R decreases significantly. The aim of this step is to obtain the model satisfying the requirements of penalties to a higher degree.

6. The weights of all penalty terms are returned to the initial values, except for the penalty for the particle centroid displacement from the search domain center, which is decreased to 5% of the initial value (this is safe since the small displacement is already obtained at step 4). The starting temperature is set to be T_init = 1.5σ_Φ(X) or 1.5–2 times smaller than the initial value to retain the basic features of the model. We should note that the minimization of the penalty for body looseness results not infrequently in the particle orientation in the search domain so that some portions of its surface are aligned along the planes of sphere packing, and the shape appears to be faceted. The value of the penalty w_LP_L becomes so small that the obtained shape can be kept in the subsequent solutions. To avoid such a situation, the DAMMINV program envisages at this step the body rotation relative to the (fixed) search domain by Euler angles about the X and Z axes with the corresponding recalculation of bead coordinates so that the face directions would not coincide with the packing planes of spatial sites. Since new bead coordinates of the rotated model do not coincide with the spatial network, the particle structure is recalculated to the nearest sites. Then the passage to step 3 is performed, at which the program continues to search for the solution that should decrease the residual R. The latter is the main objective of this search phase. The iterations are continued until the total number of search cycles with a fixed temperature of 500–600 is reached.

The above tactic is aimed at deriving different solutions and, at the same time, increasing the probability of finding a deeper minimum of the objective function. Using the DAMAVER and DAMCLUST procedures, it is possible to estimate the solution stability from the spread of obtained structures (usually, 6 to 10 models), as was done, e.g., in [7].

An additional feature of the DAMMINV program is the accounting of scattering by the model beads, which contributes significantly at large angles. The form factor of the spherical beads is replaced by scattering from ellipsoids [8] with an axis ratio of 0.71 : 1.0 : 1.4, which corresponds to typical thermal atomic vibrations. This fact decreases the influence of the diffraction by spatial element packing on the scattering curve shape, which makes it possible to determine more adequately the structures whose models consist of a small number of beads (less than 50–100), without the need for adding or subtracting a constant from scattering data. If such necessity does exist (e.g., at inadequate subtraction of the scattering by a cell with a solvent), the corresponding option is envisaged in the program.

The uniqueness of the structure determination can be expressed in terms of the solution variance for a specific problem. Information about the difference between models is provided by the DAMAVER and DAMCLUST programs. Due to the absence of a linear relationship between the structure parameters (bead coordinates) and the input scattering data, it is impossible to derive the expression for the solution variance in the analytical form. Nevertheless, it is possible to answer the question on the degree of uniqueness (or stability) by analyzing the values of the pair correlations of models in a series of solutions that are obtained by the random search method and are thus independent. Of course, such an answer is always incomplete, and the package ATSAS provides additional procedures (AMBIMETER program [6, 9]), designed to obtain additional information about the uniqueness.

In the general case, it is difficult to distinguish the ambiguity of a solution of the problem of structural model determination and the stability of this solution. Both lead to a difference in the found particle models if the angular range of scattering data is varied, the search starts from different approximations, or the parameters of the minimization method themselves are changed. To obtain the final answer, it is necessary to perform a series of numerical experiments with the variation of search conditions, analyze individual solutions from the viewpoint of “physical sense,” select groups of similar solutions (e.g., similar in the R-factor in the real space), etc. Thus, the analysis of the SAS data proves to be a rather difficult expert problem, although in many cases it is possible to derive a final answer without a large number of numerical experiments. In this paper, we do not discuss all factors affecting the solution since their systematic analysis can be a subject of more than one paper.

The examples of experimental data were taken from the base of protein particle models determined from SAS data [https://www.sasbdb.org/data]. The samples were selected based on the linearity of the Guinier plot and a moderate noise level.

An Example of Particle Model Ambiguity

The fact of ambiguity was noted by many researchers; however, no examples of bodies different in structure but causing identical SAS have been reported in the literature. The identity of scattering curves implies that the same pair distance functions p(r) (1) should correspond to the bodies, a fact suggesting the identity of maximum sizes D_max, volumes V, and radii of gyration R_g [8]. This circumstance restricts the number of possible particle shapes. There is an example of two ways of the arrangement of five points on a plane with identical sets of pair distances between graph vertices and, additionally, identical sets of triangle areas in the literature [10]. An experiment with published example showed that, if the central points of two structures are displaced out of the plane by identical distances (which provides equality of the volumes of obtained pyramids) and the bodies are assumed to be homogeneous in density, a numerical calculation of the distance functions p(r) with decreasing sphere radii yields distribution curves that tend to coincide. The shapes of these models are shown in Fig. 1.

Fig. 1.

Example of two pyramidal bodies of the same height relative to the figure plane (points P₄ and Q₄ are displaced out of the plane) and identical pair distance functions p(r): (a) published planar model [10], (b) volume spherical-bead models composed of approximately 20 000 beads, and (c) pair distance functions calculated from bead models (coincide accurately to the curve width in the plot).

Effect of Scattering Intensity Weighing Parameter

Figure 2 presents scattering curves for the particle shown in Fig. 3 (1), weighted according to formula (4). The model in Fig. 3 (2) is obtained using the DAMMIN program with default settings and weight W = s². When using the same weight, the DAMMINV program, despite the alternating mode, did not satisfactory reconstruct the shape (Fig. 3 (3)), whereas the weight W = s¹ (Fig. 2 (2)) allows one to find a shape close to the exact model (Fig. 3 (4)). The values of fitting criterion R are calculated for the non-weighted data.

Fig. 2.

Weighted scattering intensities used in the calculation of residual R. Circles represent the theoretical scattering by the particle shown in Fig. 3 (1), solid curves are typical scattering curves for the found models shown in Fig. 3 (2–4). The weight functions in the plot are (1) W = s² and (2) W = s¹.

Fig. 3.

Typical results of the particle shape reconstruction: (1) from the theoretical scattering data shown in Fig. 2 and using (2) the DAMMIN program (R = 1.3 × 10^–3, W = s²), (3) the DAMMINV program (R = 0.73 × 10^–4, W = s², alternating mode), and (4) the DAMMINV program (R = 0.71 × 10^–4, W = s¹, alternating mode).

Search for the Particle Shape in the Alternating Mode

An example demonstrating the search with periodic changes in relative contributions of the objective function terms is shown in Figs. 4 and 5. When using the DAMMINV program, we applied the weight W = s¹. Other search parameters were default ones. In all cases, the quantity R was (1 ± 0.2) × 10^–4. It can be seen that a single search using the DAMMIN and DAMMIF programs with default settings and the DAMMINV program (shapes 4–6 in Fig. 5) did not yield any acceptable result despite good correspondence between scattering curves (Fig. 4). Sequential search in the alternating mode yields acceptable reconstruction at the fifth iteration, which is retained at further iterations. As was noted above, an increase in the number of modifications accepted at a fixed temperature relative to the total number of trials up to 0.5 (100 000 instead of 20 000) results in finding an adequate model in all three cases.

Fig. 4.

(a) The results of the fitting of model scattering intensity (circles) calculated for the structure 1 in Fig. 5. Solid curves show the scattering by the structures found with different programs: (1) DAMMIN, (2) DAMMIF, and (3) DAMMINV (structure 6 in Fig. 5). (b) Weighted normalized scattering intensity for the calculation of residual R.

Fig. 5.

The results of simulation of the initial structure (1): (2) DAMMIN, (3); DAMMIF with default settings, (4) DAMMIF with the number of modifications accepted at the fixed temperature increased up to 100 000, (5–7) DAMMINV after the (5) first, (6) second, and (7) fifth iterations. The odd numbers of iterations correspond to step 4 of the alternating mode. This step corresponds to initial (large) relative contribution of the R term to the objective function.

Shapes of Bovine Albumin Molecule As an Example of Data Analysis with Partial Protein Aggregation

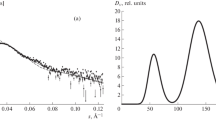
Below we report the results of a typical complex case of study of protein in a solution. Figure 6a shows SAS curves for the albumin solution. The calculation of pair distance functions showed that the distribution has an extended shoulder in the range of large (above 9 nm) portion lengths (Fig. 7), which suggests a partial protein aggregation in the solution, although the Guinier region is rectilinear (Fig. 6b) and does not indicate it. The corresponding radii of gyration found from the Guinier region and the pair distance function are, respectively, 3.25 ± 0.02 and 3.26 ± 0.04 nm. Their closeness also does not indicate the aggregation, also the radius of gyration calculated with the CRYSOL program [11] based on the crystal structure of the protein is smaller, 2.84–2.89 nm, even with allowance made for hydration shell. In fact, the typical models of molecular shape (Fig. 8) found in the alternating search mode by the DAMMINV program demonstrate the presence of artifacts, which unnaturally increase the length of the maximum chord in the structure. The molecular shapes were determined using the weighing W = s¹ since the weighing W = s² increases too much the scattering intensity at large angles, and the results prove to be somewhat worse. Since the shape artifacts appear in the solutions in different places of structures, the structure averaged with the aid of the DAMAVER program does not coincide well with the experiment (χ² = 10.4) and is not presented here. The basic result of this study is the versions of macromolecular shapes after omitting the aggregation artifacts marked in Fig. 8 by grey circles. Due to the proposed search tactics, these versions should be different when covering the set of possible shapes.

Fig. 6.

(a) Experimental scattering intensity for the bovine albumin solution (circles) and typical model curve for the structures shown in Fig. 8 and (b) the Guinier plot for the estimation of the radius of gyration R_g.

Fig. 7.

Pair distance function calculated from the data presented in Fig. 6a.

Fig. 8.

(1) Crystal structure of bovine albumin molecule from the protein database 3V03 and (2–5) sequential DAMMINV solutions after step 3. Circles indicate artifacts caused by aggregation (presumably due to partial aggregation in the solution).

Determination of Molecular Shape from Published Data

The data for analysis were taken from the SAS database SASBDB for protein solutions [12]. The scattering data and references to the publications are not presented since they can be found using the sample code. Proceeding from the scattering data, we calculated the distributions over distances p(r) without a forced decrease in the maximum distance D_max. The theoretical scattering curves for the obtained shape models describe the data with accuracy no worse than χ² = 1.12 and are of no interest for discussion. Therefore, we only present the sets of obtained structures.

Figure 9 shows the published and calculated distance distribution curves for the SASDAF5 structure (the structure of FRET biosensor). Figure 10 shows the published and calculated structures. It can be seen that the calculation using extended p(r) yielded structures closer in character to the molecular model, which can serve as its confirmation. The small-size voids in the found models are not the structure details but only reflect an attempt to describe the structure sparseness in the adjacent region. An analysis of the structures with the DAMCLUST program shows a small spread of the models; the most different ones are presented in Fig. 10.

Fig. 9.

Pair distance functions for the FRET biosensor sample (database code is SASDAF5). Circles denote published data and the curve represents the calculated distribution that was used as input data for the DAMMINV program.

Fig. 10.

Models of FRET biosensor particle (database code SASDAF5): (a, b) atomic and spherical-bead published models and (c–f) the models found by the DAMMINV program using the data presented in Fig. 9. The structures in the right column are rotated by 90° around the vertical axis.

CONCLUSIONS

Some results of numerical experiments on the determination of particle shapes based on the SAS data for diluted isotropic monodisperse systems were reported, and a scheme of sequential calculations using the program of simulation by bead structures was proposed. It is impossible to cover the whole variety of possible cases in one publication. However, the main result of the performed study can be formulated as follows: a preliminary simulation using artificial structures and sequential search for the solutions involving variation in the search algorithm parameters may help in answering the question on the reliability of solutions obtained when studying protein objects.