1 INTRODUCTION

In pioneering papers [1–3] and other studies, it was noted that the conclusion about the nonstationarity of the Universe and the law of its dynamic evolution can be obtained from Newton theory without resorting to Einstein theory. Since then, the presentation of the cosmological problem in popular books (see, for example, [4–6]) has, as a rule, been done using Newtonian theory. Furthermore, even professional monographs often begin expositions of cosmology with the Newtonian theory (see, for example, [7–10]). With this approach, it is emphasized that the Newton law of gravitation, which describes the acceleration created by gravity, is an asymptotically correct expression of the Einstein law in the case of weak gravitational fields and spherical distributions of matter and the motion velocity of the volume elements, where the velocities must be small compared to the light velocity. As a rule, when comparing the laws of Einstein and Newton, this is limited. In this paper, we show that such a restriction is not enough to understand the essence of the matter and, moreover, leads to errors.

2 NEWTONIAN COSMOLOGY

As already mentioned, starting from the pioneering pioneering papers [1–3] and other studies, Newtonian cosmology is used for a “simple” introduction to modern cosmology. To highlight the main ideas, consider the simplest ideal cosmological model. Let a homogeneous matter without pressure uniformly fill the entire Universe. In such a model, galaxies are considered in a large volume as points in such matter. Let us mentally separate in this matter a ball of arbitrary radius centered at an arbitrary point. Let us first consider the gravitational forces created on the surface of this ball only by the matter of the ball itself, and we will not yet consider the remaining matter of the Universe. Let the radius of the ball be chosen not too large, so that the gravitational field created by the matter of the ball is relatively weak, and Newton theory is applicable to calculate the gravitational force. Then the points located on the boundary sphere will be attracted to the center of the ball with a force proportional to the mass \(M\) of the ball and inversely proportional to the square of its radius \(R\).

Now let’s remember the remaining matter of the Universe outside the ball and try to consider the gravitational forces created by it. To do this, we will consider sequentially spherical shells of larger and larger radius, enclosing the ball. But it is known that spherically symmetric layers of matter do not create any gravitational forces inside the cavity. Consequently, all these spherically symmetric shells (i.e., all the rest of the matter of the Universe) will not add anything to the force of attraction experienced by the point \(A\) on the surface of the ball to its center \(O\).

Thus, we can calculate the acceleration of one point \(A\) with respect to another point \(O\). We took \(O\) as the center of the ball, and the point \(A\) is at a distance \(R\) from \(O\). This acceleration is due to the gravitation of only the matter of the ball with a radius \(R\). According to Newton law, it is

$$\ddot {R} = - \frac{{GM}}{{{{R}^{2}}}}.$$
(1)

The minus sign means that acceleration corresponds to attraction, not repulsion. So, any two points located in a homogeneous Universe at a distance \(R\) experience a relative acceleration (negative) \(\ddot {R}\) given by formula (1). This means that the Universe must be non-stationary. Indeed, if we imagine that at some time point the galaxies are at rest, i.e., \(\dot {R} = 0\), and the density of matter in the Universe does not change, then at the next time moment the galaxies would receive speeds under the action of the mutual gravitation of all matter, since there is a gravitational acceleration given by formula (1). Thus, the rest of galaxies relative to each other is possible only momentarily. At the initial time, we can choose not to rest, but to expand relative to each other. In the general case, galaxies must move— they must either move away or approach each other, the radius of the ball \(R\) must change with time, and the density of matter must also change with time.

The Universe must be non-stationary, because gravity acts in it—this is the main conclusion of the theory. Formula (1) can be rewritten by replacing the mass in it with the expression \(M = \frac{4}{3}\pi {{R}^{3}}\rho \), then we obtain the gravitational force per unit mass in the form

$$\ddot {R} = - \frac{4}{3}\pi G\rho R.$$
(2)

The dot symbol denotes the time derivative and \(\rho \) is the matter density. The choice of point \(O\) was arbitrary. Our model is homogeneous, therefore, Eq. (2) is valid for any point in the space of the Universe. Formula (2) describes the law of radius variation of an arbitrary ball with time and also describes the law of matter density variation with time, since the density of matter is \(\rho \sim \frac{1}{{{{R}^{3}}}}\) for dust when the pressure is \(P = 0\). Given this relation, Eq. (2) can be integrated:

$$\frac{1}{2}{{\dot {R}}^{2}} = \frac{4}{3}\pi G\rho {{R}^{2}} + E,$$
(3)

where \(E\) is the arbitrary constant of integration. Formula (3) makes it easy to analyze the dynamics of evolution of different scales and the evolution of the density of the Universe. Expression (3) can be considered as the law of conservation of energy during the evolution of the surface of the ball: \(E\) is the total energy equal to the sum of the kinetic (term with \({{\dot {R}}^{2}}\)) and potential (term with constant \(G\)). The negative term in the expression \(E = \left( {\frac{1}{2}} \right){\kern 1pt} {{\dot {R}}^{2}} - \left( {\frac{4}{3}} \right){\kern 1pt} \pi G\rho {{R}^{2}}\) is called the potential, it is shown in Fig. 1. The evolution of the model occurs with a constant energy \(E = {\text{const}}\), shown by horizontal line in Fig. 1. If \({{E}_{1}} > 0\), then expansion occurs from \(R = 0\) until \(R = \infty \). If \({{E}_{2}} < 0\), then the expansion occurs from \(R = 0\) until it meets the potential curve, and then compression occurs to \(R = 0\). The value \(E = {\text{const}}\) can be chosen arbitrarily, since the initial conditions in the Newtonian theory are in no way connected with the equation of gravitation. Furthermore, it is also added that the ball is small enough so that not only the gravitational forces on its surface are small, but also the matter velocities are also small compared to the light velocity \(c\). This is the essence of Newtonian cosmology, which is considered to coincide locally with relativistic cosmology. But as we will see, this statement requires significant clarifications.

Fig. 1.
figure 1

Graphical representation of the potential \(E = - {\kern 1pt} \frac{4}{3}\pi G\rho {{R}^{2}}\) of the Newtonian model, \(\rho = \frac{{{{\rho }_{0}}{\kern 1pt} R_{0}^{3}}}{{{{R}^{3}}}}\). \({{E}_{1}}\) and \({{E}_{2}}\) are the lines of constant energy values along which the evolution of the model takes place.

Full size image

3 EINSTEIN EQUATIONS

The mechanics of relativistic cosmology (Friedmann theory) is based on Einstein equations. Einstein equations describe the structure and evolution of the space-time geometry with the metric tensor \({{g}_{{ik}}}\) (see, for example, [11]) together with the evolution of the physical properties of matter [11] described by the tensor \({{T}_{{ik}}}\). Unlike the Newton equation of gravity, Einstein equations contain an equation of motion. The whole system is a system of differential equations of partial derivatives of the second order of the components of the metric tensor with respect to the coordinates \({{x}^{0}},\;{{x}^{1}},\;{{x}^{2}},\;{{x}^{3}}\). The system can be written as

$$G_{i}^{k} = \frac{{8\pi G}}{{{{c}^{4}}}}{\kern 1pt} T_{i}^{k}.$$
(4)

Here, \(G\) is the gravitational constant; \(i,\;k = 0,{\kern 1pt} \;1,{\kern 1pt} \;2,{\kern 1pt} \;3\); \(G_{i}^{k}\) is the Einstein curvature tensor; and \(T_{i}^{k}\) is the matter momentum energy tensor. These equations are divided into two groups.

(1) Equations that do not contain second time derivatives \({{x}^{0}}\). These are the equations for the initial conditions at \({{x}^{0}} = 0\):

$$G_{i}^{0} = \frac{{8\pi G}}{{{{c}^{4}}}}{\kern 1pt} T_{i}^{0}.$$
(5)

(2) Evolution equations containing second derivatives with respect to \({{x}^{0}}\):

$$G_{\alpha }^{\beta } = \frac{{8\pi G}}{{{{c}^{4}}}}{\kern 1pt} T_{\alpha }^{\beta },\quad \alpha ,\;\beta \ne 0.$$
(6)

In this case, if equations (5) are satisfied for \({{x}^{0}} = 0\), and equations (6) are satisfied for all \({{x}^{0}},\;{{x}^{1}},\;{{x}^{2}},\;{{x}^{3}}\), then equations (5) are also satisfied for all \({{x}^{0}},\;{{x}^{1}},\;{{x}^{2}},\;{{x}^{3}}\). We consider that \(\Lambda \)-term of the relativistic theory is included in the expression for the tensor \(T_{i}^{k}\). In this paper, we assume that \(\Lambda = 0\).

4 INITIAL CONDITIONS IN RELATIVISTIC COSMOLOGY

We will consider homogeneous isotropic relativistic models. Their structure and evolution are described by the radius of curvature of the three-dimensional space \(a(t)\). We will consider the pressure \(P = 0\). For such models, the Einstein equations are rewritten as

$$\ddot {a} = - {\kern 1pt} \frac{{4\pi G}}{3}a\rho ,\quad $$
(7)
$$\frac{1}{2}{\kern 1pt} {{\dot {a}}^{2}} = \frac{{4\pi G}}{3}{\kern 1pt} {{a}^{2}}\rho - \frac{{k{{c}^{2}}}}{2},$$
(8)

where \(k\) can take values \(k = 0,\; \pm {\kern 1pt} 1\). The case \(k = 0\) is degenerate and we do not consider it here. In our case, \(P = 0\) and \(\rho = {{\rho }_{0}}{{\left( {\frac{{{{a}_{0}}}}{a}} \right)}^{3}}\). Equations (7) and (8) are similar to Eqs. (2) and (3), but instead of an arbitrary sphere radius \(R\), here a specific radius of curvature \(a\) is set, which characterizes the scale of the entire Universe. In addition to this, we note that Eq. (8) is similar to the integral (3) of Newton theory, differing only in that instead of an arbitrary constant \(E\) here \( - \frac{{k{{c}^{2}}}}{2}\) is set. The difference is quite significant, because without an arbitrary \(E\), Eq. (8) is a restriction on the initial c-onditions, which is fundamentally absent in Newton theory.

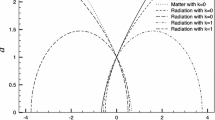
For comparison with the Newton theory, we introduce the function \(E = \frac{{{{{\dot {a}}}^{2}}}}{2} - \frac{{4\pi G}}{3}{{a}^{2}}\rho \), \(\rho \sim \frac{1}{{{{a}^{3}}}}\), for dust, when \(P = 0\). We will call this function as the energy. The value \(E = E(a)\) at \(\frac{{{{{\dot {a}}}^{2}}}}{2} = 0\) will be called as the potential; it is shown in Fig. 2. The similarity of systems (2), (3) and (7), (8) made it possible to replace the second system with the first one for the analysis of local quantities. In this case, the difference between Eq. (3) and Eq. (8) was not given importance and was not discussed. And the fundamental difference is that now in Eq. (8), we are not talking about a ball of an arbitrary chosen size \(R\), but about a specific value a—the radius of curvature of the three-dimensional section of the Universe, and Eq. (8) becomes a condition on the initial values of the parameters of the problem.

Fig. 2.
figure 2

Graphical representation of the potential \(E = E(a)\). The dashed-dotted lines are the constant energy values along which the evolution of the model occurs.

Full size image

5 INITIAL DATA IN RELATIVISTIC THEORY AND NEWTONIAN COSMOLOGY

In order to discuss the difference in the approach of the two theories—Newtonian and relativistic—to the description of even local properties of the Universe, let’s perform the operation of selecting a small ball in the relativistic theory, as we did in the Newtonian theory in Section 2, and then analyze the resulting differences. In the Newtonian theory, we mentally separated a small ball of arbitrary radius \(R\) with the center at an arbitrary point \(O\) in the homogeneous matter of the Universe at an arbitrary time \({{t}_{0}}\), when the matter density is equal to \({{\rho }_{0}}\). In this case, it was required that the acceleration \(\ddot {R}\), calculated according to Eq. (1), differ little from the acceleration according to the relativistic formula (7). For this, as is known, Eq. (8) is necessary so that the gravitational radius \({{r}_{g}}\) of a ball with a mass \(M\) is much less than the physical radius \(R\):

$${{r}_{g}} = \frac{{2GM}}{{{{c}^{2}}}} \ll R.$$
(9)

In addition, it was sometimes added or assumed that the matter motion velocities must be non-relativistic,

$$v \ll c{\kern 1pt} .$$
(10)

From Eq. (9) it follows

$$R \ll \frac{c}{{\sqrt {\frac{8}{3}\pi G{{\rho }_{0}}} }}{\kern 1pt} .$$
(11)

In Newtonian theory, to build a specific cosmological model, i.e., to integrate the only equation of the model (2), it is required to set the initial conditions at the time \({{t}_{0}}\):

$$t = {{t}_{0}},$$
(12)
$$R = {{R}_{0}},\quad \rho = {{\rho }_{0}},\quad \dot {R} = {{\dot {R}}_{0}}.$$
(13)

After that, the solution is found unambiguously. The model has been built. Let’s turn to relativistic theory. Let us indicate how much the radius of the ball \(R\) chosen by us is less than \(a\):

$$N \equiv \frac{a}{R}.$$
(14)

This relationship \(N \equiv \frac{a}{R}\) is constant over time. First of all, dynamic equation (7), rewritten for the surface of the ball \(R\), must be satisfied for our small ball. Substitute (13) into (7):

$$\ddot {R} = - \frac{{4\pi }}{3}GR\rho .$$
(15)

But in addition to this equation, the equation for the initial data (8), rewritten again for the surface of the ball \(R\), must also hold in the Friedmann theory. Substitute (14) into (8), we get:

$$\frac{{{{{\dot {R}}}^{2}}}}{2} = \frac{{4\pi }}{3}G{{R}^{2}}\rho - \frac{{k{{c}^{2}}}}{{2{{N}^{2}}}}{\kern 1pt} .$$
(16)

This condition imposes strict relations on the initial data at the time \(t = {{t}_{0}}\). Initial data

$$R = {{R}_{0}},\quad \rho = {{\rho }_{0}},\quad \dot {R} = {{\dot {R}}_{0}},$$
(17)

are bound by conditions (16). This is something that is not in the Newtonian theory. It follows from the above consideration that in order to make the Newtonian theory close to the relativistic one, it is not enough to take the ball small and set the speed of its uniform expansion to be much less than the speed of light. It is also necessary that, for given \({{R}_{0}}\) and \({{\rho }_{0}}\), the velocity on the surface of the ball satisfies relation (16). Neglect of this condition leads to errors. To illustrate, consider the ball at the initial time \({{t}_{0}}\). Let us set \(N\frac{a}{R}\), i.e., choose the size of the ball in relation to \(a\). Let this choice satisfy the necessary conditions of smallness. But now we cannot arbitrarily choose a sufficiently small expansion rate. It must be such that the total energy is equal to \(\frac{{ - k{{c}^{2}}}}{{2{{N}^{2}}}}\) (see (16)). In the plot of Fig. 1, this corresponds to the motion of a point representing the solution of the equations of evolution along a horizontal line of constant energy

$$E = - \frac{{k{{c}^{2}}}}{{2{{N}^{2}}}}{\kern 1pt} .$$
(18)

The reason for the significant difference between Figs. 1 and 2 becomes clear. In Fig. 2, the horizontals \(E = \pm \frac{{{{c}^{2}}}}{2},\;0\) depict the evolution of the entire Universe at \(k = \pm 1,\;{\kern 1pt} 0\), respectively. In Fig. 1, the horizontals \(E = {\text{const}}\) depict the evolution of the spherical part. In this case, \({{E}_{{1,2}}} = {\text{const}}\) can take not any values, but only the values indicated by us, determined by the necessary initial conditions of the relativistic theory, given by expression (16).

Thus, it should be remembered that the correct approximation of the Newtonian cosmology to the relativistic theory requires considering not only the close value of the acceleration according to both theories, i.e., condition (11), but also the obligatory fulfillment of conditions (16). When constructing the dynamics of a homogeneous, isotropic cosmological model, Einstein relativistic theory is indispensable. Non-fulfillment of conditions (16) leads to a completely different wrong picture of evolution.